1. Introduction
Most of the water resource problems, such as the operation of reservoir systems, are multi-purposes and commonly considered as multi-objective optimization problems. The complex, large scale, and nonlinear nature of these problems requires special treatment to successfully find their optimal solutions. Many researches have, therefore, focused on developing robust multi-objective optimization methods to solve multi-objective operation of the reservoir systems.
Most of the previous studies generally report two types of approaches for solving multi-objective problems. The first one uses classical approaches in which the multi-objective problem is first converted to a series of single-objective problems, which are then solved using traditional methods. The weighted sum method, goal programming, and the constraint method have been the most common approaches to convert multi-objective problems into the single-objective problems. Deb [
1] and Coello et al. [
2] presented a comprehensive study on different types of classical approaches used in the past and discussed the ways to convert multi-objective problems into single-objective ones. Labadie [
3] evaluated the performance of different classical methods for multi-objective operation of the reservoir systems. Linear programming, non-linear programming, and dynamic programming can be mentioned as the most popular classical methods used in the past to solve the multi-objective operation of reservoir systems.
Croley and Raja Rao [
4] used the ε-constraint approach for bi-objective operation of a single reservoir system with flood control and recreation purposes. Tauxe et al. [
5] developed a multi-objective dynamic programming method using the constraint method for optimal operation of a single reservoir system. Yeh and Becker [
6] developed a practical procedure for the multi-objective operation of multi-reservoir systems using the constraint technique and a modified linear programming and dynamic programming to solve the single objective problems. Mohan and Raipure [
7] developed a linear multi-objective programming model using the constraint method for optimal operation of a large-scale multi-reservoir system in India with the objectives of maximizing the irrigation releases and hydropower generation. Liang et al. [
8] used the constraint method and combined stochastic and deterministic modeling for bi-objective operation of the Upper Colorado River multi-reservoir system. They used an aggregate reservoir as a surrogate for the multi-reservoir system to avoid the curse of dimensionality in their model.
Foued and Sameh [
9] used a method based on the stochastic goal programming for multi-objective operation of a multi-reservoir system. Water supply, flood control, drought control, hydropower generation, salinity control and the pumping cost were considered as the objectives of the problem. Higgins et al. [
10] developed a multi-objective method based on the weighting technique and stochastic non-linear programming for optimal allocation of water resources in a three-reservoir system. Verma et al. [
11] applied a different three approaches of the goal programming methodology for optimal operation of a multi-reservoir system. Akbari et al. [
12] developed a simulation-optimization approach for multi-objective operation of the Abbaspour reservoir in Iran during emergency conditions with the objectives of maximization of the expected value of hydropower generation and minimization of the its variance. A weighting method was used to convert the multi-objective problem into single-objective problems and stochastic dynamic programming was developed to solve the resulting single-objective problems. Mamun et al. [
13] developed a multi-objective optimization model using the goal programming technique, which was subsequently solved by a combination of the lexicographic and weighted goal-programming method. This method was used to model the conditions of Supplemental Operation Agreements of the Columbia River Treaty (CRT). Haguma and Leconte [
14] presented deterministic and stochastic dynamic programming models for long-term planning of a water system consisting of three run-of-river plants and two hydropower plants with reservoirs. Bian et al. [
15] developed a multi-objective method for the optimal operation of a Yellow River multi-reservoir system with the objectives of power generation, water supply, and flood and ice control using the constraint technique. Power generation was the main objective and the other objectives were considered as the constraints of the optimization problem. He et al. [
16] introduced a multi-objective dynamic programming method with a new mechanism based on the reference lines for the optimal operation of reservoirs systems. Their results indicated that the proposed model was superior to the common multi-objective evolutionary algorithm.
While single-objective problems have only one single optimal solution, a set of optimal solutions known as Pareto optimal solutions can be obtained for multi-objective problems. The classical methods, therefore, are not efficient for solving multi-objective problems as they are not capable of finding the Pareto solutions all at once and need many simulation runs to find the Pareto front. Moreover, as the complexity, scale, and nonlinearity of the problems increases, performance of the classical methods deteriorates.
The second approach uses Multi-Objective Evolutionary Algorithms (MOEAs) to solve multi-objective optimization problems with the advantage of finding the Pareto solution in a single run. Given the limitations of classical methods and the capabilities of MOEAs in solving multi-objective problems, many attempts have been made to develop MOEAs for multi-objective operation of single and multi-reservoirs systems.
Kim et al. [
17] used the non-dominated sorting genetic algorithm (NSGAII) for multi-objective operation of a multi-reservoir system in the Han River basin, indicating the capability of the NSGAII algorithm in solving large-scale optimization problems. Chen et al. [
18] optimized the rule curves of a multi-objective single reservoir system in Taiwan using a macro-evolutionary multi-objective genetic algorithm. Water supply and hydropower generation were considered as the objective functions and the results showed a better-spread Pareto front compared to the NSGAII. Afshar et al. [
19] developed a multi-colony ant algorithm for the bi-objective operation of the multi-purpose Des reservoir in Iran with water supply, hydropower generation and flood control as the objective functions. Their results indicated that the proposed algorithm was superior to the weighting approach in finding the Pareto optimal set. Chang and Chang [
20] applied a multi-objective evolutionary algorithm for the operation of a multi-reservoir system in Taiwan using NSGAII to minimize the shortage indices of each reservoir. Liu et al. [
21] used a simulation-optimization framework and hybrid multi-objective genetic algorithm for deriving the optimal refill rules of a multi-objective reservoir system. Fallah-Mehdipour et al. [
22] developed three multi-objective optimization models based on the multi-objective particle swarm optimization algorithm and used them for multi-objective operation of a single and a multi-reservoir system. Wu and Chen [
23] proposed a multi-objective optimization model to derive reservoir operating rules for the East River Basin in China with water supply and hydropower generation objectives.
Hajiabadi and Zarghami [
24] solved the optimal operation of the Sefidrud reservoir in Iran for water supply, hydropower generation and sediment evacuation objectives. They used the non-dominated sorting genetic algorithm (NSGAII) for finding the optimal Pareto set of the problem and then defined various scenarios based on the weighting approach. Yang et al. [
25] introduced an improved evolutionary optimization algorithm for multi-objective operation of the reservoir systems. They also conducted a comparative study among the proposed models and other evolutionary algorithms using the benchmark problems.
Amirkhani et al. [
26] used the non-dominated sorting genetic algorithm (NSGAII) coupled with a water quality model for bi-objective operation of the Karaj reservoir in Iran. Minimization of the total dissolved solids and temperature difference between reservoir inflow and outflow were considered as the objective functions. Qi et al. [
27] developed a memetic multi-objective immune algorithm for multi-objective reservoir flood control and compared the results with those of the other evolutionary algorithms. Adeyemo and Stretch [
28] presented a review of various hybrid evolutionary algorithms used to solve the reservoir operations with different objectives. Karami et al. [
29] introduced a hybrid gravitational algorithm to minimize the water supply deficits in a two-reservoir system in Iran and compared the results with those of the common evolutionary algorithms. Li [
30] developed a data-driven optimization-simulation tool based on the fuzzy logic control and genetic algorithm for real-time control of downstream flooding.
These researches indicated that MOEAs are more effective in solving multi-objective problems compared to classical methods. These methods, however, may suffer from inefficiency, especially in large scale problems. Consequently, the development of efficient and effective methods with an emphasis on reducing the computational costs can lead to significant progress in solving multi-objective reservoir operation problems.
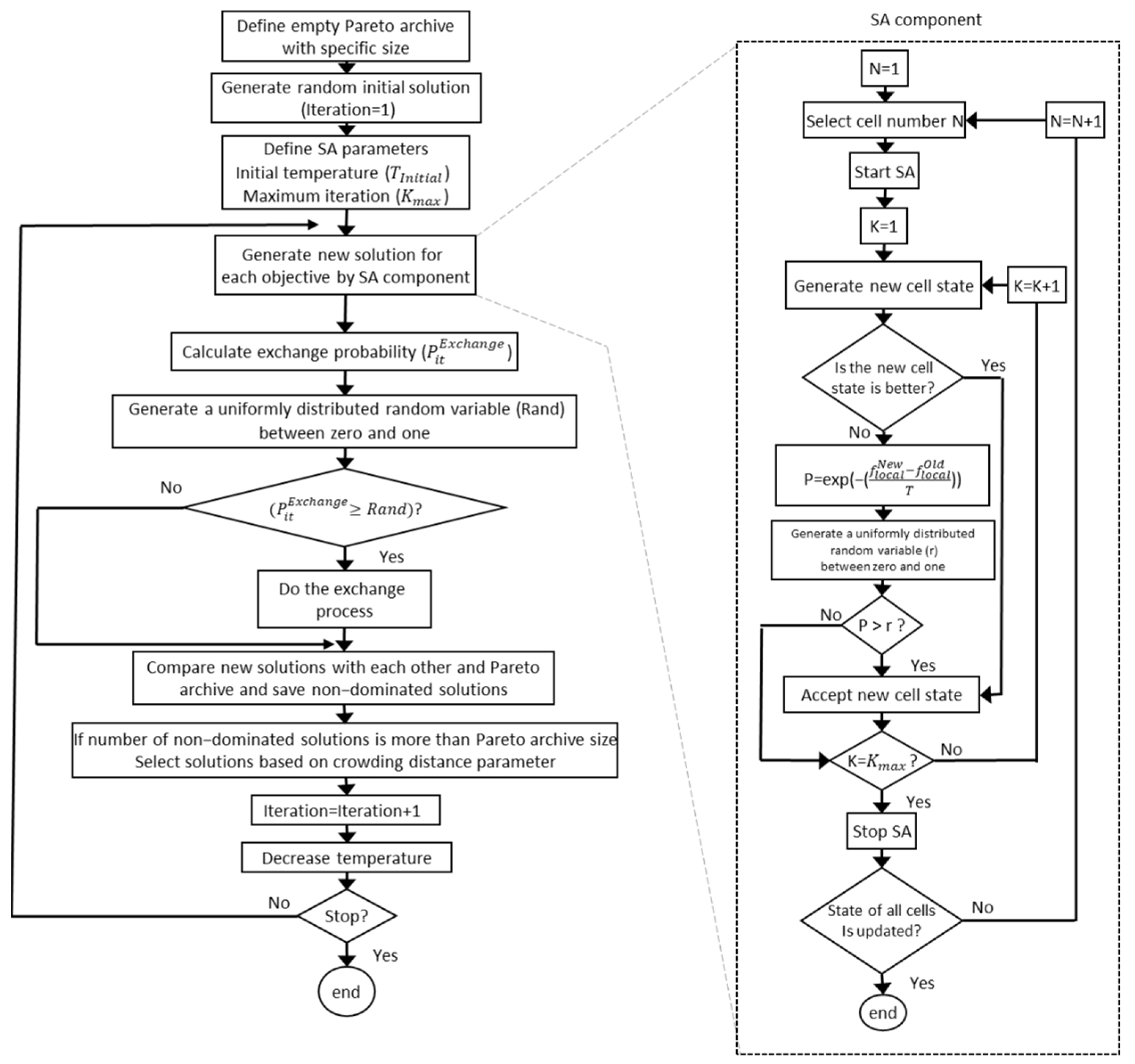
This paper presents a CA-based methodology for the multi-objective operation of multi-reservoir systems. The proposed method consists of two parallel CA methods which are used to solve each of the single objective problems using an SA-based numerical transition rule. An interaction mechanism between the CA methods is devised at each iteration of the CA method to guide the solution process to find the optimal front of the original multi-objective problem. An exchange mechanism is devised for implementing the interaction between two parallel CA methods in which each CA method is randomly fed with the solution found by other CA methods at each iteration of the CA. In order to investigate the performance of the proposed method, the problem of bi-objective monthly operation of the Dez–Gotvand–Masjed Soleyman system in Iran with water supply and hydropower production objectives is solved and the results are presented and compared with those of the non-dominated sorting genetic algorithm (NSGAII) as one of the well-known multi-objective evolutionary algorithms. The results indicate that the proposed methodology is highly efficient and capable of producing comparable solution to those of NSGAII while requiring much less computational efforts.
3. Multi-Reservoir Parallel Cellular Automata-Simulated Annealing (MPCA-SA)
The first step in using the cellular automata method to solve any optimization problem is to define the four main components of the method, including cell, cell state, neighborhood, and transition rule. These components are generally defined based on the physical characteristics of the problem in hand and can, therefore, significantly/marginally vary from one problem to another. However, proper definition of these components and in particular the transition rule significantly affects the efficiency and effectiveness of the method.
The proposed MPCA-SA method is an extended version of the PCA method first introduced by Afshar and Hajiabadi [
31] for the bi-objective operation of single-reservoir systems. The PCA method has been developed in line with the conditions governing single-reservoir problems, and the use of this method in multi-reservoir problems needs fundamental modifications and changes in the components of cellular automata. In particular, the PCA method uses analytical transition rules which cannot be readily extended to multi-reservoir problems due to limitation stemming from strong nonlinearity and non-convexity of multi-reservoir problems.
In the proposed MPCA-SA method, a set of single-objective CA methods are devised, which operate in parallel with each other. An interaction between the parallel CA methods is devised and carried out during the solution process, which leads to the optimal front rather than single objective solutions. The components of cellular automata are defined based on the characteristics of the multi-reservoir problems for improved efficiency and effectiveness.
In this method, each instance of the time at the beginning and the end of each operation period is considered as the cell and the storage volume of the reservoirs are considered as the cell state. The cell state is, therefore, defined as a vector with a dimension equal to the number of reservoirs in the system whose members show the values of the storage volume of each reservoir, shown as follows:
The neighborhood of each internal cell is defined as the collection of the previous and next cells, while only one cell is considered as the neighborhood of the boundary cells which is schematically shown in
Figure 1.
Definition of the transition rules as the vital part of CA is the last step of each CA-based formulation. In CA, the transition rule is normally defined as the solution of a local optimization sub-problem, which is defined in connection with the original optimization problem considering the physical characteristics of the multi-reservoir system problem and localized property of the storage volumes. Referring to the neighborhood definition shown in
Figure 1, the local transition rule for the cell
j is defined as the problem of minimizing the original objective functions projected onto the cell level. Projection of the problems objective functions along with their constraints to the
jth cell level can be easily achieved by assuming all cell states to be constant, except for the
jth cell state, to arrive at the local optimization problems as follows:
Subject to:
where
and
are local objective functions for the water supply and hydropower generation, respectively.
Using a penalty method, the constrained local problem for the
jth cell can be converted to the unconstrained local problem as follows:
where
is the violation of local constraints in the
jth cell for the nth reservoir and α
p is the penalty factor.
The local optimization sub-problem represented by Equations (18) and (19) with decision variables equal to the number of reservoirs in the system is a small-scale optimization problem which can be solved by any optimization methods. The local optimization problem, however, is a nonlinear and nonconvex optimization problem, which rules out the use of traditional optimization methods. On the other hand, using the evolutionary population-based methods can undermine the efficiency of the method, since many local optimization problems equal to the number of operation periods is solved at each iteration of CA. It therefore seems that using an iterative evolutionary algorithm to solve the local sub-problems would be more appropriate as it leads to more efficiency of the CA method. Here, the simulated annealing (SA) method acting as a numerical transition rule is used to solve the local sub-problems.
Simulated Annealing (SA)
Simulated annealing is a probabilistic optimization method proposed by Kirkpatrick et al. [
32] in 1983. The standard simulation annealing algorithm starts by defining an initial point and initial temperature and continues by searching for the optimal solution via two nested loops. The inner loop is responsible for the thermal equilibrium of the search while the outer loop relates to the cooling process. In the thermal equilibrium loop, the search process starts with a random initial solution. The fitness of the solution is then calculated using the problem objective function. A new solution point is generated in the neighborhood of the initial solution using a generation function, and its fitness is calculated. If the new solution has a better fitness, it is accepted as the new solution of the problem; otherwise, it is accepted with the accepting probability defined as:
where Δ
F is the fit difference between the fitness of old and generated solutions and
T is a parameter referred to as the temperature. The temperature parameter is initially set to be a large value and its value is reduced to a small value via the cooling process. Normally several iterations are carried out in the thermal equilibrium loop at a constant temperature. After the number of iterations of the inner loop is completed, the temperature is reduced in the cooling loop, and again the searches continue for new solutions at the new constant temperature. The cooling process is continued until the stopping criteria are met.
Here, in the MPCA-SA method, the SA component, employed as a numerical transition rule to update the cell states, is not carried out in its standard form and only the thermal equilibrium loop is used, and the cooling process is combined with the CA method. It has already been shown that this leads to higher efficiency of the method without any adverse effect on the effectiveness.
The process of solving the problem starts with randomly generating a set of initial guesses for the cell state, here the reservoirs storage volumes and setting a high enough value for the temperature. Then, the local optimization problems defined on each cell are considered in turn and solved using only the equilibrium loop of the SA method at the constant temperature and a limited number of iterations. Once all the cells are covered, the cell states are simultaneously updated, and an iteration of the CA is completed. The temperature is then reduced using the cooling strategy and the next CA iteration is carried out and the new set of cell states are obtained. The CA iteration are continued until the convergence criteria is met.
Figure 2 schematically describes the solution process by the proposed MPCA-SA method.
The cooling strategy is defined here by the following equation:
Here, Tit is temperature value at the current iteration, T0 is the initial temperature and α is cooling rate that ranges usually between 0.8 and 0.99.
The solution process described so far would logically lead to solutions of the two single-objective optimization problems defined by Equations (1)–(9). In order to use this solution process for finding the optimal front of the bi-objective optimization problem in hand, an interaction mechanism between these two CA methods and their solutions at each CA iteration is devised. This interaction is implemented by using the solution found by one of the CAs as the initial solution of the other one in a probabilistic manner referred to as an exchange mechanism. Three different exchange mechanism are considered are as follows:
The first approach (MPCA-SA1): In the first approach, the probability of performing the exchange process in all CA iterations is set to a constant value set by the user.
The second approach (MPCA-SA2): In this approach, the probability of performing the exchange process in each iteration of MPCA-SA2 is not constant and decreases as the method progresses.
where
—Probability of exchange in the iteration it
—Initial exchange probability factor set by the user
it—Current iteration number
itmax—Maximum number of iterations
According to Equation (23), the exchange probability starts with a high initial value at the beginning of the process and decreases as the method progresses so that the exchange probability reaches a small value near zero at the final iterations of the method.
The third approach (MPCA-SA3): this approach is similar to MPCA-SA1 with the difference being that the initial solutions of the CAs are randomly decided from the Pareto archive, if an exchange of the solutions is required, while the probability of performing the exchange process in all CA iterations is set to a constant value set by the user.
5. Results and Discussion
In this section, the bi-objective operation of the Dez-Gotvand-Masjed Soleyman, a three-reservoir system, has been considered to evaluate the efficiency and performance of MPCA-SA. Furthermore, the problem is also solved using the NSGAII method, as one of the most common evolutionary algorithms, in order to assess the performance of MPCA-SA in terms of solutions quality and computational costs.
The hypervolume parameter is used to evaluate the quality of the Pareto set and compare the results obtained by the proposed methods quantitatively. The hypervolume parameter is defined as the area of coverage of obtained Pareto set with respect to the objective space for a bi-objective problem. Here, the objective space is determined by a reference point and the hypervolume is considered as the ratio of objective space that is dominated by the obtained Pareto set. Hence, the best value for the hypervolume parameter is 1 and the worst value is 0.
Figure 5 schematically shows how to calculate the hypervolume parameter for a bi-objective minimization problem.
Table 3 shows the results obtained by NSGAII for the three-reservoir system Dez–Gotvand–Masjed Soleyman. MPCA-SA solutions are obtained using only 10 iterations for the thermal equilibrium loop (inner loop) of the SA component. The size of the Pareto archive is set to be 20 in all methods. The values of the parameter
λ in the first, second, and third approaches are set to be 0.1, 0.15, and 0.1, respectively, and the maximum number of iterations is considered to be 8000 for all methods. The reference point with coordinates (18, 35) is considered to determine the objective space used to calculate the hypervolume parameter for all methods. Moreover, the minimum value of the objective functions which represent the end points of the Pareto front are shown in
Table 3 for all methods.
In NSGAII method, a single-point crossover and one-bit mutation is used and crossover and mutation operator is applied to 70 and 10 percent of population. The maximum number of iterations is equal to 200,000 and a population size of 200 is considered for the NSGAII method.
As shown in
Table 3, while the two of proposed methods produce results comparable to that of NSGAII, the MPCA-SA3 clearly outperforms the NSGAII in both the quality of endpoint solutions and computational effort. In fact, the computational cost of MPCA-SA methods is only 1.2% of the computational cost of the NSGAII method.
All MPCA-SA methods perform better than NSGAII in finding the minimum value of hydropower objective; however, in finding the minimum value of water supply objective, only MPCA-SA3 has a better solution than NSGAII. Moreover, the hypervolume parameter shows that the quality of Pareto solutions obtained by all MPCA-SA methods is as good as NSGAII.
Figure 6 shows the Pareto fronts produced by various methods.
As seen in
Figure 6, while the first two MPCA-SA methods produce a front comparable to NSAGII, the MPCA-SA3 Pareto front extends far beyond that of NSAGII, and in particular dominates the NSAGII front as we move the front water supply endpoint to the hydropower endpoint.
Early experiments showed that the exchange probability factor
λ had a significant effect on the efficiency and quality of the solutions obtained. This is due to the fact that the exchange probability balances between exploration and exploitation characteristics of the method. For this, a set of experiments are carried out to assess the effect of the exchange probability factor
λ on the final solution and find its optimal value.
Figure 7 shows the effect of the number of CA iteration and the value of the
λ parameter on the efficiency represented by the computational time and effectivity represented by the hypervolume ratio defined as:
A value of Hypervolume Ratio greater than 1 for a method shows better performance compared to the NSAGII method, and vice versa.
The results indicate that increasing the value of the parameter λ leads to a deterioration of the results of the method if the first and third approaches are used to perform the exchange process. However, the MPCA-SA2 method is seen to be less sensitive to the value of the λ parameter. Additionally, the results indicate that the first and second exchange approaches will enjoy a higher convergence rate when an optimal value of the λ parameter is used.
The results of
Figure 7 and values of the hypervolume ratio show that while the MPCA-SA3 method can find a comparable Pareto set to that of NSGAII in half of its computational time, the MPCA-SA1 and MPCA-SA2 require only 20% of their computational effort to achieve a high rate of convergence and the good quality of the Pareto set, which can be comparable to that of NSGAII.
Another experiment is also carried out to assess the effect of the number of the thermal equilibrium loop iterations on the quality of the final solution and computational costs.
Figure 8 shows the effect of the number of iterations of the thermal equilibrium loop of the SA component on the results of the MPCA-SA2 method and the computational cost for the value of
λ parameter equal to 0.15.
As can be seen from
Figure 8, increasing the number of iterations of the SA thermal equilibrium loop up to 10 reduces the number of the CA iterations needed for the convergence of the MPCA-SA2 method without any significant effect on the computational cost of the method. On the other hand, the results show that increasing the number of the equilibrium iteration beyond 10 would only increases the computational time without any significant effect on the quality of the solution.