Next Article in Journal
Vertical Electrical Sounding (VES) for Estimation of Hydraulic Parameters in the Porous Aquifer
Next Article in Special Issue
Spatial and Temporal Evolution of Leaching Zones within Potash Seams Reproduced by Reactive Transport Simulations
Previous Article in Journal
Future Changes in Wave Conditions at the German Baltic Sea Coast Based on a Hybrid Approach Using an Ensemble of Regional Climate Change Projections
Previous Article in Special Issue
Application of Fractional Flow Theory for Analytical Modeling of Surfactant Flooding, Polymer Flooding, and Surfactant/Polymer Flooding for Chemical Enhanced Oil Recovery
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 13
Issue 2
10.3390/w13020169
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Review on Numerical Simulation of the Internal Soil Erosion Mechanisms Using the Discrete Element Method

by
Xiukai Wang
1,2,
Yao Tang
1,2,*,
Bo Huang
1,2,
Tiantian Hu
1,2 and
Daosheng Ling
1,2
1
MOE Key Laboratory of Soft Soils and Geoenvironmental Engineering, Department of Civil Engineering, Zhejiang University, Hangzhou 310058, China
2
Center for Hypergravity Experimental and Interdisciplinary Research, Zhejiang University, Hangzhou 310058, China
*
Author to whom correspondence should be addressed.
Water 2021, 13(2), 169; https://doi.org/10.3390/w13020169
Submission received: 18 December 2020 / Revised: 7 January 2021 / Accepted: 8 January 2021 / Published: 13 January 2021
(This article belongs to the Special Issue Modeling of Flow and Transport in Saturated and Unsaturated Porous Media)
Browse Figures
Review Reports Versions Notes

Abstract

:
Internal erosion can trigger severe engineering disasters, such as the failure of embankment dams and uneven settlement of buildings and sinkholes. This paper comprehensively reviewed the mechanisms of soil internal erosion studied by numerical simulation, which can facilitate uncovering the internal erosion mechanism by tracing the movement of particles. The initiation and development of internal erosion are jointly influenced by the geometric, mechanical, and hydraulic conditions, which determine the pore channels and force chains in soil. The geometric conditions are fundamental to erosion resistance, whereas the mechanical conditions can significantly change the soil erosion resistance, and the hydraulic conditions determine whether erosion occurs. The erosion process can be divided into particle detachment, transport, and clogging. The first is primarily affected by force chains, whereas the latter two are mostly affected by the pore channels. The stability of the soil is mainly determined by force chains and pore channels, whereas the hydraulic conditions act as external disturbances. The erosion process is accompanied by contact failure, force chain bending, kinetic energy burst of particles, and other processes due to multi-factor coupling.

1. Introduction

Internal erosion may be induced by the protective layer being stripped by sediment deposits [1] which are piled up by sediment transport [2], causing significant global economic losses. According to Foster [3] and Richards [4], approximately 0.5% of the embankment dams worldwide exhibit failure due to internal erosion, which is the primary failure mode, accounting for about 46% of all failure types. Dam failure induced by internal erosion and even overtopping [5] is subject to early detection, which is important to ensure their safety and security [6]. Besides, internal erosion can cause uneven settlement of buildings [7], extensive ground collapse or sinkholes [8,9,10,11,12,13] (as shown in Figure 1), damages in shield tunnels [14] and in dike foundations [15], and clogging of oil wells [16]. Internal erosion can be classified as suffusion, backward erosion, concentrated erosion, or contact erosion [17,18,19,20,21], of which induced failure was fully surveyed and reviewed by [22,23]. Suffusion is a long-term phenomenon in which fine soil particles are washed away through pore channels between coarse particles [24]. Soils susceptible to suffusion are described as internally unstable [25], and those non-susceptible to suffusion are called internally stable soils. Backward erosion refers to a process by which pipes are formed due to the removal of soil at the exit. As the erosion further develops, pipes extend in the opposite direction of the seepage. Concentrated leak erosion mainly occurs at cracks, whereas contact erosion exists at the interface of two layers of soil with significant differences in particle size.
The pore channels can be simplified as relatively large “chambers” and relatively small “constrictions” connecting the chambers [26]. The mechanism of internal erosion (as shown in Figure 2) is complex due to three coupled processes [27,28,29,30,31]: Particles are detached from the soil skeleton, the detached particles are transported through pore channels, and clogging occurs near constrictions.
Detachment is a process in which the equilibrium state is broken under the action of fluid flow and is the result of the destruction of the force chain [32,33,34]. Therefore, the most easily detached particles are fine particles that are deposited solely due to gravity or have a relatively small contact force. On this basis, Hosn [35] distinguished detached particles according to their unbalanced force. Although gravity-deposited particles cannot transmit effective stress, they provide lateral support for force-chain particles. However, the force-chain particle detachment can lead to stress redistribution and large volume deformation [36,37], significantly changing the soil structure and mechanical properties.
The transport process of the detached particles is typically determined by the constriction size distribution (CSD) [38,39]. According to Hosn [35], a detached particle can be transported through the pore channels and is considered an eroded particle if its diameter is smaller than Dc35 (i.e., 35% of the constrictions are finer than this size). Meanwhile, particle clogging may occur because the particle diameter exceeds the constriction size or arch formation occurs [7,40]. However, clogging can reduce permeability, leading to an increase in excess pore pressure and strength degradation. Finally, the arch can be destroyed by fluid flow, causing permeability reduction and abrupt erosion.
Numerous studies have been carried out to clarify the internal soil erosion mechanism, including theoretical analyses [27,41], experiments [42,43,44], and numerical simulations [34,45,46]. Numerical simulations can accurately model the internal erosion mechanism under fluid flow by tracing the movement of detached particles, visualizing the evolution of the pore channels, and quantifying the force chain variation, unlike experiments. In early research, Hu [47,48], Luo [49], Cividini [50,51], and Sterpi [7] investigated internal erosion using the continuous medium finite element method (FEM), which cannot capture the discrete behavior of geomaterials. The introduction of the discrete element method (DEM) coupled with hydro-mechanical models allowed for modeling the soil deformation characteristic and particle migration, as well as the evolution of the pore channels and force chains at the particle scale.
Therefore, this article first briefly introduces commonly used numerical simulation methods for analyzing internal erosion and then systematically summarizes the internal erosion mechanism from geometric, mechanical, and hydraulic perspectives. Several issues that require further study are highlighted to improve the accuracy and applicability of numerical simulations and improve our understanding of soil erosion mechanisms.

2. Fluid-Particle Coupled Method in Numerical Simulations of Internal Erosion

Internal erosion is a coupling process of fluid flow and particle migration; thus, a suitable coupled model is required for the analysis. Generally, the DEM is used to compute the motion of particles, but there are various solutions for fluid motion.

2.1. DEM Model of Particle Migration

The motion of particles in the DEM is computed by Newton’s second law that considers the gravity, contact force, and interaction force between the particles and fluid. Commonly used contact models include linear models and the nonlinear Hertz–Mindlin model. However, the contact properties considered by different scholars are substantially different, as listed in Table 1. Hu [52] and Kawano [24] adopted a large modulus which is similar to the natural sandy soil. Due to the negative correlation between the soil modulus and the DEM time step, Cai [53], Guo [54], Zou [55], Abdoulaye [56], and Tao [18,34] used a relatively small modulus to increase the time step. The influence of a relatively small modulus should be further analyzed and corrected to improve the applicability and accuracy of the simulation results.

2.2. DEM and Fluid Flow Coupled Method

Several scholars have proposed coupled methods to consider the influence of fluid flow in the DEM. Hakuno and Tarumi [57] developed a fluid network model coupled with the DEM. The flow channel between the pores was assumed to follow the Hagen-Poiseuille pipe flow, as shown in Figure 3a. Cui [16], Tang [9], and Goodarzi [58] coupled Darcy’s law with the DEM. Tsuji [59] and Xu and Yu [60] proposed the volume-averaged coarse-grid approach to mesh the fluid domain into cells, in which the physical domains overlapped with the soil particles. The locally averaged Navier–Stokes (N–S) equation [61] was solved in each cell, and the impact of the particles was incorporated by considering the porosity and interaction force. This model is called the computational fluid dynamics (CFD)-DEM method (Figure 3b). The Lattice–Boltzmann method (LBM) does not solve the N–S equation directly, but solves the kinetic gas theory equation, which discretizes the fluid domains and particles into fluid nodes and solid nodes, and simulates the fluid flow by tracking the evolution of the density distribution of the fluid nodes [62], as shown in Figure 3c. The LBM-DEM has been widely used to simulate the particle–fluid interaction since it does not require solving the complex N–S equation [63,64,65]. The smoothed particle hydrodynamics (SPH) model was developed using a mesh-free method [66], which discretizes the fluid domains into fluid particles, as shown in Figure 3d. By introducing the equation of state, the fluid pressure can be determined explicitly, and the N–S equation can be solved. The value of the fluid variable at any position can be obtained by interpolating the value of the fluid particles in the kernel.
The coupling process of the DEM and fluid flow is shown in Figure 4. The fluid network method does not require discretization and meshing, but its parameters are difficult to obtain. The Darcy model, which only needs the permeability, has a straightforward calculation, but the low Reynolds number limits its application. The CFD-DEM solves the fluid flow in cells larger than the particle size, which reduces the accuracy, but the model has relatively high computational efficiency; thus, it is widely used. The LBM-DEM can solve the fluid flow at a pore-scale far smaller than the particle size, capturing the fluid flow characteristics between the pores and achieving high calculation accuracy. However, the computing cost is high, and only less than ten thousand particles can be simulated [29,45,62,68,69]. The SPH does not suffer from accuracy reduction caused by mesh distortion in large deformation and can handle complex boundaries easily; however, its dynamic fluid pressure is not accurate.

3. Research on Factors Affecting Internal Erosion and Its Mechanism

Many scholars [69,70,71,72] unanimously agree that the initiation and development of internal erosion are jointly influenced by the geometric, mechanical, and hydraulic conditions, as shown in Figure 5. The coupling of these conditions affects the pore channels and force chains, influencing the particle detachment, transport, and clogging, which, in turn, determine the occurrence, initiation time, and the amount of erosion.

3.1. Geometric Conditions

Geometric conditions are inherent to the soil, representing a key factor determining erosion resistance. Compared with widely graded soils, gap-graded soils are more prone to internal erosion. In gap-graded soils, the fines content (F), gap ratio (G, defined by the ratio of the diameter of the smallest coarse particle to the largest fine particle), and density (Dr) have significant impacts on erosion. Besides, the particle shape is crucial for erosion resistance due to its impact on pore channels and interlocking. However, few studies have investigated the particle shape due to the difficulty of simulating irregular particles.

3.1.1. Effect of Geometric Conditions on Stress Distribution

Gap-graded soils can be divided into three fabric states based on two critical fines contents (S* and Smax): (1) “Underfilled” fabric when F < S* and the fines do not fill the pores; (2) “filled” fabric when S* < F < Smax and the fines fill the pores; (3) “overfilled” fabric when F > Smax and the coarse particles are separated from the fine particles [74], as shown in Figure 6. Skempton [75] proposed that Smax = 35%, and S* was between 24% and 29% due to the density. The fabric determines the stress distribution in the soil and influences the particle detachment process. Meanwhile, it also affects the pore channels, which are the transport paths of the detached particles.
The stress distribution can be quantified by the stress reduction factor α, which is the ratio of the average effective stress in the fines to the stress in the sample [75]. As the fines’ content and density increase and the gap ratio decreases, the contact force between the particles strengthens, and the connectivity increases, as reported by Li [76], Ahmadi [28], and Shire [71,74]. Shire [71,74] investigated the relationship between α and the fines content, the density, and the gap ratio, as shown in Figure 7. It was found that α decreased rapidly with the gap ratio in the underfilled state since more particles were deposited due to gravity, and there were weak contacts. α remained at a relatively high level, and the contribution of the coarse and fine particles to the stress transmission was equivalent in the overfilled state. α decreased linearly with the gap ratio in the filled state (Figure 7a). Moreover, the density had the largest impact in the sample with the largest gap ratio sample since the pore channels were wider in this sample, as shown in Figure 7b. This can confirm that the soil fabric is closely related to fines content, gap ratio, and density.

3.1.2. Effect of Soil Fabric on Pore Channels and Force Chains

In addition to affecting the stress distribution, the soil fabric also has a substantial impact on the pore channels and soil skeleton. The pore channels are wide and have high connectivity, making the transport of detached particles less tortuous in the underfilled soil fabric. Therefore, the soil is susceptible to erosion, and the higher the fines content, the more intense the erosion is. This phenomenon was confirmed by the numerical simulation results of Zou [55], Hu [46], and Cai [53], who found that the erosion ratio gradually increased with an increase in the fines content when the fines content was less than 30%. However, the filled and overfilled soil fabrics show more complex behavior. On the one hand, the pore channels become narrower, and the pore connectivity worsens with an increase in the fines content, resulting in a more tortuous transport path of the detached particles and increased clogging probability. On the other hand, the coarse particles, the main components of the soil skeleton, are separated by the fine particles which weaken the stability of the skeleton, as the fines content increases. In addition, the erosion of fine particles, bearing effective stress, leads to disturbance of the soil skeleton. The soil skeleton failure will happen when the soil skeleton can’t resist the drag force.
Therefore, in the underfilled fabric, with an increase in the fines content, more fine particles with low stress lead to a more intense erosion. However, it is not clear in the filled and overfilled fabric due to the complex effects, which deserve careful investigation.

3.1.3. Effect of Gap Ratio on Pore Channels and Flow Velocity

In addition to the fines content, the gap ratio also determines the pore channels. Tao [77], Cai [53], and Zhang [68] analyzed the effect of the gap ratio on the erosion ratio. Tao [77] found that the erosion ratio decreased gradually as the gap ratio increased from 1.25 to 2.75. However, Cai [53] found that the erosion ratio increased as the gap ratio increased from 2 to 6; these results were similar to those of Zhang [68].
Tao [77] obtained results opposite to those of Cai [53] and Zhang [68] under constant flow rate boundary conditions since the size of pore channels enlarges with the gap ratio, resulting in two effects. First, the expansion of pore channels reduces the local flow velocity, which lowers the driving force and decreases the number of detached particles under constant flow rate conditions. Second, the expansion of the pore channels allows for easier migration of the detached particles through the constriction, thus enhancing particle transport and weakening clogging. The first effect dominates the erosion process at low gap ratios since the fine particles readily form arches, causing clogging and resulting in fewer detached particles. In contrast, the second effect dominates the erosion process at high gap ratios since few arches form, and clogging is less common. Therefore, there should be a critical gap ratio (Gcr) where the two effects are equivalent. It is meaningful to fully investigate the relationship between Gcr and soil fabric and mechanical conditions.

3.2. Mechanical Conditions

Mechanical conditions, including the confining pressure and stress state, have substantial influences on the mechanical behavior of soil. To date, several studies were conducted on the influence of the mechanical conditions on contact anisotropy [78,79] and soil shear behavior [80,81], whereas few studies focused on soil erosion.

3.2.1. Effect of Confining Pressure

As the confining pressure increases, the contact force increases, which strengthens the friction between particles. Therefore, a strong driving force is needed to detach the force-chain particles from the soil skeleton, which significantly reduces the quantity of erodible soil particles. However, the increase in the confining pressure has no inhibitory effect on the detachment of gravity-deposited particles since these particles hardly transfer any effective stress [68]. Moreover, the pore channels are compacted at a high confining pressure, slowing the transport of detached particles. In addition, both numerical simulations [69] and experiments [82] have proved the existence of compression arches (here, the compression arch is part of the force chain, unlike the arch that forms clogging), which bear most of the driving force and form a protective zone behind them [69], as shown in Figure 8. However, negative effects also occur with an increase in confining pressure. The erosion of the force-chain particles can destroy the equilibrium state of the soil skeleton, leading to a large unbalanced force in the remainder of the force chain due to the loss of the large contact force, as shown in Figure 9. As a result, force-chain bending and local soil kinetic energy bursts may occur, reducing the soil stability. A suitable confining pressure can strengthen the friction, enhance the compression arch, and narrow the pore channels, improving the soil stability. However, excessive confining pressure may destroy the compression arches and soil skeleton [82] due to a relatively large unbalanced force, resulting in an unstable state.

3.2.2. Effect of Anisotropic Stress State

Numerous experiments [42,43,83,84] have proved that the erosion process varied significantly under different stress states, such as isotropy, triaxial compression, and the triaxial extension stress path. Since the soil is uniformly compressed in the isotropic stress state, the pore channels become narrower; thus, some constrictions are smaller than the diameter of the fine particles, blocking the transport path of the detached particles and weakening the erosion process. The anisotropic stress state is relatively complex. Since the force chains evolve towards the direction of the major principal stress in anisotropic stress states [29,45,85], the pore distribution shows anisotropy, which also follows the direction of the major principal stress. Therefore, the transport path of the detached particles is relatively unobstructed, and the erosion develops rapidly when the seepage flows in the direction of major principal stress. In contrast, the seepage direction is perpendicular to the pore channel when the anisotropy is perpendicular to the major principal stress; thus, the detached particles are prone to be redeposited on the soil skeleton. Moreover, the transport path is relatively tortuous, and clogging occurs readily. It deserves attention that the anisotropic stress state may have a relatively larger impact on the pore channels in underfilled soils and on the force chains in filled and overfilled soils [76], emphasizing the importance of the soil fabric. Besides, in anisotropic stress states, the soil may dilate or contract, leading to the widening or narrowing of the pore channels, which affects the transport rate of the detached particles [29,45]. Foroutan [85] assessed the influence of the medium stress ratio b = (σ1 − σ2)/(σ1 − σ3) on the macro- and micro-features of undrained granular samples. It was found that the effective mobilized friction angle reached the maximum when b was 0.5, indicating that the stress state has a significant influence on soil friction.
The influence of the mechanical conditions is relatively complex because it affects the friction and compression arches and causes contraction or dilatation of the soil. Thus, the mechanical conditions affect particle detachment, transport, and clogging by changing the force chains and pore channels. Additional research is required to understand this process comprehensively. For example, research should be conducted to (1) quantify the impact of friction on erosion, (2) explore the impact of the unbalanced force on compression arch failure due to the detachment of the force-chain particles, (3) investigate the geometry and mechanical boundaries of soil contraction and dilation, and (4) clarify the relationship between the soil fabric and the mechanical conditions.

3.3. Hydraulic Conditions

3.3.1. The Process of Soil Structure Reorganization

Soil may lose stability, causing changes in the soil structure and mechanical properties when suffering external disturbance. The hydraulic conditions are external disturbance factors. Wautier [86] used the second-order work criterion to prove that the soil stability varied with the direction. When the stress increment exceeds the threshold value, which depends on the loading rate, the direction of loading, the soil properties (the geometric conditions and mechanical conditions), and the microstructural reorganization will be induced, i.e., soil instability is triggered. Therefore, the direction of hydraulic loading, the hydraulic gradient, and the hydraulic loading rate are crucial factors affecting soil stability. As the fluid flows through the soil, the additional driving force destroys several contacts, reaching the Mohr-Coulomb limit sliding condition, which indicates the occurrence of local particle detachment. Subsequently, the contact quantity and contact force decrease [34,62], leading to the continuous loss of lateral support and resulting in unjamming and bending of a few local force chains associated with a local burst of kinetic energy. This burst of kinetic energy propagates to the entire soil sample and provokes a generalized unjamming of the force chains [86], leading to microstructural reorganization until a new stable state is reached, as shown in Figure 10.

3.3.2. Three Effects of Hydraulic Loading Direction

The importance of the hydraulic loading direction, i.e., the seepage direction, is reflected in three aspects: (a) The soil stability is directional; (b) the seepage direction determines the effect of gravity; (c) the pore channel’s direction affects the seepage action. Gravity has a pronounced influence on the number of detached particles since it is the driving force when the seepage is in the direction of gravity. In contrast, gravity is the resistant force when the seepage is opposite to it. Unlike stress disturbance which is transmitted through the force chain, the hydraulic disturbance is affected by the direction of the pore channels. When the pore channel direction is close to the direction of the force chain [42] or the same as the seepage direction, the seepage flow is unobstructed, and the migration of the detached particles is significantly enhanced [45]. On the contrary, when the pore channel direction is inconsistent with the seepage direction, the contact hindering the flow will cause continuous failure and restructuring under the impact of fluid flow. Therefore, as erosion continues, the contact direction will evolve toward the seepage direction [87,88]. Xiong [36] analyzed the effect of the seepage direction and found that the erosion ratio decreased rapidly as the angle of the seepage direction and gravity direction increased from 0° to 90°. It deserves attention that the directivity of the soil stability is likely related to the directivity of the force chains and pore channels, although the quantitative relationship is unclear. Further, the stability index of the soil in different directions may change during the erosion process since the erosion changes the pore channels and force chain.

3.3.3. The Critical Hydraulic Gradient

When the hydraulic disturbance is insufficient to cause contact failure and force-chain bending, a small amount of erosion due to detached particles does not result in the reorganization of the microstructure. Therefore, similar to the stress disturbance, suffusion occurs when the hydraulic gradient exceeds the threshold value [62,89,90,91], i.e., the critical hydraulic gradient. As the hydraulic gradient increases, the number of detached particles increases because more and more particles overcome the resistance force. In addition, with the increase in the hydraulic gradient, an increased number of force chains are destroyed and recombined, leading to periodic clogging and blowout of the clogging clusters [46]. The clogging-unclogging events lead to abrupt permeability and porosity changes, increasing soil instability [46,92] and releasing some of the fine particles blocking the pores, thereby increasing the transport distance of the detached particles. Therefore, the final erosion amount and erosion rate increase with an increase in the hydraulic gradient [89]. Moreover, Zhang [68] found that the erosion ratio increased roughly linearly with the hydraulic gradient. Since the erosion process changes the microstructure of soil, the mechanical properties of the soil will change after erosion [36,87]; this topic requires additional in-depth research.
The critical hydraulic gradient decreases with an increase in the hydraulic loading rate [34]. One interpretation is that the soil does not have sufficient time to restructure in response to the failure of the force chains since the rapidly increasing hydraulic loading rate will lead to a rapid increase in soil kinetic energy, which will be quickly transferred to the entire sample. In addition, experimental research showed that the hydraulic loading path and salt concentration had a significant and complex impact on erosion [93,94,95]. It is necessary to carry out in-depth research on the relevant hydraulic conditions to understand the impact of hydraulic conditions at the microscopic scale to deal with complex engineering applications.

3.4. Comprehensive Mechanism of Internal Erosion at the Microscopic Level

The previous analysis revealed the micro-mechanism of internal soil erosion, as depicted in the conceptual model in Figure 11. It was found that the geometric conditions and mechanical conditions determine the number and morphology of the pore channels and force chains in the soil, whereas the hydraulic conditions act as an external disturbance. The soil stability has directivity, which may result from the direction of the pore channels and force chains. Particle detachment can occur when the driving force overcomes the resistant force, indicating that the process is primarily affected by the hydraulic gradient and the force chains. The erosion is initiated when numerous particles are detached from the skeleton. Further, force-chain bending occurs due to lateral support loss, which can trigger a local kinetic energy burst in the soil. This effect is transferred to the entire sample, resulting in large-scale force-chain bending. Some detached particles are redeposited in the pores or become part of the force chain due to microstructural reorganization. Meanwhile, some of the remaining detached particles are transported through the constrictions and are removed from the soil sample; this process is influenced by the pore channels and seepage direction. The other detached particles are clogged near the constrictions due to their size or the arch formation. These particles will be transported after microstructural reorganization. The processes of redeposition, transport, and clogging determine the erosion amount. The contributory factors to internal erosion at the macroscopic level (see Figure 5) are considered at the microscopic level in the conceptual model in Figure 11.

4. Conclusions

Soils exhibit complex erosion characteristics due to the coupled effects of the geometric, mechanical, and hydraulic conditions. This article provides an in-depth review of the erosion mechanism at the microscopic level. The main findings and recommendations for future work are as follows:
(1)
Soil fabric is the primary factor affecting erosion. In the underfilled fabric, with an increase in the fines content, although the pore channels become narrower, more particles with low stress lead to a more intense erosion. In the filled and overfilled fabric, fine particles bear a higher stress than the underfilled fabric. However, a large unbalanced force induced by the detachment of force-chain particles results in a local kinetic energy burst in the soil. The combination of these effects causes the complex behavior of soils with filled and overfilled fabrics, which deserves careful investigation.
(2)
A critical gap ratio Gcr exists since the gap ratio impacts the local flow velocity and pore channel size, below which the erosion weakens when the gap ratio increases; otherwise, the erosion significantly intensifies. It is meaningful to fully research the relationship between Gcr and soil fabric and mechanical conditions.
(3)
Like the response to an increase in the fines content, the pore channels become narrower, and the contact force increases with an increase in the confining pressure. However, a larger confining pressure, resulting in a relatively large unbalanced force, can destroy the compression arches in the soil. In addition, the anisotropic stress state causes directionality of the pore channels and force chains. Therefore, it is necessary to quantify the effects of soil anisotropy coupled with seepage direction on erosion characteristics.
(4)
The coupling of geometric, mechanical, and hydraulic conditions affects the pore channels and force chains, influencing particle detachment, transport, and clogging, which, in turn, determine the occurrence, initiation time, and the amount of erosion, which are hard to quantify from available studies. The following mechanical effects deserve further in-depth investigations: The impact of unbalanced force on compression arch failure, the boundary of soil contraction and dilation, the relationship between soil fabric and mechanical conditions. Besides, the critical hydraulic gradient depends on the hydraulic loading rate and direction, and the soil properties, which is not quantitatively clear.

Author Contributions

Writing—original draft preparation, X.W.; writing—review and editing, B.H., Y.T., and D.L.; help and discussion, T.H.; funding acquisition, Y.T. All authors have read and agreed to the published version of the manuscript.

Funding

The work presented in this article was supported by the National Natural Science Foundation of China (Grant Nos. 51908493, 41961144018, 51988101), the Natural Science Foundation of Zhejiang Province (grant number LCZ19E080002), the Fundamental Research Funds for the Central Universities (grant number 2019FZA4016, 2019QNA4035).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

CFDComputation fluid dynamics
CSDConstriction size distribution
DEMDiscrete element method
Dc3535% of the constrictions are finer than this size
DrDensity
FFines content
FEMFinite element method
GGap ratio
GcrCritical gap ratio
LBMLattice-Boltzmann method
SPHSmoothed particle hydrodynamics
S*Critical fines content between underfilled and filled
SmaxCritical fines content between filled and overfilled
σ1Major principal stress
σ2Intermediate principal stress
σ3Minor principal stress

References

  1. Caldeira, L. Internal Erosion in Dams: Studies and Rehabilitation. Int. J. Civ. Eng. 2018, 17, 457–471. [Google Scholar] [CrossRef]
  2. Zarris, D.; Lykoudi, E.; Panagoulia, D. Assessing the Impacts of Sediment Yield on the Sustainability of Major Hydraulic Systems. In Proceedings of the Protection and Restoration of the Environment VIII, Chania, Greece, 3–7 July 2006; pp. 3–7. [Google Scholar]
  3. Foster, M.; Fell, R.; Spannagle, M. The Statistics of Embankment Dam Failures and Accidents. Can. Geotech. J. 2000, 37, 1000–1024. [Google Scholar] [CrossRef]
  4. Richards, K.S.; Reddy, K.R. Critical Appraisal of Piping Phenomena in Earth Dams. Bull. Int. Assoc. Eng. Geol. 2007, 66, 381–402. [Google Scholar] [CrossRef]
  5. Jandora, J.; Říha, J. The Failure of Embankment Dams Due to Overtopping; Vutium: Brno, Czech, 2008; Volume 47. [Google Scholar]
  6. Khan, A.A.; Vrabie, V.; Beck, Y.-L.; Mars, I.J.; D’Urso, G. Monitoring and Early Detection of Internal Erosion: Distributed Sensing and Processing. Struct. Heal. Monit. 2014, 13, 562–576. [Google Scholar] [CrossRef] [Green Version]
  7. Sterpi, D. Effects of the Erosion and Transport of Fine Particles due to Seepage Flow. Int. J. Géoméch. 2003, 3, 111–122. [Google Scholar] [CrossRef]
  8. Tang, Y.; Chan, D.H.; Zhu, D.Z. Numerical Investigation of Sand-Bed Erosion by an Upward Water Jet. J. Eng. Mech. 2017, 143, 04017104. [Google Scholar] [CrossRef]
  9. Tang, Y.; Chan, D.H.; Zhu, D.Z. A Coupled Discrete Element Model for the Simulation of Soil and Water Flow through an Orifice. Int. J. Numer. Anal. Methods Géoméch. 2017, 41, 1477–1493. [Google Scholar] [CrossRef]
  10. Tang, Y.; Zhu, D.Z.; Chan, D.H. Experimental Study on Submerged Sand Erosion through a Slot on a Defective Pipe. J. Hydraul. Eng. 2017, 143, 04017026. [Google Scholar] [CrossRef]
  11. Tang, Y.; Zhu, D.Z.; Chan, D.H. Modeling Soil Loss by Water Infiltration through Sewer Pipe Defects. In Proceedings of the World Environmental and Water Resources Congress 2018; American Society of Civil Engineers (ASCE): Minneapolis, MN, USA, 2018; pp. 254–262. [Google Scholar]
  12. Indiketiya, S.; Jegatheesan, P.; Rajeev, P. Evaluation of Defective Sewer Pipe–Induced Internal Erosion and Associated Ground Deformation Using Laboratory Model Test. Can. Geotech. J. 2017, 54, 1184–1195. [Google Scholar] [CrossRef]
  13. Wood, D.M. The Magic of Sands. In Proceedings of the 20th Bjerrum Lecture: Oslo, Norway, 25 November 2005. Can. Geotech. J. 2007, 44, 1329–1350. [Google Scholar] [CrossRef]
  14. Ye, Z.; Liu, H. Modeling the Effects of Internal Erosion on the Structural Damage of a Shield Tunnel. Int. J. Géoméch. 2020, 20, 04020053. [Google Scholar] [CrossRef]
  15. Yang, J.; Yin, Z.; Laouafa, F.; Hicher, P.-Y. Internal Erosion in Dike-On-Foundation Modeled by a Coupled Hydromechanical Approach. Int. J. Numer. Anal. Methods Géoméch. 2019, 43, 663–683. [Google Scholar] [CrossRef]
  16. Cui, Y.; Nouri, A.; Chan, D.; Rahmati, E. A New Approach to DEM Simulation of Sand Production. J. Pet. Sci. Eng. 2016, 147, 56–67. [Google Scholar] [CrossRef]
  17. Yang, J.; Yin, Z.-Y.; Laouafa, F.; Hicher, P.-Y. Analysis of Suffusion in Cohesionless Soils with Randomly Distributed Porosity and Fines Content. Comput. Geotech. 2019, 111, 157–171. [Google Scholar] [CrossRef]
  18. Tao, J.; Tao, H. Factors Affecting Piping Erosion Resistance: Revisited with a Numerical Modeling Approach. Int. J. Géoméch. 2017, 17, 04017097. [Google Scholar] [CrossRef]
  19. Horikoshi, K.; Takahashi, A. Suffusion-Induced Change in Spatial Distribution of Fine Fractions in Embankment Subjected to Seepage Flow. Soils Found. 2015, 55, 1293–1304. [Google Scholar] [CrossRef] [Green Version]
  20. Suits, L.D.; Sheahan, T.C.; Chang, D.S.; Zhang, L.M. A Stress-Controlled Erosion Apparatus for Studying Internal Erosion in Soils. Geotech. Test. J. 2011, 34, 103889. [Google Scholar] [CrossRef]
  21. Richards, K.; Reddy, K. Experimental Investigation of Initiation of Backward Erosion Piping in Soils. Géotechnique 2012, 62, 933–942. [Google Scholar] [CrossRef]
  22. Mattsson, H.; Hellström, J.G.I.; Lundström, S. On Internal Erosion in Embankment Dams: A Literature Survey of the Phenomenon and the Prospect to Model It Numerically; Luleå Tekniska Universitet: Lulea, Sweden, 2008. [Google Scholar]
  23. Robbins, B.; Griffiths, D.V. Internal Erosion of Embankments: A Review and Appraisal. In Proceedings of the Rocky Mountain Geo-Conference, Westminster, CO, USA, 16 April 2020; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 61–75. [Google Scholar] [CrossRef]
  24. Kawano, K.; Shire, T.; O’Sullivan, C. Coupled Particle-Fluid Simulations of the Initiation of Suffusion. Soils Found. 2018, 58, 972–985. [Google Scholar] [CrossRef]
  25. Shire, T.; O’Sullivan, C. Micromechanical Assessment of an Internal Stability Criterion. Acta Geotech. 2012, 8, 81–90. [Google Scholar] [CrossRef] [Green Version]
  26. Zhuang, P.-Z.; Ma, G.; Dai, Z.; Ming, R.; Cui, X.; She, R. Numerical Study on Pore Clogging Mechanism in Pervious Pavements. J. Hydrol. 2018, 565, 589–598. [Google Scholar] [CrossRef]
  27. Kodieh, A.; Gelet, R.; Marot, D.; Fino, A.Z. A Study of Suffusion Kinetics Inspired from Experimental Data: Comparison of Three Different Approaches. Acta Geotech. 2020, 1–19. [Google Scholar] [CrossRef]
  28. Shire, T.; Shire, T.; Mehdizadeh, A.; Disfani, M. DEM Modelling to Assess Internal Stability of Gap-Graded Assemblies of Spherical Particles under Various Relative Densities, Fine Contents and Gap Ratios. Comput. Geotech. 2020, 126, 103710. [Google Scholar] [CrossRef]
  29. Wautier, A.; Bonelli, S.; Nicot, F. Scale Separation between Grain Detachment and Grain Transport in Granular Media Subjected to an Internal Flow. Granul. Matter 2017, 19, 595. [Google Scholar] [CrossRef] [Green Version]
  30. Abdou, H.; Emeriault, F.; Plé, O. New Approach to Describe Hydro-Mechanical Phenomenon of Suffusion: Erosion, Transport and Deposition. Eur. J. Environ. Civ. Eng. 2020, 24, 2342–2360. [Google Scholar] [CrossRef]
  31. Yang, J.; Yin, Z.; Laouafa, F.; Hicher, P.-Y. Modeling Coupled Erosion and Filtration of Fine Particles in Granular Media. Acta Geotech. 2019, 14, 1615–1627. [Google Scholar] [CrossRef]
  32. Indraratna, B.; Vafai, F. Analytical Model for Particle Migration within Base Soil-Filter System. J. Geotech. Geoenviron. Eng. 1997, 123, 100–109. [Google Scholar] [CrossRef]
  33. Wautier, A.; Bonelli, S.; Nicot, F. Flow Impact on Granular Force Chains and Induced Instability. Phys. Rev. E 2018, 98, 042909. [Google Scholar] [CrossRef] [Green Version]
  34. Tao, H.; Tao, J. Quantitative Analysis of Piping Erosion Micro-Mechanisms with Coupled CFD and DEM Method. Acta Geotech. 2017, 12, 573–592. [Google Scholar] [CrossRef]
  35. Hosn, R.A.; Sibille, L.; Benahmed, N.; Chareyre, B. A Discrete Numerical Model Involving Partial Fluid-Solid Coupling to Describe Suffusion Effects in Soils. Comput. Geotech. 2018, 95, 30–39. [Google Scholar] [CrossRef] [Green Version]
  36. Xiong, H.; Yin, Z.; Zhao, J.; Yang, Y. Investigating the Effect of Flow Direction on Suffusion and Its Impacts on Gap-Graded Granular Soils. Acta Geotech. 2020, 1–21. [Google Scholar] [CrossRef]
  37. Rousseau, Q.; Sciarra, G.; Gelet, R.; Marot, D. Modelling the Poroelastoplastic Behaviour of Soils Subjected to Internal Erosion by Suffusion. Int. J. Numer. Anal. Methods Géoméch. 2019, 44, 117–136. [Google Scholar] [CrossRef]
  38. Sjah, J.; Vincens, E. Determination of the Constriction Size Distribution of Granular Filters by Filtration Tests. Int. J. Numer. Anal. Methods Géoméch. 2012, 37, 1231–1246. [Google Scholar] [CrossRef]
  39. Vincens, E.; Witt, K.-J.; Homberg, U. Approaches to Determine the Constriction Size Distribution for Understanding Filtration Phenomena in Granular Materials. Acta Geotech. 2014, 10, 291–303. [Google Scholar] [CrossRef]
  40. Valdes, J.R.; Santamarina, J.C. Particle Clogging in Radial Flow: Microscale Mechanisms. SPE J. 2006, 11, 193–198. [Google Scholar] [CrossRef] [Green Version]
  41. Moraci, N.; Mandaglio, M.C.; Ielo, D. A New Theoretical Method to Evaluate the Internal Stability of Granular Soils. Can. Geotech. J. 2012, 49, 45–58. [Google Scholar] [CrossRef]
  42. Chang, D.S.; Zhang, L. Critical Hydraulic Gradients of Internal Erosion under Complex Stress States. J. Geotech. Geoenviron. Eng. 2013, 139, 1454–1467. [Google Scholar] [CrossRef]
  43. Luo, Y.; Luo, B.; Xiao, M. Effect of Deviator Stress on the Initiation of Suffusion. Acta Geotech. 2020, 15, 1607–1617. [Google Scholar] [CrossRef]
  44. Bendahmane, F.; Marot, D.; Alexis, A. Experimental Parametric Study of Suffusion and Backward Erosion. J. Geotech. Geoenviron. Eng. 2008, 134, 57–67. [Google Scholar] [CrossRef]
  45. Wautier, A.; Bonelli, S.; Nicot, F. DEM Investigations of Internal Erosion: Grain Transport in the Light of Micromechanics. Int. J. Numer. Anal. Methods Géoméch. 2018, 43, 339–352. [Google Scholar] [CrossRef] [Green Version]
  46. Hu, Z.; Zhang, Y.; Yang, Z. Suffusion-Induced Deformation and Microstructural Change of Granular Soils: A Coupled CFD–DEM Study. Acta Geotech. 2019, 14, 795–814. [Google Scholar] [CrossRef]
  47. Ya-yuan, H.; Pan, M. The Numerical Simulation of Piping in the Two-Dimensional Embankment. Eng. Mech. 2015, 32, 110–119. [Google Scholar] [CrossRef]
  48. Ya-yuan, H.; Pan, M. Mechanism Study and Finite Element Simulation of Three-Phase Coupling Seepage Erosion Piping. Rock Soil Mech. 2013, 34, 913–921. [Google Scholar] [CrossRef]
  49. Yulong, L.; Hua, P.; Jin, Z. Design and Validation of 1D Three-Phase Seepage Erosion Coupled Piping Program. Chin. J. Solid Mech. 2008, 29, 118–121. [Google Scholar] [CrossRef]
  50. Cividini, A.; Bonomi, S.; Vignati, G.C.; Gioda, G. Seepage-Induced Erosion in Granular Soil and Consequent Settlements. Int. J. Géoméch. 2009, 9, 187–194. [Google Scholar] [CrossRef]
  51. Cividini, A.; Gioda, G. Finite-Element Approach to the Erosion and Transport of Fine Particles in Granular Soils. Int. J. Géoméch. 2004, 4, 191–198. [Google Scholar] [CrossRef]
  52. Hu, Z.; Zhang, Y.; Yang, Z. Suffusion-Induced Evolution of Mechanical and Microstructural Properties of Gap-Graded Soils Using CFD-DEM. J. Geotech. Geoenviron. Eng. 2020, 146, 04020024. [Google Scholar] [CrossRef]
  53. Yuanqiang, C.; Zhixiang, Z.; Zhigang, C.; Shuhao, Y. Mesoscopic numerical simulation for suffusion process of gap-graded sandy soil. J. Cent. South Univ. (Sci. Technol.) 2019, 50, 1144–1153. [Google Scholar] [CrossRef]
  54. Guo, Y.; Yang, Y.; Yu, X. (Bill) Influence of Particle Shape on the Erodibility of Non-Cohesive Soil: Insights from Coupled CFD–DEM Simulations. Particuology 2018, 39, 12–24. [Google Scholar] [CrossRef]
  55. Zou, Y.; Chen, C.; Zhang, L. Simulating Progression of Internal Erosion in Gap-Graded Sandy Gravels Using Coupled CFD-DEM. Int. J. Géoméch. 2020, 20, 04019135. [Google Scholar] [CrossRef]
  56. Hama, N.A.; Ouahbi, T.; Taibi, S.; Souli, H.; Fleureau, J.-M.; Pantet, A. Analysis of Mechanical Behaviour and Internal Stability of Granular Materials Using Discrete Element Method. Int. J. Numer. Anal. Methods Géoméch. 2016, 40, 1712–1729. [Google Scholar] [CrossRef]
  57. Hakuno, M.; Tarumi, Y. A Granular Assembly Simulation for the Seismic Liquefaction of Sand. Doboku Gakkai Ronbunshu 1988, 398, 129–138. [Google Scholar] [CrossRef] [Green Version]
  58. Goodarzi, M.; Kwok, C.Y.; Tham, L.G. A Continuum-Discrete Model Using Darcy’s Law: Formulation and Verification. Int. J. Numer. Anal. Methods Géoméch. 2014, 39, 327–342. [Google Scholar] [CrossRef]
  59. Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Discrete Particle Simulation of Two-Dimensional Fluidized Bed. Powder Technol. 1993, 77, 79–87. [Google Scholar] [CrossRef]
  60. Xu, B.; Yu, A. Numerical Simulation of the Gas-Solid Flow in a Fluidized Bed by Combining Discrete Particle Method with Computational Fluid Dynamics. Chem. Eng. Sci. 1997, 52, 2785–2809. [Google Scholar] [CrossRef]
  61. Anderson, T.B.; Jackson, R. Fluid Mechanical Description of Fluidized Beds. Equations of Motion. Ind. Eng. Chem. Fundam. 1967, 6, 527–539. [Google Scholar] [CrossRef]
  62. Fukumoto, Y.; Ohtsuka, S. 3-D Direct Numerical Model for Failure of Non-cohesive Granular Soils with Upward Seepage Flow. Comput. Part. Mech. 2018, 5, 443–454. [Google Scholar] [CrossRef]
  63. Lominé, F.; Scholtès, L.; Sibille, L.; Poullain, P. Modeling of Fluid-Solid Interaction in Granular Media with Coupled Lattice Boltzmann/Discrete Element Methods: Application to Piping Erosion. Int. J. Numer. Anal. Methods Géoméch. 2011, 37, 577–596. [Google Scholar] [CrossRef] [Green Version]
  64. Wang, M.; Feng, Y.; Wang, C. Coupled Bonded Particle and Lattice Boltzmann Method for Modelling Fluid-Solid Interaction. Int. J. Numer. Anal. Methods Géoméch. 2016, 40, 1383–1401. [Google Scholar] [CrossRef]
  65. Han, Y.; Cundall, P.A. LBM-DEM Modeling of Fluid-Solid Interaction in Porous Media. Int. J. Numer. Anal. Methods Géoméch. 2013, 37, 1391–1407. [Google Scholar] [CrossRef]
  66. Gingold, R.A.; Monaghan, J.J. Smoothed Particle Hydrodynamics: Theory and Application to Non-spherical Stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
  67. Han, Y. Construction of a LBM-DEM Coupling System and Its Applications in Modeling Fluid Particle Interaction in Porous Media Flow. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2012. [Google Scholar]
  68. Zhang, F.; Wang, T.; Liu, F.; Peng, M.; Furtney, J.; Zhang, L. Modeling of Fluid-Particle Interaction by Coupling the Discrete Element Method with a Dynamic Fluid Mesh: Implications to Suffusion in Gap-Graded Soils. Comput. Geotech. 2020, 124, 103617. [Google Scholar] [CrossRef]
  69. Tran, D.; Prime, N.; Froiio, F.; Callari, C.; Vincens, E. Numerical Modelling of Backward Front Propagation in Piping Erosion by DEM-LBM Coupling. Eur. J. Environ. Civ. Eng. 2016, 21, 960–987. [Google Scholar] [CrossRef]
  70. Fonseca, J.; Sim, W.; Shire, T.; O’Sullivan, C. Microstructural Analysis of Sands with Varying Degrees of Internal Stability. Géotechnique 2014, 64, 405–411. [Google Scholar] [CrossRef]
  71. Shire, T.; O’Sullivan, C.; Hanley, K.J.; Fannin, R.J. Fabric and Effective Stress Distribution in Internally Unstable Soils. J. Geotech. Geoenviron. Eng. 2014, 140, 04014072. [Google Scholar] [CrossRef] [Green Version]
  72. Chang, D.S.; Zhang, L. Extended Internal Stability Criteria for Soils under Seepage. Soils Found. 2013, 53, 569–583. [Google Scholar] [CrossRef] [Green Version]
  73. Garner, S.J.; Fannin, R.J. Understanding Internal Erosion: A Decade of Research Following a Sinkhole Event. Int. J. Hydropower Dams 2010, 17, 93–100. [Google Scholar]
  74. Shire, T.; O’Sullivan, C.; Hanley, K.J. The Influence of Fines Content and Size-Ratio on the Micro-Scale Properties of Dense Bimodal Materials. Granul. Matter 2016, 18, 52. [Google Scholar] [CrossRef] [Green Version]
  75. Skempton, A.W.; Brogan, J.M. Experiments on Piping in Sandy Gravels. Géotechnique 1994, 44, 449–460. [Google Scholar] [CrossRef]
  76. Li, W.C.; Deng, G.; Liang, X.Q.; Sun, X.X.; Wang, S.W.; Lee, M.L. Effects of Stress State and Fine Fraction on Stress Transmission in Internally Unstable Granular Mixtures Investigated via Discrete Element Method. Powder Technol. 2020, 367, 659–670. [Google Scholar] [CrossRef]
  77. Tao, H. Numerical Modeling of Soil Internal Erosion Mechanism. Ph.D. Thesis, The University of Akron, Columbus, OH, USA, 2018. [Google Scholar]
  78. Liu, J.; Zhou, W.; Ma, G.; Yang, S.; Chang, X. Strong Contacts, Connectivity and Fabric Anisotropy in Granular Materials: A 3D Perspective. Powder Technol. 2020, 366, 747–760. [Google Scholar] [CrossRef]
  79. Pouragha, M.; Duriez, J.; Wautier, A.; Wan, R.; Nicot, F.; Darve, F. Preferential Growth of Force Network in Granular Media. Granul. Matter 2019, 21, 67. [Google Scholar] [CrossRef] [Green Version]
  80. Xie, Y.H.; Yang, Z.; Barreto, D.; Jiang, M.D. The Influence of Particle Geometry and the Intermediate Stress Ratio on the Shear Behavior of Granular Materials. Granul. Matter 2017, 19, 35. [Google Scholar] [CrossRef] [Green Version]
  81. Gong, J.; Liu, J. Mechanical Transitional Behavior of Binary Mixtures via DEM: Effect of Differences in Contact-Type Friction Coefficients. Comput. Geotech. 2017, 85, 1–14. [Google Scholar] [CrossRef]
  82. Tomlinson, S.S.; Vaid, Y.P. Seepage Forces and Confining Pressure Effects on Piping Erosion. Can. Geotech. J. 2000, 37, 1–13. [Google Scholar] [CrossRef]
  83. Liang, Y.; Yeh, T.-C.J.; Chen, Q.; Xu, W.; Dang, X.; Hao, Y. Particle Erosion in Suffusion under Isotropic and Anisotropic Stress States. Soils Found. 2019, 59, 1371–1384. [Google Scholar] [CrossRef]
  84. Liang, Y.; Yeh, T.-C.J.; Wang, J.; Liu, M.; Zha, Y.; Hao, Y. Onset of Suffusion in Upward Seepage under Isotropic and Anisotropic Stress Conditions. Eur. J. Environ. Civ. Eng. 2019, 23, 1520–1534. [Google Scholar] [CrossRef]
  85. Foroutan, T.; Mirghasemi, A.A. CFD-DEM Model to Assess Stress-Induced Anisotropy in Undrained Granular Material. Comput. Geotech. 2020, 119, 103318. [Google Scholar] [CrossRef]
  86. Wautier, A.; Bonelli, S.; Nicot, F. Micro-Inertia Origin of Instabilities in Granular Materials. Int. J. Numer. Anal. Methods Géoméch. 2018, 42, 1037–1056. [Google Scholar] [CrossRef] [Green Version]
  87. Hu, Z.; Yang, Z.; Zhang, Y. CFD-DEM Modeling of Suffusion Effect on Undrained Behavior of Internally Unstable Soils. Comput. Geotech. 2020, 126, 103692. [Google Scholar] [CrossRef]
  88. Mahabadi, N.; Jang, J. The Impact of Fluid Flow on Force Chains in Granular Media. Appl. Phys. Lett. 2017, 110, 41907. [Google Scholar] [CrossRef]
  89. Gu, D.M.; Huang, D.; Liu, H.L.; Zhang, W.G.; Gao, X.C. A DEM- Based Approach for Modeling the Evolution Process of Seepage-Induced Erosion in Clayey Sand. Acta Geotech. 2019, 14, 1629–1641. [Google Scholar] [CrossRef]
  90. Nguyen, T.T.; Indraratna, B. A Coupled CFD–DEM Approach to Examine the Hydraulic Critical State of Soil under Increasing Hydraulic Gradient. Int. J. Géoméch. 2020, 20, 04020138. [Google Scholar] [CrossRef]
  91. Wang, Y.; Chai, J.; Xu, Z.; Qin, Y.; Wang, X. Numerical Simulation of the Fluid–Solid Coupling Mechanism of Internal Erosion in Granular Soil. Water 2020, 12, 137. [Google Scholar] [CrossRef] [Green Version]
  92. Bianchi, F.; Wittel, F.K.; Thielmann, M.; Trtik, P.; Herrmann, H.J. Tomographic Study of Internal Erosion of Particle Flows in Porous Media. Transp. Porous Media 2018, 122, 169–184. [Google Scholar] [CrossRef] [Green Version]
  93. Luo, Y.-L.; Qiao, L.; Liu, X.-X.; Zhan, M.-L.; Sheng, J.-C. Hydro-Mechanical Experiments on Suffusion under Long-Term Large Hydraulic Heads. Nat. Hazards 2013, 65, 1361–1377. [Google Scholar] [CrossRef]
  94. Rochim, A.; Marot, D.; Sibille, L.; Le, V.T. Effects of Hydraulic Loading History on Suffusion Susceptibility of Cohesionless Soils. J. Geotech. Geoenviron. Eng. 2017, 143, 04017025. [Google Scholar] [CrossRef]
  95. Benamar, A. Effect of Hydraulic Load and Water Chemistry on Soil Suffusion. In Proceedings of the Scour and Erosion; Informa UK Limited: Perth, Australia, 2014; pp. 197–202. [Google Scholar]
Water 13 00169 g001 550
Figure 1. Pavement collapse and sinkholes caused by internal erosion. (a) Sinkhole 1 at W.A.C Bennett Dam in 1996 ([13]); (b) sinkhole in Ottawa in 2016 (https://www.hallo-muenchen.de/bilder/2016/06/09/6474588/1248773444-krater-strassenloch-ottawa.jpg).
Figure 1. Pavement collapse and sinkholes caused by internal erosion. (a) Sinkhole 1 at W.A.C Bennett Dam in 1996 ([13]); (b) sinkhole in Ottawa in 2016 (https://www.hallo-muenchen.de/bilder/2016/06/09/6474588/1248773444-krater-strassenloch-ottawa.jpg).
Water 13 00169 g001
Water 13 00169 g002 550
Figure 2. Schematic diagram of the internal erosion process.
Figure 2. Schematic diagram of the internal erosion process.
Water 13 00169 g002
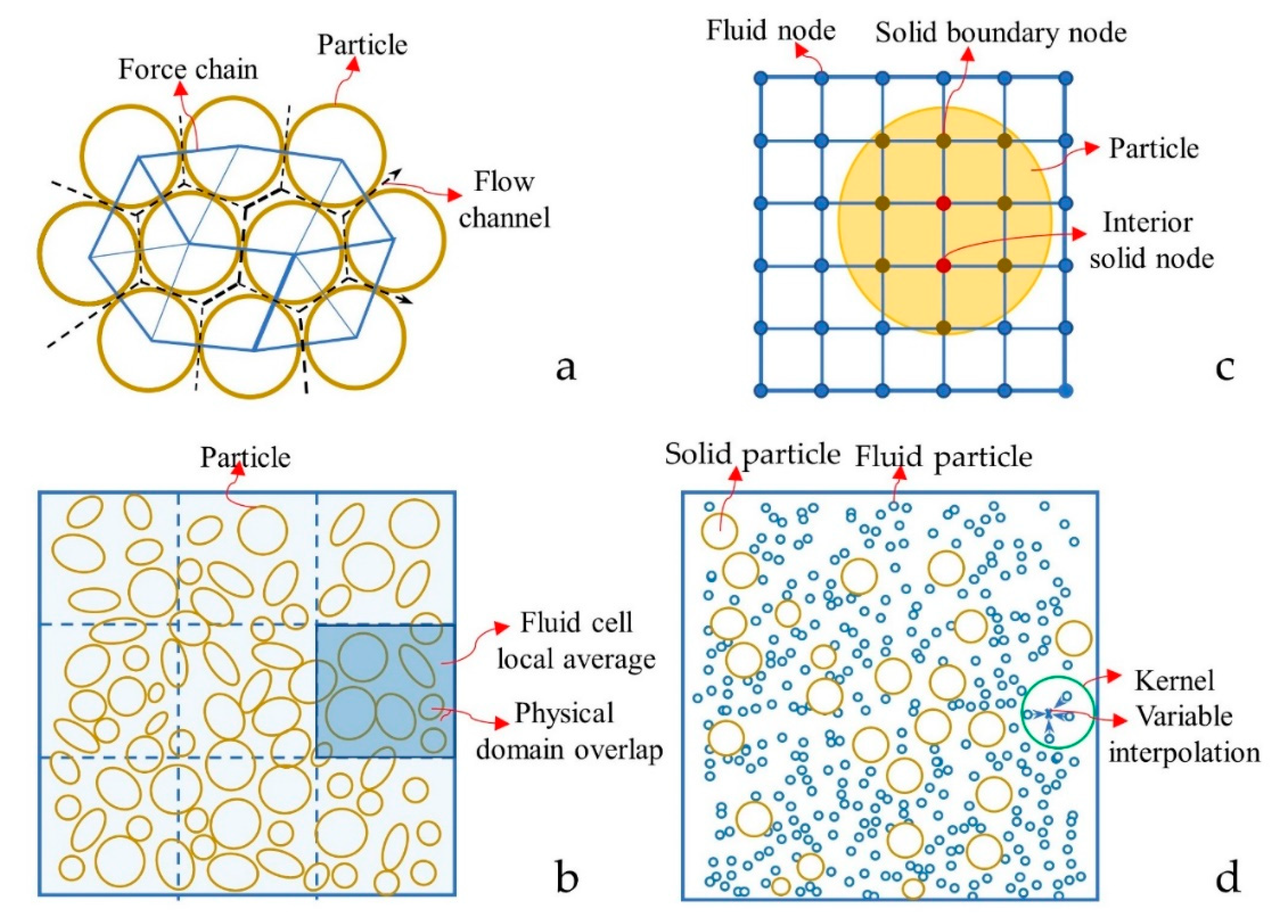
Water 13 00169 g003 550
Figure 3. Four coupled fluid flow-DEM (discrete element method) models. (a) Fluid network model; (b) computational fluid dynamics (CFD)-DEM model [24]; (c) Lattice–Boltzmann method (LBM)-DEM model [67]; (d) smoothed particle hydrodynamics (SPH)-DEM model.
Figure 3. Four coupled fluid flow-DEM (discrete element method) models. (a) Fluid network model; (b) computational fluid dynamics (CFD)-DEM model [24]; (c) Lattice–Boltzmann method (LBM)-DEM model [67]; (d) smoothed particle hydrodynamics (SPH)-DEM model.
Water 13 00169 g003
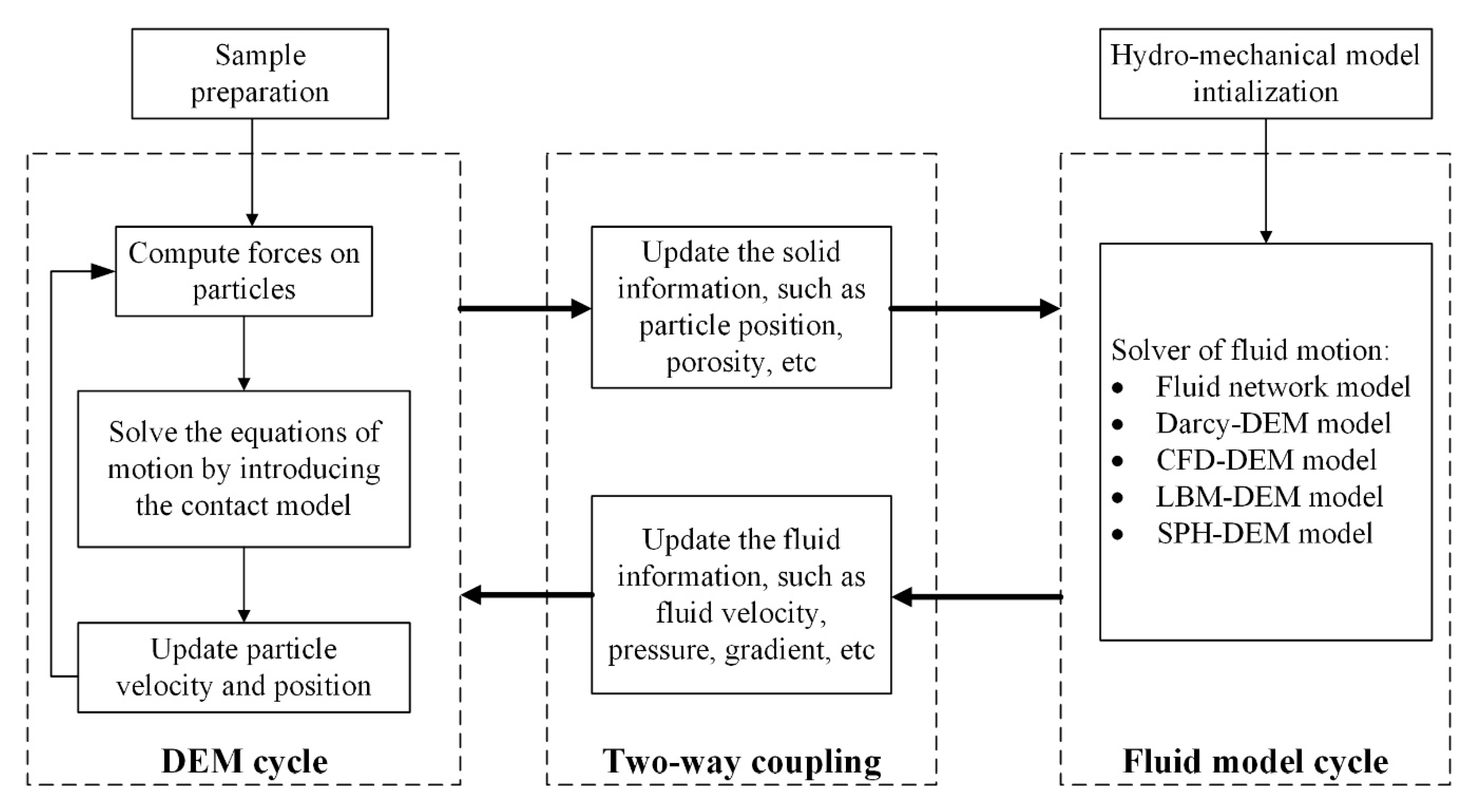
Water 13 00169 g004 550
Figure 4. Flowchart of fluid flow-DEM coupling.
Figure 4. Flowchart of fluid flow-DEM coupling.
Water 13 00169 g004
Water 13 00169 g005 550
Figure 5. Venn diagram showing the contributing factors to internal erosion (reprinted from [73]).
Figure 5. Venn diagram showing the contributing factors to internal erosion (reprinted from [73]).
Water 13 00169 g005
Water 13 00169 g006 550
Figure 6. Soil fabric states: (a) Underfilled; (b) filled; (c) overfilled ([75]).
Figure 6. Soil fabric states: (a) Underfilled; (b) filled; (c) overfilled ([75]).
Water 13 00169 g006
Water 13 00169 g007 550
Figure 7. The relationship between the stress reduction factor α and the fines content, gap ratio, and density (reprinted from [71,74]). (a) The relationship between the stress reduction factor α and the fines content and gap ratio in dense samples. (b) The relationship between the stress reduction factor α and the density and gap ratio at a fines content of 30%.
Figure 7. The relationship between the stress reduction factor α and the fines content, gap ratio, and density (reprinted from [71,74]). (a) The relationship between the stress reduction factor α and the fines content and gap ratio in dense samples. (b) The relationship between the stress reduction factor α and the density and gap ratio at a fines content of 30%.
Water 13 00169 g007
Water 13 00169 g008 550
Figure 8. Protective effect of the compression arches during erosion ([69]).
Figure 8. Protective effect of the compression arches during erosion ([69]).
Water 13 00169 g008
Water 13 00169 g009 550
Figure 9. Schematic diagram of the unbalanced force due to the detachment of force-chain particles.
Figure 9. Schematic diagram of the unbalanced force due to the detachment of force-chain particles.
Water 13 00169 g009
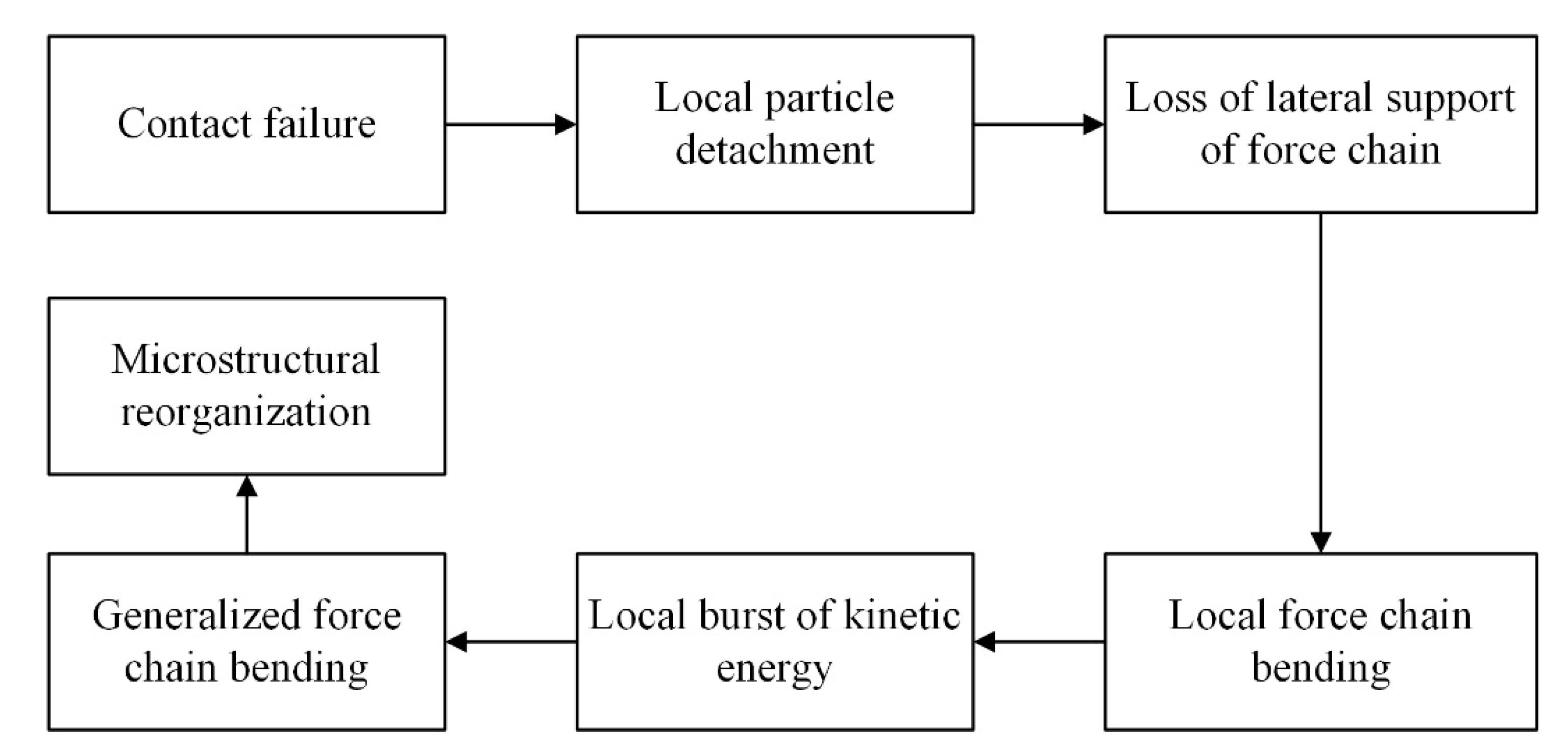
Water 13 00169 g010 550
Figure 10. The process of microstructural reorganization caused by hydraulic loading.
Figure 10. The process of microstructural reorganization caused by hydraulic loading.
Water 13 00169 g010
Water 13 00169 g011 550
Figure 11. Conceptual model of internal erosion mechanism on a microscopic scale.
Figure 11. Conceptual model of internal erosion mechanism on a microscopic scale.
Water 13 00169 g011
Table
Table 1. Particle contact properties considered in different studies. Kn, Ks, E, and G, respectively, represent the normal stiffness, tangential stiffness, Young’s modulus, and shear modulus.
Table 1. Particle contact properties considered in different studies. Kn, Ks, E, and G, respectively, represent the normal stiffness, tangential stiffness, Young’s modulus, and shear modulus.
PropertyCai [53]Guo [54]Zou [55] Hu [52] Abdoulaye [56] Tao [18,34] Kawano [24]
Kn (N/m)1.5 × 1052 × 1051 × 106—1 × 108——
Ks (N/m)1.0 × 1052 × 1051 × 106—1 × 108——
E (Pa)———7 × 1010—5 × 106/5 × 107—
G (Pa)——————2.7 × 1010
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Wang, X.; Tang, Y.; Huang, B.; Hu, T.; Ling, D. Review on Numerical Simulation of the Internal Soil Erosion Mechanisms Using the Discrete Element Method. Water 2021, 13, 169. https://doi.org/10.3390/w13020169

AMA Style

Wang X, Tang Y, Huang B, Hu T, Ling D. Review on Numerical Simulation of the Internal Soil Erosion Mechanisms Using the Discrete Element Method. Water. 2021; 13(2):169. https://doi.org/10.3390/w13020169

Chicago/Turabian Style

Wang, Xiukai, Yao Tang, Bo Huang, Tiantian Hu, and Daosheng Ling. 2021. "Review on Numerical Simulation of the Internal Soil Erosion Mechanisms Using the Discrete Element Method" Water 13, no. 2: 169. https://doi.org/10.3390/w13020169

APA Style

Wang, X., Tang, Y., Huang, B., Hu, T., & Ling, D. (2021). Review on Numerical Simulation of the Internal Soil Erosion Mechanisms Using the Discrete Element Method. Water, 13(2), 169. https://doi.org/10.3390/w13020169

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop