Two-Dimensional Flood Inundation Modeling in the Godavari River Basin, India—Insights on Model Output Uncertainty
Abstract
:1. Introduction
2. Materials and Methods
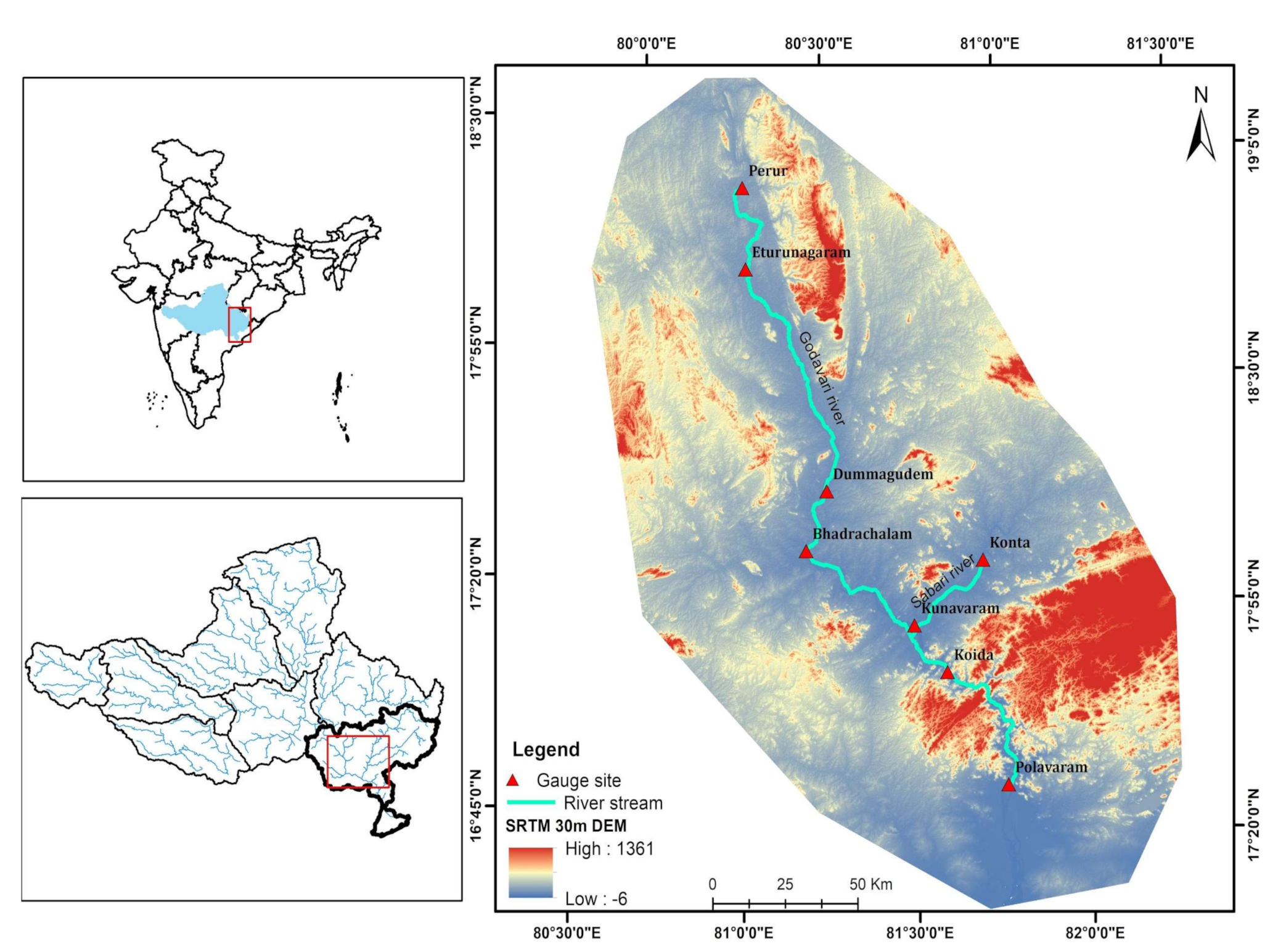
2.1. Study Area
2.2. Data
2.3. HEC-RAS 2D Model Setup
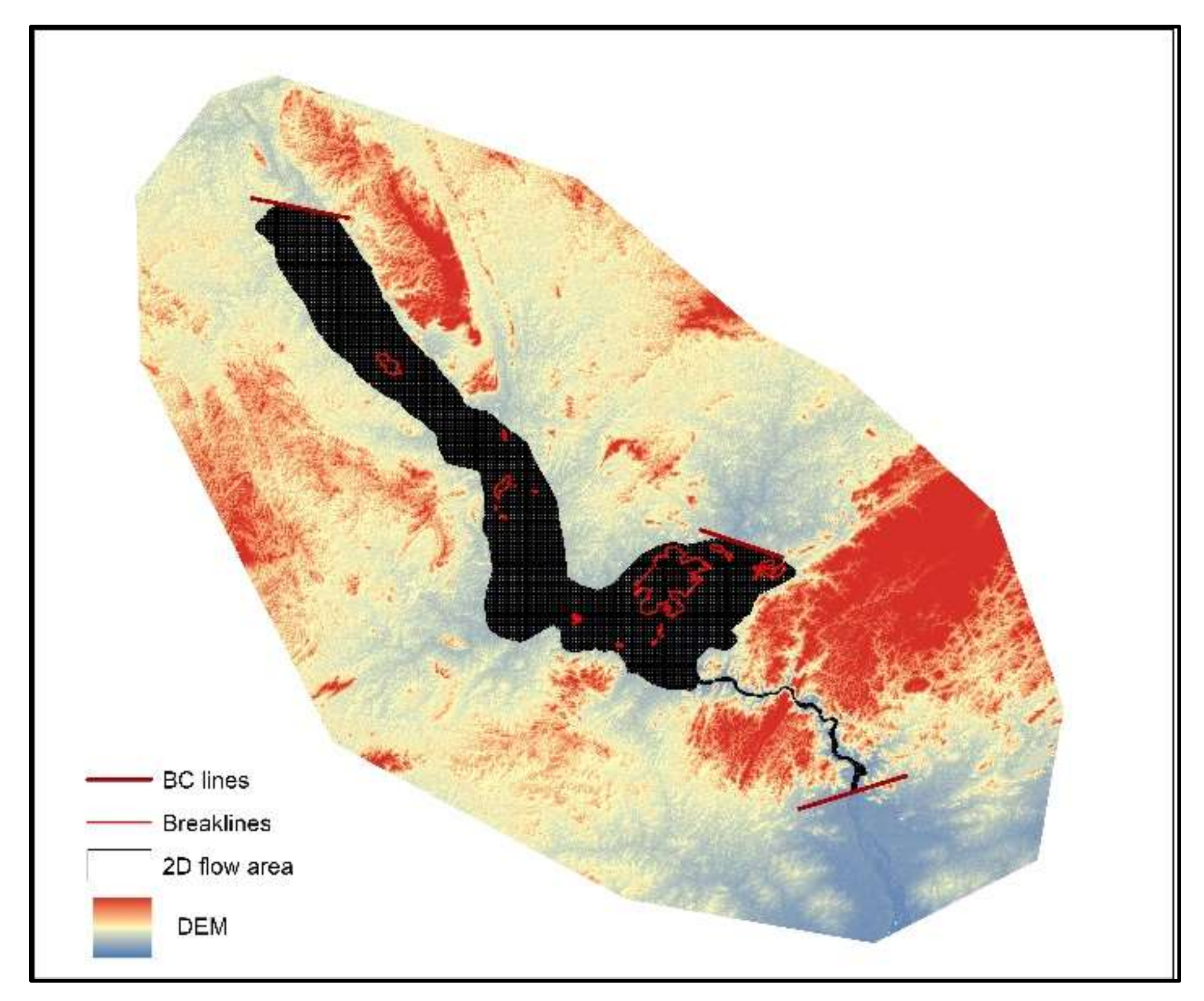
2.3.1. Developing 2D Flow Area
2.3.2. Manning’s n Values
2.3.3. Governing Equations
2.3.4. Model Parameters
2.3.5. Model Simulations
2.3.6. Model Performance
3. Results
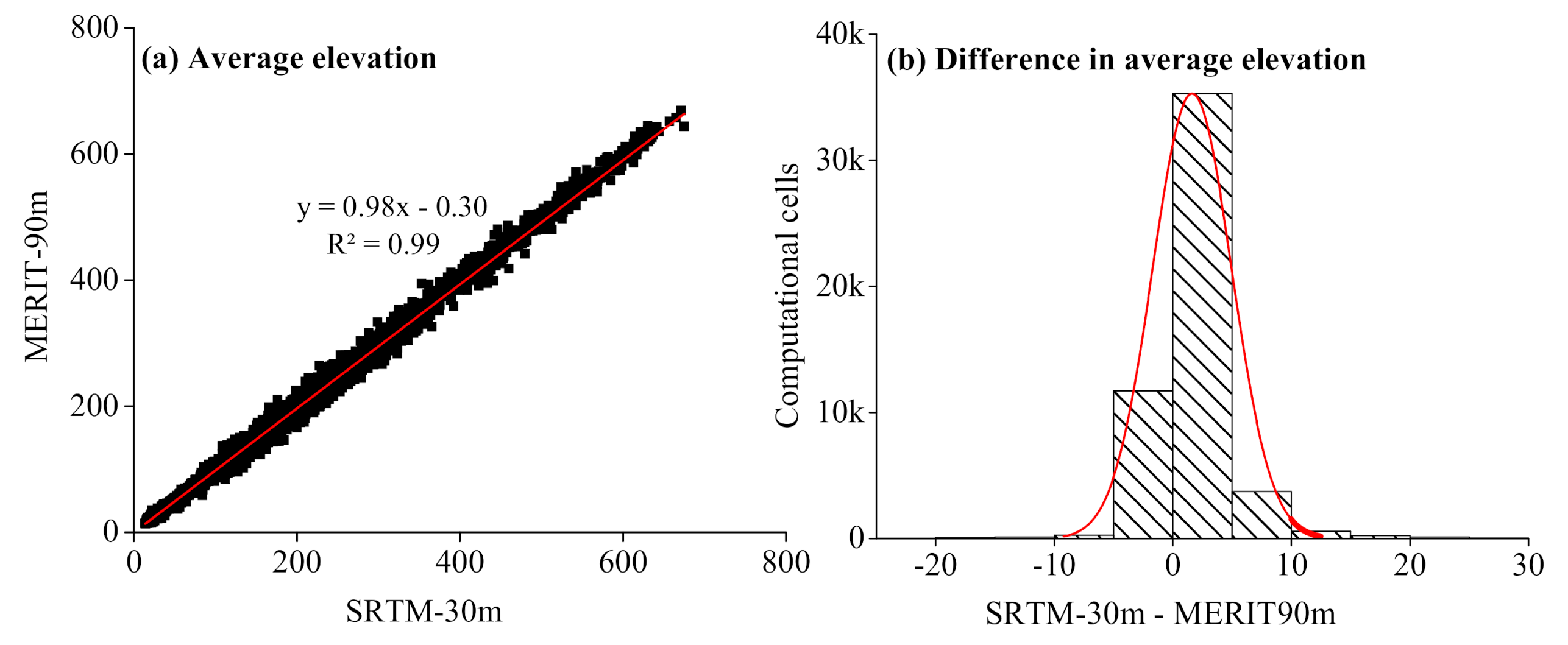
3.1. Comparison of DEMs
3.2. Model Calibration
3.3. Analysis of HError
3.4. Comparison of Stage Hydrographs
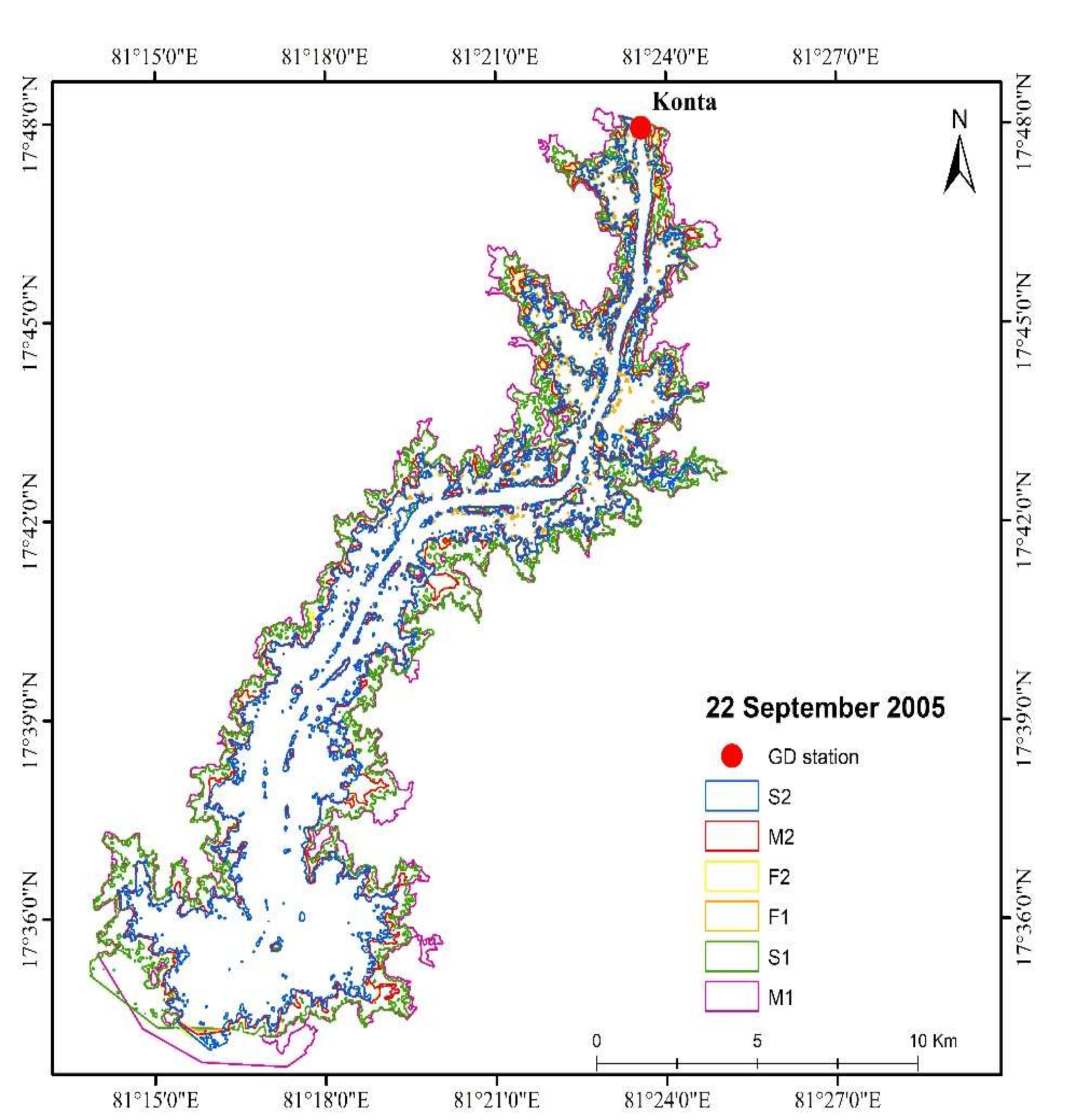
3.5. Comparison of Flood Inundation Maps for the Event E2
3.6. Model Performance
3.7. Event Hydrodynamics
3.8. Insights on the Uncertainty
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hooke, J.M.; Mant, J.M. Geomorphological impacts of a flood event on ephemeral channels in SE Spain. Geomorphology 2000, 34, 163–180. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; Ferraro, D.; Macchione, F.; Petaccia, G. Performances of the new HEC-RAS version 5 for 2-D hydrodynamic-based rainfall-runoff simulations at basin scale: Comparison with a state-of-the art model. Water 2020, 12, 2326. [Google Scholar] [CrossRef]
- Pender, G.; Néelz, S. Use of computer models of flood inundation to facilitate communication in flood risk management. Environ. Hazards 2007, 7, 106–114. [Google Scholar] [CrossRef]
- Rampinelli, C.G.; Knack, I.; Smith, T. Flood mapping uncertainty from a restoration perspective: A practical case study. Water 2020, 12, 1948. [Google Scholar] [CrossRef]
- Bates, P.D.; Pappenberger, F.; Romanowicz, R.J. Uncertainty in flood inundation modelling. In Applied Uncertainty Analysis for Flood Risk Management; Imperial College Press: London, UK, 2014. [Google Scholar]
- Pappenberger, F.; Beven, K.; Horritt, M.; Blazkova, S. Uncertainty in the calibration of effective roughness parameters in HEC-RAS using inundation and downstream level observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- Willis, T.; Wright, N.; Sleigh, A. Systematic analysis of uncertainty in 2D flood inundation models. Environ. Model. Softw. 2019, 122. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Merwade, V.; Olivera, F.; Arabi, M.; Edleman, S. Uncertainty in flood inundation mapping: Current issues and future directions. J. Hydrol. Eng. 2008, 13, 608–620. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Merwade, V.; Jafarzadegan, K. Investigating the role of model structure and surface roughness in generating flood inundation extents using one- and two-dimensional hydraulic models. J. Flood Risk Manag. 2019, 12, e12347. [Google Scholar] [CrossRef] [Green Version]
- Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
- Liu, Z.; Merwade, V. Accounting for model structure, parameter and input forcing uncertainty in flood inundation modeling using Bayesian model averaging. J. Hydrol. 2018, 565, 138–149. [Google Scholar] [CrossRef]
- Todini, E. Predictive uncertainty assessment in real time flood forecasting: Part of NATO Science for Peace and Security Series. In Uncertainties in Environmental Modelling and Consequences for Policy Making; Springer: Dordrecht, The Netherlands, 2009; pp. 205–228. [Google Scholar] [CrossRef]
- Aghakouchak, A.; Nakhjiri, N.; Habib, E. An educational model for ensemble streamflow simulation and uncertainty analysis. Hydrol. Earth Syst. Sci. 2013, 17, 445–452. [Google Scholar] [CrossRef] [Green Version]
- Harrigan, S.; Prudhomme, C.; Parry, S.; Smith, K.; Tanguy, M. Benchmarking ensemble streamflow prediction skill in the UK. Hydrol. Earth Syst. Sci. 2018, 22, 2023–2039. [Google Scholar] [CrossRef] [Green Version]
- Schick, S.; Rössler, O.; Weingartner, R. Monthly streamflow forecasting at varying spatial scales in the Rhine basin. Hydrol. Earth Syst. Sci. 2018, 22, 929–942. [Google Scholar] [CrossRef] [Green Version]
- Demeritt, D.; Nobert, S.; Cloke, H.L.; Pappenberger, F. The European Flood Alert System and the communication, perception, and use of ensemble predictions for operational flood risk management. Hydrol. Process. 2013, 27, 147–157. [Google Scholar] [CrossRef]
- Alfieri, L.; Pappenberger, F.; Wetterhall, F.; Haiden, T.; Richardson, D.; Salamon, P. Evaluation of ensemble streamflow predictions in Europe. J. Hydrol. 2014, 517, 913–922. [Google Scholar] [CrossRef] [Green Version]
- Bischiniotis, K.; van den Hurk, B.; Zsoter, E.; Coughlan de Perez, E.; Grillakis, M.; Aerts, J.C.J.H. Evaluation of a global ensemble flood prediction system in Peru. Hydrol. Sci. J. 2019, 64, 1171–1189. [Google Scholar] [CrossRef] [Green Version]
- Fleischmann, A.S.; Paiva, R.C.D.; Collischonn, W.; Siqueira, V.A.; Paris, A.; Moreira, D.M.; Papa, F.; Bitar, A.A.; Parrens, M.; Aires, F.; et al. Trade-Offs Between 1-D and 2-D Regional River Hydrodynamic Models. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Neelz, S.; Pender, G. Desktop Review of 2D Hydraulic Modelling Packages; Environment Agency: Bristol, UK, 2009. [Google Scholar]
- Bates, P.D.; De Roo, A.P.J. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Patro, S.; Chatterjee, C.; Mohanty, S.; Singh, R.; Raghuwanshi, N.S. Flood inundation modeling using MIKE FLOOD and remote sensing data. J. Indian Soc. Remote Sens. 2009, 37, 107–118. [Google Scholar] [CrossRef]
- Sampson, C.C.; Smith, A.M.; Bates, P.B.; Neal, J.C.; Alfieri, L.; Freer, J.E. A high-resolution global flood hazard model. Water Resour. Res. 2015, 51, 7358–7381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yamazaki, D.; Kanae, S.; Kim, H.; Oki, T. A physically based description of floodplain inundation dynamics in a global river routing model. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Schumann, G.J.P.; Neal, J.C.; Voisin, N.; Andreadis, K.M.; Pappenberger, F.; Phanthuwongpakdee, N.; Hall, A.C.; Bates, P.D. A first large-scale flood inundation forecasting model. Water Resour. Res. 2013, 49, 6248–6257. [Google Scholar] [CrossRef]
- Abily, M.; Bertrand, N.; Delestre, O.; Gourbesville, P.; Duluc, C.-M. Spatial Global Sensitivity Analysis of High Resolution classified topographic data use in 2D urban flood modelling. Environ. Model. Softw. 2016, 77, 183–195. [Google Scholar] [CrossRef] [Green Version]
- Baugh, C.A.; Bates, P.D.; Schumann, G.; Trigg, M.A. SRTM vegetation removal and hydrodynamic modeling accuracy. Water Resour. Res. 2013, 49, 5276–5289. [Google Scholar] [CrossRef] [Green Version]
- Pappenberger, F.; Matgen, P.; Beven, K.J.; Henry, J.B.; Pfister, L.; Fraipont, P. Influence of uncertain boundary conditions and model structure on flood inundation predictions. Adv. Water Resour. 2006, 29, 1430–1449. [Google Scholar] [CrossRef]
- Sampson, C.C.; Bates, P.D.; Neal, J.C.; Horritt, M.S. An automated routing methodology to enable direct rainfall in high resolution shallow water models. Hydrol. Process. 2013, 27, 467–476. [Google Scholar] [CrossRef]
- Sanders, B.F. Evaluation of on-line DEMs for flood inundation modeling. Adv. Water Resour. 2007, 30, 1831–1843. [Google Scholar] [CrossRef]
- Casas, A.; Benito, G.; Thorndycraft, V.R.; Rico, M. The topographic data source of digital terrain models as a key element in the accuracy of hydraulic flood modelling. Earth Surf. Process. Landf. 2006, 31, 444–456. [Google Scholar] [CrossRef]
- Saksena, S.; Merwade, V. Incorporating the Effect of DEM Resolution and Accuracy for Improved Flood Inundation Mapping Integrated Flood Modeling for Improved Understanding of River-Floodplain Hydrodynamics View project Prediction in data-scarce regions: Regionalization and catchment classification from a general perspective View project Incorporating the effect of DEM resolution and accuracy for improved flood inundation mapping. Artic. J. Hydrol. 2015, 530. [Google Scholar] [CrossRef] [Green Version]
- Prakash Mohanty, M.; Nithya, S.; Nair, A.S.; Indu, J.; Ghosh, S.; Mohan Bhatt, C.; Srinivasa Rao, G.; Karmakar, S. Sensitivity of various topographic data in flood management: Implications on inundation mapping over large data-scarce regions. J. Hydrol. 2020, 590, 125523. [Google Scholar] [CrossRef]
- Yan, K.; Di Baldassarre, G.; Solomatine, D.P. Exploring the potential of SRTM topographic data for flood inundation modelling under uncertainty. J. Hydroinf. 2013, 15. [Google Scholar] [CrossRef]
- Haque, M.M.; Seidou, O.; Mohammadian, A.; Gado Djibo, A. Development of a time-varying MODIS/2D hydrodynamic model relationship between water levels and flooded areas in the Inner Niger Delta, Mali, West Africa. J. Hydrol. Reg. Stud. 2020, 30. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Aronica, G.; Beven, K. Bayesian updating of flood inundation likelihoods conditioned on flood extent data. Hydrol. Process. 2004, 18, 3347–3370. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Romanowicz, R.; Beven, K. Estimation of flood inundation probabilities as conditioned on event inundation maps. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Apel, H.; Aronica, G.T.; Kreibich, H.; Thieken, A.H. Flood risk analyses—How detailed do we need to be? Nat. Hazards 2009, 49, 79–98. [Google Scholar] [CrossRef]
- De Almeida, G.A.M.; Bates, P. Applicability of the local inertial approximation of the shallow water equations to flood modeling. Water Resour. Res. 2013, 49, 4833–4844. [Google Scholar] [CrossRef]
- Loi, N.K.; Liem, N.D.; Tu, L.H.; Hong, N.T.; Truong, C.D.; Tram, V.N.Q.; Nhat, T.T.; Anh, T.N.; Jeong, J. Automated procedure of real-time flood forecasting in Vu Gia—Thu Bon river basin, Vietnam by integrating SWAT and HEC-RAS models. J. Water Clim. Chang. 2019, 10, 535–545. [Google Scholar] [CrossRef]
- Ferguson, C.; Fenner, R. The impact of Natural Flood Management on the performance of surface drainage systems: A case study in the Calder Valley. J. Hydrol. 2020, 590, 125354. [Google Scholar] [CrossRef]
- Doong, D.J.; Lo, W.; Vojinovic, Z.; Lee, W.L.; Lee, S.P. Development of a new generation of flood inundation maps—A case study of the coastal city of Tainan, Taiwan. Water 2016, 8, 521. [Google Scholar] [CrossRef] [Green Version]
- Patel, D.P.; Ramirez, J.A.; Srivastava, P.K.; Bray, M.; Han, D. Assessment of flood inundation mapping of Surat city by coupled 1D/2D hydrodynamic modeling: A case application of the new HEC-RAS 5. Nat. Hazards 2017, 89, 93–130. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Rahimzadeh, O.; Bahremand, A.; Noura, N.; Mukolwe, M. Evaluating flood extent mapping of two hydraulic models, 1D HEC-RAS and 2D LISFLOOD-FP in comparison with aerial imagery observations in Gorgan flood plain, Iran. Nat. Resour. Model. 2019, 32, e12214. [Google Scholar] [CrossRef]
- Shustikova, I.; Domeneghetti, A.; Neal, J.C.; Bates, P.; Castellarin, A. Comparing 2D capabilities of HEC-RAS and LISFLOOD-FP on complex topography. Hydrol. Sci. J. 2019, 64, 1769–1782. [Google Scholar] [CrossRef]
- Neelz, S.; Pender, G. Benchmarking the Latest Generation of 2D Hydraulic Modelling Packages; Environment Agency: Bristol, UK, 2013. [Google Scholar]
- Hunter, N.M.; Bates, P.D.; Neelz, S.; Pender, G.; Villanueva, I.; Wright, N.G.; Liang, D.; Falconer, R.A.; Lin, B.; Waller, S.; et al. Benchmarking 2D hydraulic models for urban flooding. Proc. Inst. Civ. Eng. Water Manag. 2008, 161, 13–30. [Google Scholar] [CrossRef] [Green Version]
- Roberts, S.; Nielsen, O.; Gray, D.; Sexton, J. ANUGA User Manual; Geoscience Australia: Symonston, ACT, Australia, 2015. [Google Scholar]
- Savage, J.T.S.; Bates, P.; Freer, J.; Neal, J.; Aronica, G. When does spatial resolution become spurious in probabilistic flood inundation predictions? Hydrol. Process. 2016, 30, 2014–2032. [Google Scholar] [CrossRef] [Green Version]
- Jafarzadegan, K.; Merwade, V. A DEM-based approach for large-scale floodplain mapping in ungauged watersheds. J. Hydrol. 2017, 550, 650–662. [Google Scholar] [CrossRef]
- Yamazaki, D.; Baugh, C.A.; Bates, P.D.; Kanae, S.; Alsdorf, D.E.; Oki, T. Adjustment of a spaceborne DEM for use in floodplain hydrodynamic modeling. J. Hydrol. 2012, 436–437, 81–91. [Google Scholar] [CrossRef]
- Medeiros, S.C.; Hagen, S.C.; Weishampel, J.F. Comparison of floodplain surface roughness parameters derived from land cover data and field measurements. J. Hydrol. 2012, 452–453, 139–149. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Vatanchi, S.M.; Maghrebi, M.F. Uncertainty in Rating-Curves Due to Manning Roughness Coefficient. Water Resour. Manag. 2019, 33, 5153–5167. [Google Scholar] [CrossRef]
- Bellos, V.; Kourtis, I.M.; Moreno-Rodenas, A.; Tsihrintzis, V.A. Quantifying roughness coefficient uncertainty in urban flooding simulations through a simplified methodology. Water 2017, 9, 944. [Google Scholar] [CrossRef] [Green Version]
- Ozdemir, H.; Sampson, C.C.; De Almeida, G.A.M.; Bates, P.D. Evaluating scale and roughness effects in urban flood modelling using terrestrial LIDAR data. Hydrol. Earth Syst. Sci. 2013, 17, 4015–4030. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Qin, X. Uncertainty analysis for flood inundation modelling with a random floodplain roughness field. Environ. Syst. Res. 2014, 3, 9. [Google Scholar] [CrossRef] [Green Version]
- Praskievicz, S.; Carter, S.; Dhondia, J.; Follum, M. Flood-inundation modeling in an operational context: Sensitivity to topographic resolution and Manning’s n. J. Hydroinf. 2020, 22, 1338–1350. [Google Scholar] [CrossRef]
- Fent, I.; Putti, M.; Gregoretti, C.; Lanzoni, S. Modeling shallow water flows on general terrains. Adv. Water Resour. 2018, 121, 316–332. [Google Scholar] [CrossRef] [Green Version]
- Smart, G.M. Improving flood hazard prediction models. Int. J. River Basin Manag. 2018, 16, 449–456. [Google Scholar] [CrossRef]
- Freer, J.; Beven, K.; Ambroise, B. Bayesian estimation of uncertainty in runoff prediction and the value of data: An application of the GLUE approach. Water Resour. Res. 1996, 32, 2161–2173. [Google Scholar] [CrossRef]
- Hunter, N.M.; Bates, P.D.; Horritt, M.S.; de Roo, P.J.; Werner, M.G.F. Utility of different data types for calibrating flood inundation models within a GLUE framework. Hydrol. Earth Syst. Sci. 2005, 9, 412–430. [Google Scholar] [CrossRef]
- Jung, Y.; Merwade, V. Uncertainty Quantification in Flood Inundation Mapping Using Generalized Likelihood Uncertainty Estimate and Sensitivity Analysis. J. Hydrol. Eng. 2012, 17, 507–520. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.J.; Ratto, M.; Matgen, P. Multi-method global sensitivity analysis of flood inundation models. Adv. Water Resour. 2008, 31, 1–14. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.J.; Hunter, N.M.; Bates, P.D.; Gouweleeuw, B.T.; Thielen, J.; de Roo, A.P.J. Cascading model uncertainty from medium range weather forecasts (10 days) through a rainfall-runoff model to flood inundation predictions within the European Flood Forecasting System (EFFS). Hydrol. Earth Syst. Sci. 2005, 9, 381–393. [Google Scholar] [CrossRef] [Green Version]
- Di Mauro, C.; Hostache, R.; Matgen, P.; Pelich, R.; Chini, M.; van Leeuwen, P.J.; Nichols, N.; Blöschl, G. Assimilation of probabilistic flood maps from SAR data into a hydrologic-hydraulic forecasting model: A proof of concept. Hydrol. Earth Syst. Sci. 2020, 1–24. [Google Scholar] [CrossRef]
- De Luca, D.L.; Biondi, D. Bivariate return period for design hyetograph and relationship with T-year design flood peak. Water 2017, 9, 673. [Google Scholar] [CrossRef] [Green Version]
- Yue, S.; Rasmussen, P. Bivariate frequency analysis: Discussion of some useful concepts in hydrological application. Hydrol. Process. 2002, 16, 2881–2898. [Google Scholar] [CrossRef]
- Volpi, E.; Fiori, A. Design event selection in bivariate hydrological frequency analysis. Hydrol. Sci. J. 2012, 57, 1506–1515. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: Berlin/Heidelberg, Germany, 1998; Available online: https://www.springer.com/gp/book/9780387286594 (accessed on 5 January 2021).
- Krishna and Godavari Basin Organization, KGBO. Available online: http://cwc.gov.in/kgbo/home (accessed on 5 November 2020).
- Das, J.; Umamahesh, N.V. Downscaling Monsoon Rainfall over River Godavari Basin under Different Climate-Change Scenarios. Water Resour. Manag. 2016, 30, 5575–5587. [Google Scholar] [CrossRef]
- Garg, S.; Mishra, V. Role of extreme precipitation and initial hydrologic conditions on floods in Godavari river basin, India. Water Resour. Res. 2019, 55. [Google Scholar] [CrossRef]
- Raju, K.S.; Kumar, D.N. Impact of Climate Change on Water Resources With Modeling Techniques and Case Studies Introduction. In Impact of Climate Change on Water Resources: With Modeling Techniques and Case Studies; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–25. [Google Scholar]
- Mujumdar, P.P.; Nagesh Kumar, D. Floods in a Changing Climate: Hydrologic Modeling; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bhatt, C.M.; Rao, G.S.; Diwakar, P.G.; Dadhwal, V.K. Development of flood inundation extent libraries over a range of potential flood levels: A practical framework for quick flood response. Geomat. Nat. Hazards Risk 2017, 8, 384–401. [Google Scholar] [CrossRef] [Green Version]
- Amarnath, C.R.; Thatikonda, S. Study on backwater effect due to Polavaram Dam Project under different return periods. Water 2020, 12, 576. [Google Scholar] [CrossRef] [Green Version]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high-accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef] [Green Version]
- Farr, T.G.; Kobrick, M. Shuttle radar topography mission produces a wealth of data. Eos 2000, 81, 583–585. [Google Scholar] [CrossRef]
- Bhuvan. Thematic Data Dissemination, Free GIS Data, OGC Services, Clip and Ship. Available online: https://bhuvan-app1.nrsc.gov.in/thematic/thematic/index.php (accessed on 5 November 2020).
- McCuen, R.H. Hydrologic Analysis and Design; Prentice-Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Brunner, G. HEC-RAS River Analysis System, Hydraulic Reference Manual, Version 4.1; Hydrologic Engineering Center: Davis, CA, USA, 2010. [Google Scholar]
- Brunner, G.W. HEC-RAS River Analysis System, 2D Modeling User’s Manual Version 5.0; Hydrologic Engineering Center: Davis, CA, USA, 2016. [Google Scholar]
- De Moura, C.A.; Kubrusly, C.S. The Courant–Friedrichs–Lewy (CFL) Condition; Birkhäuser Boston: Cambridge, MA, USA, 2013. [Google Scholar]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Ghostine, R.; Mose, R.; Vazquez, J.; Ghenaim, A.; Grégoire, C. Two-Dimensional Simulation of Subcritical Flow at a Combining Junction: Luxury or Necessity? J. Hydraul. Eng. 2010, 136, 799–805. [Google Scholar] [CrossRef] [Green Version]
- Ghostine, R.; Vazquez, J.; Terfous, A.; Mose, R.; Ghenaim, A. Comparative study of 1D and 2D flow simulations at open-channel junctions. J. Hydraul. Res. 2012, 50, 164–170. [Google Scholar] [CrossRef]
- Roy, A.G.; Woldenberg, M.J. A Model for Changes in Channel form at a River Confluence. J. Geol. 1986, 94, 402–411. [Google Scholar] [CrossRef]
- Wang, X.; Yan, X.; Duan, H.; Liu, X.; Huang, E. Experimental study on the influence of river flow confluences on the open channel stage–discharge relationship. Hydrol. Sci. J. 2019, 64, 2025–2039. [Google Scholar] [CrossRef]
- Roca, M.; Martín-Vide, J.P.; Moreta, P.J.M. Modelling a torrential event in a river confluence. J. Hydrol. 2009, 364, 207–215. [Google Scholar] [CrossRef]







| Event | Perur | Konta | Polavaram | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| t (Days) | Qp (m3/s) | Hp (m) | Tp (Date) | Qp (m3/s) | Q*p (m3/s) | Tp (Date) | Qp (m3/s) | Hp (m) | Tp (Date) | |
| 22-07-1986 to 02-09-1986 (E1) | 42 | 62,889.13 | 87.42 | 15-08-1986 | 20,187.04 | 10,400.1 | 17-08-1986 | 57,310.57 | 28.017 | 16-08-1986 |
| 11-09-2005 to 28-09-2005 (E2) | 18 | 24,436.1 | 81.13 | 18-09-2005 | 8853.78 | 9224.6 | 20-09-2005 | 43,703.04 | 25.897 | 21-09-2005 |
| 10-06-2015 to 30-06-2015) (E3) | 21 | 22,779.00 | 80.08 | 22-06-2015 | 7468 | 9107.40 | 21-06-2015 | 22.82 | 22433.00 | 23-06-2015 |
| Metric | Equation | Range |
|---|---|---|
| Correlation coefficient, r | −1 to 1 | |
| Index of agreement, d | 0 to1 | |
| Mean Absolute Error, MAE | 0 to ∞ | |
| Root Mean Squared Error, RMSE | 0 to ∞ | |
| Percent bias, PBIAS | −∞ to ∞ | |
| Kling-Gupta Efficiency, KGE | −∞ to 1 |
| Metric | E1 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dummugudem | Koida | |||||||||||
| S1 | S2 | M1 | M2 | F1 | F2 | S1 | S2 | M1 | M2 | F1 | F2 | |
| r | 0.88 | 0.92 | 0.89 | 0.97 | 0.95 | 0.95 | 0.93 | 0.95 | 0.92 | 0.95 | 0.96 | 0.95 |
| KGE | 0.81 | 0.88 | 0.82 | 0.85 | 0.85 | 0.85 | 0.64 | 0.7 | 0.63 | 0.7 | 0.82 | 0.77 |
| d | 0.79 | 0.79 | 0.77 | 0.74 | 0.84 | 0.81 | 0.86 | 0.88 | 0.83 | 0.88 | 0.92 | 0.88 |
| MAE | 3.58 | 3.69 | 4.06 | 2.96 | 2.99 | 3.49 | 6.02 | 5.59 | 7.07 | 5.57 | 4.37 | 5.64 |
| RMSE | 4.07 | 3.95 | 4.5 | 3.25 | 3.2 | 3.67 | 7.11 | 6.33 | 8.08 | 6.32 | 4.81 | 6.11 |
| PBIAS | 7.8 | 8.2 | 9 | 5 | 6.5 | 7.7 | 87.6 | 77.9 | 99.4 | 77.8 | 59.1 | 75.2 |
| Metric | E2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dummugudem | Koida | |||||||||||
| S1 | S2 | M1 | M2 | F1 | F2 | S1 | S2 | M1 | M2 | F1 | F2 | |
| R | 0.98 | 0.98 | 0.97 | 0.98 | 0.98 | 0.97 | 0.88 | 0.92 | 0.87 | 0.91 | 0.93 | 0.93 |
| KGE | 0.98 | 0.7 | 0.79 | 0.77 | 0.66 | 0.74 | 0.39 | 0.7 | 0.33 | 0.66 | 0.68 | 0.68 |
| D | 0.97 | 0.89 | 0.93 | 0.93 | 0.87 | 0.95 | 0.68 | 0.83 | 0.64 | 0.78 | 0.85 | 0.79 |
| MAE | 0.69 | 0.99 | 1.16 | 0.79 | 1.04 | 0.64 | 7.91 | 4.76 | 8.86 | 5.71 | 4.37 | 5.29 |
| RMSE | 0.75 | 1.21 | 1.24 | 0.98 | 1.27 | 0.82 | 8.65 | 5.1 | 9.72 | 6.14 | 4.79 | 5.8 |
| PBIAS | 1.3 | −2 | 2 | −1.6 | −2 | −1 | 25.9 | 15 | 29.5 | 18.7 | 13.7 | 17.8 |
| Metric | E3 | |||||
|---|---|---|---|---|---|---|
| Bhadrachalam | ||||||
| S1 | S2 | M1 | M2 | F1 | F2 | |
| R | 0.93 | 0.96 | 0.94 | 0.96 | 0.96 | 0.96 |
| KGE | 0.78 | 0.94 | 0.85 | 0.94 | 0.94 | 0.95 |
| D | 0.96 | 0.97 | 0.96 | 0.98 | 0.97 | 0.98 |
| MAE | 1.05 | 0.76 | 1.04 | 0.7 | 0.77 | 0.7 |
| RMSE | 1.53 | 1.12 | 1.42 | 0.89 | 1.13 | 0.9 |
| PBIAS | −0.1 | −1.2 | 1.1 | 0 | −1.2 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, V.C.; Regonda, S.K. Two-Dimensional Flood Inundation Modeling in the Godavari River Basin, India—Insights on Model Output Uncertainty. Water 2021, 13, 191. https://doi.org/10.3390/w13020191
Sharma VC, Regonda SK. Two-Dimensional Flood Inundation Modeling in the Godavari River Basin, India—Insights on Model Output Uncertainty. Water. 2021; 13(2):191. https://doi.org/10.3390/w13020191
Chicago/Turabian StyleSharma, Vimal Chandra, and Satish Kumar Regonda. 2021. "Two-Dimensional Flood Inundation Modeling in the Godavari River Basin, India—Insights on Model Output Uncertainty" Water 13, no. 2: 191. https://doi.org/10.3390/w13020191
APA StyleSharma, V. C., & Regonda, S. K. (2021). Two-Dimensional Flood Inundation Modeling in the Godavari River Basin, India—Insights on Model Output Uncertainty. Water, 13(2), 191. https://doi.org/10.3390/w13020191






