Hydrogeochemical Characterization and Its Seasonal Changes of Groundwater Based on Self-Organizing Maps
Abstract
:1. Introduction
2. Description of the Study Area
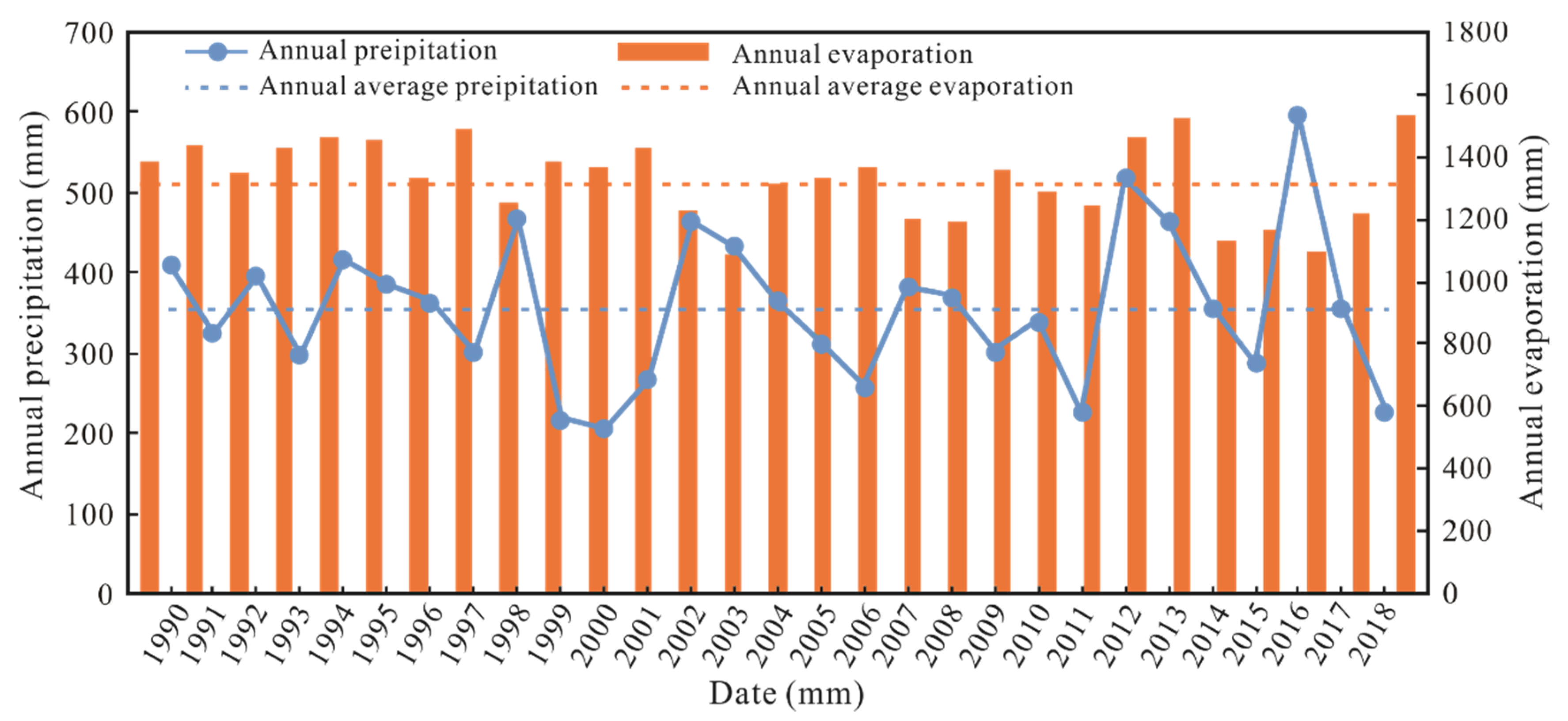
2.1. Study Location and Climate
2.2. Hydrogeological Setting
3. Data and Methods
3.1. Sample Collection and Analysis
3.2. Methods
4. Results and Discussion
4.1. Hydrochemical Characteristics of Groundwater
4.2. Formation of the Hydrochemical Composition of the Groundwater
4.3. Analysis of Mineral Dissolution
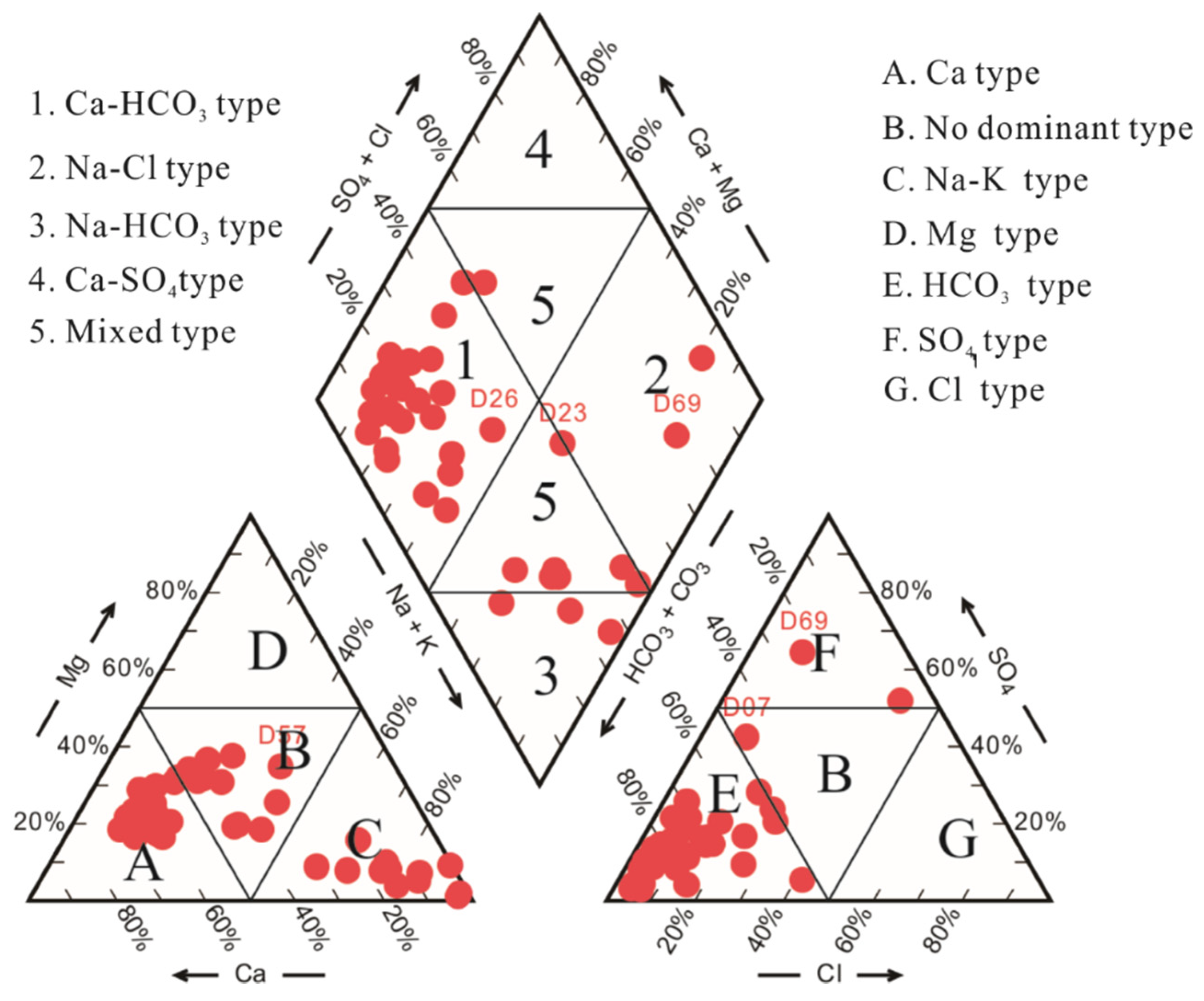
4.4. Hydrochemical Facies of Groundwater
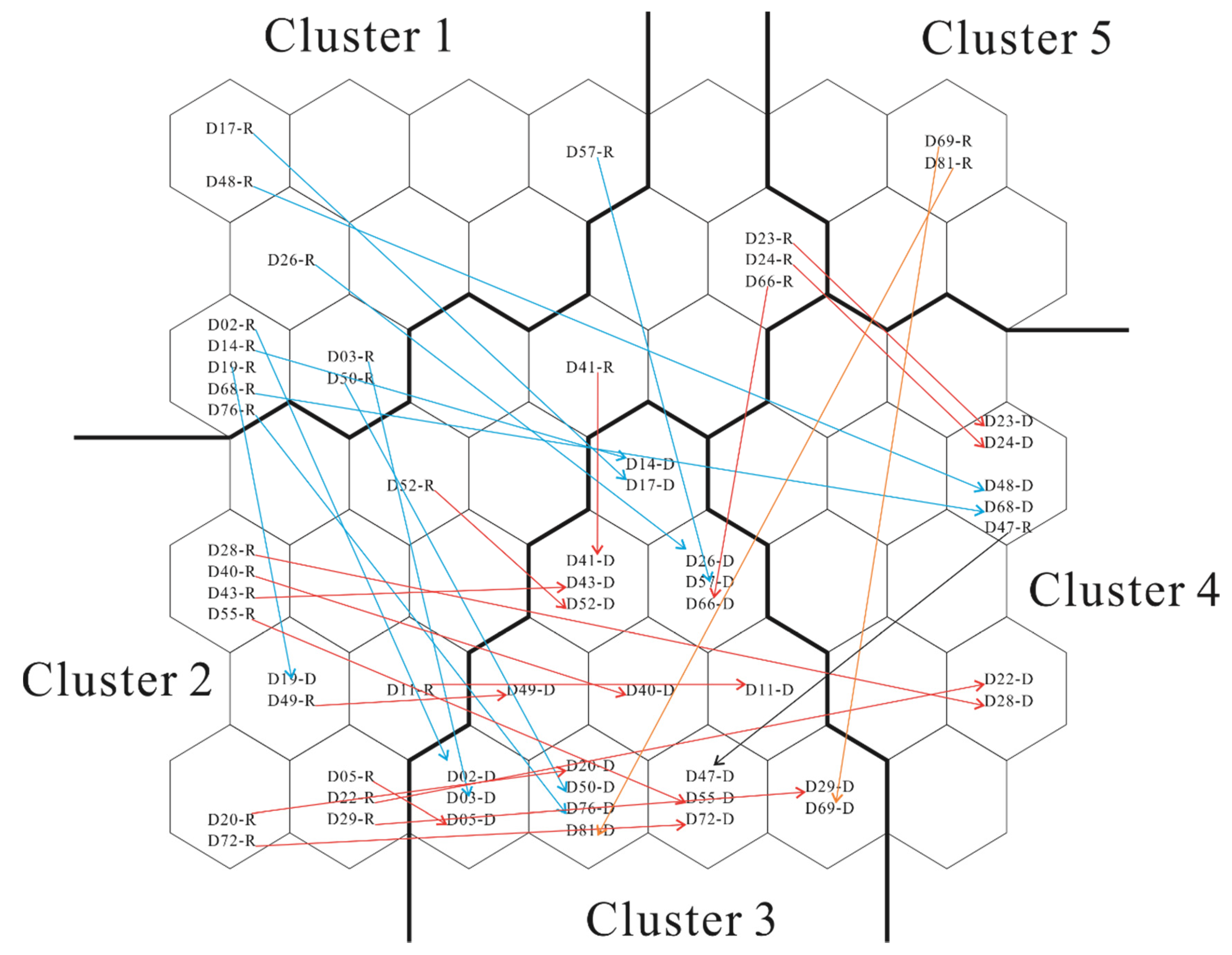
4.5. SOM-Based Clustering
4.6. Analysis of Clustered Hydrochemical Characteristics
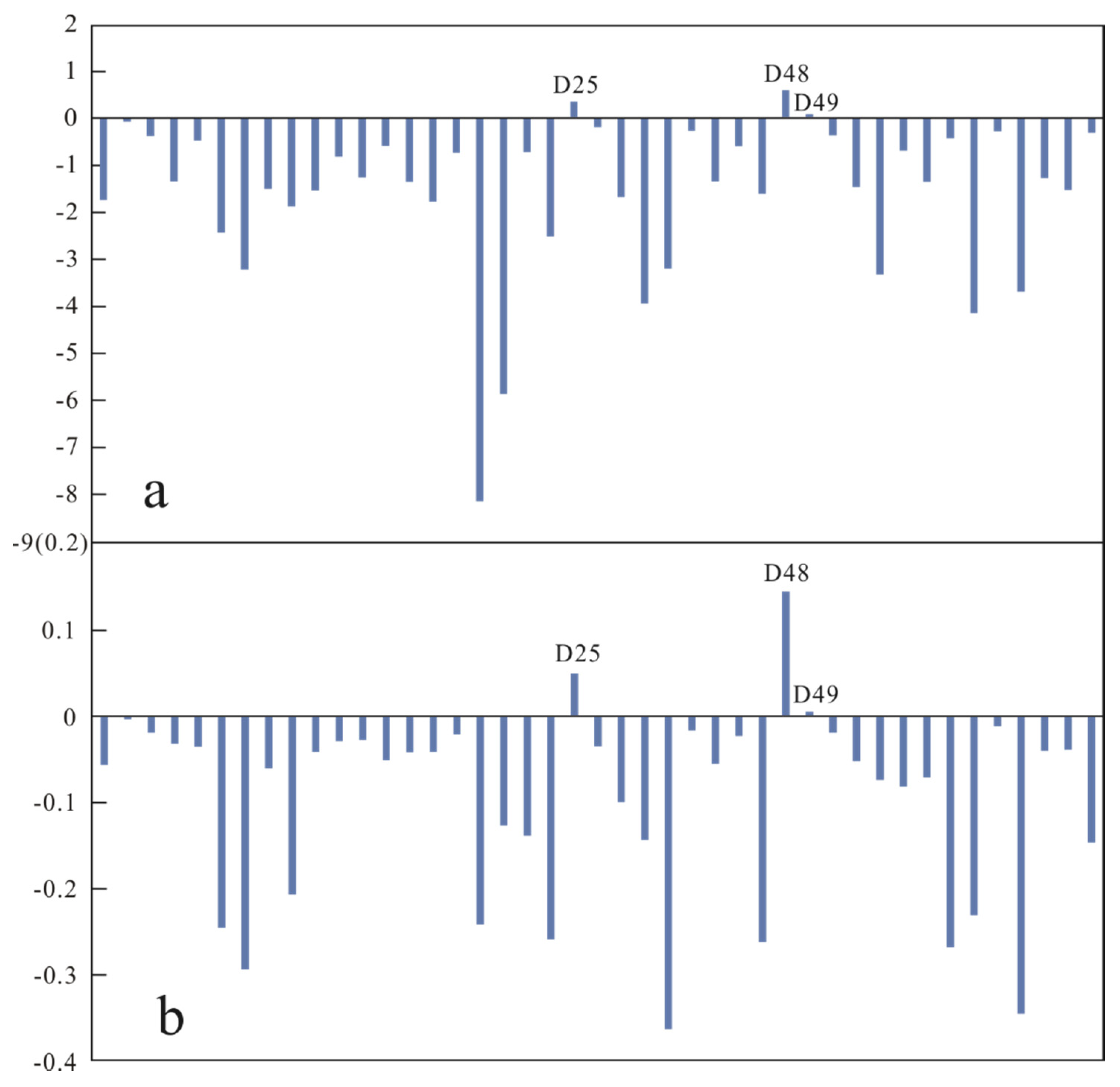
4.7. Seasonal Variability
5. Conclusions
- (1)
- The formation of the hydrochemical composition of the groundwater in the study area during the rainy and dry seasons is controlled by water–rock interactions and cation exchange. Three hydrochemical facies, HCO3–Ca type, HCO3–Na type, and Cl–Na type, dominate the groundwater in the study area, whose composition is controlled primarily by silicate weathering and carbonate dissolution. Halite, gypsum, and fluorite are the dominant sources of ions in the groundwater in the study area. Dolomite and calcite exist mostly in the form of precipitates or reactive minerals in the groundwater of the study area, in which a small amount of feldspar is dissolved.
- (2)
- SOMs were used to cluster the data of the hydrochemical parameters of the groundwater in the rainy and wet seasons. Based on the QE, the TE, and the empirical equation, the number of neurons was optimized to 7 × 7. The results derived from the neuron matrices are consistent with those of the Pearson correlation analysis. The number of clusters was optimized through DBI minimization. The groundwater samples collected from the study area during the rainy and dry seasons are grouped into five clusters, with Ca2+, Mg2+, K+, and HCO3− identified as the dominant ions in cluster 1 and Na+, K+, Cl−, and SO42− identified as the dominant ions in cluster 5.
- (3)
- HCO3–Ca type is the hydrochemical facies of the groundwater samples in clusters 1, 2, and 3, while HCO3–Na type and Cl–Na type are the hydrochemical facies of the groundwater samples in clusters 4 and 5, respectively. Cation exchange is the dominant factor controlling the formation of the hydrochemical composition of the groundwater at the sites where the groundwater samples in cluster 4 were collected, compared to water–rock interactions for the sites where the groundwater samples in other clusters were collected. The clustering of 30 sampling sites changes with the transition from the rainy season to the dry season. Of these sites, significant seasonal variability was observed in the hydrochemical characteristics of the groundwater at nine sites. Overall, there was no significant seasonal variability in the hydrochemical characteristics of the groundwater in the study area.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Sample | Ca2+ | Mg2+ | Na+ | K+ | HCO3− | SO42− | Cl− | CO32− |
|---|---|---|---|---|---|---|---|---|
| D02-R | 42.80 | 15.60 | 33.80 | 1.10 | 93.50 | 94.80 | 16.70 | 0.00 |
| D03-R | 35.00 | 16.80 | 15.40 | 2.04 | 129.00 | 48.40 | 15.70 | 0.00 |
| D04-R | 44.20 | 16.50 | 23.10 | 2.50 | 203.00 | 40.50 | 20.70 | 0.00 |
| D05-R | 37.40 | 10.70 | 9.94 | 1.37 | 142.00 | 29.30 | 5.10 | 0.00 |
| D07-R | 116.00 | 27.40 | 58.40 | 1.70 | 204.00 | 255.00 | 43.30 | 0.00 |
| D09-R | 10.70 | 2.89 | 121.00 | 1.01 | 197.00 | 48.50 | 35.20 | 6.85 |
| D10-R | 13.50 | 6.67 | 120.00 | 1.15 | 244.00 | 42.20 | 27.60 | 14.10 |
| D11-R | 30.90 | 14.10 | 31.60 | 1.11 | 156.00 | 27.80 | 9.11 | 8.98 |
| D13-R | 16.80 | 7.62 | 54.40 | 0.56 | 177.00 | 22.60 | 4.67 | 8.98 |
| D14-R | 76.70 | 13.30 | 18.50 | 0.59 | 220.00 | 51.90 | 8.30 | 10.00 |
| D15-R | 46.60 | 16.00 | 18.30 | 2.09 | 192.00 | 20.20 | 8.17 | 8.08 |
| D16-R | 50.10 | 10.70 | 10.60 | 1.20 | 188.00 | 21.20 | 5.28 | 5.39 |
| D17-R | 62.20 | 16.20 | 18.60 | 1.06 | 209.00 | 45.40 | 10.90 | 8.78 |
| D18-R | 50.90 | 12.30 | 16.90 | 0.85 | 205.00 | 23.20 | 6.97 | 0.00 |
| D19-R | 45.30 | 13.60 | 19.40 | 1.09 | 201.00 | 23.70 | 8.43 | 0.00 |
| D20-R | 41.70 | 11.00 | 12.80 | 0.90 | 109.00 | 36.30 | 7.94 | 4.64 |
| D21-R | 16.20 | 4.65 | 67.50 | 0.41 | 181.00 | 24.80 | 7.14 | 7.46 |
| D22-R | 18.70 | 5.14 | 66.80 | 0.64 | 182.00 | 25.20 | 4.10 | 10.70 |
| D23-R | 5.38 | 1.30 | 139.00 | 0.61 | 221.00 | 54.20 | 37.30 | 11.00 |
| D24-R | 5.12 | 0.05 | 177.00 | 0.67 | 237.00 | 94.50 | 37.90 | 13.30 |
| D25-R | 79.00 | 35.30 | 37.80 | 2.51 | 189.00 | 60.80 | 61.20 | 10.30 |
| D26-R | 19.10 | 22.30 | 84.50 | 1.08 | 181.00 | 20.50 | 59.60 | 12.20 |
| D28-R | 11.70 | 4.72 | 79.50 | 0.40 | 198.00 | 28.00 | 5.67 | 11.60 |
| D29-R | 36.60 | 11.60 | 17.20 | 0.66 | 132.00 | 21.00 | 7.68 | 9.03 |
| D39-R | 6.22 | 1.88 | 137.00 | 0.96 | 213.00 | 58.90 | 31.80 | 12.30 |
| D40-R | 25.70 | 21.90 | 21.00 | 1.16 | 144.00 | 13.10 | 13.60 | 7.65 |
| D41-R | 42.50 | 25.30 | 28.90 | 0.88 | 155.00 | 41.50 | 24.00 | 7.73 |
| D43-R | 39.20 | 21.00 | 13.10 | 1.14 | 179.00 | 16.50 | 11.90 | 6.37 |
| D47-R | 33.80 | 10.50 | 12.80 | 0.77 | 114.00 | 24.80 | 5.71 | 5.51 |
| D48-R | 3.30 | 1.66 | 127.00 | 0.27 | 202.00 | 42.80 | 43.80 | 9.91 |
| D49-R | 54.90 | 17.70 | 25.40 | 1.43 | 155.00 | 61.00 | 45.00 | 4.84 |
| D50-R | 37.00 | 13.90 | 13.50 | 1.29 | 93.00 | 15.70 | 15.60 | 5.09 |
| D52-R | 43.50 | 20.10 | 23.10 | 2.41 | 146.00 | 57.30 | 27.00 | 9.76 |
| D55-R | 44.70 | 12.10 | 15.30 | 1.32 | 148.00 | 17.40 | 9.48 | 6.96 |
| D57-R | 30.10 | 17.70 | 24.20 | 0.75 | 172.00 | 7.90 | 5.36 | 10.30 |
| D61-R | 45.70 | 14.80 | 15.90 | 5.75 | 180.00 | 9.51 | 20.90 | 12.40 |
| D66-R | 25.30 | 27.10 | 39.50 | 0.83 | 158.00 | 23.90 | 22.90 | 10.60 |
| D68-R | 11.30 | 13.40 | 117.00 | 0.72 | 255.00 | 43.70 | 23.00 | 18.20 |
| D69-R | 19.90 | 11.30 | 21.10 | 0.78 | 122.00 | 8.57 | 4.57 | 8.08 |
| D72-R | 31.80 | 14.70 | 13.00 | 1.18 | 122.00 | 37.70 | 6.24 | 7.91 |
| D76-R | 32.90 | 11.40 | 14.60 | 1.61 | 114.00 | 39.10 | 8.30 | 5.57 |
| D81-R | 30.30 | 15.80 | 12.20 | 0.43 | 110.00 | 12.90 | 12.80 | 4.71 |
| D02-D | 88.00 | 14.80 | 32.90 | 1.31 | 270.00 | 78.90 | 12.50 | 0.00 |
| D03-D | 68.10 | 19.70 | 12.80 | 1.99 | 241.00 | 35.20 | 13.80 | 0.00 |
| D04-D | 63.30 | 14.10 | 16.70 | 2.42 | 247.00 | 31.30 | 13.90 | 0.00 |
| D05-D | 49.30 | 10.10 | 10.10 | 1.55 | 182.00 | 23.50 | 4.98 | 0.00 |
| D07-D | 147.00 | 23.50 | 59.60 | 1.91 | 323.00 | 228.00 | 41.70 | 0.00 |
| D09-D | 18.20 | 5.25 | 95.50 | 0.78 | 220.00 | 36.00 | 28.10 | 0.00 |
| D10-D | 10.50 | 5.45 | 122.00 | 0.72 | 261.00 | 47.10 | 29.10 | 0.00 |
| D11-D | 41.20 | 16.70 | 22.50 | 1.40 | 187.00 | 30.20 | 9.56 | 0.00 |
| D13-D | 15.30 | 5.09 | 92.30 | 0.68 | 227.00 | 38.00 | 32.40 | 0.00 |
| D14-D | 89.50 | 13.10 | 24.20 | 0.76 | 277.00 | 62.70 | 9.85 | 0.00 |
| D15-D | 35.00 | 15.40 | 15.20 | 1.97 | 234.00 | 19.90 | 9.49 | 0.00 |
| D16-D | 56.20 | 11.00 | 10.40 | 1.24 | 216.00 | 20.50 | 5.16 | 0.00 |
| D17-D | 87.70 | 40.00 | 64.20 | 9.73 | 481.00 | 55.40 | 46.60 | 0.00 |
| D18-D | 54.00 | 10.70 | 16.50 | 0.96 | 206.00 | 18.00 | 7.43 | 0.00 |
| D19-D | 74.70 | 13.20 | 19.80 | 1.12 | 301.00 | 21.20 | 7.56 | 0.00 |
| D20-D | 67.20 | 10.70 | 12.30 | 0.93 | 214.00 | 26.30 | 7.62 | 0.00 |
| D21-D | 18.40 | 3.61 | 59.00 | 0.48 | 190.00 | 18.00 | 6.50 | 0.00 |
| D22-D | 36.00 | 9.47 | 34.30 | 0.57 | 192.00 | 14.30 | 5.08 | 0.00 |
| D23-D | 67.10 | 11.40 | 152.00 | 0.95 | 301.00 | 112.00 | 89.10 | 0.00 |
| D24-D | 21.80 | 9.04 | 131.00 | 1.04 | 294.00 | 55.50 | 37.60 | 0.00 |
| D25-D | 95.20 | 34.30 | 35.90 | 2.42 | 271.00 | 58.40 | 59.40 | 0.00 |
| D26-D | 58.30 | 29.00 | 92.90 | 1.10 | 333.00 | 38.20 | 79.10 | 0.00 |
| D28-D | 55.40 | 15.70 | 55.90 | 0.59 | 247.00 | 30.60 | 21.10 | 0.00 |
| D29-D | 29.80 | 8.63 | 38.30 | 0.61 | 183.00 | 14.60 | 7.88 | 0.00 |
| D39-D | 3.37 | 0.72 | 138.00 | 0.75 | 202.00 | 58.10 | 33.10 | 14.60 |
| D40-D | 56.40 | 21.90 | 22.70 | 0.84 | 231.00 | 22.00 | 18.60 | 0.00 |
| D41-D | 40.10 | 21.60 | 24.20 | 1.33 | 252.00 | 6.26 | 10.90 | 6.29 |
| D43-D | 52.00 | 16.60 | 14.20 | 1.39 | 246.00 | 9.42 | 9.79 | 0.00 |
| D47-D | 2.51 | 1.18 | 132.00 | 0.38 | 198.00 | 93.80 | 50.80 | 11.00 |
| D48-D | 119.00 | 27.60 | 39.50 | 1.80 | 330.00 | 102.00 | 104.00 | 0.00 |
| D49-D | 63.90 | 14.10 | 13.20 | 1.40 | 187.00 | 15.60 | 16.10 | 0.00 |
| D50-D | 69.50 | 15.90 | 19.20 | 2.45 | 254.00 | 49.20 | 15.90 | 0.00 |
| D52-D | 54.40 | 11.70 | 22.10 | 2.31 | 236.00 | 22.60 | 9.92 | 0.00 |
| D55-D | 40.20 | 17.40 | 24.00 | 0.78 | 226.00 | 8.02 | 5.74 | 0.00 |
| D57-D | 39.10 | 32.30 | 68.50 | 2.04 | 327.00 | 14.20 | 41.80 | 12.30 |
| D61-D | 49.90 | 32.10 | 42.00 | 4.38 | 300.00 | 71.60 | 19.70 | 0.00 |
| D66-D | 27.00 | 14.30 | 115.00 | 0.75 | 351.00 | 48.80 | 22.50 | 0.00 |
| D68-D | 88.00 | 17.90 | 19.30 | 0.52 | 321.00 | 35.50 | 15.60 | 0.00 |
| D69-D | 40.10 | 12.60 | 410.00 | 4.07 | 286.00 | 646.00 | 88.40 | 7.08 |
| D72-D | 58.30 | 11.10 | 16.70 | 1.48 | 221.00 | 31.70 | 8.00 | 0.00 |
| D76-D | 63.50 | 16.20 | 18.80 | 0.93 | 298.00 | 7.74 | 7.82 | 0.00 |
| D81-D | 135.00 | 20.70 | 834.00 | 4.72 | 219.00 | 1120.00 | 641.00 | 0.00 |
References
- Ben-Hur, M.; Cohen, R.; Danon, M.; Nachshon, U.; Katra, I. Evaluation of groundwater salinization risk following application of anti-dust emission solutions on Unpaved Roads in arid and semiarid regions. Appl. Sci. 2021, 11, 1771. [Google Scholar] [CrossRef]
- Wu, C.; Fang, C.; Wu, X.; Zhu, G.; Zhang, Y. Hydrogeochemical characterization and quality assessment of groundwater using self-organizing maps in the Hangjinqi gasfield area, Ordos Basin, NW China. Geosci. Front. 2021, 12, 781–790. [Google Scholar] [CrossRef]
- Su, Y.; Yang, F.; Chen, Y.; Zhang, P.; Zhang, X. Optimization of groundwater exploitation in an irrigation area in the arid upper Peacock River, NW China: Implications for sustainable agriculture and ecology. Sustainability 2021, 13, 8903. [Google Scholar] [CrossRef]
- Su, H.; Kang, W.; Xu, Y.; Wang, J. Assessment of Groundwater Quality and Health Risk in the Oil and Gas Field of Dingbian County, Northwest China. Expo. Health 2017, 9, 227–242. [Google Scholar] [CrossRef]
- Wu, C.; Fang, C.; Wu, X.; Zhu, G. Health-Risk Assessment of arsenic and groundwater quality classification using random forest in the Yanchi region of Northwest China. Expo. Health 2020, 12, 761–774. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, H.; Xing, S.; Liu, H. Hydrogeochemical and geothermal controls on the formation of high fluoride groundwater. J. Hydrol. 2021, 598, 126372. [Google Scholar] [CrossRef]
- Cendón, D.I.; Haldorsen, S.; Chen, J.; Hankin, S.; Nogueira, G.E.H.; Momade, F.; Achimo, M.; Muiuane, E.; Mugabe, J.; Stigter, T.Y. Hydrogeochemical aquifer characterization and its implication for groundwater development in the Maputo district, Mozambique. Quat. Int. 2020, 547, 113–126. [Google Scholar] [CrossRef]
- Wu, C.; Wu, X.; Qian, C.; Zhu, G. Hydrogeochemistry and groundwater quality assessment of high fluoride levels in the Yanchi endorheic region, northwest China. Appl. Geochem. 2018, 98, 404–417. [Google Scholar] [CrossRef]
- Liang, K. Quantifying streamflow variations in ungauged lake basins by integrating remote sensing and water balance modelling: A case study of the erdos larus relictus national nature reserve, China. Remote Sens. 2017, 9, 588. [Google Scholar] [CrossRef] [Green Version]
- Qian, C.; Wu, X.; Mu, W.-P.; Fu, R.-Z.; Zhu, G.; Wang, Z.-R.; Wang, D.-D. Hydrogeochemical characterization and suitability assessment of groundwater in an agro-pastoral area, Ordos Basin, NW China. Environ. Earth Sci. 2016, 75, 1356. [Google Scholar] [CrossRef]
- Shen, J.; Wang, Y.; Yang, X.; Zhang, E.; Yang, B.; Ji, J. Paleosandstorm characteristics and lake evolution history deduced from investigation on lacustrine sediments-The case of Hongjiannao Lake, Shaanxi Province. Chin. Sci. Bull. 2005, 50, 2355–2361. [Google Scholar]
- Jiang, X.-W.; Wan, L.; Wang, X.-S.; Wang, D.; Wang, H.; Wang, J.-Z.; Zhang, H.; Zhang, Z.-Y.; Zhao, K.-Y. A multi-method study of regional groundwater circulation in the Ordos Plateau, NW China. Hydrogeol. J. 2018, 26, 1657–1668. [Google Scholar] [CrossRef]
- Liang, K.; Yan, G. Application of landsat imagery to investigate lake area variations and relict gull habitat in hongjian lake, Ordos Plateau, China. Remote Sens. 2017, 9, 1019. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Yan, Z.; Gao, F. Monitoring spatio-temporal changes of water area in Hongjiannao Lake from 1957 to 2015 and its driving forces analysis. Trans. Chin. Soc. Agric. Eng. 2018, 34, 265–271. [Google Scholar]
- Dou, Y.; Hou, G.; Qian, H. Groundwater circulation by hydrochemistry and isotope method. Water Resour. Environ. 2016, 13–16. [Google Scholar]
- Wu, C.; Wu, X.; Mu, W.; Zhu, G. Using isotopes (H, O and Sr) and major ions to identify hydrogeochemical characteristics of groundwater in the Hongjiannao Lake Basin, Northwest China. Water 2020, 12, 1467. [Google Scholar] [CrossRef]
- Mu, W.; Wu, X.; Wu, C.; Hao, Q.; Deng, R.; Qian, C. Hydrochemical and environmental isotope characteristics of groundwater in the Hongjiannao Lake Basin, Northwestern China. Environ. Earth Sci. 2021, 80, 51. [Google Scholar] [CrossRef]
- Zhang, B.; Song, X.; Zhang, Y.; Han, D.; Tang, C.; Yu, Y.; Ma, Y. Hydrochemical characteristics and water quality assessment of surface water and groundwater in Songnen plain, Northeast China. Water Res. 2012, 46, 2737–2748. [Google Scholar] [CrossRef]
- Belkhiri, L.; Boudoukha, A.; Mouni, L. A multivariate Statistical Analysis of Groundwater Chemistry Data. Int. J. Environ. Res. 2011, 5, 537–544. [Google Scholar]
- Nguyen, T.T.; Kawamura, A.; Tong, T.N.; Nakagawa, N.; Amaguchi, H.; Gilbuena, R. Clustering spatio–seasonal hydrogeochemical data using self-organizing maps for groundwater quality assessment in the Red River Delta, Vietnam. J. Hydrol. 2015, 522, 661–673. [Google Scholar] [CrossRef]
- Olkowska, E.; Kudłak, B.; Tsakovski, S.; Ruman, M.; Simeonov, V.; Polkowska, Z. Assessment of the water quality of Kodnica River catchment using self-organizing maps. Sci. Total Environ. 2014, 476, 477–484. [Google Scholar] [CrossRef]
- Panaskar, D.B.; Wagh, V.M.; Muley, A.A.; Mukate, S.V.; Pawar, R.S.; Aamalawar, M.L. Evaluating groundwater suitability for the domestic, irrigation, and industrial purposes in Nanded Tehsil, Maharashtra, India, using GIS and statistics. Arab. J. Geosci. 2016, 9, 615. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Neurocomputing 1998, 21, 1–6. [Google Scholar] [CrossRef]
- He, S.; Li, P.; Wu, J.; Elumalai, V.; Adimalla, N. Groundwater quality under land use/land cover changes: A temporal study from 2005 to 2015 in Xi’an, Northwest China. Hum. Ecol. Risk Assess. 2020, 26, 2771–2797. [Google Scholar] [CrossRef]
- Hilario, L.; Ivan, G. Self-organizing map and clustering for wastewater treatment monitoring. Eng. Appl. Artif. Intell. 2004, 17, 215–225. [Google Scholar]
- Choi, B.Y.; Yun, S.T.; Kim, K.H.; Kim, J.W.; Kim, H.M.; Koh, Y.K. Hydrogeochemical interpretation of South Korean groundwater monitoring data using Self-Organizing Maps. J. Geochem. Explor. 2014, 137, 73–84. [Google Scholar] [CrossRef]
- SGQC (Standard for Groundwater Quality of China); Ministry of Land and Resources of the People’s Republic of China: Beijing, China, 2015.
- Davies, D.; Bouldin, D. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Zhao, D.; Zhou, P.; Qu, S.; Liao, F.; Wang, G. Hydrochemical characteristics of groundwater and dominant water–rock interactions in the Delingha Area, Qaidam Basin, Northwest China. Water 2020, 12, 836. [Google Scholar] [CrossRef] [Green Version]
- Apollaro, C.; Fuoco, I.; Bloise, L.; Calabrese, E.; Marini, L.; Vespasiano, G.; Muto, F. Geochemical modeling of water-rock interaction processes in the Pollino National Park. Geofluids 2021, 4, 1–17. [Google Scholar] [CrossRef]
- Gaillardet, J.; Dupre, B.; Allegre, C.J.; Négrel, P. Chemical and physical denudation in the Amazon River Basin. Chem. Geol. 1997, 142, 141–173. [Google Scholar] [CrossRef]
- Schoeller, H. Qualitative evaluation of ground water resources: Methods and techniques of groundwater investigation and development. Water Resour. 1967, 33, 44–52. [Google Scholar]











| Na+ | K+ | Mg2+ | Ca2+ | Cl− | SO42− | HCO3− | CO32− | TDS | pH | |
|---|---|---|---|---|---|---|---|---|---|---|
| Minimum | 10.10 | 0.38 | 0.72 | 2.51 | 4.98 | 6.26 | 182.00 | 0.00 | 285.00 | 7.34 |
| Maximum | 834.00 | 9.73 | 40.00 | 147.00 | 641.00 | 1120.00 | 481.00 | 14.60 | 2985.00 | 8.87 |
| Mean | 76.18 | 1.66 | 15.62 | 55.94 | 40.60 | 82.77 | 256.74 | 1.22 | 551.31 | 7.84 |
| Standard deviation | 138.37 | 1.63 | 8.86 | 32.16 | 98.22 | 192.46 | 59.33 | 3.54 | 439.34 | 0.33 |
| Calcite | Halite | Gypsum | Fluorite | Dolomite | |
|---|---|---|---|---|---|
| Minimum | −0.24 | −8.86 | −3.14 | −4.12 | −0.62 |
| Maximum | 1.09 | −4.55 | −0.74 | −1.10 | 2.13 |
| Mean | 0.44 | −7.59 | −2.25 | −2.29 | 0.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Wu, X.; Lu, C.; Sun, Q.; He, X.; Yan, L.; Qin, T. Hydrogeochemical Characterization and Its Seasonal Changes of Groundwater Based on Self-Organizing Maps. Water 2021, 13, 3065. https://doi.org/10.3390/w13213065
Wu C, Wu X, Lu C, Sun Q, He X, Yan L, Qin T. Hydrogeochemical Characterization and Its Seasonal Changes of Groundwater Based on Self-Organizing Maps. Water. 2021; 13(21):3065. https://doi.org/10.3390/w13213065
Chicago/Turabian StyleWu, Chu, Xiong Wu, Chuiyu Lu, Qingyan Sun, Xin He, Lingjia Yan, and Tao Qin. 2021. "Hydrogeochemical Characterization and Its Seasonal Changes of Groundwater Based on Self-Organizing Maps" Water 13, no. 21: 3065. https://doi.org/10.3390/w13213065
APA StyleWu, C., Wu, X., Lu, C., Sun, Q., He, X., Yan, L., & Qin, T. (2021). Hydrogeochemical Characterization and Its Seasonal Changes of Groundwater Based on Self-Organizing Maps. Water, 13(21), 3065. https://doi.org/10.3390/w13213065






