Mechanisms and Countermeasures on Sediment and Wood Damage in Sediment Retarding Basins

Abstract

Improvements in sediment retarding basin design are required to mitigate flood damage caused by bed load and wood debris outflow in lower river reaches. We used a scaled sediment retarding basin model to optimize our basin design, with the goal of improving sediment and wood debris transport and capture. Changes to the structural dimensions and elements of the sediment retarding basin were assessed under experimental debris flow conditions. The results obtained from the experiments and simulations were in good agreement regarding sediment flow and containment. The proposed one-dimensional model is useful for showing the effects of flow conditions within a sediment retarding basin on sediment transport.

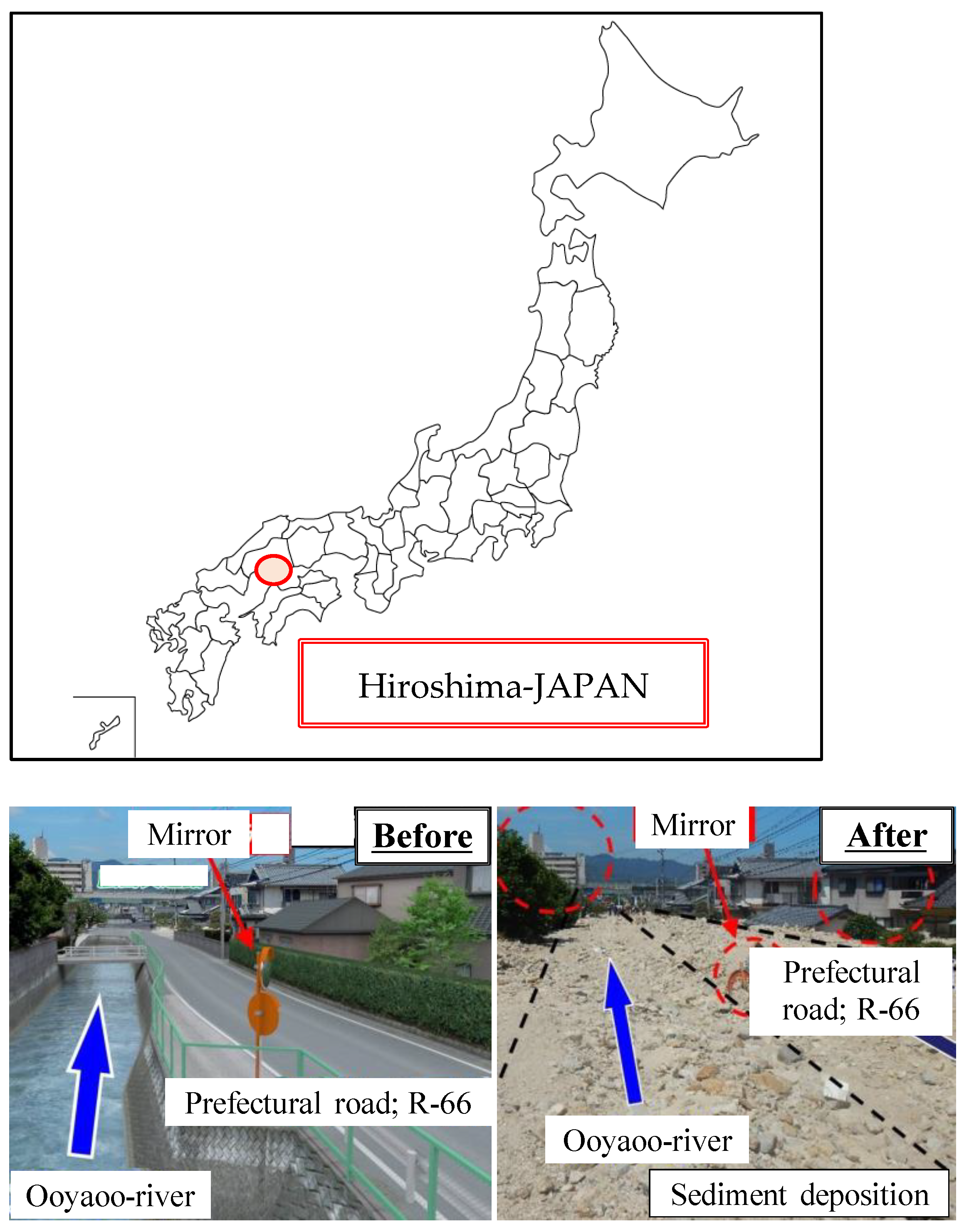
1. Introduction

In recent years, many large-scale sediment-related disasters due to unexpected torrential rains have been reported (for example, the Japan-Hiroshima heavy rain disaster in July 2018, as shown in Figure 1) [1]. Countermeasures against these disasters are vital for mitigating the damage to communities and loss of life. Figure 2 and Figure 3 show typical damage situations [2] and the rainfall conditions [3] at the time of multiple sediment-related disasters (August 2014 and July 2018) that occurred in Hiroshima. The landslide event in 2014 (Figure 2) was mainly caused by a gravel-type sediment flow, mixed with wood debris [4]. The right side of Figure 2 shows the sediment flooding of 2018, in which the outflow of fine-grain sediment and wood debris damaged areas downstream [5]. The difference in damage caused by the 2014 and 2018 events was due to the effects of re-erosion that occurred under the extended torrential rainfall conditions in 2018 (Figure 3: right axis). To address this, new measures which employ sediment retarding basins have been proposed [3]. The relationship between the shape of the sediment retarding basin and the effectiveness of the structure to control sediment flow have been discussed in numerous experimental studies and analyses [6,7]. Matsumura et al. (2001) proposed sediment dynamics for sediment retarding basins; the width of the proposed sediment retarding basin is more than three times that of the upstream channel, and the length is more than 1.33 times the width, for effective sedimentation [6]. In addition, Takahashi and Satofuka (1999) proposed a riverbed variability model for analyzing fluctuations in sediment movement in a planar flow path in a sediment retarding basin, and accurately reproduced the experimental results [7].

Computational models for debris flows are challenging to devise; many researchers have made significant efforts to build models with high accuracy and computational efficiency. Computational models for debris flow usually involve a two-phase approach, in which fluid flows (water including small grains) and motions of large scale obstacles, such as boulders or driftwood, are modeled separately. In the fluid phase, computational fluid dynamics (CFD), smoothed particle hydrodynamics (SPH), and the lattice Boltzmann method (LBM) have been applied. For modeling obstacles, the discrete element method (DEM) and finite element method (FEM) were used in most of the existing models. Hasanupour et al. (2021) employed a SPH-FEM coupling model, in which fluid motion was modeled using a particle-based Lagrange approach (SPH), and debris and structures were modeled using a mesh-based FEM [8]. The model was applied to tsunami and debris interactions and showed excellent applicability. Leonardi (2015) developed a DEM-LBM coupling model for simulating debris flow [9]. In the model, the granular phase of the debris flow was modeled using DEM and the fluid phase was modeled using LBM. Leonordi successfully computed the spatial reorganization of particles and fluid in debris flows. In addition, the DEM-LBM model was combined with FEM and applied to the interaction of debris flows with cable-net type barriers. Trujillo-Vela et al. (2020) used an SPH-DEM coupling model for computing debris flows. In the model, fluid and soil were modeled using SPH, while immersed bodies such as boulders and solid boundaries were modeled using DEM [10]. The computed results aligned with experimental results and field observations. Zhao (2014) developed the DEM-CFD model, in which fluid flows were computed with a Eulerian-type CFD model and grain motions were modeled using DEM [11]. The model was applied to landslide-induced debris flow in terrestrial and submarine conditions. Zischg et al. (2018) proposed an interesting driftwood dynamic model in a real river. Since the spatial scale targeted of the model was larger than that of the models discussed above, the computational efficiency was much more important [12]. Therefore, the river flow was modeled using a two-dimensional shallow flow model. The dynamics of the driftwood, including the generation process (recruitment of standing trees), transport process (floating, rolling and sliding conditions), and clogging at bridges, were modeled using conceptual and statistical approaches. The model was applied under extreme flood conditions and its accuracy was examined through comparison with observed data. However, the general design guidelines [13] do not sufficiently describe the processing functions of various components of the basin structure, thus limiting the ability to optimize their configuration. In this regard, the recent revision of standards in Japan has provided the opportunity to formulate new countermeasures to control sediment and debris damage. Many numerical analyses of the basin structure have been conducted to develop a model to better predict sediment transport and capture under various conditions, and to determine the ability of the sediment basin to minimize damage [3].

In this study, we investigated the structural design of sediment retarding basins using a scaled basin–waterway model for controlling the transport of sediment and simulated driftwood debris. Based on our experimental results, we constructed an analysis model to describe the functionality of the sediment retarding basin and its ability to contain sediment and debris flow [14,15].

2. Analysis of the Sediment Control Function of Sediment Retarding Basins

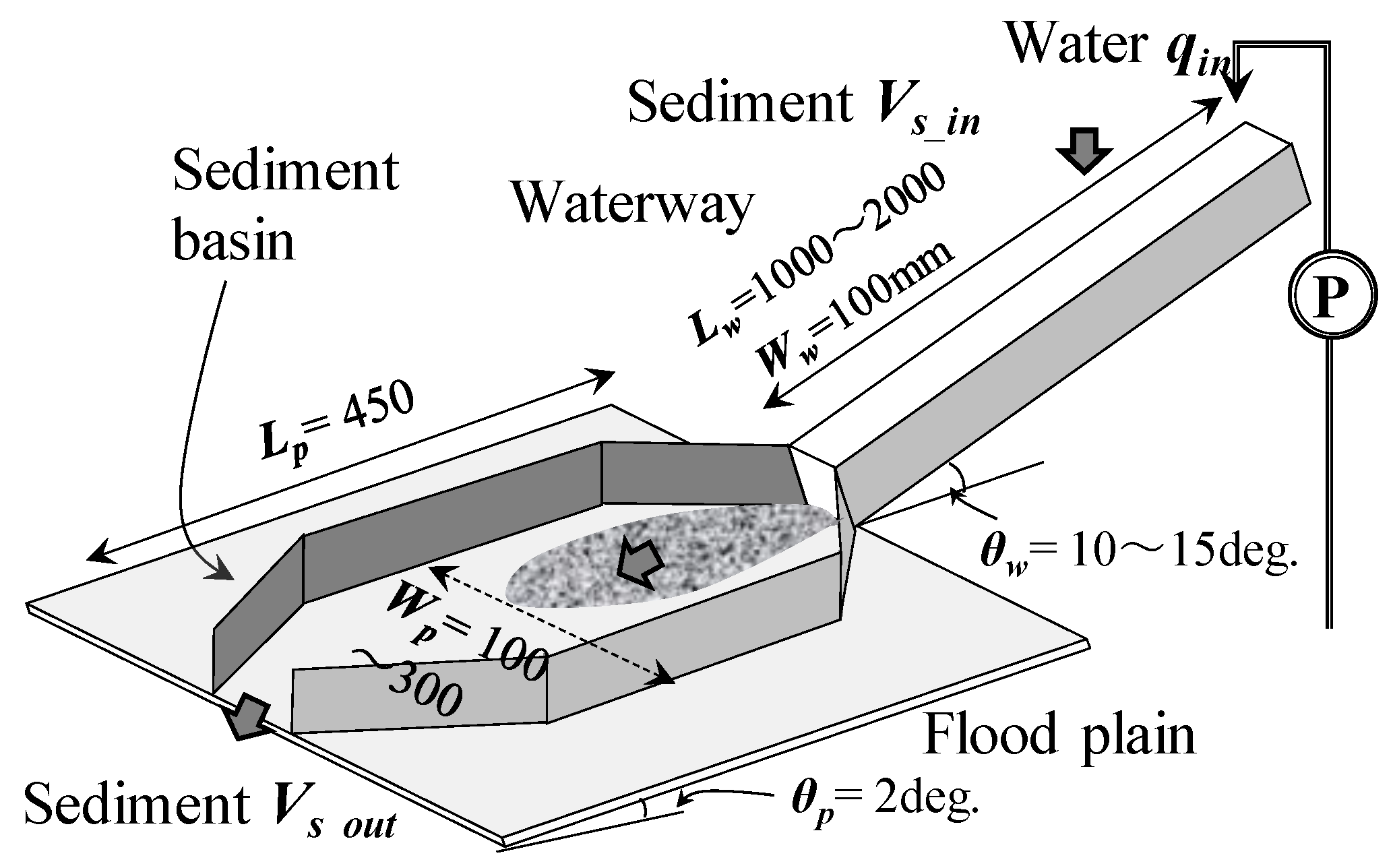
2.1. Experimental Outline

Figure 4 shows the waterway set-up used in the sediment-control experiments for the sediment retarding basin, in which the installation was assumed to be in the proximity of a valley exit. A scale of 1/100 was used for our basin model with reference to the experimental scale of previous studies [6,7]. As shown in the figure, a straight channel (width, W_w = 100 mm) was connected upstream of the planar flooding platform (θ_p = 2°: maximum and minimum gradient of the debris flow). Water (at a rate of q_in) and earth and sand (V_{s_in}, silica sand [15] was injected independently) were supplied from upstream of the channel (θ_w = 10° to 15°). The sediment basin had a length (L_p) of 450 mm and a width (W_p) of 100 to 300 mm. We measured the amount of sediment (V_{s_out}) that passed through the sediment retarding basin and flowed downstream [13]. The amount of sediment supply V_{s_in} was approximately equal to the maximum amount captured by the sediment retarding basin under each condition of the preliminary experiment. In the experiments, sediment was laid on the bottom of the straight channel in advance. Running water was then allowed to flow through the channel, which gradually eroded away the sediment. The sediment was transported from the upstream channel downstream to the basin as a sediment flow. Here, the water supply was limited to the time at which all of the upper sediment had been eroded away and flowed downstream. The maximum width of the sediment retarding basin (W_{p_max} = 300 mm) was set as the width required for sedimentation when no side wall was present in the preliminary experiment. The length of the sediment retarding basin (L_p = 450 mm) was set with reference to the current construction guidelines. In the preliminary experiment, L_w = 2000 mm was applied, in consideration of the influence of the change in the channel length L_w.

There is a need to understand the effects of different conditions (e.g., rainfall rate or water supply rate, q_in) and basin configurations (e.g., basin width W_p and installation of corners Figure 5 and Ref. [13]) on the effectiveness of the basin to control the sediment and debris flow. Considering the non-uniformity of the experimental results, we conducted three experimental trials under the same conditions and averaged the results. In the preliminary experiment, the average error of the extreme value with respect to the average value of the results of the three experiments was approximately 5%.

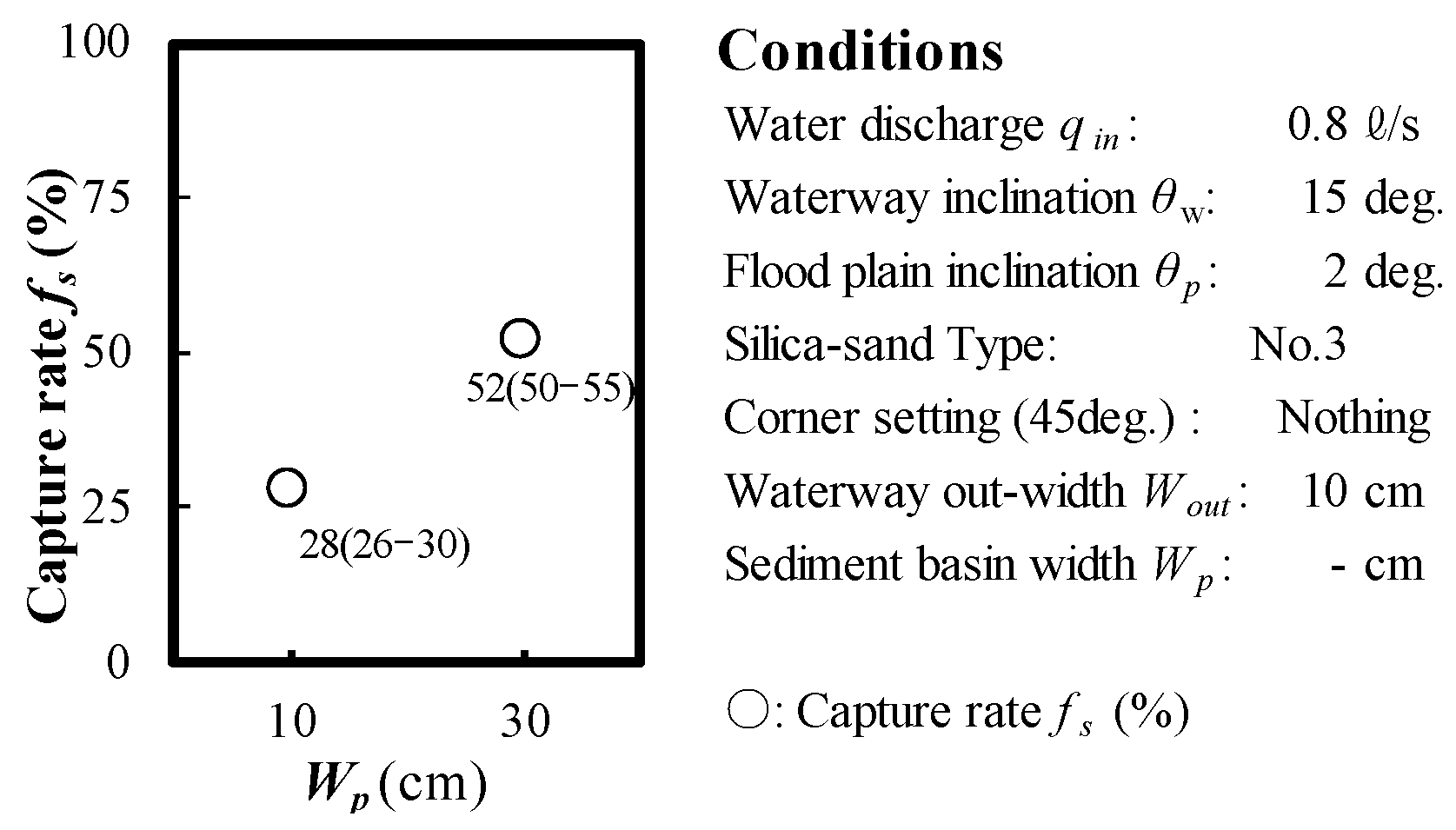
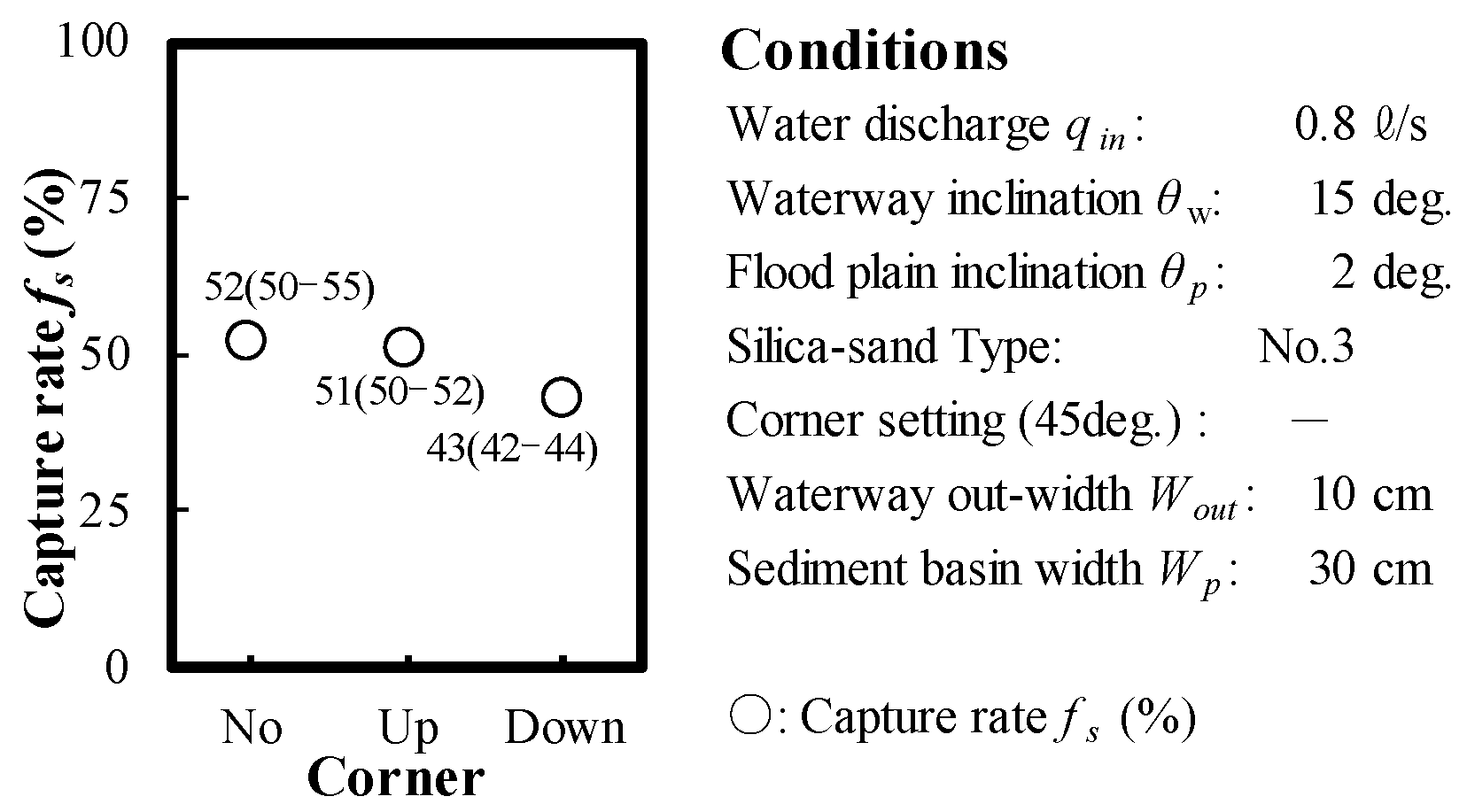
2.2. Experimental Results and Discussion

The sediment capture rate f_s of our sediment retarding basin is given by

f_s = (V_{s_in} − V_{s_out})/V_{s_in}.

(1)

Hereafter, we describe our experimental results with respect to the basic basin design shown in Figure 4.

Figure 6 and Figure 7 show the effects of changing the basin width W_p on the capture rate f_s of the basin. The numbers in the figure indicate the result range and average value of the three trials. When W_p was 10 cm (i.e., identical to the width of the upstream straight channel W_w), the average value of f_s was approximately 28% (minimum value: 26%; maximum value: 30%). When the width was widened to W_p = 30 cm, the f_s was approximately 52%; under these conditions (Figure 7), a large amount of sand passed through the sediment retarding basins and flowed downstream. Notably, changing the longitudinal gradient to θ_w/θ_p = 15°/2° improved the functionality by 30%, while widening the flow path to W_p/W_w = 30 cm/10 cm provided an improvement of approximately 20% in functionality. According to our observations during the experiment, the sediment was captured at some point by the sediment retarding basin. However, this sediment was then eroded away gradually by subsequent flow to the downstream area; thus, the final capture rate f_s was approximately 50%. When the water supply time was further extended, and water was supplied until there were no significant changes, the sediment capture rate f_s changed by approximately 10% (e.g., decreased from 52% to 42%). Thus, these results indicate that the shape of the sediment retarding basin is an important factor for sediment capture.

Figure 8 shows the effects of changing the water supply flow rate q_in on the sediment capture rate f_s, in which f_s increased with q_in. According to our observations during the experiment, when the flow rate is large, a large amount of sediment transports the sediment in the canal downstream. Additionally, a large amount of sediment is trapped in the sediment retarding basin, which is significantly affected by the change in flow between the canal and sediment retarding basin.

Figure 9 shows the effect of the presence or absence of corners in the basin (referring to Figure 5 that shows 45° corners [13]) on the capture rate f_s. There was little to no effect on f_s between the absence of corners (Corner: NO) and the presence of upstream corners (Up). Conversely, when corners were installed on the downstream side (Down), f_s decreased by approximately 10% with respect to the absence of corners (i.e., NO).

Figure 10 shows the effects of changing the downstream opening width W_out of the sediment retarding basin on the sediment capture rate f_s. When W_out was gradually contracted with respect to the inflow width W_w, the capture rate f_s significantly improved (Figure 11).

Figure 12 shows diagrams of the changes in the sediment flow with respect to the basin shape. When W_out was wide and corners were installed in the basin (Figure 12, left), a planar flow was generated from the area upstream to the area downstream inside the basin, with outward flow of the sediment from the basin to further downstream. In contrast, when W_out was narrow and no corners were installed (Figure 12, right), sediment capture improved, due to the influence of a planar outward vortex generated in the downstream area inside the sediment basin.

Taken together, these results indicate that the shape of the sediment retarding basin and the backwater effect in the flooded area due to gradual flow contraction at the downstream opening, as well as the width of this opening, affect the sediment control function of sediment retarding basins. In the future, further detailed studies will be needed to resolve the effects of differences in the flow rate, sand supply conditions, longitudinal gradient changes (θ_w/θ_p), and other aspects over time on the sediment treatment function. This was a small-scale (1/100) experiment due to the restrictions of the experimental conditions, but a large-scale experiment should be conducted in the future. Furthermore, the average value was obtained from three experiments for each condition, so it will be necessary to increase the number of experiments in future studies.

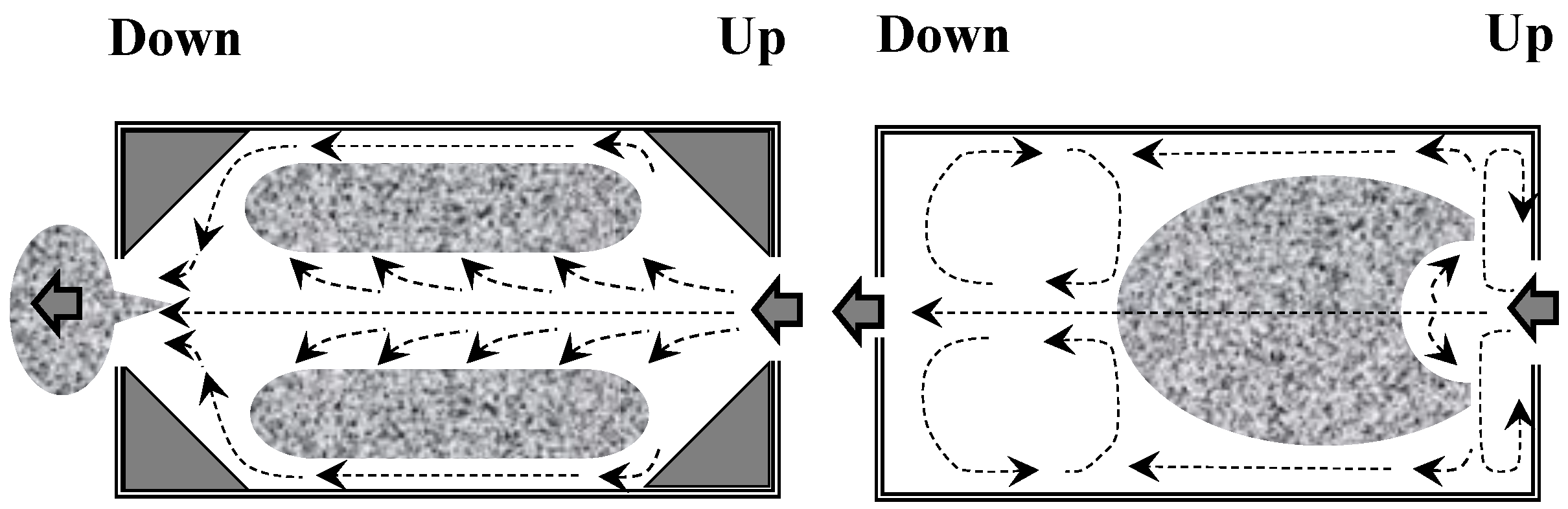
3. Analysis of Sediment Control Function of Wood Debris Retarding Basins

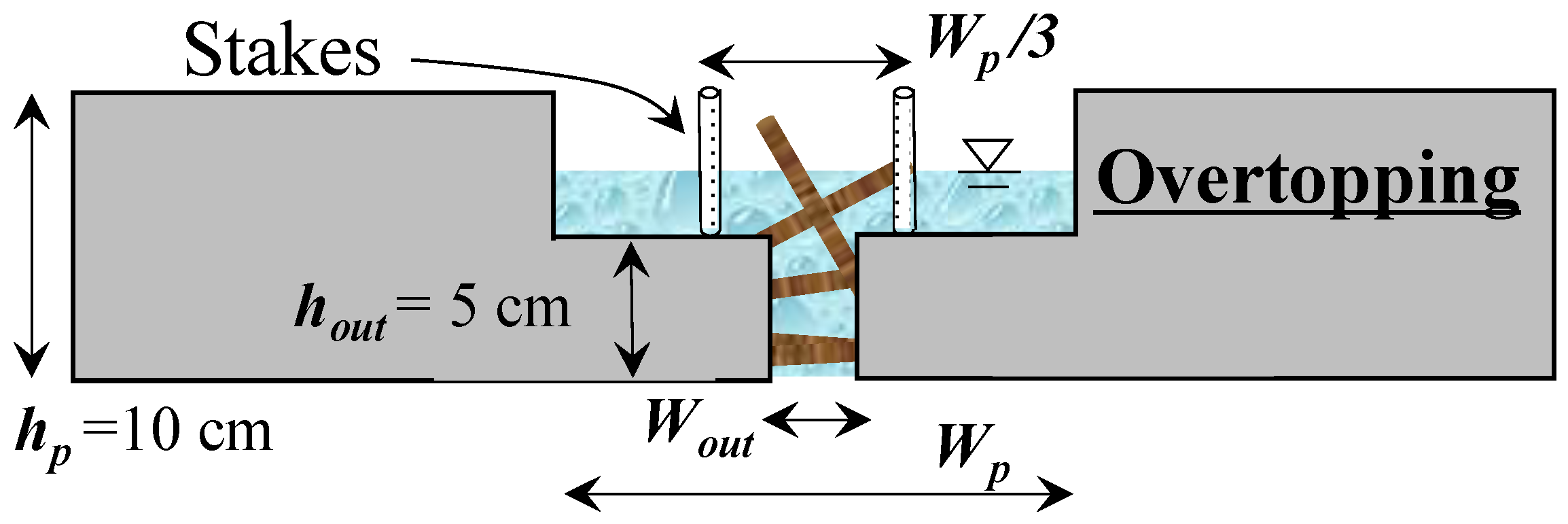
3.1. Experimental Outline

Figure 13 shows the waterway used in the experiment for the sediment retarding basin. As shown in Figure 4, water (q_in) and wood debris (number: N_{w_in}) were supplied from upstream of the straight channel, and the amount of wood debris (N_{w_out}) that flowed out of the basin was measured. The wood debris consisted of cylindrical pieces of wood (diameter: 3 mm; length L_w = 5 to 10 cm; specific gravity: 0.75). The wood debris was added manually (the amount of wood debris input per hour was approximately 1 piece every 0.5 s [16]), and the amount of debris captured was measured [14].

As a potential countermeasure against the outflow of wood debris from the basin due to overflow when the downstream opening width W_out of the basin becomes narrowed, we proposed a countermeasure stake structure, as shown in Figure 14. Figure 15 shows verification of the effectiveness of the capture structure. In the preliminary experiments, in the absence of this countermeasure, a large amount of wood debris flowed downstream due to the overflow caused by the narrow opening.

The effects of each condition on the capture function in the sediment retarding basin and the behavior of the wood debris in the basin were examined with respect to corner installations (Figure 5). These aspects were also examined by changing q_in, W_p, the downstream opening width W_out of the basin, and the number of supplied wood debris pieces N_{w_in} (32 cases) (Figure 13). To address the non-uniformity of the experimental results, we conducted three experimental trials under the same conditions and averaged the results of these trials. In the preliminary experiment, the average error of the extreme value with respect to the average value of the results of the three experiments was approximately 7%.

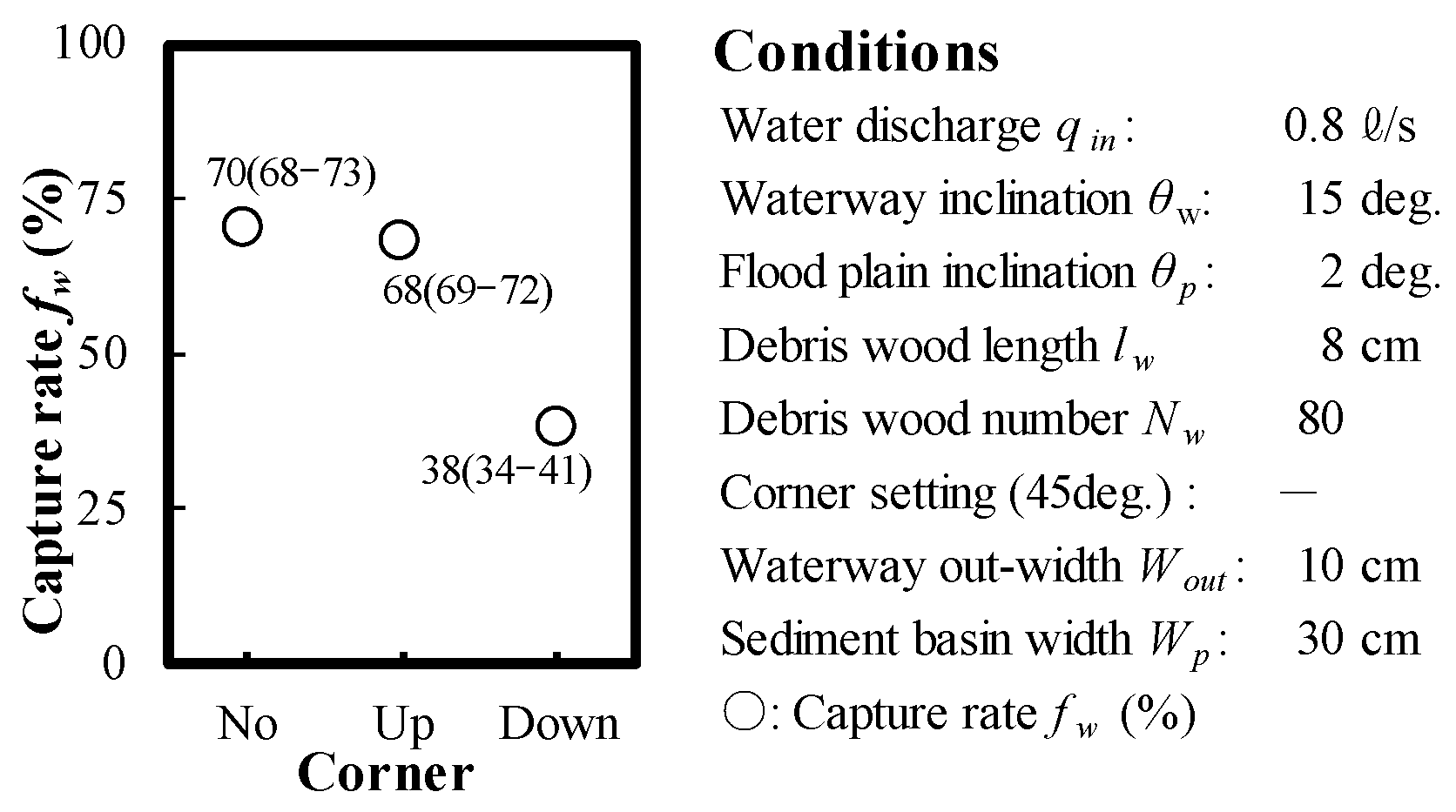
3.2. Experimental Results and Discussion

From our experimental results on wood debris control, the wood debris capture rate f_w of the sediment retarding basin is given by

f_w = (N_{w_in} − N_{w_out})/N_{w_in}.

(2)

Hereafter, we consider experimental results for the basin set-up shown in Figure 13.

Figure 16 shows the effects of changes in the downstream opening width W_out of sediment retarding basins on the wood debris capture rate f_w. When the sediment retarding basin opening width W_out was narrowed, the wood debris capture rate f_w significantly improved. Figure 17 shows the effect of the difference in the presence or absence of corners (Figure 5) installed upstream and downstream in the sediment retarding basin on wood debris capture_. There was no significant difference in f_w between a configuration without corners installed (Corner: NO) and a configuration with upstream corners installed (Up), similar to the sediment findings. However, when corners were installed on the downstream side (Down), the control function was significantly reduced (by approximately 30%) compared with the control function in the absence of corner installations; similar to the sediment capture effect shown in Figure 9.

Figure 18 shows the effect of the difference in the shape of the sediment retarding basin on the flow conditions and the capture function. When W_out was wide and downstream corners were installed (Figure 18, left), a smooth flow downstream occurred in the sediment retarding basin, and most of the wood debris flowed out of the basin to areas downstream. In contrast, when W_out was narrow and no corners were installed (Figure 18, right), the wood debris accumulated as a flat vortex in the transverse direction, which was affected by the narrowing of the downstream opening width. In the presence of a large water level difference due to backwater near the sediment retarding basin opening, the generated planar vortex became more prominent, and a large amount of wood debris was captured. With the addition of stakes installed as a debris flow countermeasure (Figure 14), a large amount of the wood was captured by the basin. There was no outflow of wood debris downstream due to changes in the flow conditions, such as the disappearance of backwater due to suspension of the water supply. Although there is some concern that these capture mechanisms are affected by the specific gravity and shape of the wood debris, these countermeasures are considered generally appropriate, compared with earlier configurations described in the literature [2].

Figure 19 shows the effects of changes in the supply flow rate q_in on the wood debris capture rate f_w of the sediment retarding basins. The capture rate f_w decreased with the supply flow rate q_in. From our observations during the experiment, the flat vortex flow became remarkable due to the backwater effect, and most of the wood debris was captured by the sediment retarding basin.

Finally, Figure 20 shows the effects of changes in the amount of supplied wood debris N_{w_in} on the sediment capture rate f_w. Although the change was not remarkable, f_w slightly improved as the amount of supplied wood debris increased. According to our observations during the experiment, when the amount of supplied wood was large, the wood debris that flowed down after the initial influx of wood debris was easily captured at the opening by the blockage [16].

These experimental results were applied to devise the shape of the sediment retarding basin. Future studies should further investigate the effects and necessity of downstream corners; we will focus on this and the differences in other conditions using additional experiments and analytical models [17]. In addition, the average value was obtained from three experiments for each condition, so it will be necessary to increase the number of experiments in future studies. As shown in previous studies ([11,18,19]), it is necessary to pay attention to the load-bearing performance of stakes in the actual design. In this experiment, the water depth was shallow, and the three-dimensional effect of the water flow was small. Future studies should examine the effect of the load on structures due to the change in water depth when the flow rate is high [20].

4. Numerical Analysis of the Control Function of Sediment Retarding Basins

Numerical analysis was used to simulate the ability of the sediment retarding basin to control sediment flow; the simulation results were compared with the experimental results described in the previous section. In this study, a one-dimensional analysis model was used for the manual [21].

4.1. Flow Equation

As the basic equation of flow in a fluidized bed, one-dimensional unsteady flow was applied for uniform gravel [4,15]. The equation of motion of the flow, the continuous equation of the total volume, the continuous equation of the sediment in running water, and the continuous equation of the riverbed are expressed as Equation (3), Equation (6), respectively, as follows:

$$\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} = -g\frac{\partial H}{\partial x} - \frac{{\tau }_b}{{\rho }_{m}h} ,$$

(3)

$$\frac{\partial h}{\partial t} + \frac{\partial uh}{\partial x}{ = i}_b ,$$

(4)

$$\frac{\partial \left(Ch\right)}{\partial t} + \frac{\partial \left(uhC\right)}{\partial x}{ = i}_{b}C* ,$$

(5)

$$\frac{\partial z}{\partial t}{ + i}_b = 0 ,$$

(6)

where h is the flow depth, u is the cross-sectional average flow velocity, g is the acceleration due to gravity, H is the flow surface elevation, z is the riverbed height, C is the sediment concentration of the fluid layer, t is the time, C* is the sediment concentration of the sedimentary layer, Ρ_m is the unit volume weight of the liquid phase containing fine particles (fine gravel), τ_b is the riverbed shear stress, and i_b is the erosion rate.

The riverbed shear force considering the motion form [4] is as follows, with respect to the sediment concentration:

When C ≥ 0.4 C* (debris flow):

$$\frac{{\tau }_b}{\rho h} = \frac{1}{8}\frac{d_m^2}{h^3}\frac{u\left|u\right|}{G\left(C\right)} ,$$

(7)

$$G \left(C\right) = \left\{C + \left(1 - C\right)\frac{\rho }{\mathsf{\sigma }}\right\}{\left\{{\left(\frac{C*}{C}\right)}^{1/3} - 1\right\}}^2.$$

(8)

When 0.01 < C < 0.4 C* (bed load collective flow):

$$\frac{{\tau }_b}{\rho h} = \frac{d_m^2}{h^3}\frac{u\left|u\right|}{0.49} .$$

(9)

When C < 0.01 or h/d ≥ 30 (quicksand):

$$\frac{{\tau }_b}{\rho h} = \frac{{gn}_m^{2}u\left|u\right|}{h^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}} .$$

(10)

Here, ρ is the unit volume weight of the sand particles, n_m is the Manning roughness coefficient, and d_m is the particle size. The erosion and sedimentation of the riverbeds are described as follows:

Erosion (i_b ≥ 0):

$$i_b = \mathsf{\delta }e\frac{C_{\infty } - C}{C* -{ C}_{\infty }}\frac{uh}{d_m} .$$

(11)

Sedimentation (i_b < 0):

$$i_b = \mathsf{\delta }d\frac{C_{\infty } - C}{C*}\frac{uh}{h} ,$$

(12)

$$C_{\infty }= \frac{{\rho }_{m}tan\mathsf{\theta }}{\left(\mathsf{\sigma }‐\rho \right)\left(tan\varphi - tan\mathsf{\theta }\right)} .$$

where δ_d is the deposition rate coefficient, δ_e is the erosion rate coefficient, C_∞ is the equilibrium sand concentration, θ is the water surface gradient, and φ is the internal friction angle of the gravel. For others, refer to the literature [4].

4.2. Analysis Conditions

For the analysis conditions, we assumed the following: a unit volume weight of sand particles (σ) of 2650 kg/m³, a unit volume weight of the liquid phase containing fine particles (fine grain gravel, ρ_m) of 1100 kg/m³, an internal friction angle of the sand gravel (φ) of 37°, a sediment concentration (C*) of the sedimentary layer of 0.65, acceleration due to gravity (g) of 9.8 m/s², an erosion rate coefficient (δ_e) of 0.0007, a sedimentation rate coefficient (δ_d) of 0.1, Δt of 0.001 s, Δx of 0.5 m, rough Manning, and a degree coefficient nm of 0.01 m^−1/3s. The other conditions were varied to determine the effect.

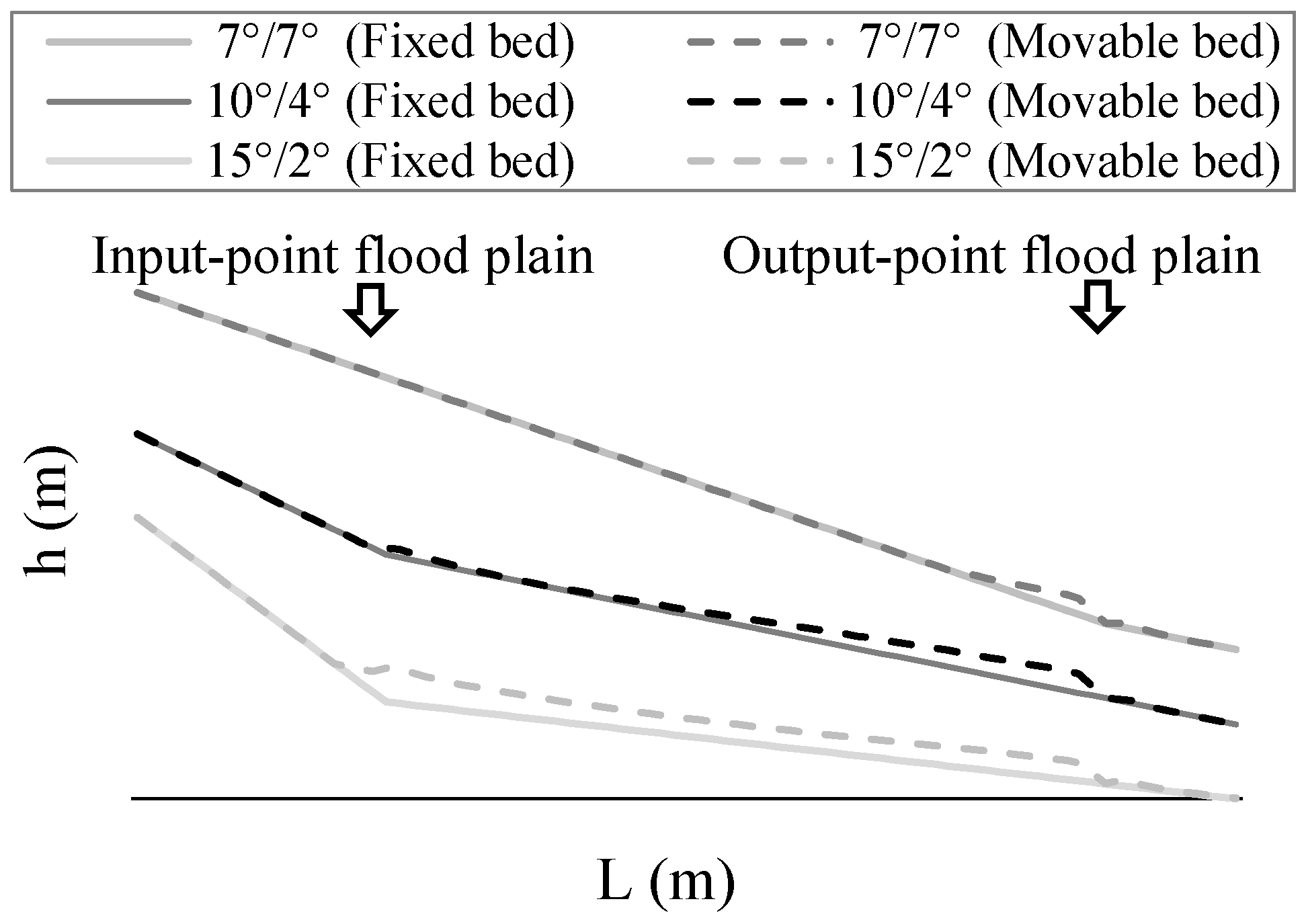
4.3. Reproduction of the Experimental Results

Using the one-dimensional analysis model constructed for the sediment control function of sediment retarding basins, the experimental results (scale: 1/100) were reproduced and calculated to determine the applicability of the proposed analysis model. Figure 21 shows a comparison between the experimental and simulation results with respect to changes in the sediment retarding basin width W_p (Figure 4) on the sediment capture rate f_s with respect to the straight channel width W_w. Figure 21 generally shows good agreement between the model and the results. The analysis results were more susceptible to widening, compared with the experimental results. As one of the factors, the one-dimensional analysis model was presumed to be significantly affected by the change in flow velocity due to the widening.

Figure 22 shows the reproduction results for changes in the most downstream outlet opening width W_out (Figure 5) of the sediment retarding basin. General reproducibility was confirmed (correlation coefficient: 0.98). The reproducibility associated with the change in the downstream opening width was smaller than the experimental results, in contrast to the tendency shown in Figure 18. In this case, the backwater effect and the flow in the transverse direction due to the narrowing of the opening width could not be sufficiently reproduced by the one-dimensional analysis model.

Figure 23 shows the reproduction results for changes in the supply flow rate q_in (Figure 4) from the upstream; as shown in Figure 23, general reproducibility was confirmed (correlation coefficient: 0.95).

Figure 24 shows the reproduction results of sediment trapping f_s when corners were added to the sediment retarding basin (Figure 5). As shown in Figure 24, the reproducibility decreased, dissimilar to the previous trends (correlation coefficient: 0.59). In particular, the installation of downstream corners (Down) could not be reproduced. In this case, the one-dimensional analysis model was unable to describe the planar flow in the transverse direction in the basin due to the corner installations.

The results thus far indicate that the proposed one-dimensional analysis model was able to reproduce the experimental results regarding the sediment trapping function of the sediment retarding basins. However, local changes in the flow (e.g., the backwater effect and cross-sectional flow) require further consideration. From the experimental results, the control functions for sediment and wood debris tended to be similar. It was found that the conditions that enhance the soil capture effect also contribute to the wood debris capture effect. In addition, we will investigate study measures to describe backwater and downstream corner effects that we were unable to address with the one-dimensional model.

5. Understanding the Impact on Sediment Control Function Using an Analytical Model

The proposed one-dimensional analysis model can be applied to describe the effects of changes in the width W_p, planar shape, and inflow slope (Figure 4: θ_w/θ_p) of the sediment retarding basin on sediment control. Regarding the shape of the sediment retarding basin, the length L_p and width W_p of the basin can be changed, such that the installation area A_p (L_p·W_p) of the sediment retarding basin remains constant.

Figure 25 shows the effects of changing the width (W_p/W_w) and vertical gradient (θ_w/θ_p) of the sediment retarding basin directly upstream on the sediment capture rate f_s. The results showed that widening of the sand area and changing the slope upstream affect sediment capture. This is likely due to changes in the water depth and flow velocity that affect sedimentation.

Figure 26 shows the effects of the downstream opening width (W_out/W_p) of the sediment retarding basin and the gradient change (θ_w/θ_p) directly upstream on sediment capture f_s. A backwater effect is expected due to narrowing of the downstream opening width of the basin; changes in the water depth and flow velocity are also expected with changes in the gradient. When the gradient change was small and there was no gradual contraction of the basin opening width, most sediment flowed downstream from the basin.

Figure 27 shows the effects of changes in the plane shape (L_p/W_p) of the sediment retarding basin, in which the installation area A_p of the sediment retarding basin is constant, and changes in the supply flow rate q_in on sediment capture f_s. When the ratio of the sediment retarding basin width to the basin length (L_w/L_p) was 1 or more (long shape in the longitudinal direction), there was little to no change in f_s.

Figure 28 shows the effects of the planar shape (L_p/W_p) of the sediment retarding basin and the gradient change (θ_w/θ_p) immediately upstream of the sediment retarding basin on sediment capture f_s. The change in the gradient showed a different tendency in the relationship between the shape of the sediment retarding basin and the sediment capture.

Figure 29 shows the sedimentation shape (longitudinal view) in the final sediment retarding basin for each gradient change (7°/7°, 10°/4°, and 15°/2°). When the gradient change was small (θ_w/θ_p = 10°/4°), a large amount of debris was deposited near the downstream opening. In contrast, when the gradient change was large (θ_w/θ_p = 15°/2°), the entire debris amount was deposited in the basin. This suggests that a wide river channel (L_p/W_p <<) shape is significant for sediment capture f_s in the sediment retarding basin with a small gradient change. The change in L_p/W_p is related to W_p/W_w; thus, the difference in these ratios affects sediment capture. This also explains why the sediment was transported continuously while the flow velocity remained high, because the water depth increased significantly due to narrowing of the basin width due to the side wall, despite the change in the gradient.

Based on the results shown in Figure 27 and Figure 28, we suggest that a sediment retarding basin with a width aspect ratio (L_p/W_p) of approximately 1 (nearly square planar shape) is more effective, compared with existing land constraints. Furthermore, regarding the installation position of the sediment retarding basin, the effectiveness of countermeasures near the gradient change point close to the valley exit should also be considered, as discussed in Section 3.

In the future, further detailed examinations are required, because there are many parameters and conditions to consider for achieving a highly functional sediment retarding basin design. In particular, the one-dimensional model adopted in this study cannot reproduce the effect of the planar eddy current shown in Figure 12 in detail, so we plan to upgrade it with a two- or three-dimensional model in the future.

6. Conclusions

In this study, the detailed structure of sediment retarding basins was examined experimentally and through simulations to optimize the functionality of the basin and its ability to control sediment and wood debris runoff during serious flooding conditions. We constructed a one-dimensional analysis model to describe our basic experimental results and verified its reproducibility. Finally, using our analysis model, we considered the effects of different conditions (for example, changes in the gradient and opening widths of the waterway and basin) on the control aspects of the basin.

According to the results of the channel experiment, the ability of the sediment retarding basin to control flood water and debris depended on the flow conditions, the shape of the basin, and the opening width of the basin at the downstream end. The installation of downstream corners reduced the control function; however, continuing investigation is necessary.

A one-dimensional analysis model was constructed to describe the sediment and wood debris transport observed in our experiments. We confirmed that our model could reproduce our experimental results. However, more detailed structures and basin configurations will likely require a more complex model. Finally, our results indicated that the overall shape of the basin could be optimized to allow for better control over sediment and debris flow. Specifically, an aspect ratio (basin extension/length-to-width ratio) of approximately 1 (square or nearly square) was especially effective in capturing the sediment and wood debris; this would also need to be examined in greater detail to adjust for variations in the runoff gradient and the conditions leading to flooding.