The Effect of Temporal Characteristics on Developing a Practical Rainfall-Induced Landslide Potential Evaluation Model Using Random Forest Method

Abstract

With the unique rainfall patterns of typhoons, plum rains, and short-term heavy rainfalls, the frequent landslide and debris flow disasters have caused severe loss to people in Taiwan. In the studies of landslide susceptibility, the information of factors used for analysis was usually annual-based content, and it was assumed that the same elements from different years were independent between each year. However, the occurrence of landslides was usually not simply due to the changes within a year. Instead, landslides were triggered because the factors that affected the potential of landslides reached critical conditions after a cumulative change with time. Therefore, this study had well evaluated the influence of temporal characteristics and the ratios of antecedent landslide areas in the past five years in the landslide potential evaluation model. The analysis was conducted through the random forest (RF) algorithm. Additional rainfall events of 2017 were used to test the proposed model’s performance to understand its practicality. The analysis results show that in the study area, the RF model had considerably acceptable performance. The results have also demonstrated that the antecedent landslide ratios in the past five years were essential to describe the significance of cumulative change with time when conducting potential landslide evaluation.

1. Introduction

Taiwan is an island located in the hot zone of the Circurm-Pacific Earthquake Belt, typhoons, and subtropics monsoon climatic region. About 70% or more of the island’s area is hillsides and mountains. Because of the steep topography and geological vulnerability, two or more natural disasters are common in Taiwan. Landslide disasters have become a critical issue in recent years due to their increasing frequency of occurrence caused by extreme weather and climate change.

To better understand and deal with the increase in landslide disasters, researchers conducted studies on the potential for landslide and occurrence probability by considering environmental conditions. Most researchers used the landslide susceptibility analysis (LSA) to develop landslide evaluation models. Factors that describe the environmental conditions and triggering behavior of landslides were usually used in the LSA method. The LSA-based models can be divided into qualitative and quantitative methods [1,2]. The approaches of statistical analysis, geotechnical engineering analysis (deterministic and probability), artificial intelligence [3,4,5,6,7,8,9], and data mining were commonly used for quantitative LSA modeling. Artificial intelligence has become a popular data analysis method in recent years [8] utilizing machine learning, and deep learning algorithms have become more efficient and reliable in recent years. The machine learning algorithm, Random Forest (RF), was often used for landslide potential evaluation [9,10,11,12,13,14,15] and was the study focus of this paper.

Landslide risk analysis (LRA) is another approach to study the landslide disaster. The concept of the risk triangle, proposed by Crichton [16], including hazard, vulnerability, and exposure, is usually used to develop an LRA model, in which probability assessment is performed to describe the risk level. A recently developed landslide evaluation model using the landslide fragility curves (LFC) was a model of LRA [1,2,17]. LFC model used spatial statistics and GIS for data processing on the grid base. Rainfall data over the study areas and landslide cases were obtained and analyzed by constructing a fragility curve to describe the exceeding probability of landslide for given environmental conditions. Fragility curves were built for each combination of factors in the model. With the fragility curves, the critical hazard potential and critical fragility potential were determined to express the probability of exceeding a damage state of landslides under certain conditions of rainfall intensity and accumulated rainfall [2].

Both LSA and LRA models use factors to describe the potential of landslides. These factors, such as rainfall intensity, accumulated rainfall, slope degree, etc., were categorized as environmental factors and triggering factors. The development of the landslide potential evaluation model was usually conducted by considering the effectiveness of each chosen factor for a given period, e.g., the accumulated rainfall of each heavy rainfall event used for developing the model. Among the rainfall-induced researches, the rainfall thresholds are usually the main factor when evaluating the landslide susceptibility [18], and the temporal resolution of rainfall affects the thresholds significantly [19]. In these studies, the rainfall factors were included in the evaluation procedure by yearly-based input, not considering the consecutive influence from previous years.

In addition to rainfall factors, previous studies [1,2,20,21] on landslides usually used other annual factors of each year to establish a potential evaluation model. The variation of the same factors between each year was typically assumed to be independent and uncorrelated. However, landslides were usually caused not simply due to the change that occurred within a year. The cumulative impacts of the factors had affected the landslide potential over time, and the landslide was triggered when the critical condition was reached. Therefore, not only the spatial factors but the temporal consecutive characteristics should be considered in the model. For this purpose, a novelty attempt was made by including the consecutive changes of landslide areas in this study. The antecedent landslide area was adopted as a temporal characteristic factor in the proposed model, and its effect was discussed in this paper.

Finally, the performance of the proposed RF model was evaluated, and two events of heavy rainfalls in 2017 were used for specific event-driven performance tests. The insights from the newly developed RF model were also included in this paper.

2. Study Areas and Environmental Factor Database

2.1. Study Areas

In the middle south of Taiwan, the watershed areas of the ChenYuLan River, the Lao- nong River, and the Qishan River (Figure 1) were chosen to develop the landslide potential evaluation model. The ChenYuLan River watershed is located in the mountainous area of Nantou County. The mainstream ChenYuLan River is one of the important tributaries of the Zhuoshui River, with a total length of about 42 km. The terrain of the ChenYuLan River is characterized by a significant height difference and steep slope. The watershed area of ChenYuLan River is about 448 km², and the average gradient is over 55%. Most of the Laonong River watershed area is located in Kaohsiung City. The mainstream of the Laonong River is the first tributary of the Gaoping River basin, with a total length of about 137 km. The terrain of the Laonong River is characterized as the valley topography, and the downstream is a suddenly widened sediment area. The watershed area of the Laonong River is extensive, with an area of 1408.71 km² and an average slope of over 65%. The Qishan River watershed area is located in Kaohsiung City and Chiayi County. The mainstream Qishan River is a tributary of the Gaoping River, with a total length of about 117 km. The terrain of the Qishan River is characterized as the terraces valley. The river is suddenly widened at the downstream section. The watershed of Qishan River is about 750.79 km² and with an average slope of more than 55%.

To better understand what has occurred in the region, satellite images from 2011 to 2016 were used to build the model factor for this study. The images had undergone a radiometric correction and orthorectification process. The satellite images of 2011 and 2016 are shown as examples in Figure 2.

2.2. Slope Units

To develop the RF models, the area impacted by landslides was first calculated based on slope units. A slope unit is defined as one slope part or the left/right part of a watershed. Slope units can be topologically divided by the watershed divide and drainage line (Figure 3) with the help of the GIS tool [22]. We used the slope unit as the analysis basis to physically and adequately represent the local conditions. Then, the environmental database was applied in accordance with the slope units at the site of interest. The ChenYuLan River, Laonong River, and Qishan River watersheds are 6651, 21,279, and 10,985 units, respectively (Figure 4).

2.3. Environmental Database and Model Factors

From research and studies, the landslide factor used for analysis included slope, lithology, aspect, elevation, land use, river system-related (including distance, density, etc.), vegetation-related (including species, density, age, etc.), geology (including distance, type, geological structure, etc.), soil-related (including type, thickness, content, etc.), slope shape, curvature (including horizontal, vertical, etc.), rainfall (including accumulated rainfall, rainfall intensity), and many more.

Factors directly or indirectly related to landslide occurrence were analyzed by their importance to establish the model for landslide potential evaluation. These factors were generally classified as environmental and triggering factors [23,24,25]. The rainfall was the primary concern, and the rainfall intensity (maximum hourly precipitation, I_max) and effective accumulated rainfall (R_te) were used as triggering factors in this study. In addition, elevation, slopes, slope aspects, normalized difference vegetation index (NDVI), distance to the river (stream), geology type, and the ratio of incremental landslide area were used as environmental factors of hillside slope in the study. These factors (

Table 1. Environmental database of factors.

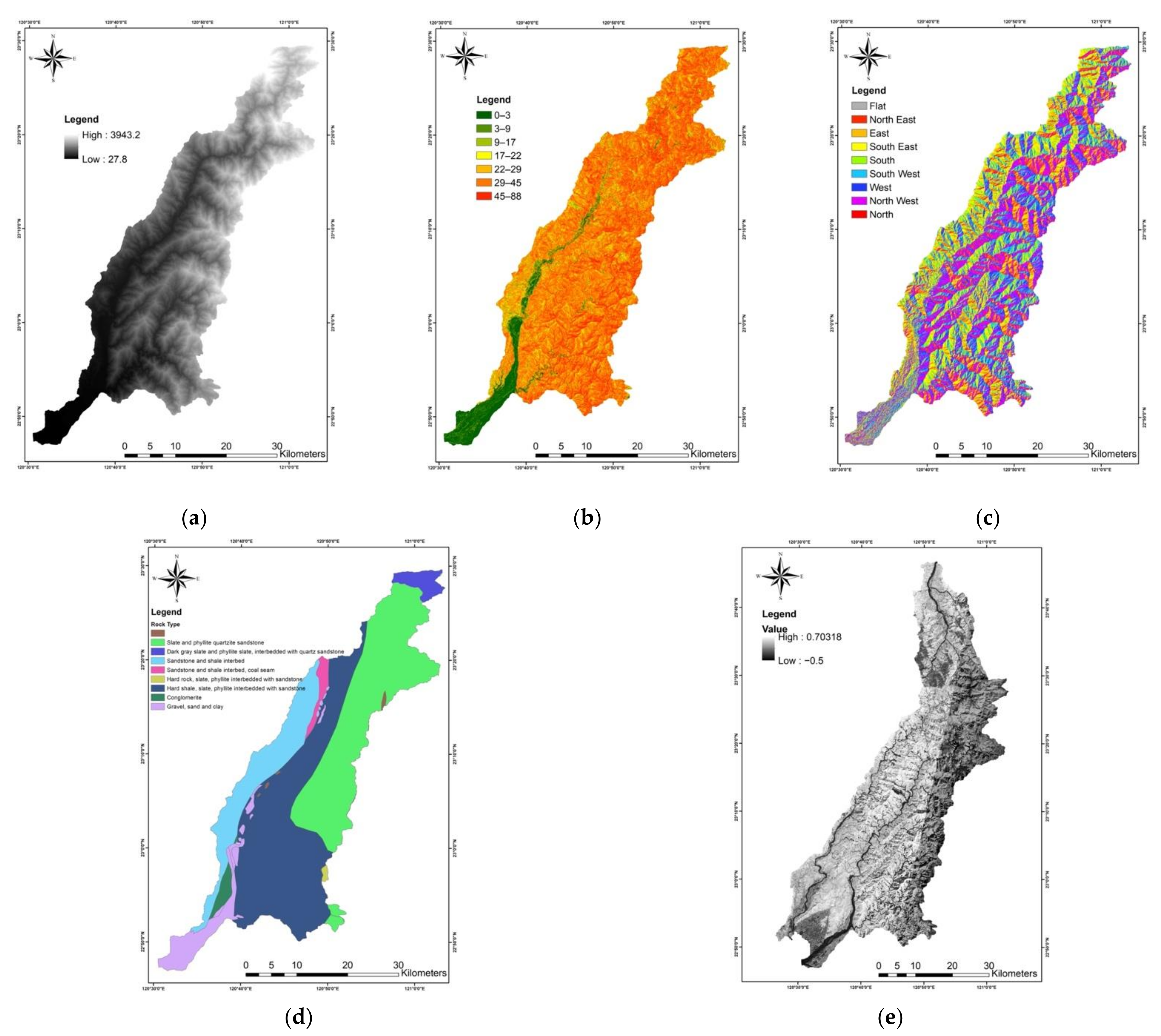
Type	Source	Factors	Data Format
Grid	DEM	Elevation Slope (degree) Aspect	Raster, 5 m
	SPOT satellite images	NDVI (from 2011 to 2016)	Raster, 20 m
	Rainfall	Maximum hourly rainfall (Imax) of events from 2006 to 2016 Effective accumulated rainfall (Rte) of events from 2006 to 2016	Raster, 20 m
Vector	River system	River system Distance to river (stream)	Shapefile, Polygon
	Geology Map	Geology type
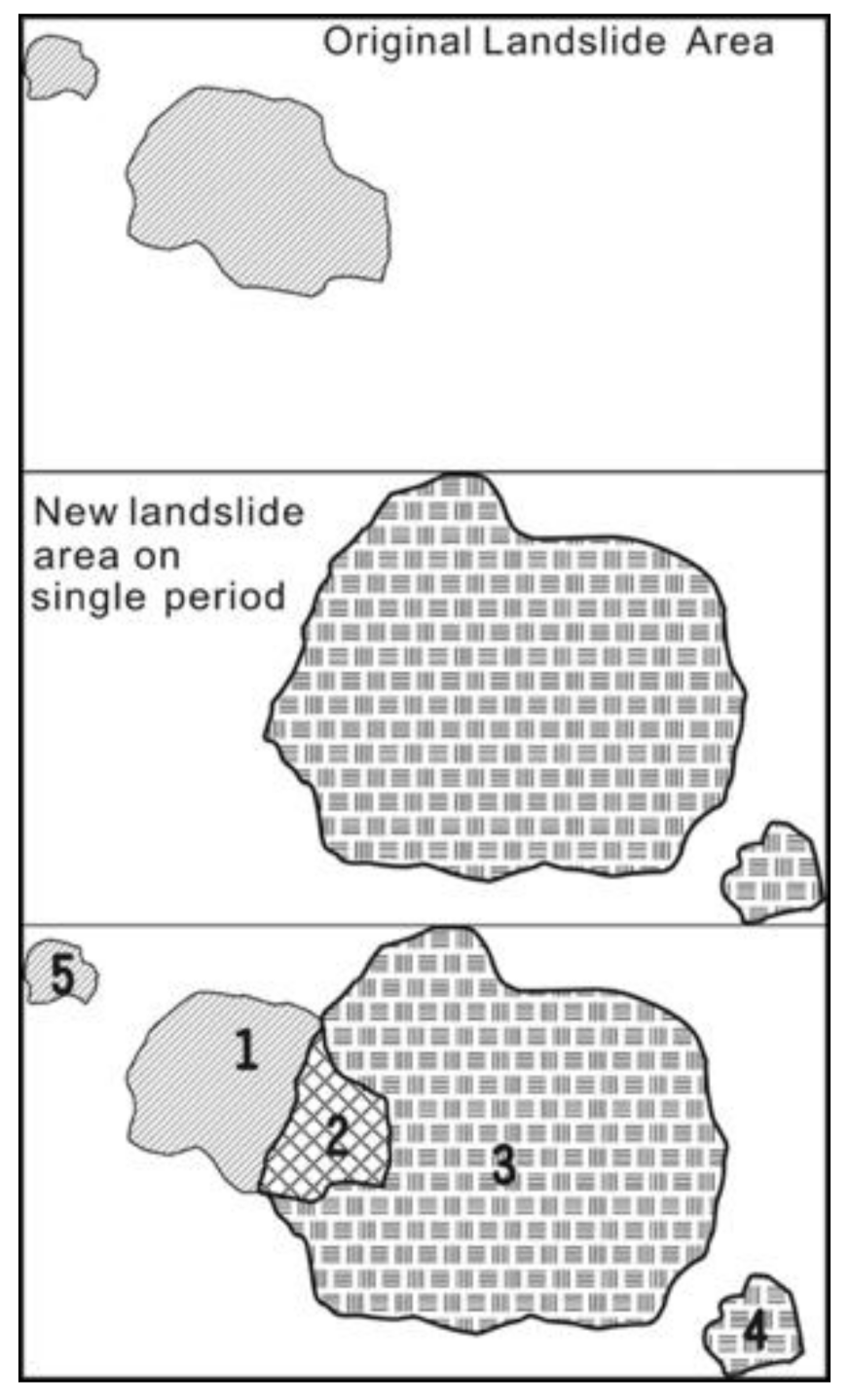
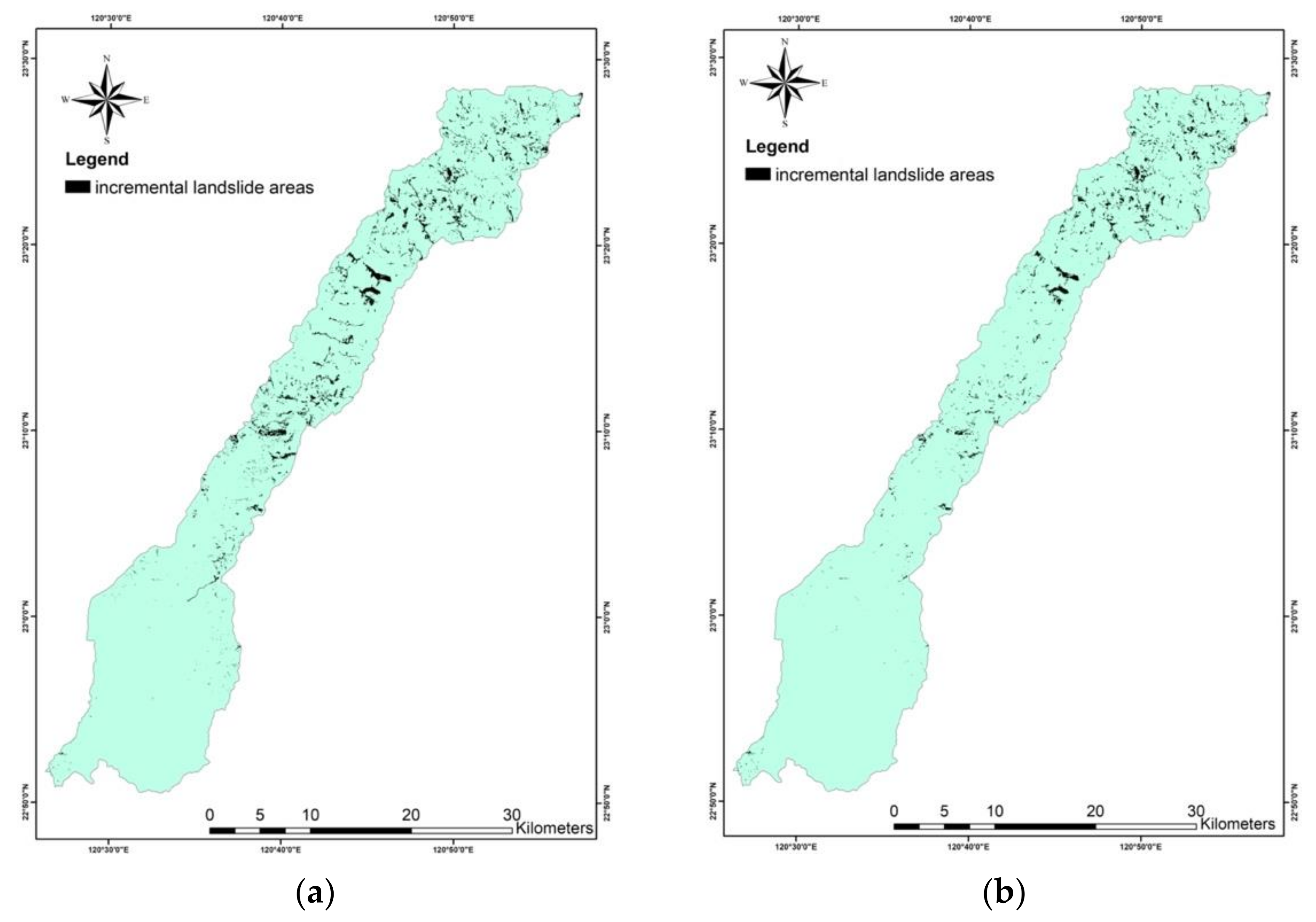
	Landslide 1	Incremental landslide areas, from 2011 to 2016

¹ the source of satellite images was from Taiwan’s government open data platform (https://data.gov.tw accessed on: 27 August 2021).

) were collected from satellite images, digital elevation model (DEM), and monitoring records, and a GIS database was created to obtain and process the necessary content of factors. The basic statistical information of the database is shown in

Table 2. Statistical information of database.

Watersheds	Year	Imax (mm) (Mean, SD)	Rte (mm) (Mean, SD)	NDVI (Average)	Slope (Degree) (Average)	Elevation (m) (Average)	Distance to the River (m) (Average)
ChenYuLan River	2011	(46.7, 14.2)	(289, 84)	0.1261	33.7	1591.2	287.3
	2012	(40.1, 9.9)	(223, 46)	−0.1072
	2013	(53.2, 23.1)	(166, 39)	0.0344
	2014	(21.4, 4.0)	(202, 75)	0.0497
	2015	(31.7, 3.5)	(139, 28)	0.0055
	2016	(55.4, 6.8)	(509, 58)	0.0893
Laonong River	2011	(50.4, 11.8)	(509, 152)	0.1016	32.2	1508.0	265
	2012	(49.5, 10.7)	(248, 85)	−0.1372
	2013	(62.9, 18.7)	(289, 73)	0.0225
	2014	(41.4, 13.4)	(322, 74)	−0.0051
	2015	(53.7, 13.9)	(347, 179)	0.0235
	2016	(58.8, 9.8)	(421, 161)	−0.0010
Qishan River	2011	(49.8, 12.1)	(322, 117)	0.0956	24.7	926.8	190.6
	2012	(49.0, 8.2)	(187, 58)	−0.0376
	2013	(56.1, 15.1)	(311, 130)	−0.2053
	2014	(40.9, 6.9)	(278, 74)	0.0799
	2015	(50.3, 9.9)	(287, 103)	0.0997
	2016	(64.1, 8.8)	(473, 70)	−0.0062

.

In the database, the landslide area, especially the incremental landslide area, was considered significant when describing the landslide situation in each target area. Figure 5 illustrates the difference of landslide areas between two periods of SPOT image. The total area, labeled as No. 3 and No. 4 in the figure, was treated as the new landslide areas during a single period. The ratios related to landslide areas, i.e., the proportions of No. 1, No. 2, No. 3, No.4, and No. 5 in Figure 5 were calculated for each slope unit after satellite image processing and interpretation. The condition of a slope unit would be classified as landslide when the ratio of incremental landslide area (No. 3 + No. 4) was greater or equal to 5%. The landslide ratios on each period from 2006 to 2016 were estimated and used in the proposed model.

According to the Soil and Water Conservation Bureau (SWCB), Taiwan, a rainfall event starts when the hourly rainfall is greater than 4 mm. The event ends when the accumulated rainfall of continuous 6 h does not exceed 24 mm, and any hourly rain is less than 10 mm during the 6-h period (Figure 6).

The factor, effective accumulated rainfall, R_te, was calculated by the expression as follows.

$$R_{te}=R_0+{\displaystyle \sum }_{i=1}^7{\left(0.7\right)}^i{R}_i$$

(1)

where the R₀ is the current daily rainfall, and R_i represents the daily rainfall i-th day before.

The maximum hourly rainfall, I_max, was used to label the timing of landslides by assuming that the landslide occurred when the hourly precipitation reached Imax. First, for a given rainfall event, each grid’s I_max and R_te were calculated by applying Kriging interpolation based on the data of reference weather stations. Then, the I_max and R_te of a slope unit were determined by averaging the values of grids within the slope unit. Figure 7 shows the processed results of factors in the study areas, and Figure 8 shows an example of the interpolation of rainfall of given rainfall events in 2011.

3. Development of Landslide Potential Evaluation Model

Machine learning, a branch of artificial intelligence (AI), has become popular in various fields. Computer algorithms are necessary and essential in machine learning to robustly analyze and predict information based on learning from training data [22]. Among its applications, the use of machine learning has increased in landslide susceptibility analysis [10]. The methods of artificial neural network (ANN) [26,27], logistic regression [28], support vector machine (SVM) [29], and random forest [11,12] have been popular for landslide-related analysis.

The random forest is a classifier based on the ensemble method and consists of many decision trees. Each tree must meet the basic classification ability and certain accuracy conditions. The built-in classifier performance will eventually be better than the result predicted by a single classifier. The random forest will randomly take the data for training, and the output will be based on the voting in each decision tree. At present, random forests are also widely used due to the advantages of accurate classification, the capability of large amounts of data processing, multi-variable data, and fast calculations.

In the analysis of landslide prediction, rainfalls and landslides in the past years may cause the current site condition to be unstable in the investigated areas. Therefore, the impacts of temporal characteristics should be taken into account in the analysis. Thus, the antecedent rainfalls and landslides were used as the temporal characteristics in the proposed random forest model. The data of the past five years were considered to represent the previous environmental impacts related to current landslide conditions.

In addition to the six environmental factors of elevation, slope, slope aspects, geology type, distance to the river, and NDVI, the temporal factors of annual landslide areas in the past five years were also considered. Therefore, these temporal factors were included in the model in annual area ratios of five-type landslides (Figure 5) in a slope unit. Furthermore, the triggering factors of annual I_max and annual R_te of a slope unit in the past five years were also treated as temporal characteristics in the model. Therefore, there was a total of 43 factors (6 environmental factors, 25 annual landslide area ratios in the past five years, ten annual factors of I_max and R_te in the past five years, and current yearly I_max and R_te) in the model database. The examples of annual landslide areas are shown in Figure 9.

The program WEKA (Waikato Environment for Knowledge Analysis) was used to develop the random forest model. The data were processed by standardization method, Z-Score, and normalization procedure (values of 0 to 1). From a total of 38,915 slope units, 10,000 units were randomly selected for model development, with a landslide to a non-landslide ratio of 1:1. In total, 50% of data were used for training during the development, and the 50% left were used for internal validation. The supervised classification algorithm was applied in training.

Validation indices are usually used to evaluate the performance of a model. In machine learning, the validation indices can be divided into classification metrics and regression metrics. The proposed model was mainly a binary case. Thus, the confusion matrix of classification metrics (

Table 3. The confusion matrix of landslide evaluation.

Predicted\Actual	Landslide (1)	Non-Landslide (0)
Landslide (1)	True Positive (TP)	False Positive (FP)
Non-Landslide (0)	False Positive (FP)	True Negative (TN)

) was used to validate the model performance.

The validation indices from Table 2 include accuracy (ACC), precision, sensitivity (or recall), Kappa (kappa index of agreement, KIA), and receiver operating characteristic curve (ROC) and area under the curve (AUC). These indices were used to validate the performance of the proposed model.

The random forest model was trained using data from 2006 to 2010 to obtain the 5-year temporal factors (rainfall factors of I_max and R_te, and ratios of antecedent landslides) and the data from 2011 as the input to represent the current state. After establishing the RF model, the landslide area data from 2012 to 2016 and the annual I_max and R_te were used as the external validation to analyze the model performance of prediction. In addition to the confirmation of the 43-factor model, the version of the model using only eight factors (elevation, slope, slope aspects, geology type, distance to river, and NDVI, and I_max and R_te) in 2011, i.e., without factors of antecedent landslide ratios, was also evaluated. The training and validation results were represented by the indices of the confusion matrix, as shown in

Table 4. RF Model training and validation results.

Training/Validation Year	Accuracy	Precision	Recall	Kappa	AUC
2011 (model training)	0.808	0.791	0.833	0.616	0.889
2012	0.716	0.860	0.515	0.431	0.839
2013	0.706	0.870	0.485	0.412	0.844
2014	0.839	0.773	0.708	0.622	0.901
2015	0.833	0.664	0.828	0.616	0.898
2016	0.834	0.619	0.819	0.592	0.897
2011 (8 factors)	0.702	0.680	0.758	0.406	0.776

. The examples of training and validation results are shown in Figure 10 and Figure 11.

From Table 4, the analysis showed that the accuracy and sensitivity (recall) of the RF model had been greatly improved after adding factors of antecedent landslide ratios, which indicated a noticeable improvement in the model’s capability of classification. Although the overall ACC of the model was improved due to a large amount of TN, the lower missing rate, i.e., 1-recall, from the RF model, was critical to denote more landslide samples. The Kappa value showed fair to good accuracy [30], within an acceptable range (0.4~0.74).

It was also noted that the precision values from 2012 to 2014 were at the same level of around 80% as 2011, and the precision from 2015 and 2016 was slightly lower than the level of the trained model. The precision variation from the tests had indicated that the proposed RF model was valuable and referential when applied to predict future landslide potential without re-training the RF model. However, it was also noted that the model might need to update every three years if precision performance was a concern.

In any subsequent year (2012 to 2016), the AUC value of the temporal-factor-added RF model was higher than that of the model that did not include factors of antecedent landslide ratios. The validation results show that the RF model with temporal characteristics had better performance than the model without those temporal factors.

4. Model Performance Evaluation for Individual Rainfall Events

Instead of using annual I_max and R_te for analysis, the selected rainfall events in 2017 (

Table 5. Selected landslide disaster cases in 2017 [31,32].

Event	Imax/Rte (mm) 1	Disaster Location 2	Time & Date	Rainfalls at Occurrence 3	Disaster Overview	Disaster Scale	Hazard Type
0601 Heavy Rainfall (2017/06/02 ~ 2017/06/04)	76.7/749.0	Shuili Township/Xinshan Village (X:236472 Y:2628694)	8:00 on 3 June	I = 43 mm/h R = 270 mm (Rainfall Sta.: XiLuan 01H47)	During the 0601 Heavy Rainfall, the landslide of Renlun Forest Road had caused blockage of about 10 m on Taiwan Provincial Highways 21.	The landslide scale was about 20 m in length, 10 m in width, and 2 m in depth. The landslide area was 200 m2, and the amount of debris accumulated was about 400 m3.	landslide
		Xinyi Township/Mingde Village (X:235029 Y: 2622652)	15:00 on 3 June	I = 17 mm/h R = 430 mm (Rainfall Sta.: Xinyi C0I080)	During the heavy rainfall, the slopes on both sides of potential debris flow torrent DF187 collapsed. As a result, existing rivers were piled up with soil and rocks, and a large amount of debris could not be discharged in time, resulting in blockage of 87 k~88 k of Taiwan Provincial Highways 21.	The landslide was about 10 m long, 5 m wide, 2 m deep and covered an area of 100 m2. The accumulation of debris was about 600 m3, with the length about 100 m, the width about 3 m, and the depth about 2 m.	landslide
Typhoons Nesat and Haitang	62.2/307.8	Xinyi Township/Tongfu Village (X:239004 Y:2607456)	7:50 on 30 July	I = 0 mm/h R = 150 mm (Rainfall Sta.: Heshe C1I070)	During Typhoons Nesat and Haitang, the slope at 115 k+540 of Taiwan Provincial Highways 21 collapsed and caused road blockage.	The landslide was about 15 m long, 10 m wide, and 2 m deep. The area of soil and debris was 150 m2, and the accumulated earth volume was about 3500 m3.	rock-fall, landslide

¹ Reference rainfall station: Nan Tian Chih (0601 event); San Di Men (Typh. Nesat and Haitang). ² at Nantou County, coordinate using TWD97. ³ The recorded rainfalls when the landslide occurred. R: accumulated rainfall; I: hourly rainfall.

) were used to test the model’s ability of landslide potential prediction if only short-period data were available. The test results would help to understand the capability of the RF model in practical applications during disaster response operations.

Based on the data from the 73 rainfall stations surrounding the study area, the I_max and R_te of each event (Table 5) were determined and inputted into the model as the factors of current annual rainfall indices. The in-situ rainfall conditions, I and R, disaster overview, and disaster scale were available from the disaster case reports, as shown in Table 5. The proposed RF model obtained the predicted landslide areas using events’ rainfall conditions, and the result of the ChenYuLan River watershed was shown in Figure 12. The local government reported the landslide disasters, and three locations were in the study areas. Figure 13 shows the predicted landslide locations and observed ones from the disaster reports of events. It is noted that the reported three locations of landslides are not precisely at the expected locations by the proposed RF model. The model did not capture the two landslide locations at the northern ChenYuLan River watershed. However, the third landslide location at Tongfu Village was close to the predicted area by the model. The results imply that the “hit rate” of the RF model might not perform well when targeting event-based predictions. A rational inference was that the rainfall conditions used in the model input were different from the actual local rainfall conditions since the maximum rainfall intensity was determined from the surrounding rainfall stations, which might not be suitable to represent the local conditions. Another possible explanation of the model’s miss-hit was the lack of past five years’ data of landslides at the two northern locations in the ChenYuLan River watershed. Nevertheless, the proposed RF model had a promising performance for landslide potential evaluation when applied to rainfall events.

5. Conclusions

Based on the analysis results from the study, the importance of antecedent landslide areas in the past five years has been emphasized and discussed. Furthermore, the performance of the proposed RF model was also highlighted by conducting annual validation from 2011 to 2016. As a result, the following conclusions were derived.

• According to the analysis results, adding temporal characteristics had significantly improved the performance of landslide potential prediction by the proposed random forest model.
• The contribution of antecedent landslide ratios was significant in improving the model performance. The performance improvement of the model indicated that the time-dependent factors should be taken into consideration, in terms of a series of inputs within a period, such as the five years in this study.
• The results of better model performance had shown the significance of cumulative change with time. Therefore, a relevant factor, e.g., the antecedent landslide ratios of the past five years, to describe the time effects was significant in landslide potential evaluation.
• The trained model by considering annual temporal factors provided an angle to estimate the landslide potential in event-type disaster responses.