Impact of Fully Coupled Hydrology-Atmosphere Processes on Atmosphere Conditions: Investigating the Performance of the WRF-Hydro Model in the Three River Source Region on the Tibetan Plateau, China
Abstract
1. Introduction
2. Study Area, Model Description and the Numerical Experiment Design
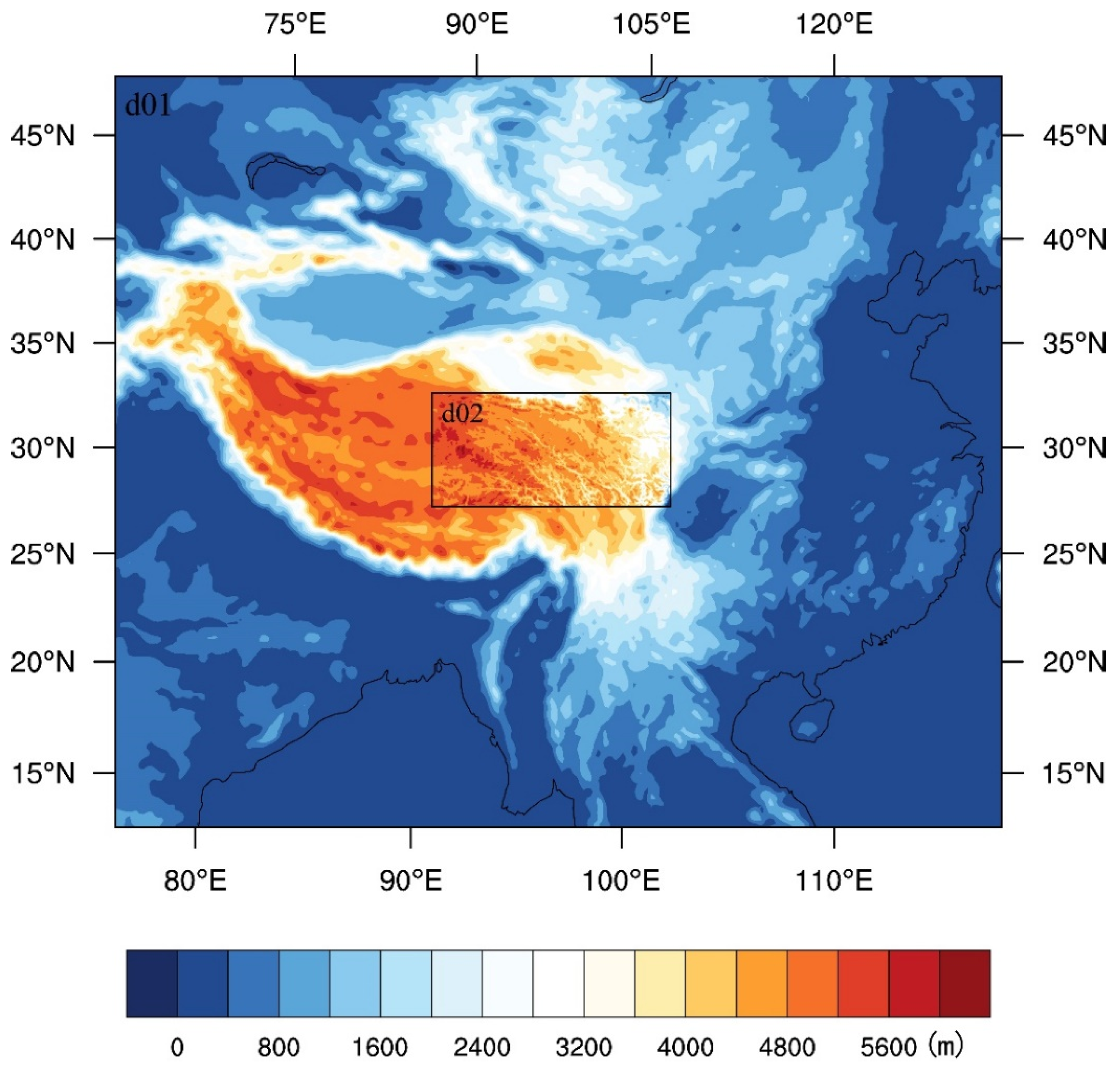
2.1. Study Area
2.2. Model Description
2.2.1. WRF-ARW and NOAH-MP
2.2.2. WRF-Hydro
2.3. Numerical Experiment Design
2.3.1. Model Calibration
2.3.2. Coupled Simulations
3. Validation Data and Analysis Metrics
3.1. Validation Data
3.2. Skill Metrics
4. Results
4.1. Streamflow Simulation
4.2. Comparison with In-Situ Observations
4.2.1. Comparison with CMA Data
4.2.2. Comparison with Turbulent Heat Flux Observation
4.3. Pattern Difference and Time Variation
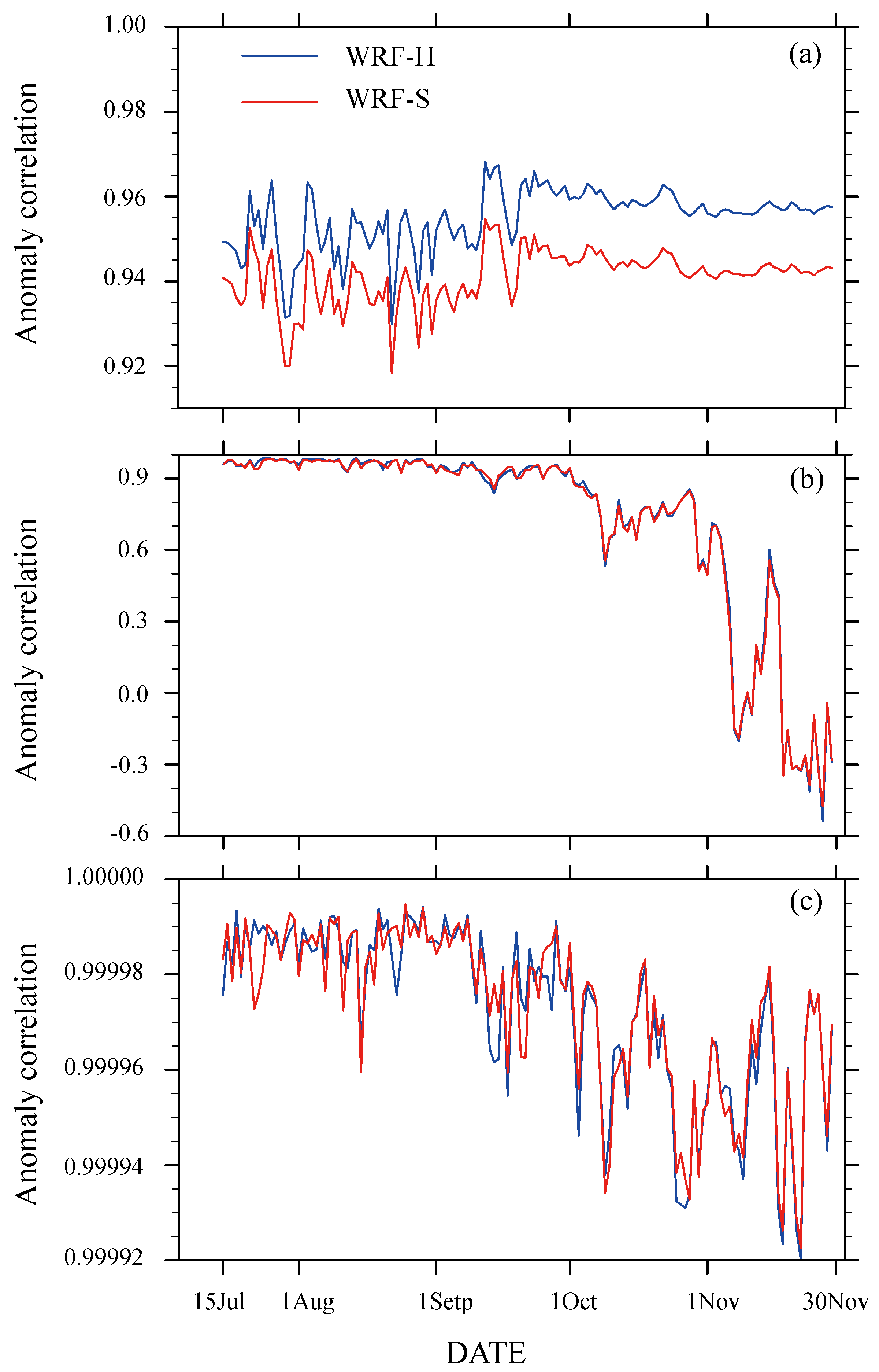
4.3.1. Spatial Validation
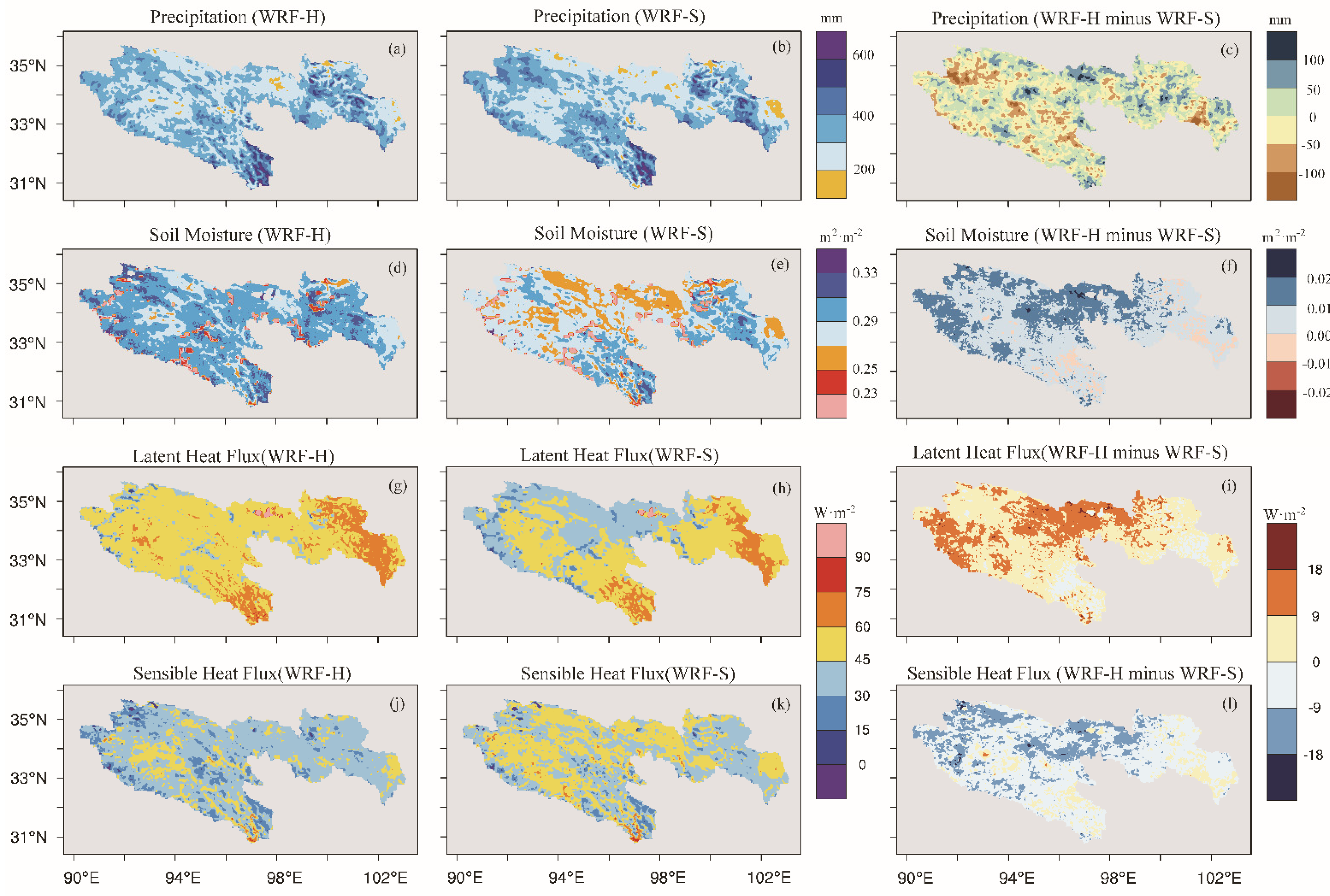
4.3.2. Spatial Distribution
4.3.3. Time Variation
4.4. Precipitation Structure and Boundary Layer Variables
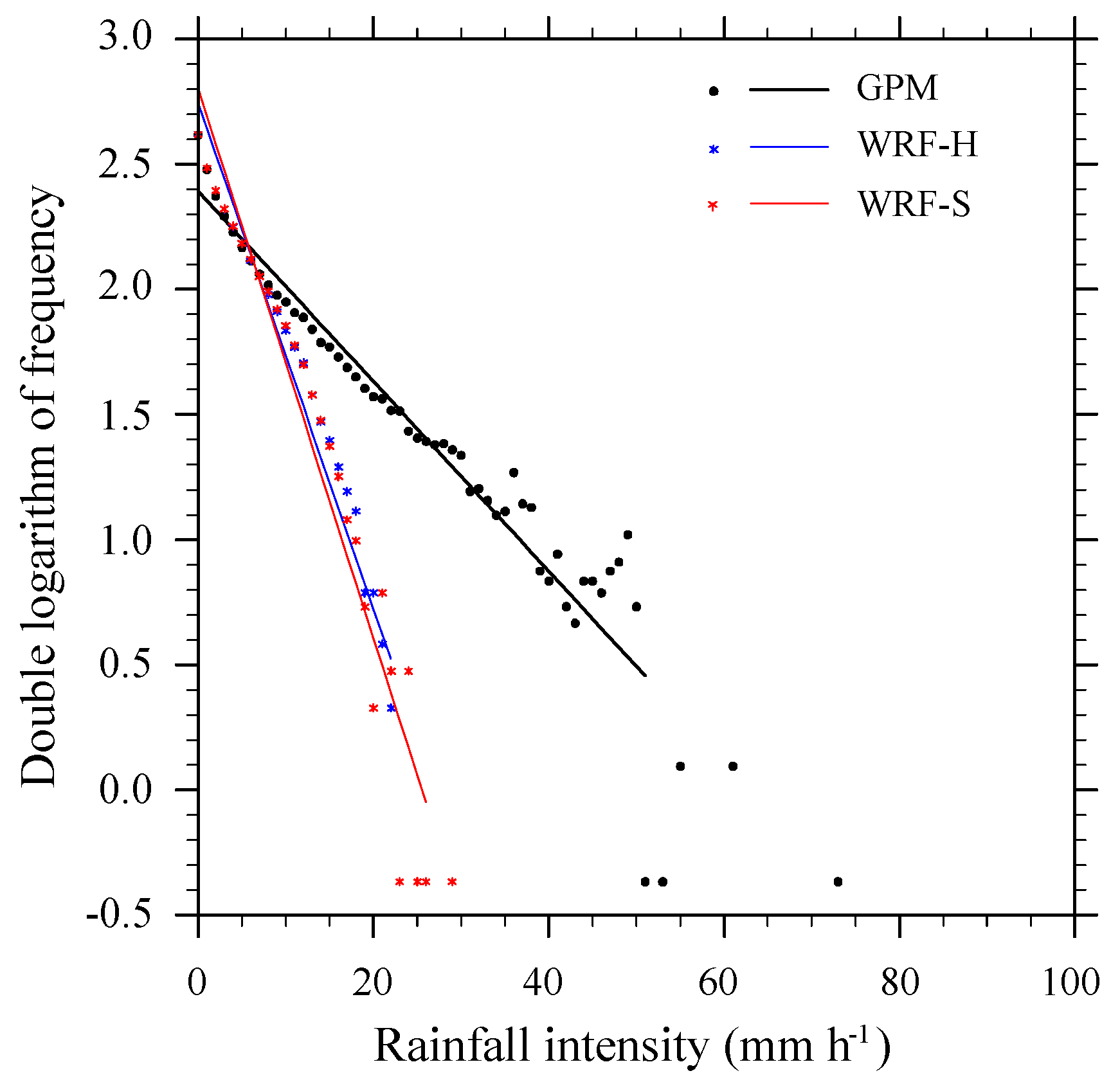
4.4.1. Precipitation Frequency-Intensity Structure
4.4.2. Boundary Layer Variables
5. Discussion
- The reproduction of the daily discharge amount of the three stations has a Nash-Sutcliffe model efficiency generally above 0.55, demonstrating the potential of WRF-Hydro for hydrological forecasting in SRTR.
- In the coupled experiment, WRF-Hydro made an improvement of 13.48% in RMSE and 8.31% in CC above WRF-ARW when compared against CMA data, and an improvement of 6.6% in RMSE and 1% in CC when compared against turbulent heat fluxes observation. WRF-Hydro tends to overestimate the soil moisture of the western part of the SRTR, but less so in the eastern part and areas with wetter soil moisture. This difference occurs mainly during the period when the soil is not frozen. Although the root mean square error of WRF-Hydro is larger than that of WRF-ARW compared against SMAP and GLEAM, WRF-Hydro scores higher in the anomaly correlation coefficient. These findings show the significance of lateral flow in soil moisture simulation.
- The coupled WRF-Hydro results in an increase in latent heat flux, a decrease in sensible heat flux, and a decrease in soil surface temperature due to the moist soil. The change in turbulent heat flux gives the WRF-Hydro simulation an enormous CAPE and easier convection, reducing precipitation intensity-frequency errors.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fersch, B.; Senatore, A.; Adler, B.; Arnault, J.; Mauder, M.; Schneider, K.; Voelksch, I.; Kunstmann, H. High-resolution fully coupled atmospheric-hydrological modeling: A cross-compartment regional water and energy cycle evaluation. Hydrol. Earth Syst. Sci. 2020, 24, 2457–2481. [Google Scholar] [CrossRef]
- Oleson, K.W.; Niu, G.Y.; Yang, Z.L.; Lawrence, D.M.; Thornton, P.E.; Lawrence, P.J.; Stoeckli, R.; Dickinson, R.E.; Bonan, G.B.; Levis, S.; et al. Improvements to the Community Land Model and their impact on the hydrological cycle. J. Geophys. Res. Biogeosci. 2008, 113, G01021. [Google Scholar] [CrossRef]
- Arnault, J.; Wagner, S.; Rummler, T.; Fersch, B.; Bliefernicht, J.; Andresen, S.; Kunstmann, H. Role of runoff-infiltration partitioning and resolved overland flow on land-atmosphere feedbacks: A case study with the WRF-hydro coupled modeling system for west Africa. J. Hydrometeorol. 2016, 17, 1489–1516. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Naabil, E.; Lamptey, B.L.; Arnault, J.; Olufayo, A.; Kunstmann, H. Water resources management using the WRF-Hydro modelling system: Case-study of the Tono dam in West Africa. J. Hydrol. Reg. Stud. 2017, 12, 196–209. [Google Scholar] [CrossRef]
- Shen, M.; Piao, S.; Jeong, S.-J.; Zhou, L.; Zeng, Z.; Ciais, P.; Chen, D.; Huang, M.; Jin, C.-S.; Li, L.Z.X.; et al. Evaporative cooling over the Tibetan Plateau induced by vegetation growth. Proc. Natl. Acad. Sci. USA 2015, 112, 9299–9304. [Google Scholar] [CrossRef] [PubMed]
- Avolio, E.; Cavalcanti, O.; Furnari, L.; Senatore, A.; Mendicino, G. Brief communication: Preliminary hydro-meteorological analysis of the flash flood of 20 August 2018 in Raganello Gorge, southern Italy. Nat. Hazards Earth Syst. Sci. 2019, 19, 1619–1627. [Google Scholar] [CrossRef]
- Schaake, J.C.; Koren, V.I.; Duan, Q.Y.; Mitchell, K.; Chen, F. Simple water balance model for estimating runoff at different spatial and temporal scales. J. Geophys. Res. Atmos. 1996, 101, 7461–7475. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.-L. Effects of frozen soil on snowmelt runoff and soil water storage at a continental scale. J. Hydrometeorol. 2006, 7, 937–952. [Google Scholar] [CrossRef]
- Swenson, S.C.; Lawrence, D.M.; Lee, H. Improved simulation of the terrestrial hydrological cycle in permafrost regions by the Community Land Model. J. Adv. Model. Earth Syst. 2012, 4, M08002. [Google Scholar] [CrossRef]
- Clark, M.P.; Fan, Y.; Lawrence, D.M.; Adam, J.C.; Bolster, D.; Gochis, D.J.; Hooper, R.P.; Kumar, M.; Leung, L.R.; Mackay, D.S.; et al. Improving the representation of hydrologic processes in Earth System Models. Water Resour. Res. 2015, 51, 5929–5956. [Google Scholar] [CrossRef]
- Wood, E.F.; Roundy, J.K.; Troy, T.J.; Van Beek, L.P.H.; Bierkens, M.F.P.; Blyth, E.; De Roo, A.; Doll, P.; Ek, M.; Famiglietti, J. Hyperresolution global land surface modeling: Meeting a grand challenge for monitoring Earth’s terrestrial water. Water Resour. Res. 2011, 47, W05301. [Google Scholar] [CrossRef]
- Ji, P.; Yuan, X.; Liang, X.-Z. Do lateral flows matter for the hyperresolution land surface modeling? J. Geophys. Res. Atmos. 2017, 122, 12077–12092. [Google Scholar] [CrossRef]
- Wagner, S.; Fersch, B.; Yuan, F.; Yu, Z.; Kunstmann, H. Fully coupled atmospheric-hydrological modeling at regional and long-term scales: Development, application, and analysis of WRF-HMS. Water Resour. Res. 2016, 52, 3187–3211. [Google Scholar] [CrossRef]
- Arnault, J.; Wei, J.; Rummler, T.; Fersch, B.; Zhang, Z.; Jung, G.; Wagner, S.; Kunstmann, H. A Joint soil-vegetation-atmospheric water tagging procedure with WRF-hydro: Implementation and application to the case of precipitation partitioning in the upper danube river basin. Water Resour. Res. 2019, 55, 6217–6243. [Google Scholar] [CrossRef]
- Yuan, X.; Ji, P.; Wang, L.; Liang, X.-Z.; Yang, K.; Ye, A.; Su, Z.; Wen, J. High-resolution land surface modeling of hydrological changes over the sanjiangyuan region in the eastern Tibetan Plateau: 1. Model development and evaluation. J. Adv. Model. Earth Syst. 2018, 10, 2806–2828. [Google Scholar] [CrossRef]
- Yang, K.; Wu, H.; Qin, J.; Lin, C.; Tang, W.; Chen, Y. Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle: A review. Glob. Planet. Chang. 2014, 112, 79–91. [Google Scholar] [CrossRef]
- Wu, G.X.; Zhang, Y.S. Tibetan Plateau forcing and the timing of the monsoon onset over South Asia and the South China Sea. Mon. Weather Rev. 1998, 126, 913–927. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, K.; Zhou, X.; Chen, D.; Lu, H.; Ouyang, L.; Chen, Y.; Lazhu; Wang, B. Synergy of orographic drag parameterization and high resolution greatly reduces biases of WRF-simulated precipitation in central Himalaya. Clim. Dyn. 2020, 54, 1729–1740. [Google Scholar] [CrossRef]
- Xu, X.; Lu, C.; Shi, X.; Gao, S. World water tower: An atmospheric perspective. Geophys. Res. Lett. 2008, 35, L20815. [Google Scholar] [CrossRef]
- Liu, X.D.; Yin, Z.Y. Spatial and temporal variation of summer precipitation over the eastern Tibetan Plateau and the North Atlantic oscillation. J. Clim. 2001, 14, 2896–2909. [Google Scholar] [CrossRef]
- Tao, S.Y.; Ding, Y.H. Observational evidence of the influence of the Qinghai-Xizang (Tibet) Plateau on the occurrence of heavy rain and severe convective storms in China. Bull. Am. Meteorol. Soc. 1981, 62, 23–30. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, M.; Chen, J.; Bian, L.; Zhang, G.; Liu, H.; Li, S.; Zhang, H.; Zhao, Y.; Suolongduoji; et al. A comprehensive physical pattern of land-air dynamic and thermal structure on the Qinghai-Xizang Plateau. Sci. China Ser. D 2002, 45, 577–594. [Google Scholar] [CrossRef]
- Wang, J.Z.; Yang, Y.Q.; Xu, X.D.; Zhang, G.Z. A monitoring study of the 1998 rainstorm along the Yangtze River of China by using TIPEX data. Adv. Atmos. Sci. 2003, 20, 425–436. [Google Scholar] [CrossRef]
- Yasunari, T.; Miwa, T. Convective cloud systems over the Tibetan Plateau and their impact on meso-scale disturbances in the Meiyu/Baiu frontal zone—A case study in 1998. J. Meteorol. Soc. Jpn. 2006, 84, 783–803. [Google Scholar] [CrossRef][Green Version]
- Zhao, Y.; Xu, X.; Chen, B.; Wang, Y. The upstream “strong signals” of the water vapor transport over the Tibetan Plateau during a heavy rainfall event in the Yangtze River Basin. Adv. Atmos. Sci. 2016, 33, 1343–1350. [Google Scholar] [CrossRef]
- Lu, C.; Yu, G.; Xie, G. Tibetan plateau serves as a water tower. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, IGARSS’05, Seoul, Korea, 25–29 July 2005; pp. 3120–3123. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, Y. Preliminary applicable analysis of SWAT model in the three rivers source area. Meteorol. Environ. Sci. 2014, 37, 102–107. (In Chinese) [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Yao, T.; Liu, X.; Wang, N. The magnitude of climate change in the Tibet Plateau. Chin. Sci. Bull. 2000, 45, 98–106. [Google Scholar] [CrossRef]
- Prein, A.F.; Heymsfield, A.J. Increased melting level height impacts surface precipitation phase and intensity. Nat. Clim. Chang. 2020, 10, 771–776. [Google Scholar] [CrossRef]
- FU, Y.; Liu, Q.; ZI, Y.; Feng, S.; LI, Y.; Liu, G. Summer precipitation and latent heating over the Tibetan Plateau based on TRMM measurements. Plateau Mt. Meteorol. Res. 2008, 28, 8–18. (In Chinese) [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Yang, T.; Liang, K.; Liu, C. Evaluation of streamflow simulation results of land surface models in GLDAS on the Tibetan plateau. J. Geophys. Res. Atmos. 2016, 121, 12180–12197. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment—Part 1: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land-surface water and energy fluxes for general-circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Oleson, K.W.; Flanner, M.G.; Thornton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, X.; Yang, Z.-L.; Levis, S.; Sakaguchi, K.; et al. Parameterization improvements and functional and structural advances in Version 4 of the community land model. J. Adv. Model. Earth Syst. 2011, 3, M03001. [Google Scholar] [CrossRef]
- Niu, G.; Yang, Z.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116, D12109. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R.; Debele, B.; Hao, F. Runoff simulation of the headwaters of the Yellow River using the SWAT model with three snowmelt algorithms. J. Am. Water Resour. Assoc. 2008, 44, 48–61. [Google Scholar] [CrossRef]
- Cuo, L.; Zhang, Y.X.; Gao, Y.H.; Hao, Z.C.; Cairang, L.S. The impacts of climate change and land cover/use transition on the hydrology in the upper Yellow River Basin, China. J. Hydrol. 2013, 502, 37–52. [Google Scholar] [CrossRef]
- Sheng, M.Y.; Lei, H.M.; Jiao, Y.; Yang, D.W. Evaluation of the runoff and river routing schemes in the community land model of the Yellow River Basin. J. Adv. Modeling Earth Syst. 2017, 9, 2993–3018. [Google Scholar] [CrossRef]
- Zheng, D.; van der Velde, R.; Su, Z.; Wen, J.; Wang, X.; Yang, K. Impact of soil freeze-thaw mechanism on the runoff dynamics of two Tibetan rivers. J. Hydrol. 2018, 563, 382–394. [Google Scholar] [CrossRef]
- Fang, Y.; Zhang, X.; Niu, G.; Zeng, W.; Zhu, J.; Zhang, T. Study of the spatiotemporal characteristics of meltwater contribution to the total runoff in the upper changjiang river basin. Water 2017, 9, 165. [Google Scholar] [CrossRef]
- Gochis, D.J.; Barlage, M.; Cabell, R.; Casali, M.; Dugger, A.; FitzGerald, K.; McAllister, M.; McCreight, J.; RafieeiNasab, A.; Read, L.; et al. The NCAR WRF-Hydro® Modeling System Technical Description, NCAR Technical Note. 2020. 107p. Available online: https://ral.ucar.edu/sites/default/files/public/WRFHydroV511TechnicalDescription.pdf (accessed on 24 January 2020). [CrossRef]
- Senatore, A.; Mendicino, G.; Gochis, D.J.; Yu, W.; Yates, D.N.; Kunstmann, H. Fully coupled atmosphere-hydrology simulations for the central Mediterranean: Impact of enhanced hydrological parameterization for short and long time scales. J. Adv. Model. Earth Syst. 2015, 7, 1693–1715. [Google Scholar] [CrossRef]
- Wang, W.; Liu, J.; Li, C.; Liu, Y.; Yu, F.; Yu, E. An evaluation study of the fully coupled WRF/WRF-hydro modeling system for simulation of storm events with different rainfall evenness in space and time. Water 2020, 12, 1209. [Google Scholar] [CrossRef]
- Rummler, T.; Arnault, J.; Gochis, D.; Kunstmann, H. Role of lateral terrestrial water flow on the regional water cycle in a complex terrain region: Investigation with a fully coupled model system. J. Geophys. Res. Atmos. 2019, 124, 507–529. [Google Scholar] [CrossRef]
- Xiang, T.; Vivoni, E.R.; Gochis, D.J.; Mascaro, G. On the diurnal cycle of surface energy fluxes in the North American monsoon region using the WRF-Hydro modeling system. J. Geophys. Res. Atmos. 2017, 122, 9024–9049. [Google Scholar] [CrossRef]
- Zhang, Z.; Arnault, J.; Wagner, S.; Laux, P.; Kunstmann, H. Impact of lateral terrestrial water flow on land-atmosphere interactions in the Heihe River Basin in China: Fully Coupled Modeling and Precipitation Recycling Analysis. J. Geophys. Res. Atmos. 2019, 124, 8401–8423. [Google Scholar] [CrossRef]
- Kerandi, N.; Arnault, J.; Laux, P.; Wagner, S.; Kitheka, J.; Kunstmann, H. Joint atmospheric-terrestrial water balances for East Africa: A WRF-Hydro case study for the upper Tana River basin. Theor. Appl. Climatol. 2018, 131, 1337–1355. [Google Scholar] [CrossRef]
- Li, L.; Gochis, D.J.; Sobolowski, S.; Mesquita, M.D.S. Evaluating the present annual water budget of a Himalayan headwater river basin using a high-resolution atmosphere-hydrology model. J. Geophys. Res. Atmos. 2017, 122, 4786–4807. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, J.; Shao, Q. Characteristic analysis of land cover change in nature reserve of three river’s source regions. Sci. Geogr. Sin. 2010, 30, 415–420. (In Chinese) [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, L.; Liu, C.; Shao, Q.; Fukushima, Y. Changes in stream flow regime in headwater catchments of the Yellow River basin since the 1950s. Hydrol. Process. 2007, 21, 886–893. [Google Scholar] [CrossRef]
- Jiang, C.; Ll, F.; Gao, Y.; Wang, D.; Zhang, L.; Guo, Y. Streamflow variation in the three-river headwaters region during 1956–2012. Res. Environ. Sci. 2017, 30, 30–39. (In Chinese) [Google Scholar] [CrossRef]
- Liu, L.; Zhang, W.J.; Lu, Q.F.; Jiang, H.R.; Tang, Y.; Xiao, H.M.; Wang, G.X. Hydrological impacts of near-surface soil warming on the Tibetan Plateau. Permafr. Periglac. Process. 2020, 31, 324–336. [Google Scholar] [CrossRef]
- Wu, P.; Liang, S.; Wang, X.-S.; McKenzie, J.M.; Feng, Y. Climate change impacts on cold season runoff in the headwaters of the Yellow River considering frozen ground degradation. Water 2020, 12, 602. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J. Comput. Phys. 2008, 227, 3465–3485. [Google Scholar] [CrossRef]
- Maussion, F.; Scherer, D.; Moelg, T.; Collier, E.; Curio, J.; Finkelnburg, R. Precipitation seasonality and variability over the Tibetan Plateau as resolved by the high asia reanalysis. J. Clim. 2014, 27, 1910–1927. [Google Scholar] [CrossRef]
- Gao, Y.; Xiao, L.; Chen, D.; Chen, F.; Xu, J.; Xu, Y. Quantification of the relative role of land-surface processes and large-scale forcing in dynamic downscaling over the Tibetan Plateau. Clim. Dyn. 2017, 48, 1705–1721. [Google Scholar] [CrossRef]
- Huang, H.; Wang, C.; Chen, G.T.; Carbone, R.E. The role of diurnal solenoidal circulation on propagating rainfall episodes near the eastern Tibetan Plateau. Mon. Weather Rev. 2010, 138, 2975–2989. [Google Scholar] [CrossRef]
- Wang, Z.; Duan, A.; Wu, G. Time-lagged impact of spring sensible heat over the Tibetan Plateau on the summer rainfall anomaly in East China: Case studies using the WRF model. Clim. Dyn. 2014, 42, 2885–2898. [Google Scholar] [CrossRef]
- Gao, Y.; Li, K.; Chen, F.; Jiang, Y.; Lu, C. Assessing and improving Noah-MP land model simulations for the central Tibetan Plateau. J. Geophys. Res. Atmos. 2015, 120, 9258–9278. [Google Scholar] [CrossRef]
- Zheng, D.; Van der Velde, R.; Su, Z.; Wen, J.; Wang, X. Assessment of Noah land surface model with various runoff parameterizations over a Tibetan river. J. Geophys. Res. Atmos. 2017, 122, 1488–1504. [Google Scholar] [CrossRef]
- Koch, M. Dupuit-Forchheimer formulation of a transport finite element model: Application to remediation of a shallow, unconfined aquifer. Water Stud. 1998, 26, 509–518. [Google Scholar] [CrossRef]
- Julien, P.Y.; Saghafian, B.; Ogden, F.L. Raster-based hydrologic modeling of spatially-varied surface runoff. Water Resour. Bull. AWRA 1995, 31, 523–536. [Google Scholar] [CrossRef]
- Garbrecht, J.; Martz, L.W. Automated channel ordering and node indexing for raster channel networks. Comput. Geosci. 1997, 23, 961–966. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.; Rao, V.; Orr, A.; Yan, E.; Kotamarthi, R. A parallel workflow implementation for PEST version 13.6 in high-performance computing for WRF-Hydro version 5.0: A case study over the midwestern United States. Geosci. Model Dev. 2019, 12, 3523–3539. [Google Scholar] [CrossRef]
- Shangguan, W.; Dai, Y.; Liu, B.; Zhu, A.; Duan, Q.; Wu, L.; Ji, D.; Ye, A.; Yuan, H.; Zhang, Q.; et al. A China data set of soil properties for land surface modeling. J. Adv. Model. Earth Syst. 2013, 5, 212–224. [Google Scholar] [CrossRef]
- Grell, G.A.; Devenyi, D. A generalized approach to parameterizing convection combining ensemble and data assimilation techniques. Geophys. Res. Lett. 2002, 29, 38-1–38-4. [Google Scholar] [CrossRef]
- Gao, Y.; Cheng, G.; Cui, W.; Chen, F.; David, G.; Yu, W. Coupling of enhanced land surface hydrology with atmospheric mesoscale model and its implement in Heihe River Basin. Adv. Earth Sci. 2006, 21, 1283–1293. (In Chinese) [Google Scholar] [CrossRef]
- Li, L.; Pontoppidan, M.; Sobolowski, S.; Senatore, A. The impact of initial conditions on convection-permitting simulations of a flood event over complex mountainous terrain. Hydrol. Earth Syst. Sci. 2020, 24, 771–791. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. GPM IMERG Final Precipitation L3 1 Day 0.1 Degree x 0.1 Degree V06; Andrey Savtchenko, A., Ed.; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2019. [CrossRef]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; Garcia-Ortega, E.; Machado, L.A.T.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104, 70–97. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Reichle, R.H.; De Lannoy, G.J.M.; Liu, Q.; Ardizzone, J.V.; Colliander, A.; Conaty, A.; Crow, W.; Jackson, T.J.; Jones, L.A.; Kimball, J.S.; et al. Assessment of the SMAP Level-4 surface and root-zone soil moisture product using in situ measurements. J. Hydrometeorol. 2017, 18, 2621–2645. [Google Scholar] [CrossRef]
- Reichle, R.H.; Liu, Q.; Koster, R.D.; Crow, W.; De Lannoy, G.J.M.; Kimball, J.S.; Ardizzone, J.V.; Bosch, D.; Colliander, A.; Cosh, M.; et al. Version 4 of the SMAP Level-4 soil moisture algorithm and data product. J. Adv. Model. Earth Syst. 2019, 11, 3106–3130. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernandez-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Ma, Y.; Tang, G.; Long, D.; Yong, B.; Zhong, L.; Wan, W.; Hong, Y. Similarity and error intercomparison of the GPM and its predecessor-TRMM multisatellite precipitation analysis using the best available hourly gauge network over the Tibetan Plateau. Remote Sens. 2016, 8, 569. [Google Scholar] [CrossRef]
- Xu, R.; Tian, F.; Yang, L.; Hu, H.; Lu, H.; Hou, A. Ground validation of GPM IMERG and TRMM 3B42V7 rainfall products over southern Tibetan Plateau based on a high-density rain gauge network. J. Geophys. Res.-Atmos. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Lu, D.; Yong, B. Evaluation and hydrological utility of the latest GPM IMERG V5 and GSMaP V7 precipitation products over the Tibetan Plateau. Remote Sens. 2018, 12, 2022. [Google Scholar] [CrossRef]
- Ma, L.; Zhao, L.; Tian, L.-M.; Yuan, L.-M.; Xiao, Y.; Zhang, L.-L.; Zou, D.-F.; Qiao, Y.-P. Evaluation of the integrated multi-satellite retrievals for global precipitation measurement over the Tibetan Plateau. J. Mt. Sci. 2019, 16, 1500–1514. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, K.; Qin, J.; Cui, Q.; Lu, H.; La, Z.; Han, M.; Tang, W. Evaluation of SMAP, SMOS, and AMSR2 soil moisture retrievals against observations from two networks on the Tibetan Plateau. J. Geophys. Res. Atmos. 2017, 122, 5780–5792. [Google Scholar] [CrossRef]
- Li, X.; Long, D.; Han, Z.; Scanlon, B.R.; Sun, Z.; Han, P.; Hou, A. Evapotranspiration estimation for Tibetan Plateau headwaters using conjoint terrestrial and atmospheric water balances and multisource remote sensing. Water Resour. Res. 2019, 55, 8608–8630. [Google Scholar] [CrossRef]
- Ding, L.; Zhou, J.; Zhang, X.; Liu, S.; Cao, R. Downscaling of surface air temperature over the Tibetan Plateau based on DEM. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 136–147. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- DelSole, T.; Shukla, J. Specification of wintertime north american surface temperature. J. Clim. 2006, 19, 2691–2716. [Google Scholar] [CrossRef][Green Version]
- Miyakoda, K.; Hembree, G.D.; Strickler, R.F.; Shulman, I. Cumulative results of extended forecast experiments.1. model performance for winter cases. Mon. Weather Rev. 1972, 100, 836–855. [Google Scholar] [CrossRef][Green Version]
- Li, J.; Yu, R.C. A Method to Linearly evaluate rainfall frequency-intensity distribution. J. Appl. Meteorol. Climatol. 2014, 53, 928–934. [Google Scholar] [CrossRef]
- Li, J.; Yu, R.; Yuan, W.; Chen, H.; Sun, W.; Zhang, Y. Precipitation over East Asia simulated by NCAR CAM5 at different horizontal resolutions. J. Adv. Model. Earth Syst. 2015, 7, 774–790. [Google Scholar] [CrossRef]
- Li, J. Hourly station-based precipitation characteristics over the Tibetan Plateau. Int. J. Climatol. 2018, 38, 1560–1570. [Google Scholar] [CrossRef]
- Meng, X.; Lyu, S.; Zhang, T.; Zhao, L.; Li, Z.; Han, B.; Li, S.; Ma, D.; Chen, H.; Ao, Y.; et al. Simulated cold bias being improved by using MODIS time-varying albedo in the Tibetan Plateau in WRF model. Environ. Res. Lett. 2018, 13, 044028. [Google Scholar] [CrossRef]
- Abbaszadeh, P.; Gavahi, K.; Moradkhani, H. Multivariate remotely sensed and in-situ data assimilation for enhancing community WRF-Hydro model forecasting. Adv. Water Resour. 2020, 145, 103721. [Google Scholar] [CrossRef]
- Mendoza, P.A.; Clark, M.P.; Barlage, M.; Rajagopalan, B.; Samaniego, L.; Abramowitz, G.; Gupta, H. Are we unnecessarily constraining the agility of complex process-based models? Water Resour. Res. 2015, 51, 716–728. [Google Scholar] [CrossRef]
- Sarkar, S.; Himesh, S. Evaluation of the skill of a fully-coupled atmospheric-hydrological model in simulating extreme hydrometeorological event: A case study over Cauvery river catchment. Pure Appl. Geophys. 2021, 178, 1063–1086. [Google Scholar] [CrossRef]
- Lin, P.; Yang, Z.-L.; Gochis, D.J.; Yu, W.; Maidment, D.R.; Somos-Valenzuela, M.A.; David, C.H. Implementation of a vector-based river network routing scheme in the community WRF-Hydro modeling framework for flood discharge simulation. Environ. Model. Softw. 2018, 107, 1–11. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, H.; Yu, W. Uncertainties of 3D soil hydraulic parameters in streamflow simulations using a distributed hydrological model system. J. Hydrol. 2018, 567, 12–24. [Google Scholar] [CrossRef]
- Arnault, J.; Rummler, T.; Baur, F.; Lerch, S.; Wagner, S.; Fersch, B.; Zhang, Z.; Kerandi, N.; Keil, C.; Kunstmann, H. Precipitation sensitivity to the uncertainty of terrestrial water flow in WRF-Hydro: An ensemble analysis for central Europe. J. Hydrometeorol. 2018, 19, 1007–1025. [Google Scholar] [CrossRef]
- Lahmers, T.M.; Castro, C.L.; Hazenberg, P. Effects of lateral flow on the convective environment in a coupled hydrometeorological modeling system in a semiarid environment. J. Hydrometeorol. 2020, 21, 615–642. [Google Scholar] [CrossRef]
- Gao, Y.; Xu, J.; Chen, D. Evaluation of WRF mesoscale climate simulations over the Tibetan Plateau during 1979–2011. J. Clim. 2015, 28, 2823–2841. [Google Scholar] [CrossRef]
- Hong, S.Y.; Dudhia, J.; Chen, S.H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Collins, W.; Rasch, P.J.; Boville, B.A.; McCaa, J.; Williamson, D.L.; Kiehl, J.T.; Briegleb, B.P.; Bitz, C.; Lin, S.-J.; Zhang, M.; et al. Description of the NCAR community atmosphere model (CAM 3.0) (No. NCAR/TN-464+STR). Univ. Corp. Atmos. Res. 2004, 226, 1326–1334. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Ball, J.T.; Woodrow, I.E.; Berry, J.A. A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. Prog. Photosynth. Res. 1987, 5, 221–224. [Google Scholar] [CrossRef]
- Brutsaert, W. Energy fluxes at the earth’s surface. In Evaporation into the Atmosphere; Springer: Dordrecht, The Netherlands, 1982; pp. 128–153. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Verseghy, D.L. Class—A canadian land surface scheme for gcms 1. soil model. Int. J. Climatol. 1991, 11, 111–133. [Google Scholar] [CrossRef]
- Jordan, R. A One-Dimensional Temperature Model for a Snow Cover: Technical Documentation for SNTHERM. 89; Special Report 91-16; US Army Corps of Engineers: Washington, DC, USA, 1991; Volume 89.






| Data Set | Type | Variable | Spatial Resolution | Time Interval |
|---|---|---|---|---|
| CAM (China Meteorological Administration observation data) | in situ | Precipitation, surface skin temperature and pressure, 2 m air temperature and humidity, wind speed | point | six-hourly |
| Hydrologic data | in situ | Discharge | point | daily |
| Eddy covariance | in situ | Heat flux | point | 30 min |
| GPM level_3 IMERG final | remote sensing | Precipitation | 0.1° | 30 min |
| SMAP level-4 | remote sensing | Soil moisture | 9 km | three-hourly |
| GLEAM | remote sensing | Evapotranspiration | 0.25° | daily |
| CMFD | Fusion of reanalysis and in-situ data | Air temperature at 2 m | 0.1° | three-hourly |
| Station ID | Stations | Latitude (° N) | Longitude (° E) | Elevation (m) |
|---|---|---|---|---|
| Runoff gauge1 | Changdu | 31.13 | 97.18 | 3306 |
| Runoff gauge2 | Tangnag | 35.5 | 100.15 | 4989 |
| Runoff gauge3 | Zhimenda | 33.01 | 97.25 | 3531 |
| Eddy covariance1 | Elinghu | 34.91 | 97.55 | 4322 |
| Eddy covariance2 | Huahu | 33.92 | 102.82 | 3432 |
| CMA 1 | Wudaoliang | 35.22 | 93.08 | 4612 |
| CMA 2 | Tuotuohe | 34.22 | 92.43 | 4533 |
| CMA 3 | Qumalai | 34.13 | 95.78 | 4175 |
| CMA 4 | Zaduo | 32.9 | 95.3 | 4066 |
| CMA 5 | Nangqian | 32.2 | 96.48 | 3644 |
| CMA 6 | Chagndu | 31.15 | 97.17 | 3306 |
| CMA 7 | Maduo | 34.92 | 98.22 | 4272 |
| CMA 8 | Dari | 33.75 | 99.65 | 3968 |
| CMA 9 | Guoluo | 34.47 | 100.25 | 3719 |
| CMA 10 | Henan | 34.73 | 101.6 | 3530 |
| CMA 11 | Maqu | 34 | 102.08 | 3471 |
| CMA 12 | Jiuzhi | 33.43 | 101.48 | 3629 |
| CMA 13 | Hongyuan | 32.8 | 102.55 | 3492 |
| CMA 14 | Ruoergai | 33.58 | 102.97 | 3440 |
| Variables | RMSE | CC | Number of Sites | |||
|---|---|---|---|---|---|---|
| WRF-H | WRF-S | WRF-H | WRF-S | WRF-H | WRF-S | |
| Precipitation (mm) | 5.9 | 6.1 | 0.33 | 0.23 | 13 | 11 |
| Air temperature at 2 m (k) | 3.1 | 3.2 | 0.97 | 0.97 | 14 | 14 |
| Surface skin temperature (k) | 6.8 | 7.0 | 0.91 | 0.91 | 14 | 14 |
| Surface pressure (hPa) | 15.7 | 15.8 | 0.91 | 0.91 | 14 | 14 |
| Relative humidity (%) | 15.7 | 15.7 | 0.6 | 0.59 | 14 | 14 |
| Wind speed (ms−1) | 1.0 | 1.1 | 0.29 | 0.28 | 12 | 12 |
| Stations | Variables | RMSE | CC | ||
|---|---|---|---|---|---|
| WRF-H | WRF-S | WRF-H | WRF-S | ||
| Elinghu | LH | 55.7 | 39.8 | 0.75 | 0.74 |
| HFX | 45.9 | 69.7 | 0.76 | 0.74 | |
| Huahu | LH | 77.4 | 80.4 | 0.73 | 0.72 |
| HFX | 67.9 | 74.4 | 0.78 | 0.79 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Meng, X.; Blyth, E.; Chen, H.; Shu, L.; Li, Z.; Zhao, L.; Ma, Y. Impact of Fully Coupled Hydrology-Atmosphere Processes on Atmosphere Conditions: Investigating the Performance of the WRF-Hydro Model in the Three River Source Region on the Tibetan Plateau, China. Water 2021, 13, 3409. https://doi.org/10.3390/w13233409
Li G, Meng X, Blyth E, Chen H, Shu L, Li Z, Zhao L, Ma Y. Impact of Fully Coupled Hydrology-Atmosphere Processes on Atmosphere Conditions: Investigating the Performance of the WRF-Hydro Model in the Three River Source Region on the Tibetan Plateau, China. Water. 2021; 13(23):3409. https://doi.org/10.3390/w13233409
Chicago/Turabian StyleLi, Guangwei, Xianhong Meng, Eleanor Blyth, Hao Chen, Lele Shu, Zhaoguo Li, Lin Zhao, and Yingsai Ma. 2021. "Impact of Fully Coupled Hydrology-Atmosphere Processes on Atmosphere Conditions: Investigating the Performance of the WRF-Hydro Model in the Three River Source Region on the Tibetan Plateau, China" Water 13, no. 23: 3409. https://doi.org/10.3390/w13233409
APA StyleLi, G., Meng, X., Blyth, E., Chen, H., Shu, L., Li, Z., Zhao, L., & Ma, Y. (2021). Impact of Fully Coupled Hydrology-Atmosphere Processes on Atmosphere Conditions: Investigating the Performance of the WRF-Hydro Model in the Three River Source Region on the Tibetan Plateau, China. Water, 13(23), 3409. https://doi.org/10.3390/w13233409








