Generation of Homogeneous Slope Units Using a Novel Object-Oriented Multi-Resolution Segmentation Method
Abstract
:1. Introduction
2. Automatic Delineation of Slope Units
2.1. Dataset Establishment
2.1.1. The Segmented Dataset
2.1.2. The Restricted Dataset
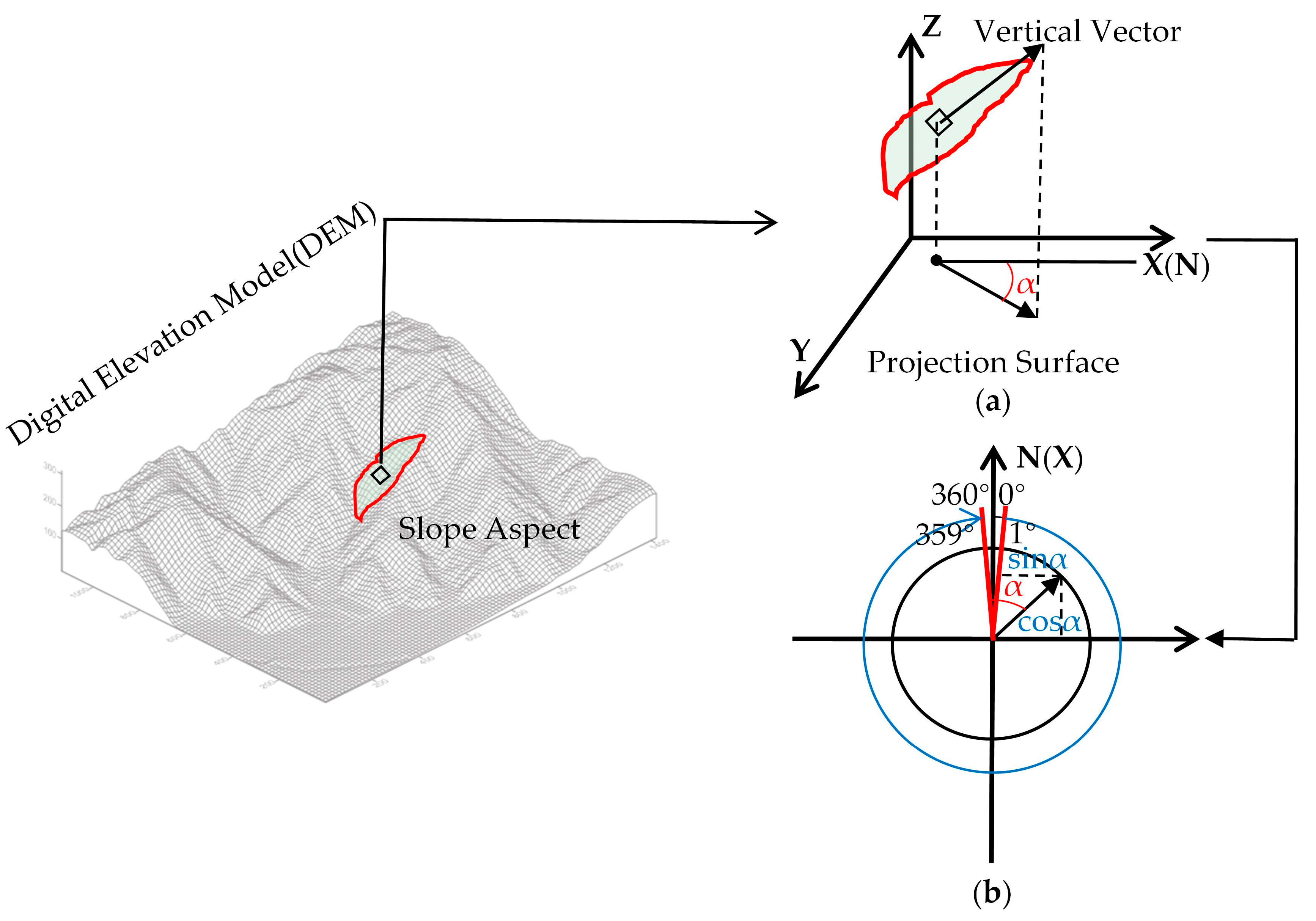
2.2. Object-Oriented Multiresolution Segmentation Method
2.2.1. Determination of Segmentation Parameters
2.2.2. Object-Oriented Multiresolution Segmentation Algorithm
- Data import: The regional DEM data should be imported to generate a slope aspect dataset, which is used as the basic layer for image segmentation. Ridge lines extracted from the forward catchment area can also be obtained using DEM data, and then are considered as the thematic restriction layer.
- Parameter setting: the ROC-LV method is used to determine the optimal segmentation scale, and the optimal shape factor and compactness are determined according to the requirements.
- Segmentation: Multiresolution image segmentation adopts a bottom-up segmentation method. The first segmentation starts from any pixel in the image, and the initial heterogeneity parameter is calculated. After the first segmentation, the second segmentation is performed based on the new image region. If the heterogeneity parameter f is small compared with the square of the segmentation scale, the segmentation is continued; if the heterogeneity parameter f is small compared with the square of the segmentation scale, the segmentation is continued according to the minimum heterogeneity criterion, and the segmentation ends when all the pixels in the image are divided into different image objects.
2.3. Segmentation Metric of Slope Unit Segmentation Method
3. Case Study
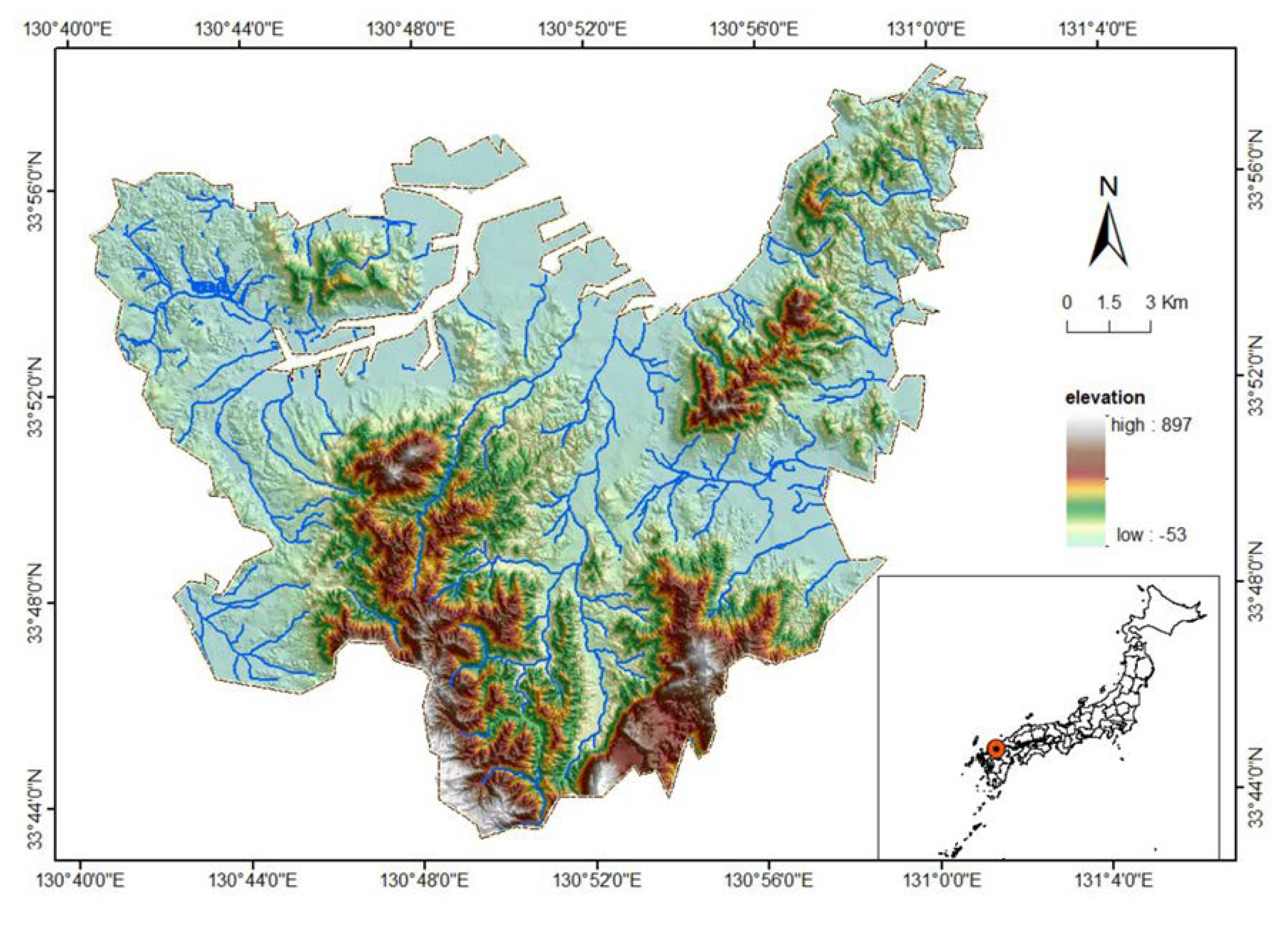
3.1. Study Area
3.2. Results
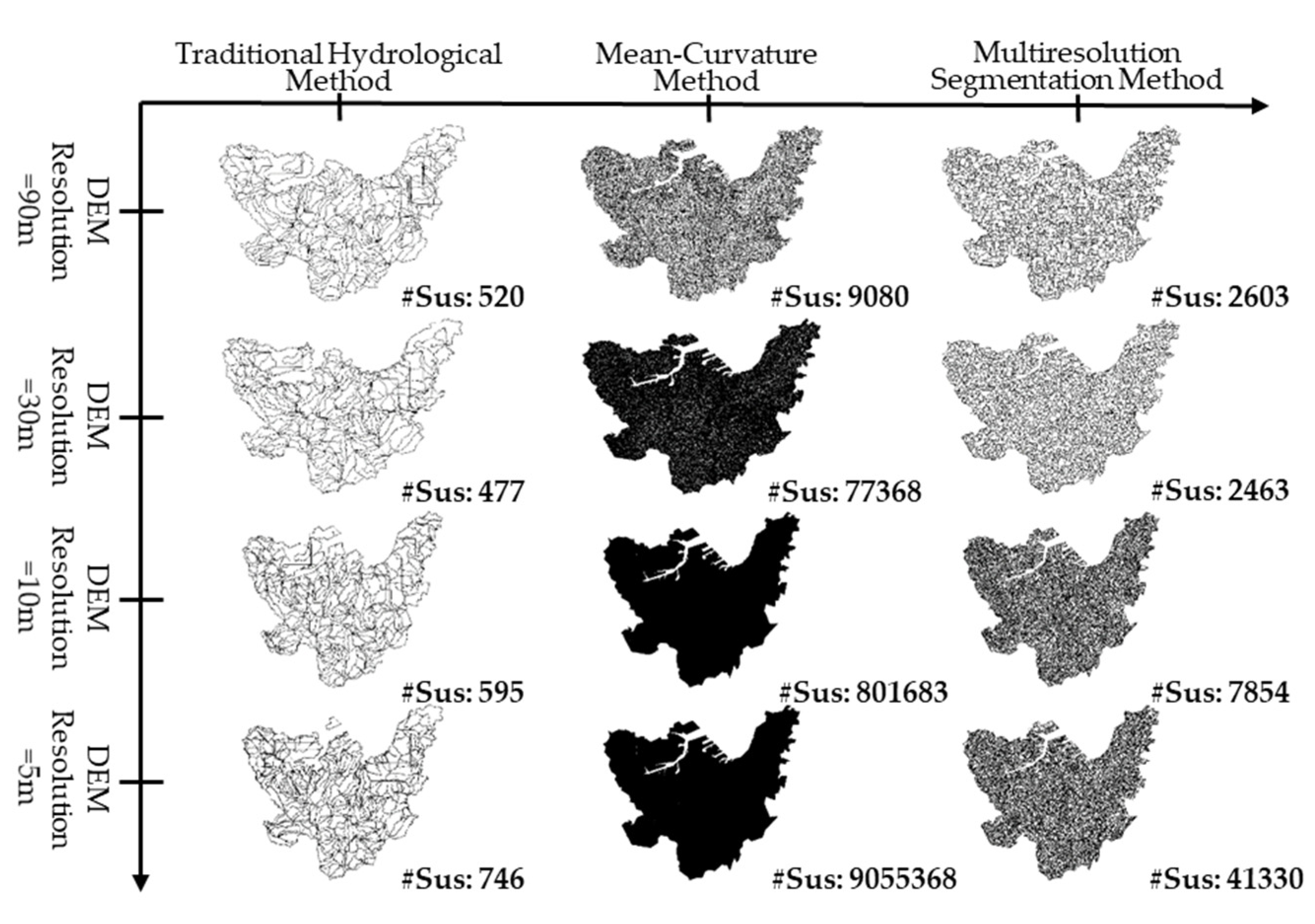
4. Comparison
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, P.; Stumpf, A.; Kerle, N.; Casagli, N. Object-Oriented Change Detection for Landslide Rapid Mapping. IEEE Geosci. Remote Sens. Lett. 2011, 8, 701–705. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the quality of landslide susceptibility models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
- Saito, H.; Nakayama, D.; Matsuyama, H. Comparison of landslide susceptibility based on a decision-tree model and actual landslide occurrence: The Akaishi Mountains, Japan. Geomorphology. 2009, 109, 108–121. [Google Scholar] [CrossRef]
- Li, Y.G.; Liu, X.T.; Han, Z.; Dou, J. Spatial proximity-based geographically weighted regression model for landslide susceptibility assessment: A case study of Qingchuan area, China. Appl. Sci. 2020, 10, 1107. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.D.; He, Z.L.; Han, Z.; Li, Y.G.; Dou, J.; Huang, J.L. Mapping the susceptibility to landslides based on the deep belief network: A case study in Sichuan Province, China. Natural Hazards. 2020, 103, 3239–3261. [Google Scholar] [CrossRef]
- Huabin, W.; Gangjun, L.; Weiya, X.; Gonghui, W. GIS-based landslide hazard assessment: An overview. Prog. Phys. Geogr. Earth Environ. 2016, 29, 548–567. [Google Scholar] [CrossRef]
- Lopes, R.P.; Madeira, M.; Arsénio, P. Mapping of Land Units and Land Capability Classification in Portugal. The Case of the Municipality of LourinhÃ. Finisterra 2018, 52. [Google Scholar] [CrossRef] [Green Version]
- Saha, S.; Paul, G.C.; Hembram, T.K. Classification of terrain based on geo-environmental parameters and their relationship with land use/land cover in Bansloi River basin, Eastern India: RS-GIS approach. Appl. Geomat. 2019, 12, 55–71. [Google Scholar] [CrossRef]
- Can, T.; Nefeslioglu, H.A.; Gokceoglu, C.; Sonmez, H.; Duman, T.Y. Susceptibility assessments of shallow earthflows triggered by heavy rainfall at three catchments by logistic regression analyses. Geomorphology 2005, 72, 250–271. [Google Scholar] [CrossRef]
- Li, J.Y.; Wang, W.D.; Han, Z.; Li, Y.G.; Chen, G.Q. Exploring the Impact of Multitemporal DEM Data on the Susceptibility Mapping of Landslides. Appl. Sci. 2020, 10, 2518. [Google Scholar] [CrossRef] [Green Version]
- Conoscenti, C.; Di Maggio, C.; Rotigliano, E. Soil erosion susceptibility assessment and validation using a geostatistical multivariate approach: A test in Southern Sicily. Nat. Hazards. 2008, 46, 287–305. [Google Scholar] [CrossRef]
- Han, Z.; Ma, Y.F.; Li, Y.G.; Zhang, H.; Chen, N.S.; Hu, G.S.; Chen, G.Q. Hydrodynamic and topography based cellular automaton model for simulating debris flow run-out extent and entrainment behavior. Water Res. 2021, 193, 116872. [Google Scholar] [CrossRef]
- Amorim, D.S.; Santos, C.M.D. Flies, endemicity, and the Atlantic Forest: A biogeographical study using topographic units of analysis. Aust. Syst. Bot. 2017, 30, 439–469. [Google Scholar] [CrossRef]
- Hassani, H.; Ghazanfari, M. Landslide susceptibility zonation of the Qazvin-Rasht-Anzali railway track, North Iran. In Proceedings of the 10th International Symposium on Landslides and Engineered Slopes, Xi’an, China, 30 June–30 July 2008; p. 1911. [Google Scholar]
- Neelakantan, R.; Yuvaraj, S. Relative effect-based landslide hazard zonation mapping in parts of Nilgiris, Tamil Nadu, South India. Arab. J. Geosci. 2012, 6, 4207–4213. [Google Scholar] [CrossRef]
- Mergili, M.; Marchesini, I.; Alvioli, M.; Rossi, M.; Santangelo, M.; Cardinali, M.; Ardizzone, F.; Fiorucci, F.; Schneider-Muntau, B.; Fellin, W.; et al. GIS-Based Deterministic Analysis of Deep-Seated Slope Stability in a Complex Geological Setting. In Engineering Geology for Society and Territory; Springer: Berlin/Heidelberg, Germany, 2015; Volume 2, pp. 1437–1440. [Google Scholar]
- Cardinali, M.; Reichenbach, P.; Guzzetti, F.; Ardizzone, F.; Antonini, G.; Galli, M.; Cacciano, M.; Castellani, M.; Salvati, P. A geomorphological approach to the estimation of landslide hazards and risks in Umbria, Central Italy. Nat. Hazards Earth Syst. Sci. 2002, 2, 57–72. [Google Scholar] [CrossRef] [Green Version]
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic landslide hazard assessment at the basin scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
- Rossi, M.; Guzzetti, F.; Reichenbach, P.; Mondini, A.C.; Peruccacci, S. Optimal landslide susceptibility zonation based on multiple forecasts. Geomorphology 2010, 114, 129–142. [Google Scholar] [CrossRef]
- Alvioli, M.; Marchesini, I.; Reichenbach, P.; Rossi, M.; Ardizzone, F.; Fiorucci, F.; Guzzetti, F. Automatic delineation of geomorphological slope units with r.slopeunits v1.0 and their optimization for landslide susceptibility modeling. Geosci. Model Dev. 2016, 9, 3975–3991. [Google Scholar] [CrossRef] [Green Version]
- Shafique, M.; van der Meijde, M.; Khan, M.A. A review of the 2005 Kashmir earthquake-induced landslides; from a remote sensing prospective. J. Asian Earth Sci. 2016, 118, 68–80. [Google Scholar] [CrossRef]
- Zhou, G.; Esaki, T.; Qiu, C.; Sasaki, Y. A GIS-based approach of identifying slope unit from natural terrain for slope stability evaluation. Soil Found. 2004, 52, 26–28. [Google Scholar]
- Jia, N.; Mitani, Y.; Xie, M.; Djamaluddin, I. Shallow landslide hazard assessment using a three-dimensional deterministic model in a mountainous area. Comput. Geotech. 2012, 45, 1–10. [Google Scholar] [CrossRef]
- Romstad, B.; Etzelmüller, B. Mean-curvature watersheds: A simple method for segmentation of a digital elevation model into terrain units. Geomorphology 2012, 139–140, 293–302. [Google Scholar] [CrossRef] [Green Version]
- Yan, G.; Liang, S.; Zhao, H. An Approach to Improving Slope Unit Division Using GIS Technique. Sci. Geogr. Sinica. 2017, 37, 1764–1770. [Google Scholar] [CrossRef]
- Li, Y.G.; Chen, G.Q.; Wang, B.; Zheng, L.; Zhang, Y.B.; Tang, C. A new approach of combining aerial photography with satellite imagery for landslide detection. Nat. Hazards 2013, 66, 649–669. [Google Scholar] [CrossRef]
- Drăguţ, L.; Blaschke, T. Automated classification of landform elements using object-based image analysis. Geomorphology 2006, 81, 330–344. [Google Scholar] [CrossRef]
- Aplin, P.; Smith, G.M. Introduction to object-based landscape analysis. Int. J. Geogr. Inf. Sci. 2011, 25, 869–875. [Google Scholar] [CrossRef]
- Etzelmueller, B.; Romstad, B.; Fjellanger, J. Automatic regional classification of topography in Norway. Nor. J. Geol. 2007, 87, 167–180. [Google Scholar]
- Ermini, L.; Catani, F.; Casagli, N. Artificial Neural Networks applied to landslide susceptibility assessment. Geomorphology 2005, 66, 327–343. [Google Scholar] [CrossRef]
- Lassueur, T.; Joost, S.; Randin, C.F. Very high resolution digital elevation models: Do they improve models of plant species distribution? Ecol. Model. 2006, 198, 139–153. [Google Scholar] [CrossRef]
- Smith, M.P.; Zhu, A.X.; Burt, J.E.; Stiles, C. The effects of DEM resolution and neighborhood size on digital soil survey. Geoderma 2006, 137, 58–69. [Google Scholar] [CrossRef]
- Wells, A.F.; Frost, G.V.; Macander, M.J.; Jorgenson, M.T.; Roth, J.E.; Davis, W.A.; Pullman, E.R. Integrated terrain unit mapping on the Beaufort Coastal Plain, North Slope, Alaska, USA. Landsc. Ecol. 2020, 36, 549–579. [Google Scholar] [CrossRef]
- Chen, N.; Wang, Q. Selection of DEM Resolutions Based on the Information Amount of Terrain Factors—A Case Study of Loess Plateau Area. J. Wuhan Univ. Inf. Sci. Ed. 2009, 34, 692–695. [Google Scholar]
- Jedlička, K. Accuracy of Surface Models Acquired from Different Sources-Important Information for Geomorphological Research. Geomorphol. Slovaca Et Bohem. 2009, 9, 17–28. [Google Scholar]
- Papastergios, G.; Fernandez-Turiel, J.-L.; Filippidis, A.; Gimeno, D. Determination of geochemical background for environmental studies of soils via the use of HNO3 extraction and Q-Q plots. Environ. Earth Sci. 2010, 64, 743–751. [Google Scholar] [CrossRef] [Green Version]
- Drǎguţ, L.; Tiede, D.; Levick, S.R. ESP: A tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci. 2010, 24, 859–871. [Google Scholar] [CrossRef]
- Kong, C. Classification and Extraction of Urban Land-Use Information from High-Resolution Image Based on Object Multi-features. J. China Univ. Geosci. 2006, 17, 151–157. [Google Scholar] [CrossRef]
- Han, Z.; Su, B.; Li, Y.G.; Ma, Y.F.; Wang, W.D.; Chen, G.Q. An enhanced image binarization method incorporating with Monte-Carlo simulation. J. Cent. South Univ. 2019, 26, 1661–1671. [Google Scholar] [CrossRef]
- Han, Z.; Li, Y.G.; Du, Y.F.; Wang, W.D.; Chen, G.Q. Noncontact detection of earthquake-induced landslides by an enhanced image binarization method incorporating with Monte-Carlo simulation. Geomat. Nat. Hazards Risk 2019, 10, 219–241. [Google Scholar] [CrossRef]
- Zhu, H.; Cai, L.; Liu, H.; Huang, W. Information Extraction of High Resolution Remote Sensing Images Based on the Calculation of Optimal Segmentation Parameters. PLoS ONE 2016, 11, e0158585. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Alexandridis, T.K.; Sotiropoulou, A.M.; Bilas, G.; Karapetsas, N.; Silleos, N.G. The Effects of Seasonality in Estimating the C-Factor of Soil Erosion Studies. Land Degrad. Dev. 2015, 26, 596–603. [Google Scholar] [CrossRef]
- Kim, M.; Madden, M.; Warner, T. Estimation of optimal image object size for the segmentation of forest stands with multispectral IKONOS imagery. In Object-Based Image Analysis; Springer: Berlin/Heidelberg, Germany, 2008; pp. 291–307. [Google Scholar]
- Drǎguţ, L.; Eisank, C. Object representations at multiple scales from digital elevation models. Geomorphology 2011, 129, 183–1891. [Google Scholar] [CrossRef] [Green Version]
- Drǎgut, L.; Eisank, C.; Strasser, T. Local variance for multi-scale analysis in geomorphometry. Geomorphology 2011, 130, 162–172. [Google Scholar] [CrossRef] [Green Version]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Duan, G.; Gong, H.; Li, X.; Chen, B. Shadow extraction based on characteristic components and object-oriented method for high-resolution images. J. Remote Sens. 2014, 18, 760–770. [Google Scholar]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multi-scale approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Myint, S.W.; Gober, P.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Per-pixel vs. object-based classification of urban land cover extraction using high spatial resolution imagery. Remote Sens. Environ. 2011, 115, 1145–1161. [Google Scholar] [CrossRef]
- Espindola, G.M.; Camara, G.; Reis, I.A.; Bins, L.S.; Monteiro, A.M. Parameter selection for region-growing image segmentation algorithms using spatial autocorrelation. Int. J. Remote Sens. 2007, 27, 3035–3040. [Google Scholar] [CrossRef]
- Dongping, M.; Tianyu, C.; Hongyue, C.; Longxiang, L.; Cheng, Q.; Jinyang, D. Semivariogram-Based Spatial Bandwidth Selection for Remote Sensing Image Segmentation With Mean-Shift Algorithm. IEEE Geosci. Remote Sens. Lett. 2012, 9, 813–817. [Google Scholar] [CrossRef]
- Tong, H.; Maxwell, T.; Zhang, Y.; Dey, V. A Supervised and Fuzzy-based Approach to Determine Optimal Multi-resolution Image Segmentation Parameters. Photogramm. Eng. Remote Sens. 2012, 78, 1029–1044. [Google Scholar] [CrossRef]
- Schlögel, R.; Marchesini, I.; Alvioli, M.; Reichenbach, P.; Rossi, M.; Malet, J.P. Optimizing landslide susceptibility zonation: Effects of DEM spatial resolution and slope unit delineation on logistic regression models. Geomorphology 2018, 301, 10–20. [Google Scholar] [CrossRef]
- Tian, Y.; XiaO, C.; Liu, Y.; Wu, L. Effects of raster resolution on landslide susceptibility mapping: A case study of Shenzhen. Sci. China Ser. E Technol. Sci. 2009, 51, 188–198. [Google Scholar] [CrossRef]
- Claessens, L.; Heuvelink, G.B.M.; Schoorl, J.M.; Veldkamp, A. DEM resolution effects on shallow landslide hazard and soil redistribution modelling. Earth Surf. Process. Landf. 2005, 30, 461–477. [Google Scholar] [CrossRef]
- Penna, D.; Borga, M.; Aronica, G.T.; Brigandì, G.; Tarolli, P. The influence of grid resolution on the prediction of natural and road-related shallow landslides. Hydrol. Earth Syst. Sci. 2014, 18, 2127–2139. [Google Scholar] [CrossRef] [Green Version]




| DEM Data Resolution | Shape Factor | Compactness Factor | Optimum Segmentation Scale |
|---|---|---|---|
| 90 m | 0.15 | 0.5 | 8 |
| 30 m | 0.3 | 0.5 | 8 |
| 10 m | 0.1 | 0.5 | 9 |
| 5 m | 0.1 | 0.5 | 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; He, J.; Chen, F.; Han, Z.; Wang, W.; Chen, G.; Huang, J. Generation of Homogeneous Slope Units Using a Novel Object-Oriented Multi-Resolution Segmentation Method. Water 2021, 13, 3422. https://doi.org/10.3390/w13233422
Li Y, He J, Chen F, Han Z, Wang W, Chen G, Huang J. Generation of Homogeneous Slope Units Using a Novel Object-Oriented Multi-Resolution Segmentation Method. Water. 2021; 13(23):3422. https://doi.org/10.3390/w13233422
Chicago/Turabian StyleLi, Yange, Jianhua He, Fang Chen, Zheng Han, Weidong Wang, Guangqi Chen, and Jianling Huang. 2021. "Generation of Homogeneous Slope Units Using a Novel Object-Oriented Multi-Resolution Segmentation Method" Water 13, no. 23: 3422. https://doi.org/10.3390/w13233422
APA StyleLi, Y., He, J., Chen, F., Han, Z., Wang, W., Chen, G., & Huang, J. (2021). Generation of Homogeneous Slope Units Using a Novel Object-Oriented Multi-Resolution Segmentation Method. Water, 13(23), 3422. https://doi.org/10.3390/w13233422








