Simulation-Optimization Model for Conjunctive Management of Surface Water and Groundwater for Agricultural Use
Abstract
:1. Introduction
2. Materials and Methods
2.1. Area of Study
2.2. ANNs
2.3. JA
2.4. S-O Model
3. Results
3.1. Predictive Capability
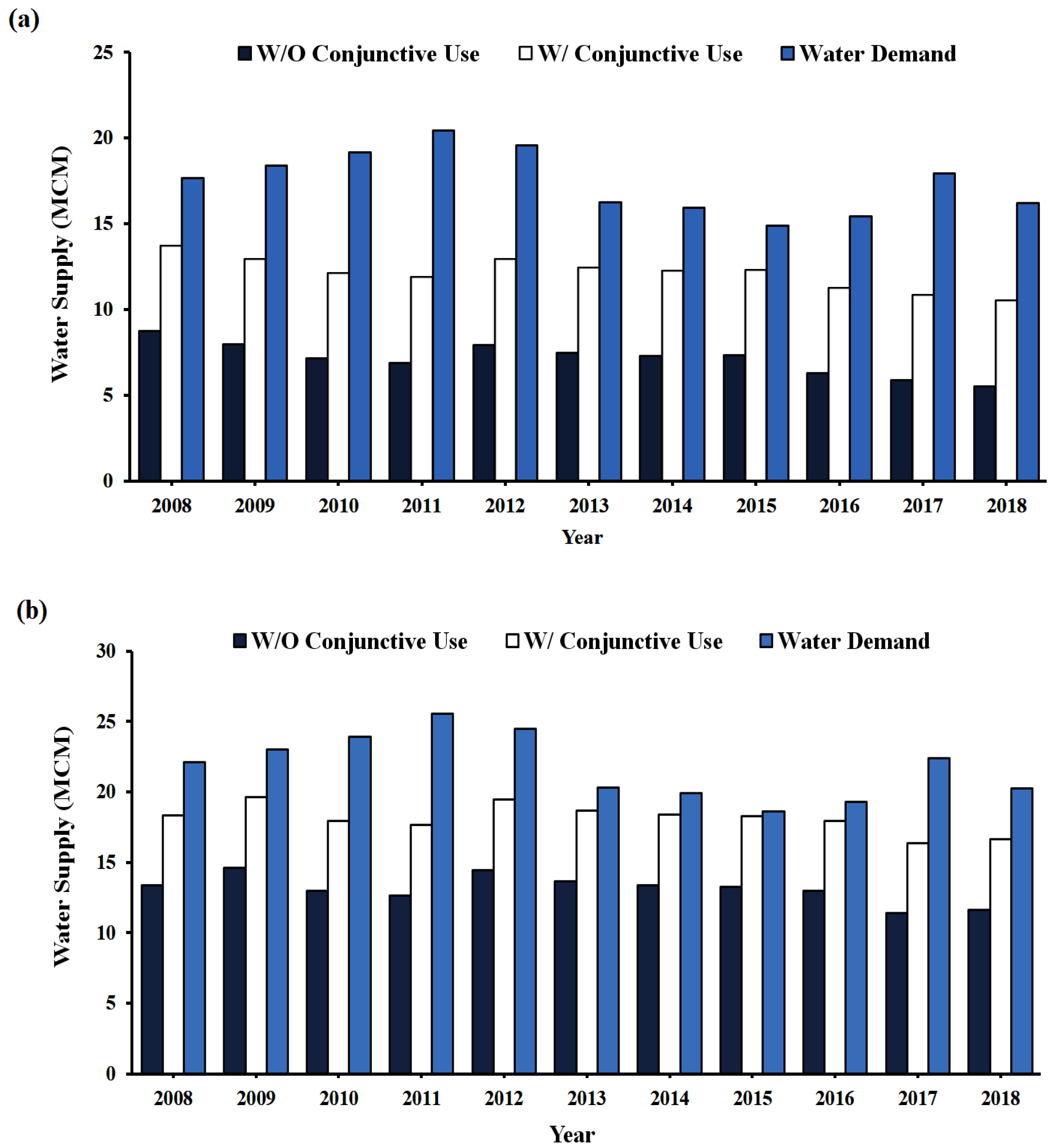
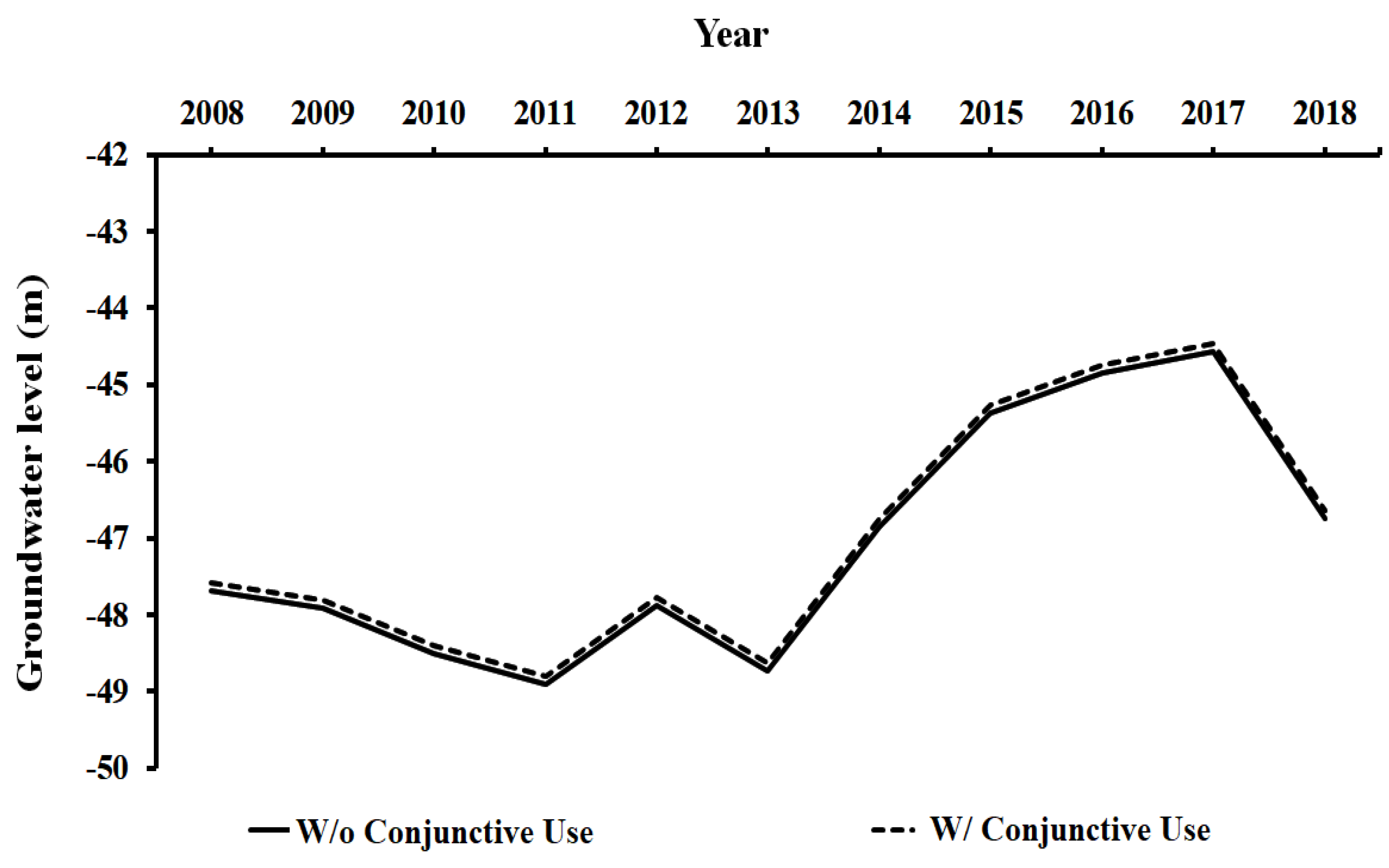
3.2. Optimal Conjunctive Use
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nayak, P.C.; Rao, Y.R.S.; Sudheer, K.P. Groundwater level forecasting in a shallow aquifer using artificial neural network approach. Water Resour. Manag. 2006, 20, 77–90. [Google Scholar] [CrossRef]
- Sepahvand, R.; Safavi, H.R.; Rezaei, F. Multi-objective planning for conjunctive use of surface and ground water resources using genetic programming. Water Resour. Manag. 2019, 33, 2123–2137. [Google Scholar] [CrossRef]
- Fischer, G.; Tubiello, F.N.; van Velthuizen, H.V.; Wiberg, D.A. Climate change impacts on irrigation water requirements: Effects of mitigation, 1990–2080. Technol. Forecast. Soc. Chang. 2007, 74, 1083–1107. [Google Scholar] [CrossRef] [Green Version]
- Ministry of Environment. Wastewater Reuse Guidebook; MOE: Seoul, Korea, 2009. (In Korean)
- Ministry of Construction and Transportation. National Water Resource Plan; MOCT: Seoul, Korea, 2012. (In Korean)
- Jeong, H.; Kim, H.; Jang, T. Irrigation water quality standards for indirect wastewater reuse in agriculture: A contribution toward sustainable wastewater reuse in South Korea. Water 2016, 8, 169. [Google Scholar] [CrossRef] [Green Version]
- Ashu, A.B.; Lee, S.-I. The effects of climate change on the reuse of agricultural drainage water in irrigation. KSCE J. Civ. Eng. 2021, 2, 51116–51129. [Google Scholar] [CrossRef]
- Ministry of Construction and Transportation. Comprehensive Water Resources Plan—Water Vision 2020; MOCT: Seoul, Korea, 2006. (In Korean)
- Yoo, S.-H.; Choi, J.-Y.; Lee, S.-H.; Kim, T. Estimating water footprint of paddy rice in Korea. Paddy Water Environ. 2014, 12, 43–54. [Google Scholar] [CrossRef]
- Pathare, V.G.; Jagtap, S.A. Attributes of conjunctive use of surface water and sub-surface water. Int. J. Eng. Technol. Manag. Arts Sci. 2016, 4, 27–30. [Google Scholar]
- American Society of Civil Engineers. Total Maximum Daily Load Analysis and Modeling: Assessment of the Practice; ASCE Press: Reston, VA, USA, 2017. [Google Scholar]
- Safavi, H.; Enteshari, S. Conjunctive use of surface and ground water resources using the ant system optimization. Agric. Water Manag. 2016, 173, 23–34. [Google Scholar] [CrossRef]
- Portoghese, I.; Giannoccaro, G.; Giordanoa, R.; Paganoa, A. Modeling the impacts of volumetric water pricing in irrigation districts with conjunctive use of surface and groundwater resources. Agric. Water Manag. 2021, 244, 106561. [Google Scholar] [CrossRef]
- Azaiez, M.N. A model for conjunctive use of ground and surface water with opportunity costs. Eur. J. Oper. Res. 2002, 143, 611–624. [Google Scholar] [CrossRef]
- Cosgrove, D.M.; Johnson, G.S. Aquifer management zones based on simulated surface-water response functions. J. Water Resour. Plan. Manag. 2005, 131, 89–100. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, A.; Nelson, K.; Hipke, W. Cloud computing for integrated stochastic groundwater uncertainty analysis. Int. J. Digit. Earth 2013, 6, 313–337. [Google Scholar] [CrossRef]
- Singh, A. Optimizing the use of land and water resources for maximizing farm income by mitigating the hydrological imbalances. J. Hydrol. Eng. 2014, 19, 1447–1451. [Google Scholar] [CrossRef]
- Barlow, P.M.; Ahlfeld, D.P.; Dickerman, D.C. Conjunctive-management models for sustained yield of stream-aquifer systems. J. Water Resour. Plan. Manag. 2003, 129, 35–48. [Google Scholar] [CrossRef]
- Singh, A. Simulation–optimization modeling for conjunctive water use management. Agric. Water Manag. 2014, 141, 23–29. [Google Scholar] [CrossRef]
- Shi, F.; Zhao, C.; Sun, D.; Peng, D.; Han, M. Conjunctive use of surface and groundwater in central Asia area: A case study of the Tailan River Basin. Stoch. Environ. Res. Risk Assess. 2012, 26, 961–970. [Google Scholar] [CrossRef]
- Safavi, H.R.; Esmikhani, M. Conjunctive use of surface water and groundwater: Application of support vector machines (SVMs) and genetic algorithms. Water Resour. Manag. 2013, 27, 2623–2644. [Google Scholar] [CrossRef]
- Dawson, D.; Wilby, R. An artificial neural network approach to rainfall-runoff modeling. Hydrol. Sci. J. 1998, 43, 47–65. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; ASCE Task Committee on Application of Artificial Neural Networks in Hydrology. Artificial neural networks in hydrology. I: Preliminary concepts. ASCE J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar]
- Jain, S.K.; Nayak, P.C.; Sudheer, K.P. Models for estimating evapotranspiration using artificial neural networks, and their physical interpretation. Hydrol. Process. 2008, 22, 2225–2234. [Google Scholar] [CrossRef]
- Babel, M.S.; Shinde, V.R. Identifying prominent explanatory variables for water demand prediction using artificial neural networks: A case study of Bangkok. Water Resour. Manag. 2011, 25, 1653–1676. [Google Scholar] [CrossRef]
- Javan, K.; Lialestani, M.R.F.H.; Nejadhossein, M. A comparison of ANN and HSPF models for runoff simulation in Gharehsoo River watershed, Iran. Model. Earth Syst. Environ. 2015, 1, 41. [Google Scholar] [CrossRef] [Green Version]
- Kasiviswanathan, K.S.; Sudheer, K.P. Methods used for quantifying the prediction uncertainty of artificial neural network based hydrologic models. Stoch. Environ. Res. Risk Assess. 2017, 31, 1659–1670. [Google Scholar] [CrossRef]
- Modaresi, F.; Araghinejad, S.; Ebrahimi, K. A comparative assessment of artificial neural network generalized regression neural network, least square support vector regression, and K-nearest neighbor regression for monthly streamflow forecasting in linear and nonlinear conditions. Water Resour. Manag. 2018, 32, 243–258. [Google Scholar] [CrossRef]
- Vidyarthi, V.K.; Jain, A. Knowledge extraction from trained ANN drought classification model. J. Hydrol. 2020, 585, 124804. [Google Scholar] [CrossRef]
- Vidyarthi, V.K.; Jain, A.; Chourasiya, S. Modeling rainfall-runoff process using artificial neural network with emphasis on parameter sensitivity. Model. Earth Syst. Environ. 2020, 6, 2177–2188. [Google Scholar] [CrossRef]
- Govindraraju, R.S.; Rao, A.R. (Eds.) Artificial Neural Networks in Hydrology; Kluwer: Dordrecht, The Netherlands, 2000; pp. 1–7. [Google Scholar]
- Matanga, G.B.; Mariño, M.A. Irrigation planning: 1. Cropping pattern. Water Resour. Res. 1979, 15, 672–678. [Google Scholar] [CrossRef]
- Loucks, D.P.; Stedginger, J.R.; Haith, D.A. Water Resource Systems Planning and Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1981. [Google Scholar]
- Hantush, M.S.M.; Marino, M.A. Chance-constrained model for management of stream-aquifer system. J. Water Res. Plan. Manag. 1989, 115, 259–277. [Google Scholar] [CrossRef]
- Kite, G.; Droogers, P. Comparing evapotranspiration estimates from satellites, hydrological models, and field data. J. Hydrol. 2000, 229, 3–18. [Google Scholar] [CrossRef]
- Mantoglou, A. Pumping management of coastal aquifers using analytical models of salt water intrusion. Water Resour. Res. 2003, 39, 1–12. [Google Scholar] [CrossRef]
- Liu, L.; Cui, Y.; Luo, Y. Integrated modeling of conjunctive water use in a canal-well irrigation district in the lower Yellow River Basin, China. J. Irrig. Drain. Eng. 2013, 139, 775–784. [Google Scholar] [CrossRef]
- Singh, A.; Panda, S.N.; Saxena, C.K.; Verma, C.L. Optimization modeling for conjunctive use planning of surface water and groundwater for irrigation. J. Irrig. Drain. Eng. 2016, 142, 1–9. [Google Scholar] [CrossRef]
- Jha, M.K.; Peralta, R.C.; Sahoo, S. Simulation-optimization for conjunctive water resources management and optimal crop planning in Kushabhadra-Bhargavi river delta of Eastern India. Int. J. Environ. Res. Public Health 2020, 17, 3521. [Google Scholar] [CrossRef]
- Soleimani, S.; Bozorg-Haddad, O.; Boroomandnia, B.; Loáiciga, H.A. A review of conjunctive GW-SW management by simulation–optimization tools. J. Water Supply Res. Technol. AQUA 2021, 70, 239–256. [Google Scholar] [CrossRef]
- Chakrae, I.; Safavi, H.R.; Dandy, G.C.; Golmohammadi, M.H. Integrated simulation-optimization framework for water allocation based on sustainability of surface water and groundwater resources. J. Water Resour. Plan. Manag. 2021, 147, 05021001. [Google Scholar] [CrossRef]
- Wang, M.; Zheng, C. Ground water management optimization using genetic algorithms and simulated annealing: Formulation and comparison. J. Am. Water Resour. Assoc. 1998, 34, 519–530. [Google Scholar] [CrossRef]
- Yang, C.C.; Chang, L.C.; Chen, C.S.; Yeh, M.S. Multi-objective planning for conjunctive use of surface and subsurface water using genetic algorithm and dynamics programming. Water Resour. Manag. 2009, 23, 417–437. [Google Scholar] [CrossRef]
- Singh, A. Irrigation planning and management through optimization modeling. Water Resour. Manag. 2013, 28, 1–14. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, Y.; Wu, B.; Tian, Y.; Han, F.; Zheng, C. Optimizing conjunctive use of surface water and groundwater for irrigation to address human-nature water conflicts: A surrogate modeling approach. Agric. Water Manag. 2016, 163, 380–392. [Google Scholar] [CrossRef]
- Ashu, A.; Lee, S.-I. Reuse of agriculture drainage water in a mixed land-use watershed. Agronomy 2019, 9, 6. [Google Scholar] [CrossRef] [Green Version]
- Ashu, A.B.; Lee, S.-I. Assessing climate change effects on water balance in a monsoon watershed. Water 2020, 12, 2564. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Kwon, K.D. Current status of groundwater monitoring networks in Korea. Water 2016, 8, 168. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.Y. Environmental issues of groundwater in Korea: Implications for sustainable use. Environ. Conserv. 2011, 38, 64–74. [Google Scholar] [CrossRef]
- Ministry of Land, Transport and Maritime Affairs; Korea Water Resources Corporation. A Revised National Master Plan for Groundwater Management; MLTM, K-Water: Gwacheon, Korea, 2007. (In Korean)
- Smith, M. CROPWAT: A Computer Program for Irrigation Planning and Management; Food and Agriculture Organization of the United Nations: Rome, Italy, 1992. [Google Scholar]
- Tayfur, G.; Singh, V.P. ANN and fuzzy logic models for simulating event-based rainfall-runoff. J. Hydraul. Eng. 2006, 132, 1321–1330. [Google Scholar] [CrossRef] [Green Version]
- Adamowski, J.; Sun, K. Development of a coupled wavelet transform and neural network method for flow forecasting of non-perennial rivers in semi-arid watersheds. J. Hydrol. 2010, 390, 85–91. [Google Scholar] [CrossRef]
- Yoon, H.; Jun, S.-C.; Hyun, Y.; Bae, G.-O.; Lee, K.-K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet neural network and wavelet support vector regression models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Ketabchi, H.; Ataie-Ashtiani, B. Evolutionary algorithms for the optimal management of coastal groundwater: A comparative study toward future challenges. J. Hydrol. 2015, 520, 193–213. [Google Scholar] [CrossRef]
- Daliakopoulos, I.; Coulibaly, P.; Tsanis, I. Groundwater level forecasting using artificial neural networks. J. Hydrol. 2005, 309, 229–240. [Google Scholar] [CrossRef]
- Coppola, E.; Szidarovszky, F.; Poulton, M.; Charles, E. Artificial neural network approach for predicting transient water levels in a multi-layered groundwater system under variable state, pumping, and climate conditions. J. Hydrol. Eng. 2003, 8, 348–360. [Google Scholar] [CrossRef]
- Rao, R. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar]
- Rao, R.; More, K. Design optimization and analysis of selected thermal devices using self-adaptive Jaya algorithm. Energy Convers. Manag. 2017, 140, 24–35. [Google Scholar] [CrossRef]
- Rao, R.V.; Saroj, A. A self-adaptive multi-population-based Jaya algorithm for engineering optimization. Swarm Evol. Comput. 2017, 37, 1–26. [Google Scholar]
- Rao, R.V.; Saroj, A. Constrained economic optimization of shell-and-tube heat exchangers using elitist-Jaya algorithm. Energy 2017, 128, 785–800. [Google Scholar] [CrossRef]
- Ha, K.; Lee, E.; An, H.; Kim, S.; Park, C.; Kim, G.-B.; Ko, K.-S. Evaluation of Seasonal Groundwater Quality Changes Associated with Groundwater Pumping and Level Fluctuations in an Agricultural Area, Korea. Water 2021, 13, 51. [Google Scholar] [CrossRef]
- Safavi, H.R.; Darzi, F.; Mariño, M.A. Simulation-optimization modeling of conjunctive use of surface water and groundwater. Water Resour. Manag. 2010, 24, 1965–1988. [Google Scholar] [CrossRef]

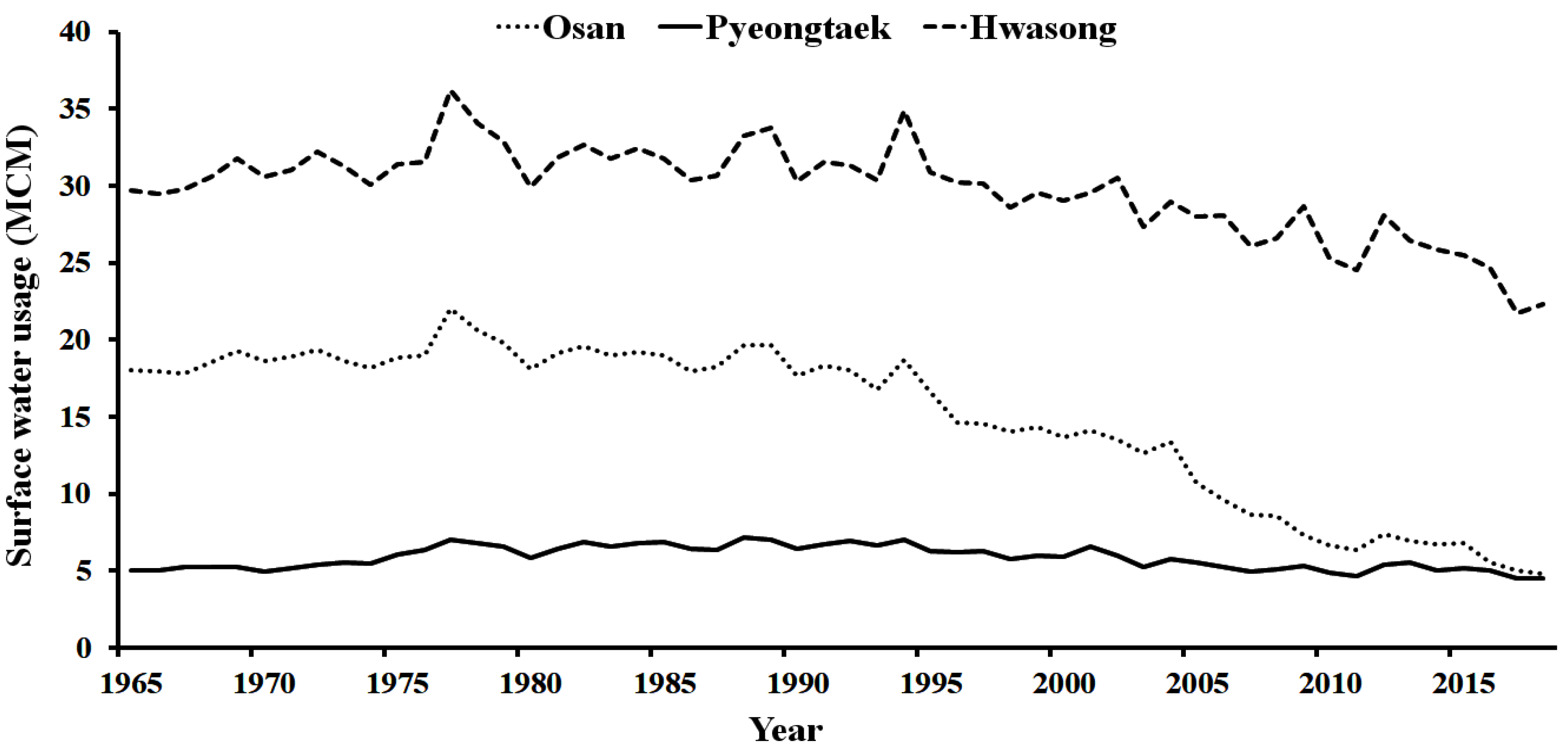


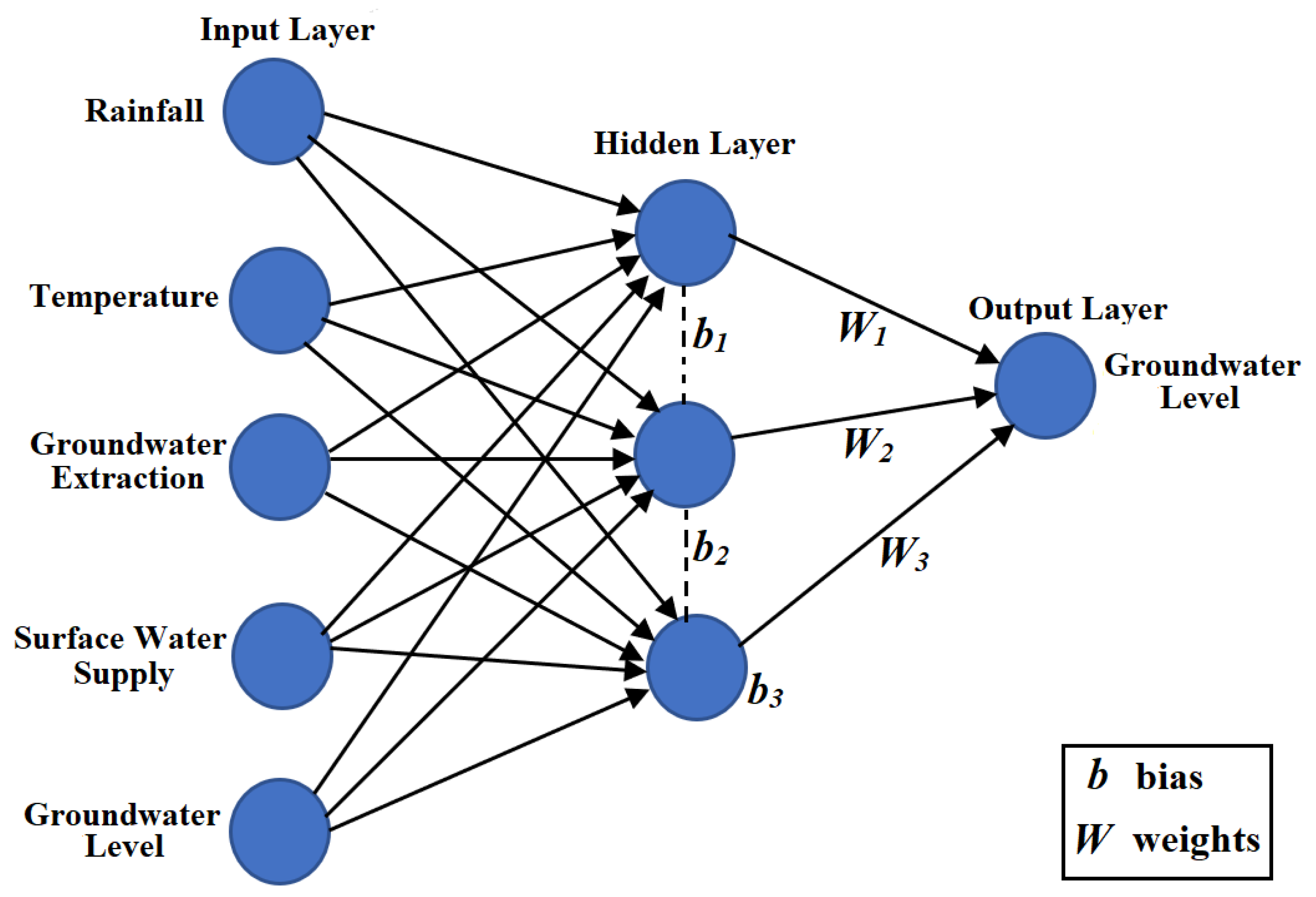
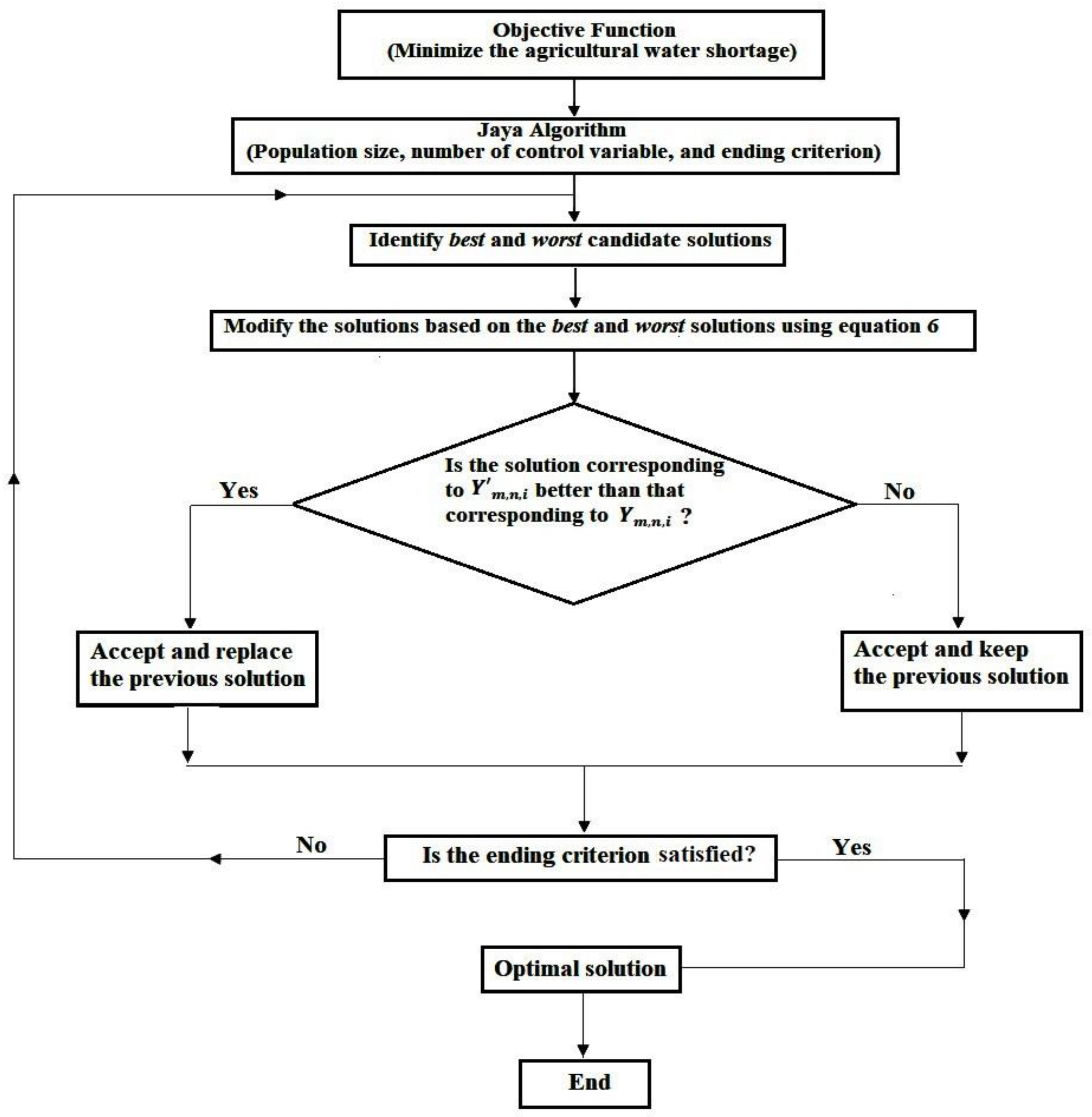

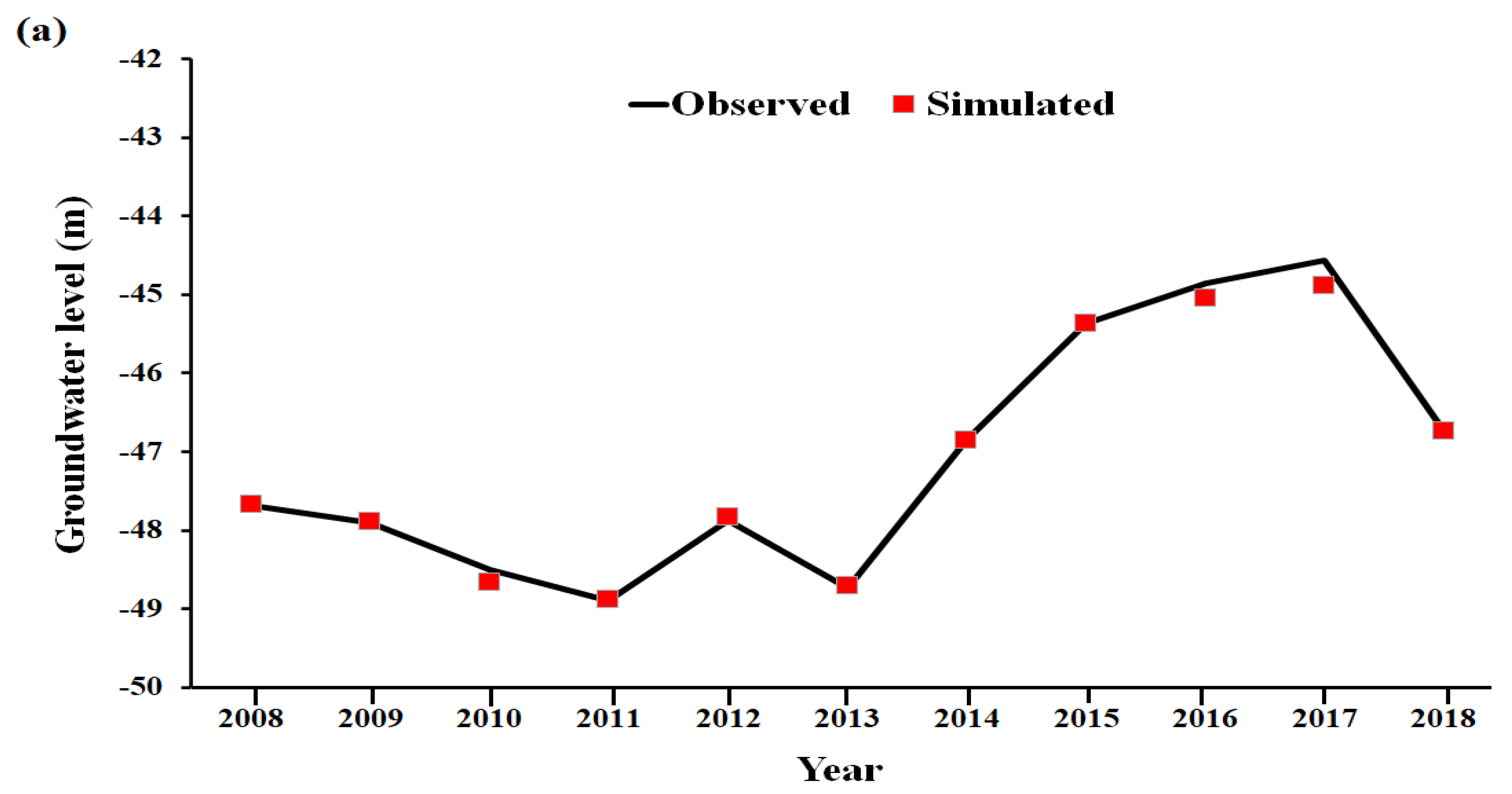



| Year | Crop Water Requirement (mm) | Groundwater Supply (MCM) | Surface Water Supply (MCM) | Water Demand (MCM) |
|---|---|---|---|---|
| 2008 | 1833.4 | 0.34 | 24.78 | 44.18 |
| 2009 | 1909 | 1.20 | 25.52 | 46.01 |
| 2010 | 1986.1 | 1.12 | 22.79 | 47.87 |
| 2011 | 2118.6 | 1.18 | 22.14 | 51.06 |
| 2012 | 2031.8 | 1.21 | 25.33 | 48.97 |
| 2013 | 1686 | 1.20 | 24.12 | 40.63 |
| 2014 | 1653.3 | 1.27 | 23.41 | 39.84 |
| 2015 | 1545.5 | 1.32 | 23.42 | 37.25 |
| 2016 | 1602.6 | 1.60 | 22.04 | 38.62 |
| 2017 | 1858.5 | 1.51 | 19.62 | 44.79 |
| 2018 | 1679 | 1.30 | 19.51 | 40.46 |
| Subarea | Training (R) | Testing (R) | Overall (R) | Overall (R2) | RMSE | MSE | MAPE |
|---|---|---|---|---|---|---|---|
| Osan | 0.95 | 0.92 | 0.92 | 0.85 | 0.12 | 0.02 | 0.15 |
| Hwasong | 0.85 | 0.98 | 0.90 | 0.81 | 0.01 | 0 | 0.01 |
| Pyeongtaek | 0.99 | 0.97 | 0.99 | 0.98 | 0.02 | 0 | 0.08 |
| Subarea | Without Conjunctive Use (MCM) | With Conjunctive Use (MCM) | ||||||
|---|---|---|---|---|---|---|---|---|
| Surface Water Supply | Groundwater Supply | Total Water Supply | Deficit | Surface Water Supply | Groundwater Supply | Total Water Supply | Deficit | |
| Osan | 4.79–8.57 | 0.17–0.89 | 5.52–8.74 | 7.57–13.53 | 9.47–12.37 | 1.05–1.37 | 10.52–13.74 | 2.57–8.53 |
| Hwasong | 10.86–14.35 | 0.04–0.60 | 11.38–14.62 | 5.36–11.01 | 14.75–17.66 | 1.64–1.96 | 16.38–19.62 | 1.36–7.87 |
| Pyeongtaek | 2.26–2.75 | 0.02–0.13 | 2.30–2.88 | 1.03–2.65 | 2.97–3.49 | 0.33–0.39 | 3.30–3.88 | 0.03–1.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ashu, A.B.; Lee, S.-I. Simulation-Optimization Model for Conjunctive Management of Surface Water and Groundwater for Agricultural Use. Water 2021, 13, 3444. https://doi.org/10.3390/w13233444
Ashu AB, Lee S-I. Simulation-Optimization Model for Conjunctive Management of Surface Water and Groundwater for Agricultural Use. Water. 2021; 13(23):3444. https://doi.org/10.3390/w13233444
Chicago/Turabian StyleAshu, Agbortoko Bate, and Sang-Il Lee. 2021. "Simulation-Optimization Model for Conjunctive Management of Surface Water and Groundwater for Agricultural Use" Water 13, no. 23: 3444. https://doi.org/10.3390/w13233444
APA StyleAshu, A. B., & Lee, S.-I. (2021). Simulation-Optimization Model for Conjunctive Management of Surface Water and Groundwater for Agricultural Use. Water, 13(23), 3444. https://doi.org/10.3390/w13233444







