Analysis of Long-Term Shoreline Observations in the Vicinity of Coastal Structures: A Case Study of South Bali Beaches
Abstract
:1. Introduction
1.1. Background
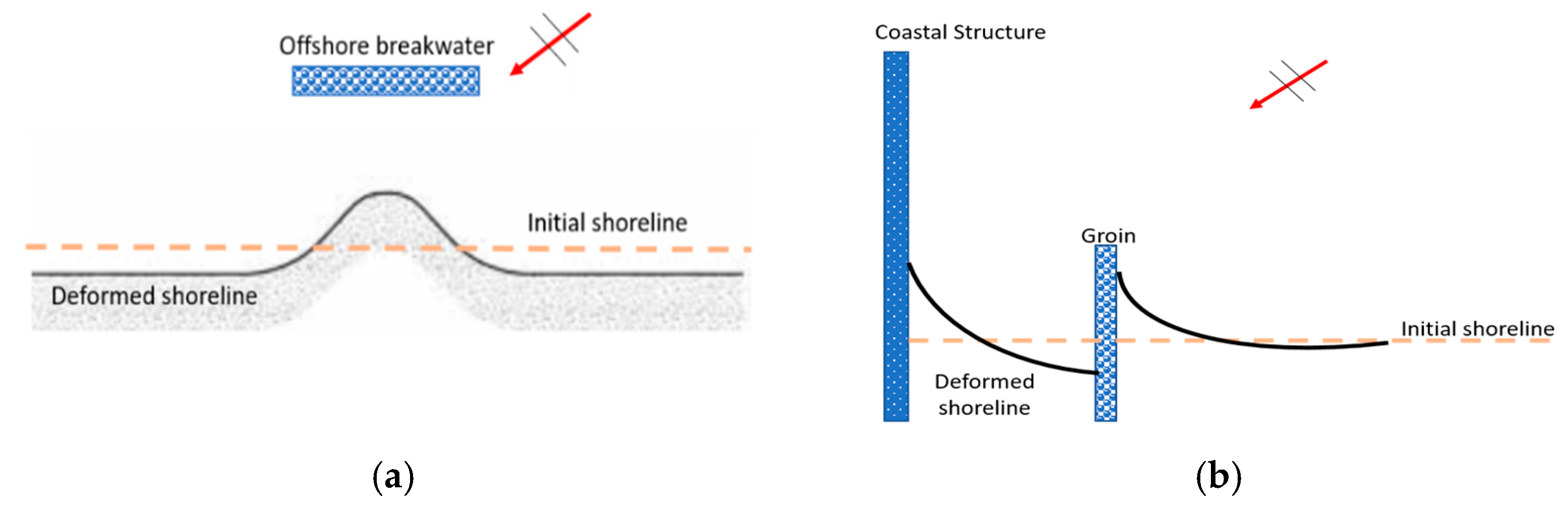
1.2. Shoreline Changes Due to Coastal Structures
2. Characteristics of Study Areas
2.1. Study Areas
2.2. Existing Structures and Projects
3. Materials and Methods
3.1. Data Collection
3.2. Shoreline Data Indicators from Beach Profile Data in HWL
3.3. Shoreline Rate Changes Based on Beach Profile Data
3.4. Littoral Sediment Transport Using the Inverse Method
3.5. MeEPASoL and QGIS Application to Define Shoreline Equilibrium
3.6. Sediment Budget Reduction Based on Mass Conservation
4. Results
4.1. Kuta Beach
4.2. Sanur Beach
4.3. Nusa Dua Beach
5. Discussion
5.1. Littoral Drift Vector and Sediment Changes at Study Areas
5.2. Effect of Structures and Littoral Drift on the Shoreline
5.3. Background Erosion in Littoral Cell
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Kraus, N.; Rosati, J. Estimating Uncertainty in Coastal-Sediment Budget at Inlets; Coast Eng. Tech. Note CETN IV-16; U.S. Army Engineering Res. Dev. Center, Coast Hydraul Lab.: Vicksburg, MS, USA, 1999.
- Crowell, M.; Leatherman, S.P.; Buckley, M.K. Historical Shoreline Change: Error Analysis and Mapping Accuracy. J. Coast. Res. 1991, 7, 839–852. [Google Scholar]
- Byrnes, M.R.; Anders, F.J. Accuracy of Shoreline Change Rates as Determined from Maps and Aerial Photographs. Shore Beach Obs. 2016, 58, 30. [Google Scholar]
- Douglas, B.C.; Crowell, M.; Winter, F. Long-term Shoreline Position Prediction and Error Propagation. J. Coast. Res. 2000, 16, 145–152. [Google Scholar]
- Lee, J.L.; Jung, J.S.; Kim, I.H.; Kweon, H.M. Estimation of Longshore Sediment Transport Rates from Shoreline Changes. Korea Coast. Ocean Eng. Proj. 2004, 248–267. [Google Scholar]
- Sui, L.; Wang, J.; Yang, X.; Wang, Z. Spatial-temporal characteristics of coastline changes in Indonesia from 1990 to 2018. Sustainability 2020, 12, 3242. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Hou, X. Characteristics of coastline changes on southeast Asia Islands from 2000 to 2015. Remote Sens. 2020, 12, 519. [Google Scholar] [CrossRef] [Green Version]
- Ariffin, E.H.; Zulfakar, M.S.Z.; Redzuan, N.S.; Mathew, M.J.; Akhir, M.F.; Baharim, N.B.; Awang, N.A.; Mokhtar, N.A. Evaluating the effects of beach nourishment on littoral morphodynamics at Kuala Nerus, Terengganu (Malaysia). J. Sustain. Sci. Manag. 2020, 15, 29–42. [Google Scholar] [CrossRef]
- Raj, J.K. Net directions and rates of present-day beach transport by littoral drift along the East Coast of Peninsular Malaysia. Bull. Geol. Soc. Malays. 1982, 15, 57–70. [Google Scholar] [CrossRef]
- Thoai, D.T.; Dang, A.N.; Kim, O.N.T. Analysis of coastline change in relation to meteorological conditions and human activities in Ca mau cape, Viet Nam. Ocean Coast. Manag. 2019, 171, 56–65. [Google Scholar] [CrossRef]
- Lim, C.B.; Lee, J.; Lee, J.L. Simulation of bay-shaped shorelines after the construction of large-scale structures by using a parabolic bay shape equation. J. Mar. Sci. Eng. 2021, 9, 43. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J.L. Estimation of background erosion rate at janghang beach due to the construction of geum estuary tidal barrier in Korea. J. Mar. Sci. Eng. 2020, 8, 551. [Google Scholar] [CrossRef]
- Lim, C.; Kim, T.; Lee, S.; Yeon, Y.J.; Lee, J.L. Quantitative interpretation of risk potential of beach erosion due to coastal zone development. Nat. Hazards Earth Syst. Sci. 2021, 180. [Google Scholar] [CrossRef]
- Uda, T.; Onaka, S.; Serizawa, M. Beach erosion downcoast of Pengambengan fishing port in western part of Bali Island. Procedia Eng. 2015, 116, 494–501. [Google Scholar] [CrossRef] [Green Version]
- Onaka, S.; Endo, S.; Uda, T. Bali beach conservation project and issues related to beach maintenance after completion of project. In Proceedings of the Seventh International Conference on Asian and Pacific Coasts, Bali, Indonesia, 24–26 September 2013; pp. 198–203. [Google Scholar]
- Carpi, L.; Bicenio, M.; Mucerino, L.; Ferrari, M. Detached breakwaters, yes or not? A modelling approach to evaluate and plan their removal. Ocean Coast Manag. 2021, 210, 105668. [Google Scholar] [CrossRef]
- Vaidya, A.M.; Kori, S.K.; Kudale, M.D. Shoreline Response to Coastal Structures. Aquat Procedia. 2015, 4, 333–340. [Google Scholar] [CrossRef]
- Uda, T. Advanced Series on Ocean Engineering. In Japan’s Beach Erosion Reality and Future Measures; Angewandte Chemie International Edition: Singapore, 1967; Volume 31, pp. 951–952. [Google Scholar]
- Badan Pusat Statistik (BPS). Provinsi Bali 2020. In Provinsi Bali Dalam Angka 2020; CV Bhineka Raya: Bali, Indonesia, 2020; Volume 148, pp. 148–162. [Google Scholar]
- Saputra, H. Studi Pola Sebaran Sedimen Dasar Akibat Arus Sepanjang Pantai di Sekitar Pemecah Gelombang Pantai Kuta Bali. J. Oseanografi. 2013, 2, 161–170. [Google Scholar]
- Putro, A.H.S.; Lee, J.L. Analysis of longshore drift patterns on the littoral system of Nusa Dua beach in Bali, Indonesia. J. Mar. Sci. Eng. 2020, 8, 749. [Google Scholar] [CrossRef]
- Patil, B.M. Littoral Drift and Shoreline Evolution. Train Course Coast Eng Coast Zo Manag; Central Water and Power Research Station: Pune, India, 2012; pp. 1–12. [Google Scholar]
- Ferreira, A.; Coelho, C. Artificial Nourishments Effects on Longshore Sediments Transport. J. Mar. Sci. Eng. 2021, 9, 240. [Google Scholar] [CrossRef]
- Solihuddin, T.; Husrin, S.; Salim, H.L.; Kepel, T.L.; Mustikasari, E.; Heriati, A.; Ati, R.N.A.; Purbani, D.; Mbay, L.O.N.; Indriasari, V.Y.; et al. Coastal erosion on the north coast of Java: Adaptation strategies and coastal management. In IOP Conference Series: Earth and Environmental; IOP Publishing: Bristol, UK, 2021; Volume 777. [Google Scholar]
- Rashidi, A.M.; Jamal, M.; Hassan, M.; Sendek, S.M.; Sopie, S.M.; Hamid, M.A. Coastal Structures as Beach Erosion Control and Sea Level Rise Adaptation in Malaysia: A Review. Water 2021, 13, 1741. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Turner, I.L. Shoreline response to submerged structures: A review. Coast. Eng. 2006, 53, 65–79. [Google Scholar] [CrossRef]
- Hanson, H. GENESIS—A generalized shoreline change numerical model. J. Coast. Res. 1989, 5, 1–27. [Google Scholar]
- Himmelstoss, E.A.; Henderson, R.E.; Kratzmann, M.G.; Farris, A.S. Digital Shoreline Analysis System (DSAS) Version 5.0 User Guide; U.S. Geological Survey: Reston, VR, USA, 2018.
- Baig, M.R.I.; Ahmad, I.A.; Shahfahad; Tayyab, M.; Rahman, A. Analysis of shoreline changes in Vishakhapatnam coastal tract of Andhra Pradesh, India: An application of digital shoreline analysis system (DSAS). Ann. GIS 2020, 26, 361–376. [Google Scholar] [CrossRef]
- Das, S.K.; Sajan, B.; Ojha, C.; Soren, S. Shoreline change behavior study of Jambudwip island of Indian Sundarban using DSAS model. Egypt. J. Remote Sens. Space Sci. 2021. [Google Scholar] [CrossRef]
- Nassar, K.; Mahmod, W.E.; Fath, H.; Masria, A.; Nadaoka, K.; Negm, A. Shoreline change detection using DSAS technique: Case of North Sinai coast, Egypt. Mar. Georesour. Geotechnol. 2019, 37, 81–95. [Google Scholar] [CrossRef]
- Klein, A.H.D.F.; Vargas, A.; Raabe, A.L.A.; Hsu, J.R. Visual assessment of bayed beach stability with computer software. Comput. Geosci. 2003, 29, 1249–1257. [Google Scholar] [CrossRef]
- Benedet, L.; Klein, A.H.; Hsu, J.R.-C.; Smith, J.M. Practical insights and applicability of empirical bay shape equations. Coast. Eng. 2005, 2181–2193. [Google Scholar] [CrossRef]
- Valsamidis, A.; Figlus, J.; Ritt, B.; Reeve, D.E. Modelling the morphodynamic evolution of Galveston beach, Gulf of Mexico, following Hurricane Ike in 2008. Cont. Shelf Res. 2021, 218, 104373. [Google Scholar] [CrossRef]
- Hsu, J.R.-C.; Yu, M.-J.; Lee, F.-C.; Benedet, L. Static bay beach concept for scientists and engineers: A review. Coast. Eng. 2010, 57, 76–91. [Google Scholar] [CrossRef]
- Ab Razak, M.S.; Reyns, J.; Roelvink, D. Beach response due to sand nourishment on the east coast of Malaysia. Proc. Inst. Civ. Eng.-Marit. Eng. 2013, 166, 151–174. [Google Scholar] [CrossRef]
- Ab Razak, M.S.; Jamaludin, N.; Nor, N.A.Z.M. The Planform Stability of Embayed Beached on the west coast of Peninsular Malaysia. J. Teknol. 2018, 80, 33–42. [Google Scholar] [CrossRef] [Green Version]
- Ab Razak, M.S.; Suryadi, F.X.; Jamaluddin, N.; Nor, N.A.Z.M. Shoreline Planform Stability of Embayed Beaches Along the Malaysian Peninsular Coast. J. Coast. Res. 2018, 85, 631–635. [Google Scholar] [CrossRef]
- Sudiarta, I.N.; Suardana, I.W. Tourism Destination Planning Strategy: Analysis and Implementation of Marketing City Tour in Bali. Procedia-Soc. Behav. Sci. 2016, 227, 664–670. [Google Scholar] [CrossRef] [Green Version]
- Makfiya, N.; Siladharma, I.G.B.; Gede, I.W.; Karang, A. Analisis Perubahan Garis Pantai dengan Menggunakan Metode One-Line Model (Studi Kasus: Pantai Kecamatan Kuta, Bali). J. Mar. Aquat. Sci. 2020, 6, 196–204. [Google Scholar]
- Tsuchiya, Y. Formation of Stable Sandy Beaches and Beach Erosion Control: A Methodology for Beach Erosion Control Using Headlands and Its Applications. Bull. Disaster Prev. Res. Inst. 1994, 44, 139–173. [Google Scholar]
- Litbang Sumber Daya Air Bali. Kolokium Hasil Litbang Sumber Daya Air 2014; Litbang Sumber Daya Air Bali: Bali, Indonesia, 2014; pp. 1–11. [Google Scholar]
- Senjaya, E.S.; Sila, D.I.B.; Suputra, I.K. Evolusi Perubahan Garis Pantai Setelah Pemasangan Bangunan Pantai. J. Spektran. 2015, 3, 65–74. [Google Scholar] [CrossRef]
- Jean, M.; Leatherman, S.; Spring, F.; Pajak, M.J. The High Water Line as Shoreline Indicator. J. Coast. Res. 2002, 18, 329–337. [Google Scholar]
- Boak, E.H.; Turner, I.L. Shoreline definition and detection: A review. J. Coast. Res. 2005, 21, 688–703. [Google Scholar] [CrossRef] [Green Version]
- Gibson, A.W.M.; Shalowitz Aaron, L. Shore and Sea Boundaries. In Interpretation and Use of Coast and Geodetic Survey Data; U.S. Department of Commerce: Washington, DC, USA, 1965; Volume 2. [Google Scholar]
- Jaramillo, C.; Jara, M.S.; González, M.; Medina, R. A shoreline evolution model considering the temporal variability of the beach profile sediment volume (sediment gain/loss). Coast. Eng. 2020, 56, 103612. [Google Scholar] [CrossRef]
- Smith, G.L.; Zarillo, G.A. Calculating long-term shoreline recession rates using aerial photographic and beach profiling techniques. J. Coast. Res. 1990, 6, 111–120. [Google Scholar]
- Ozturk, D.; Beyazit, I.; Kilic, F. Spatiotemporal Analysis of Shoreline Changes of the Kizilirmak Delta. J. Coast. Res. 2015, 316, 1389–1402. [Google Scholar] [CrossRef]
- Romine, B.M.; Fletcher, C.H.; Frazer, L.; Genz, A.S.; Barbee, M.M.; Lim, S.-C. Historical Shoreline Change, Southeast Oahu, Hawaii; Applying Polynomial Models to Calculate Shoreline Change Rates. J. Coast. Res. 2009, 256, 1236–1253. [Google Scholar] [CrossRef]
- Douglas, B.C.; Crowell, M.; Leatherman, S.P. Considerations for Shoreline Position Prediction. J. Coast. Res. 1998, 14, 1025–1033. [Google Scholar]
- Department of the army, U.S. Center. Shore Protection Manual; Coastal Engineering U.S. Army Water-way Experiment Station, Corps of Engineers Coastal Engineering Research Center: Vicksburg, MS, USA, 1984. [Google Scholar]
- Sayao, O.J. Discussion of “Alongshore Sediment Transport Rate” by J. W. Kamphuis (November/December, 1991, Vol. 117, No. 6). J. Waterw. Port Coast. Ocean Eng. 1993, 119, 344–346. [Google Scholar] [CrossRef]
- Bayram, A.; Larson, M.; Hanson, H. A new formula for the total longshore sediment transport rate. Coast. Eng. 2007, 54, 700–710. [Google Scholar] [CrossRef]
- van Rijn, L.C. A simple general expression for longshore transport of sand, gravel and shingle. Coast. Eng. 2014, 90, 23–39. [Google Scholar] [CrossRef]
- Shaeri, S.; Etemad-Shahidi, A.; Tomlinson, R. Revisiting Longshore Sediment Transport Formulas. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04020009. [Google Scholar] [CrossRef]
- Samaras, A.G.; Koutitas, C.G. Comparison of three longshore sediment transport rate formulae in shoreline evolution modeling near stream mouths. Ocean Eng. 2014, 92, 255–266. [Google Scholar] [CrossRef]
- Klonaris, G.; Memos, C.D.; Drønen, N.K.; Deigaard, R. Boussinesq-Type Modeling of Sediment Transport and Coastal Morphology. Coast. Eng. J. 2017, 59, 1750007-1. [Google Scholar] [CrossRef]
- Pelnard-Considère, R. Essai de théorie de l’évolution des formes de rivage en plages de sables et de gâlets. In Proceedings of the Soc Hydro-technique Fr Proc 4th Journees L’Hydraulique Quest III, Rapport, Paris, France, 13–15 June 1956; p. 74-1–10. [Google Scholar]
- Gunawan, P.H.; Pudjaprasetya, S.R. Simulation of shoreline development in a groyne system, with a case study Sanur Bali beach. J. Phys. Conf. Ser. 2018, 971, 012027. [Google Scholar] [CrossRef]
- Walton, T.L.; Dean, R.G. Longshore sediment transport via littoral drift rose. Ocean Eng. 2010, 37, 228–235. [Google Scholar] [CrossRef]
- Mehaute, B.L.; Soldate, M. Mathematical Modeling of Shoreline Evolution. Coast. Eng. 1978, 1978, 1163–1179. [Google Scholar]
- Thomas, T.; Williams, A.; Rangel-Buitrago, N.; Phillips, M.; Anfuso, G. Assessing Embayed Equilibrium State, Beach Rotation and Environmental Forcing Influences; Tenby Southwest Wales, UK. J. Mar. Sci. Eng. 2016, 4, 30. [Google Scholar] [CrossRef] [Green Version]
- Zhilong, L.; Zishen, C. Progress in Studies on the Equilibrium Shape of Headland-bay Shoreline. Mar. Sci. Bull. 2007, 9, 74–83. [Google Scholar]
- Lim, C.B.; Lee, J.L.; Kim, I.H. Performance test of parabolic equilibrium shoreline formula by using wave data observed in east sea of Korea. J. Coast. Res. 2019, 91, 101–105. [Google Scholar] [CrossRef]
- Lee, J.L.; Hsu, J.R.C. Numerical Simulation of Dynamic Shoreline Changes Behind a Detached Breakwater by Using an Equilibrium Formula. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering OMAE 2017, Throndhein, Norway, 25–30 June 2017; pp. 1–9. [Google Scholar]
- Hsu, J.R.C.; Evans, C. Parabolic bay shapes and applications. Proc. Inst. Civ. Eng. 1989, 87, 557–570. [Google Scholar] [CrossRef]
- Rosati, J.D. Concepts in Sediment Budgets. J. Coast. Res. 2005, 2005, 307–322. [Google Scholar] [CrossRef]
- Young, R.S.; Pilkey, O.H.; Bush, D.M.; Thieler, E.R. A discussion of the generalized model for simulating shoreline change (GENESIS). J. Coast. Res. 1995, 11, 875–886. [Google Scholar]

















| Beach | Hs (m) 1 | Ts (s) 1 | D50 (mm) 1 | Beach Nourishment (×1000 m3) 2 |
|---|---|---|---|---|
| Kuta: Kuta Beach | 1.1–2.8 | 4–8 s | 0.201 | 520 |
| Sanur: Karang Beach | 1.7–5.5 | 5–16 s | 0.606 | 300 |
| Nusa Dua: Samuh Beach | 1.7–5.5 | 5–16 s | 0.606 | 340 |
| Beach | Beach Length (m) | Existing Structure | Dimension (m) |
|---|---|---|---|
| Kuta: Kuta Beach | 676 | offshore breakwater BWN 1 | L = 150 |
| offshore breakwater BWN 2 | L = 120 | ||
| reef flat restoration | - | ||
| Sanur: Karang Beach | 250 | Headland T groin G4 | L = 76.5 W = 3 |
| Headland L groin G16 | L = 71.1 W = 3 | ||
| offshore breakwater BWN 1 | L = 80 W = 7 | ||
| Nusa dua: Samuh Beach | 210 | Groin type L GN1 | L = 85 W = 3 |
| Groin type L G9 | L = 80 W = 73 |
| Beach | Beach Length (m) | Cross-Line Observation | Beach Width (m) | Year Observation | Berm + Closure Depth (m) 1 |
|---|---|---|---|---|---|
| Kuta: Kuta Beach | 676 | 13 | 52 | 2008–2021 | 5 |
| Sanur: Karang Beach | 250 | 7 | 40 | 2004–2019 | 4.0 |
| Nusa Dua: Samuh Beach | 210 | 6 | 36 | 2003–2021 | 4.5 |
| Beach | Area Change (m2) | Note | |
|---|---|---|---|
| Initial | Mean Area | ||
| Kuta | 48,620.68 | 47,636.62 | retreat |
| Sanur | 8406.00 | 8549.30 | advance |
| Nusa Dua | 9866.13 | 8583.09 | retreat |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahmawati, R.R.; Putro, A.H.S.; Lee, J.L. Analysis of Long-Term Shoreline Observations in the Vicinity of Coastal Structures: A Case Study of South Bali Beaches. Water 2021, 13, 3527. https://doi.org/10.3390/w13243527
Rahmawati RR, Putro AHS, Lee JL. Analysis of Long-Term Shoreline Observations in the Vicinity of Coastal Structures: A Case Study of South Bali Beaches. Water. 2021; 13(24):3527. https://doi.org/10.3390/w13243527
Chicago/Turabian StyleRahmawati, Ria Rista, Anthony Harlly Sasono Putro, and Jung Lyul Lee. 2021. "Analysis of Long-Term Shoreline Observations in the Vicinity of Coastal Structures: A Case Study of South Bali Beaches" Water 13, no. 24: 3527. https://doi.org/10.3390/w13243527
APA StyleRahmawati, R. R., Putro, A. H. S., & Lee, J. L. (2021). Analysis of Long-Term Shoreline Observations in the Vicinity of Coastal Structures: A Case Study of South Bali Beaches. Water, 13(24), 3527. https://doi.org/10.3390/w13243527






