Flow Turbulence Characteristics and Mass Transport in the Near-Wake Region of an Aquaculture Cage Net Panel
Abstract
:1. Introduction
2. Methodology
2.1. Experimental Setup and Instrumentation
2.2. Experimental Procedures
3. Results and Discussion
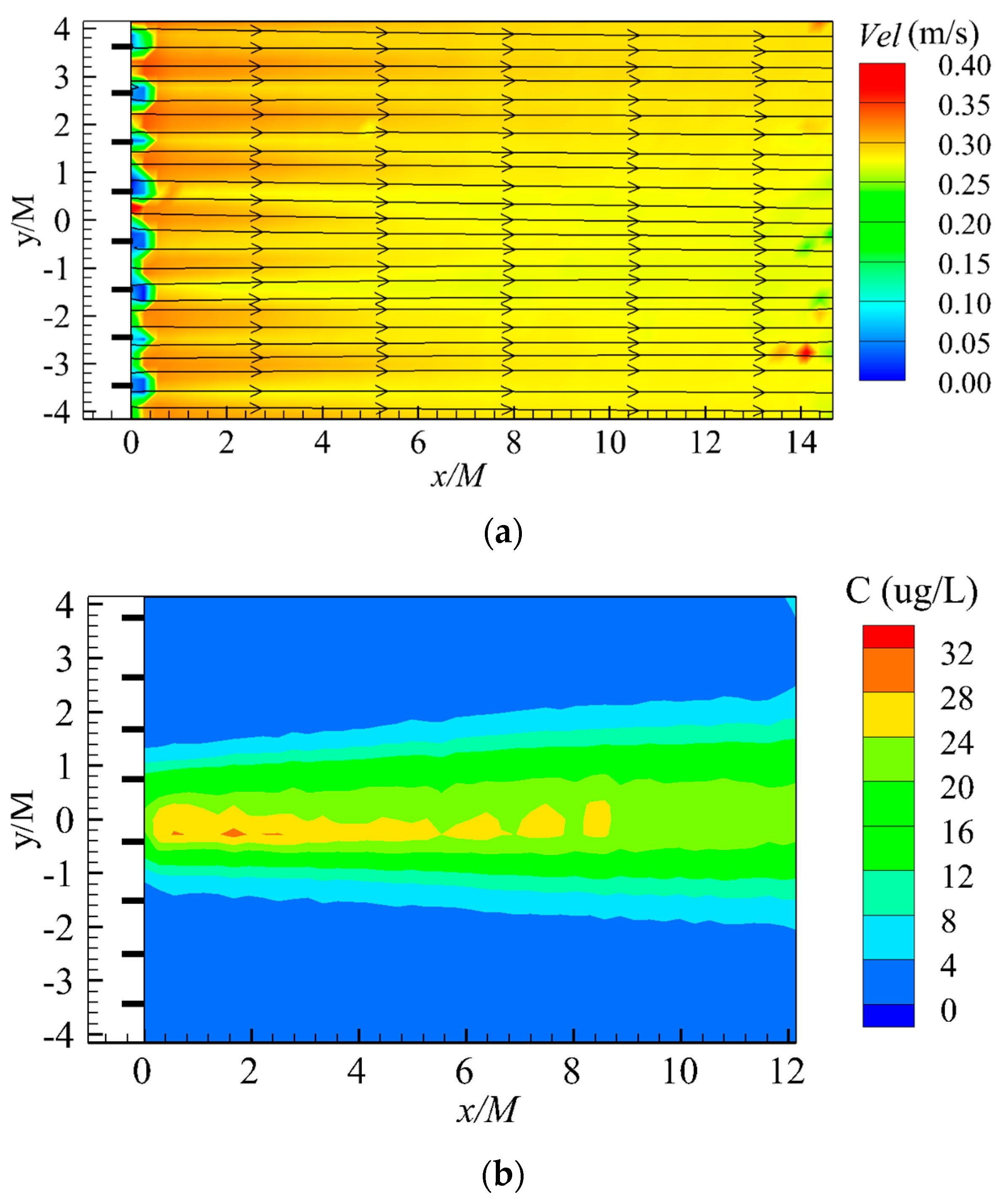
3.1. Time-Averaged Velocity and Concentration Field
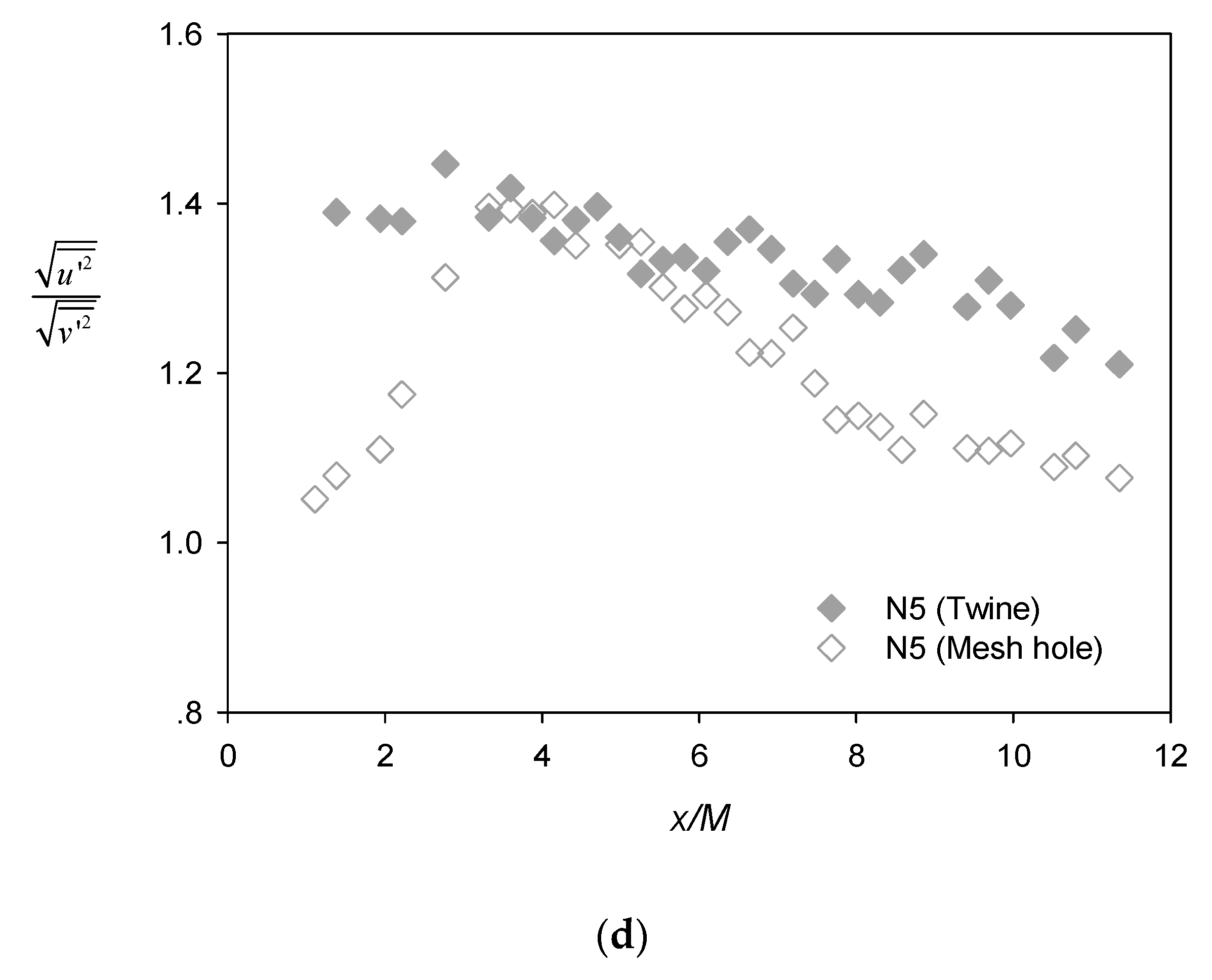
3.2. Turbulence Characteristics
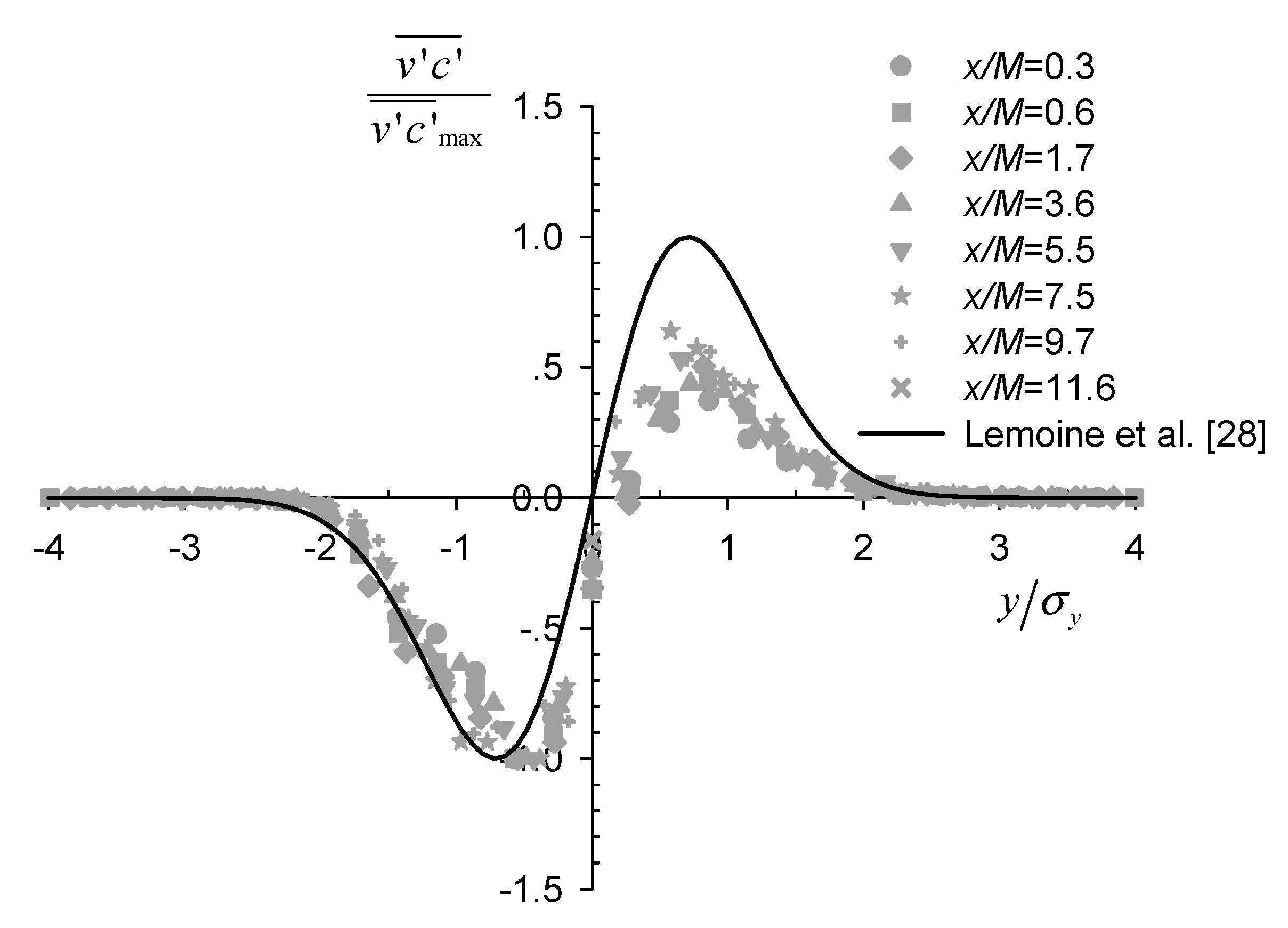
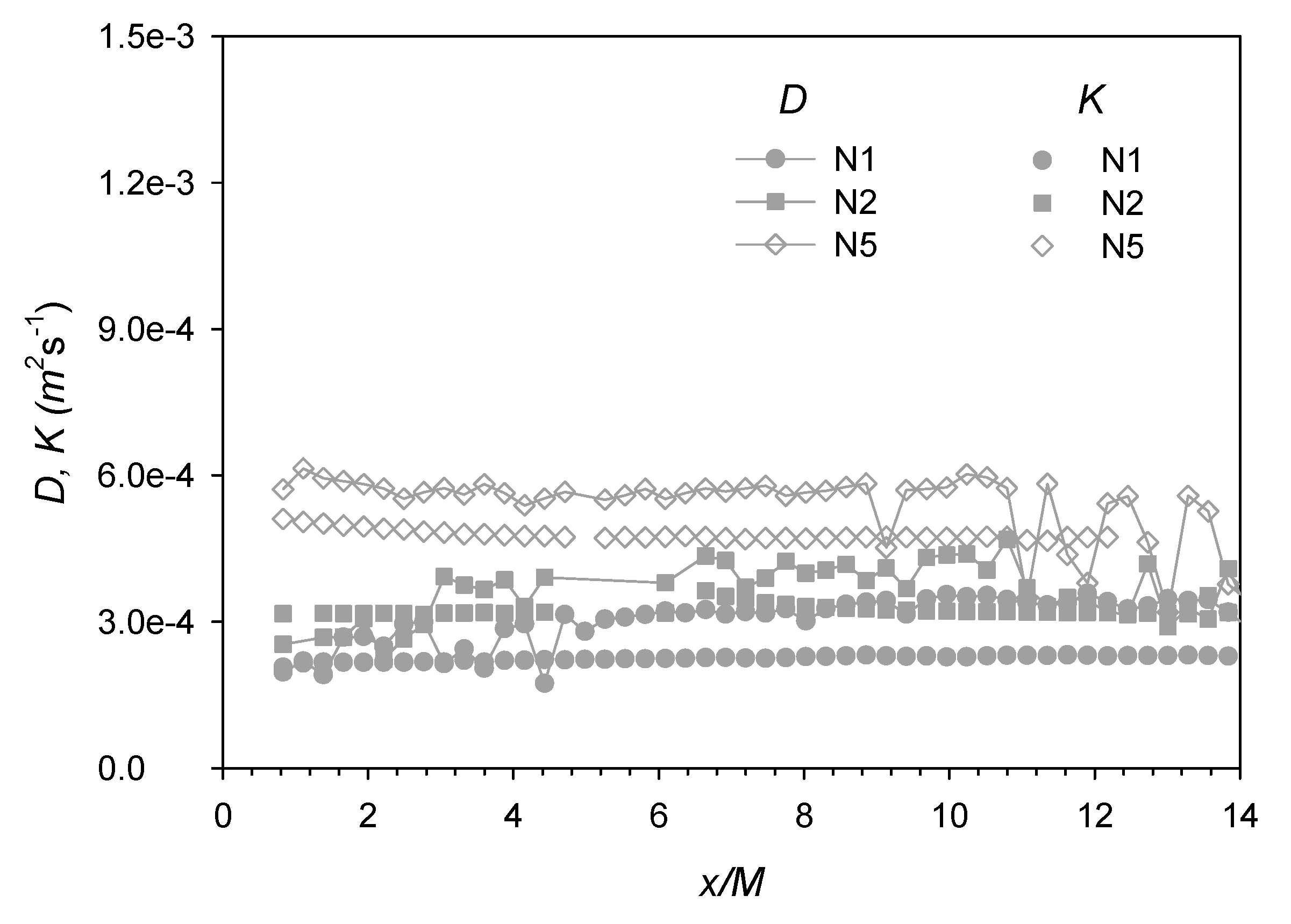
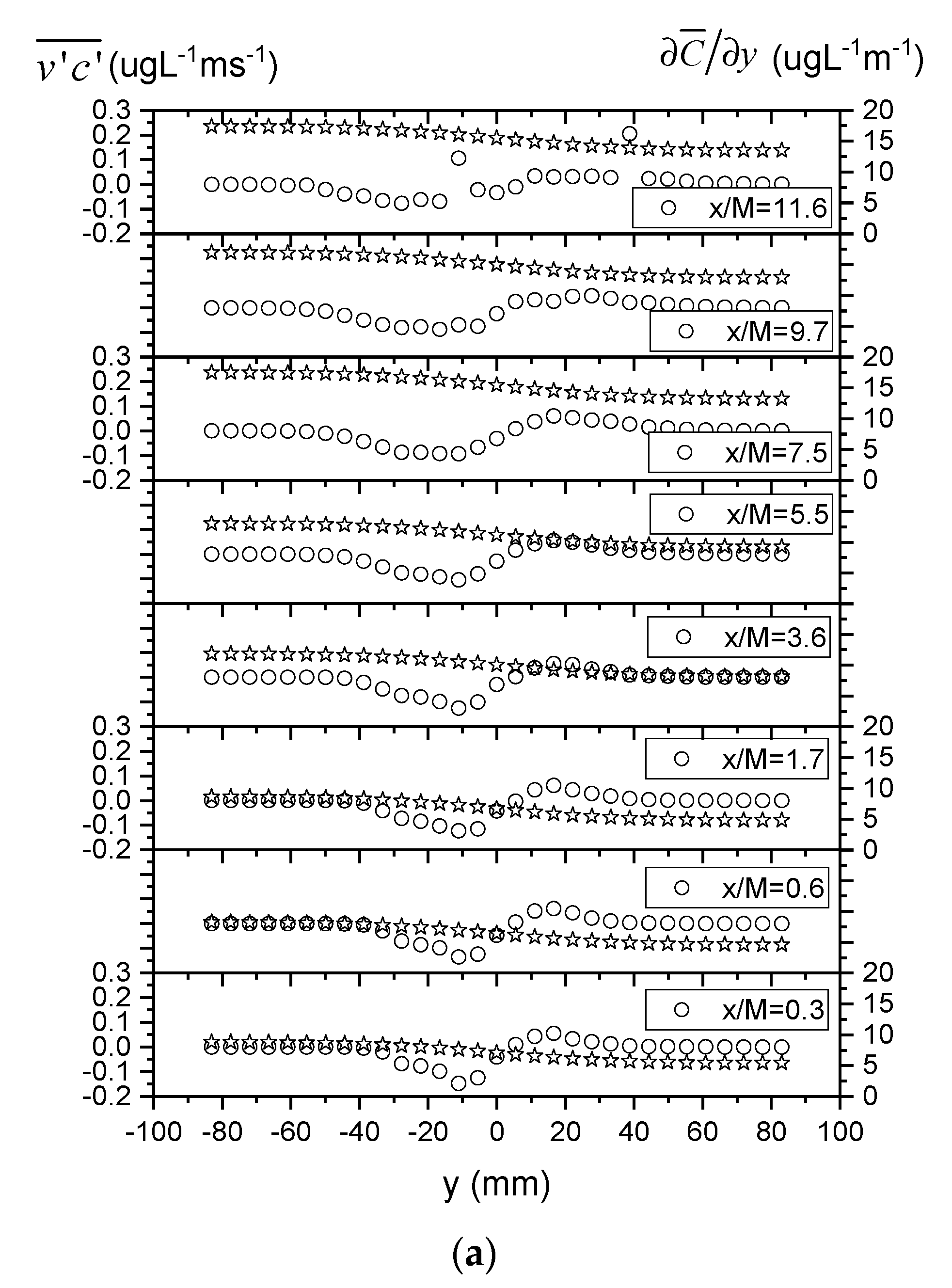
3.3. Turbulent Mass Transport
4. Conclusions
- The wake flow downstream of the model fishing net panel showed a marked reduction and increase in time-averaged streamwise velocity immediately behind the net twine and at the adjacent mesh holes, respectively. The opposite trend was found for the streamwise turbulence intensity. For x > ~3M, the flow field became more homogeneous and entered the turbulence decay region. However, complete recovery of incoming velocity and development of isotropic turbulence was not observed to occur within the downstream extent of experimental measurements (i.e., x → ~15M). Corroborating with these changes in the turbulent flow field, the mean concentration began to decay steadily after x = ~3M.
- Similar to decaying grid-generated turbulence, the turbulence intensity followed a power-law decay over a short range of x = ~4M to 10M. However, the fitted decay exponent was much smaller than reported values for grid turbulence in previous wind-tunnel and water-channel experimental studies. Lateral profiles of the mean scalar concentration and concentration fluctuation exhibited self-similar Gaussian distributions, while those for the transverse turbulent scalar flux were nearly self-similar and antisymmetric about the centerline. These profiles started from a downstream location x = 0.3M, which was much closer to the net panel, with a strongly inhomogeneous wake flow field, than previous findings on scalar plume development downstream of point sources in grid turbulence.
- The presence of the net panel tended to break larger coherent eddies into smaller vortices, leading to a reduction in the transverse integral length scale. In so doing, the panel also accelerated the transition of plume development from the turbulent-convective regime to the more effective turbulent-diffusive regime, with the combined effects leading to slightly enhanced lateral spreading of the scalar plume.
- Direct comparison of the plume spreading width and the transverse integral length scale of the flow indicated that the development of the scalar plume was still transitioning from turbulent-convective regime to turbulent-diffusive regime within the downstream extent of the experimental measurements. This was confirmed by the invalidity of the gradient-diffusion hypothesis in predicting the transverse scalar transport. Nevertheless, the apparent turbulent diffusivity, estimated from the gross plume parameters (i.e., time-averaged velocity and spreading width), appeared to be in reasonable agreement with the Taylor diffusivity calculated as the product of the transverse velocity fluctuation and integral length scale.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | constant associated with the power law turbulence decay |
| mean concentration (µg/L) | |
| mean concentration at the plume centerline (µg/L) | |
| mean concentration at the net panels (µg/L) | |
| c’ | concentration fluctuation (µg/L) |
| d | diameter of the net twine (mm) |
| D | Taylor (turbulent) diffusivity (m2/s) |
| ey | transverse unit vector |
| h | water depth in the flume (m) |
| K | apparent turbulent diffusivity (m2/s) |
| Lt | integral length scale of transverse velocity fluctuations (mm) |
| M | mesh size of the net/grid (mm) |
| n | decay rate (exponent) of the power law turbulence decay |
| r | separation in the transverse direction |
| Red | Reynolds number with respect to water depth (=U0 h/ν) |
| Rem | Reynolds number with respect to net twine (=U0 d/ν) |
| Rew | Reynolds number with respect to mesh size (=U0M/ν) |
| S | net solidity defined as the ratio between the projected area and the total area enclosed by the net panel () |
| mean streamwise velocity behind the net (m/s) | |
| U0 | incoming current velocity in the flume (m/s) |
| u’ | velocity fluctuation in the streamwise direction (m/s) |
| v’ | velocity fluctuation in the transverse direction (m/s) |
| transverse turbulent mass flux (µg/L⋅m/s) | |
| x,y,z | Cartesian coordinates in the longitudinal, transverse and vertical directions, respectively (mm) |
| x0 | virtual origin associated with the power law turbulence decay (mm) |
| spreading width of the scalar plume (mm) | |
| spreading with of the concentration fluctuations (mm) | |
| normalized transverse coordinate ( |
References
- Dudley, R.W.; Panchang, V.G.; Newell, C.R. Application of a comprehensive modeling strategy for the management of net-pen aquaculture waste transport. Aquaculture 2000, 187, 319–349. [Google Scholar] [CrossRef]
- Corner, R.A.; Davies, P.A.; Cuthbertson, A.J.S.; Telfer, T.C. A flume study to evaluate the processes governing retention of sea lice therapeutants using skirts in the treatment of sea lice infestation. Aquaculture 2011, 319, 459–465. [Google Scholar] [CrossRef]
- Buryniuk, M.; Petrell, R.J.; Baldwin, S.; Lo, K.V. Accumulation and natural disintegration of solid wastes caught on a screen suspended below a fish farm cage. Aquac. Eng. 2006, 35, 78–90. [Google Scholar] [CrossRef]
- Klebert, P.; Lader, P.; Gansel, L.; Oppedal, F. Hydrodynamic interactions on net panel and aquaculture fish cages: A review. Ocean Eng. 2013, 58, 260–274. [Google Scholar] [CrossRef]
- Price, C.; Black, K.D.; Hargrave, B.T.; Morris, J.A. Marine cage culture and the environment: Effects on water quality and primary production. Aquac. Environ. Interact. 2015, 6, 151–174. [Google Scholar] [CrossRef] [Green Version]
- Laws, E.M.; Livesey, J.L. Flow through Screens. Annu. Rev. Fluid Mech. 1978, 10, 247–266. [Google Scholar] [CrossRef]
- Katopodis, C.; Ead, S.A.; Standen, G.; Rajaratnam, N. Structure of flow upstream of vertical angled screens in open channels. J. Hydraul. Eng. 2005, 131, 294–304. [Google Scholar] [CrossRef]
- Teitel, M.; Dvorkin, D.; Haim, Y.; Tanny, J.; Seginer, I. Comparison of measured and simulated flow through screens: Effects of screen inclination and porosity. Biosyst. Eng. 2009, 104, 404–416. [Google Scholar] [CrossRef]
- Bi, C.W.; Zhao, Y.P.; Dong, G.H.; Xu, T.J.; Gui, F.K. Experimental investigation of the reduction in flow velocity downstream from a fishing net. Aquac. Eng. 2013, 57, 71–81. [Google Scholar] [CrossRef]
- Batchelor, G.K. The Theory of Homogeneous Turbulence; University Press: Cambridge, UK, 1953; 197p. [Google Scholar]
- Mohamed, M.S.; Larue, J.C. The Decay Power Law in Grid-Generated Turbulence. J. Fluid Mech. 1990, 219, 195–214. [Google Scholar] [CrossRef]
- Comte-bellot, G.; Corrsin, S. Use of a Contraction to Improve Isotropy of Grid-Generated Turbulence. J. Fluid Mech. 1966, 25, 657–682. [Google Scholar] [CrossRef]
- Isaza, J.C.; Salazar, R.; Warhaft, Z. On grid-generated turbulence in the near- and far field regions. J. Fluid Mech. 2014, 753, 402–426. [Google Scholar] [CrossRef]
- Cardesa, J.I.; Nickels, T.B.; Dawson, J.R. 2D PIV measurements in the near field of grid turbulence using stitched fields from multiple cameras. Exp. Fluids 2012, 52, 1611–1627. [Google Scholar] [CrossRef]
- Gan, L.; Krogstad, P.A. Evolution of turbulence and in-plane vortices in the near field flow behind multi-scale planar grids. Phys. Fluids 2016, 28. [Google Scholar] [CrossRef] [Green Version]
- Hopfinger, E.J.; Toly, J.A. Spatially Decaying Turbulence and Its Relation to Mixing across Density Interfaces. J. Fluid Mech. 1976, 78, 155–175. [Google Scholar] [CrossRef]
- Desilva, I.P.D.; Fernando, H.J.S. Oscillating Grids as a Source of Nearly Isotropic Turbulence. Phys. Fluids 1994, 6, 2455–2464. [Google Scholar] [CrossRef]
- Cuthbertson, A.J.S.; Dong, P.; Davies, P.A. Non-equilibrium flocculation characteristics of fine-grained sediments in grid-generated turbulent flow. Coast. Eng. 2010, 57, 447–460. [Google Scholar] [CrossRef]
- Nakamura, I.; Sakai, Y.; Miyata, M. Diffusion of matter by a non-buoyant plume in grid-generated turbulence. J. Fluid Mech. 1987, 178, 379–403. [Google Scholar] [CrossRef]
- Lemoine, F.; Antoine, Y.; Wolff, M.; Lebouche, M. Mass transfer properties in a grid generated turbulent flow: Some experimental investigations about the concept of turbulent diffusivity. Int. J. Heat Mass Transf. 1998, 41, 2287–2295. [Google Scholar] [CrossRef]
- Cuthbertson, A.J.S.; Malcangio, D.; Davies, P.A.; Mossa, M. The influence of a localised region of turbulence on the structural development of a turbulent, round, buoyant jet. Fluid Dyn. Res. 2006, 38, 683–698. [Google Scholar] [CrossRef]
- Nedic, J.; Tavoularis, S. Measurements of passive scalar diffusion downstream of regular and fractal grids. J. Fluid Mech. 2016, 800, 358–386. [Google Scholar] [CrossRef]
- Taylor, G.I. Diffusion by continuous movements. Proc. Lond. Math. Soc. 1922, 20, 196–212. [Google Scholar] [CrossRef]
- Lader, P.; Jensen, A.; Sveen, J.K.; Fredheim, A.; Enerhaug, B.; Fredriksson, D. Experimental investigation of wave forces on net structures. Appl. Ocean Res. 2007, 29, 112–127. [Google Scholar] [CrossRef]
- Zhan, J.M.; Jia, X.P.; Li, Y.S.; Sun, M.G.; Guo, G.X.; Hu, Y.Z. Analytical and experimental investigation of drag on nets of fish cages. Aquac. Eng. 2006, 35, 91–101. [Google Scholar] [CrossRef]
- Patursson, O.; Swift, M.R.; Tsukrov, I.; Simonsen, K.; Baldwin, K.; Fredriksson, D.W.; Celikkol, B. Development of a porous media model with application to flow through and around a net panel. Ocean Eng. 2010, 37, 314–324. [Google Scholar] [CrossRef]
- Løland, G. Current forces on, and water flow through and around, floating fish farms. Aquac. Int. 1993, 1, 72–89. [Google Scholar] [CrossRef]
- Lemoine, F.; Antoine, Y.; Wolff, M.; Lebouche, M. Some experimental investigations on the concentration variance and its dissipation rate in a grid generated turbulent flow. Int. J. Heat Mass Transf. 2000, 43, 1187–1199. [Google Scholar] [CrossRef]
- Lemoine, F.; Wolff, M.; Lebouché, M. Experimental investigation of mass transfer in a grid-generated turbulent flow using combined optical methods. Int. J. Heat Mass Transf. 1997, 40, 3255–3266. [Google Scholar] [CrossRef]
- Ito, Y.; Watanabe, T.; Nagata, K.; Sakai, Y. Turbulent mixing of a passive scalar in grid turbulence. Phys. Scr. Int. J. Exp. Theor. Phys. 2016, 91, 074002. [Google Scholar] [CrossRef]
- Warhaft, Z. The interference of thermal fields from line sources in grid turbulence. J. Fluid Mech. 1984, 144, 363–387. [Google Scholar] [CrossRef]
- Li, J.D.; Bilger, R.W. The diffusion of conserved and reactive scalars behind line sources in homogeneous turbulence. J. Fluid Mech. 2006, 318, 339–372. [Google Scholar] [CrossRef]










| No. | Current Velocity U0 (m/s) | Twine Diameter d (mm) | Mesh Size M (mm) | Net Solidity S (%) | Reynolds Number w.r.t. Water Depth Rew = U0h/ν | Reynolds Number w.r.t. Net Twine Red = U0d/ν | Reynolds Number w.r.t. Mesh Size Rem = U0M/ν |
|---|---|---|---|---|---|---|---|
| N0 | 0.290 | / | / | / | 87,000 | / | / |
| N1 | 0.142 | 2 | 20 | 19.0 | 42,600 | 284 | 2840 |
| N2 | 0.290 | 2 | 20 | 19.0 | 87,000 | 580 | 5800 |
| N5 | 0.290 | 1 | 20 | 9.8 | 87,000 | 290 | 5800 |
| References | Experimental Conditions | Decay Rate n (n with x0 = 0) | Constant a (a with x0 = 0) |
|---|---|---|---|
| Nakamura et al. (1987) [19] | Water channel Regular biplane grids S = 36% ReM = 1480–2970 | 1.45 | 0.0566 |
| Isaza et al. (2014) [13] | Wind tunnel Regular biplane grids S = 34% ReM = 42,000 | (1.90) | (0.489) |
| Nedic and Tavoularis (2016) [22] | Wind tunnel Steel regular grids S = 25% ReM = 51,000–102,000 | 2.34–2.87 (1.82–1.93) | |
| Present study | Water flume Polyethylene knotless square nets S = 9.8–19.0% ReM = 2840–5800 | 0.67–0.85 (0.43–0.55) | 0.023–0.047 (0.011–0.018) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, D.; Huang, L.; Wang, R.-Q.; Gualtieri, C.; Cuthbertson, A. Flow Turbulence Characteristics and Mass Transport in the Near-Wake Region of an Aquaculture Cage Net Panel. Water 2021, 13, 294. https://doi.org/10.3390/w13030294
Shao D, Huang L, Wang R-Q, Gualtieri C, Cuthbertson A. Flow Turbulence Characteristics and Mass Transport in the Near-Wake Region of an Aquaculture Cage Net Panel. Water. 2021; 13(3):294. https://doi.org/10.3390/w13030294
Chicago/Turabian StyleShao, Dongdong, Li Huang, Ruo-Qian Wang, Carlo Gualtieri, and Alan Cuthbertson. 2021. "Flow Turbulence Characteristics and Mass Transport in the Near-Wake Region of an Aquaculture Cage Net Panel" Water 13, no. 3: 294. https://doi.org/10.3390/w13030294
APA StyleShao, D., Huang, L., Wang, R.-Q., Gualtieri, C., & Cuthbertson, A. (2021). Flow Turbulence Characteristics and Mass Transport in the Near-Wake Region of an Aquaculture Cage Net Panel. Water, 13(3), 294. https://doi.org/10.3390/w13030294








