Modeling the Effectiveness of Cooling Trenches for Stormwater Temperature Mitigation
Abstract
:1. Introduction
2. Model Assumptions
- There is heat flux between the media and water and between the media and the surrounding soil as shown in Figure 2. All heat loss/gain for the fluid is through contact with a solid phase, such as rocks, there are no other sources/sinks such as groundwater inflow or outflow or radiation;
- There is no vertical or lateral variation in water temperature or solid temperature;
- There is no temporal or longitudinal variation of water diffusivity coefficient (E);
- There is no temporal of spatial variation of the solid–solid heat diffusivity coefficient (D).
3. Model Simplifications
4. Model Examples
4.1. Base Case Example
4.2. Steady-State Mixing of Stormwater and Media in a Batch Operation
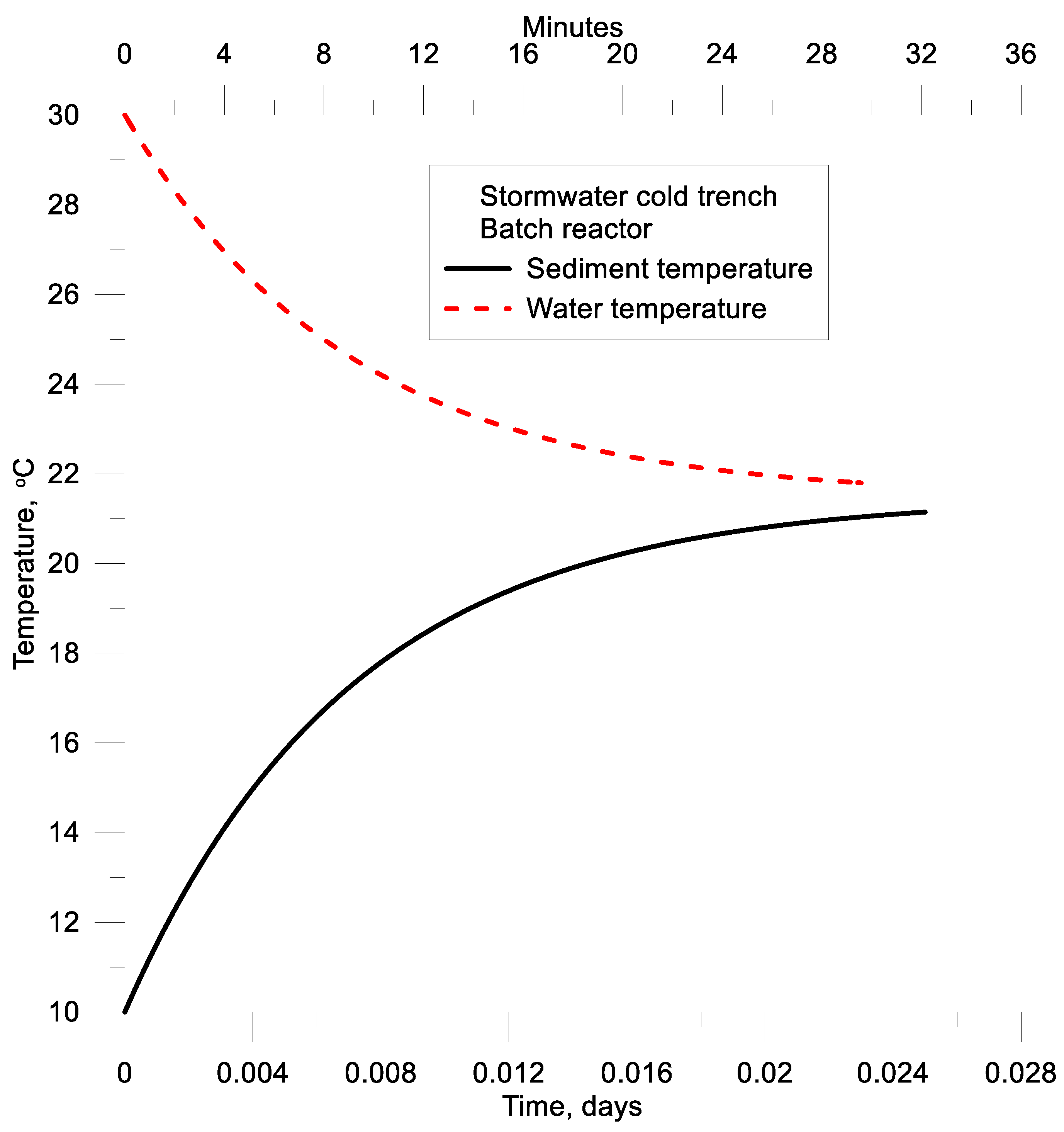
4.3. Dynamic Mixing of Stormwater and Media in a Batch Operation
4.4. Dynamic Well-Mixed Stormwater and Media with Inflow and Outflow
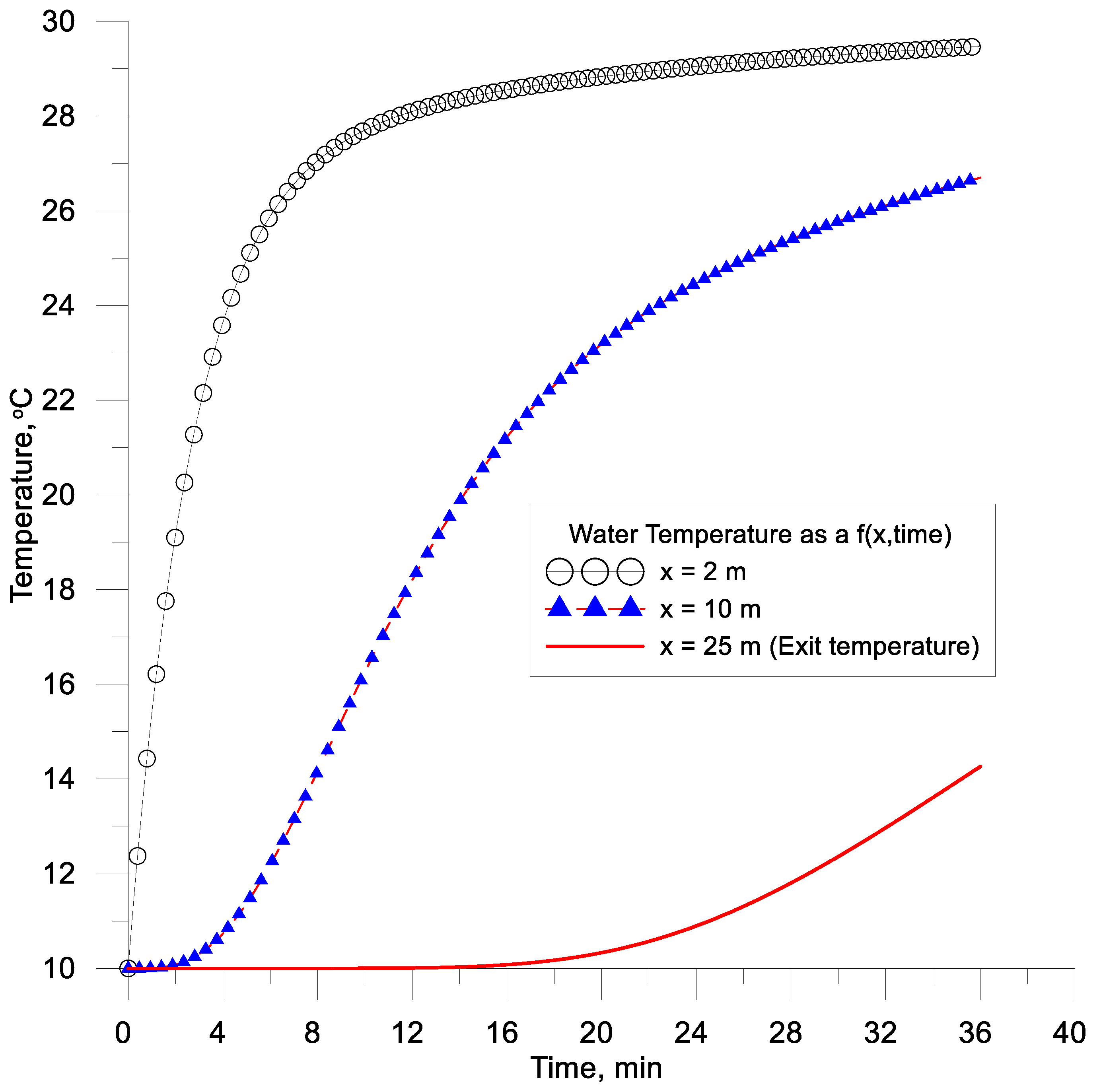
4.5. Dynamic Inflow-Outflow Plug Flow with Spatially Variable Water Temperature
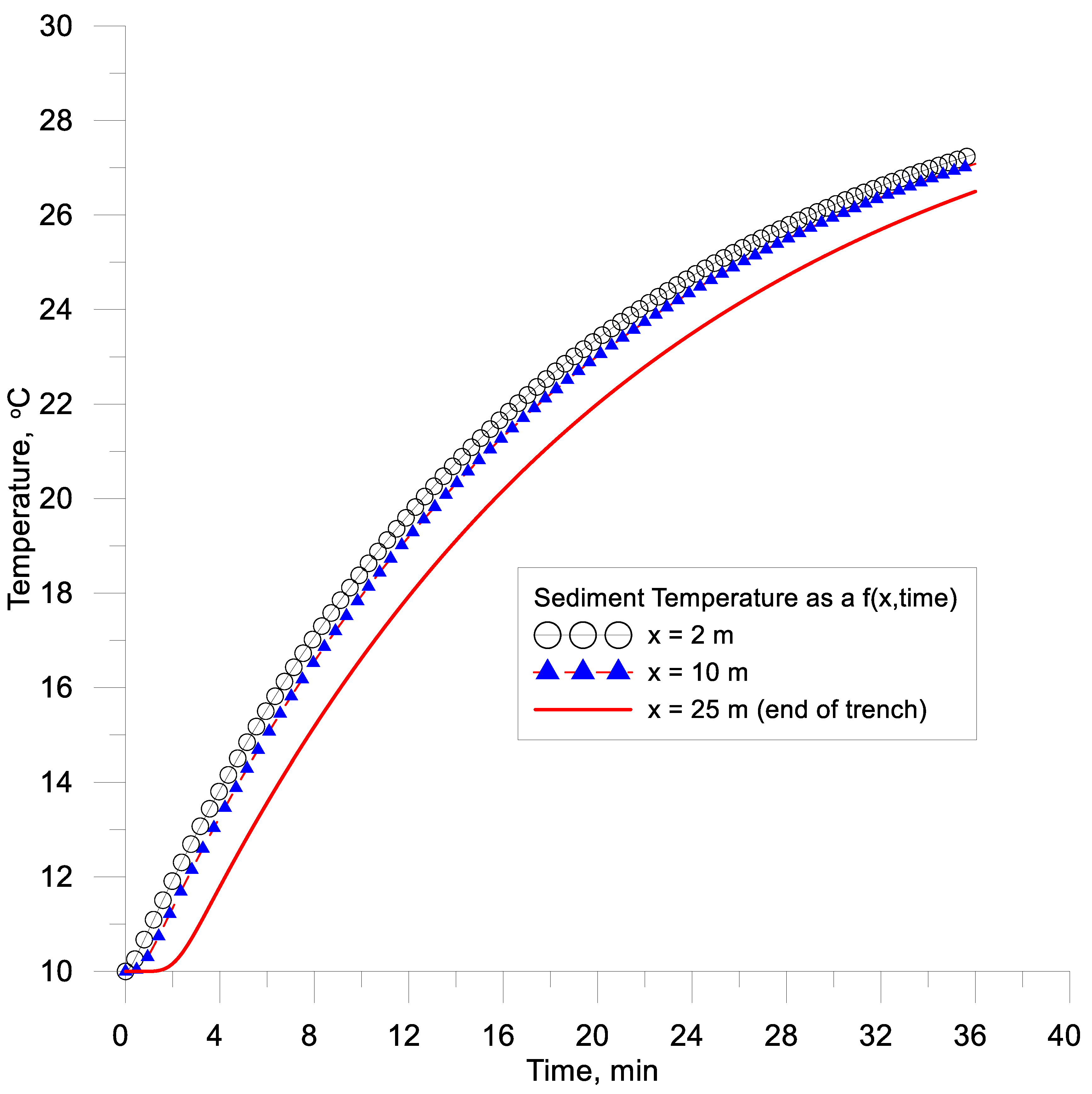
4.6. Dynamic Well-Mixed Stormwater and Media with Inflow and Outflow with Soil Cooling
5. Summary
- Dynamic changes in water and rock media temperatures along the axis of the cooling trench with cooling from surrounding soil;
- Equilibrium temperature of a batch reactor of rock and stormwater as a function of porosity;
- Dynamic temperature change of rock and stormwater in a batch reactor;
- dynamic changes in temperature of stormwater and rock in cooling trench conceptualized as a complete-mix, continuous flow reactor;
- Dynamic changes in temperature of stormwater and rock in cooling trench conceptualized as a plug-flow, continuous flow reactor;
- Dynamic changes in temperature of stormwater and rock in cooling trench conceptualized as a complete-mix, continuous flow reactor with cooling from the surrounding soil.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Haq, R.U.; James, W. Thermal Enrichment of Stream Temperature by Urban Storm Waters. In Proceedings of the Ninth International Conference on Urban Drainage (9ICUD), Portland, OR, USA, 8–13 September 2002; American Society of Civil Engineers: Portland, OR, USA, 2002. [Google Scholar] [CrossRef]
- Jenkins, P. Methods to Reduce or Avoid Thermal Impacts to Surface Water: A Manual For Small Municipal Wastewater Treatment Plants; Ecology Publication 07-10-088; Washington Department of Ecology Water Quality Program: Olympia, WA, USA, 2007; 109p.
- Roseen, R.M.; DiGennaro, N.; Watts, A.; Ballestero, T.P.; Houle, J. Preliminary Results of the Examination of Thermal Impacts from Stormwater BMPs. In Proceedings of the World Environmental and Water Resources Congress 2010, Providence, RI, USA, 16–20 May 2010; American Society of Civil Engineers: Portland, OR, USA, 2012. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency (USEPA). Technical Guidance on Implementing the Stormwater Runoff Requirements for Federal Projects under Section 438 of the Energy Independence and Security Act; No. EPA 841-B-09-001; United States Environmental Protection Agency, Office of Water: Washington, DC, USA, 2009.
- Gulliver, J.S.; Erickson, A.J.; Weiss, P.T. Stormwater Treatment: Assessment and Maintenance. Available online: http://stormwaterbook.safl.umn.edu/ (accessed on 30 January 2021).
- DiGennaro, N. Examination of thermal impacts from stormwater BMPs. Master’s Thesis, University of New Hampshire, Durham, NH, USA, May 2010. [Google Scholar]
- Hathaway, J.M.; Winston, R.J.; Brown, R.A.; Hunt, W.F.; McCarthy, D.T. Temperature Dynamics of stormwater runoff in Australia and the USA. Sci. Total Environ. 2016, 559, 141–150. [Google Scholar] [CrossRef] [PubMed]
- Sabouri, F. Dissipation of Thermal Enrichment of Stormwater Management Ponds. Ph.D. Thesis, The University of Guelph, Guelph, ON, Canada, December 2013. [Google Scholar]
- Thompson, A.M.; Vandermuss, A.J.; Norman, J.M.; Roa-Espinosa, A. Modeling the Effect of a Rock Crib on Reducing Stormwater Runoff Temperature. Trans. ASABE 2008, 51, 947–960. [Google Scholar] [CrossRef]
- Fang, X.; Stefan, H. Temperature variability in lake sediments. Water Resour. Res. 1998, 34, 717–729. [Google Scholar] [CrossRef]
- Silliman, S.E.; Ramirez, J.; McCabe, R.L. Quantifying downflow through creek sediments using temperature time series: One-dimensional solution incorporating measured surface temperature. J. Hydrol. 1995, 167, 99–119. [Google Scholar] [CrossRef]
- Carslaw, H.C.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- Jobson, H.E. Bed Conduction Computation for Thermal Models. J. Hydraul. 1977, 103, 1213–1217. [Google Scholar]
- Chen, Y.; Carsel, R.; McCuthcheon, S.; Nutter, W. Stream Temperature Simulation of Forested Riparian Areas: I. Watershed-Scale Model Development. J. Environ. Eng. 1998, 124, 304–315. [Google Scholar] [CrossRef]
- Kim, K.; Chapra, S. Temperature Model for Highly Transient Shallow Streams. J. Hydraul. Eng. 1997, 123, 30–39. [Google Scholar] [CrossRef]
- Pluhowski, E.J. Urbanization and Its Effect on Temperature of the Streams on Long Island, New York; Geological Survey Professional Paper 627-D; The United States Geological Survey (USGS): Reston, VA, USA, 1970; p. 110.











| Reference | Thermal Diffusivity of Sediment, D: | Bed Thermal Conductivity, k | for Sediment | for Sediment | Description |
|---|---|---|---|---|---|
| Fang and Stefan [10] | 0.035 m2/d | 2.3 × 106 J/m3/°C | Lake sediment study, determined by calibration | ||
| Fang and Stefan [10] | 0.01–0.11 m2/d | 1.4 × 106–3.8 × 106 J/m3/°C | Literature reported range and is a function of sediment composition | ||
| Silliman et al. [11] | 0.0046 cm2/s | 0.0023 cal/cm/s/°C | 0.5 cal/cm3/°C | Taken from Carslaw and Jaeger [12] | |
| Jobson [13] | 0.01 cm2/s (range of 0.006 to 0.2 cm2/s not found to be sensitive to model results) | 0.55 cal/cm3/°C | Concrete lined channel, study length 16 miles | ||
| Jobson [13] | 0.0077 cm2/s | 0.68 cal/cm3/°C | Sand bed study length 17 miles | ||
| Chen et al. [14] | 1.18 × 10-6 m2/s or 0.0118 cm2/s | 1.491 × 106 J/m3/°C | Homogeneous rock, study length 9.3 miles | ||
| Kim and Chapra [15] | 3 × 10-7 m2/s | 795.2 J/kg/°C | Sand–dry, density of dry sand was 1750 kg/m3, study length 8.5 miles, penetration depth of heat was about 0.25 m for the diurnal case | ||
| Kim and Chapra [15] | 9 × 10-7 m2/s | 799.8 J/kg/°C | Stone–dry, density of dry sand was 2500 kg/m3 | ||
| Pluhowski [16] | 0.00394 cal/cm/s/°C | Water saturated sands and gravel mixtures, study length 0.94 miles |
| Governing Water Temperature Equation | Governing Sediment Temperature Equation | Assumptions | Equation |
|---|---|---|---|
| (3) | ||
| (4) | ||
| (5) | ||
| (6) | ||
Steady-state solution: | Ts = constant |
There are both steady-state and time dependent solutions for water temperature. | (7) |
| (8) | ||
| (9) |
| Parameter | Value | Units |
|---|---|---|
| L, length of infiltration gallery | 25 | m |
| H, height or depth of infiltration gallery | 4 | m |
| W, width of infiltration gallery | 2 | m |
| ε, porosity | 0.35 | (-) |
| Vtotal, total volume of infiltration gallery | 200 | m3 |
| Rock or solid media volume | 130 | m3 |
| ρcp density times specific heat of fluid | 1 | cal/cm3/°C |
| ρscps density times specific heat for solid media | 0.4 | cal/cm3/°C |
| k, Thermal conductivity of rock | 0.004 | cal/s/cm/°C |
| D, Thermal diffusivity, k/(ρscps), of rock | 0.01 | cm2/s |
| drock, Average diameter of stones | 0.08 | m |
| δ, B/L thickness (assume 50% of stone diameter) | 0.04 | m |
| δs-o, B/L thickness for stone to outside soil heat diffusion (assume 50% of stone diameter) | 0.04 | m |
| Asurface, Surface area - contact area | 9750 | m2 |
| Acontact, Surface area - contact area for rock and surrounding soil | 105 | m2 |
| f, Factor to decrease contact area between rocks and water | 0.5 | (-) |
| fAsurface, Actual surface area used in model | 4875 | m2 |
| Inflow temperature of water coming into trench | 30 | °C |
| Initial temperature of stones | 10 | °C |
| Temperature of surrounding soil Toutside | 10 | °C |
| Initial temperature of water in trench | 10 | °C |
| E, dispersion coefficient for water | 0.1 | m2/s |
| Q, m3/s | Detention time, days | Detention time, min |
|---|---|---|
| 0.03 | 2.1 × 10−2 | 30 |
| 0.52 | 1.3 × 10−3 | 1.8 |
| 2.72 | 2.4 × 10−4 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wells, S.A. Modeling the Effectiveness of Cooling Trenches for Stormwater Temperature Mitigation. Water 2021, 13, 373. https://doi.org/10.3390/w13030373
Wells SA. Modeling the Effectiveness of Cooling Trenches for Stormwater Temperature Mitigation. Water. 2021; 13(3):373. https://doi.org/10.3390/w13030373
Chicago/Turabian StyleWells, Scott A. 2021. "Modeling the Effectiveness of Cooling Trenches for Stormwater Temperature Mitigation" Water 13, no. 3: 373. https://doi.org/10.3390/w13030373
APA StyleWells, S. A. (2021). Modeling the Effectiveness of Cooling Trenches for Stormwater Temperature Mitigation. Water, 13(3), 373. https://doi.org/10.3390/w13030373






