Impact of Land Use Change on Non-Point Source Pollution in a Semi-Arid Catchment under Rapid Urbanisation in Bolivia
Abstract
:1. Introduction
2. Materials and Methods
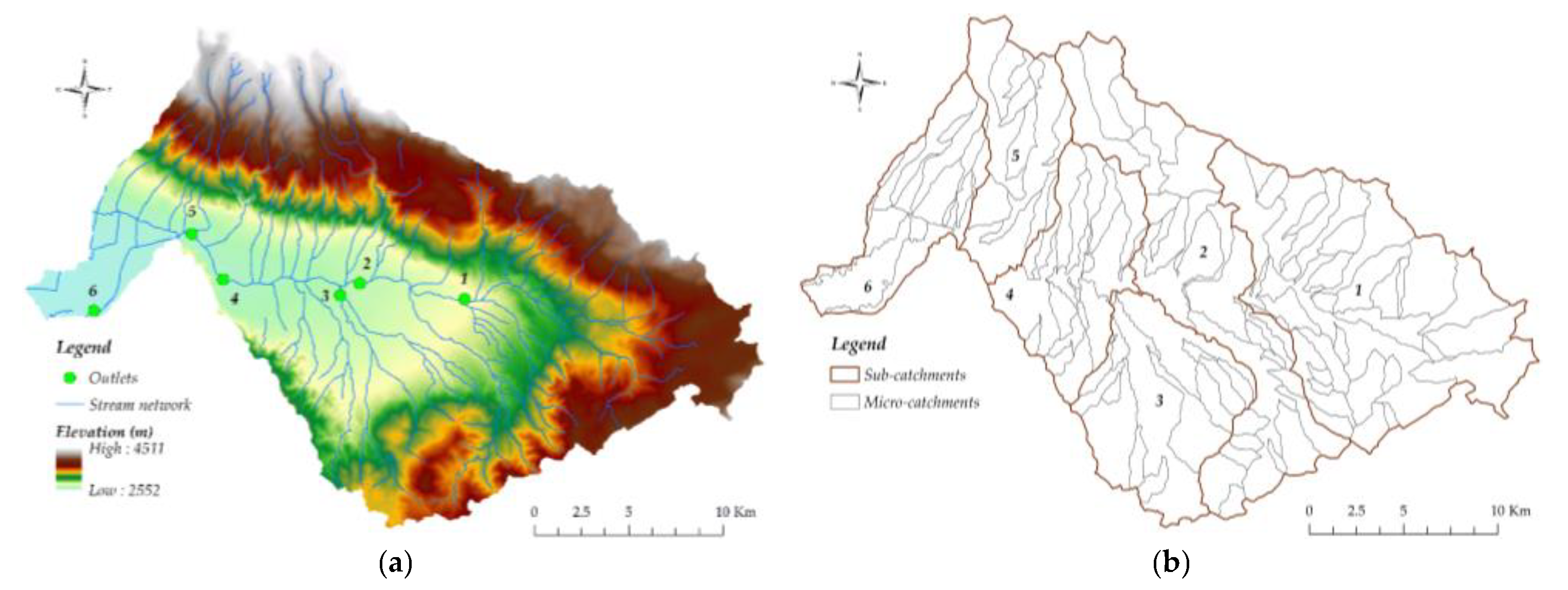
2.1. Study Area
2.2. River Network and Catchment Delineation
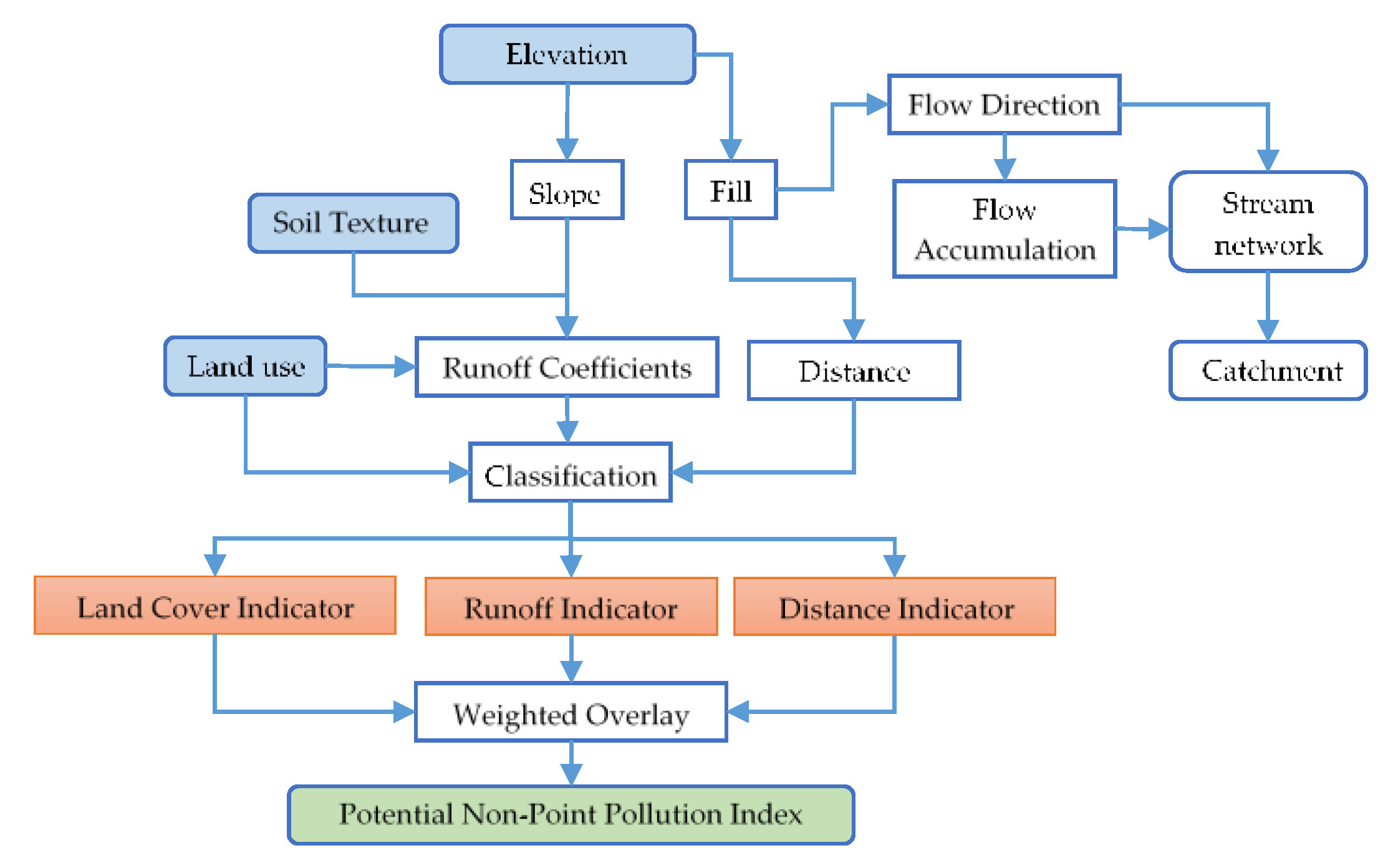
2.3. Potential Non-Point Pollution Index
2.3.1. Land Cover Indicator
2.3.2. Runoff Indicator
2.3.3. Distance Indicator
2.4. PNPI Implementation
2.5. PNPI Performance Evaluation
3. Results
3.1. Land Cover Indicator (LCI)
3.2. Runoff Indicator (RoI)
3.3. Distance Indicator (DI)
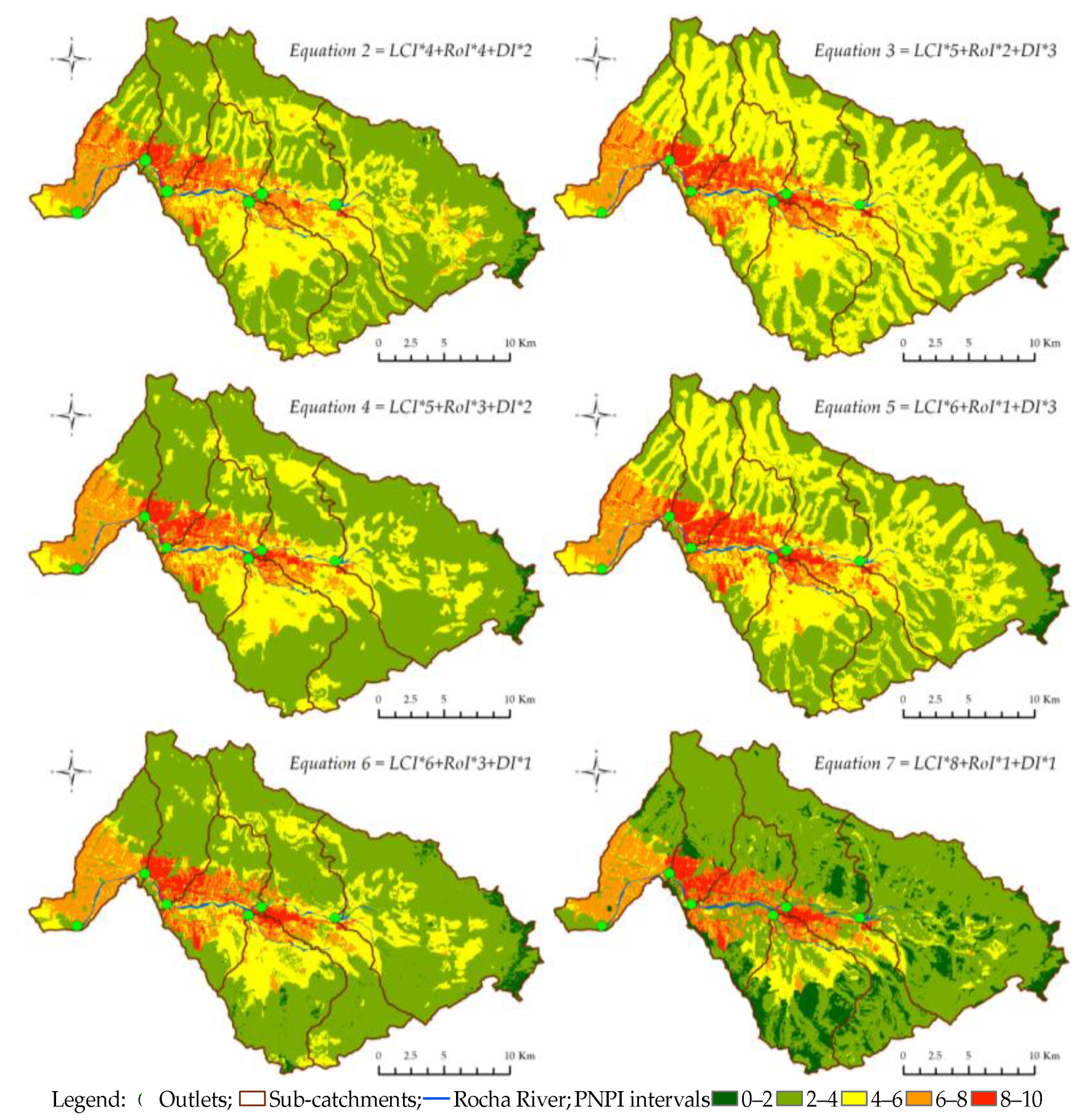
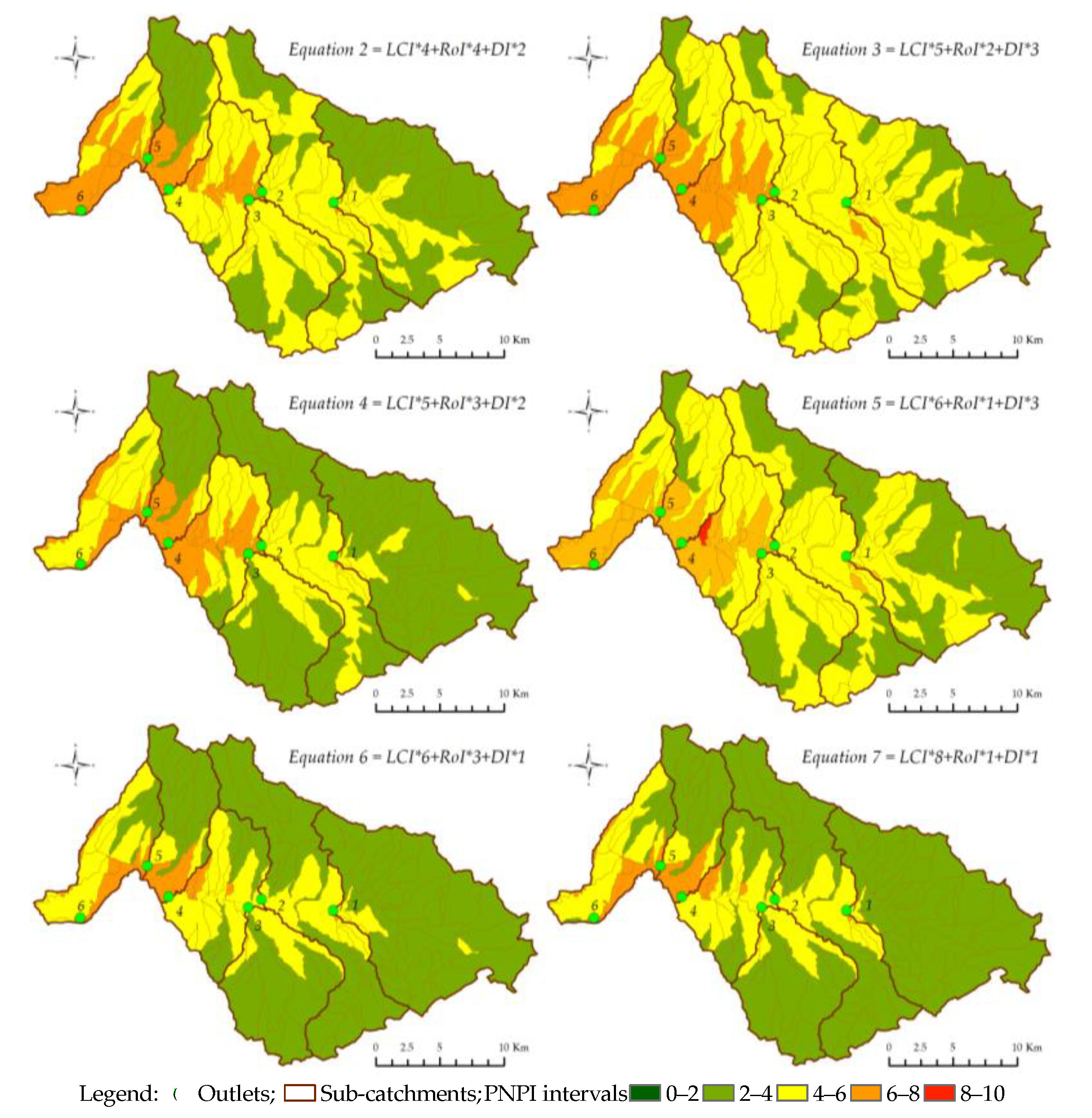
3.4. Potential Non-Point Pollution
4. Discussion
4.1. Relative Importance of Indicators
4.2. Potential Non-Point Pollution Index (PNPI)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, X.; Zhou, W.; Pickett, S.T.; Li, W.; Han, L. Spatial-Temporal Variations of Water Quality and Its Relationship to Land Use and Land Cover in Beijing, China. Int. J. Environ. Res. Public Health 2016, 13, 449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schaffner, M.; Bader, H.-P.; Scheidegger, R. Modeling the contribution of point sources and non-point sources to Thachin River water pollution. Sci. Total. Environ. 2009, 407, 4902–4915. [Google Scholar] [CrossRef]
- Novotny, V. Water Quality: Diffuse Pollution and Watershed Management; The Royal Geographical Society (with the Institute of British Geographers): London, UK, 2002. [Google Scholar]
- Mi, Y.; He, C.; Bian, H.; Cai, Y.; Sheng, L.; Ma, L. Ecological engineering restoration of a non-point source polluted river in Northern China. Ecol. Eng. 2015, 76, 142–150. [Google Scholar] [CrossRef]
- Zhu, Q.D.H.; Sun, J.H.; Hua, G.F.; Wang, J.H.; Wang, H. Runoff characteristics and non-point source pollution analysis in the Taihu Lake Basin: A case study of the town of Xueyan, China. Environ. Sci. Pollut. Res. 2015, 22, 15029–15036. [Google Scholar] [CrossRef] [PubMed]
- Corwin, D.L.; Loague, K.; Ellsworth, T.R. Introduction: Assessing non-point source pollution in the vadose zone with advanced information technologies. Hydrogeol. Chem. Weather. Soil Form. 1999, 108, 1–20. [Google Scholar] [CrossRef]
- Loague, K.; Corwin, D.L.; Ellsworth, A.T.R. Feature: The Challenge of Predicting Nonpoint Source Pollution. Environ. Sci. Technol. 1998, 32, 130A–133A. [Google Scholar] [CrossRef]
- Giri, S.; Qiu, Z. Understanding the relationship of land uses and water quality in Twenty First Century: A review. J. Environ. Manag. 2016, 173, 41–48. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Shao, J.; Wang, D.; Ni, J.; Xie, D. Identification of the “source” and “sink” patterns influencing non-point source pollution in the Three Gorges Reservoir Area. J. Geogr. Sci. 2016, 26, 1431–1448. [Google Scholar] [CrossRef]
- Zhang, J. Discussion on Non-point Source Pollution and Control in Water Source Areas. In Study of Ecological Engineering of Human Settlements; Springer Nature: Berlin/Heidelberg, Germany, 2019; pp. 197–221. [Google Scholar]
- Zhang, H.; Huang, G. Assessment of non-point source pollution using a spatial multicriteria analysis approach. Ecol. Model. 2011, 222, 313–321. [Google Scholar] [CrossRef]
- Maillard, P.; Pineheiro Santos, N.A. A spatial statistical approach for modeling the effect of non-point source pollution on different water quality parameters in the Velhas River watershed–Brazil. J. Environ. Manag. 2008, 86, 158. [Google Scholar] [CrossRef] [PubMed]
- Li, K.-C.; Yeh, M. Nonpoint source pollution potential index: A case study of the Feitsui Reservoir watershed, Taiwan. J. Chin. Inst. Eng. 2004, 27, 253–259. [Google Scholar] [CrossRef]
- De Oliveira, L.M.; Maillard, P.; Pinto, E.J.D.A. Application of a land cover pollution index to model non-point pollution sources in a Brazilian watershed. Catena 2017, 150, 124–132. [Google Scholar] [CrossRef]
- Shen, Z.; Hong, Q.; Chu, Z.; Gong, Y. A framework for priority non-point source area identification and load estimation integrated with APPI and PLOAD model in Fujiang Watershed, China. Agric. Water Manag. 2011, 98, 977–989. [Google Scholar] [CrossRef]
- Kliment, Z.; Kadlec, J.; Langhammer, J. Evaluation of suspended load changes using AnnAGNPS and SWAT semi-empirical erosion models. Catena 2008, 73, 286–299. [Google Scholar] [CrossRef]
- Heathwaite, L.; Sharpley, A.N.; Gburek, W. A Conceptual Approach for Integrating Phosphorus and Nitrogen Management at Watershed Scales. J. Environ. Qual. 2000, 29, 158–166. [Google Scholar] [CrossRef]
- Munafò, M.; Cecchi, G.; Baiocco, F.; Mancini, L. River pollution from non-point sources: A new simplified method of assessment. J. Environ. Manag. 2005, 77, 93–98. [Google Scholar] [CrossRef]
- Cecchi, G.; Munafò, M.; Baiocco, F.; Andreani, P.; Mancini, L. Estimating river pollution from diffuse sources in the Viterbo province using the potential non-point pollution index. Annali dell’Istituto Superiore di Sanità 2007, 43, 295–301. [Google Scholar] [PubMed]
- Ciambella, M.; Venanzi, D.; Dello, E.; Andreani, P.; Cecchi, G.; Formichetti, P.; Munafò, M.; Mancini, L. Convenzione Istituto Superiore Di Sanità-Provincia Di Viterbo: Messa a punto di uno strumento conoscitivo per la gestione delle acque superficiali della Provincia di Viterbo; Convenzione Istituto Superiore Di Sanità-Provincia Di Viterbo: Viterbo, Italy, 2005; pp. 227–238. [Google Scholar]
- CGE (Contraloria General del Estado). Informe de Auditoría Sobre el Desempeño Ambiental Respecto de los Impactos Negativos Generados en el Río Rocha (Audit Report about Environmental Performance Regarding Negative Impacts Generated on the Rocha River); K2/AP06/M11; Gestión de Evaluación Ambiental: Cochabamba, Bolivia, 2011; p. 320. [Google Scholar]
- PDC (Prefectura del Departamento de Cochabamba). Estudios Básicos de la Cuenca del Río Rocha (Rocha River Watershed Basic Studies); Dirección departamental de Recursos Naturales–DDRN: Cochabamba, Bolivia, 2005; p. 314. [Google Scholar]
- Romero, A.; Van Damme, P.; Goitia, E. Contaminación orgánica en el río Rocha (Cochabamba, Bolivia) (Organic contamination of the Rocha river (Cochabamba, Bolivia)). Rev. Boliv. Ecol. Conserv. Ambient. 1998, 8, 37–47. [Google Scholar]
- Gossweiler, B.; Wesström, I.; Messing, I.; Romero, A.M.; Joel, A. Spatial and Temporal Variations in Water Quality and Land Use in a Semi-Arid Catchment in Bolivia. Water 2019, 11, 2227. [Google Scholar] [CrossRef] [Green Version]
- Metternicht, G.; Gonzalez, S. FUERO: Foundations of a fuzzy exploratory model for soil erosion hazard prediction. Environ. Model. Softw. 2005, 20, 715–728. [Google Scholar] [CrossRef]
- Metternicht, G.; Fermont, A. Estimating Erosion Surface Features by Linear Mixture Modeling. Remote Sens. Environ. 1998, 64, 254–265. [Google Scholar] [CrossRef]
- Holdridge, L.R. Determination of World Plant Formations From Simple Climatic Data. Science 1947, 105, 367–368. [Google Scholar] [CrossRef]
- Ongaro, L. Land Evaluation of the Valley of Sacaba (Bolivia). In Remote Sensing and Natural Resources Evaluation; Istituto agronomico per l’oltremare, Ed.; Ministero degli affari esteri: Firenze, Italy, 1998; p. 177. [Google Scholar]
- MMAA (Ministerio de Medio Ambiente y Agua de Bolivia). Sistematización Sobre Tratamiento y Reúso de Aguas Residuales (Wastewater Treatment and Reuse Systematization on); Programa de Desarrollo Agropecuario Sustentable—Proagro: La Paz, Bolivia, 2013. [Google Scholar]
- INE (Instituto Nacional de Estadística). Censo Nacional de Población y Vivienda 2012. In Crecimiento Intercensal por Municipios (National Population and Housing Census 2012, Intercensal Growth by Municipalities); Estado Plutrinacional de Bolivia: La Paz, Bolivia, 2013; p. 56. [Google Scholar]
- UN-GEOBOL (United Nations-Servicio Geologico de Bolivia). Investigaciones de Aguas Subterráneas en las Cuencas de Cochabamba (Study of the Groundwaters of Basins of the Cochabamba Department). In Informe Técnico (Technical Report) 1; Proyecto Integrado de Recursos Hidricos (PIRHC): Cochabamba, Bolivia, 1978. [Google Scholar]
- Stimson, J.; Frape, S.; Drimmie, R.; Rudolph, D. Isotopic and geochemical evidence of regional-scale anisotropy and interconnectivity of an alluvial fan system, Cochabamba Valley, Bolivia. Appl. Geochem. 2001, 16, 1097–1114. [Google Scholar] [CrossRef]
- Renner, S.; Velasco, C. Geology and Hydrogeology of the Central Valley of Cochabamba; Geology and Minning National Service: La Paz, Bolivia, 2000; Volume 34, p. 125. [Google Scholar]
- Trohanis, Z.; Zaengerling, B.; Sanchez-Reaza, J. Urbanization trends in Bolivia. In Opportunities and Challenges; The World Bank: Washington, DC, USA, 2015. [Google Scholar]
- MMAA (Ministerio de Medio Ambiente y Agua de Bolivia). Inventario de Principales Fuentes de Contaminación en la Cuenca del Rio Rocha (Municipios de Sacaba, Cochabamba, Colcapirhua, Quillacollo, Vinto y Sipe Sipe) (Inventory of Main Pollution Sources in the Rocha River Watershed (Municipalities of Sacaba, Cochabamba, Colcapirhua, Quillacollo, Vinto and Sipe Sipe)); Viceministerio de Recursos Hídricos y Riego–VRHR: La Paz, Bolivia, 2017. [Google Scholar]
- Maathuis, B.H.P.; Wang, L. Digital Elevation Model Based Hydro-processing. Geocarto Int. 2006, 21, 21–26. [Google Scholar] [CrossRef]
- Wesström, I.; Joel, A. In Storage and reuse of drainage water. In Proceedings of the 9th International Drainage Symposium held jointly with CIGR and CSBE/SCGAB, Quebec City, QC, Canada, 13–16 June 2010; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2010; p. 10. [Google Scholar] [CrossRef]
- GAMS (Gobierno Autónomo Municipal de Sacaba). Plan Territorial de Desarrollo Integral—PTDT (Integral Development Territorial Plan—IDTP); Secretaria Municipal de Planificación y Desarrollo Territorial: Sacaba, Cochabamba, Bolivia, 2016; p. 294. [Google Scholar]
- Aguilera, X.; Declerck, S.A.J.; De Meester, L.; Maldonado, M.; Ollevier, F. Tropical high Andes lakes: A limnological survey and an assessment of exotic rainbow trout (Oncorhynchus mykiss). Limnologica 2006, 36, 258–268. [Google Scholar] [CrossRef] [Green Version]
- Jacobs, S.R.; Weeser, B.; Guzha, A.C.; Rufino, M.C.; Butterbach-Bahl, K.; Windhorst, D.; Breuer, L. Using High-Resolution Data to Assess Land Use Impact on Nitrate Dynamics in East African Tropical Montane Catchments. Water Resour. Res. 2018, 54, 1812–1830. [Google Scholar] [CrossRef] [Green Version]
- Smith, V.; Swaney, P.; Talaue-Mcmanus, L.; Bartley, D.; Sandhei, T.; McLaughlin, J.; Dupra, C.; Crossland, J.; Buddemeier, W.; Maxwell, A.; et al. Humans, Hydrology, and the Distribution of Inorganic Nutrient Loading to the Ocean. Bioscience 2003, 53, 235–245. [Google Scholar] [CrossRef]
- Santos, I.R.; Costa, R.C.; Freitas, U.; Fillmann, G. Influence of effluents from a Wastewater Treatment Plant on nutrient distribution in a coastal creek from southern Brazil. Braz. Arch. Biol. Technol. 2008, 51, 153–162. [Google Scholar] [CrossRef] [Green Version]
- Van Drecht, G.; Bouwman, A.F.; Harrison, J.; Knoop, J.M. Global nitrogen and phosphate in urban wastewater for the period 1970 to 2050. Glob. Biogeochem. Cycles 2009, 23, 4. [Google Scholar] [CrossRef] [Green Version]
- Puccinelli, C.; Marcheggiani, S.; Munafò, M.; Andreani, P.; Mancini, L. Evaluation of Aquatic Ecosystem Health Using the Potential Non Point Pollution Index (PNPI) Tool. In Diversity of Ecosystems; Ali, M., Ed.; InTech: London, UK, 2012; p. 16. ISBN 978-953-51-0572-5. [Google Scholar]
- Goel, M. Runoff Coefficient. In Encyclopedia of Snow, Ice and Glaciers; Singh, V.P., Singh, P., Haritashya, U.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 952–953. [Google Scholar]
- The Clean Water Team Runoff Coefficient, FS-5.1.3. (RC), SWAMP—Clean Water Team Citizen Monitoring Program, Guidance Compendium for Watershed Monitoring and Assessment. Available online: https://www.waterboards.ca.gov/water_issues/programs/swamp/docs/cwt/guidance/513.pdf (accessed on 21 November 2019).
- Schwab, G.; Frevert, R.; Edminster, T.; Barnes, K. Soil and Water Conservation Engineering; John Wiley and Sons: New York, NY, USA, 1981. [Google Scholar]
- Hudson, N. Field Measurement of Soil Erosion and Runoff; Food & Agriculture Orgriculture—FAO: Rome, Italy, 1993; Volume 68. [Google Scholar]
- Zinck, J.; Metternicht, G.; Bocco, G.; Del Valle, H. Geopedology Elements of Geomorphology for Soil and Geohazard Studies; ITC Special Lecture Notes Series: Enschede, The Netherlands, 2013. [Google Scholar]
- Metternicht, G. Detecting and Monitoring Land Degradation Features and Processes in the Cochabamba Valleys, Bolivia: A Synergistic Approach. Ph.D. Thesis, University of Ghent, Enschede, The Netherlands, 1996. [Google Scholar]
- Jenks, G. The data model concept in statistical mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Arora, J. Multi-objective Optimum Design Concepts and Methods. In Introduction to Optimum Design, 3rd ed.; Arora, J.S., Ed.; Academic Press: Boston, MA, USA, 2012; pp. 657–679. [Google Scholar]
- Stillwell, W.G.; Seaver, D.A.; Edwards, W. A comparison of weight approximation techniques in multiattribute utility decision making. Organ. Behav. Hum. Perform. 1981, 28, 62–77. [Google Scholar] [CrossRef]
- Bossard, M.; Feranec, J.; Otahel, J. CORINE Land Cover Technical Guide: Addendum; EEA (European Environment Agency): Copenhagen, Denmark, 2000; p. 105. [Google Scholar]
- Wu, B.; Zhang, X.; Xu, J.; Liu, J.; Wei, F. Assessment and management of nonpoint source pollution based on multicriteria analysis. Environ. Sci. Pollut. Res. 2019, 26, 27073–27086. [Google Scholar] [CrossRef] [PubMed]
- Chesters, G.; Schierow, J. A primer on nonpoint pollution. J. Soil Water Conserv. 1985, 40, 9. [Google Scholar]
- Ouyang, W.; Skidmore, A.K.; Toxopeus, A.; Hao, F. Long-term vegetation landscape pattern with non-point source nutrient pollution in upper stream of Yellow River basin. J. Hydrol. 2010, 389, 373–380. [Google Scholar] [CrossRef]
- Yang, H.; Wang, G.; Yang, Y.; Xue, B.; Wu, B. Assessment of the Impacts of Land Use Changes on Nonpoint Source Pollution Inputs Upstream of the Three Gorges Reservoir. Sci. World J. 2014, 2014, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Luzio, M.; Arnold, J.G.; Srinivasan, R. Effect of GIS data quality on small watershed stream flow and sediment simulations. Hydrol. Process. 2005, 19, 629–650. [Google Scholar] [CrossRef]
- Bormann, H. Sensitivity of a soil-vegetation-atmosphere-transfer scheme to input data resolution and data classification. J. Hydrol. 2008, 351, 154–169. [Google Scholar] [CrossRef]
- Ochoa-Tocachi, B.; Buytaert, W.; De Bièvre, B.; Célleri, R.; Crespo, P.; Villacís, M.; Llerena, C.; Acosta, L.; Villazón, M.; Guallpa, M.; et al. Impacts of land use on the hydrological response of tropical Andean catchments. Hydrol. Process. 2016, 30, 4074–4089. [Google Scholar] [CrossRef] [Green Version]
- Viglione, A.; Blöschl, G. On the role of storm duration in the mapping of rainfall to flood return periods. Hydrol. Earth Syst. Sci. 2009, 13, 205–216. [Google Scholar] [CrossRef] [Green Version]
- Gebresellassie, D. Spatial mapping and testing the applicability of the curve number method for ungauged catchments in Northern Ethiopia. Int. Soil Water Conserv. Res. 2017, 5, 293–301. [Google Scholar] [CrossRef]
- Rawat, K.S.; Singh, S.K. Estimation of Surface Runoff from Semi-arid Ungauged Agricultural Watershed Using SCS-CN Method and Earth Observation Data Sets. Water Conserv. Sci. Eng. 2017, 1, 233–247. [Google Scholar] [CrossRef]
- D’Alberto, L.; Lucianetti, G. Misinterpretation of the Kenessey method for the determination of the runoff coefficient: A review. Hydrol. Sci. J. 2019, 64, 288–296. [Google Scholar] [CrossRef]
- Wu, J.; Lu, J. Landscape patterns regulate non-point source nutrient pollution in an agricultural watershed. Sci. Total. Environ. 2019, 669, 377–388. [Google Scholar] [CrossRef] [PubMed]
- Wałęga, A.; Wachulec, K. Effect of a Retention Basin on Removing Pollutants from Stormwater: A Case Study in Poland. Pol. J. Environ. Stud. 2018, 27, 1795–1803. [Google Scholar] [CrossRef]
- Yoon, K.; Hwang, C. TOPSIS (Technique for Order Preference by Similarity to Ideal Solution)–A Multiple Attribute Decision Making: Multiple Attribute Decision Making–Methods and Applications; A state-of-the-at Survey; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]











| Land Use Type | LCI Values |
|---|---|
| Lakes | 0.05 |
| Forest, Shrubland | 0.10 |
| Grassland, Transitional woodland/shrubland | 0.20 |
| Cropland | 0.30 |
| Sparsely vegetated areas | 0.35 |
| Human settlements (persons per ha) | |
| <20 | 0.40 |
| 21–70 | 0.50 |
| 71–100 | 0.60 |
| 101–120 | 0.70 |
| 121–150 | 0.80 |
| >150 | 0.90 |
| Land Use Type | FAO | Slope | |||
|---|---|---|---|---|---|
| Soil Texture | 0–5% | 5–10% | 10–30% | >30% | |
| Forest, Shrubland a | >45% sand | 0.10 | 0.25 | 0.30 | 0.45 |
| clay and silt | 0.30 | 0.35 | 0.50 | 0.55 | |
| >55% clay | 0.40 | 0.50 | 0.60 | 0.70 | |
| Grassland a | >45% sand | 0.10 | 0.16 | 0.22 | 0.28 |
| clay and silt | 0.30 | 0.36 | 0.42 | 0.48 | |
| >55% clay | 0.40 | 0.55 | 0.60 | 0.75 | |
| Cropland a | >45% sand | 0.30 | 0.40 | 0.52 | 0.62 |
| clay and silt | 0.50 | 0.60 | 0.72 | 0.82 | |
| >55% clay | 0.60 | 0.70 | 0.82 | 0.92 | |
| Transitional woodland/shrubland b | >45% sand | 0.10 | 0.15 | 0.20 | 0.25 |
| clay and silt | 0.20 | 0.25 | 0.30 | 0.35 | |
| >55% clay | 0.30 | 0.35 | 0.40 | 0.45 | |
| Sparsely vegetated areas—Smooth b | >45% sand | 0.30 | 0.40 | 0.50 | 0.60 |
| clay and silt | 0.45 | 0.55 | 0.65 | 0.75 | |
| >55% clay | 0.60 | 0.75 | 0.80 | 0.90 | |
| Sparsely vegetated areas—Rough b | >45% sand | 0.20 | 0.30 | 0.40 | 0.50 |
| clay and silt | 0.35 | 0.45 | 0.55 | 0.65 | |
| >55% clay | 0.50 | 0.65 | 0.70 | 0.80 | |
| % of impervious area | |||||
| Human settlements b | <30% | 0.30 | 0.40 | 0.50 | 0.60 |
| 30–50% | 0.40 | 0.50 | 0.60 | 0.70 | |
| 50–70% | 0.55 | 0.65 | 0.75 | 0.85 | |
| >70% | 0.65 | 0.80 | 0.85 | 0.95 | |
| Distance Class (m) | 0–159 | 160–332 | 333–520 | 521–736 | 737–996 | 997–1314 | 1315–1703 | 1704–2165 | 2166–2714 | 2715–3681 |
|---|---|---|---|---|---|---|---|---|---|---|
| DI value | 1 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| PNPI Classes | PNPI Value | Representation | Pollution Potential |
|---|---|---|---|
| 0–2 | 0–2.0 | Dark green | Low |
| 2–4 | 2.1–4.0 | Light green | Low-medium |
| 4–6 | 4.1–6.0 | Yellow | Medium |
| 6–8 | 6.1–8.0 | Orange | Medium-high |
| 8–10 | 8.1–10.0 | Red | High |
| DI Class | Catchment | Sub-Catchment | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 0.8–1 | 44.5 | 37.7 | 43.6 | 46.1 | 52.9 | 48.2 | 50.2 |
| 0.6–0.8 | 35.3 | 31.7 | 38.0 | 33.8 | 37.8 | 38.1 | 36.2 |
| 0.4–0.6 | 14.6 | 16.5 | 16.1 | 17.5 | 7.4 | 11.9 | 12.6 |
| 0.4–0.2 | 4.1 | 9.0 | 2.3 | 2.6 | 1.9 | 1.8 | 0.9 |
| 0–0.2 | 1.5 | 5.1 | 0 | 0 | 0 | 0 | 0 |
| PNPI Class | Equation (2) | Equation (3) | Equation (4) | Equation (5) | Equation (6) | Equation (7) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1997 | 2017 | 1997 | 2017 | 1997 | 2017 | 1997 | 2017 | 1997 | 2017 | 1997 | 2017 | |
| 0–2 | 1% | 1% | 1% | 1% | 1% | 1% | 1% | 1% | 1% | 1% | 12% | 13% |
| 2–4 | 59% | 54% | 36% | 34% | 66% | 61% | 46% | 44% | 72% | 44% | 72% | 66% |
| 4–6 | 33% | 32% | 56% | 51% | 27% | 25% | 46% | 41% | 22% | 41% | 11% | 8% |
| 6–8 | 5% | 9% | 5% | 9% | 4% | 9% | 5% | 8% | 3% | 8% | 3% | 8% |
| 8–10 | 2% | 4% | 2% | 5% | 2% | 4% | 2% | 6% | 2% | 6% | 2% | 5% |
| Sub-Catchment PNPI Value Statistics | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equation | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1997 | 2017 | |||||||||||||
| 2 | LCI*4+RoI*4+DI*2 | Min | 1.4 | 2.0 | 1.4 | 1.4 | 1.8 | 2.0 | 1.4 | 2.0 | 1.4 | 1.4 | 1.8 | 2.0 |
| Mean | 3.7 | 4.1 | 4.2 | 4.5 | 4.1 | 5.1 | 3.7 | 4.3 | 4.3 | 5.4 | 4.4 | 5.6 | ||
| Max | 6.5 | 9.2 | 9.2 | 9.2 | 9.6 | 9.6 | 9.2 | 9.2 | 9.2 | 9.6 | 9.6 | 9.6 | ||
| 3 | LCI*5+RoI*2+DI*3 | Min | 1.5 | 2.2 | 1.6 | 1.6 | 2.2 | 2.5 | 1.3 | 2.2 | 1.6 | 1.6 | 2.2 | 2.5 |
| Mean | 4.0 | 4.4 | 4.5 | 4.9 | 4.5 | 5.4 | 4.0 | 4.5 | 4.6 | 5.7 | 4.9 | 5.9 | ||
| Max | 7.0 | 9.4 | 9.4 | 9.4 | 9.6 | 9.6 | 9.4 | 9.4 | 9.4 | 9.6 | 9.6 | 9.6 | ||
| 4 | LCI*5+RoI*3+DI*2 | Min | 1.5 | 2.0 | 1.4 | 1.4 | 1.8 | 2.0 | 1.3 | 1.9 | 1.4 | 1.4 | 1.8 | 2.0 |
| Mean | 3.6 | 3.9 | 4.0 | 4.4 | 4.0 | 5.0 | 3.6 | 4.1 | 4.2 | 5.3 | 4.4 | 5.5 | ||
| Max | 6.5 | 9.3 | 9.3 | 9.3 | 9.6 | 9.6 | 9.3 | 9.3 | 9.3 | 9.6 | 9.6 | 9.6 | ||
| 5 | LCI*6+RoI*1+DI*3 | Min | 1.6 | 2.3 | 1.6 | 1.6 | 2.2 | 2.5 | 1.1 | 2.1 | 1.6 | 1.6 | 2.2 | 2.5 |
| Mean | 3.8 | 4.2 | 4.3 | 4.7 | 4.5 | 5.3 | 3.8 | 4.4 | 4.4 | 5.6 | 4.8 | 5.8 | ||
| Max | 7.1 | 9.6 | 9.6 | 9.6 | 9.6 | 9.6 | 9.6 | 9.6 | 9.6 | 9.6 | 9.6 | 9.6 | ||
| 6 | LCI*6+RoI*3+DI*1 | Min | 1.5 | 1.5 | 1.2 | 1.2 | 1.4 | 1.5 | 1.1 | 2.1 | 1.6 | 1.6 | 2.2 | 2.5 |
| Mean | 3.0 | 3.3 | 3.4 | 3.8 | 3.4 | 4.5 | 3.8 | 4.4 | 4.4 | 5.6 | 4.8 | 5.8 | ||
| Max | 6.1 | 9.3 | 9.3 | 9.3 | 9.6 | 9.6 | 9.6 | 9.6 | 9.6 | 9.6 | 9.6 | 9.6 | ||
| 7 | LCI*8+RoI*1+DI*1 | Min | 1.5 | 1.4 | 1.2 | 1.2 | 1.5 | 0.9 | 1.2 | 1.2 | 1.2 | 1.4 | 1.5 | 1.5 |
| Mean | 4.3 | 3.2 | 3.6 | 3.1 | 3.0 | 2.7 | 2.7 | 3.2 | 3.2 | 4.7 | 3.7 | 4.9 | ||
| Max | 9.6 | 9.6 | 9.5 | 9.5 | 9.5 | 6.3 | 9.5 | 9.5 | 9.5 | 9.6 | 9.6 | 9.6 | ||
| Equation | Sub-Catchment Accumulated PNPI Average | |||||||
|---|---|---|---|---|---|---|---|---|
| Year | 1 | 2 | 3 | 4 | 5 | 6 | ||
| 2 | LCI*4+RoI*4+DI*2 | 1997 | 3.7 | 3.9 | 4.2 | 4.0 | 4.0 | 4.1 |
| 2017 | 3.7 | 3.9 | 4.3 | 4.2 | 4.3 | 4.4 | ||
| 3 | LCI*5+RoI*2+DI*3 | 1997 | 4.0 | 4.1 | 4.5 | 4.3 | 4.4 | 4.4 |
| 2017 | 4.0 | 4.2 | 4.6 | 4.5 | 4.6 | 4.7 | ||
| 4 | LCI*5+RoI*3+DI*2 | 1997 | 3.6 | 3.7 | 4.0 | 3.9 | 3.9 | 4.0 |
| 2017 | 3.6 | 3.8 | 4.2 | 4.1 | 4.1 | 4.3 | ||
| 5 | LCI*6+RoI*1+DI*3 | 1997 | 3.8 | 4.0 | 4.3 | 4.2 | 4.2 | 4.3 |
| 2017 | 3.8 | 4.1 | 4.4 | 4.4 | 4.4 | 4.6 | ||
| 6 | LCI*6+RoI*3+DI*1 | 1997 | 3.0 | 3.1 | 3.4 | 3.3 | 3.3 | 3.4 |
| 2017 | 3.0 | 3.2 | 3.6 | 3.5 | 3.6 | 3.7 | ||
| 7 | LCI*8+RoI*1+DI*1 | 1997 | 2.7 | 2.8 | 3.1 | 3.0 | 3.0 | 3.1 |
| 2017 | 2.7 | 2.9 | 3.2 | 3.2 | 3.3 | 3.5 | ||
| Year | n | Outlet of Sub-Catchment | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| NO3 (mg L−1) | 1997 | 3 | 0.07 | 0.47 | 0.16 | 0.78 | 8.54 | 8.4 |
| 2017 | 2 | 1.21 | 7.75 | 12.54 | 9.36 | 19.41 | 4.26 | |
| PO4 (mg L−1) | 1997 | 3 | 0.09 | 0.25 | 0.23 | 0.31 | 12.75 | 0.03 |
| 2017 | 2 | 0.17 | 2.98 | 33.36 | 12.8 | 36.86 | 27.87 | |
| PNPI Equation | 1997 | 2017 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NO3 | PO4 | NO3 | PO4 | ||||||
| r | p-Value | r | p-Value | r | p-Value | r | p-Value | ||
| 2 | LCI*4 + RoI*4 + DI*2 | 0.39 | 0.450 | 0.11 | 0.841 | 0.51 | 0.300 | 0.85 | 0.031 * |
| 3 | LCI*5 + RoI*2 + DI*3 | 0.48 | 0.341 | 0.85 | 0.751 | 0.51 | 0.341 | 0.85 | 0.032 * |
| 4 | LCI*5 + RoI*3 + DI*2 | 0.44 | 0.385 | 0.12 | 0.820 | 0.50 | 0.317 | 0.85 | 0.034 * |
| 5 | LCI*6 + RoI*1 + DI*3 | 0.52 | 0.290 | 0.18 | 0.735 | 0.51 | 0.306 | 0.85 | 0.034 * |
| 6 | LCI*6 + RoI*3 + DI*1 | 0.46 | 0.357 | 0.12 | 0.828 | 0.48 | 0.330 | 0.84 | 0.038 * |
| 7 | LCI*8 + RoI*1 + DI*1 | 0.58 | 0.230 | 0.17 | 0.742 | 0.47 | 0.348 | 0.83 | 0.043 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gossweiler, B.; Wesström, I.; Messing, I.; Villazón, M.; Joel, A. Impact of Land Use Change on Non-Point Source Pollution in a Semi-Arid Catchment under Rapid Urbanisation in Bolivia. Water 2021, 13, 410. https://doi.org/10.3390/w13040410
Gossweiler B, Wesström I, Messing I, Villazón M, Joel A. Impact of Land Use Change on Non-Point Source Pollution in a Semi-Arid Catchment under Rapid Urbanisation in Bolivia. Water. 2021; 13(4):410. https://doi.org/10.3390/w13040410
Chicago/Turabian StyleGossweiler, Benjamin, Ingrid Wesström, Ingmar Messing, Mauricio Villazón, and Abraham Joel. 2021. "Impact of Land Use Change on Non-Point Source Pollution in a Semi-Arid Catchment under Rapid Urbanisation in Bolivia" Water 13, no. 4: 410. https://doi.org/10.3390/w13040410
APA StyleGossweiler, B., Wesström, I., Messing, I., Villazón, M., & Joel, A. (2021). Impact of Land Use Change on Non-Point Source Pollution in a Semi-Arid Catchment under Rapid Urbanisation in Bolivia. Water, 13(4), 410. https://doi.org/10.3390/w13040410







