Two-Dimensional Numerical Modeling of Flow in Physical Models of Rock Vane and Bendway Weir Configurations
Abstract
1. Introduction
2. Materials and Methods
2.1. Physical Model Facility
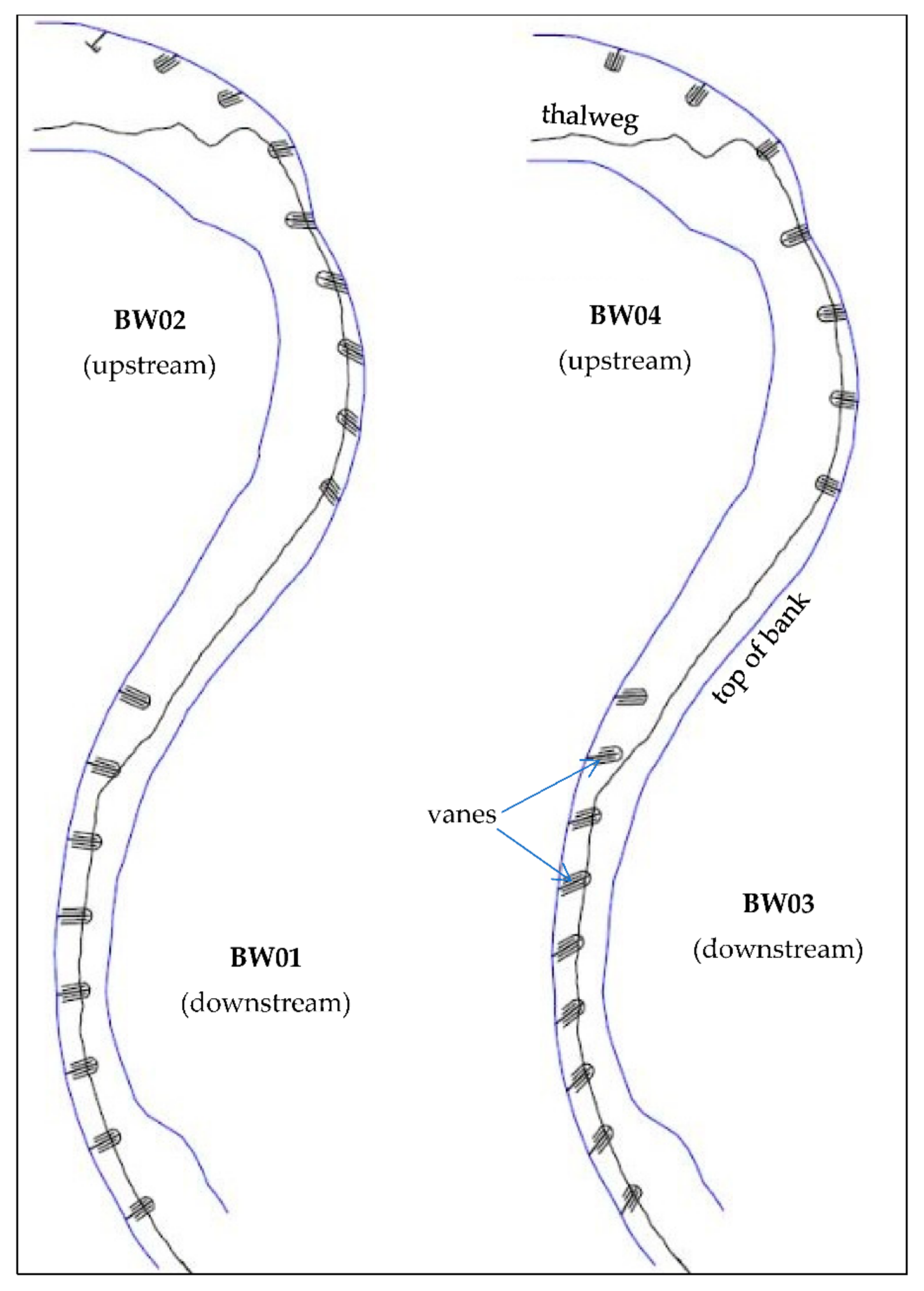
2.2. Physical Model Transverse Feature Configurations
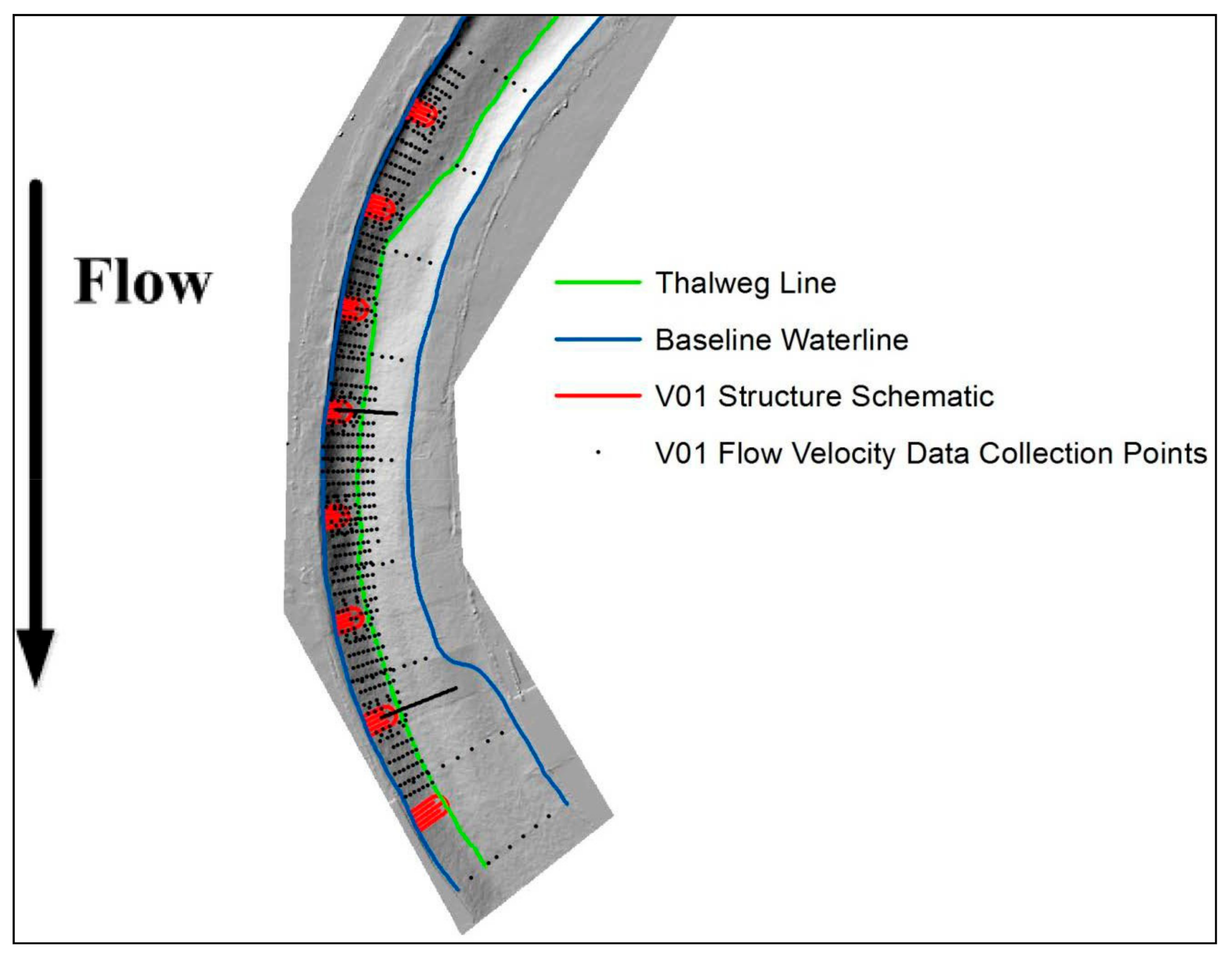
2.3. Physical Model Measurements
2.4. SRH-2D Numerical Model
2.4.1. Model Setup and Calibration
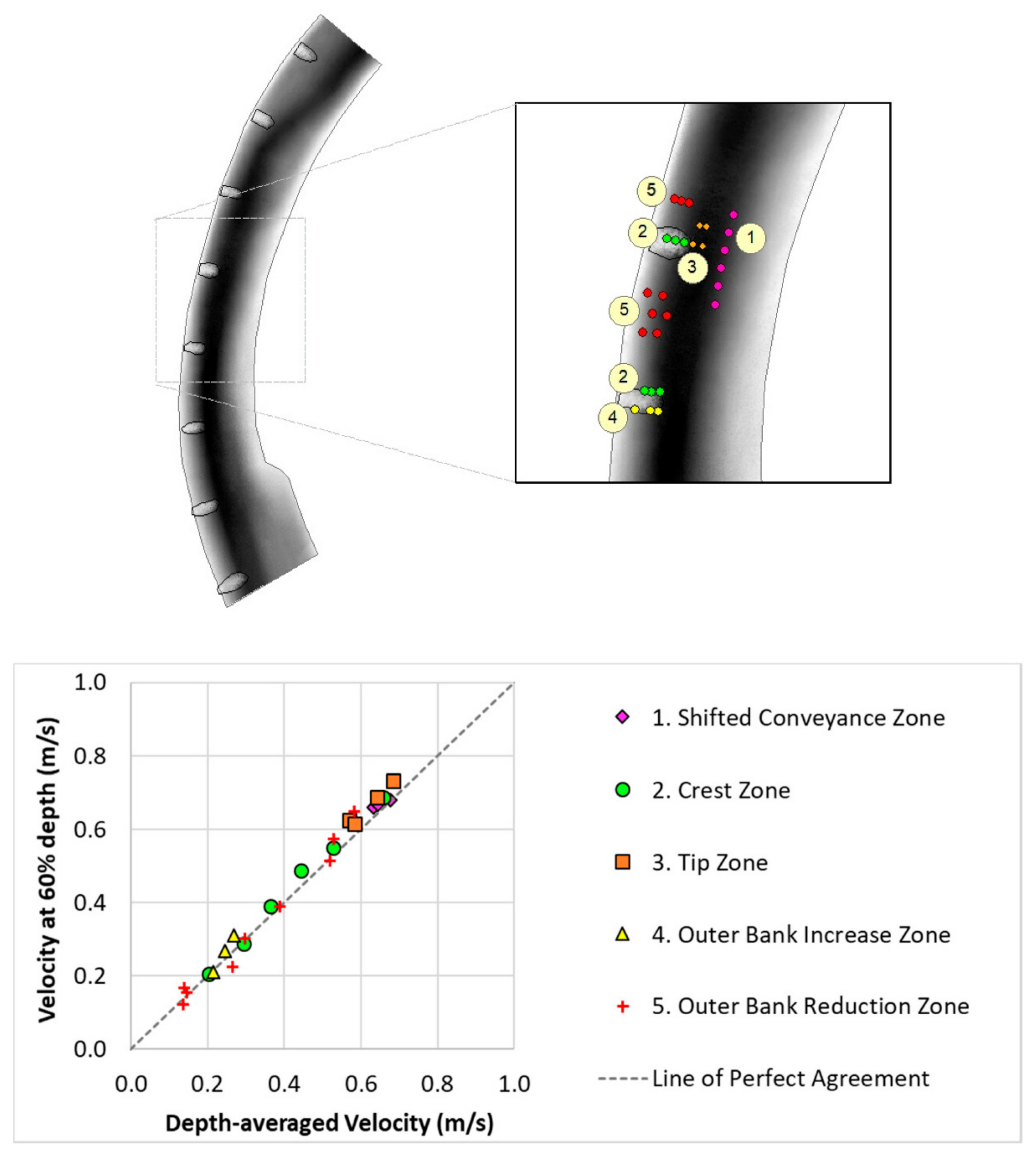
2.4.2. Velocity Zone Comparison
3. Results
3.1. Depth-Averaged Velocity Verification
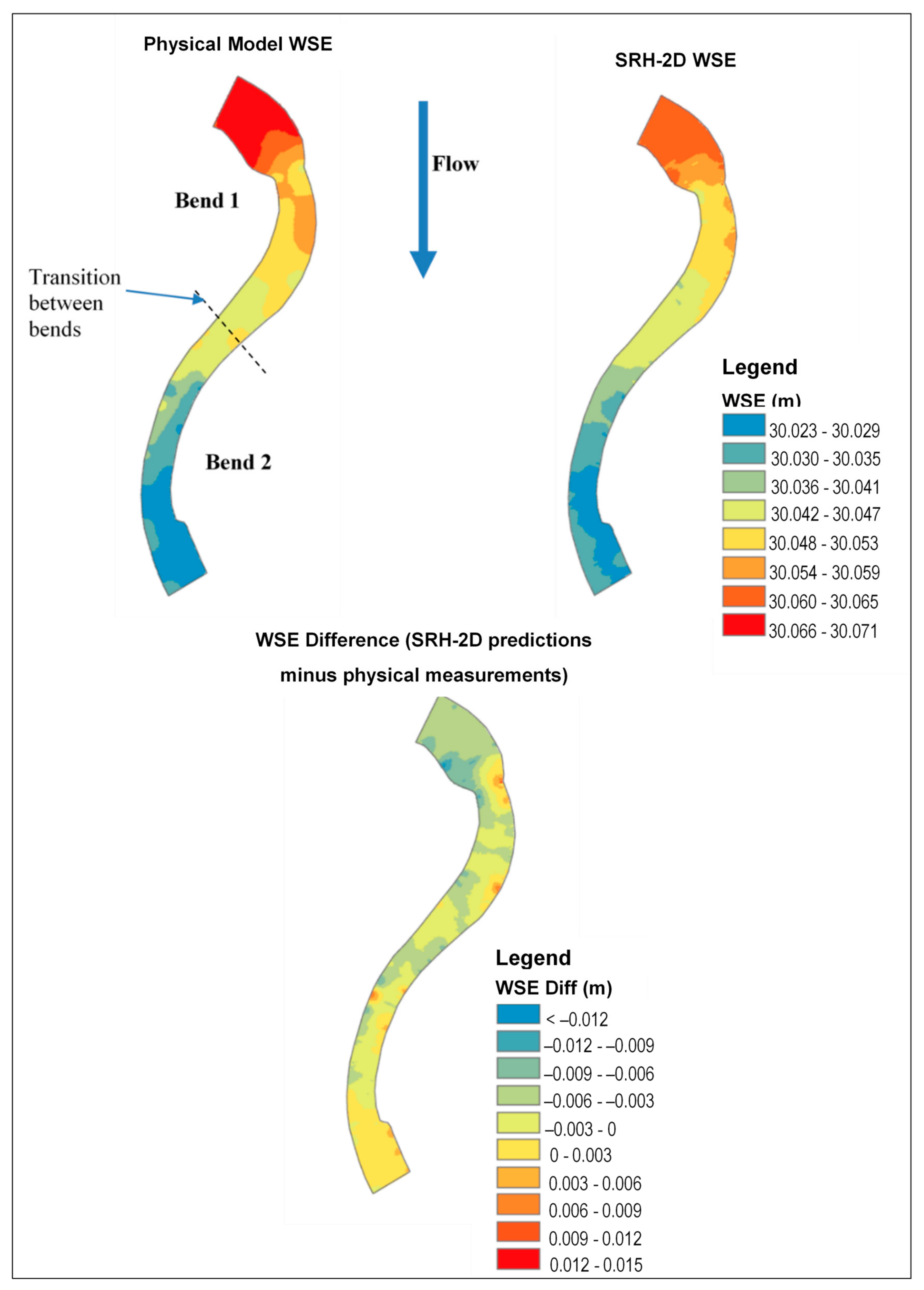
3.2. Baseline Configuration: Physical and SRH-2D Numerical Model Comparisons
- inside Bend 1,
- upper half of the outside of Bend 2,
- inside of the Bend 2 near the end of the physical model.
- along the outside of Bend 1,
- through the upper portion of the inside of Bend 2,
- on the outside of the downstream portion of Bend 2.
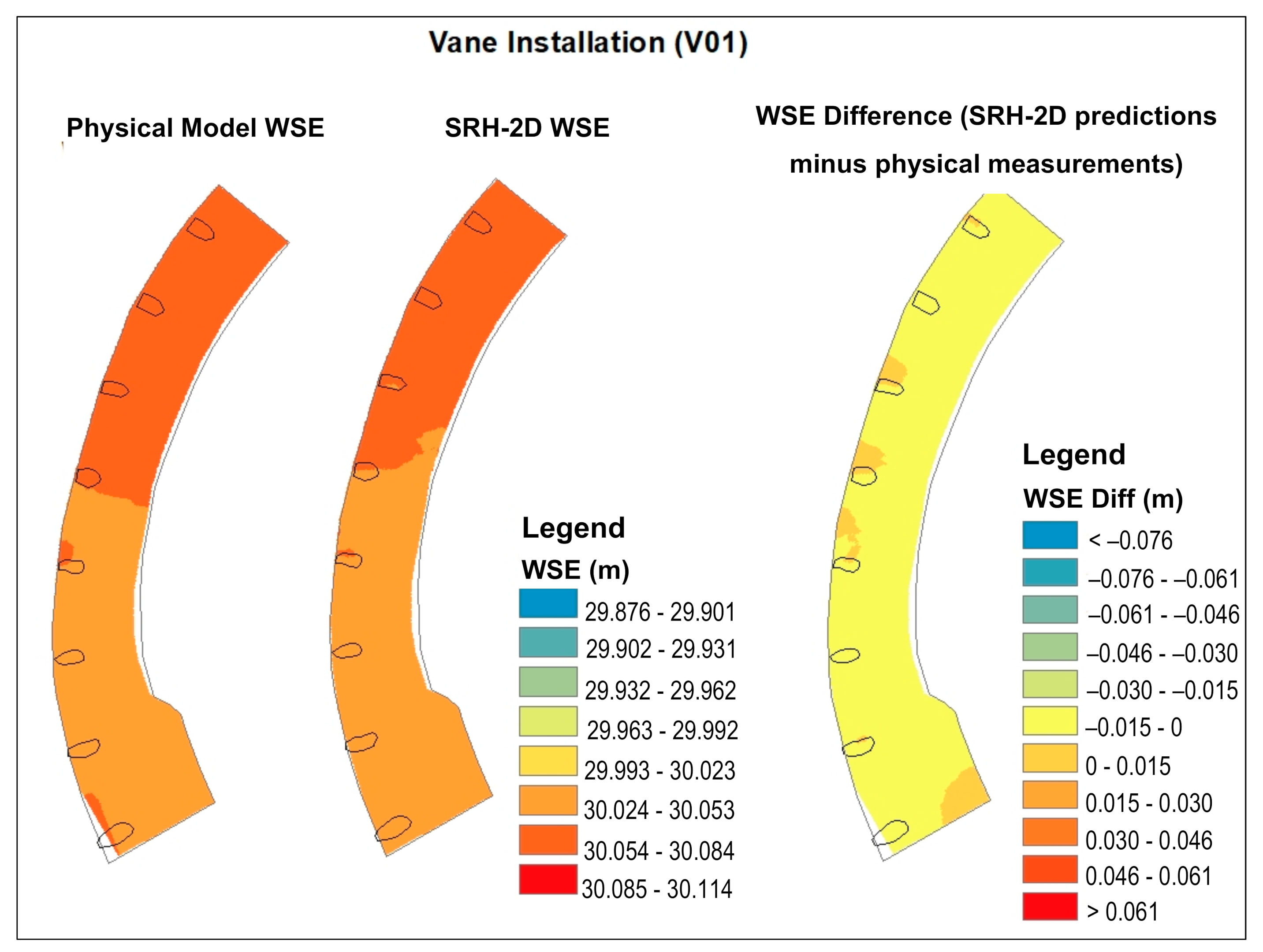
3.3. Rock Vane Configuration: Physical and SRH-2D Numerical Model Comparisons
- crest zone;
- out bank increase zone downstream of the first three upstream vanes;
- fifth vane (in the fifth vane by 0.09 to 0.18 m/s);
- sixth vane (in the sixth vane by 0 to 0.09 m/s);
- tip and shifted conveyance zones where flow has a significant vertical velocity component (Sections A-A and B-B in Figure 21);
- areas where flow vertically contracts and expands (outer bank increase zone) over the structures (Section C-C Figure 21);
- tip zone where there is vortex shedding and associated turbulence kinetic energy (Section A-A Figure 21).
- shifted conveyance zone throughout the bendway (−0.18 to 0 m/s);
- tip zone of Vanes 4, 6, 7, and 8 (−0.18 to −0.09 m/s);
- localized zones along the outer bank around Vanes 4, 6, 7, and 8 (−0.18 to −0.09 m/s);
- areas where the shifted conveyance zone is not fully captured.
3.4. Bendway Weir Scenario Configuration: Physical and SRH-2D Numerical Model Comparisons
- over the bendway weir crests;
- downstream of each weir;
- downstream of the weir tips (weir tips by about 0 to 0.18 m/s).
- at the tips of Weirs 6 and 8;
- between Weirs 7 and 8 along the bank (Weirs 7 and 8 by −0.36 to −0.27 m/s).
4. Discussion, Summary and Conclusions
4.1. SRH-2D Model Performance
4.2. Modeling Summary
4.3. Design Implications of Model Results
- SRH-2D model results matched the overall flow patterns found in physical model measurements for rock vanes and bendway weirs. Thus, SRH-2D models can be used to compare the effects of spacing, length, horizontal angle (rock vanes) and orientation angle of different structure configurations.
- SRH-2D did not compute the high-velocity zone between Bendway Weirs 7 and 8 (Figure 25). Higher velocities exist on the downstream portion of river bends (Figure 16). Additional bank erosion countermeasures such as bioengineering [35] could be employed between bendway weirs located in the downstream section of river bends, as well as between other weirs.
- SRH-2D computes increased resultant velocity when compared to physical model measurements over transverse feature crests and right at the tips where there is a vertical-velocity component and turbulent kinetic energy. Overprediction varies between approximately 15 and 25%, with a few locations over this range. This overprediction provides conservative design. And we recommend that model results be used over weir crests when designing erosion countermeasures such as bioengineering [35].
- SRH-2D may not fully resolve conveyance shifts. This failure to fully resolve can lead to both overprediction and underprediction of velocity in certain zones of the flow field by up to 25%, depending on the configuration. The highest velocity found in the shifted conveyance zone or at the tip is conservative and should be used for design tip scour and riprap sizing. Transverse feature rock sizing procedures from large-scale flume experiments [36] should be used, along with an appropriate factor of safety [37]. These higher velocities might affect sediment transport analysis, but this study did not determine the magnitude of this effect.
- SRH-2D underpredicts bankline velocity in some locations by up to about 25%. Increase bankline velocity by at least this amount during design.
4.4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Washington State Department of Transportation. Hydraulics Manual; Washington State Department of Transportation: Olympia, WA, USA, 2017. [Google Scholar]
- Natural Resources Conservation Service. Kansas Engineering Technical Note No. KS-1 (Revision 1); U.S. Department of Agriculture: Salina, KS, USA, 2013.
- Natural Resources Conservation Service. Minnesota Technical Note No. 8 Design of Stream Barbs for Low Gradient Streams; United States Department of Agriculture: St. Paul, MN, USA, 2010.
- Natural Resources Conservation Service. Wisconsin Supplement Engineering Field Handbook Chapter 16 Streambank and Shoreline Protection; United States Department of Agriculture: Madison, WI, USA, 2009.
- Natural Resources Conservation Service. Technical Supplement 14H Flow Changing Techniques Part 654 National Engineering Handbook; United States Department of Agriculture: Madison, WI, USA, 2007.
- Natural Resources Conservation Service. Technical Note 23, Version 2.0 Design of Stream Barbs; United States Department of Agriculture: Portland, OR, USA, 2005.
- Johnson, P.A.; Hey, R.D.; Tessier, M.; Rosgen, D.L. Use of vanes for control of scour at vertical wall abutments. J. Hydraul. Eng. 2001, 127, 772–778. [Google Scholar] [CrossRef]
- Maryland Department of the Environment. Maryland’s Waterway Construction Guidelines; Water Management Administration: Baltimore, MD, USA, 2000. [Google Scholar]
- Julien, P.Y.; Duncan, J.R. Optimal Design Criteria of Bendway Weirs from Numerical Simulations and Physical Model Studies; Technical Paper; Department of Civil Engineering, Colorado State University: Fort Collins, CO, USA, 2003. [Google Scholar]
- McCullah, J.A.; Gray, D. Environmentally Sensitive Channel- and Bank-Protection Measures; NCHRP Rep. 544; National Cooperative Highway Research Program, Transportation Research Board of the National Academy of Sciences: Washington, DC, USA, 2005. [Google Scholar]
- Lagasse, P.F.; Clopper, P.E.; Pagán-Ortiz, J.E.; Zevenbergen, L.W.; Arneson, L.A.; Schall, J.D.; Girard, L.G. Bridge Scour and Stream Instability Countermeasures: Experience, Selection, and Design Guidance, 3rd ed.; Rep. No. FHWA NHI HEC-23, Vols. 1 and 2; U.S. Department of Transportation, Federal Highway Administration, National Highway Institute: Washington, DC, USA, 2009.
- Abad, J.D.; Rhoads, B.L.; Guneralp, I.; Garcia, M.H. Flow Structure at Different Stages in a Meander-bend with Bendway Weirs. J. Hydraul. Eng. 2008, 134, 1052–1063. [Google Scholar] [CrossRef]
- Jia, Y.; Zhu, T.; Scott, S. Turbulent flow around submerged bendway weirs and its influence on channel navigation. In Hydrodynamics—Optimizing Methods and Tools; Schulz, H., Ed.; InTech Open: Rijeka, Croatia, 2011; ISBN 978-953-307-712-3. [Google Scholar]
- Lyn, D.A.; Cunningham, R.A. Laboratory Study of Bendway Weirs as a Bank Erosion Countermeasure; Rep. No. FHWA/IN/JTRP-2010/24, Joint Transportation Research Program (JTRP); Purdue University: West Lafayette, IN, USA, 2010. [Google Scholar]
- McCoy, A.; Constantinescu, G.; Weber, L. Hydrodynamics of flow in a channel with two lateral submerged groynes. In World Environmental and Water Resources Congress 2007: Restoring Our Natural Habitat; Kabbes, K.C., Ed.; ASCE: Reston, VA, USA, 2007; pp. 1–11. [Google Scholar]
- Jamieson, E.C.; Rennie, C.D.; Townsend, R.D. 3D flow and sediment dynamics in a laboratory channel bend with and without stream barbs. J. Hydraul. Eng. 2013, 139, 154–166. [Google Scholar] [CrossRef]
- Ottevanger, K.; Blanckaert, K.; Uijttewaal, W.S.J. Processes governing the flow redistribution in sharp river bends. Geomorphology 2012, 163, 45–55. [Google Scholar] [CrossRef]
- Bressan, F.; Wilson, C.G.; Papanicolaou, A.N. Improved streambank countermeasures: The Des Moines River (USA) case study. Int. J. River Basin Manag. 2014, 12, 69–86. [Google Scholar] [CrossRef]
- Elhakeem, M.; Papanicolaou, A.N.; Wilson, C.G. Implementing streambank erosion control measures in meandering streams: Design procedure enhanced with numerical modeling. Int. J. River Basin Manag. 2017, 15, 317–327. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Bressan, F.; Fox, J.; Kramer, C.; Kjos, L. Role of structure submergence on scour evolution in gravel-bed rivers: Application to slope-crested structures. J. Hydraul. Eng. 2018, 144, 03117008. [Google Scholar] [CrossRef]
- Thornton, C.I.; James, M.; Shin, K.S. Testing of Instream Vane Structures within the Native Topography Channel; Department of Civil Engineering, Colorado State University: Fort Collins, CO, USA, 2016. [Google Scholar]
- Thornton, C.I.; Cox, A.L.; Ursic, M.E.; Youngblood, N.A. Data Report for Completed Bendway weir Configurations within the Native Topography Model; Department of Civil Engineering, Colorado State University: Fort Collins, CO, USA, 2011. [Google Scholar]
- Scurlock, S.M.; Thornton, C.I.; Abt, S.R. Evaluation of Bendway Weir Structures within the Native-Topography Channel; Department of Civil Engineering, Engineering Research Center, Colorado State University: Fort Collins, CO, USA, 2014. [Google Scholar]
- Scurlock, S.M.; Thornton, C.I.; Abt, S.R. Middle Rio Grande Physical Modeling, Re-Evaluations and Comparison of Instream Structures within the Native-Topography Channel. Native Topography: Construction and Evaluation of Baseline Hydraulic Conditions; Department of Civil Engineering, Engineering Research Center, Colorado State University: Fort Collins, CO, USA, 2013. [Google Scholar]
- Scurlock, S.M.; Thornton, C.I.; Abt, S.R.; Cox, A.L. Middle Rio Grande Physical Modeling, Native-Topography Dataset Evaluation Summary; Department of Civil Engineering, Engineering Research Center, Colorado State University: Fort Collins, CO, USA, 2012. [Google Scholar]
- Scurlock, A.M.; Baird, D.C.; Cox, A.L.; Thornton, C.I. Bendway Weir Design—Rio Grande Physical Model; Department of Civil Engineering, Engineering Research Center, Colorado State University: Fort Collins, CO, USA, 2012. [Google Scholar]
- Scurlock, S.M.; Cox, A.L.; Baird, D.C.; Thornton, C.I.; Parker, T.R.; Abt, S.R. Middle Rio Grande Physical Modeling—Native Topography: Construction and Evaluation of Baseline Hydraulic Conditions; Department of Civil Engineering, Engineering Research Center, Colorado State University: Fort Collins, CO, USA, 2012. [Google Scholar]
- Papanicolaou, A.N.; Elhakeem, M.; Wardman, B. Calibration and verification of a 2D-hydrodynamic model for simulating flow around bendway weir structures. J. Hydraul. Eng. 2011, 137, 75–89. [Google Scholar] [CrossRef]
- Richard, G.; Julien, P. Dam impacts on and restoration of an alluvial river—Rio Grande, New Mexico. Int. J. Sediment Res. 2003, 18, 89–96. [Google Scholar]
- Walker, K.G.; Thornton, C.I.; Abt, S.R.; Cox, A.L. Comparison of a Generalized Trapezoidal Hydraulic Model to a Native Topography Patterned Bed Surface Model of the Rio Grande; Colorado State University: Fort Collins, CO, USA, 2009. [Google Scholar]
- Lai, Y.G. SRH-2D version 2: Theory and User’s Manual; Sedimentation and River Hydraulics Group, Technical Service Center, Bureau of Reclamation, U.S. Department of the Interior: Denver, CO, USA, 2008. [Google Scholar]
- Lai, Y.G. Unstructured Grid Arbitrarily Shaped Element Method for Fluid Flow Simulation. AIAA J. 2000, 38, 2246–2252. [Google Scholar] [CrossRef]
- Aquaveo. SMS User Manual: The Surface Water Modeling System; Aquaveo, Provo, Utah USA. Available online: https://www.xmswiki.com/wiki/SMS:SMS_User_Manual_13.0 (accessed on 7 February 2021).
- Scurlock, S.M.; Cox, A.L.; Thornton, C.I.; Abt, S.R. Calibration and Validation of a Numerical Model for Evaluation of Transverse In-Stream Structure Research; Department of Civil Engineering, Engineering Research Center, Colorado State University: Fort Collins, CO, USA, 2014. [Google Scholar]
- Baird, D.C.; Fotherby, L.; Klumpp, C.C. Bank Stabilization Design Guidelines; Report: SRH-2015-25; Sedimentation and River Hydraulics Group, Technical Service Center, Bureau of Reclamation, U.S. Department of the Interior: Denver, CO, USA, 2015. [Google Scholar]
- Ettema, R.; Aubuchon, J.; Holste, N.; Varyu, D.; Baird, D.; Padilla, R.; Posner, A.; Thornton, C. Large-Flume Tests on Flow Dislodgment of Rocks Forming Bendway Weirs, American Society of Civil Engineers. J. Hydraul. Eng. 2020, 146, 2020. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers. Hydraulic Design of Flood Control Channels; EM 1110-2-1601; Department of the Army, U.S. Army Corps of Engineers: Washington, DC, USA, 1994.


















| Type | Top Width (m) | Radius of Curvature (m) | Bend Angle (degrees) | Relative Curvature, Rc/Tw | Channel Length (m) |
|---|---|---|---|---|---|
| Upstream | 5.85 | 11.81 | 125 | 2.02 | 25.76 |
| Downstream | 4.57 | 20.07 | 73 | 4.39 | 25.45 |
| Configuration | Length (m) | Height (m) | Top Width (m) | Spacing (m) | θ (°) |
|---|---|---|---|---|---|
| Design Parameters | |||||
| V01, V02 | TW/3–TW/4 | 7% sloping crest | 2 d100–3 d100 | 2.69 L–4.79 L | variable |
| Values | |||||
| V01 (downstream) | 0.42–0.73 * | 0.14–0.30 | 0.3 | 2.83 | 85 |
| V02 (upstream) | 0.61–1.22 * | 0.16–0.45 | 0.3 | 2.83 | 60 |
| NRCS Design Parameters | |||||
| V07 | TW/6 | 7% sloping crest | 2 d100–3 d100 | 2.69 L–4.79 L | variable |
| Values | |||||
| V07 (downstream) | 2.60–3.00 * | 0.00–0.17 | 0.3 | 5.05–7.38 | 20–30 |
| Location | Length (m) | Height (m) | Top Width (m) | Spacing (m) | θ (°) | Transverse Slope |
|---|---|---|---|---|---|---|
| Design Parameters | ||||||
| BW01 (downstream) | TW/2 | 0.333 BF Hydr. Depth | 2 d100 | 2.69 L | 85 | 0 |
| BW02 (upstream) | TW/4 | 0.333 BF Hydr. Depth | 2 d100 | 3.37 L | 60 | 0 |
| Values | ||||||
| BW01 (downstream) | 1.2 | 0.059 | 0.3 | 3.23 | 85 | 0 |
| BW02 (upstream) | 0.9 | 0.055 | 0.3 | 3.02 | 60 | 0 |
| Design Parameters | ||||||
| BW03 (downstream) | TW/2 | 0.333 BF Hydr. Depth | 2 d100 | 2.36 L | 60 | 0 |
| BW04 (upstream) | TW/4 | 0.333 BF Hydr. Depth | 2 d100 | 4.17 L | 85 | 0 |
| Values | ||||||
| BW03 (downstream) | 1.2 | 0.059 | 0.3 | 2.83 | 60 | 0 |
| BW04 (upstream) | 0.9 | 0.055 | 0.3 | 3.73 | 85 | 0 |
| Data Collection Scheme | Description | Planimetric Distribution | Vertical Distribution |
|---|---|---|---|
| Cross-section | Direct comparison to baseline and other tests | Seven points per cross-section | 60% depth,5%, 20% depth intervals at thalweg |
| Structure | Tip, crest, key-in, and immediate vicinity hydraulics | Twelve points per structure, one inner- bank point matching spur-dike testing | 20% depth intervals, 5% depth intervals at 5th and 7th structure |
| Outer bank | Flow field hydraulics and eddies | Twelve to sixteen locations between structures | 20% depth intervals |
| 60% depth | Full resolution of 60% depth velocity field | Staggered points where needed to resolve flow field | 60% depth |
| Structure Grid | Comprehensive mapping of structure flow field | Equidistant grid of closely distributed points | 20% depth intervals |
| Root Mean Square Error (×10−3 m/s) | Mean Absolute Error (×10−3 m/s) | Mean Absolute Percentage Error | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Q1 (0.30 m3/s) | Q2 (0.325 m3/s) | Q3 (0.34 m3/s) | Q1 (0.30 m3/s) | Q2 (0.325 m3/s) | Q3 (0.34 m3/s) | Q1 (0.30 m3/s) | Q2 (0.325 m3/s) | Q3 (0.34 m3/s) | |
| n1 (0.017) | 8.83 | 8.16 | 8.24 | 6.97 | 6.37 | 6.31 | 26% | 28% | 29% |
| n2 (0.018) | 8.89 | 8.01 | 8.16 | 7.08 | 6.29 | 6.29 | 28% | 29% | 30% |
| n3 (0.021) | 9.03 | 8.10 | 8.04 | 7.28 | 6.34 | 6.20 | 31% | 32% | 33% |
| n4 (0.022) | 9.17 | 8.16 | 8.10 | 7.42 | 6.40 | 6.23 | 32% | 32% | 33% |
| Domain (Cell Type) | Fine | Medium | Coarse |
|---|---|---|---|
| Main Channel–Lateral (quad) | 23–38 mm | 46–76 mm | 198–305 mm |
| Main Channel–Longitudinal (quad) | 30–38 mm | 60–76 mm | 259–305 mm |
| Overbank | 30–76 mm | 60–152 mm | 259–610 mm |
| Total Number of Elements | 379,200 | 94,790 | 5300 |
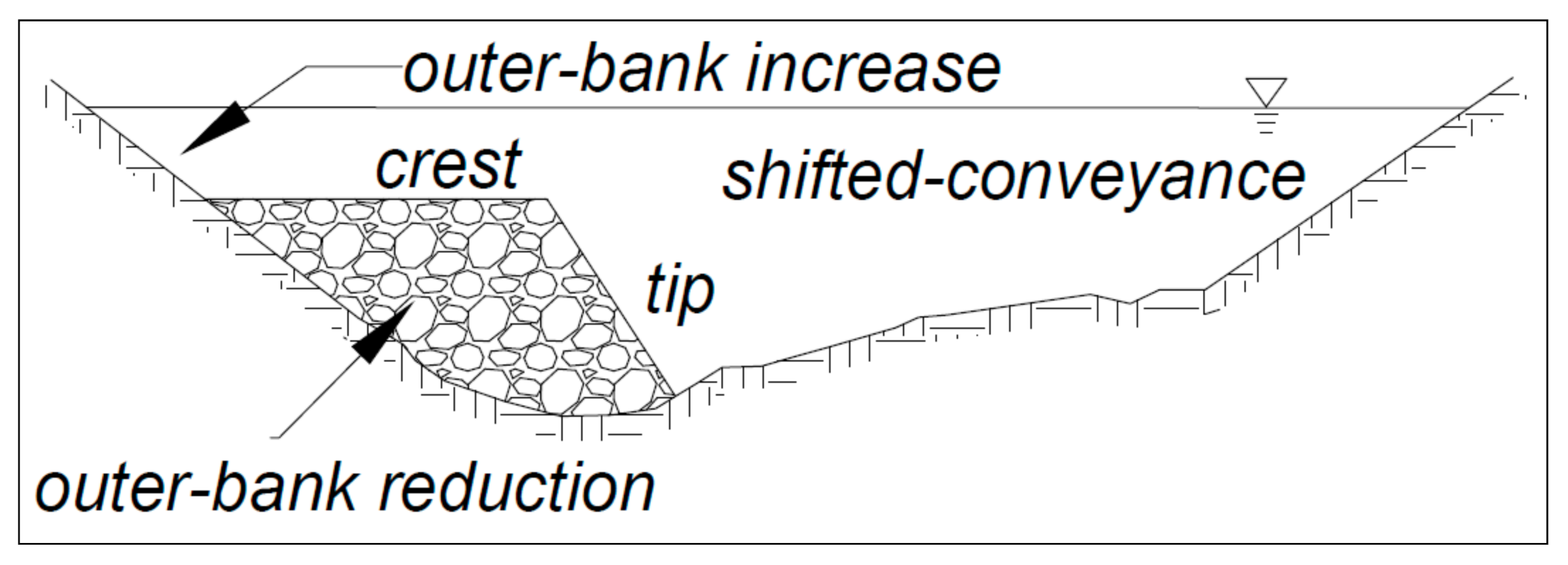
| Flow Zone | Definition |
|---|---|
| Shifted Conveyance | Zone that extends from near the structure tip to the point bar where velocity increases above baseline as longitudinal flows contract and a new thalweg location is created. |
| Crest | Zone where there is convective acceleration of flow passing over the crest of the structure. |
| Tip | Turbulent zone at the tip where flow contracts horizontally. This zone is frequently associated with vortex shedding. |
| Outer Bank Increase Zone | Zone along the outer bank shortly downstream of the crest of each structure as flow vertically expands after passing over the structure crest. |
| Outer Bank Reduction | Zone along the outer bank covering most of the bank between structures and downstream of the most downstream structure, where bank-line velocity is decreased from baseline conditions. This zone generally extends laterally from the bankline to near structure tips. |
| Configuration | Comparison between Measured and Predicted Fields |
|---|---|
| Baseline | The highest velocity area starts on the inside of upstream part of Bend 1, moves to outside of Bend 1 downstream of constriction and stays on that bank to the upstream part of Bend 2, then switches to outside of Bend 2 about the bend apex and continues to the downstream boundary. SRH-2D predicted less variability in the lateral velocity area, which continues until the wide section near model outlet. |
| V01 | Both measured and predicted results show that velocity in outer bank reduction zone is lower in the rock vane configuration than in the baseline configuration. Within the rock vane configuration, there is a higher velocity in tip zone, and the highest velocity is in the shifted conveyance zone near bend apex downstream of vane downstream to Vane 6 (predicted), and Vane 7 (measured). SRH-2D overpredicts in crest and tip zone and between Vanes 1 and 2, and 2 and 3, and downstream of Vanes 3 and 5, and in shifted conveyance zone downstream of Vane 5, but by less than ±25%. |
| BW02 | Both measured and SRH-2D results show that velocity in outer bank reduction zone is lower and is higher in the shifted conveyance zone in the bendway weir configuration than in the baseline configuration.SRH-2D overpredicts in the crest, tip, and outer bank increase zone downstream of contraction. SRH-2D both shows increase and decrease in shifted conveyance zone (overpredicted and underpredicted regions in zone). Over- and under-predictions are less than ±25%. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baird, D.C.; Abban, B.; Scurlock, S.M.; Abt, S.B.; Thornton, C.I. Two-Dimensional Numerical Modeling of Flow in Physical Models of Rock Vane and Bendway Weir Configurations. Water 2021, 13, 458. https://doi.org/10.3390/w13040458
Baird DC, Abban B, Scurlock SM, Abt SB, Thornton CI. Two-Dimensional Numerical Modeling of Flow in Physical Models of Rock Vane and Bendway Weir Configurations. Water. 2021; 13(4):458. https://doi.org/10.3390/w13040458
Chicago/Turabian StyleBaird, Drew C., Benjamin Abban, S. Michael Scurlock, Steven B. Abt, and Christopher I. Thornton. 2021. "Two-Dimensional Numerical Modeling of Flow in Physical Models of Rock Vane and Bendway Weir Configurations" Water 13, no. 4: 458. https://doi.org/10.3390/w13040458
APA StyleBaird, D. C., Abban, B., Scurlock, S. M., Abt, S. B., & Thornton, C. I. (2021). Two-Dimensional Numerical Modeling of Flow in Physical Models of Rock Vane and Bendway Weir Configurations. Water, 13(4), 458. https://doi.org/10.3390/w13040458





