Analysis of Weakening Law and Stability of Sliding Zone Soil in Thrust-Load-Induced Accumulation Landslides Triggered by Rainfall Infiltration
Abstract
:1. Introduction
- (1)
- The slope body structure of accumulation slopes has not been taken into account-the spatial structure of the weak surface controls the rainfall infiltration process and landslide failure mode [39];
- (2)
- (3)
- The characteristics of gradual creep failure in accumulation landslides have not been considered [40];
- (4)
- After rainfall infiltration, the mechanical properties of accumulation slopes exhibit gradual weakening, however the geotechnical physical parameters considered in the calculation of slope stability are all fixed values. Therefore, the spatiotemporal variability of the mechanical parameters is neglected [41,42];
- (5)
- The traditional stability calculation method cannot fully reflect the characteristics of shear stress and displacement changes in the sliding zone [43].
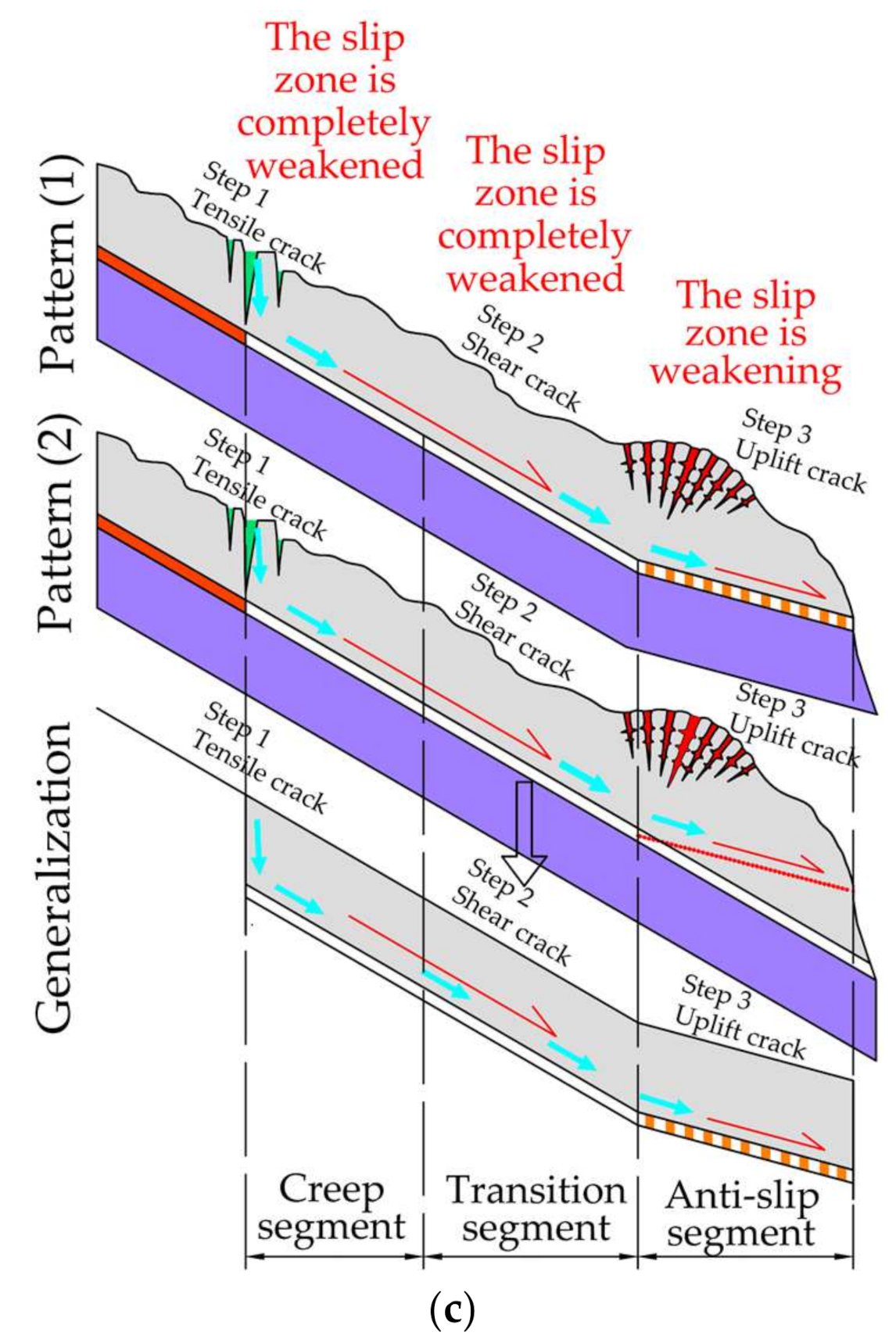
2. Failure Mode of Thrust-Load-Induced Accumulation Landslides Triggered by Rainfall Infiltration
3. Weakening Law of the Mechanical Parameters of Sliding Zone Soil of Thrust-Load-Induced Accumulation Landslides Triggered by Rainfall Infiltration
3.1. Constitutive Model of Sliding Zone Soil
3.2. Weakening Law of the Mechanical Parameters of Sliding Zone Soil
3.2.1. Basic Weakening Law of Mechanical Parameters
3.2.2. Weakening Model of Mechanical Parameters
3.2.3. State Curve Equation for the Weakening Coefficient
4. Stability Calculation of Sliding Zone Soil of Thrust-Load-Induced Accumulation Landslide Triggered by Rainfall Infiltration
- Divide the up-steep section and the down-slow section of the sliding zone into equal parts:where and and , and are the calculated step size and equal fractions of the up-steep and down-slow sections, respectively.
- The equidistant nodes can be expressed as follows:
- The sliding resistance force of the sliding zone can be calculated according to two situations: (1) If soil in the up-steep section is not completely weakened, its anti-sliding force is the joint force between the anti-sliding force of the soil in the up-steep section and the anti-sliding force of the soil in the down-slow section; (2) If soil in the up-steep section is completely weakened, its sliding resistance force is approximately equal to the sliding resistance force of the soil in the down-slow section. Under this condition, the calculation equation can be expressed as follows (1):
- The sliding force of the landslide is expressed as follows:
- The slope stability coefficient is expressed as follows:
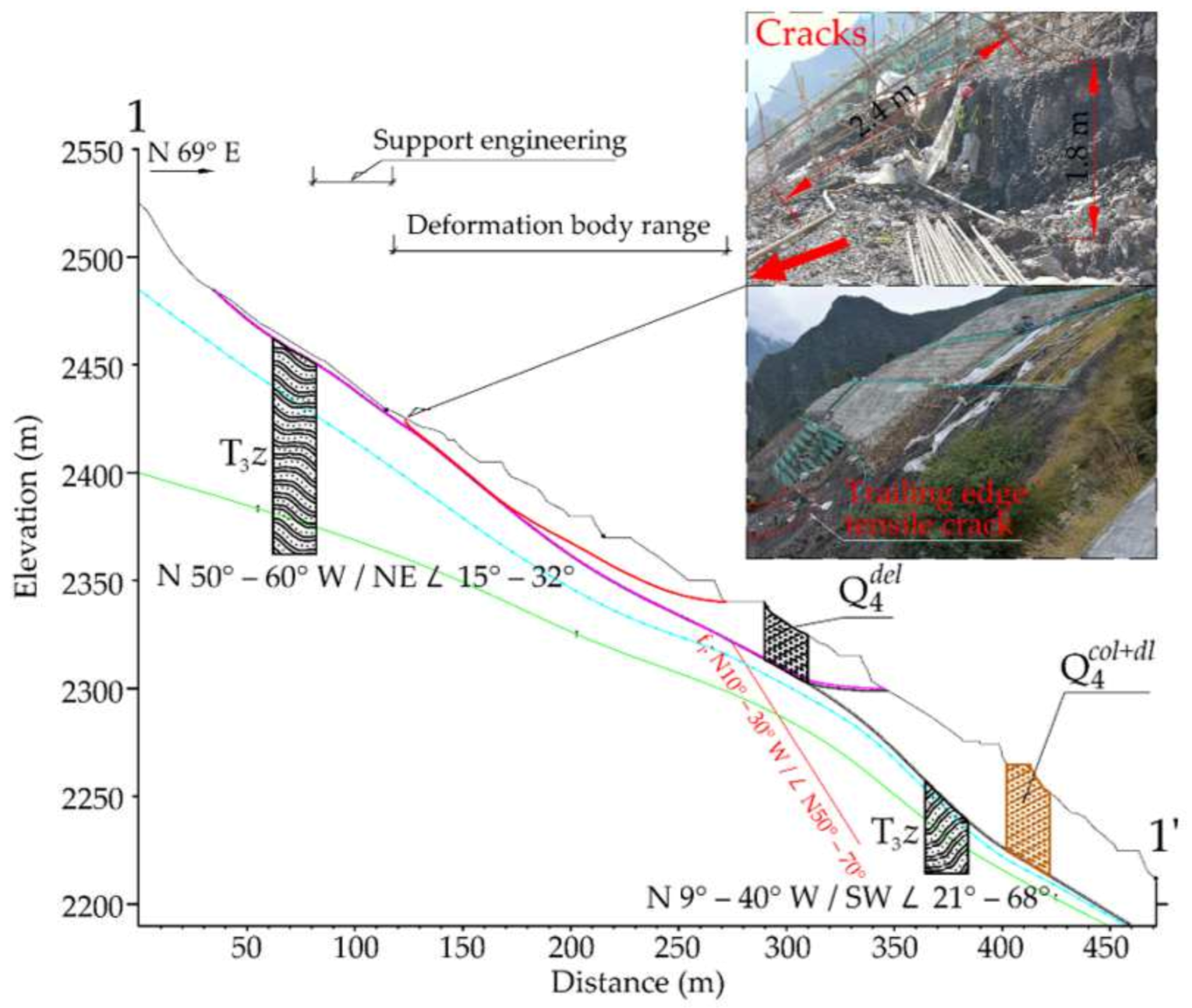
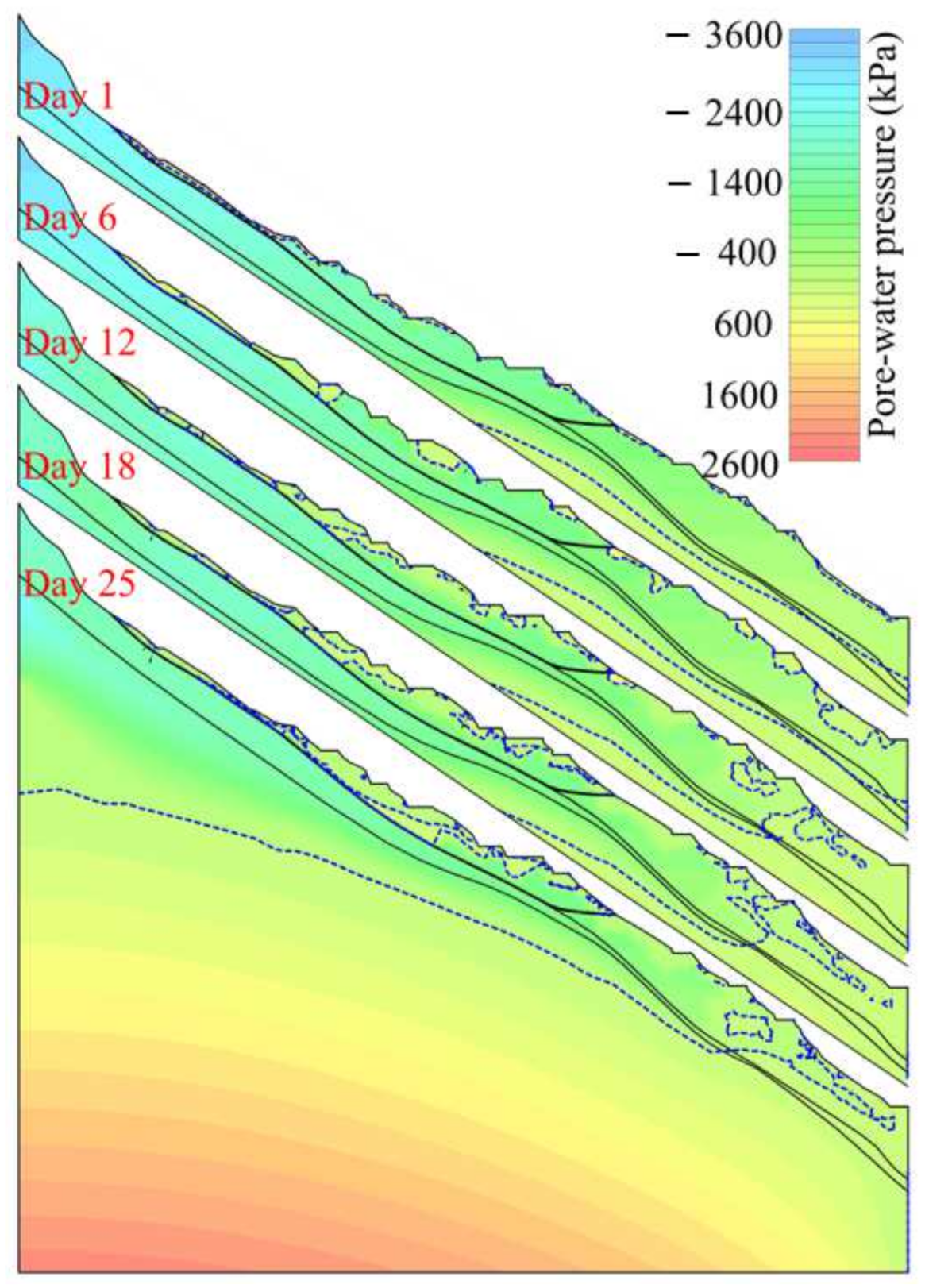
5. Case Analysis
6. Conclusions
- (1)
- It is concluded that the deformation and failure mode of thrust-load-induced accumulation landslides is triggered by rainfall infiltration, and the sliding zone is governed by the spatial morphology law of up-steep and down-slow actions. Moreover, the weakening of the sliding zone soil is gradual from the trailing edge to the front edge, with the three stages of creep, transition, and shear;
- (2)
- The negative exponential equation was introduced into the constitutive equation of the sliding zone soil and combined with the constitutive curve. The relationship between shear stress and shear strain in the weakening process of the sliding zone soil caused by rainfall infiltration was expounded in detail from the two aspects of time and space;
- (3)
- In the constitutive model, the weakening law of the mechanical parameters of sliding zone soil can be generalized to weakening shear stiffness. On this basis, the concept of the weakening coefficient is put forward and the state curve equation of the weakening coefficient of sliding zone soil is established by combining the “S”-shaped curve of the evolution of the geological body;
- (4)
- According to the level of similarity of the material composition of the up-steep section and the down-slow section of sliding zone soil in thrust-load-induced accumulation landslides induced by rainfall infiltration, the two failure modes were further divided and a formula for calculating the stability of such slopes under the two conditions of incomplete weakening of the up-steep section and complete weakening of the up-steep section was derived;
- (5)
- Taking a deformation body in the Danbo reservoir (thrust-load-induced accumulation landslide) as a geological prototype, in which the main factor controlling the landslide is the weakening of mechanical parameters due to rainfall infiltration into the sliding zone, the derived formula was applied and the relationship curve between the characteristic values of and at different weakening stages of the sliding zone soil and slope stability was established. The results reflect the progressive failure characteristics of thrust-load-induced accumulation landslides to a certain extent.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tu, G.Q.; Huang, D.; Huang, R.Q.; Deng, H. Effect of locally accumulated crushed stone soil on the infiltration of intense rainfall: A case study on the reactivation of an old deep landslide deposit. Bull. Eng. Geol. Environ. 2019, 78, 4833–4849. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, W.; Zhang, Z.Y. New Views on Forming Mechanism of Deep Overburden on River Bed in Southwest of China. Adv. Earth Sci. 2008, 23, 448–456. [Google Scholar] [CrossRef]
- Wang, Z.G. Engineering Geological Study on Large Quaternary Deposits in the Deeply Valley Southwestern China. Ph.D. Thesis, Chengdu University of Technology, Chengdu, Sichuan, China, 2015. [Google Scholar]
- Song, H.; Cui, W. A large-scale colluvial landslide caused by multiple factors: Mechanism analysis and phased stabilization. Landslides 2016, 13, 321–335. [Google Scholar] [CrossRef]
- Wang, D.J.; Tang, H.M.; Li, C.D.; Ge, Y.F.; Yi, X.L. Stability analysis of colluvial landslide due to heavy rainfall. Rock Soil Mech. 2016, 37, 439–445. [Google Scholar] [CrossRef]
- Zhang, F.Y.; Huang, X.W. Trend and spatiotemporal distribution of fatal landslides triggered by non-seismic effects in China. Landslides 2018, 15, 1663–1674. [Google Scholar] [CrossRef]
- He, K.Q.; Bai, J.Y.; Wang, S.J. Analysis of displacement dynamic features of colluvial landslide induced by rainfall. Rock Soil Mech. 2005, 26, 705–709. [Google Scholar] [CrossRef]
- Wang, Z.G. Study on Geological Disaster of Water Conservancy and Hydropower Engineering in Southwest China and Its Prevention Measures; China Water Power Press: Beijing, China, 2013. [Google Scholar]
- Wang, R.B.; Xia, R.; Xu, W.Y.; Wang, H.L.; Qi, J. Study on physical simulation of rainfall infiltration process of landslide ac-cumulation body. Adv. Eng. Sci. 2019, 51, 47–54. [Google Scholar] [CrossRef]
- Pearce, A.J. Streamflow Generation Processes: An Austral View. Water Resour. Res. 1990, 26, 3037–3047. [Google Scholar] [CrossRef]
- Okura, Y.; Kitahara, H.; Ochiai, H.; Sammori, T.; Kawanami, A. Landslide fluidization process by flume experiments. Eng. Geol. 2002, 66, 65–78. [Google Scholar] [CrossRef]
- Wang, G.H.; Sassa, K. Pore-pressure generation and movement of rainfall-induced landslides: Effects of grain size and fine-particle content. Eng. Geol. 2003, 69, 109–125. [Google Scholar] [CrossRef]
- Wu, Y. Mechanism analysis of hazards caused by the interaction between groundwater and geo-environment. Environ. Geol. 2003, 44, 811–819. [Google Scholar] [CrossRef]
- Sergio, D.N.L.O.; Sassa, K.; Fukoka, H. Failure process and hydrologic response of a two layer physical model: Implications for rainfall-induced landslides. Geomorphology 2006, 73, 115–130. [Google Scholar] [CrossRef]
- Jian, B.T.; Lu, X.B.; Wang, S.Y.; Chen, X.Q.; Cui, P. The Movement of Fine Grains and Its Effects on the Landslide and Debris Flow Caused by Raining. Chin. J. Undergr. Space Eng. 2005, 1, 1014–1016. [Google Scholar]
- Senthilkumar, V.; Chandrasekaran, S.S.; Maji, V.B. Geotechnical characterization and analysis of rainfall-induced 2009 landslide at Marappalam area of Nilgiris district, Tamil Nadu state, India. Landslides 2017, 14, 1803–1814. [Google Scholar] [CrossRef]
- Uyeturk, C.E.; Huvaj, N.; Bayraktaroglu, H.; Huseyinpasaoglu, M. Geotechnical Characteristics of Residual Soils in Rainfall-Triggered Landslides in Rize, Turkey. Eng. Geol. 2020, 264, 105318. [Google Scholar] [CrossRef]
- Lam, L.; Fredlund, D.G.; Barbour, S.L. Transient seepage model for saturated–unsaturated soil systems: A geotechnical engineering approach. Can. Geotech. J. 1987, 24, 565–580. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Jeong, S.; Park, S.; Sharma, J. Influence of rainfall-induced wetting on the stability of slopes in weathered soils. Eng. Geol. 2004, 75, 251–262. [Google Scholar] [CrossRef]
- Fredlund, D.G. The emergence of unsaturated soil mechanics. Can. Geotech. J. 2014, 51, ix–x. [Google Scholar] [CrossRef]
- Qi, S.C.; Vanapalli, S.K. Simulating hydraulic and mechanical responses of unsaturated expansive soil slope to rainfall: Case study. Int. J. Geomech. 2018, 18, 05018002. [Google Scholar] [CrossRef]
- Shao, W.; Yang, Z.J.; Ni, J.J.; Su, Y.; Nie, W.; Mao, X.Y. Comparison of single- and dual-permeability models in simulating the unsaturated hydro-mechanical behavior in a rainfall-triggered landslide. Landslides 2018, 15, 2449–2464. [Google Scholar] [CrossRef]
- Rahardjo, H.; Kim, Y.; Satyanaga, A. Role of unsaturated soil mechanics in geotechnical engineering. Int. J. Geo-Eng. 2019, 10. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.X.; Li, T.C. Review and Forecast of Landslide Research in China; Sichuan Science and Technology Press: Chengdu, Sichuan, China, 1987. [Google Scholar]
- Bicocchi, G.; Tofani, V.; D’Ambrosio, M.; Tacconi-Stefanelli, C.; Vannocci, P.; Casagli, N.; Lavorini, G.; Trevisani, M.; Catani, F. Geotechnical and hydrological characterization of hillslope deposits for regional landslide prediction modeling. Bull. Eng. Geol. Environ. 2019, 78, 4875–4891. [Google Scholar] [CrossRef] [Green Version]
- Shuzui, H. Process of slip-surface development and formation of slip-surface clay in landslides in Tertiary volcanic rocks, Japan. Eng. Geol. 2001, 61, 199–220. [Google Scholar] [CrossRef]
- Guglielmi, Y.; Vengeon, J.M.; Bertrand, C.; Mudry, J.; Follacci, J.P.; Giraud, A. Hydrogeochemistry: An investigation tool to evaluate infiltration into large moving rock masses (case study of La Clapiere and Sechilienne alpine landslides). Bull. Eng. Geol. Environ. 2002, 61, 311–324. [Google Scholar] [CrossRef]
- Chigira, M.; Nakamoto, M.; Nakata, E. Weathering mechanisms and their effects on the landsliding of ignimbrite subject to vapor-phase crystallization in the Shirakawa pyroclastic flow, northern Japan. Eng. Geol. 2002, 66, 111–125. [Google Scholar] [CrossRef]
- Bogaard, T.; Guglielmi, Y.; Marc, V.; Emblanch, C.; Bertrand, C.; Mudry, J. Hydrogeochemistry in landslide research: A review. Bull. Soc. Geol. Fr. 2002, 178, 113–126. [Google Scholar] [CrossRef]
- Martins-Champina, B.; Huneau, F.; Fabre, R. The Eaux-Bonnes landslide (Western Pyrenees, France): Overview of possible triggering factors with emphasis on the role of groundwater. Environ. Geol. 2008, 55, 397–404. [Google Scholar] [CrossRef]
- Meehan, C.L.; Brandon, T.L.; Duncan, J.M.; Twari, B. Direct shear testing of polished slickensided surfaces. Landslides 2010, 7, 157–167. [Google Scholar] [CrossRef]
- Tang, W.; Yao, Z.B.; Li, S.J.; Sun, Q.C. Effect of pore water chemistry on physical and mechanical properties of sliding-zone soil: An experimental study. Rock Soil Mech. 2016, 37, 2885–2892. [Google Scholar] [CrossRef]
- Xue, Y.; Zhang, X.; Li, S.; Qiu, D.H.; Su, M.X.; Xu, Z.H.; Zhou, B.H.; Xia, T. Sensitivity analysis of loess stability to physical and mechanical properties: Assessment model. Int. J. Geomech. 2019, 19, 06019012. [Google Scholar] [CrossRef]
- Duan, Z.; Cheng, W.C.; Peng, J.B.; Wang, Q.Y.; Chen, W. Investigation into the triggering mechanism of loess landslides in the south Jingyang platform, Shaanxi province. Bull. Eng. Geol. Environ. 2019, 78, 4919–4930. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.T. Delay Failure Mechanism of Rainfall-Caused Shallow Landslide. Geotech. Geol. Eng. 2018, 36, 2293–2304. [Google Scholar] [CrossRef]
- Mingxin, Z.; Luming, Z.; Tao, F.; Weihong, L.; Xiangying, K. Stability Analysis of Unstable Permeability Field and Unsaturated Soil of Landslide. J. East China Jiaotong Univ. 2011, 28, 44–48. [Google Scholar]
- Jin, X.G.; Li, X.H.; Liu, X.R. Stress and Displacement Numerical Modeling of Bedding Bank Slope Including Weak Inter bed. J. Chongqing Univ. 2004, 27, 129–136. [Google Scholar]
- Chen, L.H.; Jin, X.G. Study on the applicability of three criteria for slope instability using finite element strength reduction method. China Civ. Eng. J. 2012, 45, 136–146. [Google Scholar]
- Wang, L.Q.; Yin, Y.P.; Zhang, Z.H.; Huang, B.L.; Wei, Y.J.; Zhao, P.; Hu, M.J. Stability analysis of the Xinlu Village landslide (Chongqing, China) and the influence of rainfall. Landslides 2019, 16, 1993–2004. [Google Scholar] [CrossRef]
- Tiande, M.; Chongwu, M.; Shengzhi, W. Evolution Model of Progressive Failure of Landslides. J. Geotech. Geoenviron. Eng. 1999, 125. [Google Scholar] [CrossRef]
- Yu, M.D. Analysis on stability of mountain mass and numerical calculation of landslide resistance based on strength reduction method. Arab. J. Geosci. 2020, 13, 617. [Google Scholar] [CrossRef]
- Castellanos, B.A.; Brandon, T.L.; VandenBerge, D.R. Use of fully softened shear strength in slope stability analysis. Landslide 2016, 13, 697–709. [Google Scholar] [CrossRef]
- Zou, Z.X.; Yan, J.B.; Tang, H.M.; Wang, S.; Xiong, C.R.; Hu, X.L. A shear constitutive model for describing the full process of the deformation and failure of slip zone soil. Eng. Geol. 2020, 267, 105766. [Google Scholar] [CrossRef]
- Xu, Q.; Tang, M.G.; Tu, K.X.; Huang, X.B. Research on space-time evolution laws and early warning-prediction of landslides. Chin. J. Rock Mech. Eng. 2008, 27, 1104–1112. [Google Scholar] [CrossRef]
- Tang, H.M.; Zou, Z.X.; Xiong, C.R.; Wu, Y.P.; Hu, X.L.; Wang, L.Q.; Lu, S.; Criss, R.E.; Li, C. An evolution model of large consequent bedding rockslides, with particular reference to the Jiweishan rockslide in Southwest China. Eng. Geol. 2015, 186, 17–27. [Google Scholar] [CrossRef]
- Guangrun, L.I.U.; Echuan, Y.A.N.; Cao, L.I.A.N. Discussion on classification of landslides. J. Eng. Geol. 2002, 10, 339–342. [Google Scholar]
- Yong, R. Interaction between Thrust Load Caused Landslide and Antislide Pile in Jurassic Strata in Three Gorges Reservoir Region. Ph.D. Thesis, China University of Geosciences, Wuhan, Hubei, China, 2014. [Google Scholar]
- Li, Y.Y. Research on Prediction and Forecast of Progressive Bank Landslide in the Three Gorges Reservoir. Ph.D. Thesis, China University of Geosciences, Wuhan, Hubei, China, 2010. [Google Scholar]
- Zheng, M.X. Research of strength characteristic of landslide slip and revised counter calculation method. Rock Soil Mech. 2003, 24, 528–532. [Google Scholar] [CrossRef]
- Xu, P.F. Study on Weakening Effect of Deformation Strength Parameters and Stability Evolution Law of Accumulation Landslide: A Case Study of Xintan Landslide. Master’s Thesis, Qingdao Technological University, Qingdao, Shandong, China, 2012. [Google Scholar]
- Zhang, J. Study on the Unload-Load Response Ratio of Debris Landslide and its Stability Evolution-Selecting Bazimen Landslide as the Example. Master’s Thesis, Qingdao Technological University, Qingdao, Shandong, China, 2011. [Google Scholar]
- Zhu, D.P. Revival Mechanism and Deformation Prediction of Typical Accumulative Landslide in the Three Gorges Reservoir. Ph.D. Thesis, China University of Geosciences, Wuhan, Hubei, China, 2010. [Google Scholar]
- Zou, Z.X.; Tang, H.M.; Xiong, C.G.; Wu, Y.; Liao, S. Geomechanical model of progressive failure for large consequent bedding rockslide and its stability analysis. Chin. J. Rock Mech. Eng. 2012, 31, 2222–2232. [Google Scholar] [CrossRef]
- Chen, Q.J.; Wang, Q.C. Optimization calculation of design thrust for landslide. J. Zhejiang Univ. Eng. Sci. 2018, 52, 1320–1328. [Google Scholar]
- Li, Y. Study on Deformation Mechanism of DanBo Deposits in Front of Dam of Yangfanggou Hydropower Station on Yalong River. Mater’s Thesis, Chengdu University of Technology, Chengdu, Sichuan, China, 2019. [Google Scholar] [CrossRef]
- Zhou, Z.; Shen, J.H.; Shu, J.C.; Duan, W.F.; Yang, R.C.; Li, Y. Predictive and Early Warning Study on Deformation of Deposit Ahead of Dam of a Hydropower Station in Southwest China. J. Chengdu Univ. Technol. Sci. Technol. Ed. 2020, 47, 481–491. [Google Scholar] [CrossRef]
- Binghui, S.; Wenwu, C.; Weijiang, W. Experimental study of large scale direct shear test of sliding zone soil of Suoertou landslide with different moisture contents. Rock Soil Mech. 2012, 33, 77–84. [Google Scholar] [CrossRef]
- Wang, Z.M.; Jiang, G.L.; Wei, Y.X. Experimental research on parameters of Duncan-Chang model for mud-stone. Subgrade Eng. 2009, 28, 52–54. [Google Scholar] [CrossRef]
- Qin, S.Q.; Wang, Y.Y.; Ma, P. Exponential laws of critical displacement evolution for landslides and avalanches. Chin. J. Rock Mech. Eng. 2010, 29, 873–880. [Google Scholar] [CrossRef]













| Steep Upper Sliding Zone Soil | Shallow Lower Sliding Zone Soil | ||||||
|---|---|---|---|---|---|---|---|
| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
| 0.44 | 10 | 0.45 | 10 | ||||
| 0.23 | 8.66 | 0.05 | 9.14 | ||||
| 0.56 | 30 | 0.55 | 24 | ||||
| 2.2 | 2.08 | 2.3 | 2.08 | ||||
| 0.9 | 2.4 | 0.9 | 2.4 | ||||
| 3 | 2360 | 3 | 2260 | ||||
| 0.7 | 60 | 0.7 | 113 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Shen, J.; Tang, S.; Duan, W.; Wang, J.; Yang, R.; Zheng, S.; Guo, F. Analysis of Weakening Law and Stability of Sliding Zone Soil in Thrust-Load-Induced Accumulation Landslides Triggered by Rainfall Infiltration. Water 2021, 13, 466. https://doi.org/10.3390/w13040466
Zhou Z, Shen J, Tang S, Duan W, Wang J, Yang R, Zheng S, Guo F. Analysis of Weakening Law and Stability of Sliding Zone Soil in Thrust-Load-Induced Accumulation Landslides Triggered by Rainfall Infiltration. Water. 2021; 13(4):466. https://doi.org/10.3390/w13040466
Chicago/Turabian StyleZhou, Zhou, Junhui Shen, Song Tang, Weifeng Duan, Jingyong Wang, Richang Yang, Shengzhe Zheng, and Fulin Guo. 2021. "Analysis of Weakening Law and Stability of Sliding Zone Soil in Thrust-Load-Induced Accumulation Landslides Triggered by Rainfall Infiltration" Water 13, no. 4: 466. https://doi.org/10.3390/w13040466
APA StyleZhou, Z., Shen, J., Tang, S., Duan, W., Wang, J., Yang, R., Zheng, S., & Guo, F. (2021). Analysis of Weakening Law and Stability of Sliding Zone Soil in Thrust-Load-Induced Accumulation Landslides Triggered by Rainfall Infiltration. Water, 13(4), 466. https://doi.org/10.3390/w13040466







