Trend Analyses of Baseflow and BFI for Undisturbed Watersheds in Michigan—Constraints from Multi-Objective Optimization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Datasets
2.2. MOO Modeling of Baseflow
2.2.1. Conceptual Approach
2.2.2. MOO Algorithm
2.2.3. MOO Performance Evaluation
2.3. Mann–Kendall Trend Analysis
2.3.1. Conventional MK Test
2.3.2. Modified MK Test
3. Results and Discussion
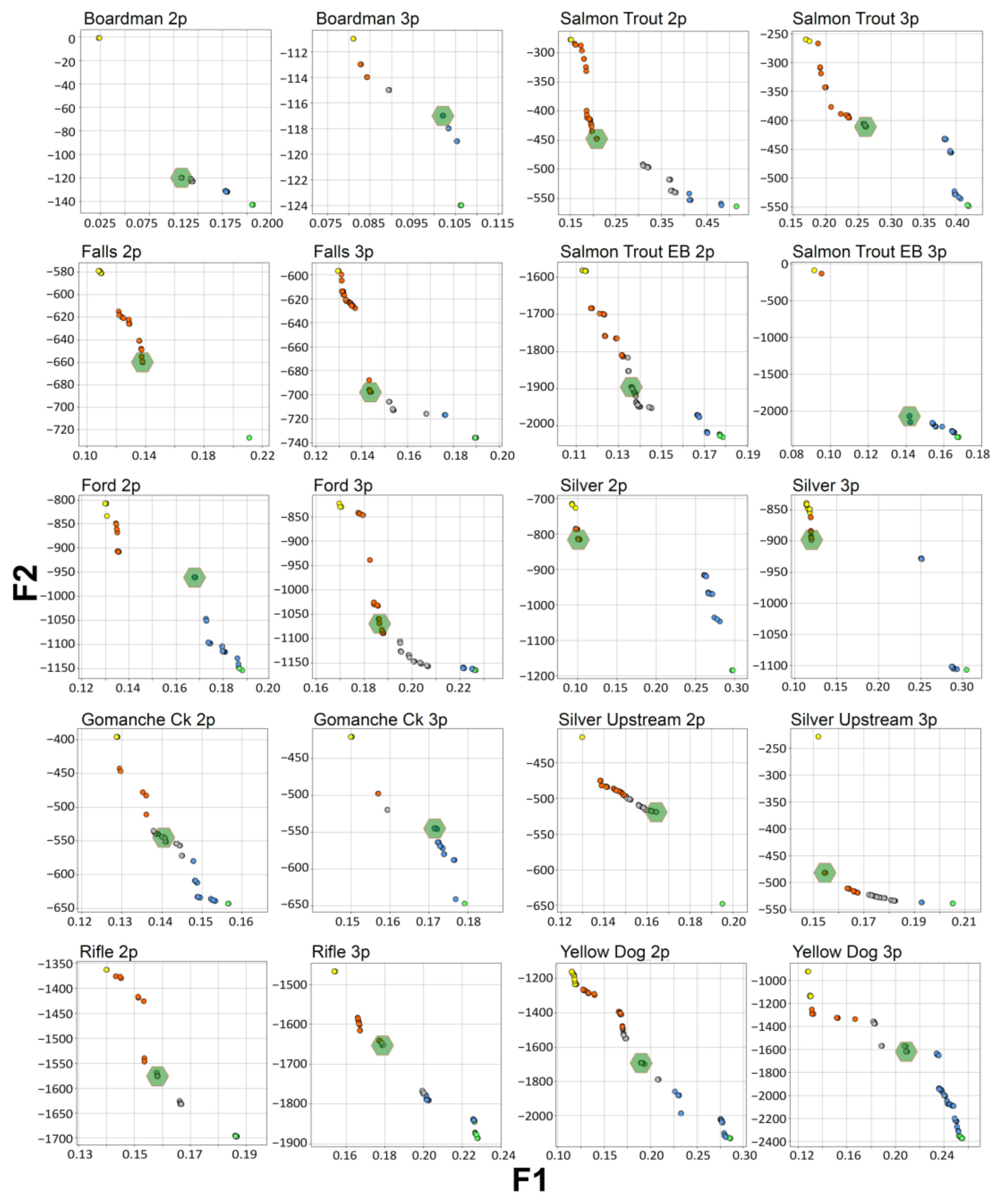
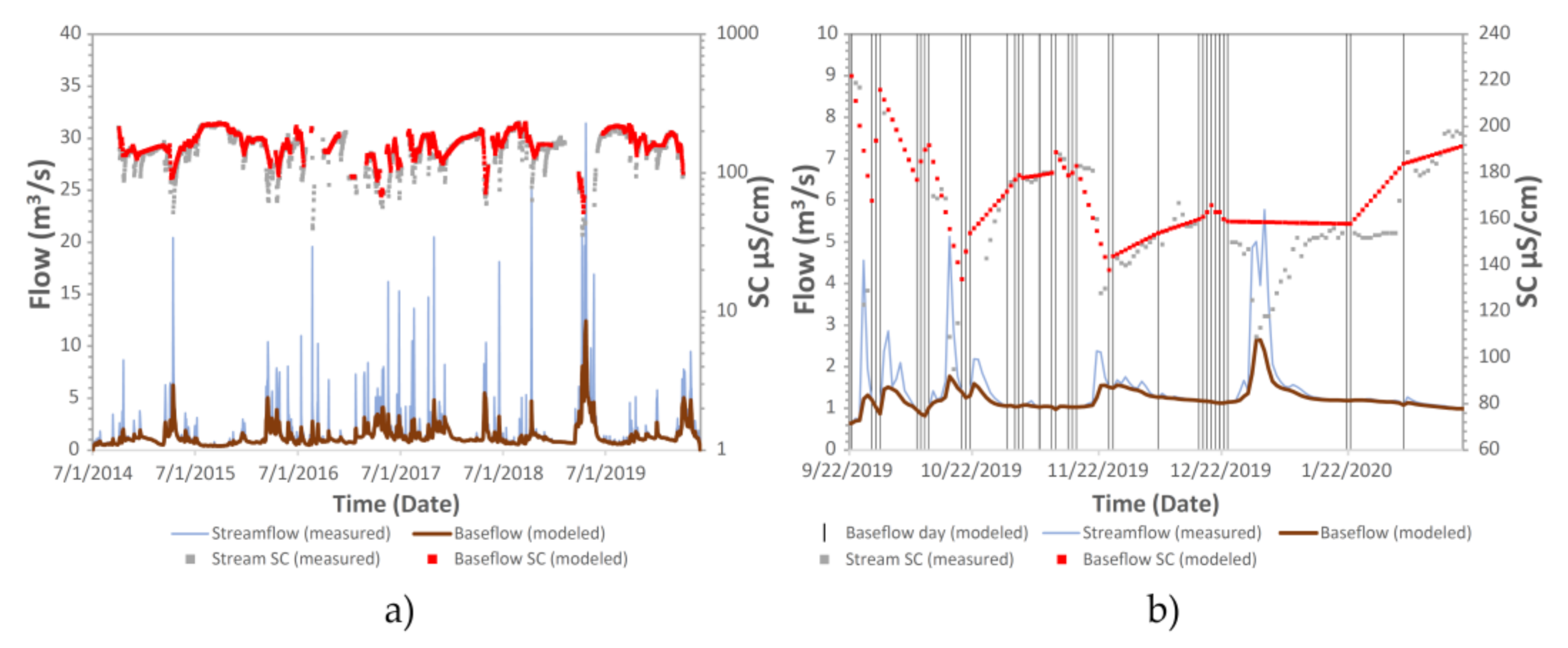
3.1. Baseflow Results
3.2. Autocorrelation Results
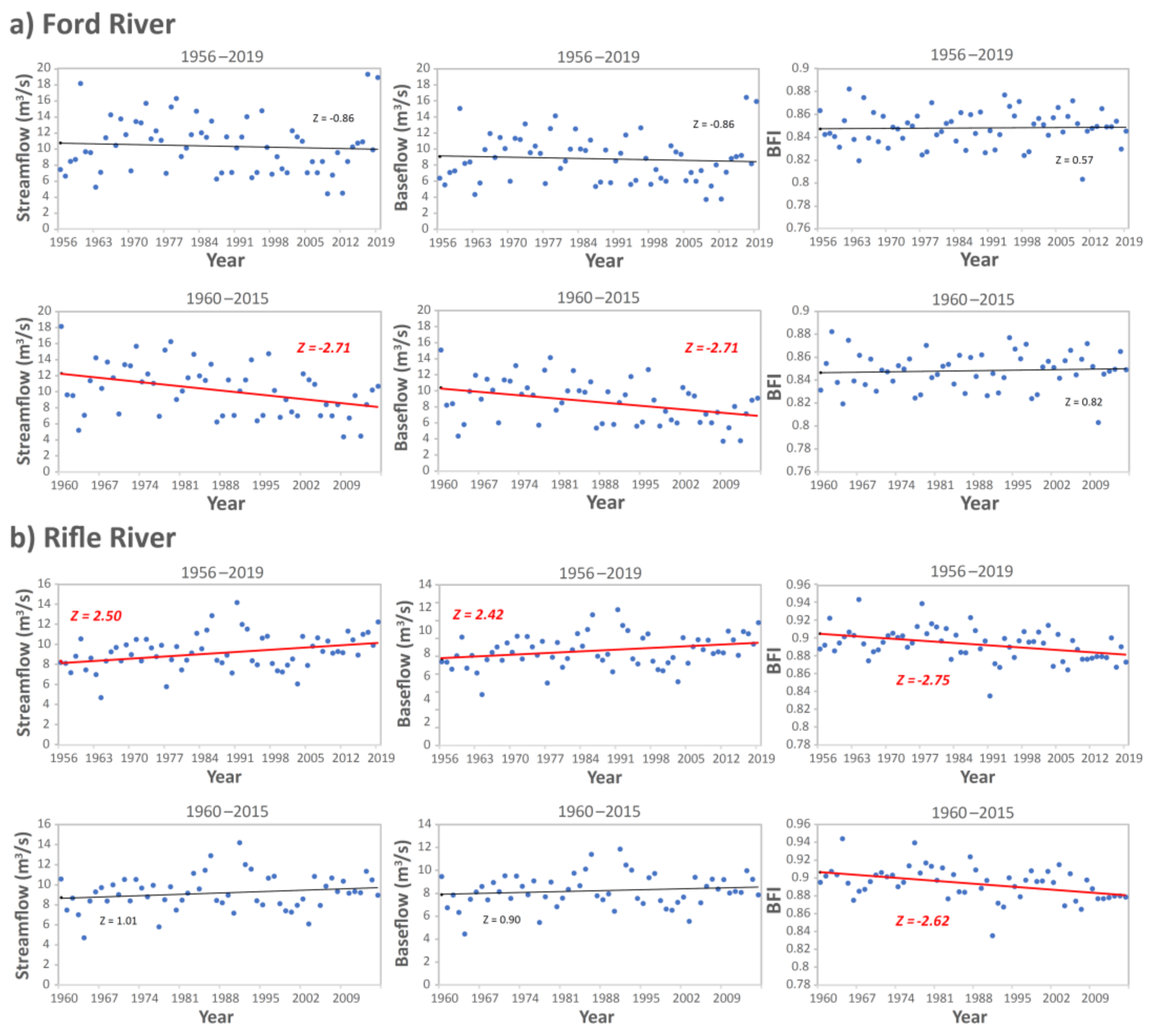
3.3. MK Test Results
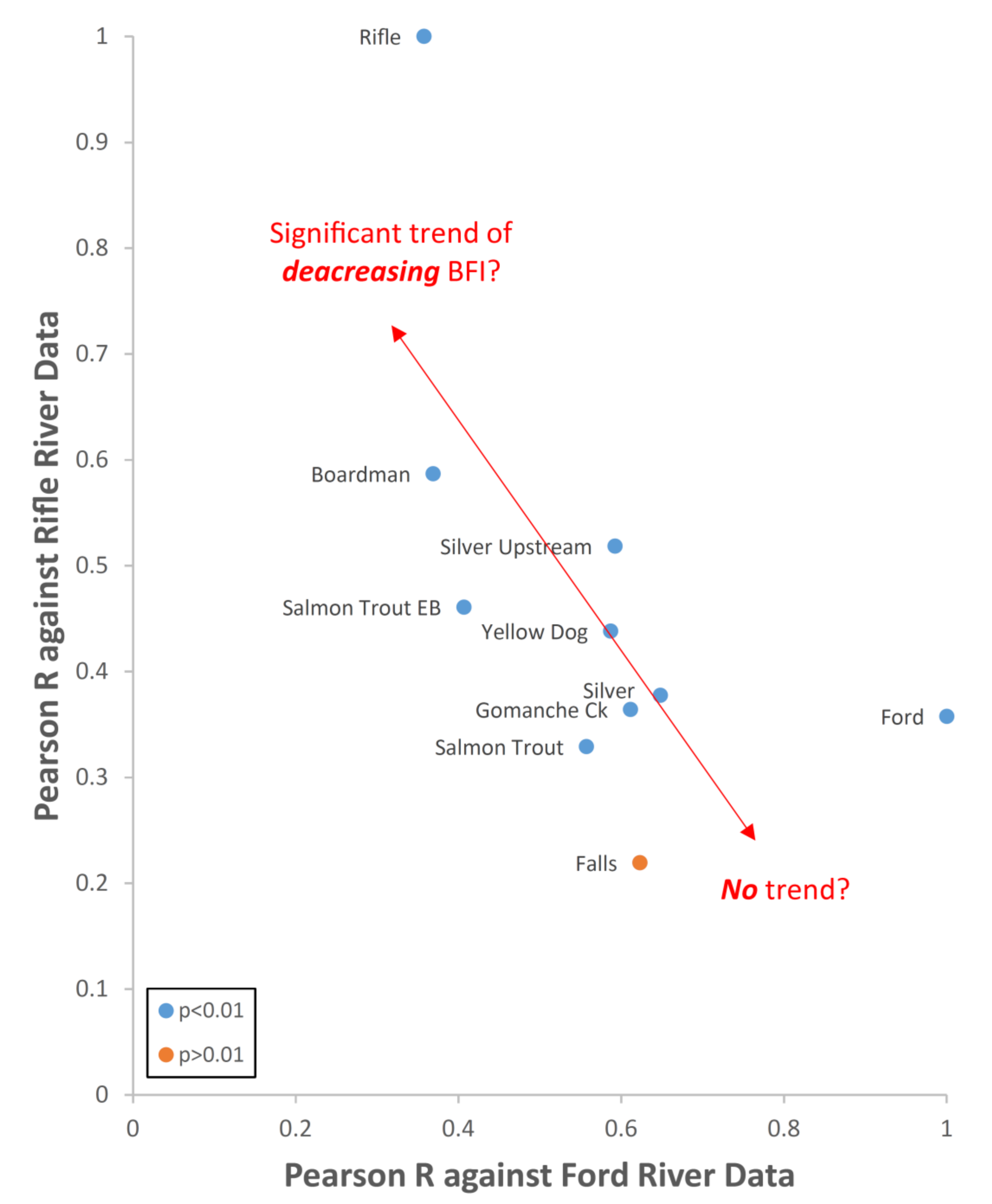
3.4. Transferability of Results
4. Conclusions and Implications
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- U.S. Global Change Research Program. Fourth National Climate Assessment Chapter 21: Midwest. Available online: https://nca2018.globalchange.gov/chapter/21 (accessed on 22 September 2020).
- Wuebbles, D.; Cardinale, B.; Cherkauer, K.; Davidson-Arnott, R.; Hellmann, J.; Infante, D.; Johnson, L.; de Loë, R.; Lofgren, B.; Packman, A.; et al. An Assessment of the Impacts of Climate Change on the Great Lakes by Scientists and Experts from Universities and Institutions in the Great Lakes Region; Environmental Law & Policy Center: Chicago, IL, USA, 2019; p. 74. [Google Scholar]
- Christiansen, D.E.; Walker, J.F.; Hunt, R.J. Basin-Scale Simulation of Current and Potential Climate Changed Hydrologic Conditions in the Lake Michigan Basin, United States; Scientific Investigations Report; U.S. Geological Survey: Reston VA, USA, 2014; p. 86. [Google Scholar]
- Markstrom, S.L.; Hay, L.E.; Ward-Garrison, D.C.; Risley, J.C.; Battaglin, W.A.; Bjerklie, D.M.; Chase, K.J.; Christiansen, D.E.; Dudley, R.W.; Hunt, R.J.; et al. Integrated Watershed-Scale Response to Climate Change for Selected Basins across the United States; Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2012; p. 153. [Google Scholar]
- Norton, P.A.; Driscoll, D.G.; Carter, J.M. Climate, Streamflow, and Lake-Level Trends in the Great Lakes Basin of the United States and Canada, Water Years 1960–2015; Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2019; p. 58. [Google Scholar]
- Gebert, W.A.; Walker, J.F.; Kennedy, J.L. Estimating 1970-99 Average Annual Groundwater Recharge in Wisconsin Using Streamflow Data; Open-File Report; U.S. Geological Survey: Reston, VA, USA, 2011. [Google Scholar]
- Neff, B.P.; Day, S.M.; Piggott, A.R.; Fuller, L.M. Base Flow in the Great Lakes Basin; Scientific Investigations Report; U.S. Geological Suvey: Reston, VA, USA, 2005. [Google Scholar]
- Hodgkins, G.A.; Dudley, R.W.; Aichele, S.S. Historical Changes in Precipitation and Streamflow in the U.S. Great Lakes Basin, 1915–2004; Scientific Investigations Report; Geological Survey (U.S.): Reston, VA, USA, 2007. [Google Scholar]
- Croley, T.; Luukkonen, C. Potential Effects of Climate Change on Ground Water in Lansing, Michigan. JAWRA J. Am. Water Resour. Assoc. 2007, 39, 149–163. [Google Scholar] [CrossRef]
- Gronewold, A.D.; Rood, R.B. Recent Water Level Changes across Earth’s Largest Lake System and Implications for Future Variability. J. Gt. Lakes Res. 2019, 45, 1–3. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Song, J.; Cheng, L. Evaluating Relative Merits of Four Baseflow Separation Methods in Eastern Australia. J. Hydrol. 2017, 549, 252–263. [Google Scholar] [CrossRef]
- Shao, G.; Zhang, D.; Guan, Y.; Sadat, M.A.; Huang, F. Application of Different Separation Methods to Investigate the Baseflow Characteristics of a Semi-Arid Sandy Area, Northwestern China. Water 2020, 12, 434. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Ahiablame, L.; Engel, B.; Liu, J. Regression Modeling of Baseflow and Baseflow Index for Michigan USA. Water 2013, 5, 1797–1815. [Google Scholar] [CrossRef] [Green Version]
- Ahiablame, L.; Chaubey, I.; Engel, B.; Cherkauer, K.; Merwade, V. Estimation of Annual Baseflow at Ungauged Sites in Indiana USA. J. Hydrol. 2013, 476, 13–27. [Google Scholar] [CrossRef]
- Beatty, S.J.; Morgan, D.L.; McAleer, F.J.; Ramsay, A.R. Groundwater Contribution to Baseflow Maintains Habitat Connectivity for Tandanus Bostocki (Teleostei: Plotosidae) in a South-Western Australian River. Ecol. Freshw. Fish 2010, 19, 595–608. [Google Scholar] [CrossRef]
- Boutt, D.F.; Hyndman, D.W.; Pijanowski, B.C.; Long, D.T. Identifying Potential Land Use-Derived Solute Sources to Stream Baseflow Using Ground Water Models and GIS. Groundwater 2001, 39, 24–34. [Google Scholar] [CrossRef]
- Choi, B.; Kang, H.; Lee, W.H. Baseflow Contribution to Streamflow and Aquatic Habitats Using Physical Habitat Simulations. Water 2018, 10, 1304. [Google Scholar] [CrossRef] [Green Version]
- McCallum, J.L.; Cook, P.G.; Brunner, P.; Berhane, D. Solute Dynamics during Bank Storage Flows and Implications for Chemical Base Flow Separation. Water Resour. Res. 2010, 46, W07541. [Google Scholar] [CrossRef] [Green Version]
- Murray, B.; Zeppel, M.; Hose, G.; Eamus, D. Groundwater-Dependent Ecosystems in Australia: It’s More than Just Water for Rivers. Ecol. Manag. Restor. 2008, 4, 110–113. [Google Scholar] [CrossRef]
- Power, G.; Brown, R.S.; Imhof, J.G. Groundwater and Fish—Insights from Northern North America. Hydrol. Process. 1999, 13, 401–422. [Google Scholar] [CrossRef]
- Reichard, J.S.; Brown, C.M. Detecting Groundwater Contamination of a River in Georgia, USA Using Baseflow Sampling. Hydrogeol. J. 2009, 17, 735–747. [Google Scholar] [CrossRef]
- Malcolm, I.A.; Soulsby, C.; Youngson, A.F.; Hannah, D.M.; McLaren, I.S.; Thorne, A. Hydrological Influences on Hyporheic Water Quality: Implications for Salmon Egg Survival. Hydrol. Process. 2004, 18, 1543–1560. [Google Scholar] [CrossRef]
- Combalicer, E.; Lee, S.-K.; Ahn, S.; Kim, D.; Im, S. Comparing Groundwater Recharge and Base Flow in the Bukmoongol Small-Forested Watershed, Korea. J. Earth Syst. Sci. 2008, 117, 553–566. [Google Scholar] [CrossRef] [Green Version]
- Arnold, J.G.; Muttiah, R.S.; Srinivasan, R.; Allen, P.M. Regional Estimation of Base Flow and Groundwater Recharge in the Upper Mississippi River Basin. J. Hydrol. 2000, 227, 21–40. [Google Scholar] [CrossRef]
- Nielsen, M.G.; Westenbroek, S.M. Groundwater Recharge Estimates for Maine Using a Soil-Water-Balance Model—25-Year Average, Range, and Uncertainty, 1999 to 2015; Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2019; p. 68. [Google Scholar]
- Zomlot, Z.; Verbeiren, B.; Huysmans, M.; Batelaan, O. Spatial Distribution of Groundwater Recharge and Base Flow: Assessment of Controlling Factors. J. Hydrol. Reg. Stud. 2015, 4, 349–368. [Google Scholar] [CrossRef] [Green Version]
- Sloto, R.A.; Crouse, M.Y. HYSEP: A Computer Program for Streamflow Hydrograph Separation and Analysis: U.S. Geological Survey Water-Resources Investigations Report 96–4040; U.S. Geological Survey: Reston, VA, USA, 1996; p. 46. [Google Scholar]
- Aksoy, H.; Kurt, I.; Eris, E. Filtered Smoothed Minima Baseflow Separation Method. J. Hydrol. 2009, 372, 94–101. [Google Scholar] [CrossRef]
- Wahl, K.L.; Wahl, T.L. Determining the Flow of Comal Springs at New Braunfels, Texas; Texas Water ’95; American Society of Civil Engineers: San Antonio, TX, USA, 1995; pp. 77–86. [Google Scholar]
- Rammal, M.; Archambeau, P.; Erpicum, S.; Orban, P.; Brouyère, S.; Pirotton, M.; Dewals, B. Technical Note: An Operational Implementation of Recursive Digital Filter for Base Flow Separation. Water Resour. Res. 2018, 54, 8528–8540. [Google Scholar] [CrossRef]
- Rorabaugh, M.I. Estimating Changes in Bank Storage and Ground-Water Contribution to Streamflow. Int. Assoc. Sci. Hydrol. 1964, 63, 432–441. [Google Scholar]
- Cartwright, I.; Gilfedder, B.; Hofmann, H. Contrasts between Estimates of Baseflow Help Discern Multiple Sources of Water Contributing to Rivers. Hydrol. Earth Syst. Sci. 2014, 18, 15–30. [Google Scholar] [CrossRef] [Green Version]
- Miller, M.P.; Susong, D.D.; Shope, C.L.; Heilweil, V.M.; Stolp, B.J. Continuous Estimation of Baseflow in Snowmelt-Dominated Streams and Rivers in the Upper Colorado River Basin: A Chemical Hydrograph Separation Approach. Water Resour. Res. 2014, 50, 6986–6999. [Google Scholar] [CrossRef]
- Ladson, A.R.; Brown, R.; Neal, B.; Nathan, R. A Standard Approach to Baseflow Separation Using The Lyne and Hollick Filter. Australas. J. Water Resour. 2013, 17, 25–34. [Google Scholar] [CrossRef]
- Nathan, R.J.; McMahon, T.A. Evaluation of Automated Techniques for Base Flow and Recession Analyses. Water Resour. Res. 1990, 26, 1465–1473. [Google Scholar] [CrossRef]
- Eckhardt, K. A Comparison of Baseflow Indices, Which Were Calculated with Seven Different Baseflow Separation Methods. J. Hydrol. 2008, 352, 168–173. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Muttiah, R.; Bernhardt, G. Automated Base Flow Separation and Recession Analysis Techniques. Groundwater 1995, 33, 1010–1018. [Google Scholar] [CrossRef]
- Rutledge, A.T. Computer Programs for Describing the Recession of Ground-Water Discharge and for Estimating Mean Ground-Water Recharge and Discharge from Streamflow Records-Update; Water-Resources Investigations Report; U.S. Geological Survey: Reston, VA, USA, 1998. [Google Scholar]
- Hagedorn, B. Hydrograph Separation through Multi Objective Optimization: Revealing the Importance of a Temporally and Spatially Constrained Baseflow Solute Source. J. Hydrol. 2020, 125349. [Google Scholar] [CrossRef]
- Rapp, G.; Liukkonen, B.W.; Allert, J.D.; Sorensen, J.A.; Glass, G.E.; Loucks, O.L. Geologic and Atmospheric Input Factors Affecting Watershed Chemistry in Upper Michigan. Environ. Geol. Water Sci. 1987, 9, 155–171. [Google Scholar] [CrossRef]
- USGS Water Data for the Nation. Available online: http://Waterdata.Usgs.Gov/Nwis (accessed on 8 December 2020).
- UM University of Michigan. Bedrock Geology of Michigan | U-M LSA Earth and Environmental Sciences. Available online: https://lsa.umich.edu/earth/community-engagement/downloadable-resources/bedrock-geology-of-michigan.html (accessed on 8 February 2021).
- Hagedorn, B.; Whittier, R.B. Solute Sources and Water Mixing in a Flashy Mountainous Stream (Pahsimeroi River, U.S. Rocky Mountains): Implications on Chemical Weathering Rate and Groundwater–Surface Water Interaction. Chem. Geol. 2015, 391, 123–137. [Google Scholar] [CrossRef]
- Harrington, G.A.; Herzceg, A.L. The Importance of Silicate Weathering of a Sedimentary Aquifer in Central Australia Indicated by Very High Sr-87/Sr-86 Ratios. Chem. Geol. 2003, 199, 281–292. [Google Scholar] [CrossRef]
- Lyne, V.; Hollick, M. Stochastic Time-Variable Rainfall-Runoff Modelling; Hydrology and Water Resources Symposium; Institution of Engineers: Perth, Australia, 1979. [Google Scholar]
- Ritter, A.; Muñoz-Carpena, R. Performance Evaluation of Hydrological Models: Statistical Significance for Reducing Subjectivity in Goodness-of-Fit Assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Khalil, B. Using Discrete Wavelet Transforms to Analyze Trends in Streamflow and Precipitation in Quebec and Ontario (1954–2008). J. Hydrol. 2012, 475, 204–228. [Google Scholar] [CrossRef]
- Chen, Y.; Guan, Y.; Shao, G.; Zhang, D. Investigating Trends in Streamflow and Precipitation in Huangfuchuan Basin with Wavelet Analysis and the Mann-Kendall Test. Water 2016, 8, 77. [Google Scholar] [CrossRef] [Green Version]
- Schlüter, M. Mixed Integer Distributed Ant Colony Optimization (MIDACO)-Solver. User Manual. Available online: http://midaco-solver.com/ (accessed on 10 February 2020).
- Blum, C. Ant Colony Optimization: Introduction and Recent Trends. Phys. Life Rev. 2005, 2, 353–373. [Google Scholar] [CrossRef] [Green Version]
- Socha, K.; Dorigo, M. Ant Colony Optimization for Continuous Domains. Eur. J. Oper. Res. 2008. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Srinivas, N.; Deb, K. Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Lenz, M.; Jöst, D.; Thiel, F.; Pischinger, S.; Sauer, D.U. Identification of Load Dependent Cell Voltage Model Parameters from Sparse Input Data Using the Mixed Integer Distributed Ant Colony Optimization Solver. J. Power Sources 2019, 437, 226880. [Google Scholar] [CrossRef]
- Zobaa, A.F. Mixed-Integer Distributed Ant Colony Multi-Objective Optimization of Single-Tuned Passive Harmonic Filter Parameters. IEEE Access 2019, 7, 44862–44870. [Google Scholar] [CrossRef]
- Schlueter, M. MIDACO Software Performance on Interplanetary Trajectory Benchmarks. Adv. Space Res. 2014, 54, 744–754. [Google Scholar] [CrossRef]
- Schlueter, M.; Erb, S.O.; Gerdts, M.; Kemble, S.; Rückmann, J.-J. MIDACO on MINLP Space Applications. Adv. Space Res. 2013, 51, 1116–1131. [Google Scholar] [CrossRef]
- Schlueter, M.; Yam, C.H.; Watanabe, T.; Oyama, A. Parallelization Impact on Many-Objective Optimization for Space Trajectory Design. Int. J. Mach. Learn. Comput. 2016, 6, 9. [Google Scholar]
- Wang, Z.; Rangaiah, G.P. Application and Analysis of Methods for Selecting an Optimal Solution from the Pareto-Optimal Front Obtained by Multiobjective Optimization. Ind. Eng. Chem. Res. 2017, 56, 560–574. [Google Scholar] [CrossRef]
- Coello, C.A. Multi-objective optimization. In Handbook of Heuristics; John Wiley & Sons: Hoboken, NJ, USA, 2018; pp. 177–204. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2001; ISBN 978-0-471-87339-6. [Google Scholar]
- Spongberg, M.E. Spectral Analysis of Base Flow Separation with Digital Filters. Water Resour. Res. 2000, 36, 745–752. [Google Scholar] [CrossRef]
- Li, L.; Maier, H.R.; Partington, D.; Lambert, M.F.; Simmons, C.T. Performance Assessment and Improvement of Recursive Digital Baseflow Filters for Catchments with Different Physical Characteristics and Hydrological Inputs. Environ. Model. Softw. 2014, 54, 39–52. [Google Scholar] [CrossRef]
- Li, L.; Maier, H.R.; Lambert, M.F.; Simmons, C.T.; Partington, D. Framework for Assessing and Improving the Performance of Recursive Digital Filters for Baseflow Estimation with Application to the Lyne and Hollick Filter. Environ. Model. Softw. 2013, 41, 163–175. [Google Scholar] [CrossRef] [Green Version]
- Hirsch, R.M.; Slack, J.R. A Nonparametric Trend Test for Seasonal Data With Serial Dependence. Water Resour. Res. 1984, 20, 727–732. [Google Scholar] [CrossRef] [Green Version]
- Adamowski, K.; Bougadis, J. Detection of Trends in Annual Extreme Rainfall. Hydrol. Process. 2003, 17, 3547–3560. [Google Scholar] [CrossRef]
- Yagbasan, O.; Demir, V.; Yazicigil, H. Trend Analyses of Meteorological Variables and Lake Levels for Two Shallow Lakes in Central Turkey. Water 2020, 12, 414. [Google Scholar] [CrossRef] [Green Version]
- Cohn, T.A.; Lins, H.F. Nature’s Style: Naturally Trendy. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Spooner, J.; Harcum, J.B.; Meals, D.W.; Dressing, S.A.; Richards, R.P. Chapter 7 Data Analysis. In Monitoring and Evaluating Nonpoint Source Watershed Projects - Monitoring Guide; U.S. Environmental Protection Agency: Washington, DC, USA, 2016; 118p. [Google Scholar]
- Ljung, G.; Box, G. On a Measure of Lack of Fit in Time Series Models. Biometrika 1978, 65. [Google Scholar] [CrossRef]
- Patakamuri, S.K.; O’Brien, N. Modifiedmk: Modified Versions of Mann Kendall and Spearman’s Rho Trend Tests. Available online: https://CRAN.R-project.org/package=modifiedmk (accessed on 4 July 2020).
- Hamed, K.H.; Rao, A.R. A Modified Mann-Kendall Trend Test for Autocorrelated Data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The Mann-Kendall Test Modified by Effective Sample Size to Detect Trend in Serially Correlated Hydrological Series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Mirabbasi, R.; Jhajharia, D.; Abianeh, H.Z.; Mostafaeipour, A. Effect of Short-Term and Long-Term Persistence on Identification of Temporal Trends. J. Hydrol. Eng. 2014, 19, 617–625. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend Detection in Hydrologic Data: The Mann–Kendall Trend Test under the Scaling Hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Gachon, P.; Sushama, L.; St-Hilaire, A. Identification of Hydrological Trends in the Presence of Serial and Cross Correlations: A Review of Selected Methods and Their Application to Annual Flow Regimes of Canadian Rivers. J. Hydrol. 2009, 368, 117–130. [Google Scholar] [CrossRef]
- Önöz, B.; Bayazit, M. Block Bootstrap for Mann–Kendall Trend Test of Serially Dependent Data. Hydrol. Process. 2012, 26, 3552–3560. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The Influence of Autocorrelation on the Ability to Detect Trend in Hydrological Series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Hamed, K.H. Enhancing the Effectiveness of Prewhitening in Trend Analysis of Hydrologic Data. J. Hydrol. 2009, 368, 143–155. [Google Scholar] [CrossRef]
- Svensson, C.; Kundzewicz, W.Z.; Maurer, T. Trend Detection in River Flow Series: 2. Flood and Low-Flow Index Series / Détection de Tendance Dans Des Séries de Débit Fluvial: 2. Séries d’indices de Crue et d’étiage. Hydrol. Sci. J. 2005, 50, 811–824. [Google Scholar] [CrossRef] [Green Version]
- Huntington, J.L.; Niswonger, R.G. Role of Surface-Water and Groundwater Interactions on Projected Summertime Streamflow in Snow Dominated Regions: An Integrated Modeling Approach. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- MDEGLE Base Flow of Michigan Streams—Michigan Department of Environment, Great Lakes and Eneregy. Available online: http://gis-michigan.opendata.arcgis.com/datasets/base-flow-of-michigan-streams (accessed on 29 August 2020).
- Chiaudani, A.; Di Curzio, D.; Palmucci, W.; Pasculli, A.; Polemio, M.; Rusi, S. Statistical and Fractal Approaches on Long Time-Series to Surface-Water/Groundwater Relationship Assessment: A Central Italy Alluvial Plain Case Study. Water 2017, 9, 850. [Google Scholar] [CrossRef] [Green Version]
- Dudley, R.; Hodgkins, G.; McHale, M.R.; Kolian, M.; Renard, B. Trends in Snowmelt-Related Streamflow Timing in the Conterminous United States. J. Hydrol. 2017. [Google Scholar] [CrossRef] [Green Version]
- Suriano, Z.; Robinson, D.; Leathers, D. Changing Snow Depth in the Great Lakes Basin: Implications and Trend. Anthropocene 2019, 26. [Google Scholar] [CrossRef]
- Xu, Y.-P.; Pan, S.; Fu, G.; Tian, Y.; Zhang, X. Future Potential Evapotranspiration Changes and Contribution Analysis in Zhejiang Province, East China. J. Geophys. Res. Atmospheres 2014, 119, 2174–2192. [Google Scholar] [CrossRef] [Green Version]
- Bai, X.; Wang, J. Atmospheric Teleconnection Patterns Associated with Severe and Mild Ice Cover on the Great Lakes, 1963–2011. Water Qual. Res. J. 2012, 47, 421–435. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Tian, L.; Wang, L.; Yu, W.; Qu, D. River Recharge Sources and the Partitioning of Catchment Evapotranspiration Fluxes as Revealed by Stable Isotope Signals in a Typical High-Elevation Arid Catchment. J. Hydrol. 2017, 549, 616–630. [Google Scholar] [CrossRef]
- Haiyan, C.; Yaning, C.; Weihong, L.; Xinming, H.; Yupeng, L.; Qifei, Z. Identifying Evaporation Fractionation and Streamflow Components Based on Stable Isotopes in the Kaidu River Basin with Mountain–Oasis System in North-West China. Hydrol. Process. 2018, 32, 2423–2434. [Google Scholar] [CrossRef]
- Simpson, H.J.; Herczeg, A.L. Salinity and Evaporation in the River Murray Basin, Australia. J. Hydrol. 1991, 124, 1–27. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources—Hydrologic Analysis and Interpretation: Techniques of Water-Resources Investigations of the U.S. Geological Survey, Chap. A3, Book 4; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Betterle, A.; Radny, D.; Schirmer, M.; Botter, G. What Do They Have in Common? Drivers of Streamflow Spatial Correlation and Prediction of Flow Regimes in Ungauged Locations. Water Resour. Res. 2017, 53, 10354–10373. [Google Scholar] [CrossRef] [Green Version]
- Partington, D.; Brunner, P.; Simmons, C.T.; Werner, A.D.; Therrien, R.; Maier, H.R.; Dandy, G.C. Evaluation of Outputs from Automated Baseflow Separation Methods against Simulated Baseflow from a Physically Based, Surface Water-Groundwater Flow Model. J. Hydrol. 2012, 458–459, 28–39. [Google Scholar] [CrossRef] [Green Version]
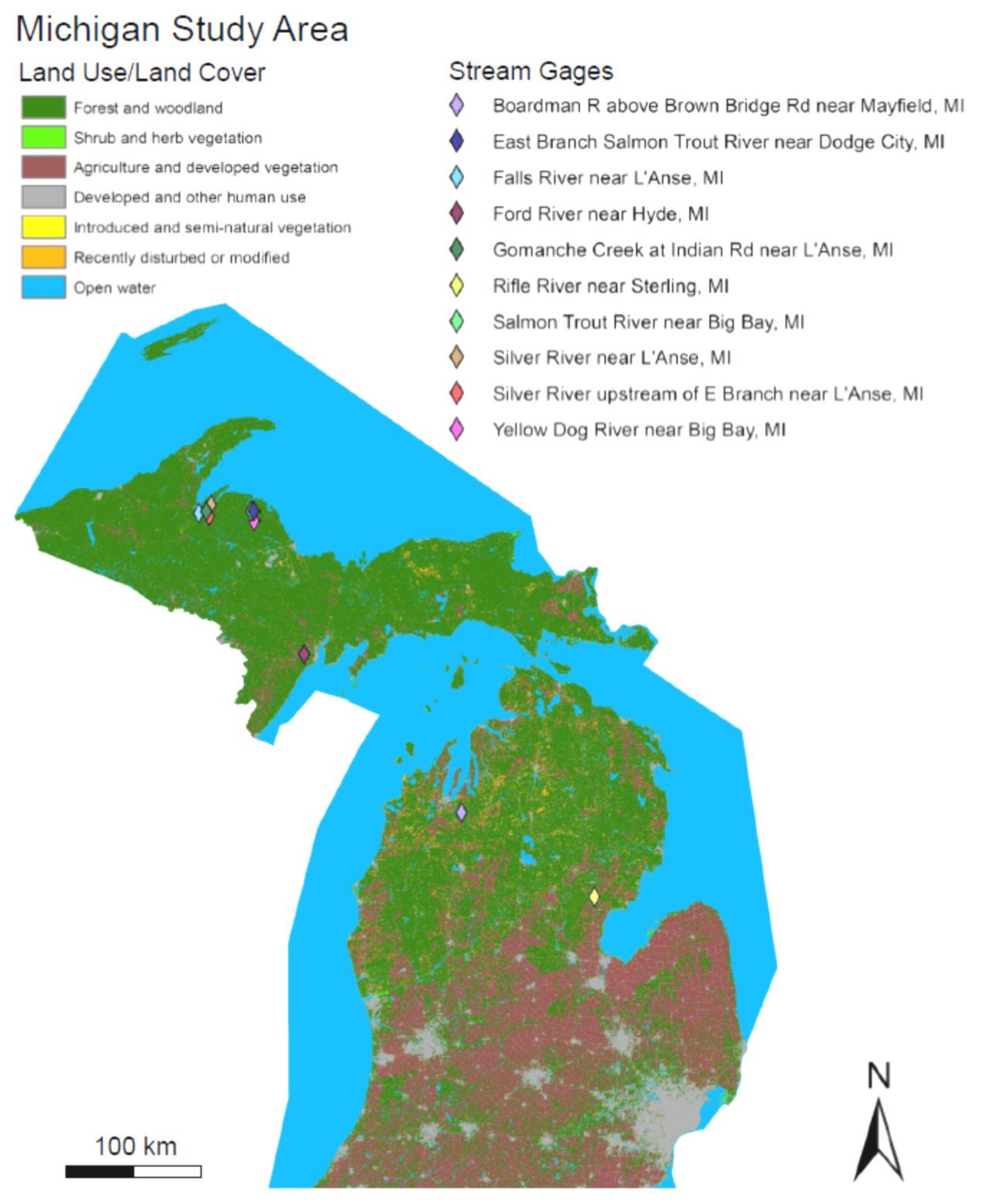



| USGS Gage ID | Lat. | Long. | Streamflow Record | Stream SC Record | Missing Data Streamflow (%) | Missing Data SC (%) |
|---|---|---|---|---|---|---|
| Boardman R above Brown Bridge Road near Mayfield | 44°39’24” | 85°26’12” | 1997-09-10–current | 1997-11-05–1998-09-30 | 0 | 9.09 |
| Falls River near L’Anse | 46°44’05” | 88°26’35” | 2014-07-01–current | 2014-09-30–2020-03-03 | 0 | 14.5 |
| Ford River near Hyde | 45°45’18” | 87°12’07” | 1954-10-01–current | 1975-09-24–current | 0 | 29.8 a |
| Gomanche Creek at Indian Road near L’Anse | 46°45’04” | 88°21’42” | 2007-10-01–2013-09-29 | 2007-10-01–2013-09-29 | 0 | 35.9 |
| Rifle River near Sterling | 44°04’21” | 84°01’12” | 1937-01-13–current | 1975-08-28–current | 0 | 12.4 b |
| Salmon Trout River near Big Bay | 46°46’56” | 87°52’39” | 2004-12-01–current | 2004-12-01–2020-07-29 | 0 | 13.5 c |
| East Branch Salmon Trout River near Dodge City | 46°47’09” | 87°51’08” | 2005-10-01–current | 2005-12-06–current | 0 | 1.95 |
| Silver River near L’Anse | 46°48’15” | 88°19’01” | 2001-10-01–current | 2005-10-15–2013-09-29 | 0 | 35.2 |
| Silver River Upstream of East Branch near L’Anse | 46°43’16” | 88°19’48” | 2008-10-01–2013-09-29 | 2008-09-30–2013-09-29 | 0 | 35.2 |
| Yellow Dog River near Big Bay | 46°42’49” | 87°50’26” | 2004-12-01–2016-10-17 | 2004-12-22–2017-01-23 | 0 | 1.86 |
| Site and Model Scenario a | F1 | F2 | k (--) | SCq Nov–Feb (µS/cm) | SCq Mar–Jun (µS/cm) | SCq Jul–Oct (µS/cm) | Mean Baseflow (m3/s) | BFI (%) b |
|---|---|---|---|---|---|---|---|---|
| Boardman 2p | 0.11 | −120 | 0.96 | 248 | 159 | 242 | 3.16 | 91.6 |
| Boardman 3p | 0.10 | −117 | 0.96 | 248 | 159 | 242 | 2.95 | 85.4 |
| Falls 2p | 0.14 | −660 | 0.74 | 77 | 73 | 103 | 1.33 | 74.6 |
| Falls 3p | 0.14 | −698 | 0.88 | 89 | 83 | 115 | 1.14 | 63.8 |
| Ford 2p | 0.17 | −961 | 0.36 | 216 | 194 | 223 | 9.22 | 90.0 |
| Ford 3p | 0.19 | −1169 | 0.56 | 246 | 219 | 259 | 8.19 | 79.9 |
| Gomanche 2p | 0.14 | −545 | 0.41 | 104 | 84 | 113 | 0.09 | 84.1 |
| Gomanche 3p | 0.17 | −545 | 0.10 | 111 | 98 | 126 | 0.10 | 86.4 |
| Rifle 2p | 0.16 | −1576 | 0.25 | 247 | 235 | 327 | 8.68 | 90.6 |
| Rifle 3p | 0.18 | −1653 | 0.27 | 309 | 280 | 354 | 8.34 | 87.1 |
| Salmon Trout 2p | 0.21 | −448 | 0.50 | 69 | 43 | 58 | 0.16 | 91.8 |
| Salmon Trout 3p | 0.26 | −411 | 0.66 | 69 | 53 | 63 | 0.15 | 87.7 |
| East Branch Salmon Trout 2p | 0.14 | −1896 | 0.79 | 77 | 55 | 88 | 0.47 | 84.9 |
| East Branch Salmon Trout 3p | 0.14 | −2067 | 0.99 | 85 | 62 | 91 | 0.39 | 69.1 |
| Silver 2p | 0.10 | −816 | 0.72 | 66 | 46 | 76 | 1.49 | 74.3 |
| Silver 3p | 0.12 | −898 | 0.71 | 76 | 55 | 84 | 1.35 | 67.3 |
| Silver Upstream 2p | 0.16 | −519 | 0.27 | 20 | 25 | 29 | 0.61 | 84.6 |
| Silver Upstream 3p | 0.15 | −482 | 0.90 | 32 | 41 | 50 | 0.37 | 51.2 |
| Yellow Dog 2p | 0.19 | −1694 | 0.89 | 28 | 13 | 46 | 0.62 | 72.1 |
| Yellow Dog 3p | 0.21 | −1620 | 0.83 | 33 | 17 | 47 | 0.61 | 70.6 |
| USGS Site | Data | Time Series | L-B Test Statistic lag 1 | p-Value Lag 1 | L-B Test Statistic Lag 2 | p-Value Lag 2 | L-B Test Statistic Lag 3 | p-Value Lag 3 | STA b |
|---|---|---|---|---|---|---|---|---|---|
| FORD RIVER NEAR HYDE, MI | Streamflow | Monthly | 104 | <0.1 | 105 | <0.1 | 136 | <0.1 | yes |
| Seasonal | 8.60 | <0.1 | 17.2 | <0.1 | 105 | <0.1 | yes | ||
| Annual | 2.15 | 0.14 | 2.84 | 0.24 | 3.20 | 0.36 | no | ||
| Baseflow | Monthly | 109 | <0.1 | 110 | <0.1 | 139 | <0.1 | yes | |
| Seasonal | 7.56 | <0.1 | 16.1 | <0.1 | 102 | <0.1 | yes | ||
| Annual | 1.99 | 0.16 | 2.64 | 0.27 | 3.05 | 0.38 | no | ||
| BFI a | Monthly | 48.0 | <0.1 | 49.7 | <0.1 | 54.4 | <0.1 | yes | |
| Seasonal | 9.49 | <0.1 | 24.1 | <0.1 | 72.8 | <0.1 | yes | ||
| Annual | 0.86 | 0.35 | 2.64 | 0.27 | 3.30 | 0.35 | no | ||
| RIFLE RIVER NEAR STERLING, MI | Streamflow | Monthly | 168 | <0.1 | 177 | <0.1 | 185 | <0.1 | yes |
| Seasonal | 7.28 | <0.1 | 17.9 | <0.1 | 101 | <0.1 | yes | ||
| Annual | 3.63 | <0.1 | 4.84 | <0.1 | 5.15 | 0.16 | no | ||
| Baseflow | Monthly | 193 | <0.1 | 206 | <0.1 | 213 | <0.1 | yes | |
| Seasonal | 7.51 | <0.1 | 18.6 | <0.1 | 105 | <0.1 | yes | ||
| Annual | 3.44 | <0.1 | 4.41 | 0.11 | 4.80 | 0.19 | no | ||
| BFI a | Monthly | 24.5 | <0.1 | 24.9 | <0.1 | 27.2 | <0.1 | yes | |
| Seasonal | 1.45 | 0.23 | 5.96 | <0.1 | 52.8 | <0.1 | no | ||
| Annual | 4.04 | <0.1 | 8.85 | <0.1 | 10.0 | <0.1 | yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hagedorn, B.; Meadows, C. Trend Analyses of Baseflow and BFI for Undisturbed Watersheds in Michigan—Constraints from Multi-Objective Optimization. Water 2021, 13, 564. https://doi.org/10.3390/w13040564
Hagedorn B, Meadows C. Trend Analyses of Baseflow and BFI for Undisturbed Watersheds in Michigan—Constraints from Multi-Objective Optimization. Water. 2021; 13(4):564. https://doi.org/10.3390/w13040564
Chicago/Turabian StyleHagedorn, Benjamin, and Christina Meadows. 2021. "Trend Analyses of Baseflow and BFI for Undisturbed Watersheds in Michigan—Constraints from Multi-Objective Optimization" Water 13, no. 4: 564. https://doi.org/10.3390/w13040564
APA StyleHagedorn, B., & Meadows, C. (2021). Trend Analyses of Baseflow and BFI for Undisturbed Watersheds in Michigan—Constraints from Multi-Objective Optimization. Water, 13(4), 564. https://doi.org/10.3390/w13040564






