Analytical Solutions of Vertical Airflow in an Unconfined Aquifer with Rising or Falling Water Table
Abstract
:1. Introduction
2. Conceptual Model and Control Equations
2.1. Conceptual Model and Assumptions
2.2. Nonlinear Control Equation of Airflow
2.3. Feedback Equation for Groundwater Flow
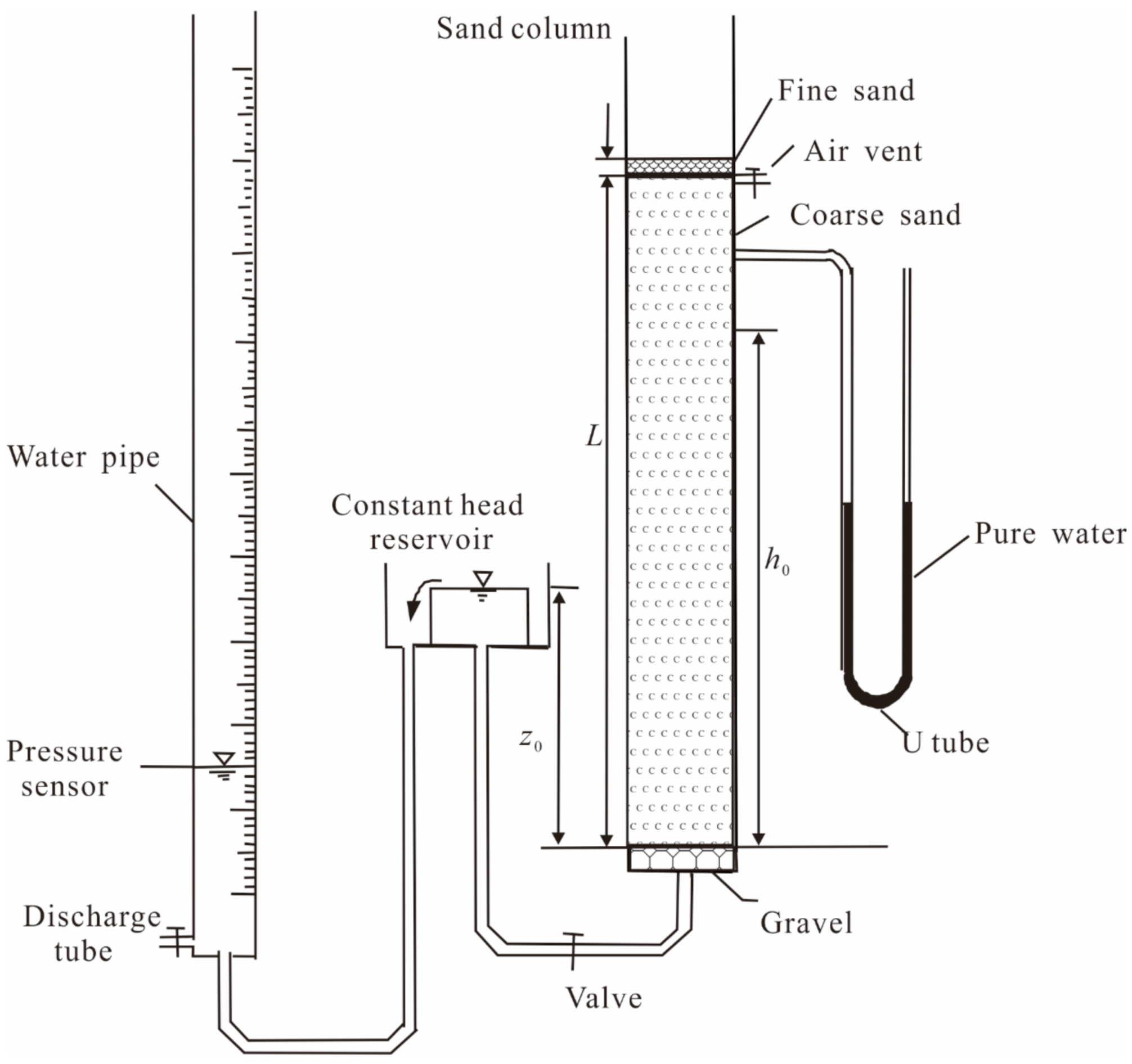
3. Experimental Studies
3.1. Experimental Setup
3.2. Type Curves of Change in the Air Pressure Beneath the Low-Permeability Cap
3.2.1. Results of the Drainage Experiments
3.2.2. Results of the Injection Experiments
3.3. Limitation Remarks of the Experiments
4. Analytical Solutions
4.1. Early Stage Analytical Solution
4.2. Middle Stage Analytical Solution
4.3. Late Stage Analytical Solution
4.4. Estimating Parameters with Semi-Analytical Solutions
4.5. The Generic Behaviors of Airflow Revealed by the Analytical Solutions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Youngs, E.G. The drainage of liquids from porous materials. J. Geophys. Res. Space Phys. 1960, 65, 4025–4030. [Google Scholar] [CrossRef]
- Ligon, J.T.; Johnson, H.P.; Kirkham, D. Unsteady-state drainage of fluid from a vertical column of porous material. J. Geophys. Res. Space Phys. 1962, 67, 5199–5204. [Google Scholar] [CrossRef]
- Kroszynski, U. Flow in a vertical porous column drained at its bottom at constant flux. J. Hydrol. 1975, 24, 135–153. [Google Scholar] [CrossRef]
- Moench, A.F. Combining the Neuman and Boulton Models for Flow to a Well in an Unconfined Aquifer. Ground Water 1995, 33, 378–384. [Google Scholar] [CrossRef]
- Tartakovsky, G.D.; Neuman, S.P. Three-dimensional saturated-unsaturated flow with axial symmetry to a partially penetrating well in a compressible unconfined aquifer. Water Resour. Res. 2007, 43, 1410-1–1410-17. [Google Scholar] [CrossRef]
- Mishra, P.K.; Neuman, S.P. Improved forward and inverse analyses of saturated-unsaturated flow toward a well in a compressible unconfined aquifer. Water Resour. Res. 2010, 46, W07508. [Google Scholar] [CrossRef]
- Mishra, P.K.; Neuman, S.P. Saturated-unsaturated flow to a well with storage in a compressible unconfined aquifer. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Vachaud, G.; Vauclin, M.; Khanji, D.; Wakil, M. Effects of air pressure on water flow in an unsaturated stratified vertical column of sand. Water Resour. Res. 1973, 9, 160–173. [Google Scholar] [CrossRef]
- Bouwer, H.; Rice, R.C. Delayed aquifer yield as a phenomenon of delayed air entry. Water Resour. Res. 1978, 14, 1068–1074. [Google Scholar] [CrossRef]
- Jiao, J.J.; Li, H. Breathing of coastal vadose zone induced by sea level fluctuations. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Jiao, J.J. One-dimensional airflow in unsaturated zone induced by periodic water table fluctuation. Water Resour. Res. 2005, 41, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.-P.; Jiao, J.J. Numerical study of airflow in the unsaturated zone induced by sea tides. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Jiao, J.J.; Guo, H. Airflow induced by pumping tests in unconfined aquifer with a low-permeability cap. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
- Kuang, X.; Jiao, J.J.; Wan, L.; Wang, X.-S.; Mao, D. Air and water flows in a vertical sand column. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Kuang, X. Air and Water Flows Induced by Water Level Change in Aquifers. Ph.D. Thesis, The University of Hong Kong, Hong Kong, China, 2013. [Google Scholar] [CrossRef]
- Kuang, X.; Jiao, J.J.; Huang, H.; Qian, J. Air and water flows in a large sand box with a two-layer aquifer system. Hydrogeol. J. 2013, 21, 977–985. [Google Scholar] [CrossRef]
- Dong, P. Experimental Study and Numerical Modeling on Coupling between Water Table Change and Air Flow in Double-Layer Media. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2013. [Google Scholar]
- An, R. Research on Typical Coupling Problems and the Decoupling Conditions for Groundwater Flow Linked with Air Flow and Thermal Flow. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2015. [Google Scholar]
- Faust, C.R. Transport of Immiscible Fluids Within and Below the Unsaturated Zone: A Numerical Model. Water Resour. Res. 1985, 21, 587–596. [Google Scholar] [CrossRef]
- Kuppusamy, T.; Sheng, J.; Parker, J.C.; Lenhard, R.J. Finite-element analysis of multiphase immiscible flow through soils. Water Resour. Res. 1987, 23, 625–631. [Google Scholar] [CrossRef]
- Faust, C.R.; Guswa, J.H.; Mercer, J.W. Simulation of three-dimensional flow of immiscible fluids within and below the unsaturated zone. Water Resour. Res. 1989, 25, 2449–2464. [Google Scholar] [CrossRef]
- Kueper, B.H.; Frind, E.O. Two-phase flow in heterogeneous porous media: Model development. Water Resour. Res. 1991, 27, 1049–1057. [Google Scholar] [CrossRef]
- Celia, M.A.; Binning, P.J. A mass conservative numerical solution for two-phase flow in porous media with application to unsaturated flow. Water Resour. Res. 1992, 28, 2819–2828. [Google Scholar] [CrossRef]
- Class, H.; Helmig, R.; Bastian, P. Numerical simulation of non-isothermal multiphase multicomponent processes in porous media. Adv. Water Resour. 2002, 25, 533–550. [Google Scholar] [CrossRef]
- Amaziane, B.; Jurak, M.; Keko, A. Žgaljić Modeling and Numerical Simulations of Immiscible Compressible Two-Phase Flow in Porous Media by the Concept of Global Pressure. Transp. Porous Media 2009, 84, 133–152. [Google Scholar] [CrossRef]
- Miller, C.T.; Christakos, G.; Imhoff, P.T.; McBride, J.F.; Pedit, J.A.; Trangenstein, J.A. Multiphase flow and transport modeling in heterogeneous porous media: Challenges and approaches. Adv. Water Resour. 1998, 21, 77–120. [Google Scholar] [CrossRef]
- McWhorter, D.B.; Sunada, D.K. Exact integral solutions for two-phase flow. Water Resour. Res. 1990, 26, 399–413. [Google Scholar] [CrossRef]
- Fokas, A.S.; Yortsos, Y.C. On the exactly solvable equation St = [(β S + γ )−2 Sx] + α (βSx + γ)−2 Sx occurring in two-phase flow in porous media. SIAM J. Appl. Math. 1982, 42, 318–332. [Google Scholar] [CrossRef]
- Rogers, C.; Stallybrass, M.; Clements, D. On two phase filtration under gravity and with boundary infiltration: Application of a bäcklund transformation. Nonlinear Anal. Theory, Methods Appl. 1983, 7, 785–799. [Google Scholar] [CrossRef]
- Sander, G.; Parlange, J.-Y.; Kühnel, V.; Hogarth, W.; Lockington, D.; O’Kane, J. Exact nonlinear solution for constant flux infiltration. J. Hydrol. 1988, 97, 341–346. [Google Scholar] [CrossRef]
- Sander, G.C.; Parlange, J.-Y.; Hogarth, W.L. Air and water flow, II. Gravitational flow with an arbitrary flux boundary condition. J. Hydrol. 1988, 99, 225–234. [Google Scholar] [CrossRef]
- Sander, G.C.; Norbury, J.; Weeks, S.W. An exact solution to the nonlinear diffusion-convection equation for two-phase flow. Q. J. Mech. Appl. Math. 1993, 46, 709–727. [Google Scholar] [CrossRef]
- Sander, G.; Parlange, J.-Y.; Lisle, I.; Weeks, S. Exact solutions to radially symmetric two-phase flow for an arbitrary diffusivity. Adv. Water Resour. 2005, 28, 1112–1121. [Google Scholar] [CrossRef]
- Sander, G.; Parlange, J.-Y. Water and Air Movement in Soils. Soil Sci. 1984, 138, 198–202. [Google Scholar] [CrossRef]
- Fučík, R.; Mikyška, J.; Beneš, M.; Illangasekare, T.H. An Improved Semi-Analytical Solution for Verification of Numerical Models of Two-Phase Flow in Porous Media. Vadose Zone J. 2007, 6, 93–104. [Google Scholar] [CrossRef]
- Charbeneau, R.J. Groundwater Hydraulics and Pollutant Transport; Prentice-Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Dong, P.; Wang, X.S.; Wan, L.; Kuang, X.X.; Chen, T.F. Sand Column Experiments and Modeling Study on Coupling between Groundwater Level Change and Air Flow. Earth Sci. J. China Univ. Geosci. 2013, 126–132. [Google Scholar] [CrossRef]
- Dong, P.; Wang, X.S.; Wan, L.; Chen, T.F. Vacuum decay effect in drainage of sand columns: Experiments and dynamic analy-sis. Rock Soil Mech. 2013, 34, 1661–1667. [Google Scholar] [CrossRef]





| Experimental Groups | Initial Water Head Difference (∆H, cm) | Fine Sand Thickness (D, cm) | Observation Duration (hour) | |
|---|---|---|---|---|
| Drainage Experiments | 1 | 30 | 0.0 | 8.5 |
| 2 | 30 | 2.0 | 5 | |
| 3 | 30 | 5.0 | 7 | |
| 4 | 30 | 7.5 | 6 | |
| 5 | 40 | 2.0 | 9 | |
| 6 | 40 | 5.0 | 5 | |
| 7 | 40 | 7.5 | 7 | |
| Injection Experiments | 1 | 30 | 2.0 | 3 |
| 2 | 30 | 5.0 | 3 | |
| 3 | 40 | 2.0 | 3 | |
| 4 | 40 | 5.0 | 3 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, R.; Dong, P.; Wang, J.-Z.; Zhang, Y.; Song, X.; Wan, L.; Wang, X.-S. Analytical Solutions of Vertical Airflow in an Unconfined Aquifer with Rising or Falling Water Table. Water 2021, 13, 625. https://doi.org/10.3390/w13050625
An R, Dong P, Wang J-Z, Zhang Y, Song X, Wan L, Wang X-S. Analytical Solutions of Vertical Airflow in an Unconfined Aquifer with Rising or Falling Water Table. Water. 2021; 13(5):625. https://doi.org/10.3390/w13050625
Chicago/Turabian StyleAn, Ran, Pei Dong, Jun-Zhi Wang, Yifan Zhang, Xianfang Song, Li Wan, and Xu-Sheng Wang. 2021. "Analytical Solutions of Vertical Airflow in an Unconfined Aquifer with Rising or Falling Water Table" Water 13, no. 5: 625. https://doi.org/10.3390/w13050625
APA StyleAn, R., Dong, P., Wang, J.-Z., Zhang, Y., Song, X., Wan, L., & Wang, X.-S. (2021). Analytical Solutions of Vertical Airflow in an Unconfined Aquifer with Rising or Falling Water Table. Water, 13(5), 625. https://doi.org/10.3390/w13050625







