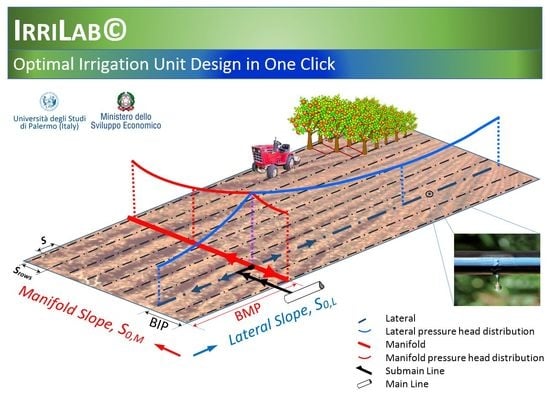
Verification of IRRILAB Software Application for the Hydraulic Design of a Micro-Irrigation System by Using IRRIPRO for an Apple Farm in Sicily
Abstract
:1. Introduction and Theoretical Background
2. IRRILAB and IRRIPRO Software
2.1. IRRILAB Software
2.2. IRRIPRO Software
2.3. Motivation of Joint Use of IRRILAB and IRRIPRO
3. IRRILAB and IRRIPRO Applications
3.1. IRRILAB Applications
3.2. IRRIPRO Applications
4. Results and Discussion
4.1. Results for the Actual “Non-Uniform” Five Sectors
4.2. Subdividing the Apple Farm in Seven and in Nine Sectors
4.3. Evaluating Energy Consumption by Using IRRILAB and IRRIPRO with Common Emitters and Pressure Compensating Emitters
5. Conclusions
- The IRRILAB application showed its sensitivity to the planform geometry and to the slope uniformity of the laterals and of the manifold, indicating that the more uniform in slope and the more rectangular the sector is, the better and better the design results (in terms of emission uniformity and energy-saving) will be.
- IRRILAB, which is based on analytical solutions and does not require attempts and the trial-and-error technique, offers a valuable solution in designing a micro-irrigation system using CEs or PCEs, and makes it possible to save energy for both emitter types, especially when sectors are almost rectangular and uniform in slope.
- The energy-saving provided by IRRILAB with respect to IRRIPRO, applied by attempts, resulted higher for CEs (−15% for five sectors and −9% for nine sectors) than for PCEs (−7% for five sectors and −6% for nine sectors). However, in absolute terms, the energy required was greater for five-sector subdivision than for nine-sector subdivision.
- PCEs could be considered a good solution for saving energy in the sloping field, but their contraindications need to be mentioned: they are more expansive, more complicated structurally, and the working mechanism is not clear, which causes difficulty in their research and development. The latter causes their damage in the short term and the increase of the manufacturing variation coefficient can frustrate the benefit found in terms of energy-saving.
- For sloping fields, CEs, usually chosen only for flat fields, should be recommended, if a design procedure such as that suggested by IRRILAB is applied, especially for sectors uniform in slopes and rectangular planform geometry.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Food and Agriculture Organization of the United Nations. The State of the World’s Land and Water Resources: Managing Systems at Risk; Earthscan: London, UK, 2011. Available online: http://www.fao.org/docrep/017/i1688e/i1688e.pdf (accessed on 25 September 2020).
- Food and Agriculture Organization of the United Nations. The Future of Food and Agriculture—Trends and Challenges; Food and Agriculture Organization of the United Nations: Rome, Italy, 2017. Available online: http://www.fao.org/3/i6583e/i6583e.pdf (accessed on 25 September 2020).
- UNESCO World Water Assessment Programme. The United Nations World Water Development Report 2020: Water and Climate Change. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000372985.locale=en (accessed on 17 January 2021).
- Postel, S.L. Water for food production: Will there be enough in 2025? BioScience 1998, 48, 629–637. [Google Scholar] [CrossRef] [Green Version]
- WRG. Charting Our Water Future. Economic Frameworks to Inform Decision-Making; The 2030 Water Resources Group: Rome, Italy, 2009. Available online: https://www.2030wrg.org/wp-content/uploads/2012/06/Charting_Our_Water_Future_Final.pdf (accessed on 27 September 2020).
- Scheierling, S.M.; Treguer, D.O. Enhancing water productivity in irrigated agriculture in the face of water scarcity. Choices 2016, 31, 1–10. [Google Scholar]
- Baiamonte, G. Advances in designing drip irrigation laterals. Agric. Water Manag. 2018, 199, 157–174. [Google Scholar] [CrossRef]
- Hamdy, A.; Ragab, R.; Scarascia Mugnozza, E. Coping with water scarcity: Water saving and increasing water productivity. Irrig. Drain. 2003, 52, 3–20. [Google Scholar] [CrossRef]
- Cullotta, S.; Bagarello, V.; Baiamonte, G.; Gugliuzza, G.; Iovino, M.; La Mela Veca, D.S.; Maetzke, F.; Palmeri, V.; Sferlazza, S. Comparing different methods to determine soil physical quality in a Mediterranean forest and pasture land. Soil Sci. Soc. Am. J. 2016, 80, 1038–1056. [Google Scholar] [CrossRef]
- Bucks, D.A.; Nakayama, F.S.; Warrick, A.W. Principles, practices, and potentialities of trickle (drip) irrigation. Adv. Irrig. 1982, 1, 219–298. [Google Scholar]
- Baiamonte, G.; Crescimanno, G.; Minacapilli, M. Effects of Biochar on Irrigation Management and Water Use Efficiency for Three Different Crops in a Desert Sandy Soil. Sustainability 2020, 12, 7678. [Google Scholar] [CrossRef]
- Tiwari, K.N. Feasibility of drip irrigation under different soil covers in tomato. J. Agric. Eng. 1998, 35, 41–49. [Google Scholar]
- Bralts, V.F.; Driscoll, M.A.; Shayya, W.H.; Cao, L. An expert system for the hydraulic analysis of microirrigation systems. Comput. Electron. Agric. 1993, 9, 275–287. [Google Scholar] [CrossRef]
- Trung, M.C.; Nishiyama, S.; Anyouji, H. Hydraulic design of drip irrigation system by the method of unsteady flow: Example in irregular slope field. Sand Dune Res. 2007, 54, 49–56. [Google Scholar]
- Zhu, D.L.; Wu, P.T.; Merkley, G.P.; Jin, J. Drip irrigation lateral design procedure based on emission uniformity and field microtopography. Irrig. Drain. 2010, 59, 535–546. [Google Scholar] [CrossRef]
- Ju, X.; Wu, P.; Weckler, R.; Zhu, D.; Zhang, L. Simplified method for designing diameter of drip irrigation laterals based on emitter flow variation. Trans. Chin. Soc. Agric. Eng. 2016, 32, 14–20. [Google Scholar]
- Myers, L.E.; Bucks, D.A. Uniform irrigation with low-pressure trickle systems. J. Irrig. Drain. Div. 1972, 98, 341–346. [Google Scholar] [CrossRef]
- Howell, T.A.; Hiler, E.A. Trickle irrigation lateral design. Trans. ASAE 1974, 17, 902–908. [Google Scholar] [CrossRef]
- Wu, I.P.; Gitlin, H.M. Energy gradient line for drip irrigation laterals. J. Irrig. Drain. Div. 1975, 101, 321–326. [Google Scholar] [CrossRef]
- Kang, Y.; Nishiyama, S. Analysis and design of microirrigation laterals. J. Irrig. Drain. Eng. 1996, 122, 75–82. [Google Scholar] [CrossRef]
- Jiang, S.; Kang, Y. Simple method for the design of microirrigation paired laterals. J. Irrig. Drain. Eng. 2010, 136, 271–275. [Google Scholar] [CrossRef]
- Baiamonte, G.; Provenzano, G.; Rallo, G. Analytical approach determining the optimal length of paired drip laterals in uniformly sloped fields. J. Irrig. Drain. Eng. 2015, 141, 04014042. [Google Scholar] [CrossRef] [Green Version]
- Xueliang, J.; Pute, W.; Paul, W.R. Newly-simplified method for hydraulic design of micro-irrigation laterals based on emission uniformity. J. Drain. Irrig. Mach. Eng. 2015, 33, 691–700. [Google Scholar]
- Baiamonte, G. Simple relationships for the optimal design of paired drip laterals on uniform slopes. J. Irrig. Drain. Eng. ASCE 2016, 142, 04015054. [Google Scholar] [CrossRef]
- Keller, J.; Karmeli, D. Trickle irrigation design parameters. Trans. ASAE 1974, 17, 678–684. [Google Scholar] [CrossRef]
- Juana, L.; Losada, A.; Rodrigues-Sinobas, L.; Sanchez, R. Analytical relationships for designing rectangular drip irrigation units. J. Irrig. Drain. Eng. ASCE 2004, 130, 47–59. [Google Scholar] [CrossRef]
- Di Dio, P.; Provenzano, G.; Provenzano, C.; Savona, P. IRRIPRO: A Powerful Software to Graphic and Hydraulic Design of Irrigation Plants. In Proceedings of the International Conference on Agricultural and Biosystem Engineering for a Sustainable world, Crete, Greece, 23–25 June 2008; Curran Associates, Inc.: Red Hook, NY, USA, 2008; Volume 1, pp. 1–14. [Google Scholar]
- García, I.F.; Montesinos, P.; Poyato, E.C.; Díaz, J.R. Energy cost optimization in pressurized irrigation networks. Irrig. Sci. 2016, 34, 1–13. [Google Scholar] [CrossRef]
- Baiamonte, G. Explicit relationships for optimal designing rectangular microirrigation units on uniform slopes: The IRRILAB software application. Comput. Electron. Agric. 2018, 153, 151–168. [Google Scholar] [CrossRef]
- Zayani, K.; Alouini, A.; Lebdi, F.; Lamaddalena, N. Design of drip irrigationsystems using the energy drop ratio approach. Trans. ASAE 2001, 44, 1127–1133. [Google Scholar] [CrossRef]
- Wu, I.P. An assessment of hydraulic design of micro-irrigation systems. Agric. Water Manag. 1997, 32, 275–284. [Google Scholar] [CrossRef]
- Vallesquino, P.; Luque-Escamilla, P.L. Equivalent friction factor method for hydraulic calculation in irrigation laterals. J. Irrig. Drain. Eng. ASCE 2002, 128, 278–286. [Google Scholar] [CrossRef]
- Baiamonte, G.; Mangiapane, G. Il software IRRILAB per gli impianti microirrigui: Verifiche numeriche e sperimentali. Conference Proceeding “Attualità dell’idraulica Agraria e delle Sistemazioni Idraulico-Forestali al cambiare dei tempi”, Dipartimento di Scienze Agrarie e Forestali, Palermo. Quad. di Idron. Mont. 2018, 35, 209–218. [Google Scholar]
- Arshad, I.; Savona, P.; Khan, Z.A. Analysis of Trickle/Drip Irrigation Uniformity by IRRIPRO Simulations. Int. J. Res. 2014, 1, 635–649. [Google Scholar]
- Baiamonte, G. Linking kinetic energy fraction and equivalent length method to determine local losses in trickle irrigation. J. Irrig. Drain. Eng. ASCE 2020, 146, 04020024. [Google Scholar] [CrossRef]
- Keller, J.; Bliesner, R.D. Sprinkle and Trickle Irrigation; Van Nostrand Reinhod: New York, NY, USA, 1990. [Google Scholar]
- Baiamonte, G. Minor Losses and Best Manifold Position in the Optimal Design of Paired Sloped Drip Laterals. Irrig. Drain. 2018, 67, 893–908. [Google Scholar] [CrossRef]
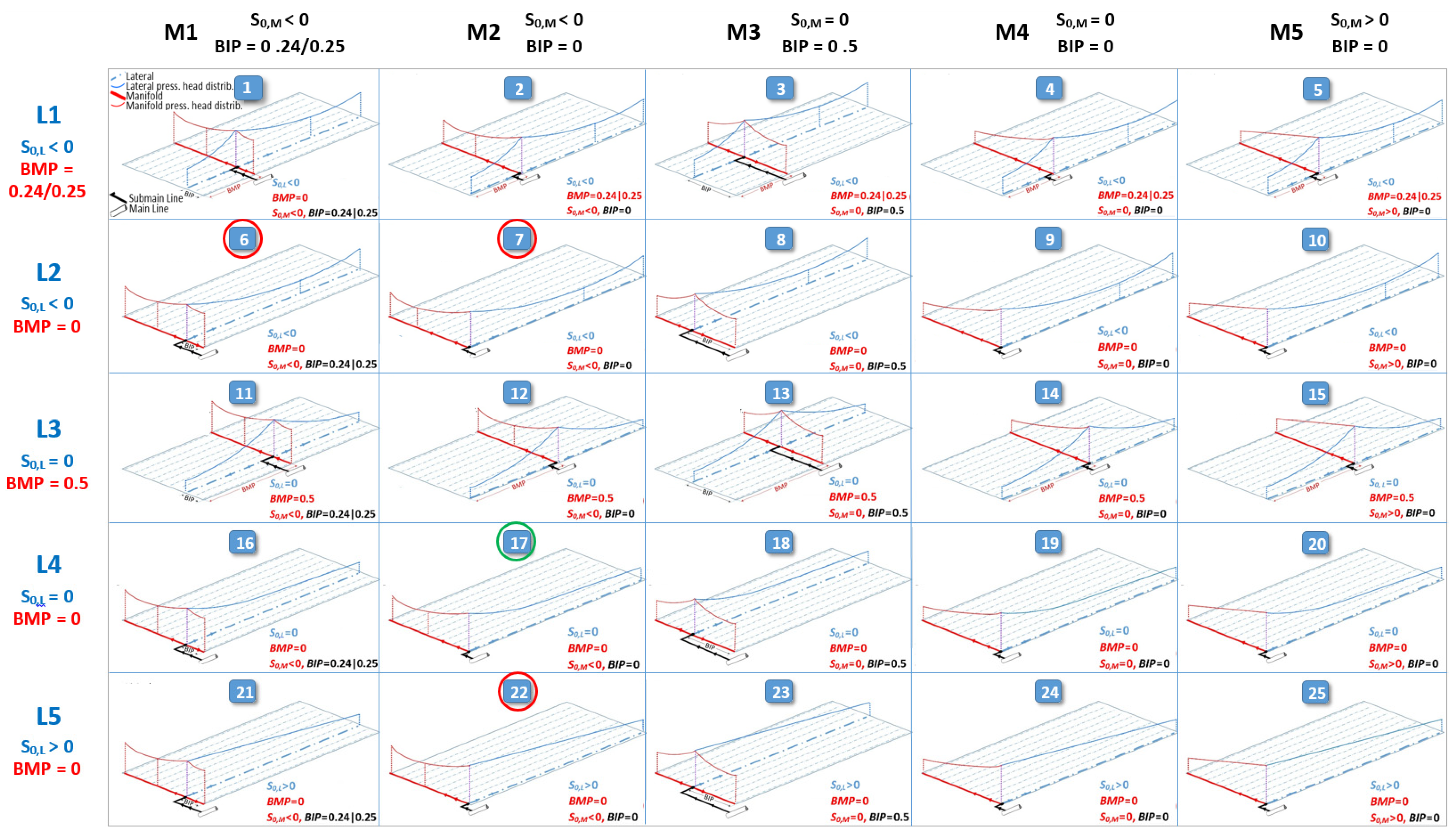







| (a) | |||||
| Lateral Layout (Figure 1) | Slope, S0,L | BMP | Lateral’s Sketch | Nominal Pressure Head Coefficient α Equation (1) | Nominal Flow Rate Coefficient α′ Equation (2) |
| L2 | < 0 | 0 |  | ||
| L5 | > 0 | 0 |  | ||
| (b) | |||||
| Manifold Layout (Figure 1) | Slope, S0,M | BIP | Manifold’s Sketch | ||
| M1 | < 0 | 0.24 | 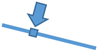 | ||
| M2 | < 0 | 0 | 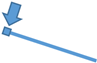 | ||
| Resistance Equation | rL | sL | kL | BMP | B1 | B2 |
|---|---|---|---|---|---|---|
| Blasius | 1.750 | 4.750 | 7.788 10−4 | 0.24 | 7.35 | 2.34 |
| Hazen-Williams | 1.852 | 4.871 | 10.675 C−r | 0.25 | 7.07 | 2.34 |
| Layout | Lateral Layout | Manifold Layout | β | Different Resistance Equation for L and M β′ | Same Resistance Equationfor L and M β′ | ||||
|---|---|---|---|---|---|---|---|---|---|
| # | S0,L | BMP | # | S0,M | BIP | ||||
| 6 | L2 | <0 | 0 | M1 | <0 | 0.24 | |||
| 7 | L2 | <0 | M2 | <0 | 0 | ||||
| 22 | L5 | >0 | M2 | <0 | |||||
| Geometric Parameters | ||||||||||||||
| Sector | #Layout | BMP | BIP | nrows | Lopt,L (m) | Lopt,M (m) | S0,L | S0,M | CE | PCE | ||||
| DL (mm) | DM (mm) | DL (mm) | DM (mm) | |||||||||||
| 1 | 6 | 0 | 0.24 | 72 | 88.96 | 273.6 | −0.0210 | −0.1202 | 12.98 | 39.3 | 12.98 | 39.3 | ||
| 2 | 49 | 78.49 | 186.2 | −0.0898 | −0.1259 | 45.8 | 45.8 | |||||||
| 3 | 37 | 99.17 | 140.6 | −0.0747 | −0.0586 | 46.7 | 46.7 | |||||||
| 4 | 7 | 0 | 42 | 90.33 | 159.6 | −0.0540 | −0.1799 | 39.9 | 39.9 | |||||
| 5 | 37 | 84.04 | 140.6 | −0.0414 | −0.1566 | 37.1 | 37.1 | |||||||
| Hydraulic parameters for common emitters (CE) with x = 0.5 | ||||||||||||||
| Sector | δ | δL | δM | ke | hn (m) | qn (L/h) | hin (m) | hmin (m) | hmean (m) | hmax (m) | Qs (m3/h) | hs (m) | CV | EU (%) |
| 1 | 0.06 | 0.004 | 0.056 | 0.400 | 80.2 | 3.58 | 85.0 | 73.2 | 84.7 | 102.3 | 22.98 | 196.7 | 3.23 | 89.2 |
| 2 | 0.08 | 0.023 | 0.056 | 1.247 | 55.7 | 9.30 | 60.1 | 49.7 | 55.8 | 71.1 | 34.45 | 157.3 | 4.21 | 89.4 |
| 3 | 0.05 | 0.027 | 0.022 | 0.947 | 49.0 | 6.63 | 51.4 | 41.9 | 47.2 | 58.8 | 23.12 | 145.3 | 3.60 | 89.9 |
| 4 | 0.10 | 0.015 | 0.084 | 0.779 | 60.2 | 6.04 | 66.2 | 49.1 | 54.5 | 70.0 | 21.15 | 189.9 | 4.71 | 89.3 |
| 5 | 0.09 | 0.012 | 0.077 | 0.784 | 50.7 | 5.58 | 55.3 | 43.2 | 49.0 | 58.8 | 16.11 | 176.0 | 3.59 | 89.7 |
| Hydraulic parameters for pressure compensating emitters (PCE) with x = 0 | ||||||||||||||
| Sector | δ | δL | δM | ke | hn (m) | hin (m) | hmin (m) | hmean (m) | hmax (m) | Qs (m3/h) | hs (m) | CV | EU (%) | |
| 1 | 0.425 | 0.030 | 0.384 | 3.578 | 11.3 | 16.1 | 5.1 | 16.6 | 34.9 | 22.35 | 128.2 | 0 | 100 | |
| 2 | 0.342 | 0.097 | 0.223 | 9.301 | 13.0 | 17.5 | 6.3 | 13.3 | 29.4 | 34.42 | 115.4 | |||
| 3 | 0.168 | 0.091 | 0.071 | 6.627 | 14.6 | 17.0 | 6.9 | 12.6 | 24.4 | 23.56 | 111.2 | |||
| 4 | 0.26 | 0.038 | 0.214 | 6.044 | 23.1 | 29.2 | 7.4 | 13.7 | 33.3 | 22.26 | 155.9 | |||
| 5 | 0.29 | 0.040 | 0.241 | 5.582 | 15.7 | 20.3 | 6.2 | 12.9 | 23.9 | 16.39 | 142.5 | |||
| Geometric Parameters | |||||||||||
| Sector | Area (m2) | nrows | LL (m) | LM (m) | S0,L | S0,M | CE | PCE | |||
| DL (mm) | DM (mm) | DL (mm) | DM (mm) | ||||||||
| 1 | 24,339 | 72 | 87.3 | 328.3 | −0.0210 | −0.1202 | 17.8 | 78.0 | 12.98 | 41.6 | |
| 2 | 14,616 | 49 | 75.8 | 213.5 | −0.0898 | −0.1259 | 38.0 | ||||
| 3 | 13,944 | 37 | 96.3 | 139.4 | −0.0747 | −0.0586 | 38.0 | ||||
| 4 | 14,416 | 42 | 87.9 | 263.2 | −0.0540 | −0.1799 | 41.6 | ||||
| 5 | 11,815 | 37 | 79.6 | 152.5 | −0.0414 | −0.1566 | 38.0 | ||||
| Hydraulic parameters (CE) | |||||||||||
| Sector | ke | x | qn (L/h) | Qs (m3/h) | hs (m) | hin (m) | hmin (m) | hmean (m) | hmax (m) | CV | EU (%) |
| 1 | 1.253 | 0.5 | 12.87 | 80.36 | 239.6 | 100.2 | 94.2 | 105.6 | 131.6 | 4.33 | 89.3 |
| 2 | 1.253 | 0.5 | 11.71 | 43.33 | 183.6 | 82.4 | 77.4 | 87.4 | 105 | 3.79 | 89.6 |
| 3 | 1.253 | 0.5 | 9.04 | 32.12 | 146.8 | 49.8 | 46.2 | 52.1 | 62.1 | 3.57 | 89.9 |
| 4 | 1.253 | 0.5 | 12.32 | 45.39 | 219.2 | 84.5 | 84.3 | 96.8 | 115.3 | 2.97 | 89.8 |
| 5 | 1.253 | 0.5 | 12.46 | 36.59 | 213.1 | 84.8 | 85.1 | 98.9 | 108.9 | 2.45 | 89.9 |
| Hydraulic parameters (PCE) | |||||||||||
| Sector | ke | x | Qs (m3/h) | hs (m) | hin (m) | hmin (m) | hmean (m) | hmax (m) | CV | EU (%) | |
| 1 | 5 | 0 | 31.23 | 140.7 | 25.7 | 9.1 | 20.6 | 37.2 | 0 | 100 | |
| 2 | 7 | 25.91 | 113.7 | 19.2 | 9.1 | 14.6 | 25.8 | ||||
| 3 | 7 | 24.89 | 126.2 | 31.4 | 9.1 | 19.7 | 33.8 | ||||
| 4 | 7 | 25.78 | 163.6 | 34.8 | 9.1 | 16.2 | 38.3 | ||||
| 5 | 7 | 20.56 | 159.6 | 35.6 | 9.1 | 18.6 | 38.5 | ||||
| Geometric Parameters | ||||||||||||||
| Sector | #Layout | BMP | BIP | nrows | Lopt,L (m) | Lopt,M (m) | S0,L | S0,M | CE | PCE | ||||
| DL (mm) | DM (mm) | DL (mm) | DM (mm) | |||||||||||
| 1 | 7 | 0 | 0 | 63 | 55.5 | 239.4 | −0.0911 | −0.0993 | 12.98 | 58.7 | 12.98 | 58.7 | ||
| 1A | 22 | 43 | 23.5 | 165 | 0.0429 | −0.0610 | 31.5 | 31.5 | ||||||
| 1B | 7 | 63 | 39.3 | 239.4 | −0.1148 | −0.1260 | 58.6 | 58.6 | ||||||
| 2 | 7 | 44 | 45.1 | 167.2 | −0.0203 | −0.1476 | 34.5 | 34.5 | ||||||
| 3 | 22 | 43 | 82.3 | 163.4 | 0.0351 | −0.1463 | 25.1 | 25.1 | ||||||
| 4 | 7 | 50 | 66.8 | 190 | −0.0143 | −0.1486 | 33.5 | 33.5 | ||||||
| 5 | 7 | 33 | 65.5 | 125.4 | −0.1639 | −0.0918 | 53.2 | 53.2 | ||||||
| 6 | 7 | 44 | 73.6 | 167.2 | −0.0631 | −0.1740 | 42.3 | 42.3 | ||||||
| 7 | 7 | 40 | 81.5 | 152 | −0.0335 | −0.1503 | 36.8 | 36.8 | ||||||
| 7A | 7 | 39 | 55.7 | 148.2 | −0.0322 | −0.1502 | 36.2 | 36.2 | ||||||
| 7B | 7 | 21 | 51.7 | 79.8 | −0.0403 | −0.1528 | 30.1 | 30.1 | ||||||
| Hydraulic parameters for common emitters (CE) with x = 0.5 | ||||||||||||||
| Sector | δ | δL | δM | ke | hn (m) | qn (L/h) | hin (m) | hmin (m) | hmean (m) | hmax (m) | Qs (m3/h) | hs (m) | CV | EU (%) |
| 1 | 0.04 | 0.007 | 0.033 | 1.167 | 129.1 | 13.26 | 134.2 | 103.7 | 116.9 | 145.9 | 44.07 | 243.2 | 4.01 | 89.43 |
| 1A | 0.07 | 0.017 | 0.052 | 1.109 | 33.7 | 6.43 | 36.0 | 24.6 | 27.3 | 39.3 | 5.46 | 136.3 | 4.52 | 89.51 |
| 1B | 0.1 | 0.013 | 0.086 | 2.713 | 62.1 | 21.38 | 68.3 | 51.3 | 56.8 | 79.4 | 47.68 | 179.3 | 4.99 | 89.18 |
| 2 | 0.1 | 0.004 | 0.096 | 1.022 | 45.8 | 6.92 | 50.4 | 43.1 | 46.2 | 54.6 | 13.01 | 154.1 | 2.98 | 92.88 |
| 3 | 0.1 | 0.028 | 0.070 | 0.213 | 59.2 | 1.64 | 65.1 | 49.8 | 54.8 | 65.6 | 5.56 | 153.7 | 2.57 | 92.25 |
| 4 | 0.1 | 0.003 | 0.096 | 0.529 | 52.3 | 3.83 | 57.5 | 43.4 | 49.0 | 60.6 | 12.32 | 147.0 | 4.04 | 89.36 |
| 5 | 0.08 | 0.039 | 0.040 | 2.227 | 49.8 | 15.72 | 53.8 | 41.8 | 47.5 | 56.0 | 32.88 | 148.9 | 3.27 | 89.95 |
| 6 | 0.1 | 0.014 | 0.085 | 1.043 | 60.4 | 8.11 | 66.5 | 52.8 | 57.7 | 68.5 | 25.55 | 187.6 | 2.71 | 92.45 |
| 7 | 0.06 | 0.006 | 0.053 | 0.584 | 76.3 | 5.10 | 80.9 | 63.8 | 71.0 | 86.2 | 15.7 | 199.1 | 3.96 | 90.13 |
| 7A | 0.1 | 0.007 | 0.092 | 1.111 | 43.1 | 7.29 | 47.4 | 38.2 | 42.1 | 51.6 | 14.96 | 164.0 | 4.08 | 90.44 |
| 7B | 0.08 | 0.012 | 0.068 | 1.577 | 32.0 | 8.92 | 34.5 | 28.1 | 31.6 | 37.2 | 8.92 | 134.1 | 3.80 | 89.86 |
| Hydraulic parameters for pressure compensating emitters (PCE) with x = 0 | ||||||||||||||
| Sector | δ | δL | δM | ke | hn (m) | hin (m) | hmin (m) | hmean (m) | hmax (m) | Qs (m3/h) | hs (m) | CV | EU (%) | |
| 1 | 0.150 | 0.026 | 0.121 | 13.263 | 34.4 | 39.6 | 5.3 | 20.3 | 49.8 | 46.35 | 149.9 | 0 | 100 | |
| 1A | 0.132 | 0.032 | 0.097 | 6.433 | 17.9 | 20.2 | 7.2 | 10.2 | 21.9 | 6.06 | 120.5 | |||
| 1B | 0.316 | 0.041 | 0.264 | 21.377 | 19.7 | 25.9 | 7.1 | 13.1 | 35.8 | 49.94 | 138.5 | |||
| 2 | 0.467 | 0.017 | 0.443 | 6.921 | 9.8 | 14.4 | 7.1 | 10.3 | 18.8 | 12.96 | 118.2 | |||
| 3 | 0.337 | 0.093 | 0.223 | 1.638 | 17.6 | 23.5 | 6.8 | 11.8 | 23.5 | 5.78 | 112.2 | |||
| 4 | 0.286 | 0.009 | 0.274 | 3.825 | 18.3 | 23.5 | 7.9 | 13.8 | 25.4 | 12.73 | 113.2 | |||
| 5 | 0.241 | 0.116 | 0.112 | 15.720 | 16.5 | 20.5 | 6.6 | 13.6 | 22.8 | 33.7 | 116.3 | |||
| 6 | 0.368 | 0.051 | 0.302 | 8.108 | 16.4 | 22.5 | 7.0 | 12.3 | 24.9 | 26.16 | 144.0 | |||
| 7 | 0.211 | 0.023 | 0.184 | 5.099 | 21.7 | 26.3 | 5.5 | 13.8 | 31.7 | 16.28 | 144.8 | |||
| 7A | 0.323 | 0.024 | 0.292 | 7.295 | 13.3 | 17.6 | 7.1 | 11.3 | 22.0 | 15.16 | 134.4 | |||
| 7B | 0.222 | 0.032 | 0.184 | 8.917 | 11.5 | 14.1 | 7.2 | 11.0 | 16.8 | 8.99 | 113.7 | |||
| Geometric Parameters | |||||||||||
| Sector | Area (m2) | nrows | LL (m) | LM (m) | S0,L | S0,M | CE | PCE | |||
| DL (mm) | DM (mm) | DL (mm) | DM (mm) | ||||||||
| 1 | 13,275 | 63 | 55.7 | 274.8 | −0.0911 | −0.0993 | 17.80 | 78.0 | 12.98 | 41.6 | |
| 1A | 3876 | 43 | 22.2 | 159.6 | 0.0429 | −0.0610 | 12.98 | 50.0 | 38.0 | ||
| 1B | 9399 | 63 | 37.3 | 248.7 | −0.1148 | −0.1260 | 12.98 | 50.0 | 38.0 | ||
| 2 | 7540 | 44 | 42.8 | 170.9 | −0.0203 | −0.1476 | 12.98 | 50.0 | 38.0 | ||
| 3 | 13,437 | 43 | 82.3 | 195.3 | 0.0351 | −0.1463 | 17.80 | 78.0 | 41.6 | ||
| 4 | 12,681 | 50 | 66.8 | 218.9 | −0.0143 | −0.1486 | 17.80 | 78.0 | 41.6 | ||
| 5 | 8215 | 33 | 65.2 | 121.2 | −0.1639 | −0.0918 | 12.98 | 78.0 | 38.0 | ||
| 6 | 12,282 | 44 | 73.6 | 192.4 | −0.0631 | −0.1740 | 12.98 | 50.0 | 41.6 | ||
| 7 | 12,386 | 40 | 80.1 | 187.7 | −0.0335 | −0.1503 | 17.80 | 78.0 | 41.6 | ||
| 7A | 8256 | 39 | 53.6 | 184.1 | −0.0322 | −0.1502 | 12.98 | 50.0 | 38.0 | ||
| 7B | 4129 | 21 | 48.3 | 76.0 | −0.0403 | −0.1528 | 12.98 | 50.0 | 38.0 | ||
| Hydraulic parameters (CE) | |||||||||||
| Sector | ke | x | qn (L/h) | Qs (m3/h) | hs (m) | hin (m) | hmin (m) | hmean (m) | hmax (m) | CV | EU (%) |
| 1 | 1.253 | 0.5 | 11.86 | 42.49 | 203.9 | 95.6 | 85.0 | 94.3 | 122.0 | 4.12 | 90.05 |
| 1A | 7.05 | 6.64 | 135.6 | 35.3 | 29.0 | 31.7 | 44.8 | 3.99 | 91.00 | ||
| 1B | 10.35 | 24.18 | 175.4 | 72.4 | 61.5 | 68.4 | 90.5 | 4.26 | 89.80 | ||
| 2 | 10.41 | 19.49 | 168.3 | 63.5 | 63.2 | 69.0 | 81.5 | 3.42 | 91.60 | ||
| 3 | 11.14 | 39.28 | 173.4 | 75.7 | 70.2 | 79.1 | 96.3 | 3.07 | 90.60 | ||
| 4 | 11.46 | 38.15 | 173.4 | 76.2 | 76.0 | 83.8 | 100.6 | 4.00 | 90.50 | ||
| 5 | 10.13 | 21.71 | 153.0 | 61.4 | 57.8 | 65.4 | 75.2 | 3.10 | 90.40 | ||
| 6 | 9.89 | 31.91 | 188.7 | 64.9 | 57.0 | 62.3 | 72.3 | 2.28 | 92.90 | ||
| 7 | 11.62 | 37.09 | 198.85 | 74.6 | 75.1 | 86.0 | 96.2 | 2.81 | 90.11 | ||
| 7A | 9.74 | 20.24 | 171.3 | 53.3 | 53.3 | 60.5 | 68.4 | 2.59 | 90.90 | ||
| 7B | 9.04 | 9.11 | 148.9 | 49.3 | 46.2 | 52.1 | 59.6 | 3.55 | 90.00 | ||
| Hydraulic parameters (PCE) | |||||||||||
| Sector | ke | x | Qs (m3/h) | hs (m) | hin (m) | hmin (m) | hmean (m) | hmax (m) | CV | EU (%) | |
| 1 | 5 | 0 | 17.48 | 133.1 | 32.0 | 9.1 | 19.3 | 43.4 | 0 | 100 | |
| 1A | 9 | 8.48 | 121.0 | 20.4 | 9.1 | 12.1 | 24.5 | ||||
| 1B | 9 | 21.02 | 143.5 | 41.1 | 9.1 | 19.4 | 41.2 | ||||
| 2 | 9 | 16.86 | 121.4 | 17.0 | 9.1 | 12.6 | 21.3 | ||||
| 3 | 7 | 24.69 | 131.8 | 39.2 | 9.1 | 19.0 | 39.2 | ||||
| 4 | 7 | 23.30 | 123.5 | 31.3 | 9.1 | 18.4 | 32.4 | ||||
| 5 | 9 | 19.30 | 112.7 | 21.7 | 9.1 | 14.1 | 23.2 | ||||
| 6 | 9 | 29.04 | 157.0 | 34.3 | 9.1 | 15.8 | 36.0 | ||||
| 7 | 6 | 19.16 | 146.6 | 27.7 | 9.1 | 20.4 | 32.8 | ||||
| 7A | 9 | 18.70 | 142.3 | 24.6 | 9.1 | 14.3 | 28.6 | ||||
| 7B | 9 | 9.07 | 113.0 | 13.3 | 9.1 | 14.5 | 21.6 | ||||
| Sector | IRRILAB | IRRIPRO | ||
|---|---|---|---|---|
| E (kWh) | E (kWh) | |||
| CE | PCE | CE | PCE | |
| 1 | 34,866 | 22,100 | 41,292 | 24,249 |
| 2 | 16,074 | 11,789 | 18,743 | 11,611 |
| 3 | 13,991 | 10,905 | 14,398 | 12,386 |
| 4 | 18,342 | 15,846 | 22,291 | 16,624 |
| 5 | 14,021 | 11,546 | 17,272 | 12,938 |
| SUM | 97,295 | 72,187 | 113,996 | 77,807 |
| Sector | IRRILAB | IRRIPRO | ||
|---|---|---|---|---|
| E (kWh) | E (kWh) | |||
| CE | PCE | CE | PCE | |
| 1 | 22,306 | 14,456 | 20,164 | 12,845 |
| 1A | 3192 | 3134 | 3525 | 3145 |
| 1B | 11,037 | 8928 | 11,308 | 9252 |
| 2 | 7994 | 6107 | 8693 | 6276 |
| 3 | 14,401 | 10,925 | 16,868 | 12,829 |
| 4 | 13,070 | 10,396 | 15,926 | 11,344 |
| 5 | 8592 | 6877 | 9047 | 6670 |
| 6 | 16,317 | 12,824 | 16,797 | 13,978 |
| 7 | 16,914 | 12,758 | 17,516 | 12,917 |
| 7A | 9280 | 7705 | 9824 | 8159 |
| 7B | 3702 | 3164 | 4140 | 3142 |
| TOTAL 7 sectors | 99,594 | 74,343 | 105,011 | 76,859 |
| TOTAL 9 sectors | 87,585 | 70,060 | 96,128 | 74,795 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baiamonte, G.; Di Dio, P.; Elfahl, M. Verification of IRRILAB Software Application for the Hydraulic Design of a Micro-Irrigation System by Using IRRIPRO for an Apple Farm in Sicily. Water 2021, 13, 694. https://doi.org/10.3390/w13050694
Baiamonte G, Di Dio P, Elfahl M. Verification of IRRILAB Software Application for the Hydraulic Design of a Micro-Irrigation System by Using IRRIPRO for an Apple Farm in Sicily. Water. 2021; 13(5):694. https://doi.org/10.3390/w13050694
Chicago/Turabian StyleBaiamonte, Giorgio, Pietro Di Dio, and Mustafa Elfahl. 2021. "Verification of IRRILAB Software Application for the Hydraulic Design of a Micro-Irrigation System by Using IRRIPRO for an Apple Farm in Sicily" Water 13, no. 5: 694. https://doi.org/10.3390/w13050694
APA StyleBaiamonte, G., Di Dio, P., & Elfahl, M. (2021). Verification of IRRILAB Software Application for the Hydraulic Design of a Micro-Irrigation System by Using IRRIPRO for an Apple Farm in Sicily. Water, 13(5), 694. https://doi.org/10.3390/w13050694