Incorporating the Effects of Complex Soil Layering and Thickness Local Variability into Distributed Landslide Susceptibility Assessments
Abstract
:1. Introduction
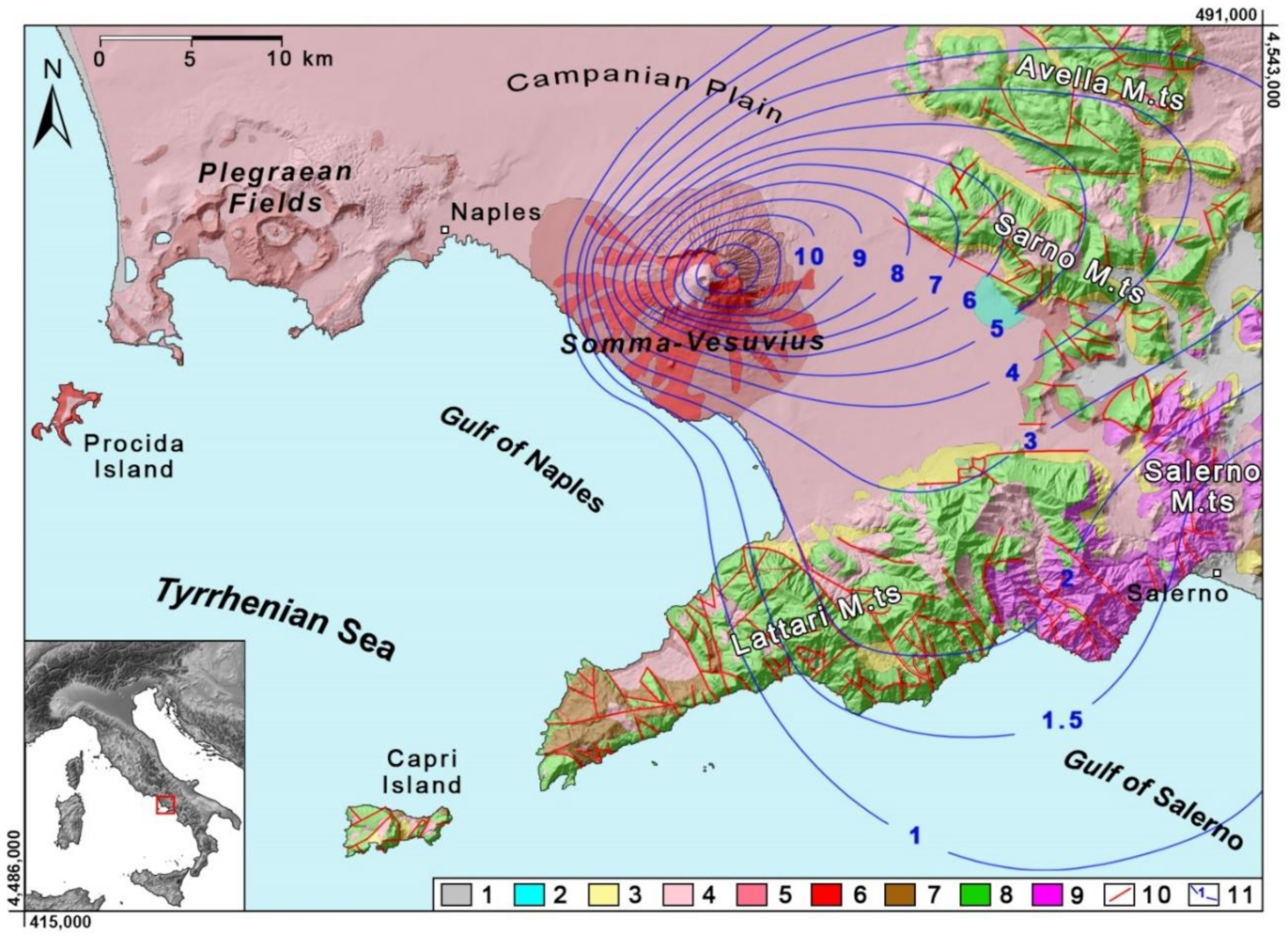
2. Overview of the Testing Area
2.1. Geological and Stratigraphic Settings
2.2. Flow-Type Landslides Involving Ash-Fall Pyroclastic Coverings
3. Data and Methods
3.1. Overview of TRIGRS
3.2. Parameterizing TRIGRS
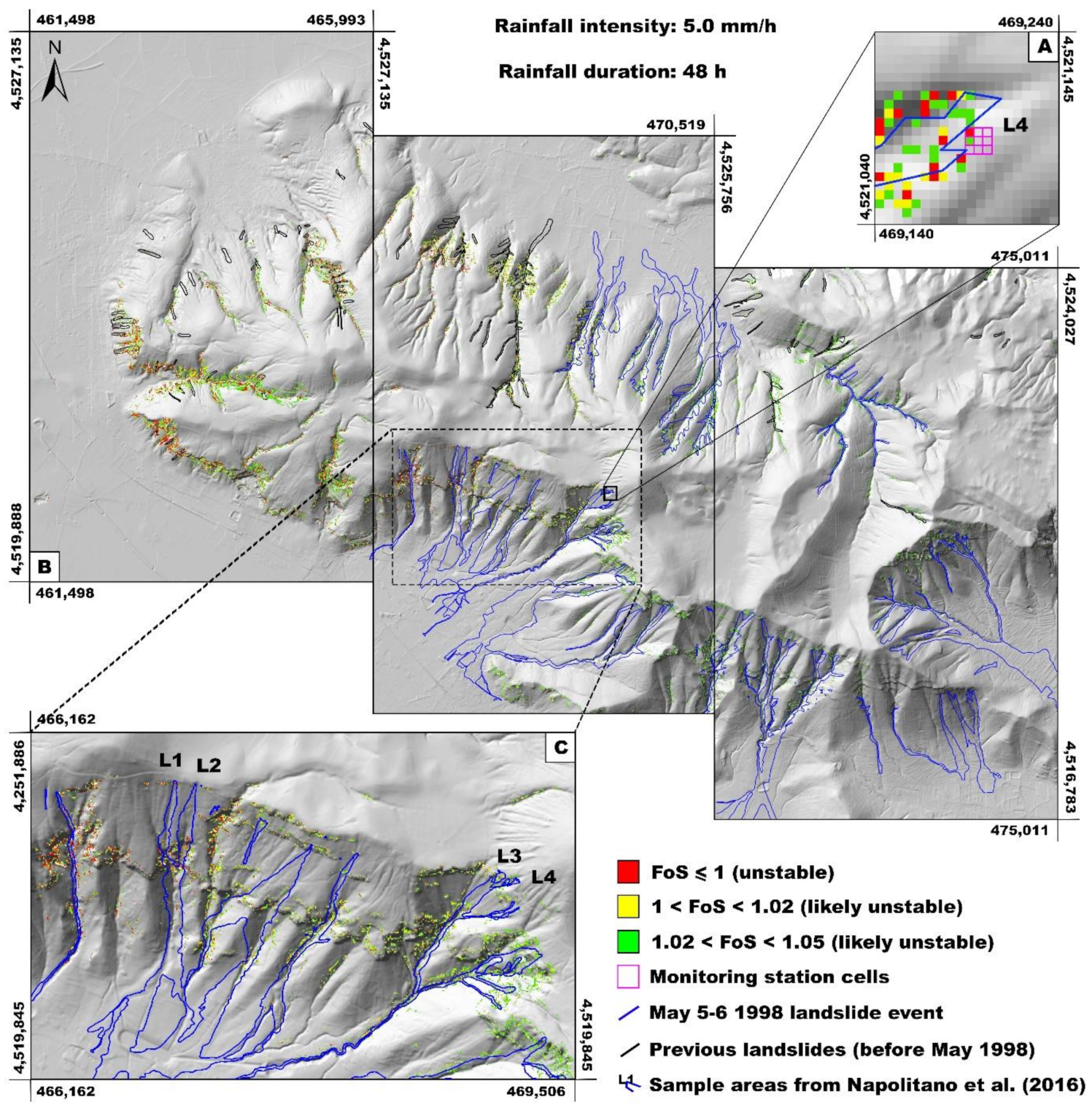
4. Results
4.1. TRIGRS Model Calibration
4.2. Slope Stability Maps for Initial Landslides
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sidle, R.C.; Swanston, D.N. Analysis of a small debris slide in coastal Alaska. Can. Geotech. J. 1983, 19, 167–174. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Morgenstern, N.R. Stress state variables for unsaturated soils. J. Geotech. Eng. Div. 1977, 103, 447–466. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed–form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Baum, R.L.; Godt, J.W.; Coe, J.A. Assessing susceptibility and timing of shallow landslide and debris flow initiation in the Oregon Coast Range, USA. Ital. J. Eng. Geol. Environ. 2011, 825–834. [Google Scholar] [CrossRef]
- Wu, W.; Sidle, R.C. A distributed slope stability model for steep forested basins. Water Res. Res. 1995, 31, 2097–2110. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically–based landslide susceptibility models. Earth Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Aleotti, P. A warning system for rainfall-induced shallow failures. Eng. Geol. 2004, 73, 247–265. [Google Scholar] [CrossRef]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi–scale study, central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Reichenbach, P.; Galli, M.; Cardinali, M.; Guzzetti, F.; Ardizzone, F. Geomorphologic mapping to assess landslide risk: Concepts, methods and applications in the Umbria region of central Italy. In Landslide Risk Assessment; Glade, T., Anderson, M.G., Crozier, M.J., Eds.; John Wiley: Chichester, UK, 2005; pp. 429–468. [Google Scholar] [CrossRef]
- Carrara, A. Multivariate models for landslide hazard evaluation. Math. Geol. 1983, 15, 402–426. [Google Scholar] [CrossRef]
- Mandal, S.; Mondal, S. Statistical Approaches for Landslide Susceptibility Assessment Prediction; Springer: Berlin/Heidelberg, Germany, 2019; ISBN 978-3-319-93896-7. [Google Scholar] [CrossRef]
- Huabin, W.; Gangjun, L.; Gonghui, W. GIS-based landslide hazard assessment: An overview. Prog. Phys. Geogr. 2005, 29, 548–567. [Google Scholar] [CrossRef]
- Chacón, J.; Irigaray, C.; Fernandez, T.; El Hamdouni, R. Engineering geology maps: Landslides and geographical information systems. Bull. Eng. Geol. Environ. 2006, 65, 341–411. [Google Scholar] [CrossRef]
- van Westen, C.J.; Castellanos, E.; Kuriakose, S.L. Spatial data for landslide susceptibility, hazard, and vulnerability assessment: An overview. Eng. Geol. 2008, 102, 112–131. [Google Scholar] [CrossRef]
- Hammond, C.; Hall, D.; Miller, S.; Swetik, P. Level I Stability Analysis (LISA) Documentation for Version 2.0; (324 25th St., Ogden 84401); U.S. Department of Agriculture, Forest Service, Intermountain Research Station: Ogden, UT, USA, 1992; 285.
- Montgomery, D.R.; Dietrich, W.E. A Physically based model for the topographic control on shallow landsliding. Water Res. Res. 1994, 30, 83–92. [Google Scholar] [CrossRef]
- Borga, M.; Dalla Fontana, G.; De Ros, D.; Marchi, L. Shallow landslide hazard assessment using a physically based model and digital elevation data. Environ. Geol. 1998, 35, 81–88. [Google Scholar] [CrossRef]
- Pack, R.T.; Tarboton, D.G.; Goodwin, C.N. The Sinmap Approach to Terrain Stability Mapping. In Proceedings of the 8th Congress of the International Association of Engineering Geology, Vancouver, BC, Canada, 21–25 September 1998. [Google Scholar]
- Baum, R.L.; Godt, J.W. Early warning of rainfall-induced shallow landslides and debris flows in the USA. Landslides 2010, 7, 259–272. [Google Scholar] [CrossRef]
- Chen, H.X.; Zhang, L.M. A physically based distributed cell model for predicting regional rainfall-induced shallow slope failures. Eng. Geol. 2014, 176, 79–92. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2001; ISBN 978-0-470-71459-1. [Google Scholar]
- Loague, K.; Heppner, C.S.; Mirus, B.B.; Ebel, B.A.; Ran, Q.; Carr, A.E.; Be Ville, S.H.; Vander Kwaak, J.E. Physics-based hydrologic-response simulation: Foundation for hydroecology and hydrogeomorphology. Hydrol. Process. 2006, 20, 1231–1237. [Google Scholar] [CrossRef]
- Mirus, B.B. Evaluating the importance of characterizing soil structure and horizons in parameterizing a hydrologic process model. Hydrol. Process. 2015, 29, 4611–4623. [Google Scholar] [CrossRef]
- Fatichi, S.; Dani, O.; Walko, R.; Vereecken, H.; Young, M.H.; Ghezzehei, T.A.; Hengl, T.; Kollet, S.; Agam, N.; Avissar, R. Soil structure is an important omission in Earth system models. Nat. Commun. 2020, 11. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, R.M.; Kollet, S.J. Interdependence of groundwater dynamics and land-energy feedbacks under climate change. Nat. Geosci. 2008, 1, 665–669. [Google Scholar] [CrossRef]
- Goderniaux, P.; Brouyere, S.; Fowler, H.J.; Blenkinsop, S.; Therrien, R.; Orban, P.; Dassargues, A. Large scale surface–subsurface hydrological model to assess climate change impacts on groundwater reserves. J. Hydrol. 2009, 373, 122–138. [Google Scholar] [CrossRef]
- Camporese, M.; Daly, E.; Dreseld, P.E.; Webb, J.A. Simplified modeling of catchment-scale evapotranspiration via boundary condition switching. Adv. Water Resour. 2014, 69, 95–105. [Google Scholar] [CrossRef]
- Condon, L.E.; Maxwell, R.M. Feedbacks between managed irrigation and water availability: Diagnosing temporal and spatial patterns using an integrated hydrologic model. Water Resour. Res. 2014, 50, 2600–2616. [Google Scholar] [CrossRef]
- Zhu, J.H.; Anderson, S.A. Determination of shear strength of Hawaiian residual soil subjected to rainfall-induced landslides. Geotechnique 1998, 48, 73–82. [Google Scholar] [CrossRef]
- Gerscovich, D.M.S.; Vargas, E.A., Jr.; de Campos, T.M.P. On the evaluation of unsaturated flow in a natural slope in Rio de Janeiro, Brazil. Eng. Geol. 2006, 88, 23–40. [Google Scholar] [CrossRef]
- Mirus, B.B.; Ebel, B.A.; Loague, K.; Wemple, B.C. Simulated effect of a forest road on near–surface hydrologic respeartonse: Redux. Earth Surf. Proc. Landf. 2007. [Google Scholar] [CrossRef]
- Zhao, H.F.; Zhang, L.M. Instability of saturated and unsaturated coarse granular soils. J. Geotech. Geoenviron. 2014, 140, 25–35. [Google Scholar] [CrossRef]
- Fusco, F.; De Vita, P.; Allocca, V. Hydro-geomorphological modelling of ash-fall pyroclastic soils for debris flow initiation and groundwater recharge in Campania (Southern Italy). Catena 2017, 158, 235–249. [Google Scholar] [CrossRef]
- Yang, H.; Rahardjo, H.; Leong, E.C. Behavior of unsaturated layered soil columns during infiltration. J. Hydrol. Eng. 2006, 11, 329–337. [Google Scholar] [CrossRef]
- Schneider, P.; Pool, S.; Strouhal, L.; Seibert, J. True colors-experimental identification of hydrological processes at a hillslope prone to slide. Hydrol. Earth Syst. Sci. 2014, 18, 875–892. [Google Scholar] [CrossRef] [Green Version]
- Hübner, R.; Günther, T.; Heller, K.; Noell, U.; Kleber, A. Impacts of a capillary barrier on infiltration and subsurface stormflow in layered slope deposits monitored with 3-D ERT and hydrometric measurements. Hydrol. Earth Syst. Sci. 2017, 21, 5181–5199. [Google Scholar] [CrossRef] [Green Version]
- Formetta, G.; Capparelli, G. Quantifying the three-dimensional effects of anisotropic soil horizons on hillslope hydrology and stability. J. Hydrol. 2019, 570, 329–342. [Google Scholar] [CrossRef]
- Au, S.W.C. Rain-induced slope instability in Hong Kong. Eng. Geol. 1998, 51, 1–36. [Google Scholar] [CrossRef]
- Chen, H.; Lee, C.F.; Law, K.T. Causative mechanisms of rainfall-induced fill slope failures. J. Geotech. Geoenviron. Eng. 2004, 130, 593–602. [Google Scholar] [CrossRef]
- Collins, B.D.; Znidarcic, D. Stability analyses of rainfall induced landslides. J. Geotech. Geoenviron. Eng. 2004, 130, 362–372. [Google Scholar] [CrossRef]
- Zhang, L.L.; Zhang, J.; Zhang, L.M.; Tang, W.H. Stability analysis of rainfall-induced slope failure: A review. Proc. Inst. Civ. Eng. Geotech. Eng. 2011, 164, 299–316. [Google Scholar] [CrossRef] [Green Version]
- Perkins, J.P.; Reid, M.E.; Schmidt, K.M. Control of landslide volume and hazard by glacial stratigraphic architecture, northwest Washington State, USA. Geology 2017, 45, 1139–1142. [Google Scholar] [CrossRef]
- Yeh, T.C.J.; Ye, M. Estimation of effective unsaturated hydraulic conductivity tensor using spatial moments of observed moisture plume. Water Res. Res. 2005, 41, W03014. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W. Hillslope hydrology and stability. In Hillslope Hydrology and Stability; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Greco, R.; Comegna, L.; Damiano, E.; Guida, A.; Olivares, L.; Picarelli, L. Hydrological modelling of a slope covered with shallow pyroclastic deposits from field monitoring data. Hydrol. Earth Syst. Sci. 2013, 17, 4001–4013. [Google Scholar] [CrossRef] [Green Version]
- Cascini, L.; Sorbino, G.; Cuomo, S. Seasonal effects of rainfall on the shallow pyroclastic deposits of the Campania region (southern Italy). Landslides 2014, 11, 779–792. [Google Scholar] [CrossRef]
- Fusco, F.; De Vita, P. Hydrological monitoring of ash-fall pyroclastic soil mantled slopes in Campania (Southern Italy). In Advancing Culture of Living with Landslides; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- De Vita, P.; Fusco, F.; Tufano, R.; Cusano, D. Seasonal and event-based hydrological response of ash-fall pyroclastic cover in Campania (Southern Italy) for debris flow hazard assessment. Water 2018, 10, 1140. [Google Scholar] [CrossRef] [Green Version]
- Fusco, F.; De Vita, P.; Mirus, B.B.; Baum, R.L.; Allocca, V.; Tufano, R.; Calcaterra, D. Physically Based Estimation of Rainfall Thresholds Triggering Shallow Landslides in Volcanic Slopes of Southern Italy. Water 2019, 11, 1915. [Google Scholar] [CrossRef] [Green Version]
- Patacca, E.; Scandone, P. Geology of the Southern Apennines. Ital. J. Geosci. 2007, 7, 75–119. [Google Scholar]
- Brancaccio, L.; Cinque, A.; Russo, F.; Sgambati, D. Le frane del 5–6 maggio 1998 sul gruppo montuoso Pizzo D’Alvano (Campania): Osservazioni gemorfologiche sulla loro distribuzione e sulla dinamica delle connesse colate. Quad. Geol. Appl. 2002, 7, 5–36. [Google Scholar]
- Rolandi, G.; Bertolini, F.; Cozzolino, G.; Esposito, N.; Sannino, D. Sull’origine delle coltri piroclastiche presenti sul versante occidentale del Pizzo d’Alvano (Sarno—Campania). Quad. Geol. Appl. 2000, 7, 213–235. (In Italian) [Google Scholar]
- Shoji, S.; Dahlgren, R.; Nanzyo, M. Morphology of volcanic ash soils. In Volcanic Ash Soils; Elsevier: Amsterdam, The Netherlands, 1993; pp. 7–35. [Google Scholar]
- Guadagno, F.M.; Magaldi, S. Considerazioni suelle proprietà geotecniche dei suoli allofanici di copertura delle dorsali carbonatiche campane. Quad. Geol. Appl. 2000, 7, 143–155. (In Italian) [Google Scholar]
- Terribile, F.; Basile, A.; De Mascellis, R.; Di Gennaro, A.; Vingiani, S. I suoli delle aree di crisi di Quindici e Sarno: Proprietà e comportamenti in relazione ai fenomeni franosi del 1998. Quad. Geol. Appl. 2000, 7, 60–79. (In Italian) [Google Scholar]
- Scognamiglio, S.; Basile, A.; Calcaterra, D.; Iamarino, M.; Langella, G.; Moretti, P.; Vingiani, S.; Terribile, F. Andic soils and flow-like landslides: Cause–effect evidence from Italy. Land Degrad. Dev. 2018, 30. [Google Scholar] [CrossRef]
- De Vita, P.; Celico, P.; Siniscalchi, P.; Panza, R. Distribution, hydrogeological features and landslide hazard of pyroclastic soils on carbonate slopes in the area surrounding Mount Somma–Vesuvius (Italy). Ital. J. Eng. Geol. Environ. 2006, 1, 75–98. [Google Scholar] [CrossRef]
- Fusco, F.; De Vita, P.; Napolitano, E.; Allocca, V.; Manna, F. Monitoring the soil suction regime of landslide–prone ash-fall pyroclastic deposits covering slopes in the Sarno area (Campania-Southern Italy). Rend. Online Soc. Geol. Ital. 2013, 24, 146–148. [Google Scholar]
- De Vita, P.; Aquino, D.; Celico, P.B. Small-Scale Factors Controlling Onset of the Debris Avalanche of 4 March 2005 at Nocera Inferiore (Southern Italy). Adv. Cult. Living Landslides 2017, 467–475. [Google Scholar] [CrossRef]
- Tufano, R.; Annunziata, L.; Di Clemente, E.; Falgiano, G.; Fusco, F.; De Vita, P. Analysis of Shear Strength Variability of Ash-Fall Pyroclastic Soils Involved in Flow-Like Landslides. Underst. Reducing Landslide Disaster Risk 2021, 4, 329–334. [Google Scholar] [CrossRef]
- De Vita, P.; Nappi, M. Regional distribution of ash-fall pyroclastic deposits in Campania (Southern Italy) for landslide susceptibility assessment. In Landslide Science and Practice; Margottini, C., Canuti, P., Sassa, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 3, pp. 103–110. ISBN 978-3-642-31310-3. [Google Scholar]
- Del Soldato, M.; Pazzi, V.; Segoni, S.; De Vita, P.; Tofani, V.; Moretti, S. Spatial modeling of pyroclastic cover deposit thickness (depth to bedrock) in peri-volcanic area of Campania (Southern Italy). Earth Surf. Process. Landf. 2018, 43, 1757–1767. [Google Scholar] [CrossRef] [Green Version]
- USDA. Keys to Soil Taxonomy, 12th ed.; United States Department of Agriculture Natural Resources Conservation Service: Washington, DC, USA, 2014; 372p.
- De Vita, P.; Agrello, D.; Ambrosino, F. Landslide susceptibility assessment in ash-fall pyroclastic deposits surrounding Mount Somma-Vesuvius: Application of geophysical surveys for soil thickness mapping. J. Appl. Geophys. 2006, 59, 126–139. [Google Scholar] [CrossRef]
- Calcaterra, D.; Parise, M.; Palma, B.; Pelella, L. The May 5th 1998, landsliding event in Campania (Southern Italy): Inventory of slope movements in the Quindici area. In Proceedings of the International Symposium on Slope Stability Engineering, Shikoku, Japan, 8–11 November 1999; Volume 2, pp. 1361–1366. [Google Scholar]
- Mele, R.; Del Prete, S. Lo studio della franosita storica come utile strumento per la valutazione della pericolosita da frane. Un esempio nell’area di Gragnano (Campania). Bull. Soc. Geol. Ital. 1999, 118, 91–111. [Google Scholar]
- Calcaterra, D.; Parise, M.; Palma, B.; Pelella, L. The influence of meteoric events in triggering shallow landslides in pyroclastic deposits of Campania, Italy. In Landslides in Research, Theory and Practice, Proceedings of the 8th International Symposium on Landslides, Cardiff, UK, 26–30 June 2000; Bromhead, E., Dixon, N., Ibsen, M.L., Eds.; Thomas Telford: London, UK, 2000; Volume 1, pp. 209–214. [Google Scholar]
- Calcaterra, D.; de Riso, R.; Evangelista, A.; Nicotera, M.V.; Santo, A.; Scotto Di Santolo, A. Slope instabilities in the pyroclastic deposits of the Phlegraean district and the carbonate Apennine (Campania, Italy). In Proceedings of the International Workshop on Occurrence and Mechanisms of Flows in Natural Slopes and Earthfills, Sorrento, Italy, 14–16 May 2003; pp. 61–75. [Google Scholar]
- Cascini, L.; Cuomo, S.; Guida, D. Typical source areas of May 1998 flow-like mass movements in the Campania region, Southern Italy. Eng. Geol. 2008, 96, 107–125. [Google Scholar] [CrossRef]
- Esposito, E.; Porfido, S.; Violante, C.; Biscardini, C.; Alaia, F.; Esposto, G. Water events and historical flood recurrences in the Vietri sul Mare coastal area (Costiera Amalfitana, Southern Italy). Int. Assoc. Hydrol. Sci. 2004, 286, 95–106. [Google Scholar]
- Del Prete, M.; Guadagno, F.M.; Hawkins, A.B. Preliminary report on the landslides of 5 May 1998, Campania, Southern Italy. Bull. Eng. Geol. Environ. 1998, 57, 41–50. [Google Scholar] [CrossRef]
- Celico, P.; Guadagno, F.M. L’instabilità delle coltri piroclastiche delle dorsali carbonatiche in Campania: Attuali conoscenze. Quad. Geol. Appl. 1998, 5, 129–188. (In Italian) [Google Scholar]
- Fiorillo, F.; Wilson, R.C. Rainfall induced debris flows in pyroclastic deposits, Campania (Southern Italy). Eng. Geol. 2004, 75, 263–289. [Google Scholar] [CrossRef]
- Fiorillo, F.; Guadagno, F.M.; Aquini, S.; De Blasio, A. The December 1999 Cervinara landslides: Further debris flows in the pyroclastic deposits of Campania (Southern Italy). Bull. Eng. Geol. Environ. 2001, 60, 171–184. [Google Scholar] [CrossRef]
- Guadagno, F.M.; Revellino, P. Debris avalanches and debris flows of the Campania Region (Southern Italy). In Debris–Flow Hazard and Related Phenomena; Jacob, M., Hungr, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 2, pp. 489–518. [Google Scholar]
- De Vita, P.; Napolitano, E.; Godt, J.; Baum, R. Deterministic estimation of hydrological thresholds for shallow landslide initiation and slope stability models: Case study from the Somma-Vesuvius area of Southern Italy. Landslides 2013, 10, 713–728. [Google Scholar] [CrossRef]
- Napolitano, E.; Fusco, F.; Baum, R.L.; Godt, J.W.; De Vita, P. Effect of antecedent-hydrological conditions on rainfall triggering of debris flows in ash-fall pyroclastic mantled slopes of Campania (Southern Italy). Landslides 2016, 13, 967–983. [Google Scholar] [CrossRef]
- Hungr, O.; Evans, S.G.; Bovis, M.J.; Hutchinson, J.N. A review of the classification of landslides of flow type. Environ. Eng. Geosci. 2001, 7, 221–238. [Google Scholar] [CrossRef]
- Jakob, M.; Hungr, O. Debris–Flow Hazards and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 2005; Volume 739. [Google Scholar] [CrossRef]
- UNESCO Working Party on World Landslide Inventory. A suggested method for describing the activity of a landslide. Bull. Int. Assoc. Eng. Geol. 1993, 47, 53–57. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.B.; Fusi, N.; Dal Negro, P. Shallow landslides in pyroclastic soils: A distributed modelling approach for hazard assessment. Eng. Geol. 2004, 73, 277–295. [Google Scholar] [CrossRef]
- Di Crescenzo, G.; Santo, A. Debris Slide–Rapid Earth Flow in the Carbonate Massifs of the Campania Region (Southern Italy): Morphological and Morphometric Data for Evaluating Triggering Susceptibility. Geomorphology 2005, 66, 255–276. [Google Scholar] [CrossRef]
- Palma, B.; Calcaterra, D.; Parise, M. Modelli geologici e meccanismi di innesco di frane da scorrimento-colata rapida nei depositi vulcanoclastici della Campania. Geol. Ambient. E Min. 2009, 1, 21–48. [Google Scholar]
- Perriello Zampelli, S.; Sessa, E.B.; Cavallaro, M. Application of a GIS-aided method for the assessment of volcaniclastic soil sliding susceptibility to sample areas of Campania (Southern Italy). Nat. Hazards 2011, 61, 155–168. [Google Scholar] [CrossRef]
- Lizarraga, J.L.; Buscarnera, G. Spatially distributed modeling of rainfall-induced landslides in shallow layered slopes. Landslides 2018. [Google Scholar] [CrossRef]
- Sepe, C.; Confuorto, P.; Angrisani, A.C.; Di Martire, D.; Di Napoli, M.; Calcaterra, D. Application of a Statistical Approach to Landslide Susceptibility Map Generation in Urban Settings. In IAEG/AEG Annual Meeting Proceedings, San Francisco, California, USA, 17–21 September 2018; Shakoor, A., Cato, K., Eds.; Springer: Cham, Switzerland, 2018; Volume 1, pp. 155–162. [Google Scholar] [CrossRef]
- Campbell, R.H. Soil Slips, Debris Flows, and Rainstorms in the Santa Monica Mountains and Vicinity, Southern California; US Geological Survey Professional Paper 851; U.S. Government Printing Office: Washington, DC, USA, 1975; 51p.
- Caine, N. The rainfall intensity–duration control of shallow landslides and debris flows. Geogr. Ann. 1980, 62A, 23–27. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Baum, R.L.; Godt, J.W. Correction to “Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration”. J. Geophys. Res. Earth Surf. 2013, 118, 1. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Luciani, S.; Vennari, C.; Guzzetti, F. Lithological and seasonal control on rainfall thresholds for the possible initiation of landslides in central Italy. Geomorphology 2012, 139/140, 79–90. [Google Scholar] [CrossRef]
- Celico, P.; Guadagno, F.M.; Vallario, A. Proposta di un modello interpretativo per lo studio delle frane nei terreni piroclastici. Geol. Appl. E Idrogeol. 1986, 21, 173–193. [Google Scholar]
- Cascini, L.; Cuomo, S.; Pastor, M.; Sorbino, G. Modeling of rainfall-induced shallow landslides of the Flow type. J. Geotech. Geo Environ. Eng. 2010, 85–98. [Google Scholar] [CrossRef]
- Crosta, G.B.; Dal Negro, P. Observations and modelling of soil slip-debris flow initiation processes in piroclastica deposits: The Sarno 1998 event. Nat. Hazards Earth Syst. Sci. 2003, 3, 53–69. [Google Scholar] [CrossRef] [Green Version]
- De Vita, P.; Fusco, F.; Napolitano, E.; Tufano, R. Physically based models for estimating rainfall triggering debris flows in Campania (Southern Italy). In Advancing Culture of Living with Landslides; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef] [Green Version]
- Wieczorek, G.F.; Glade, T. Climatic factors influencing the occurrence of debris flows. In Debris-flow Hazards and Related Phenomena; Jakob, M., Hungr, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 325–362. [Google Scholar]
- Tufano, R.; Cesarano, M.; Fusco, F.; De Vita, P. Probabilistic approaches for assessing rainfall thresholds triggering shallow landslides. The case study of the peri-Vesuvian area (Southern Italy). Ital. J. Eng. Geol. Environ. 2019, 1, 105–110. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef] [Green Version]
- Gardner, W. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Srivastava, R.; Yeh, T.C.J. Analytical solutions for one dimensional, transient infiltration toward the water table in homogeneous and layered soils. Water Resour. Res. 1991, 27, 753–762. [Google Scholar] [CrossRef]
- Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS—A Fortran Program for Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Analysis, Version 2.0; Open-File Report 2008-1159; U.S. Geological Survey: Reston, VA, USA, 2008; 75p.
- Taylor, D.W. Fundamentals of soil mechanics. Soil Sci. 1948, 66, 700. [Google Scholar] [CrossRef]
- Hsieh, P.A.; Wingle, W.; Healy, R.W. VS2DI—A Graphical Software Package for Simulating Fluid Flow and Solute or Energy Transport in Variably Saturated Porous Media; Water-Resources Investigations Report 99-4130; U.S. Geological Survey: Lakewood, CO, USA, 2000.
- Allocca, V.; De Vita, P.; Manna, F.; Nimmo, J.R. Groundwater recharge assessment at local and episodic scale in a soil mantled perched karst aquifer in Southern Italy. J. Hydrol. 2015, 529, 843–854. [Google Scholar] [CrossRef]
- De Vita, P.; Allocca, V.; Celico, F.; Fabbrocino, S.; Mattia, C.; Monacelli, G.; Musilli, I.; Piscopo, V.; Scalise, A.R.; Summa, G.; et al. Hydrogeology of continental Southern Italy. J. Maps 2018, 14, 230–241. [Google Scholar] [CrossRef] [Green Version]
- Thomas, M.A.; Mirus, B.B.; Smith, J.B. Hillslopes in humid-tropical climates aren’t always wet: Implications for hydrologic response and landslide initiation in Puerto Rico. Hydrol. Process. 2020. [Google Scholar] [CrossRef]
- Raia, S.; Alvioli, M.; Rossi, M. Improving predictive power of physically based rainfall-induced shallow landslide models: A probabilistic approach. Geosci. Model. Dev. 2014, 7, 495–514. [Google Scholar] [CrossRef] [Green Version]
- Gioia, E.; Speranza, G.; Ferretti, M.; Godt, J.W.; Baum, R.L.; Marincioni, F. Application of a process-based shallow landslide hazard model over a broad area in central Italy. Landslides 2015, 13, 1197–1214. [Google Scholar] [CrossRef]
- Mirus, B.B.; Loague, K. How runoff begins (and ends): Characterizing hydrologic response at the catchment scale. Water Resour. Res. 2013, 49, 2987–3006. [Google Scholar] [CrossRef]
- Capparelli, G.; Damiano, E.; Greco, R.; Olivares, L.; Spolverino, G. Physical modeling investigation of rainfall infiltration in steep layered volcanoclastic slopes. J. Hydrol. 2019, 580. [Google Scholar] [CrossRef]
- Salciarini, D.; Castorino, G.C.; Cuomo, S.; Tamagnini, C. A New Tool for Large-Area Analysis of Transient Pore Water Pressures in Layered Shallow Covers Prone to Failure. Geotech. Saf. Risk V 2015, 2000, 772–778. [Google Scholar] [CrossRef]
- Damiano, E.; Greco, R.; Guida, A.; Olivares, L.; Picarelli, L. Investigation on rainwater infiltration into layered shallow covers in pyroclastic soils and its effect on slope stability. Eng. Geol. 2017, 220, 208–218. [Google Scholar] [CrossRef]
- Guadagno, F.M.; Palmieri, M.; Siviero, V.; Vallario, A. La frana di Palma Campania del 22 Febbraio 1986. Geol. Tec. 1988, 4I, 18–29. [Google Scholar]
- Furcolo, P.; Pelosi, A. Orographic Effects on Extreme Rainfall at Different Durations: A Case Study in Campania Region (Southern Italy). J. Geosci. Environ. Prot. 2018, 6, 77–88. [Google Scholar] [CrossRef] [Green Version]










| (a) | Hydro–Mechanical Properties | ||||||||
| Ksat (m/s) | θs (ad.) | θr (ad.) | α (cm−1) | n (ad.) | ’ (°) | c′ (kPa) | |||
| Soil horizons (USDA) | B | 4.82 × 10−5 | 0.505 | 0.083 | 0.884 | 1.307 | 32.0 | 4.500 | |
| C | 2.82 × 10−3 | 0.500 | 0.001 | 20.39 | 1.081 | 37.0 | 0.000 | ||
| Bb | 6.00 × 10−6 | 0.663 | 0.001 | 0.884 | 1.307 | 34.0 | 1.800 | ||
| Bbbasal | 2.48 × 10−7 | 0.505 | 0.083 | 0.884 | 1.307 | 35.0 | 8.100 | ||
| (b) Test site | Soil column and thickness (m) | Weighted Harmonic Mean | |||||||
| Ksat (m/s) | θs (ad.) | θr (ad.) | α (cm−1) | n (ad.) | ’(°) | c′ (kPa) | |||
| L1 | 1a | 4.85 | 8.53 × 10−6 | 0.590 | 0.132 | 3.059 | 1.294 | 34.0 | 3.820 |
| 1b | 4.34 | 4.78 × 10−6 | 0.581 | 0.111 | 3.851 | 1.316 | 33.8 | 4.350 | |
| 1c | 1.62 | 1.68 × 10−6 | 0.584 | 0.118 | 3.590 | 1.307 | 33.9 | 4.186 | |
| L2 | 2a | 3.23 | 5.68 × 10−6 | 0.589 | 0.143 | 2.689 | 1.299 | 34.0 | 3.493 |
| 2b | 3.13 | 5.30 × 10−6 | 0.565 | 0.122 | 3.618 | 1.372 | 33.5 | 3.884 | |
| 2c | 1.75 | 2.06 × 10−6 | 0.567 | 0.099 | 4.384 | 1.356 | 33.5 | 4.585 | |
| L3 | 3a | 3.99 | 2.65 × 10−6 | 0.580 | 0.073 | 5.174 | 1.302 | 33.8 | 5.496 |
| 3b | 3.35 | 3.34 × 10−6 | 0.573 | 0.098 | 4.347 | 1.335 | 33.7 | 4.659 | |
| 3c | 2.43 | 5.20 × 10−6 | 0.557 | 0.122 | 3.689 | 1.399 | 33.3 | 3.806 | |
| L4 | 4a | 3.21 | 2.88 × 10−6 | 0.574 | 0.089 | 4.673 | 1.328 | 33.7 | 4.959 |
| 4b | 3.09 | 3.78 × 10−6 | 0.556 | 0.080 | 5.109 | 1.385 | 33.3 | 5.027 | |
| 4c | 1.47 | 7.16 × 10−6 | 0.558 | 0.097 | 4.512 | 1.386 | 33.3 | 4.539 | |
| TRIGRS model | 4.28 × 10−6 | 0.574 | 0.105 | 4.099 | 1.332 | 33.7 | 4.445 | ||
| Rainfall Intensity (mm/h) | 2.5 | 5.0 | 10 | 20 | 40 | |
| Winter Threshold [77] | Duration (hours) | 77 | 47 | 22 | 11 | 6 |
| Frequency of May 1998 source areas, unstable under TRIGRS modelling | 1% | 90 | 47 | 22 | 14 | 14 |
| 5% | 92 | 49 | 23 | 15 | 15 | |
| 50% | 109 | 55 | 33 | 27 | 27 | |
| 95% | 170 | 120 | 77 | 49 | 34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fusco, F.; Mirus, B.B.; Baum, R.L.; Calcaterra, D.; De Vita, P. Incorporating the Effects of Complex Soil Layering and Thickness Local Variability into Distributed Landslide Susceptibility Assessments. Water 2021, 13, 713. https://doi.org/10.3390/w13050713
Fusco F, Mirus BB, Baum RL, Calcaterra D, De Vita P. Incorporating the Effects of Complex Soil Layering and Thickness Local Variability into Distributed Landslide Susceptibility Assessments. Water. 2021; 13(5):713. https://doi.org/10.3390/w13050713
Chicago/Turabian StyleFusco, Francesco, Benjamin B. Mirus, Rex L. Baum, Domenico Calcaterra, and Pantaleone De Vita. 2021. "Incorporating the Effects of Complex Soil Layering and Thickness Local Variability into Distributed Landslide Susceptibility Assessments" Water 13, no. 5: 713. https://doi.org/10.3390/w13050713
APA StyleFusco, F., Mirus, B. B., Baum, R. L., Calcaterra, D., & De Vita, P. (2021). Incorporating the Effects of Complex Soil Layering and Thickness Local Variability into Distributed Landslide Susceptibility Assessments. Water, 13(5), 713. https://doi.org/10.3390/w13050713








