Adaptive Prediction of Water Droplet Infiltration Effectiveness of Sprinkler Irrigation Using Regularized Sparse Autoencoder–Adaptive Network-Based Fuzzy Inference System (RSAE–ANFIS)
Abstract
1. Introduction
2. Calibration of Droplet Infiltration Effectiveness
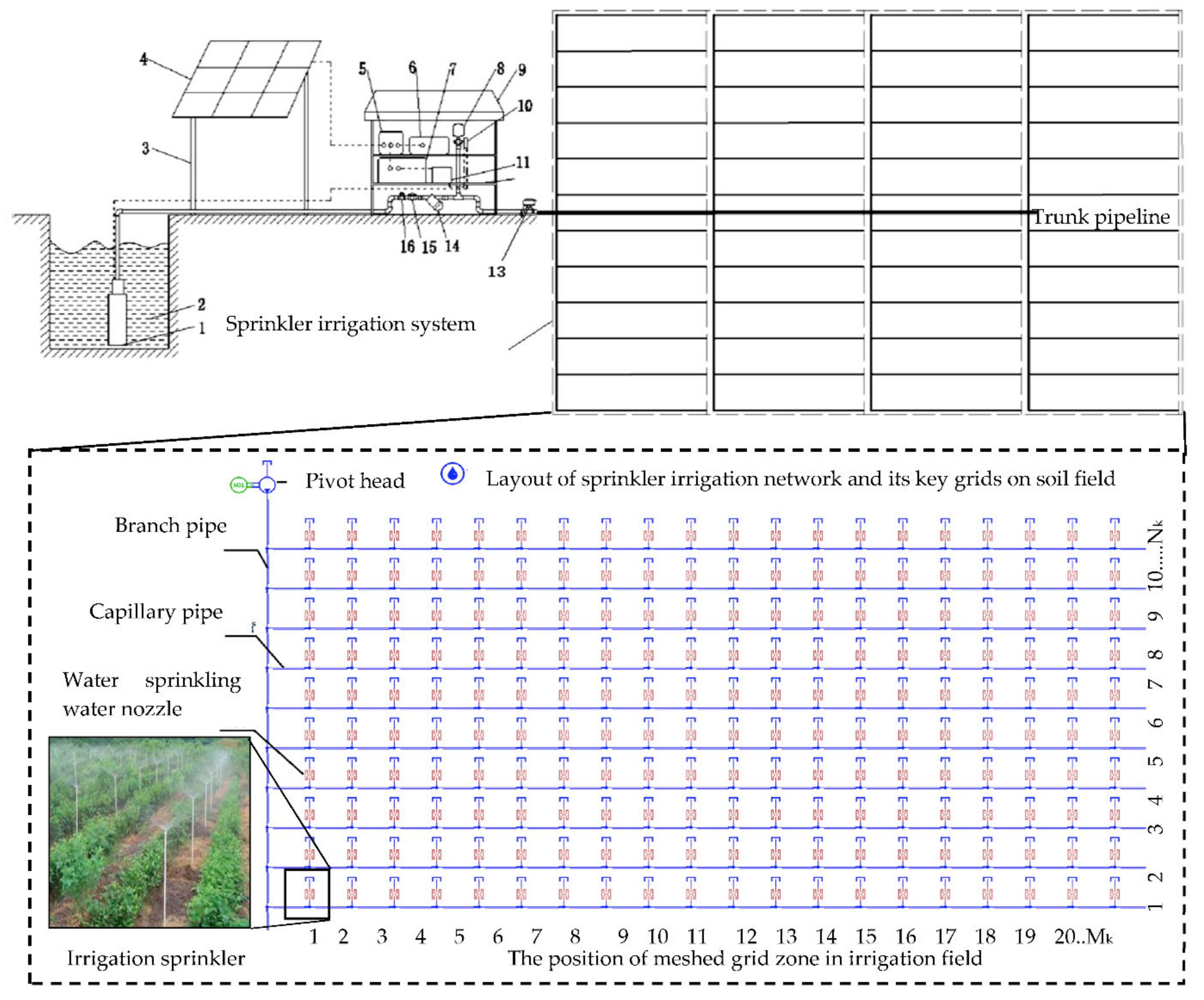
3. Experimental Environment of Sprinkler Irrigation
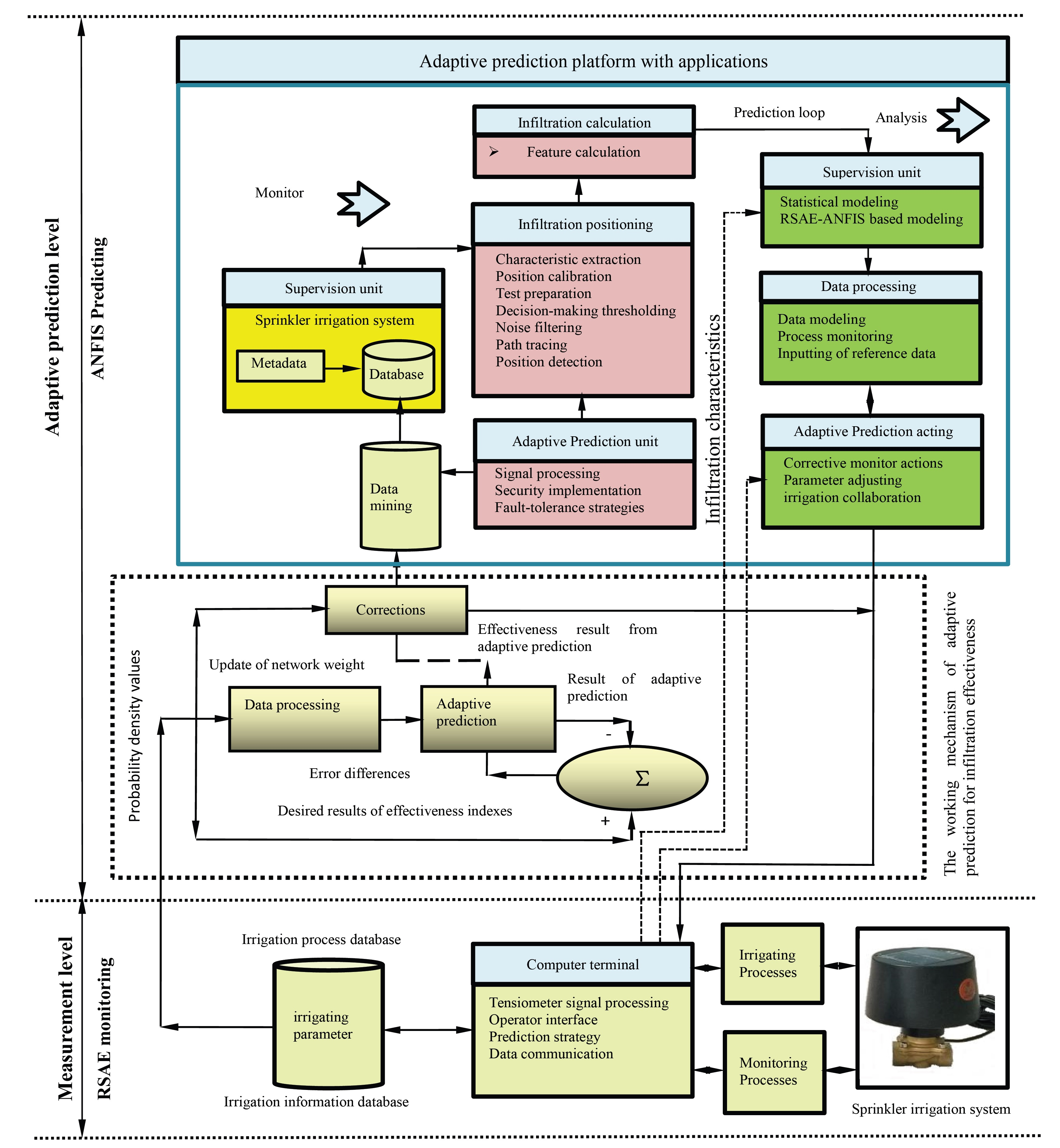
4. Regularized Sparse Autoencoder–Adaptive Network-Based Fuzzy Inference System
4.1. Working Mechanism of Regularized Sparse Autoencoder (RSAE)
4.2. Working Mechanism of ANFIS (Adaptive Network-Based Fuzzy Inference System) Integrated with RSAE
5. Adaptive Prediction of Water Droplet Infiltration Effectiveness
5.1. Sprinkler Irrigation System
5.2. Adaptive Prediction of Droplet Infiltration Effectiveness
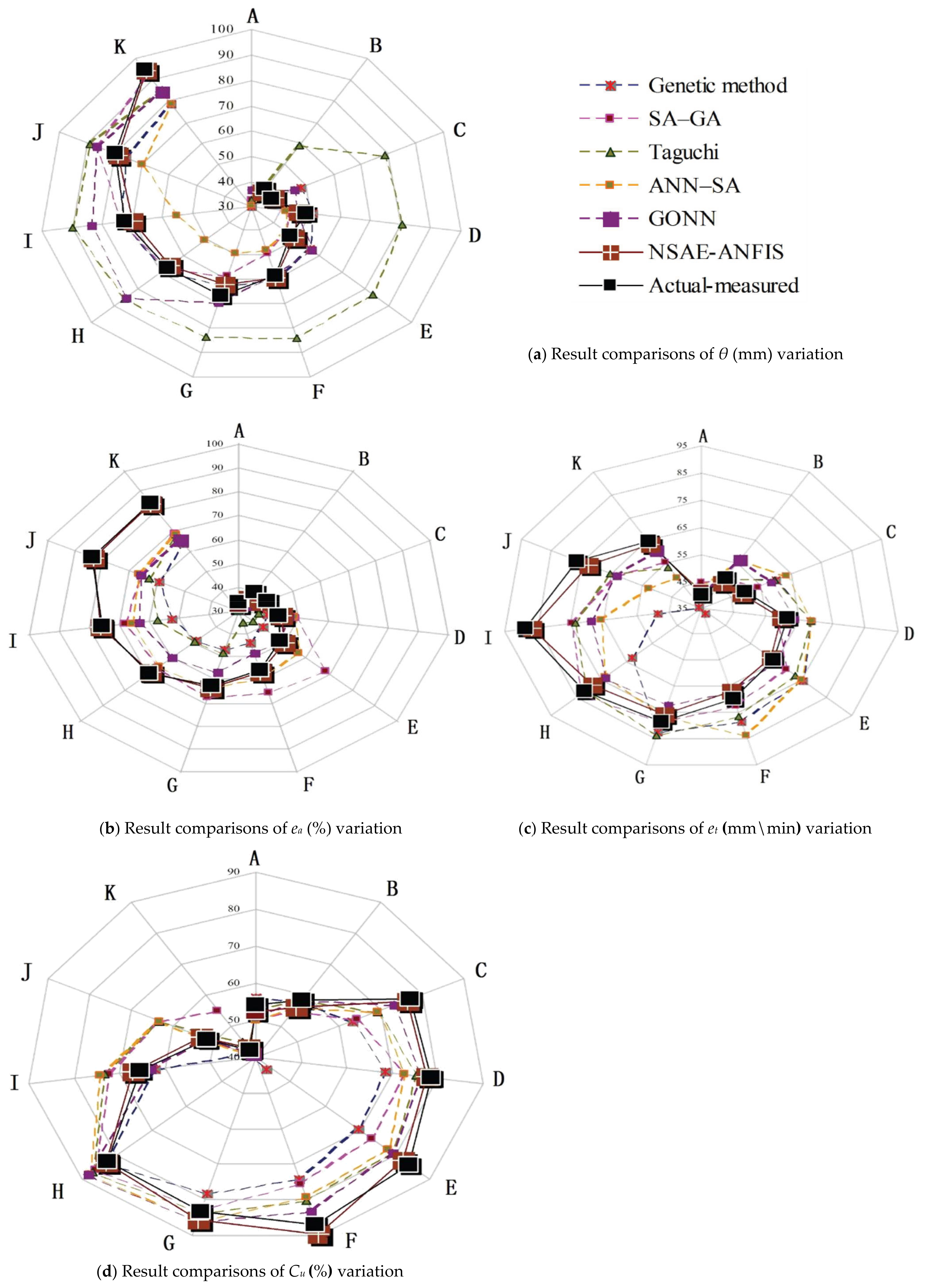
6. Assessments of Adaptive Prediction Quality
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| The averaged value of soil moisture proportion (%) | |
| (xk,yk)th | The meshed grid zone of the soil field |
| The mathematical features of probability density | |
| The probability density of droplet infiltration at a given meshed grid zone | |
| ∇J | The gradient of JRSAE |
| Cf | The cumulative irrigation flow depth (mm) |
| Cu | The uniformity coefficient of soil moisture infiltration (%) |
| E | evaporation |
| ea | The irrigation infiltration efficiency |
| et | The irrigation turn duration efficiency, or the ratio of net infiltrated moisture depth per unit of irrigation time (mm/min) |
| Ev | The cumulative water flow depth evaporated at the end of irrigation turn (mm) |
| f | The mapping function of the RSAE decoder |
| F1 | The recursive complexity index |
| F2 | The functional inclusion index |
| F3 | The computational compactness index |
| F4 | The cluster validity index |
| F5 | The Kullback–Leibler divergence index |
| F6 | The fuzzy clustering uniformity index |
| Fa | The flow rate of water (kg/min) |
| gRSAE | The mapping function for the RSAE decoder |
| H(i,j) | The inverse of the Hessian matrix |
| i | The ith intervals of the update process of WRSAE |
| Id((xk,yk); μ, σ2) | The probability density of water droplet infiltration at the investigated area |
| IT | The irrigation time (h) |
| j | The jth intervals of the update process of WRSAE |
| Mk | The number of meshed grids in length directions |
| N(μ,σ) | Normal distribution of droplet infiltration positions on an objective meshed grid zone |
| Nk | The number of meshed grids in width directions |
| Pw | The jetting pressure in the nozzle tube (kPa) |
| Q | The spray discharge amount (L/h) |
| RH | The average air relative humidity (%) |
| sgn | The result of the sign function of σr(W∙(xk,yk)) |
| SR | The solar radiation |
| T | The average air temperature (℃) |
| t | The irrigation turn duration (min) |
| Tc | The continuous irrigation time (min) |
| Wa | The impinge angle (º) |
| WRSAE | The weight matrix of the Regularized Sparse Autoencoder |
| xk | The horizontal coordinates of the specific position where water droplet infiltration happens |
| yk | The vertical coordinates of the specific position where water droplet infiltration happens |
| η | The step size of the update process |
| θ | The average soil moisture depth increment (mm) |
| θantecedent | The average antecedent soil moisture depths (mm) |
| θend | The average achieved soil moisture depths (mm) |
| θxk,yk | The soil moisture proportion at one infiltration measurement position (%) |
| λxkyk | The regular coefficient of RSAE corresponding to the mesh grid zone |
| μ | The mean value of the infiltration position coordinate |
| σ | The corresponding distribution variance |
| σr(z) | The rectified linear unit employed as the activation function in the RSAE decoder |
| σr’ | The derivative function of rectified linear unit σr |
References
- Goodchild, M.; Jenkins, M.; Whalley, W.; Watts, C. A novel dielectric moisture probe enabling precision PID-based irrigation control of polytunnel-grown strawberries in coir. Biosyst. Eng. 2018, 165, 70–76. [Google Scholar] [CrossRef]
- Zapata-Sierra, A.; Agugliaro, F. Controlled deficit irrigation for orange trees in Mediterranean countries. J. Clean. Prod. 2017, 162, 130–140. [Google Scholar] [CrossRef]
- Martí, R.; Valcárcel, M.; Leiva-Brondo, M.; Lahoz, I.; Campillo, C.; Roselló, S.; Cebolla-Cornejo, J. Influence of controlled deficit irrigation on tomato functional value. Food Chem. 2018, 252, 250–257. [Google Scholar] [CrossRef]
- Jouni, H.; Liaghat, A.; Hassanoghli, A.; Henk, R. Managing controlled drainage in irrigated farm fields, A case study in the Moghan plain, Iran. Agric. Water Manag. 2018, 208, 393–405. [Google Scholar] [CrossRef]
- Mostafa, H.; Nady, R.; Awad, M.; Ansary, M. Drip irrigation management for wheat under clay soil in arid conditions. Ecol. Eng. 2018, 121, 35–43. [Google Scholar] [CrossRef]
- Li, D.; Franssen, H.; Han, X.; Bello, M.; Vereecken, H. Evaluation of an operational real-time irrigation scheduling scheme for droplet irrigated citrus fields in Picassent, Spain. Agric. Water Manag. 2018, 208, 465–477. [Google Scholar] [CrossRef]
- Rodríguez, F.L.; Horváth, K.; Martín, J.G.; Maestre, J. Mobile Model Predictive Control for the Évora irrigation test canal. IFAC-PapersOnLine 2017, 50, 6570–6575. [Google Scholar] [CrossRef]
- Smith, R.; Uddin, M.; Gillies, M. Estimating irrigation duration for high performance furrow irrigation on cracking clay soils. Agric. Water Manag. 2018, 206, 78–85. [Google Scholar] [CrossRef]
- Oker, T.E.; Kisekka, I.; Sheshukov, A.Y.; Aguilar, J.; Rogers, D.H. Evaluation of maize production under mobile drip irrigation. Agric. Water Manag. 2018, 210, 11–21. [Google Scholar] [CrossRef]
- Dang, T.; Pedroso, R.; Laux, P.; Kunstmann, H. Development of an integrated hydrological-irrigation optimization modeling system for a typical rice irrigation scheme in Central Vietnam. Agric. Water Manag. 2018, 208, 193–203. [Google Scholar] [CrossRef]
- Salem, G.S.A.; Kazama, S.; Shahid, S.; Dey, N.C. Impacts of climate change on groundwater level and irrigation cost in a groundwater dependent irrigated region. Agric. Water Manag. 2018, 208, 33–42. [Google Scholar] [CrossRef]
- Bigelow, D.P.; Zhang, H. Supplemental irrigation water rights and climate change adaptation. Ecol. Econ. 2018, 154, 156–167. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Guo, L.; Lin, J.; Xing, S. A neural network constructed by deep learning technique and its application to intelligent fault diagnosis of machines. Neurocomputing 2018, 272, 619–628. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, X.; Xiao, J.; Liu, C. Adaptive prediction of abrasive impacting pressure effectiveness in strengthen jet grinding using NSAE-ANFIS. Int. J. Adv. Manuf. Technol. 2020, 106, 2805–2828. [Google Scholar] [CrossRef]
- Liang, Z.; Shan, S.; Liu, X.; Wen, Y. Fuzzy prediction of AWJ turbulence characteristics by using typical multi-phase flow models. Eng. Appl. Comput. Fluid Mech. 2017, 11, 225–257. [Google Scholar] [CrossRef]
- Ren, Y.; Wei, S.; Cheng, K.; Fu, Q. Valuation and Pricing of Agricultural Irrigation Water Based on Macro and Micro Scales. Water 2018, 10, 1044. [Google Scholar] [CrossRef]
- Paranage, K. Understanding the Relationship between Water Infrastructure and Socio-Political Configurations: A Case Study from Sri Lanka. Water 2018, 10, 1402. [Google Scholar] [CrossRef]
- Ćosić, M.; Stričević, R.; Djurović, N.; Lipovac, A.; Pavlović, M. Effects of irrigation regime and application of kaolin on canopy temperatures of sweet pepper and tomato. Sci. Hortic. 2018, 238, 23–31. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Liu, X.; Liang, Z.; Wen, G.; Yuan, X. Waterjet machining and research developments: A review. Int. J. Adv. Manuf. Technol. 2018, 102, 1257–1335. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, H.; Li, J.; Li, Y.; Yan, H. Estimation of irrigation requirements for droplet-irrigated maize in a sub-humid climate. J. Integr. Agric. 2018, 17, 677–692. [Google Scholar] [CrossRef]
- Liu, J.; Bi, X.; Ma, M.; Jiang, L.; Du, L.; Li, S.; Sun, Q.; Zou, G.; Liu, H. Precipitation and irrigation dominate soil water leaching in cropland in Northern China. Agric. Water Manag. 2019, 211, 165–171. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, M.; Shi, W.; Zheng, W. Construction of intelligent water saving irrigation control system based on water balance. IFAC-PapersOnLine 2018, 51, 466–471. [Google Scholar] [CrossRef]
- Du, Y.-D.; Niu, W.-Q.; Gu, X.-B.; Zhang, Q.; Cui, B.-J.; Zhao, Y. Crop yield and water use efficiency under aerated irrigation: A meta-analysis. Agric. Water Manag. 2018, 210, 158–164. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, J.; Wang, Y.; Xiang, C.; Zhou, J. Practicality of using solar energy for cassava irrigation in the Guangxi Autonomous Region, China. Appl. Energy 2018, 230, 31–41. [Google Scholar] [CrossRef]
- Elshaikh, A.E.; Jiao, X.; Yang, S.-H. Performance evaluation of irrigation projects: Theories, methods, and techniques. Agric. Water Manag. 2018, 203, 87–96. [Google Scholar] [CrossRef]
- Stärke, F.; Awiszus, F.; Lohmann, C.; Stärke, C. The effect of irrigation time and type of irrigation fluid on cartilage surface friction. J. Mech. Behav. Biomed. Mater. 2018, 77, 187–191. [Google Scholar] [CrossRef]
- Delgoda, D.; Malano, H.; Saleem, S.K.; Halgamuge, M.N. Irrigation control based on model predictive control (MPC): Formulation of theory and validation using weather forecast data and AQUACROP model. Environ. Model. Softw. 2016, 78, 40–53. [Google Scholar] [CrossRef]
- Basga, S.D.; Tsozue, D.; Temga, J.P.; Balna, J.; Nguetnkam, J.P. Land use impact on clay dispersion/flocculation in irrigated and flooded vertisols from Northern Cameroon. Int. Soil Water Conserv. Res. 2018, 6, 237–244. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, H.; Wang, L.; Yu, D.; Yang, F.; Shi, X.; Saleem, H.; Akhtar, M.S. Irrigation with sediment-laden river water affects the soil texture and composition of organic matter fractions in arid and semi-arid areas of Northwest China. Geoderma 2018, 328, 10–19. [Google Scholar] [CrossRef]
- Liang, Z.; Liao, S.; Wen, Y.; Liu, X. Working parameter optimization of strengthen waterjet grinding with the orthogonal-experiment-design-based ANFIS. J. Intell. Manuf. 2019, 30, 833–854. [Google Scholar] [CrossRef]
- Brinkhoff, J.; Hornbuckle, J.; Barton, J.L. Assessment of Aquatic Weed in Irrigation Channels Using UAV and Satellite Imagery. Water 2018, 10, 1497. [Google Scholar] [CrossRef]
- Ayyad, S.; Al Zayed, I.S.; Ha, V.T.T.; Ribbe, L. The Performance of Satellite-Based Actual Evapotranspiration Products and the Assessment of Irrigation Efficiency in Egypt. Water 2019, 11, 1913. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, X.; Wen, G.; Yuan, X. Influence analysis of sprinkler irrigation effectiveness using ANFIS. Int. J. Agric. Biol. Eng. 2019, 12, 135–148. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, X.; Wen, G.; Xiao, J. Effectiveness prediction of abrasive jetting stream of accelerator tank using normalized sparse autoencoder-adaptive neural fuzzy inference system. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2020, 234, 1615–1639. [Google Scholar] [CrossRef]
- Zaki, N.A.; Haghighi, A.T.; Rossi, P.M.; Xenarios, S.; Kløve, B. An Index-Based Approach to Assess the Water Availability for Irrigated Agriculture in Sub-Saharan Africa. Water 2018, 10, 896. [Google Scholar] [CrossRef]
- Zhang, X.; Qiu, J.; Leng, G.; Yang, Y.; Gao, Q.; Fan, Y.; Luo, J. The Potential Utility of Satellite Soil Moisture Retrievals for Detecting Irrigation Patterns in China. Water 2018, 10, 1505. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, X.; Xiong, J.; Xiao, J. Water Allocation and Integrative Management of Precision Irrigation: A Systematic Review. Water 2020, 12, 3135. [Google Scholar] [CrossRef]





| Condition | P (kPa) | IT (h) | Q (L/h) | T (°C) | RH (%) | SR (MJ/m2) | U (m/s) | E (mm) | WD |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 250 | 2.5 | 1785 | 25.6 | 88 | 15.2 | 0.5 | 20.2 | Northeast |
| 2 | 330 | 2.6 | 1744 | 24.1 | 62 | 11.4 | 1.1 | 31.4 | Southeast |
| 3 | 240 | 3.1 | 1562 | 28.6 | 75 | 17.2 | 1.2 | 28.2 | Northeast/North |
| 4 | 280 | 3.2 | 1823 | 30.2 | 74 | 19.2 | 0.9 | 26.2 | South/Southwest |
| 5 | 260 | 3.3 | 1492 | 31.2 | 69 | 15.3 | 0.5 | 30.2 | Southwest |
| 6 | 270 | 2.8 | 1522 | 32.5 | 66 | 16.5 | 0.8 | 24.3 | West |
| 7 | 330 | 2.7 | 1638 | 29.5 | 72 | 14.8 | 0.6 | 37.5 | Northeast |
| 8 | 310 | 2.9 | 1729 | 29.3 | 76 | 15.6 | 1.1 | 28.2 | Northwest |
| 9 | 350 | 2.4 | 1562 | 28.6 | 85 | 17.2 | 1.3 | 31.2 | North/Northeast |
| 10 | 360 | 2.6 | 1882 | 24.6 | 92 | 18.8 | 1.4 | 33.2 | Southeast |
| 11 | 250 | 2.6 | 1485 | 25.9 | 91 | 17.3 | 1.8 | 34.2 | East/Northeast |
| 12 | 280 | 2.1 | 1925 | 28.8 | 68 | 15.6 | 1.5 | 30.6 | Northeast |
| 13 | 290 | 2.0 | 1547 | 26.9 | 75 | 14.5 | 0.9 | 28.2 | Southeast/South |
| 14 | 320 | 2.5 | 1482 | 28.7 | 77 | 18.2 | 0.8 | 37.2 | Southeast |
| 15 | 310 | 2.5 | 1556 | 33.2 | 84 | 19.2 | 1.4 | 28.9 | North |
| 16 | 330 | 3.2 | 1572 | 33.6 | 88 | 14.2 | 1.6 | 27.6 | Northwest |
| 17 | 280 | 3.6 | 1982 | 34.5 | 86 | 16.2 | 1.8 | 24.2 | Northeast |
| 18 | 260 | 3.1 | 1563 | 26.5 | 87 | 14.5 | 1.7 | 23.2 | Southeast |
| 19 | 270 | 3.0 | 1425 | 28.5 | 82 | 17.2 | 1.5 | 34.1 | Northwest |
| 20 | 280 | 3.0 | 1825 | 24.9 | 85 | 18.2 | 1.4 | 36.2 | North |
| 21 | 260 | 2.6 | 1472 | 26.3 | 86 | 15.5 | 1.7 | 28.2 | Northeast/East |
| 22 | 240 | 2.8 | 1635 | 28.4 | 92 | 14.2 | 1.5 | 35.3 | East/North |
| 23 | 250 | 2.7 | 1852 | 26.3 | 90 | 14.6 | 1.2 | 24.7 | Northeast |
| 24 | 260 | 3.5 | 1472 | 25.8 | 86 | 16.2 | 1.6 | 35.2 | Southeast |
| 25 | 260 | 3.6 | 1882 | 24.7 | 75 | 18.2 | 1.2 | 28.2 | Southwest |
| 26 | 310 | 3.5 | 1664 | 26.3 | 74 | 15.6 | 0.8 | 33.2 | Southeast |
| 27 | 330 | 3.4 | 1592 | 25.9 | 83 | 14.2 | 0.6 | 34.2 | North |
| 28 | 350 | 3.2 | 1822 | 33.6 | 81 | 18.2 | 0.8 | 37.2 | South |
| 29 | 320 | 3.3 | 1425 | 32.5 | 88 | 14.4 | 0.4 | 26.3 | Southwest/West |
| 30 | 340 | 3.6 | 1632 | 36.2 | 86 | 16.2 | 0.8 | 32.1 | Northwest |
| 31 | 360 | 3.4 | 1472 | 34.1 | 84 | 18.2 | 1.1 | 38.2 | West |
| 32 | 380 | 3.8 | 1582 | 26.9 | 92 | 17.2 | 1.5 | 28.2 | Northeast/East |
| 33 | 370 | 2.9 | 1556 | 32.4 | 82 | 16.6 | 1.4 | 37.2 | Southeast |
| 34 | 260 | 2.5 | 1482 | 25.6 | 76 | 18.2 | 1.2 | 36.2 | North/Northwest |
| 35 | 280 | 2.7 | 1725 | 28.4 | 77 | 18.2 | 1.8 | 34.2 | Northeast |
| Irrigation Parameters | Value Levels | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Jetting pressure (Pw/kPa) | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 |
| Impinge angle (Wa/°) | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 | 35.0 | 40.0 | 45.0 | 50.0 | 55.0 |
| Flow rate of water (Fa/kg/min) | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 | 1.00 | 1.10 |
| Continuous irrigation time (Tc/min) | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 |
| Infiltration Effectiveness Indexes | Value Levels | |||||||||
| Average soil moisture depth increment (θ/mm) | 10.0 | 20.0 | 30.0 | 40.0 | 50.0 | 60.0 | 70.0 | 80.0 | 90.0 | 100.0 |
| Irrigation infiltration efficiency (ea/%) | 20.0 | 25.0 | 30.0 | 35.0 | 40.0 | 45.0 | 50.0 | 55.0 | 60.0 | 65.0 |
| Irrigation turn duration efficiency (et/mm/min) | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 | 35.0 | 40.0 | 45.0 | 50.0 | 55.0 |
| The uniformity coefficient of soil moisture infiltration (Cu/%) | 10.0 | 20.0 | 30.0 | 40.0 | 50.0 | 60.0 | 70.0 | 80.0 | 90.0 | 100.0 |
| No | IF: Experimental Run of Input Levels | THEN: Experimental Run of Output Levels | ||||||
|---|---|---|---|---|---|---|---|---|
| Pw | Wa | Fa | Tc | θ | ea | et | Cu | |
| 1 | 1 | 1 | 1 | 1 | 5 | 3 | 6 | 6 |
| 2 | 1 | 1 | 2 | 1 | 6 | 2 | 4 | 6 |
| 3 | 1 | 2 | 3 | 1 | 7 | 2 | 5 | 8 |
| 4 | 1 | 2 | 4 | 2 | 2 | 3 | 2 | 5 |
| 5 | 2 | 3 | 5 | 2 | 10 | 1 | 2 | 1 |
| 6 | 2 | 3 | 6 | 2 | 6 | 4 | 2 | 4 |
| 7 | 2 | 4 | 7 | 3 | 8 | 5 | 4 | 5 |
| 8 | 2 | 4 | 8 | 3 | 4 | 6 | 5 | 2 |
| 9 | 3 | 5 | 9 | 3 | 7 | 2 | 1 | 2 |
| 10 | 3 | 5 | 10 | 4 | 5 | 7 | 7 | 6 |
| 11 | 3 | 6 | 1 | 4 | 2 | 8 | 8 | 9 |
| 12 | 3 | 6 | 2 | 4 | 2 | 2 | 3 | 2 |
| 13 | 4 | 7 | 3 | 5 | 3 | 6 | 5 | 4 |
| 14 | 4 | 7 | 4 | 5 | 4 | 4 | 6 | 1 |
| 15 | 4 | 8 | 5 | 5 | 6 | 8 | 4 | 10 |
| 16 | 4 | 8 | 6 | 6 | 5 | 9 | 1 | 5 |
| 17 | 5 | 9 | 7 | 6 | 8 | 2 | 2 | 5 |
| 18 | 5 | 9 | 8 | 6 | 8 | 2 | 1 | 6 |
| 19 | 5 | 10 | 9 | 7 | 7 | 4 | 1 | 10 |
| 20 | 5 | 10 | 10 | 7 | 4 | 5 | 5 | 2 |
| 21 | 6 | 1 | 1 | 7 | 2 | 4 | 4 | 5 |
| 22 | 6 | 1 | 2 | 8 | 5 | 7 | 5 | 5 |
| 23 | 6 | 2 | 3 | 8 | 6 | 1 | 6 | 4 |
| 24 | 6 | 2 | 4 | 8 | 4 | 4 | 4 | 1 |
| 25 | 7 | 3 | 5 | 9 | 2 | 5 | 8 | 3 |
| 26 | 7 | 3 | 6 | 9 | 5 | 6 | 8 | 3 |
| 27 | 7 | 4 | 7 | 9 | 9 | 1 | 9 | 5 |
| 28 | 7 | 4 | 8 | 10 | 4 | 2 | 10 | 6 |
| 29 | 8 | 5 | 9 | 10 | 5 | 5 | 2 | 10 |
| 30 | 8 | 5 | 10 | 10 | 1 | 5 | 2 | 2 |
| 31 | 8 | 6 | 1 | 9 | 1 | 8 | 4 | 5 |
| 32 | 8 | 6 | 2 | 9 | 5 | 8 | 5 | 6 |
| 33 | 9 | 7 | 3 | 9 | 3 | 9 | 6 | 8 |
| 34 | 9 | 7 | 4 | 8 | 5 | 1 | 4 | 7 |
| 35 | 9 | 8 | 5 | 8 | 7 | 1 | 10 | 4 |
| 36 | 9 | 8 | 6 | 8 | 9 | 2 | 2 | 1 |
| 37 | 10 | 9 | 7 | 7 | 10 | 5 | 6 | 5 |
| 38 | 10 | 9 | 8 | 7 | 5 | 4 | 1 | 2 |
| … | …… | …… | …… | …… | …… | |||
| 100 | 10 | 10 | 10 | 6 | 5 | 8 | 5 | 6 |
| Tests | Infiltration Effectiveness Indexes Investigated in Our Experiment. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Average Soil Moisture Depth Increment (θ, mm) | Irrigation Infiltration Efficiency (ea, %) | Irrigation Turn Duration Efficiency (et, mm/min) | Uniformity Coefficient of Soil Moisture Infiltration (Cu, %) | ||||||||||
| RSAE– ANFIS | Measured | RE (%) | RSAE– ANFIS | Measured | RE (%) | RSAE– ANFIS | Measured | RE (%) | RSAE– ANFIS | Measured | RE (%) | ||
| Test A | 1 | 52.33 | 53.65 | 2.46 | 36.22 | 35.30 | 2.61 | 15.22 | 14.15 | 7.56 | 63.25 | 61.25 | 3.27 |
| 2 | 62.14 | 65.15 | 4.62 | 56.55 | 52.65 | 7.41 | 36.25 | 33.05 | 9.68 | 88.15 | 83.25 | 5.89 | |
| 3 | 82.11 | 86.32 | 4.88 | 47.21 | 43.33 | 8.95 | 33.42 | 36.14 | 7.53 | 47.25 | 45.14 | 4.67 | |
| 4 | 34.02 | 37.56 | 9.42 | 39.25 | 36.09 | 8.76 | 56.25 | 52.25 | 7.66 | 63.25 | 66.58 | 3.51 | |
| 5 | 53.26 | 50.55 | 5.36 | 55.41 | 52.00 | 6.56 | 27.55 | 26.14 | 5.39 | 33.58 | 34.92 | 3.84 | |
| Test B | 1 | 42.11 | 46.95 | 10.31 | 28.44 | 26.04 | 9.22 | 29.54 | 27.28 | 8.28 | 38.95 | 37.31 | 4.40 |
| 2 | 59.32 | 56.55 | 4.90 | 62.14 | 68.06 | 8.70 | 30.14 | 33.85 | 10.96 | 41.25 | 43.58 | 5.35 | |
| 3 | 85.14 | 86.44 | 1.50 | 60.22 | 67.11 | 10.27 | 45.22 | 41.58 | 8.75 | 46.25 | 45.22 | 6.55 | |
| 4 | 75.22 | 79.14 | 4.95 | 50.14 | 53.65 | 6.54 | 50.06 | 54.45 | 8.06 | 47.22 | 44.47 | 6.18 | |
| 5 | 64.15 | 68.14 | 5.86 | 23.04 | 25.06 | 8.06 | 48.22 | 45.58 | 5.79 | 82.62 | 86.58 | 4.57 | |
| Test C | 1 | 63.95 | 68.17 | 6.19 | 28.44 | 26.05 | 9.17 | 47.01 | 43.44 | 8.22 | 55.26 | 53.26 | 3.76 |
| 2 | 68.25 | 66.21 | 3.08 | 38.00 | 35.01 | 8.54 | 43.51 | 46.98 | 7.39 | 63.24 | 66.58 | 6.02 | |
| 3 | 47.22 | 43.54 | 8.45 | 36.14 | 38.03 | 4.97 | 39.25 | 36.48 | 7.59 | 53.26 | 57.14 | 6.79 | |
| 4 | 69.25 | 64.14 | 7.97 | 30.25 | 33.06 | 8.50 | 33.01 | 35.65 | 7.41 | 45.26 | 49.25 | 6.13 | |
| 5 | 48.22 | 46.22 | 4.33 | 46.25 | 47.25 | 2.12 | 35.05 | 36.95 | 5.14 | 90.25 | 93.55 | 3.53 | |
| Test D | 1 | 32.55 | 35.97 | 9.51 | 44.17 | 45.06 | 1.98 | 42.06 | 46.25 | 9.06 | 91.00 | 96.51 | 5.71 |
| 2 | 14.25 | 15.17 | 6.06 | 42.56 | 46.29 | 8.06 | 18.49 | 17.48 | 5.78 | 65.25 | 66.25 | 1.51 | |
| 3 | 16.55 | 15.88 | 4.22 | 63.22 | 67.22 | 5.95 | 17.22 | 16.99 | 1.35 | 48.26 | 46.66 | 4.54 | |
| 4 | 17.25 | 16.14 | 6.88 | 55.89 | 56.28 | 0.69 | 25.61 | 23.65 | 8.29 | 47.25 | 45.14 | 4.67 | |
| 5 | 82.55 | 89.17 | 7.42 | 52.47 | 57.25 | 8.35 | 28.48 | 26.48 | 7.55 | 66.32 | 63.02 | 5.24 | |
| Test E | 1 | 46.23 | 48.22 | 4.13 | 56.90 | 52.13 | 9.15 | 36.25 | 33.32 | 8.79 | 26.05 | 28.04 | 7.10 |
| 2 | 54.12 | 53.14 | 1.84 | 55.02 | 53.15 | 3.52 | 37.48 | 36.28 | 3.31 | 37.82 | 39.25 | 2.74 | |
| 3 | 66.32 | 61.47 | 7.89 | 40.36 | 44.33 | 8.96 | 33.05 | 34.25 | 3.50 | 34.26 | 36.54 | 3.98 | |
| 4 | 82.56 | 86.98 | 5.08 | 43.81 | 47.05 | 6.89 | 28.49 | 26.05 | 9.37 | 48.25 | 47.14 | 2.35 | |
| 5 | 92.14 | 98.88 | 6.82 | 48.07 | 46.11 | 4.25 | 30.15 | 32.17 | 6.28 | 46.92 | 44.15 | 6.27 | |
| Test F | 1 | 45.26 | 47.98 | 5.67 | 45.62 | 48.26 | 5.47 | 48.05 | 43.48 | 10.51 | 40.15 | 43.25 | 7.17 |
| 2 | 44.25 | 46.88 | 5.61 | 41.09 | 44.25 | 7.14 | 46.22 | 42.17 | 9.60 | 30.25 | 32.58 | 7.15 | |
| 3 | 41.56 | 43.89 | 5.31 | 35.04 | 36.33 | 3.55 | 38.15 | 36.14 | 5.56 | 36.95 | 38.75 | 3.81 | |
| 4 | 63.25 | 69.65 | 9.19 | 38.19 | 36.25 | 5.35 | 48.75 | 45.62 | 6.86 | 38.15 | 36.14 | 4.57 | |
| 5 | 65.47 | 68.95 | 5.05 | 35.62 | 39.23 | 9.20 | 53.25 | 51.84 | 2.72 | 62.15 | 66.95 | 7.17 | |
| Test G | 1 | 66.29 | 68.19 | 2.79 | 40.22 | 43.22 | 6.94 | 49.66 | 46.14 | 7.63 | 66.85 | 62.14 | 7.58 |
| 2 | 48.25 | 43.65 | 10.54 | 46.25 | 47.25 | 2.12 | 27.58 | 25.65 | 7.52 | 75.18 | 78.25 | 3.92 | |
| 3 | 39.25 | 37.14 | 5.68 | 48.22 | 44.15 | 9.22 | 39.15 | 36.84 | 6.27 | 70.02 | 73.65 | 4.93 | |
| 4 | 47.25 | 45.16 | 4.63 | 46.92 | 44.06 | 6.49 | 38.14 | 36.48 | 4.55 | 65.14 | 68.04 | 4.26 | |
| 5 | 44.56 | 48.98 | 9.02 | 50.18 | 55.33 | 9.31 | 48.15 | 47.14 | 2.14 | 73.05 | 79.25 | 7.82 | |
| Test H | 1 | 53.36 | 55.22 | 4.02 | 38.25 | 39.25 | 2.55 | 25.11 | 23.65 | 6.18 | 85.45 | 89.65 | 4.69 |
| 2 | 59.22 | 58.17 | 2.01 | 46.25 | 47.74 | 3.13 | 26.33 | 25.95 | 1.47 | 89.25 | 86.54 | 3.14 | |
| 3 | 72.13 | 74.69 | 3.43 | 43.78 | 46.22 | 5.28 | 28.14 | 27.17 | 3.57 | 87.24 | 83.62 | 4.33 | |
| 4 | 70.32 | 72.51 | 3.02 | 50.36 | 53.21 | 5.36 | 34.14 | 35.63 | 4.19 | 79.52 | 77.15 | 3.08 | |
| 5 | 59.22 | 56.38 | 5.04 | 48.72 | 46.21 | 5.44 | 26.95 | 25.85 | 4.26 | 88.32 | 84.65 | 4.34 | |
| Test I | 1 | 48.25 | 46.14 | 4.58 | 62.14 | 65.55 | 5.21 | 24.58 | 25.87 | 4.99 | 86.45 | 84.25 | 2.62 |
| 2 | 47.22 | 49.22 | 4.07 | 63.25 | 66.34 | 4.66 | 27.45 | 26.47 | 3.71 | 77.45 | 73.33 | 5.62 | |
| 3 | 63.21 | 65.89 | 4.07 | 48.29 | 46.25 | 4.41 | 26.35 | 25.65 | 2.73 | 79.21 | 75.12 | 5.45 | |
| 4 | 55.26 | 57.48 | 3.87 | 57.12 | 54.23 | 5.33 | 36.15 | 37.89 | 4.60 | 75.48 | 78.22 | 3.51 | |
| 5 | 58.14 | 55.48 | 4.80 | 66.32 | 63.68 | 4.15 | 36.55 | 35.47 | 3.05 | 82.45 | 80.11 | 2.92 | |
| Test J | 1 | 36.54 | 39.32 | 7.07 | 49.25 | 46.25 | 6.49 | 38.24 | 37.56 | 1.81 | 80.12 | 83.54 | 4.10 |
| 2 | 39.58 | 37.14 | 6.57 | 56.21 | 54.47 | 3.20 | 29.54 | 28.47 | 3.76 | 78.65 | 77.11 | 2.00 | |
| 3 | 42.15 | 45.55 | 7.47 | 43.26 | 44.98 | 3.83 | 28.48 | 29.98 | 5.01 | 77.48 | 75.96 | 2.01 | |
| 4 | 44.36 | 46.21 | 4.01 | 44.78 | 46.25 | 3.18 | 28.88 | 27.56 | 4.79 | 82.36 | 86.54 | 4.83 | |
| 5 | 42.78 | 44.47 | 3.80 | 58.25 | 54.59 | 6.71 | 35.65 | 36.98 | 3.60 | 83.14 | 87.22 | 4.68 | |
| Test K | 1 | 53.26 | 56.47 | 5.69 | 63.21 | 66.98 | 5.63 | 37.41 | 38.98 | 4.03 | 82.64 | 88.21 | 6.32 |
| 2 | 52.78 | 55.54 | 4.97 | 65.47 | 67.24 | 2.64 | 37.16 | 39.65 | 6.28 | 76.98 | 75.14 | 2.45 | |
| 3 | 55.36 | 56.98 | 2.85 | 59.25 | 56.24 | 5.36 | 29.54 | 28.56 | 3.44 | 77.25 | 75.11 | 2.85 | |
| 4 | 59.24 | 56.47 | 4.91 | 34.21 | 36.08 | 5.19 | 37.25 | 38.98 | 4.44 | 75.48 | 73.25 | 3.05 | |
| 5 | 57.15 | 56.10 | 1.88 | 39.25 | 37.25 | 5.37 | 28.41 | 27.36 | 3.84 | 78.29 | 76.21 | 2.73 | |
| Performance Accuracy and Computational Efficiency | Representative Prediction Approaches (Error Tolerance = ±5%) | ||||||
|---|---|---|---|---|---|---|---|
| RSAE–ANFIS | Genetic | SA-GA | Taguchi | ANN-SA | GONN | ||
| Network training | Computation accuracy (%) | 98.25 | 91.02 | 96.55 | 91.41 | 91.26 | 92.95 |
| Standard deviation (%) | 0.335 | 0.562 | 0.662 | 0.623 | 0.485 | 0.635 | |
| Network testing | Computation accuracy (%) | 93.47 | 87.25 | 86.33 | 87.58 | 89.25 | 84.56 |
| Standard deviation (%) | 0.402 | 0.568 | 0.596 | 0.553 | 0.563 | 0.725 | |
| Average computation storage (kb) | 1855.4 | 1556.5 | 1472.5 | 1566.2 | 1695.2 | 1475.2 | |
| Computation time (s) | 1.22s | 1.85s | 1.87s | 1.76s | 1.85s | 1.95s | |
| Standard error of prediction (%) | 3.66 | 4.78 | 5.68 | 6.65 | 5.68 | 5.85 | |
| Confidence interval 95% | Upper error limit (%) | 4.27 | 6.24 | 6.28 | 6.47 | 6.98 | 6.52 |
| Lower error limit (%) | 4.52 | 6.85 | 6.54 | 6.58 | 6.88 | 5.69 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Liu, X.; Zou, T.; Xiao, J. Adaptive Prediction of Water Droplet Infiltration Effectiveness of Sprinkler Irrigation Using Regularized Sparse Autoencoder–Adaptive Network-Based Fuzzy Inference System (RSAE–ANFIS). Water 2021, 13, 791. https://doi.org/10.3390/w13060791
Liang Z, Liu X, Zou T, Xiao J. Adaptive Prediction of Water Droplet Infiltration Effectiveness of Sprinkler Irrigation Using Regularized Sparse Autoencoder–Adaptive Network-Based Fuzzy Inference System (RSAE–ANFIS). Water. 2021; 13(6):791. https://doi.org/10.3390/w13060791
Chicago/Turabian StyleLiang, Zhongwei, Xiaochu Liu, Tao Zou, and Jinrui Xiao. 2021. "Adaptive Prediction of Water Droplet Infiltration Effectiveness of Sprinkler Irrigation Using Regularized Sparse Autoencoder–Adaptive Network-Based Fuzzy Inference System (RSAE–ANFIS)" Water 13, no. 6: 791. https://doi.org/10.3390/w13060791
APA StyleLiang, Z., Liu, X., Zou, T., & Xiao, J. (2021). Adaptive Prediction of Water Droplet Infiltration Effectiveness of Sprinkler Irrigation Using Regularized Sparse Autoencoder–Adaptive Network-Based Fuzzy Inference System (RSAE–ANFIS). Water, 13(6), 791. https://doi.org/10.3390/w13060791






