Optimal Design of District Metered Areas in a Water Distribution Network Using Coupled Self-Organizing Map and Community Structure Algorithm
Abstract
:1. Introduction
- Graph theory–based WDN partitioning, including spectral algorithms and MLRB, requires that the size and number of clusters be determined in advance [3,13,34,35,42]. Unfortunately, the optimal number of clusters (i.e., number of DMAs) is generally not known in advance. Thus, the determination of the optimal number of DMAs in a given WDN has not been addressed heretofore.
- A modularity index-based optimization approach for exploring the communities in a WDN was focused on the network topology information, whereas specific hydraulic properties of the WDN have not been considered adequately [25,26,45,46]. This means that practical engineering aspects (i.e., weighting factors of nodes/links) were not integrated/embedded into the model adequately, thus forming infeasible DMAs.
- A set of standard criteria and their degree for designing and evaluating the DMA’s performance is lacking. In reality, water utilities develop a strategy to design DMAs that focus on pressure management to ensure minimal leakage. Thus, maintaining a uniform pressure in each DMA is essential, especially in a water network with multiple sources or irregular topographical conditions. Therefore, it is desirable to propose a method that addresses these aspects.
2. Methods
2.1. Characteristics of WDN
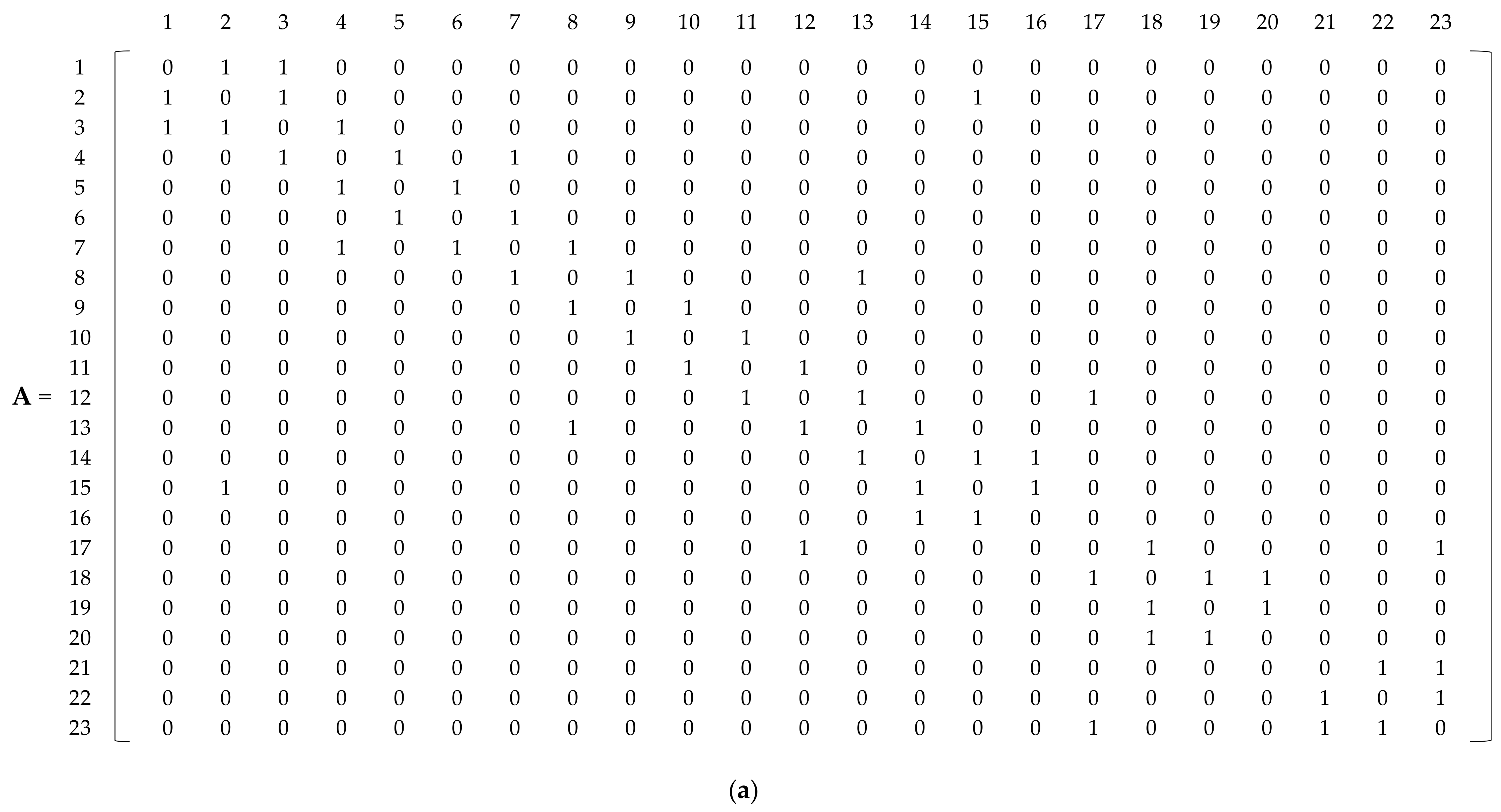
2.1.1. Adjacency Matrix
2.1.2. Topology Similarity (TS) Matrix
2.1.3. Hydraulic Similarity (HS) Matrix
- The pairs of nodes in the DMA have a high TS index and HS index;
- The pairs of nodes within a DMA must be connected directly.
- In the clustering phase, hydraulic and topological data are prepared. Then, SOM is adopted to form homologous clusters before the CSA is applied for refining cluster sizes into multiscale DMAs;
- In the sectorization phase, flowmeters and gate valves are optimally located in the boundary pipes identified in the clustering phase;
- In the MCDA phase, TOPSIS is designed to rigorously evaluate the performance of the multiscale DMA layouts that are obtained in the sectorization phase, aiming to determine the optimal DMA layout in a given WDN. The detailed methodology proposed for each phase is described in the following sections.
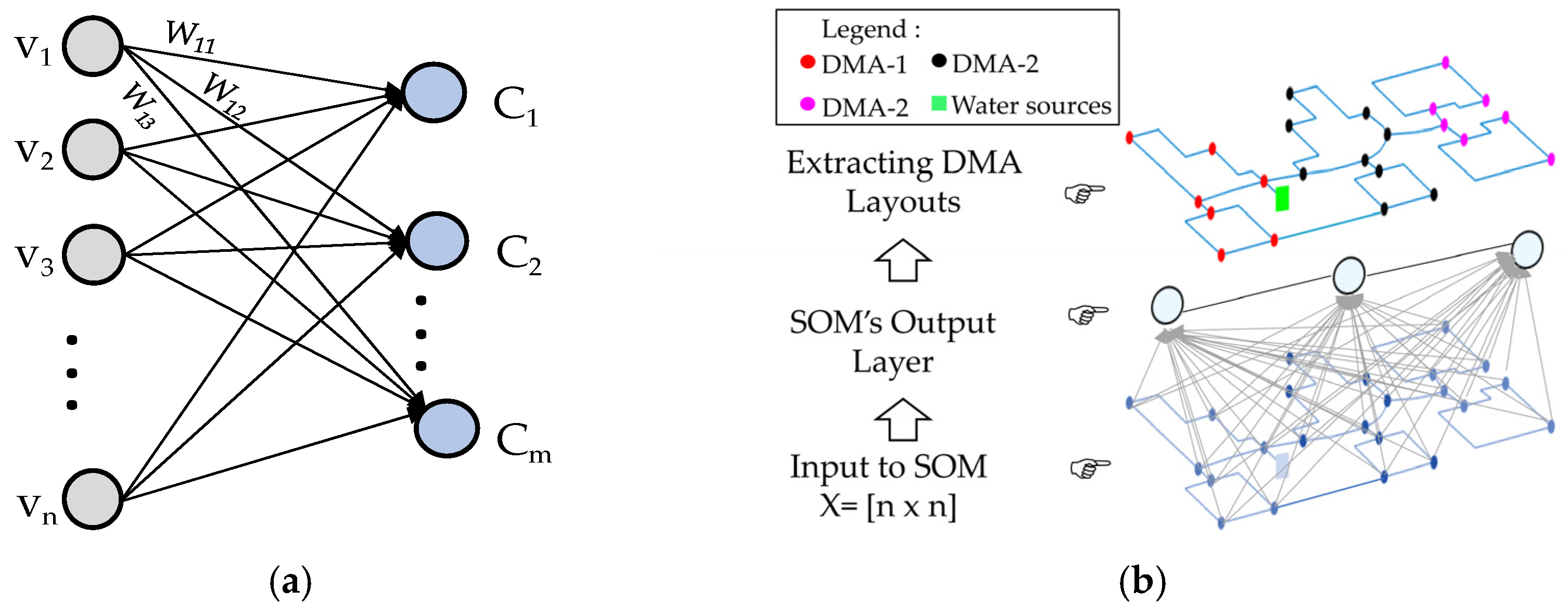
2.2. Phase 1: Coupled Model of SOM and CSA for Clustering Dynamic DMAs
2.2.1. SOM-Based Clustering of Homologous Regions in WDN
2.2.2. CSA-Based Creation of Multiscale and Dynamic DMAs
2.3. Phase 2: GA-Based Sectorization
2.4. Sample Network Demonstration of Phases 1 and 2
- The pressure variance in these layouts is relatively small and varies gently;
- The modularity index increases smoothly to a maximum of 0.5433 correspondings to five clusters (see Figure 7i).
2.5. Phase 3: MCDA-Based Comparative Analysis of Multiscale DMAs
2.5.1. Performance Indices of WNP
Demand Similarity Index (DSI)
Pressure Similarity Index (PSI)
Resilience Index (RI)
Water Age (WA)
Capital Cost
2.5.2. Multi-Criteria Decision Analysis (MCDA)
3. Results and Discussion
3.1. Case Study
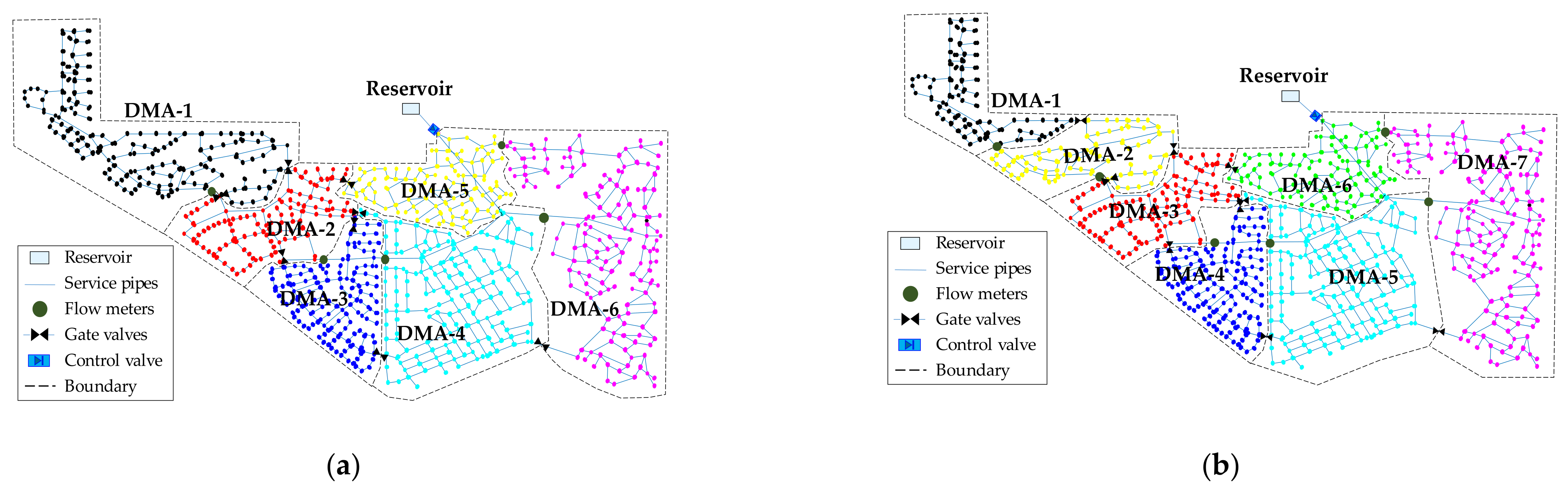
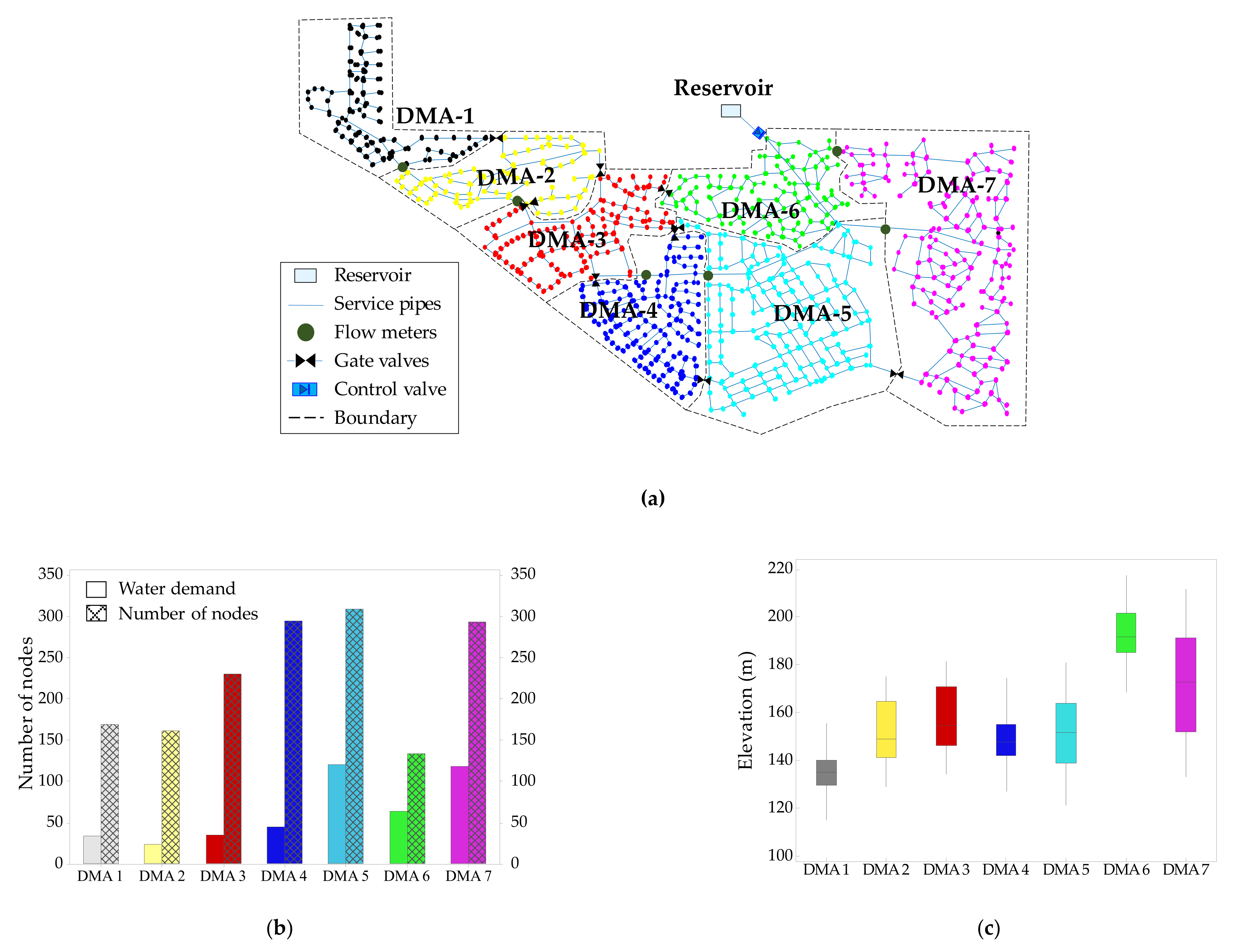
3.2. Multiscale and Dynamic DMA Layouts
3.3. Comprehensive Evaluation of Alternative DMA Layouts
3.4. Evaluation of the Optimal DMA Layout
3.5. Dynamic Operation of DMAs
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farley, M. Leakage Management and Control: A Best Practice Training Manual, No. WHO/SDE/WSH/01.1; World Health Organization: Geneva, Switzerland, 2001. [Google Scholar]
- Morrison, J.; Tooms, S.; Rogers, D. DMA Management Guidance Notes; IWA Publishing: London, UK, 2007. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.F.; Venticinque, S. An Automated Tool for Smart Water Network Partitioning. Water Resour. Manag. 2013, 27, 4493–4508. [Google Scholar] [CrossRef]
- Laucelli, D.B.; Simone, A.; Berardi, L.; Giustolisi, O. Optimal Design of District Metering Areas for the Reduction of Leakages. J. Water Resour. Plan. Manag. 2017, 143, 04017017. [Google Scholar] [CrossRef]
- Rajeswaran, A.; Narasimhan, S.; Narasimhan, S. A graph partitioning algorithm for leak detection in water distribution networks. Comput. Chem. Eng. 2018, 108, 11–23. [Google Scholar] [CrossRef] [Green Version]
- Creaco, E.; Haidar, H. Multiobjective Optimization of Control Valve Installation and DMA Creation for Reducing Leakage in Water Distribution Networks. J. Water Resour. Plan. Manag. 2019, 145, 04019046. [Google Scholar] [CrossRef]
- Brentan, B.; Meirelles, G.; Luvizotto, E.; Izquierdo, J. Hybrid SOM+ k-Means clustering to improve planning, operation and management in water distribution systems. Environ. Model. Softw. 2018, 106, 77–88. [Google Scholar] [CrossRef]
- Ferrari, G.; Savić, D. Economic Performance of DMAs in Water Distribution Systems. Procedia Eng. 2015, 119, 189–195. [Google Scholar] [CrossRef] [Green Version]
- Di Nardo, A.; Di Natale, M.; Musmarra, D.; Santonastaso, G.F.; Tzatchkov, V.; Alcocer-Yamanaka, V.H. Dual-use value of network partitioning for water system management and protection from malicious contamination. J. Hydroinform. 2014, 17, 361–376. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Musmarra, D.; Santonastaso, G.; Tuccinardi, F.; Zaccone, G. Software for partitioning and protecting a water supply network. Civ. Eng. Environ. Syst. 2015, 33, 55–69. [Google Scholar] [CrossRef]
- Ciaponi, C.; Creaco, E.; Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G.F. Reducing Impacts of Contamination in Water Distribution Networks: A Combined Strategy Based on Network Partitioning and Installation of Water Quality Sensors. Water 2019, 11, 1315. [Google Scholar] [CrossRef] [Green Version]
- Gomes, R.; Marques, A.S.A.; Sousa, J. District Metered Areas Design Under Different Decision Makers’ Options: Cost Analysis. Water Resour. Manag. 2013, 27, 4527–4543. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Santonastaso, G.F.; Tzatchkov, V.; Varela, J.M.R. Economic and Energy Criteria for District Meter Areas Design of Water Distribution Networks. Water 2017, 9, 463. [Google Scholar] [CrossRef] [Green Version]
- Herrera, M.; Abraham, E.; Stoianov, I. A Graph-Theoretic Framework for Assessing the Resilience of Sectorised Water Distribution Networks. Water Resour. Manag. 2016, 30, 1685–1699. [Google Scholar] [CrossRef] [Green Version]
- Armand, H.; Stoianov, I.; Graham, N. Impact of network sectorisation on water quality management. J. Hydroinform. 2017, 20, 424–439. [Google Scholar] [CrossRef] [Green Version]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Saldarriaga, J.; Bohorquez, J.; Celeita, D.; Vega, L.; Paez, D.; Savic, D.; Dandy, G.; Filion, Y.; Grayman, W.; Kapelan, Z. Battle of the Water Networks District Metered Areas. J. Water Resour. Plan. Manag. 2019, 145, 04019002. [Google Scholar] [CrossRef]
- Bui, X.K.; Marlim, M.S.; Kang, D. Water Network Partitioning into District Metered Areas: A State-Of-The-Art Review. Water 2020, 12, 1002. [Google Scholar] [CrossRef] [Green Version]
- Perelman, L.; Ostfeld, A. Topological clustering for water distribution systems analysis. Environ. Model. Softw. 2011, 26, 969–972. [Google Scholar] [CrossRef]
- Lifshitz, R.; Ostfeld, A. Clustering for Analysis of Water Distribution Systems. J. Water Resour. Plan. Manag. 2018, 144, 04018016. [Google Scholar] [CrossRef]
- Scarpa, F.; Lobba, A.; Becciu, G. Elementary DMA Design of Looped Water Distribution Networks with Multiple Sources. J. Water Resour. Plan. Manag. 2016, 142, 04016011. [Google Scholar] [CrossRef] [Green Version]
- Gomes, R.; Marques, A.S.; Sousa, J. Decision support system to divide a large network into suitable District Metered Areas. Water Sci. Technol. 2012, 65, 1667–1675. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [Green Version]
- Clauset, A.; Newman, M.E.J.; Moore, C. Finding community structure in very large networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef] [Green Version]
- Diao, K.; Zhou, Y.; Rauch, W. Automated Creation of District Metered Area Boundaries in Water Distribution Systems. J. Water Resour. Plan. Manag. 2013, 139, 184–190. [Google Scholar] [CrossRef]
- Campbell, E.; Ayala-Cabrera, D.; Izquierdo, J.; Pérez-García, R.; Tavera, M. Water Supply Network Sectorization Based on Social Networks Community Detection Algorithms. Procedia Eng. 2014, 89, 1208–1215. [Google Scholar] [CrossRef] [Green Version]
- Perelman, L.S.; Allen, M.; Preis, A.; Iqbal, M.; Whittle, A.J. Automated sub-zoning of water distribution systems. Environ. Model. Softw. 2015, 65, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Ciaponi, C.; Murari, E.; Todeschini, S. Modularity-Based Procedure for Partitioning Water Distribution Systems into Independent Districts. Water Resour. Manag. 2016, 30, 2021–2036. [Google Scholar] [CrossRef]
- Giustolisi, O.; Ridolfi, L. New Modularity-Based Approach to Segmentation of Water Distribution Networks. J. Hydraul. Eng. 2014, 140, 04014049. [Google Scholar] [CrossRef]
- Giustolisi, O.; Ridolfi, L. A novel infrastructure modularity index for the segmentation of water distribution networks. Water Resour. Res. 2014, 50, 7648–7661. [Google Scholar] [CrossRef]
- Creaco, E.; Cunha, M.; Franchini, M. Using Heuristic Techniques to Account for Engineering Aspects in Modularity-Based Water Distribution Network Partitioning Algorithm. J. Water Resour. Plan. Manag. 2019, 145, 04019062. [Google Scholar] [CrossRef]
- Simone, A.; Giustolisi, O.; Laucelli, D.B. A proposal of optimal sampling design using a modularity strategy. Water Resour. Res. 2016, 52, 6171–6185. [Google Scholar] [CrossRef] [Green Version]
- Alvisi, S. A New Procedure for Optimal Design of District Metered Areas Based on the Multilevel Balancing and Refinement Algorithm. Water Resour. Manag. 2015, 29, 4397–4409. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Weighted spectral clustering for water distribution network partitioning. Appl. Netw. Sci. 2017, 2, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Di Nardo, A.; Giudicianni, C.; Greco, R.; Herrera, M.; Santonastaso, G.F. Applications of Graph Spectral Techniques to Water Distribution Network Management. Water 2018, 10, 45. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Han, R. Spectral Clustering and Multicriteria Decision for Design of District Metered Areas. J. Water Resour. Plan. Manag. 2018, 144, 04018013. [Google Scholar] [CrossRef]
- Izquierdo, J.; Herrera, M.; Montalvo, I.; Pérez-García, R. Agent-based division of water distribution systems into district metered areas. In Proceedings of the 4th International Conference on Software and Data Technologies, Sofia, Bulgaria, 26–29 July 2009; pp. 83–90. [Google Scholar]
- Herrera, M.; Izquierdo, J.; Pérez-García, R.; Montalvo, I. Multi-agent adaptive boosting on semi-supervised water supply clusters. Adv. Eng. Softw. 2012, 50, 131–136. [Google Scholar] [CrossRef]
- Hajebi, S.; Barrett, S.; Clarke, A.; Clarke, S. Multi-agent simulation to support water distribution network partitioning. In Proceedings of the 27th European Simulation and Modelling Conference, Lancaster, UK, 23–25 October 2013; pp. 163–168. [Google Scholar]
- Giudicianni, C.; Herrera, M.; Di Nardo, A.; Adeyeye, K. Automatic Multiscale Approach for Water Networks Partitioning into Dynamic District Metered Areas. Water Resour. Manag. 2020, 34, 835–848. [Google Scholar] [CrossRef] [Green Version]
- Wright, R.; Stoianov, I.; Parpas, P.; Henderson, K.; King, J. Adaptive water distribution networks with dynamically reconfigurable topology. J. Hydroinform. 2014, 16, 1280–1301. [Google Scholar] [CrossRef]
- Liu, J.; Lansey, K.E. Multiphase DMA Design Methodology Based on Graph Theory and Many-Objective Optimization. J. Water Resour. Plan. Manag. 2020, 146, 04020068. [Google Scholar] [CrossRef]
- Pesantez, J.; Berglund, E.Z.; Mahinthakumar, G. Geospatial and Hydraulic Simulation to Design District Metered Areas for Large Water Distribution Networks. J. Water Resour. Plan. Manag. 2020, 146, 06020010. [Google Scholar] [CrossRef]
- Santonastaso, G.F.; Di Nardo, A.; Creaco, E. Dual topology for partitioning of water distribution networks considering actual valve locations. Urban Water J. 2019, 16, 469–479. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, H.; Zeng, H.; Xin, K.; Tao, T. A practical multi-objective optimization sectorization method for water distribution network. Sci. Total. Environ. 2019, 656, 1401–1412. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Z.Y.; Zhao, M.; Qi, J.; Huang, Y.; Zhao, H. Automatic Partitioning of Water Distribution Networks Using Multiscale Community Detection and Multiobjective Optimization. J. Water Resour. Plan. Manag. 2017, 143, 04017057. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Rana, S.M.M.; Boccelli, D.L.; Marchi, A.; Dandy, G.C. Drinking Water Distribution System Network Clustering Using Self-Organizing Map for Real-Time Demand Estimation. J. Water Resour. Plan. Manag. 2020, 146, 04020090. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Methods for Multiple Attribute Decision Making. In Optimizing Hospital-Wide Patient Scheduling; Springer: Cham, Switzerland, 2014; pp. 58–191. [Google Scholar]
- Giudicianni, C.; Di Nardo, A.; Di Natale, M.; Greco, R.; Santonastaso, G.F.; Scala, A. Topological Taxonomy of Water Distribution Networks. Water 2018, 10, 444. [Google Scholar] [CrossRef] [Green Version]
- Zhou, T.; Lü, L.; Zhang, Y.-C. Predicting missing links via local information. Eur. Phys. J. B 2009, 71, 623–630. [Google Scholar] [CrossRef] [Green Version]
- Salton, G.; McGill, M.J. Introduction to Modern Information Retrieval; McGraw Hill Book Company: New York, NY, USA, 1983. [Google Scholar]
- Miljkovic, D. Brief review of self-organizing maps. In Proceedings of the 2017 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 22–26 May 2017; pp. 1061–1066. [Google Scholar]
- Campbell, E.; Izquierdo, J.; Montalvo, I.; Pérez-García, R. A Novel Water Supply Network Sectorization Methodology Based on a Complete Economic Analysis, Including Uncertainties. Water 2016, 8, 179. [Google Scholar] [CrossRef] [Green Version]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef] [Green Version]
- Todini, E. Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Tateishi, R. Urban Flood Vulnerability and Risk Mapping Using Integrated Multi-Parametric AHP and GIS: Methodological Overview and Case Study Assessment. Water 2014, 6, 1515–1545. [Google Scholar] [CrossRef]
- Chung, E.-S.; Abdulai, P.J.; Park, H.; Kim, Y.; Ahn, S.R.; Kim, S.J. Multi-Criteria Assessment of Spatial Robust Water Resource Vulnerability Using the TOPSIS Method Coupled with Objective and Subjective Weights in the Han River Basin. Sustain. J. Rec. 2016, 9, 29. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Solano, F.J.; Iglesias-Rey, P.L.; Meliá, D.M.; Ribelles-Aguilar, J.V. Combining Skeletonization, Setpoint Curves, and Heuristic Algorithms to Define District Metering Areas in the Battle of Water Networks District Metering Areas. J. Water Resour. Plan. Manag. 2018, 144, 04018023. [Google Scholar] [CrossRef]
- Salomons, E.; Skulovich, O.; Ostfeld, A. Battle of Water Networks DMAs: Multistage Design Approach. J. Water Resour. Plan. Manag. 2017, 143, 04017059. [Google Scholar] [CrossRef]
- Lippai, I. Water System Design by Optimization: Colorado Springs Utilities Case Studies. In Pipelines 2005; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2005; pp. 1058–1070. [Google Scholar]













| No. of Clusters | Cluster Record | Variance Record | Average Variance | Q Index |
|---|---|---|---|---|
| 9 | C1 = {1,2,3}; C2 = {4,5,6,7}; C3 = {8}; C4 = {9,10,11,12}; C5 = {13}; C6 = {14,15,16}; C7 = {17}; C8 = {18,19,20}; C9 = {21,22,23}; | Var(C1) = 0.0056; Var(C2) = 0.0873; Var(C3) = 0; Var(C4) = 0.0135; Var(C5) = 0; Var(C6) = 0.0423; Var(C7) = 0; Var(C8) = 0.0261; Var(C9) = 0.0838; | 0.0287 | 0.4511 |
| 8 | C1 = {1,2,3}; C2 = {4,5,6,7}; C3 = {8, 13}; C4 = {9,10,11,12}; C5 = {14,15,16}; C6 = {17}; C7 = {18,19,20}; C8 = {21,22,23}; | Var(C1) = 0.0056; Var(C2) = 0.0873; Var(C3) = 1.0898; Var(C4) = 0.0135; Var(C5) = 0.0423; Var(C6) = 0; Var(C7) = 0.0261; Var(C8) = 0.0838 | 0.1686 | 0.4767 |
| 7 | C1 = {1,2,3}; C2 = {4,5,6,7}; C3 = {8,9,10,11,12,13}; C4 = {14,15,16}; C5 = {18,19,20}; C6 = {17}; C7 = {21,22,23}; | Var(C1) = 0.0056; Var(C2) = 0.0873; Var(C3) = 0.7191; Var(C4) = 0.0423; Var(C5) = 0.0261; Var(C6) = 0; Var(C7) = 0.0838 | 0.1377 | 0.5211 |
| 6 | C1 = {1,2,3}; C2 = {4,5,6,7}; C3 = {8,9,10,11,12,13}; C4 = {14,15,16}; C5 = {18,19,20}; C6 = {17,21,22,23}; | Var(C1) = 0.0056; Var(C2) = 0.0873; Var(C3) = 0.7191; Var(C4) = 0.0423; Var(C5) = 0.0261; Var(C6) = 0.0642; | 0.1574 | 0.5422 |
| 5 | C1 = {1,2,3}; C2 = {4,5,6,7}; C3 = {8,9,10,11,12,13}; C4 = {14,15,16}; C5 = {17,18,19,20,21,22,23}; | Var(C1) = 0.0056; Var(C2) = 0.0873; Var(C3) = 0.7191; Var(C4) = 0.0423; Var(C5) = 0.0506; | 0.1810 | 0.5433 |
| 4 | C1 = {1,2,3,14,15,16}; C2 = {4,5,6,7}; C3 = {8,9,10,11,12,13}; C4 = {17,18,19,20,21,22,23}; | Var(C1) = 7.1598; Var(C2) = 0.0873; Var(C3) = 0.7191; Var(C4) = 0.0506; | 2.0042 | 0.5422 |
| 3 | C1 = {1,2,3,14,15,16}; C2 = {4,5,6,7,8,9,10,11,12,13}; C3 = {17,18,19,20,21,22,23}; | Var(C1) = 7.1598; Var(C2) = 5.3974; Var(C3) = 0.0506; | 4.2026 | 0.4700 |
| 2 | C1 = {1,2,3,4,5,6,7,8,9,10,11,12, 13,14,15,16}; C2 = {17,18,19,20,21,22,23}; | Var(C1) = 6.1588; Var(C2) = 0.0506; | 3.1047 | 0.3389 |
| Indicator | DSI | PSI | RI | WA | Cost |
|---|---|---|---|---|---|
| Weight | 0.2 | 0.3 | 0.2 | 0.1 | 0.2 |
| Physical Characteristics | Value | Main Hydraulic Features | Value |
|---|---|---|---|
| No. of nodes | 1592 | Minimum pressure (m): | 41.2 |
| No. of pipes | 1795 | Mean of pressure (m): | 70.8 |
| No. of valves (PRVs) | 2 | Maximum pressure (m): | 107.7 |
| No. of reservoirs | 1 | Mean surplus pressure (m): | 29.1 |
| No. of pumping stations | 1 | Average WA (hour): | 6.0 |
| Main pipe diameters (mm) | 200–600 | Resilience index (RI) | 0.877 |
| No. of DMAs | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| Nbp | 9 | 10 | 12 | 13 | 15 | 23 | 25 | 27 | 30 | 33 | 35 | 36 | 38 | 39 | 44 | 48 | 51 | 53 | 54 | 55 | 56 | 58 | 59 |
| Nfm | 3 | 4 | 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| Ngv | 6 | 6 | 7 | 8 | 9 | 16 | 17 | 18 | 20 | 22 | 23 | 23 | 24 | 25 | 29 | 32 | 34 | 35 | 35 | 35 | 35 | 36 | 36 |
| No. of DMAs | Criteria | ||||
|---|---|---|---|---|---|
| DSI | PSI | RI | WA | Cost | |
| 3-DMAs | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 |
| 4-DMAs | 0.48 | 0.20 | 1.00 | 1.00 | 0.96 |
| 5-DMAs | 0.61 | 0.32 | 0.97 | 0.80 | 0.82 |
| 6-DMAs | 0.56 | 0.41 | 0.97 | 0.80 | 0.82 |
| 7-DMAs | 0.50 | 0.46 | 0.97 | 0.79 | 0.78 |
| 8-DMAs | 0.68 | 0.62 | 0.67 | 0.70 | 0.62 |
| 9-DMAs | 0.88 | 0.72 | 0.49 | 0.49 | 0.59 |
| 10-DMAs | 0.83 | 0.75 | 0.53 | 0.41 | 0.56 |
| 11-DMAs | 0.79 | 0.79 | 0.48 | 0.31 | 0.48 |
| 12-DMAs | 0.87 | 0.81 | 0.48 | 0.34 | 0.46 |
| 13-DMAs | 0.84 | 0.83 | 0.30 | 0.30 | 0.41 |
| 14-DMAs | 0.83 | 0.85 | 0.30 | 0.30 | 0.40 |
| 15-DMAs | 0.83 | 0.86 | 0.25 | 0.32 | 0.37 |
| 16-DMAs | 0.84 | 0.88 | 0.25 | 0.32 | 0.37 |
| 17-DMAs | 0.88 | 0.90 | 0.22 | 0.31 | 0.34 |
| 18-DMAs | 0.93 | 0.93 | 0.06 | 0.14 | 0.19 |
| 19-DMAs | 1.00 | 0.96 | 0.02 | 0.03 | 0.16 |
| 20-DMAs | 0.99 | 0.97 | 0.00 | 0.00 | 0.14 |
| 21-DMAs | 0.98 | 0.98 | 0.00 | 0.00 | 0.10 |
| 22-DMAs | 0.98 | 0.99 | 0.00 | 0.00 | 0.06 |
| 23-DMAs | 0.97 | 0.99 | 0.01 | 0.02 | 0.04 |
| 24-DMAs | 0.97 | 1.00 | 0.01 | 0.01 | 0.02 |
| 25-DMAs | 0.97 | 1.00 | 0.01 | 0.01 | 0.00 |
| No. of DMAs | Criterion | E+ | E− | C | Rank | ||||
|---|---|---|---|---|---|---|---|---|---|
| DSI | PSI | RI | WA | Cost | |||||
| 3 DMAs | 0.0000 | 0.0000 | 0.0777 | 0.0425 | 0.0806 | 0.0933 | 0.1198 | 0.5621 | 10 |
| 4 DMAs | 0.0244 | 0.0159 | 0.0777 | 0.0425 | 0.0775 | 0.0679 | 0.1213 | 0.6412 | 5 |
| 5 DMAs | 0.0310 | 0.0248 | 0.0754 | 0.0341 | 0.0662 | 0.0595 | 0.1131 | 0.6552 | 3 |
| 6 DMAs | 0.0285 | 0.0319 | 0.0754 | 0.0341 | 0.0659 | 0.0543 | 0.1141 | 0.6776 | 2 |
| 7 DMAs | 0.0253 | 0.0363 | 0.0753 | 0.0338 | 0.0626 | 0.0531 | 0.1126 | 0.6794 | 1 |
| 8 DMAs | 0.0343 | 0.0485 | 0.0524 | 0.0299 | 0.0497 | 0.0540 | 0.0982 | 0.6451 | 4 |
| 9 DMAs | 0.0443 | 0.0563 | 0.0380 | 0.0208 | 0.0479 | 0.0604 | 0.0965 | 0.6151 | 6 |
| 10 DMAs | 0.0419 | 0.0586 | 0.0415 | 0.0175 | 0.0448 | 0.0608 | 0.0960 | 0.6123 | 7 |
| 11 DMAs | 0.0402 | 0.0619 | 0.0377 | 0.0133 | 0.0385 | 0.0679 | 0.0923 | 0.5761 | 9 |
| 12 DMAs | 0.0438 | 0.0638 | 0.0375 | 0.0146 | 0.0367 | 0.0677 | 0.0946 | 0.5831 | 8 |
| 13 DMAs | 0.0426 | 0.0650 | 0.0232 | 0.0127 | 0.0334 | 0.0796 | 0.0886 | 0.5267 | 11 |
| 14 DMAs | 0.0419 | 0.0670 | 0.0232 | 0.0127 | 0.0319 | 0.0803 | 0.0892 | 0.5261 | 12 |
| 15 DMAs | 0.0418 | 0.0677 | 0.0194 | 0.0135 | 0.0299 | 0.0837 | 0.0883 | 0.5132 | 14 |
| 16 DMAs | 0.0425 | 0.0689 | 0.0194 | 0.0135 | 0.0296 | 0.0837 | 0.0894 | 0.5166 | 13 |
| 17 DMAs | 0.0447 | 0.0702 | 0.0169 | 0.0131 | 0.0271 | 0.0868 | 0.0901 | 0.5093 | 15 |
| 18 DMAs | 0.0471 | 0.0731 | 0.0049 | 0.0059 | 0.0150 | 0.1048 | 0.0886 | 0.4579 | 16 |
| 19 DMAs | 0.0506 | 0.0753 | 0.0019 | 0.0014 | 0.0130 | 0.1097 | 0.0916 | 0.4552 | 17 |
| 20 DMAs | 0.0500 | 0.0763 | 0.0000 | 0.0000 | 0.0112 | 0.1126 | 0.0919 | 0.4495 | 18 |
| 21 DMAs | 0.0494 | 0.0768 | 0.0000 | 0.0000 | 0.0081 | 0.1145 | 0.0916 | 0.4446 | 19 |
| 22 DMAs | 0.0497 | 0.0773 | 0.0000 | 0.0000 | 0.0051 | 0.1164 | 0.0921 | 0.4415 | 20 |
| 23 DMAs | 0.0493 | 0.0775 | 0.0008 | 0.0008 | 0.0033 | 0.1167 | 0.0920 | 0.4406 | 21 |
| 24 DMAs | 0.0491 | 0.0782 | 0.0007 | 0.0003 | 0.0015 | 0.1182 | 0.0924 | 0.4388 | 22 |
| 25 DMAs | 0.0491 | 0.0784 | 0.0007 | 0.0003 | 0.0000 | 0.1192 | 0.0925 | 0.4369 | 23 |
| Best ideal | 0.0506 | 0.0784 | 0.0777 | 0.0425 | 0.0806 | ||||
| Worst ideal | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bui, X.K.; Marlim, M.S.; Kang, D. Optimal Design of District Metered Areas in a Water Distribution Network Using Coupled Self-Organizing Map and Community Structure Algorithm. Water 2021, 13, 836. https://doi.org/10.3390/w13060836
Bui XK, Marlim MS, Kang D. Optimal Design of District Metered Areas in a Water Distribution Network Using Coupled Self-Organizing Map and Community Structure Algorithm. Water. 2021; 13(6):836. https://doi.org/10.3390/w13060836
Chicago/Turabian StyleBui, Xuan Khoa, Malvin S. Marlim, and Doosun Kang. 2021. "Optimal Design of District Metered Areas in a Water Distribution Network Using Coupled Self-Organizing Map and Community Structure Algorithm" Water 13, no. 6: 836. https://doi.org/10.3390/w13060836
APA StyleBui, X. K., Marlim, M. S., & Kang, D. (2021). Optimal Design of District Metered Areas in a Water Distribution Network Using Coupled Self-Organizing Map and Community Structure Algorithm. Water, 13(6), 836. https://doi.org/10.3390/w13060836







