Accounting for Uncertainties in the Safety Assessment of Concrete Gravity Dams: A Probabilistic Approach with Sample Optimization
Abstract
:1. Introduction
2. Related Works
3. Methodology
3.1. Sampling Strategy
3.2. Sensitivity Analysis
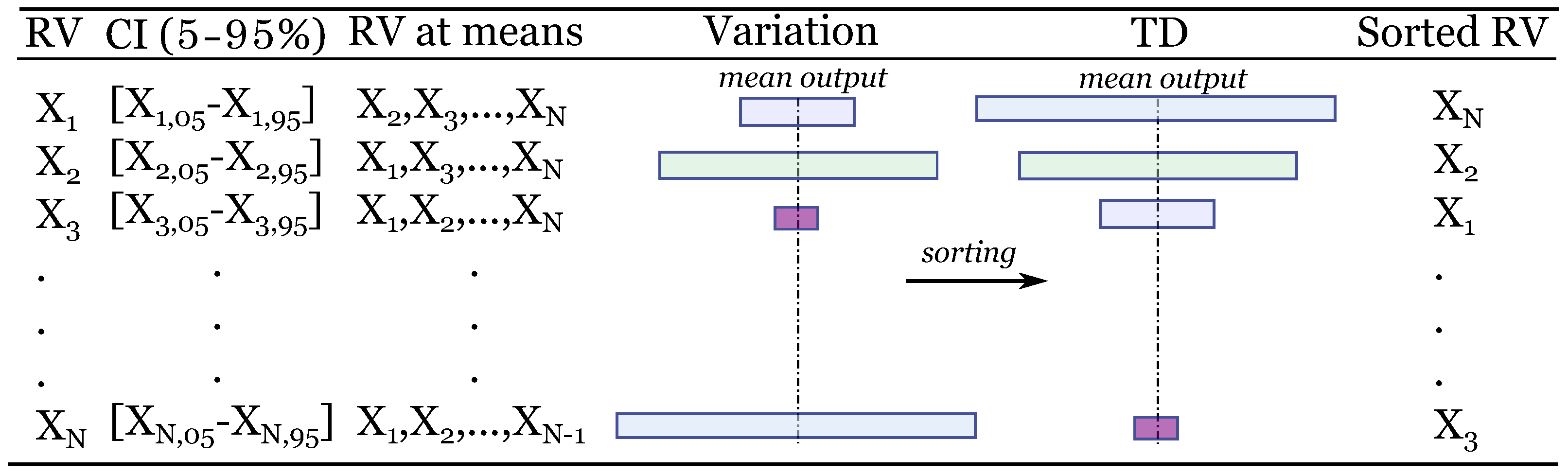
3.2.1. Tornado Diagrams
3.2.2. Variance-Based Global Sensitivity Analysis
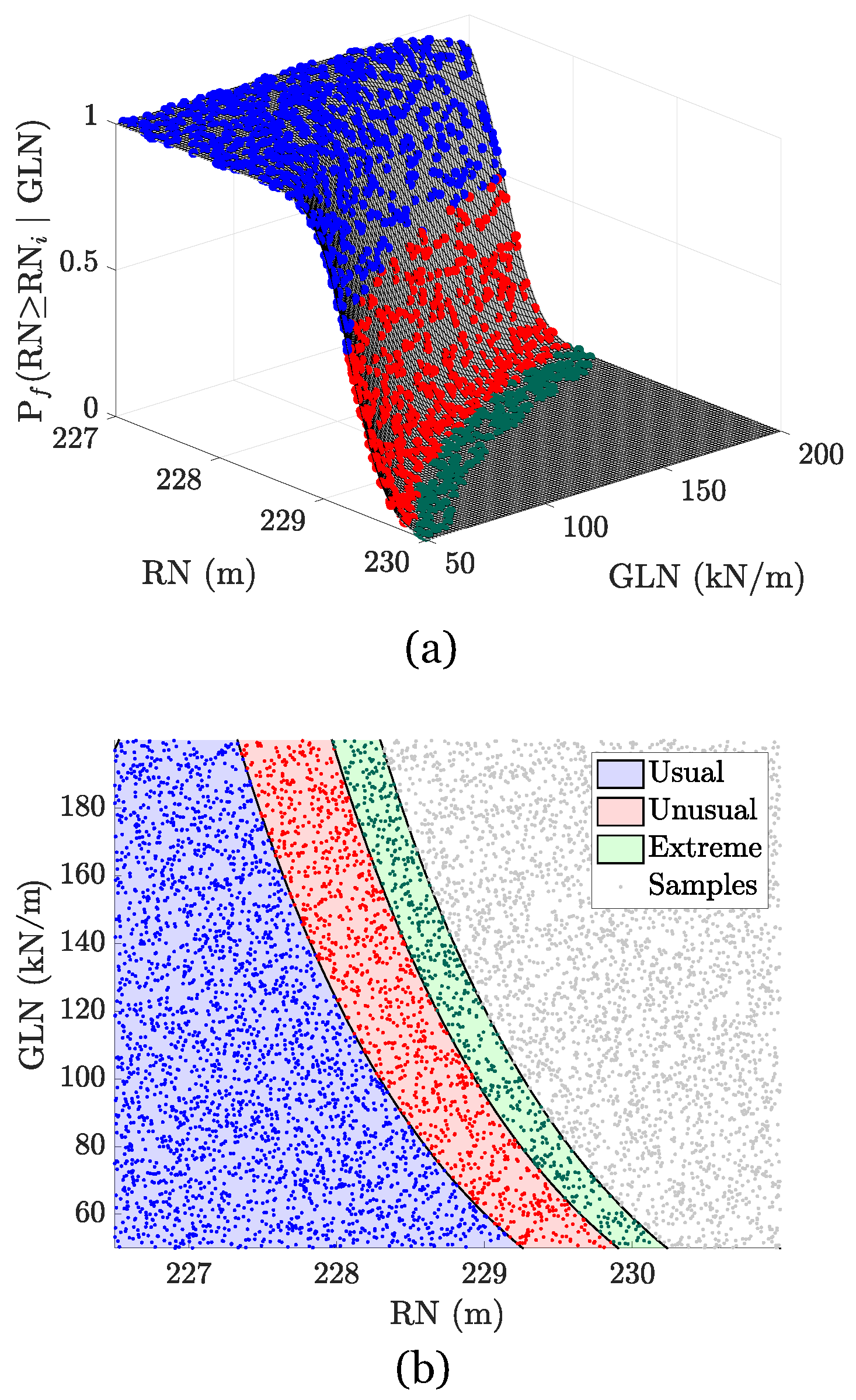
3.3. Conditional Probability of Exceedance Estimation
4. Case Study
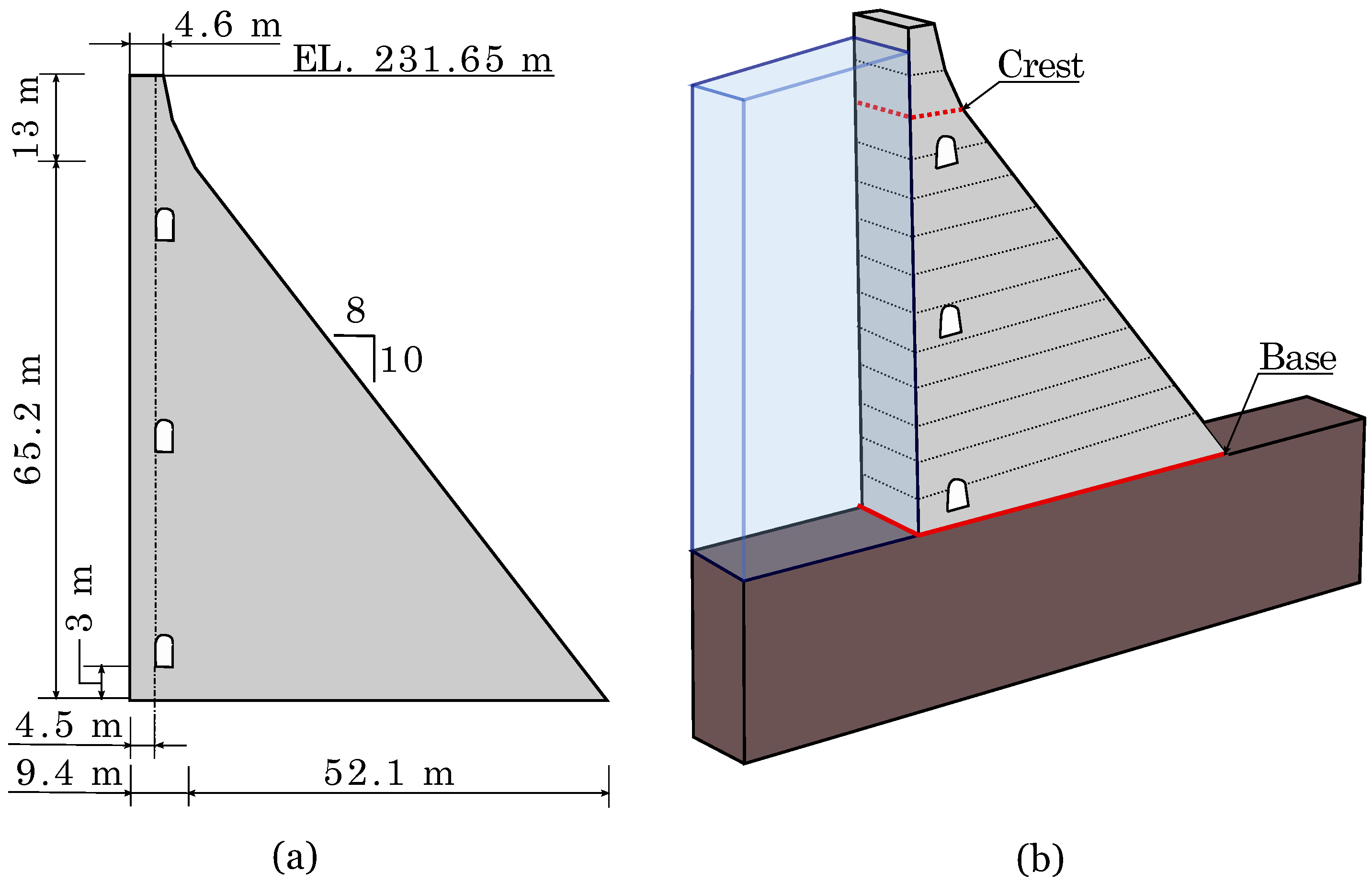
4.1. Numerical Model
4.2. Performance Indicators
4.3. Modeling Parameters and Screening Study
4.4. Load Combinations
5. Results and Discussion
5.1. Sample Size
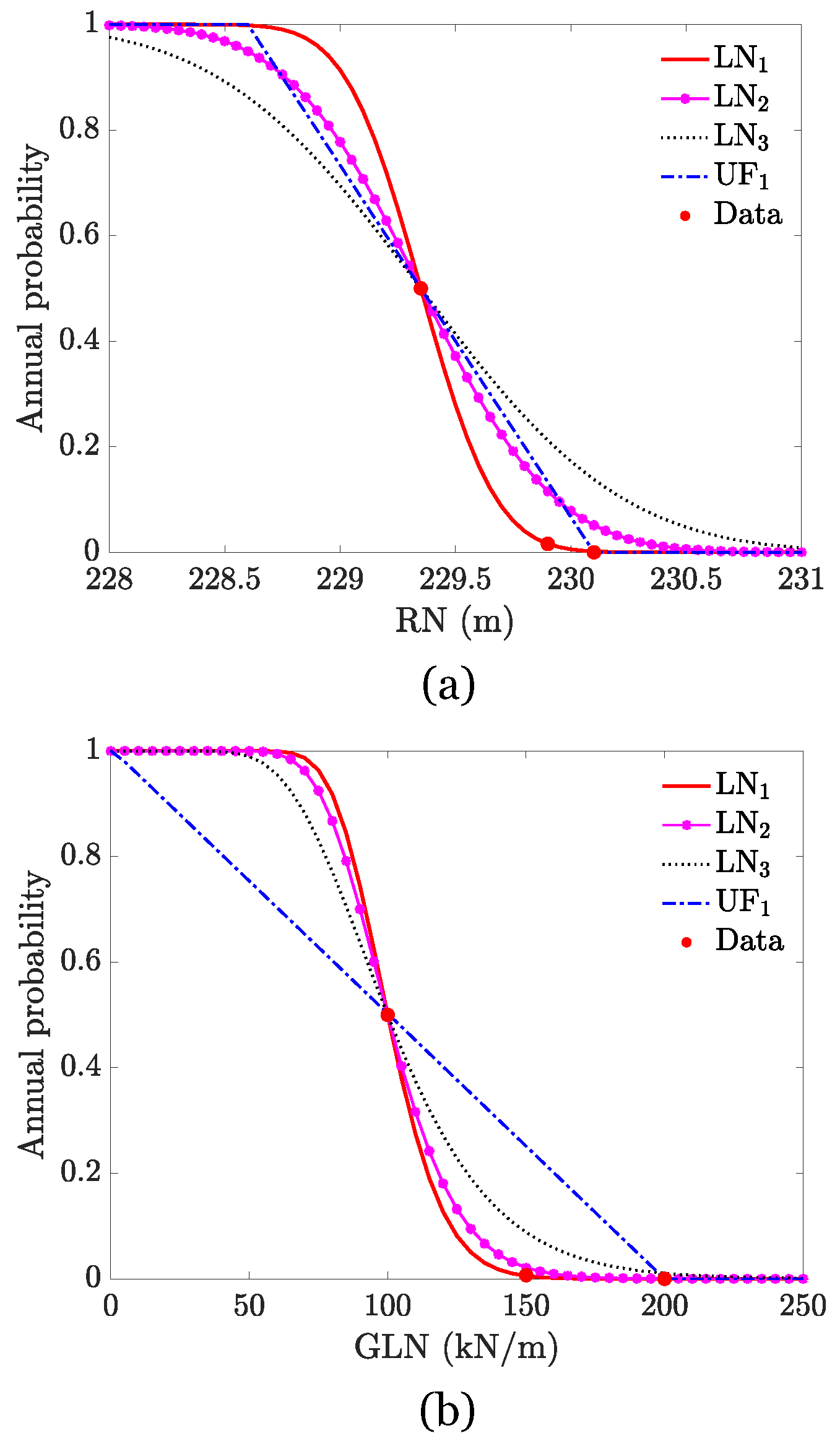
5.2. Effect of Model Demand PDF Variation in the Analysis
5.3. Model Parameter Recommendations for Adequate Performance
5.3.1. Influence of Model Parameters
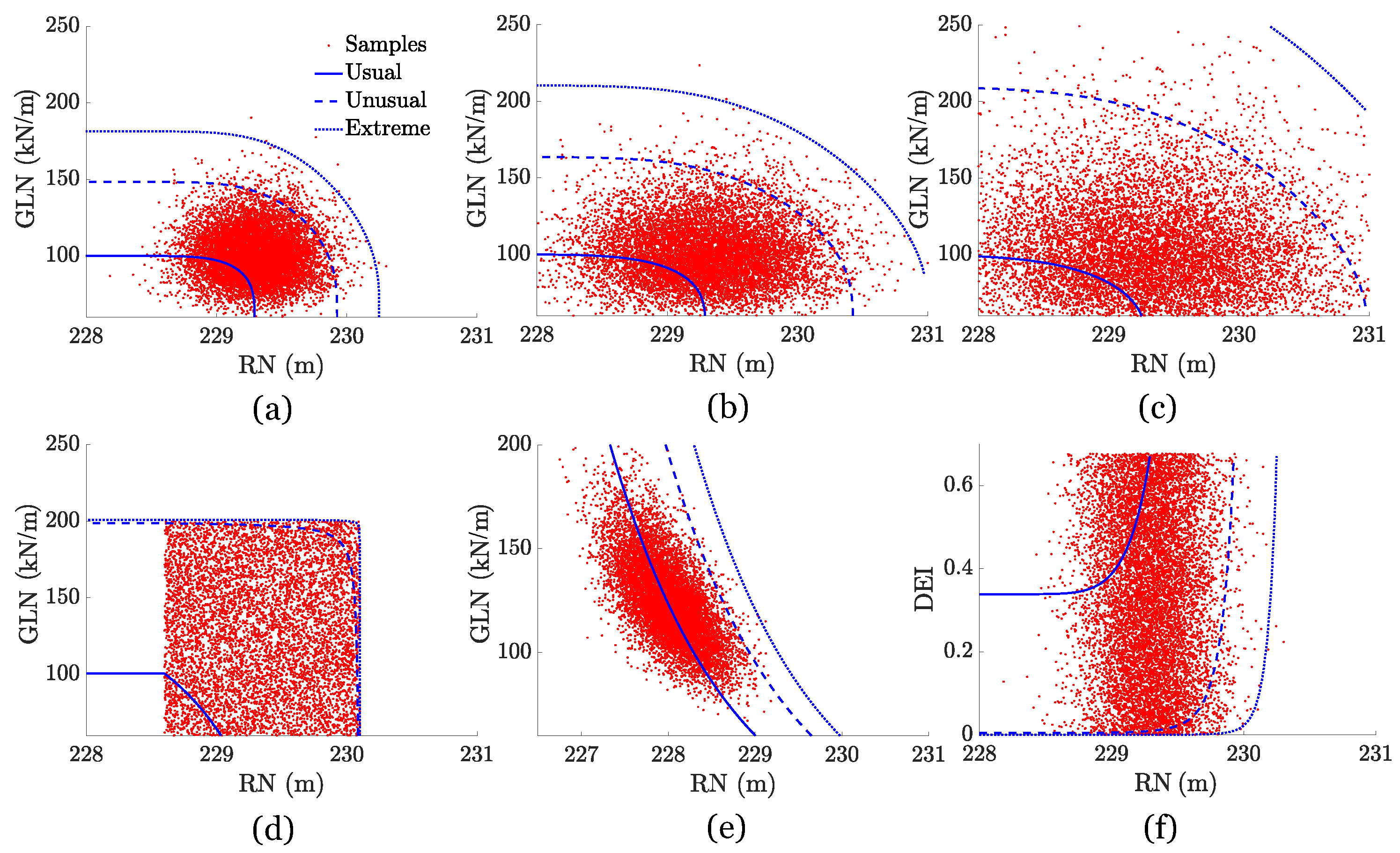
5.3.2. Stability Analysis Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z. Global Sensitivity Analysis of the Static Performance of Concrete Gravity Dam from the Viewpoint of Structural Health Monitoring. Arch. Comput. Methods Eng. 2020. [Google Scholar] [CrossRef]
- Cordier, M.; Léger, P. Structural stability of gravity dams: A progressive assessment considering uncertainties in shear strength parameters. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2018, 12, 109–122. [Google Scholar] [CrossRef]
- Westberg Wilde, M.; Johansson, F. Probability-based guidelines for design and assessment of concrete dams. In Safety, Reliability, Risk and Life-Cycle Performance of Structures & Infrastructures; Deodatis, E.F., Ed.; Taylor & Francis Group: London, UK, 2013; pp. 5187–5210. [Google Scholar]
- Kalinina, A.; Spada, M.; Marelli, S.; Burgherr, P.; Sudret, B. Uncertainties in the Risk Assessment of Hydropower Dams: State-of-the-Art and Outlook; Rapport Technique RSUQ-2016-008; ETH Zurich: Zürich, Switzerland, 2016. [Google Scholar]
- Segura, R.; Padgett, J.; Paultre, P. Metamodel-Based Seismic Fragility Analysis of Concrete Gravity Dams. J. Struct. Eng. 2020, 46, 04020121. [Google Scholar] [CrossRef] [Green Version]
- Hariri-Ardebili, M.; Pourkamali-Anaraki, F. Simplified reliability analysis of multi hazard risk in gravity dams via machine learning techniques. Arch. Civ. Mech. Eng. 2018, 18, 592–610. [Google Scholar] [CrossRef]
- Salazar, F.; Morán, R.; Toledo, M.Á.; Oñate, E. Data-based models for the prediction of dam behaviour: A review and some methodogical considerations. Arch. Comput. Methods Eng. 2015, 24, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Schleiss, A.; Pougatsch, H. Les Barrages, du Project a la Mise en Service, 1st ed.; Presses Polytechniques et Universitaires Romandes: Lausanne, Switzerland, 2011. [Google Scholar]
- CDA. Dam safety Guidelines. In Dam Safety Recommendations Section 6.1, 6.2 and 6.3, Revised in 2013; Canadian Dam Association: Winnipeg, MB, Canada, 2007. [Google Scholar]
- FERC. Engineering Guidelines for the Evaluation of Hydropower Projects; Federal Energy Regulatory Comission: Washington, DC, USA, 2002.
- USACE. Gravity Dam Design; Technical Report EM 1110-2-2200; U.S. Corps of Engineer: Washington, DC, USA, 1995.
- Lave, L.B.; Resendiz-Carrillo, D.; McMichael, F.C. Safety goals for high-hazard dams: Are dams too safe? Water Resour. Res. 1990, 26, 1383–1391. [Google Scholar]
- Tekie, P.; Ellingwood, B. Seismic fragility assessment of concrete gravity dams. Earthq. Eng. Struct. Dyn. 2003, 32, 2221–2240. [Google Scholar] [CrossRef]
- Schultz, M.; Gouldby, B.; Simm, J.; Wibowo, J. Beyond the Factor of Safety: Developing Fragility Curves to Characterize System Reliability; Technical Report ERDC SR-10-01; U.S. Army Corps of Engineers: Washington, DC, USA, 2010.
- Kreuzer, H.; Léger, P. The Adjustable Factor of Safety: A reliability-based approach to assess the factor of safety for concrete dams. Int. J. Hydropower Dams 2013, 20, 67–80. [Google Scholar]
- Westberg Wilde, M.; Johansson, F. System reliability of concrete dams with respect to foundation stability: Application to a spillway. J. Geotech. Geoenviron. Eng. 2013, 139, 308–319. [Google Scholar] [CrossRef]
- Bernier, C.; Padgett, J.; Proulx, J.; Paultre, P. Seismic fragility of concrete gravity dams with modeling parameter uncertainty and spacial variation. J. Struct. Eng. 2016, 142, 05015002. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M. Analytical failure probability model for generic gravity dam classes. Proc. Inst. Mech. Eng. J. Risk Reliab. 2017, 1–12. [Google Scholar] [CrossRef]
- Segura, R.; Bernier, C.; Durand, C.; Paultre, P. Modelling and Characterizing a Concrete Gravity Dam for Fragility Analysis. Infrastructures 2019, 4, 1–19. [Google Scholar]
- USBR and USACE. Best Practices in Dam and Levee Safety Risk Analysis; Technical Report Version 4.1; U.S. Bureau of Reclammation: Washington, DC, USA; U.S. Army Corps of Engineer: Washington, DC, USA, 2019.
- Hovde, E. Recommendations for Existing Concrete Dams: Probabilistic Analysis of Stability; Rapport Technique 12372-OO-R-001; Dr.techn.Olav Olsen AS: Trondheim, Norway, 2017. [Google Scholar]
- Westberg, M.; Johansson, F. Probabilistic Model Code for Concrete Dams; Rapport Technique 2016:292; Energiforsk: Stockholm, Sweden, 2016. [Google Scholar]
- FERC. Risk-Informed Decision Making Guidelines; Version 4.1; Federal Energy Regulatory Comission: Washington, DC, USA, 2016.
- FEMA. Federal Guidelines for Dam Safety Risk Management; Technical Report P-1025. Federal Guidelines for Dam Safety Risk Management; Federal Emergency Management Agency (FEMA): Washington, DC, USA, 2015.
- Escuder-Bueno, I.; Mazza, G.; Morales-Torres, A.; Castillo-Rodriguez, J.T. Computational Aspects of Dam Risk Analysis: Findings and Challenges. Engineering 2016, 2, 319–324. [Google Scholar] [CrossRef] [Green Version]
- Krounis, A.; Johansson, F.; Larsson, S. Effects of spatial variation in cohesion over the concrete-rock interface on dam sliding stability. J. Rock Mech. Geotech. Eng. 2015, 7, 659–667. [Google Scholar] [CrossRef] [Green Version]
- Altarejos-Garcia, L.; Escuder-Bueno, I.; Serrano-Lombillo, A.; Morales-Torres, A. Factor of safety and probability of failure in concrete dams. In Risk Analysis, Dam Safety, Dam Security and Critical Infrastructure Management; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- USBR. Dam Safety Public Protection Guidelines: A Risk Framework to Support Dam Safety Decision-Making; Technical Report August; U.S. Bureau of Reclammation: Washington, DC, USA, 2011.
- Howard, R.A. Decision analysis: Practice and promise. Manag. Sci. 1988, 34, 679–695. [Google Scholar] [CrossRef] [Green Version]
- Porter, K. An overview of PEER’s performance-based earthquake engineering methodology. In Proceedings of the 9th International Conference on Applications of Statistics and Probability in Civil Engineering, San Francisco, CA, USA, 6–9 July 2003. [Google Scholar]
- Hariri-Ardebili, M.A.; Saouma, V. Sensitivity and uncertainty quantification of the cohesive crack model. Eng. Fract. Mech. 2016, 155, 18–35. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M. MCS-based response surface metamodels and optimal design of experiments for gravity dams. Struct. Infraestruct. Eng. 2018. [Google Scholar] [CrossRef]
- Lokke, A.; Chopra, A.K. Direct-Finite-Element Method for Nonlinear Earthquake Analysis of Concrete Dams Including Dam-Water-Foundation Rock Interaction; Technical Report 2019/02; Pacific Earthquake Engineering Research Center: Richmond, CA, USA, 2019. [Google Scholar]
- Sobol, I. Global sensitivity indices for nonlinear mathematical models and their monte carlo estimates mathematics and computers in simulations. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Gaspar, A.; Lopez-Caballero, F.; Modaressi-Farahmand-Razavi, A.; Gomes-Correia, A. Methodology for a probabilistic analysis of an RCC gravity dam construction. Modelling of temperature, hydration degree and ageing degree fields. Eng. Struct. 2014, 65, 99–110. [Google Scholar] [CrossRef]
- Khaneghahi, M.H.; Alembagheri, M.; Soltani, N. Reliability and variance-based sensitivity analysis of arch dams during construction and reservoir impoundment. Front. Struct. Civ. Eng. 2018, 13, 526–541. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, M.; Chang, D.; Xu, Y. Dam Failure Mechanism and Risk Assessment; Wiley: Singapore, 2016. [Google Scholar]
- Sheikholeslami, R.; Razavi, S. Progressive Latin Hypercube Sampling: An efficient approach for robust sampling-based analysis of environmental models. Environ. Model. Softw. 2017, 93, 109–126. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; Wiley: Ispra, Italy, 2004. [Google Scholar]
- Padgett, J.; DesRoches, R. Sensitivity of Seismic Response and Fragility to Parameter Uncertainty. J. Struct. Eng. 2007, 133, 1710–1718. [Google Scholar] [CrossRef] [Green Version]
- CADAM3D; Version 2.4; Mlt Technology Inc.: Westport, IN, USA, 2020.
- Proulx, J.; Paultre, P. Experimental and numerical investigation of dam-reservoir-foundation interaction for a large gravity dam. Can. J. Civ. Eng. 1997, 24, 90–105. [Google Scholar]
- FERC. Engineering Guidelines for the Evaluation of Hydropower Projects: Chapter 3, Gravity Dams; Revised Version; Federal Energy Regulatory Comission: Washington, DC, USA, 2016.
- Rivard, P.; Champagne, K.; Quirion, M. Paramètres de résistance au cisaillement associés aux discontinuités des barrages en béton du Québec. In Proceedings of the Annual Congress of the Canadian Dam Association, Montreal, QC, Canada, 5–10 October 2013. [Google Scholar]
- Ruggeri, G. Working Group on Sliding Safety of Existing Gravity Dams; Technical Report; ICOLD European Club: Paris, France, 2004. [Google Scholar]
- Renaud, S.; Saichi, T.; Bouaanani, N.; Miquel, B.; Quirion, M.; Rivard, P. Roughness Effects on the Shear Strength of Concrete and Rock Joints in Dams Based on Experimental Data. Rock Mech. Rock Eng. 2019, 52, 3867–3888. [Google Scholar] [CrossRef]
- Griffith, A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond 1921, 221, 163–198. [Google Scholar]
- USACE. Introduction to Probability and Reliability Methods for Use in Geotechnical Engineering; U.S. Army Corps of Engineers: Washington, DC, USA, 1997.
- Razavi, S.; Sheikholeslami, R.; Gupta, H.V.; Haghnegahdar, A. VARS-TOOL: A toolbox for comprehensive, efficient, and robust sensitivity and uncertainty analysis. Environ. Model. Softw. 2018, 112, 95–107. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. UQLab: A Framework for Uncertainty Quantification in MATLAB. In Proceedings of the 2nd International Conference on Vulnerability and Risk Analysis and Management (ICVRAM 2014), Liverpool, UK, 13–16 July 2014; pp. 2554–2563. [Google Scholar]








| LC | SSF | OSF | USF | PR | ||
|---|---|---|---|---|---|---|
| No Test | Test | Residual | ||||
| Usual | 3 | 2 | 1.5 | 1.2 | 1/3 median | |
| Unusual | 2 | 1.5 | 1.3 | 1.1 | 1/2 median | |
| Extreme | 1.3 | 1.1 | 1.1 | 1.1 | within base | |
| Parameter | Designation | Distribution Parameters | ||
|---|---|---|---|---|
| Reservoir elevation (m) | RN | Uniform | L = 225 | U = 231 |
| Ice load (kN/m) | GLN | Uniform | L = 50 | U = 200 |
| Drain efficiency (%) | DEI | Uniform | L = 0 | U = 67 |
| Base peak friction angle () | BFP | Uniform | L = 42 | U = 55 |
| Base residual friction angle () | BFR | Normal | BFP | |
| Base tensile strength (kPa) | BRT | Uniform | L = 150 | U = 1500 |
| Base min. peak compressive stress (kPa) | BMCP | Normal | ||
| Base peak cohesion - Real (kPa) | BCP | Uniform | L = 300 | U = 3000 |
| Base peak cohesion - Apparent (kPa) | BCP | Uniform | L = 0 | U = 1000 |
| Joint tensile strength (kPa) | JRT | Uniform | L = 1000 | U = 3000 |
| Joint peak friction angle () | JFP | Uniform | L = 45 | U = 55 |
| Joint peak cohesion (kPa) | JCP | Uniform | L = 400 | U = 700 |
| Load Combination (LC) | Annual Probability (P) | Return Period (RP) |
|---|---|---|
| Usual | P | RP years |
| Unusual | P | RP years |
| Extreme | P | RP years |
| CDF | Distribution Parameters | |||||
|---|---|---|---|---|---|---|
| RN | GLN | DEI | ||||
| LN | 5.34 | 0.001 | 4.60 | 0.10 | – | – |
| LN | 5.34 | 0.002 | 4.60 | 0.20 | – | – |
| LN | 5.34 | 0.003 | 4.60 | 0.30 | – | – |
| UF | L | U | L | U | L | U |
| LC Distribution | Parameter | Description |
|---|---|---|
| D1 | RN-GLN | LN LN |
| D2 | RN-GLN | LN LN |
| D3 | RN-GLN | LN LN |
| D4 | RN-GLN | UF UF |
| D5 | RN-GLN | LN LN with |
| D6 | RN-DEI | LN UF |
| Model Parameter | SSF | SSFR | USF | OSF | PR | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Base | Crest | Base | Crest | Base | Crest | Base | Crest | Base | Crest | |
| RN | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| GLN | <0.05 | <0.05 | <0.05 | <0.05 | 0.657 | 0.233 | 0.070 | <0.05 | <0.05 | <0.05 |
| DEI | <0.05 | – | <0.05 | – | <0.05 | – | <0.05 | – | <0.05 | – |
| BRT | <0.05 | – | 0.087 | – | 0.215 | – | 0.191 | – | 0.151 | – |
| BMCP | <0.05 | – | <0.05 | – | <0.05 | – | 0.104 | – | <0.05 | – |
| BCP | <0.05 | – | 0.167 | – | 0.615 | – | 0.538 | – | 0.428 | – |
| BFP | <0.05 | – | 0.913 | – | 0.970 | – | 0.915 | – | 0.444 | – |
| BRF | 0.532 | – | <0.05 | – | 0.917 | – | 0.964 | – | 0.339 | – |
| JRT | – | 0.206 | – | 0.096 | – | <0.05 | – | <0.05 | – | 0.060 |
| JCP | – | <0.05 | – | 0.093 | – | <0.05 | – | <0.05 | – | 0.060 |
| JPF | – | <0.05 | – | 0.251 | – | 0.190 | – | 0.231 | – | 0.315 |
| Surface | R | RMSE |
|---|---|---|
| SSF (BCP, BFP) | 0.963 | 0.3613 |
| PR (RN, DEI) | 0.901 | 1.450 |
| PR (RN, GLN) | 0.999 | 0.101 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Segura, R.L.; Miquel, B.; Paultre, P.; Padgett, J.E. Accounting for Uncertainties in the Safety Assessment of Concrete Gravity Dams: A Probabilistic Approach with Sample Optimization. Water 2021, 13, 855. https://doi.org/10.3390/w13060855
Segura RL, Miquel B, Paultre P, Padgett JE. Accounting for Uncertainties in the Safety Assessment of Concrete Gravity Dams: A Probabilistic Approach with Sample Optimization. Water. 2021; 13(6):855. https://doi.org/10.3390/w13060855
Chicago/Turabian StyleSegura, Rocio L., Benjamin Miquel, Patrick Paultre, and Jamie E. Padgett. 2021. "Accounting for Uncertainties in the Safety Assessment of Concrete Gravity Dams: A Probabilistic Approach with Sample Optimization" Water 13, no. 6: 855. https://doi.org/10.3390/w13060855
APA StyleSegura, R. L., Miquel, B., Paultre, P., & Padgett, J. E. (2021). Accounting for Uncertainties in the Safety Assessment of Concrete Gravity Dams: A Probabilistic Approach with Sample Optimization. Water, 13(6), 855. https://doi.org/10.3390/w13060855







