Hydraulic Characteristics of Emerged Rigid and Submerged Flexible Vegetations in the Riparian Zone
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment Apparatus
2.2. Vegetation Material
2.3. Experiment Method
2.4. Experimental Conditions
2.5. Locations of Flow Measurement
3. Analytical Method
3.1. Mean Velocity
3.2. Turbulence Intensity
3.3. Flow Resistance Coefficient
4. Results and Discussions
4.1. Mean Velocity Profiles
4.2. Turbulence Intensities
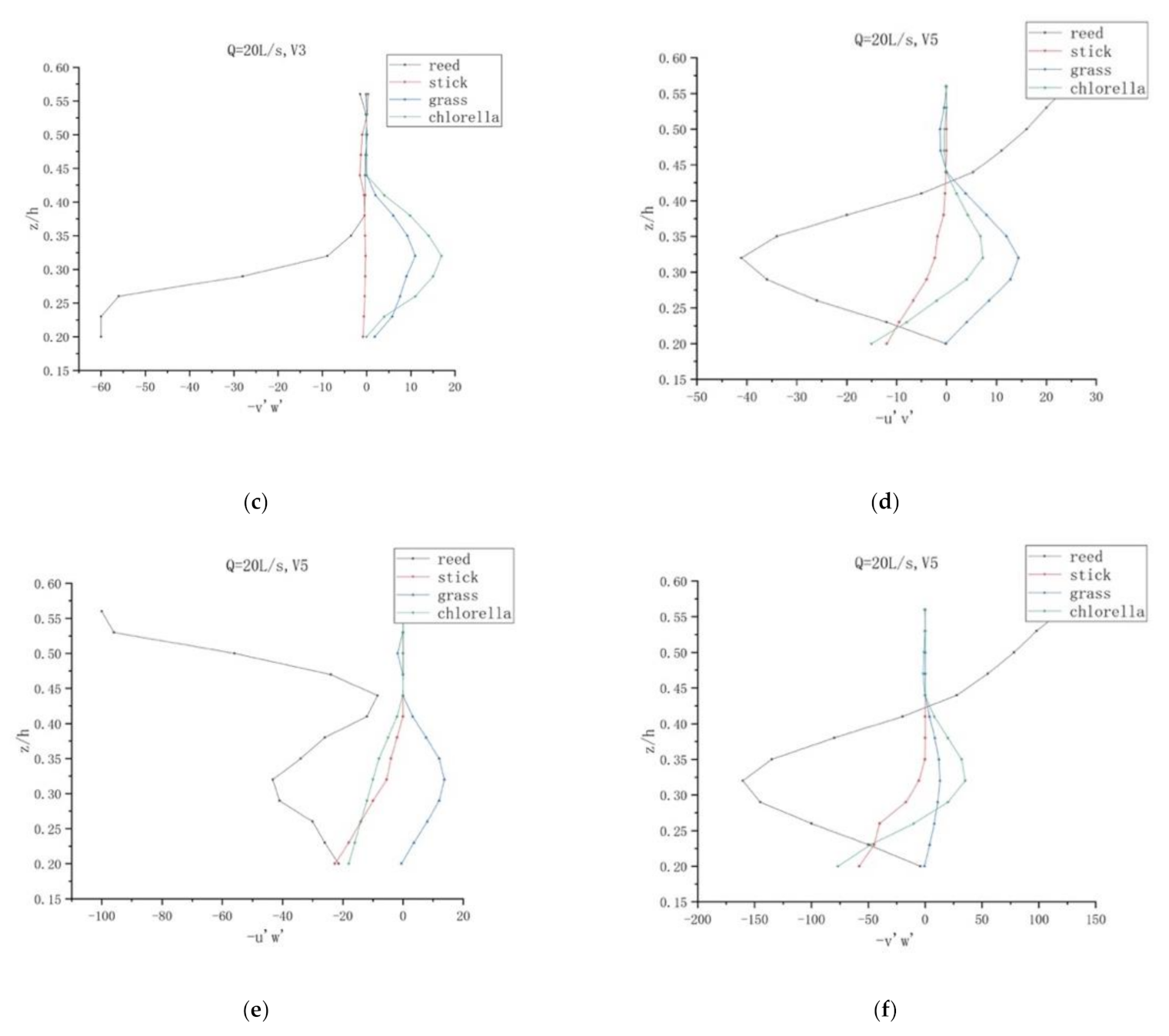
4.3. Reynold Stress
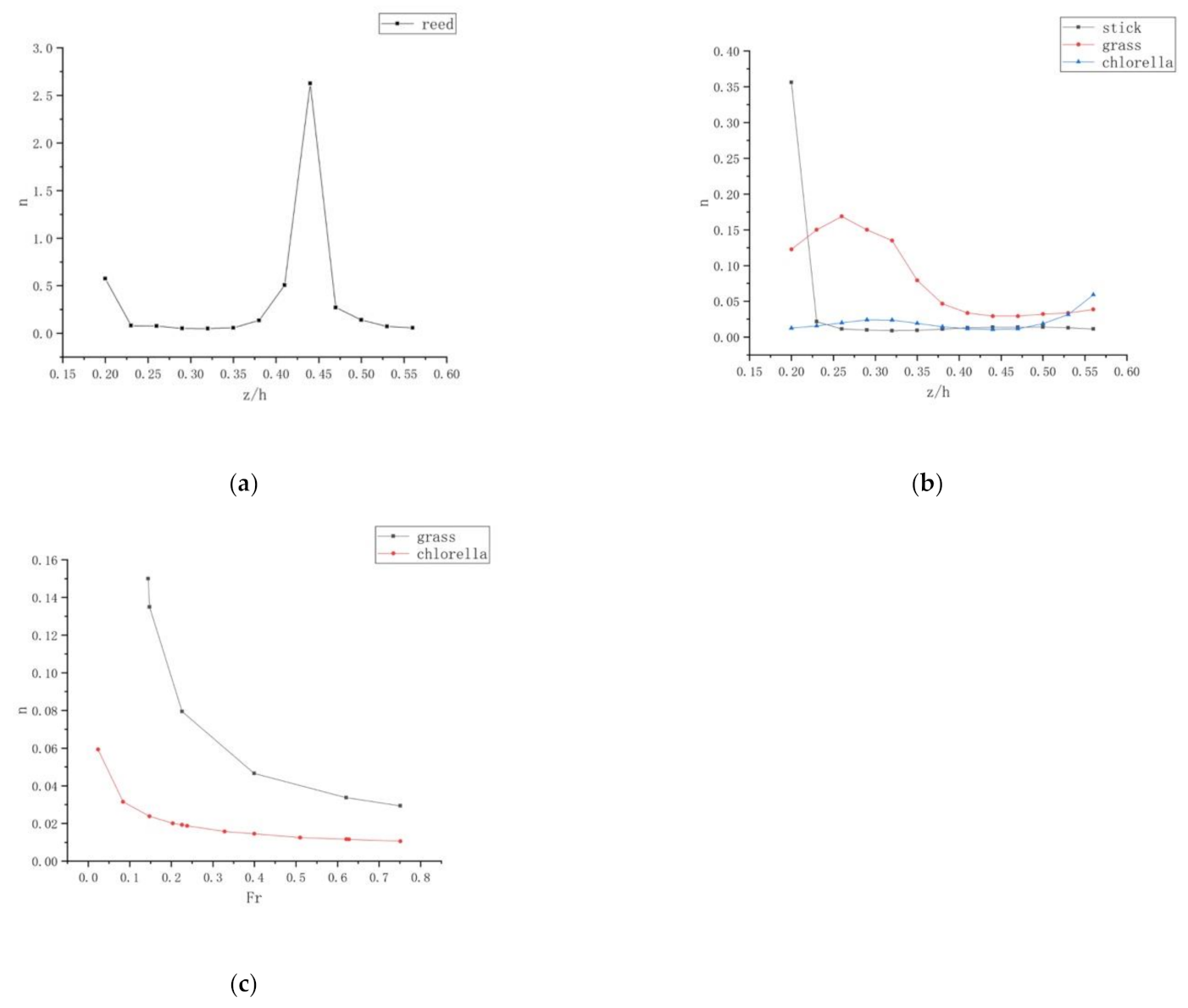
4.4. Manning Coefficient
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Szabo-Meszaros, M.; Navaratnam, C.U.; Aberle, J.; Silva, A.T.; Forseth, T.; Calles, O.; Fjeldstad, H.P.; Alfredsen, K. Experimental hydraulics on fish-friendly trash-racks: An ecological approach. Ecol. Eng. 2018, 113, 11–20. [Google Scholar] [CrossRef]
- Sonnenwald, F.; Guymer, I.; Stovin, V. A CFD-Based Mixing Model for Vegetated Flows. Water Resour. Res. 2019, 55. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Tang, C.; Nepf, H. Turbulent Kinetic Energy in Submerged Model Canopies under Oscillatory Flow. Water Resour. Res. 2018, 54, 1734–1750. [Google Scholar] [CrossRef]
- Li, D.; Huai, W.-X.; Liu, M.-Y. Investigation of the flow characteristics with one-line emergent canopy patches in open channel. J. Hydrol. 2020, 590, 125248. [Google Scholar] [CrossRef]
- Leonard, L.A.; Luther, M.E. Flow hydrodynamics in tidal marsh canopies. Limnol. Oceanogr. 1995, 40, 1474–1484. [Google Scholar] [CrossRef]
- Kemp, J.L.; Harper, D.M.; Crosa, G.A. The habitat-scale ecohydraulics of rivers. Ecol. Eng. 2000, 16, 17–29. [Google Scholar] [CrossRef]
- Chen, S.C.; Kuo, Y.M.; Li, Y.H. Flow characteristics within different configurations of submerged flexible vegetation. J. Hydrol. 2011, 398, 124–134. [Google Scholar] [CrossRef]
- Järvelä, J. Flow resistance of flexible and stiff vegetation: A flume study with natural plants. J. Hydrol. 2002, 269, 44–54. [Google Scholar] [CrossRef]
- Järvelä, J. Effect of submerged flexible vegetation on flow structure and resistance. J. Hydrol. 2005, 307, 233–241. [Google Scholar] [CrossRef]
- Stephan, U.; Gutknecht, D. Hydraulic resistance of submerged flexible vegetation. J. Hydrol. 2002, 269, 27–43. [Google Scholar] [CrossRef]
- Xia, J.; Nehal, L. Hydraulic features of flow through emergent bending aquatic vegetation in the riparian zone. Water 2013, 5, 2080–2093. [Google Scholar] [CrossRef]
- Zhang, S.; Li, G.; He, X.; Liu, Y.; Wang, Z. Water flow resistance characteristics of double-layer vegetation in different submerged states. Water Sci. Technol. Water Supply 2019, 19, 2435–2442. [Google Scholar] [CrossRef]
- Weltz, M.A.; Arslan, A.B.; Lane, L.J. Hydraulic Roughness Coefficients for Native Rangelands. J. Irrig. Drain. Eng. 1992, 118, 776–790. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.; Abrahams, A.D. Resistance to overland flow due to bed-load transport on plane mobile beds. Earth Surf. Process. Landf. 2004, 29, 1691–1701. [Google Scholar] [CrossRef]
- Hu, S.; Abrahams, A.D. The effect of bed mobility on resistance to overland flow. Earth Surf. Process. Landf. 2005, 30, 1461–1470. [Google Scholar] [CrossRef]
- Hu, S.; Abrahams, A.D. Partitioning resistance to overland flow on rough mobile beds. Earth Surf. Process. Landf. 2006, 31, 1280–1291. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, J.; Zhou, G. Relation between crack propagation and internal damage in sandstone during shear failure. J. Geophys. Eng. 2018, 15, 2104–2109. [Google Scholar] [CrossRef] [Green Version]
- Ferro, V. Assessing flow resistance law in vegetated channels by dimensional analysis and self-similarity. Flow Meas. Instrum. 2019, 69, 101610. [Google Scholar] [CrossRef]
- Guillén-Ludeña, S.; Lopez, D.; Mignot, E.; Riviere, N. Flow Resistance for a Varying Density of Obstacles on Smooth and Rough Beds. J. Hydraul. Eng. 2020, 146. [Google Scholar] [CrossRef]
- Bialik, R.J.; Karpiński, M.; Rajwa, A.; Luks, B.; Rowiński, P. łM Bedform characteristics in natural and regulated channels: A comparative field study on the Wilga River, Poland. Acta Geophys. 2014, 62, 1413–1434. [Google Scholar] [CrossRef]
- Parsons, D.R.; Best, J.L.; Orfeo, O.; Hardy, R.J.; Kostaschuk, R.; Lane, S.N. Morphology and flow fields of three-dimensional dunes, Rio Paraná, Argentina: Results from simultaneous multibeam echo sounding and acoustic Doppler current profiling. J. Geophys. Res. Earth Surf. 2005, 110, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Shugar, D.H.; Kostaschuk, R.; Best, J.L.; Parsons, D.R.; Lane, S.N.; Orfeo, O.; Hardy, R.J. On the relationship between flow and suspended sediment transport over the crest of a sand dune, Río Paraná, Argentina. Sedimentology 2010, 57, 252–272. [Google Scholar] [CrossRef]
- Defina, A.; Bixio, A.C. Mean flow and turbulence in vegetated open channel flow. Water Resour. Res. 2005, 41, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Hui, E.Q.; Hu, X.E.; Jiang, C.B.; Ma, F.K.; Zhu, Z.D. A study of drag coefficient related with vegetation based on the flume experiment. J. Hydrodyn. 2010, 22, 329–337. [Google Scholar] [CrossRef]
- Busari, A.O.; Li, C.W. Bulk drag of a regular array of emergent blade-type vegetation stems under gradually varied flow. J. Hydro Environ. Res. 2016, 12, 59–69. [Google Scholar] [CrossRef]
- Parsons, A.J.; Abrahams, A.D.; Wainwright, J. On determining resistance to interrill overland flow. Water Resour. Res. 1994, 30, 3515–3521. [Google Scholar] [CrossRef]
- Mu, H.; Yu, X.; Fu, S.; Yu, B.; Liu, Y.; Zhang, G. Effect of stem basal cover on the sediment transport capacity of overland flows. Geoderma 2019, 337, 384–393. [Google Scholar] [CrossRef]
- Sun, Z.L.; Zheng, J.Y.; Zhu, L.L.; Chong, L.; Liu, J.; Luo, J.Y. Influence of submerged vegetation on flow structure and sediment deposition. J. Zhejiang Univ. (Eng. Sci.) 2021, 55, 71–80. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Z.; Liu, Y.; Li, G.; Chen, S.; Liu, M. The influence of combined vegetation stalk thickness on water flow resistance. Water Environ. J. 2019, 34, 455–463. [Google Scholar] [CrossRef]
- Chen, M.; Lou, S.; Liu, S.; Ma, G.; Liu, H.; Zhong, G.; Zhang, H. Velocity and turbulence affected by submerged rigid vegetation under waves, currents and combined wave–current flows. Coast. Eng. 2020, 159. [Google Scholar] [CrossRef]
- Carollo, F.G.; Ferro, V.; Termini, D. Analyzing Turbulence Intensity in Gravel Bed Channels. J. Hydraul. Eng. 2005, 131, 1050–1061. [Google Scholar] [CrossRef]
- Goring, D.G.; Nikora, V.I. Despiking Acoustic Doppler Velocimeter Data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Wahl, T.L. Analyzing ADV data using WinADV. Jt. Conf. Water Resour. Eng. Water Resour. Plan. Manag. 2000 Build. Partnerships 2004, 104, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Hydromechanics, A. Engineering Course: Applied Hydromechanics. 2020. [Google Scholar]
- Yang, K.; Cao, S.; Knight, D.W. Flow Patterns in Compound Channels with Vegetated Floodplains. J. Hydraul. Eng. 2007, 133, 148–159. [Google Scholar] [CrossRef]
- Fischenich, C. Resistance Due to Vegetation. Ecosyst. Manag. Restorat. Res. Progr. 2000, 37, 1–9. [Google Scholar]
- Fischenich, C.; Dudley, S. Determining drag coefficients and area for vegetation. Ecosyst. Manag. Restorat. Res. Progr. 1999, 2, 36. [Google Scholar]
- Wang, W.J.; Peng, W.Q.; Huai, W.X.; Katul, G.G.; Liu, X.B.; Qu, X.D.; Dong, F. Friction factor for turbulent open channel flow covered by vegetation. Sci. Rep. 2019, 9, 1–16. [Google Scholar] [CrossRef]







| Scheme | Data Number | H (cm) | Discharge (L/s) | Vegetation | Re | Fr | |
|---|---|---|---|---|---|---|---|
| S1 | Run01 | 15 | 10.00 | reed | stick | 10,967 | 0.0082 |
| S2 | Run02 | 15 | 10.00 | grass | chlorella | 10,967 | 0.0082 |
| S3 | Run03 | 15 | 15.00 | reed | stick | 16,620 | 0.0189 |
| S4 | Run04 | 15 | 15.00 | grass | chlorella | 16,620 | 0.0189 |
| S5 | Run05 | 15 | 20.00 | reed | stick | 22,134 | 0.0335 |
| S6 | Run06 | 15 | 20.00 | grass | chlorella | 22,134 | 0.0335 |
| S7 | Run07 | 15 | 25.00 | reed | stick | 27,697 | 0.0525 |
| S8 | Run08 | 15 | 25.00 | grass | chlorella | 27,697 | 0.0525 |
| S9 | Run09 | 15 | 30.00 | reed | stick | 33,200 | 0.0754 |
| S10 | Run10 | 15 | 30.00 | grass | chlorella | 33,200 | 0.0754 |
| S11 | Run11 | 20 | 10.00 | reed | stick | 9930 | 0.0035 |
| S12 | Run12 | 20 | 10.00 | grass | chlorella | 9930 | 0.0035 |
| S13 | Run13 | 20 | 15.00 | reed | stick | 14,955 | 0.0080 |
| S14 | Run14 | 20 | 15.00 | grass | chlorella | 14,955 | 0.0080 |
| S15 | Run15 | 20 | 20.00 | reed | stick | 19,944 | 0.0142 |
| S16 | Run16 | 20 | 20.00 | grass | chlorella | 19,944 | 0.0142 |
| S17 | Run17 | 20 | 25.00 | reed | stick | 24,885 | 0.0221 |
| S18 | Run18 | 20 | 25.00 | grass | chlorella | 24,885 | 0.0221 |
| S19 | Run19 | 20 | 30.00 | reed | stick | 29,910 | 0.0319 |
| S20 | Run20 | 20 | 30.00 | grass | chlorella | 29,910 | 0.0319 |
| S21 | Run21 | 25 | 10.00 | reed | stick | 9068 | 0.0018 |
| S22 | Run22 | 25 | 10.00 | grass | chlorella | 9068 | 0.0018 |
| S23 | Run23 | 25 | 15.00 | reed | stick | 13,596 | 0.0041 |
| S24 | Run24 | 25 | 15.00 | grass | chlorella | 13,596 | 0.0041 |
| S25 | Run25 | 25 | 20.00 | reed | stick | 18,082 | 0.0072 |
| S26 | Run26 | 25 | 20.00 | grass | chlorella | 18,082 | 0.0072 |
| S27 | Run27 | 25 | 25.00 | reed | stick | 22,664 | 0.0113 |
| S28 | Run28 | 25 | 25.00 | grass | chlorella | 22,664 | 0.0113 |
| S29 | Run29 | 25 | 30.00 | reed | stick | 27,191 | 0.0163 |
| S30 | Run30 | 25 | 30.00 | grass | chlorella | 27,191 | 0.0163 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Zhou, Y.; Sun, Z.; Ding, K.; Chong, L. Hydraulic Characteristics of Emerged Rigid and Submerged Flexible Vegetations in the Riparian Zone. Water 2021, 13, 1057. https://doi.org/10.3390/w13081057
Meng X, Zhou Y, Sun Z, Ding K, Chong L. Hydraulic Characteristics of Emerged Rigid and Submerged Flexible Vegetations in the Riparian Zone. Water. 2021; 13(8):1057. https://doi.org/10.3390/w13081057
Chicago/Turabian StyleMeng, Xin, Yubao Zhou, Zhilin Sun, Kaixuan Ding, and Lin Chong. 2021. "Hydraulic Characteristics of Emerged Rigid and Submerged Flexible Vegetations in the Riparian Zone" Water 13, no. 8: 1057. https://doi.org/10.3390/w13081057
APA StyleMeng, X., Zhou, Y., Sun, Z., Ding, K., & Chong, L. (2021). Hydraulic Characteristics of Emerged Rigid and Submerged Flexible Vegetations in the Riparian Zone. Water, 13(8), 1057. https://doi.org/10.3390/w13081057






