Machine Learning Modeling of Climate Variability Impact on River Runoff
Abstract
:1. Introduction
2. Related Work
3. Data and Methods
3.1. Data
3.2. Modelling
Convolution Neural Networks (CNNs)
3.3. Training and Testing Regime
3.4. Evaluation and Metrics
3.5. Baseline Models
3.6. Software
4. Results
4.1. Comparison to the Baseline
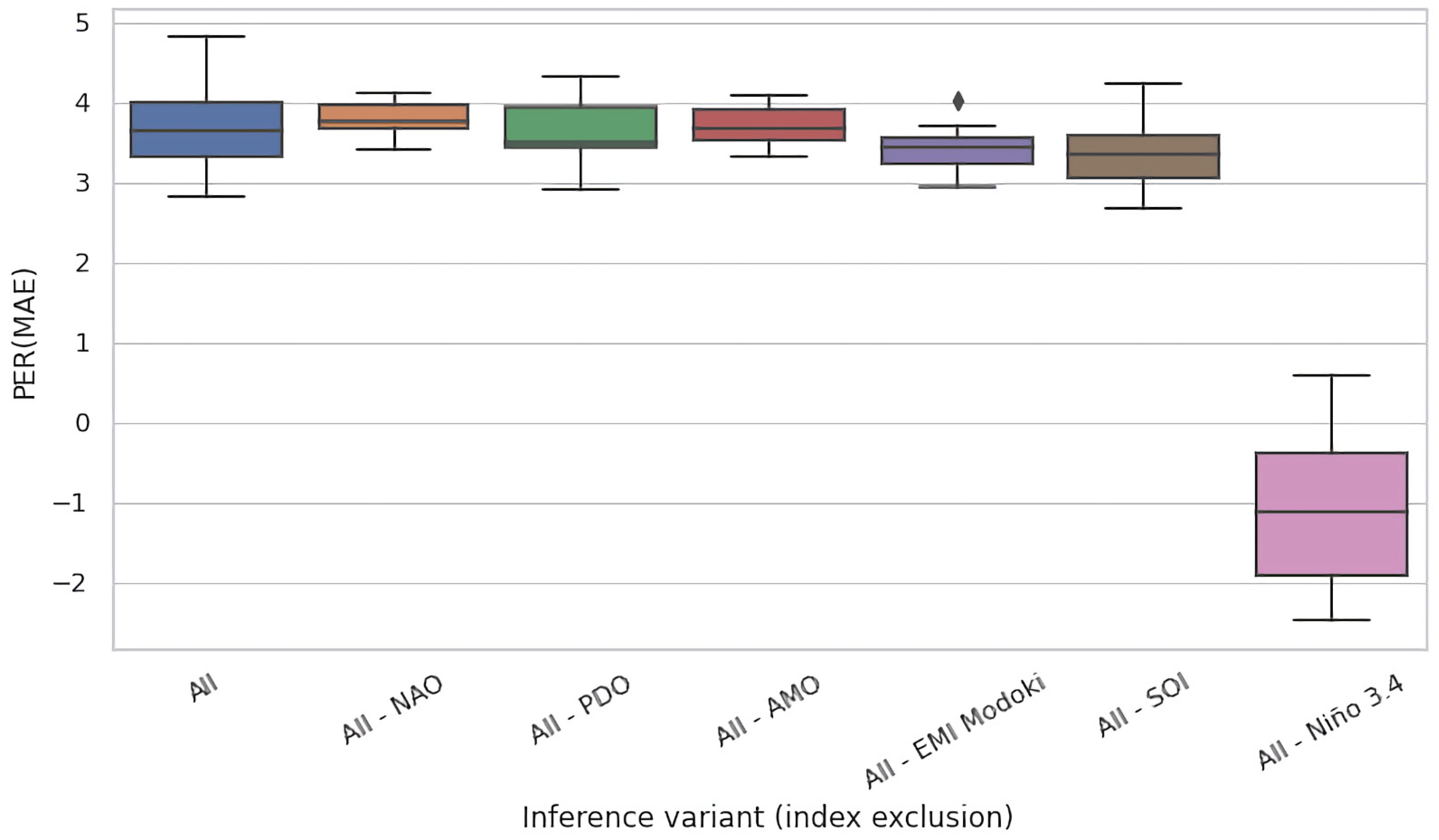
4.2. Ablation Experiments
5. Discussion and Conclusions
- (i).
- Our study areas (“rectangular” sets of cells) did not really map regions analyzed in the literature.
- (ii).
- (iii).
- No reference known to the authors includes all six climate variability indices considered in our paper.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A











References
- Kron, W.; Eichner, J.; Kundzewicz, Z.W. Reduction of flood risk in Europe-Reflections from a reinsurance perspective. J. Hydrol. 2019, 576, 197–209. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood risk and climate change: Global and regional perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Kundzewicz, Z.W.; Hegger, D.L.T.; Matczak, P.; Driessen, P.P.J. Flood risk reduction: Structural measures and diverse strategies. Proc. Nat. Acad. Sci. USA 2018, 115, 12321–12325. [Google Scholar] [CrossRef] [Green Version]
- Kundzewicz, Z.W.; Krysanova, V.; Dankers, R.; Hirabayashi, Y.; Kanae, S.; Hattermann, F.F.; Huang, S.; Milly, P.C.D.; Stoffel, M.; Driessen, P.P.J.; et al. Differences in flood hazard projections in Europe-their causes and consequences for decision making. Hydrol. Sci. J. 2017, 62, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Kundzewicz, Z.W.; Su, B.; Wang, Y.; Wang, G.; Wang, G.; Huang, J.; Jiang, T. Flood risk in a range of spatial perspectives-from global to local scales. Nat. Haz. Earth Syst. Sci. 2019, 19, 1319–1328. [Google Scholar] [CrossRef] [Green Version]
- Emerton, R.; Cloke, H.; Stephens, E.; Zsoter, E.; Woolnough, S.; Pappenberger, F. Complex picture for likelihood of ENSO-driven flood hazard. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Ward, P.J.; Eisner, S.; Flörke, M.; Dettinger, M.D.; Kummu, M. Annual flood sensitivities to El Niño–Southern Oscillation at the global scale. Hydrol. Earth Sys. Sci. 2014, 18, 47–66. [Google Scholar] [CrossRef] [Green Version]
- Ward, P.J.; Jongman, B.; Kummu, M.; Dettinger, M.D.; Weiland, F.C.S.; Winsemius, H.C. Strong influence of El Niño Southern Oscillation on flood risk around the world. Proc. Nat. Acad. Sci. USA 2014, 111, 15659–15664. [Google Scholar] [CrossRef] [Green Version]
- Hodgkins, G.A.; Whitfield, P.H.; Burn, D.H.; Hannaford, J.; Renard, B.; Stahl, K.; Fleig, A.K.; Madsen, H.; Mediero, L.; Korhonen, J.; et al. Climate-driven variability in the occurrence of major floods across North America and Europe. J. Hydrol. 2017, 552, 704–717. [Google Scholar] [CrossRef] [Green Version]
- Ward, P.J.; Kummu, M.; Lall, U. Flood frequencies and durations and their response to El Niño Southern Oscillation: Global analysis. J. Hydrol. 2016, 539, 358–378. [Google Scholar] [CrossRef] [Green Version]
- Najibi, N.; Devineni, N. Recent trends in the frequency and duration of global floods. Earth Sys. Dyn. 2018, 9, 757–783. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Yuan, X. Extending seasonal predictability of Yangtze River summer floods. Hydrol. Earth Sys. Sci. Discuss. 2018, 22, 4201–4211. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Xu, C.; Jiang, T.; Wu, Y. Possible influence of ENSO on annual maximum streamflow of the Yangtze River, China. J. Hydrol. 2007, 333, 265–274. [Google Scholar] [CrossRef]
- Tong, J.; Qiang, Z.; Deming, Z.; Yijin, W. Yangtze floods and droughts (China) and teleconnections with ENSO activities (1470–2003). Quat. Int. 2006, 144, 29–37. [Google Scholar] [CrossRef]
- Ye, X.C.; Wu, Z.W. Contrasting impacts of ENSO on the interannual variations of summer runoff between the upper and mid-lower reaches of the Yangtze River. Atmosphere 2018, 9, 478. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Gu, X.; Singh, V.P.; Xiao, M.; Chen, X. Evaluation of flood frequency under non-stationarity resulting from climate indices and reservoir indices in the East River basin, China. J. Hydrol. 2015, 527, 565–575. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Q.; Singh, V.P.; Gu, X.; Shi, P. Nonstationarity and clustering of flood characteristics and relations with the climate indices in the Poyang Lake basin, China. Hydrol. Sci. J. 2017, 62, 1809–1824. [Google Scholar] [CrossRef]
- Delgado, J.M.; Merz, B.; Apel, H. A climate-flood link for the lower Mekong River. Hydrol. Earth Syst. Sci. 2012, 16, 1533–1541. [Google Scholar] [CrossRef] [Green Version]
- Iqbal, A.; Hassan, S.A. ENSO and IOD analysis on the occurrence of floods in Pakistan. Nat. Haz. 2018, 91, 879–890. [Google Scholar] [CrossRef]
- Chowdhury, M.R. The El Niño-Southern Oscillation (ENSO) and seasonal flooding–Bangladesh. Theor. Appl. Climatol. 2003, 76, 105–124. [Google Scholar] [CrossRef]
- Saghafian, B.; Haghnegahdar, A.; Dehghani, M. Effect of ENSO on annual maximum floods and volume over threshold in the southwestern region of Iran. Hydrol. Sci. J. 2017, 62, 1039–1049. [Google Scholar] [CrossRef]
- Cullen, H.M.; Kaplan, A.; Arkin, P.A.; Demenocal, P.B. Impact of the North Atlantic Oscillation on Middle Eastern climate and streamflow. Clim. Chang. 2002, 55, 315–338. [Google Scholar] [CrossRef]
- Cayan, D.R.; Redmond, K.T.; Riddle, L.G. ENSO and hydrologic extremes in the western United States. J. Clim. 1999, 12, 2881–2893. [Google Scholar] [CrossRef] [Green Version]
- Corringham, T.W.; Cayan, D.R. The effect of El Niño on flood damages in the Western United States. Weather Clim. Soc. 2019, 11, 489–504. [Google Scholar] [CrossRef]
- Wang, S.-Y.S.; Huang, W.-R.; Hsu, H.-H.; Gillies, R.R. Role of the strengthened El Niño teleconnection in the May 2015 floods over the southern Great Plains. Geophys. Res. Lett. 2015, 42, 8140–8146. [Google Scholar] [CrossRef] [Green Version]
- Munoz, S.E.; Dee, S.G. El Nino increases the risk of lower Mississippi River flooding. Sci. Rep. 2017, 7, 1772. [Google Scholar] [CrossRef]
- Nakamura, J.; Lall, U.; Kushnir, Y.; Robertson, A.W.; Seager, R. Dynamical structure of extreme floods in the U.S. Midwest and the United Kingdom. J. Hydrometeorol. 2013, 14, 485–504. [Google Scholar] [CrossRef]
- Andrews, E.D.; Antweiler, R.C.; Neiman, P.J.; Ralph, F.M. Influence of ENSO on flood frequency along the California Coast. J. Clim. 2004, 17, 337–348. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Hakala, K.; Gillies, R.R.; Capehart, W.J. The Pacific Quasi-decadal Oscillation (QDO): An important precursor toward anticipating major flood events in the Missouri River Basin? Geophys. Res. Lett. 2014, 41, 991–997. [Google Scholar] [CrossRef] [Green Version]
- Nasser, N.; Devineni, N.; Lu, M. Hydroclimate drivers and atmospheric teleconnections of long duration floods: An application to large reservoirs in the Missouri River Basin. Adv. Water Resour. 2017, 100, 153–167. [Google Scholar]
- Beebee, R.A.; Manga, M. Variation in the relationship between snowmelt runoff in Oregon and ENSO and PDO. J. Am. Water Resour. Assoc. 2004, 40, 1011–1024. [Google Scholar] [CrossRef]
- Enfield, D.B.; Mestas-Nunez, A.M.; Trimble, P.J. The Atlantic Multidecadal Oscillation and its relation to rainfall and river flows in the continental U.S. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef] [Green Version]
- Munoz, S.E.; Giosan, L.; Therrell, M.D.; Remo, J.W.F.; Shen, Z.; Sullivan, R.M.; Wiman, C.; O’Donnell, M.; Donnelly, J.P. Climatic control of Mississippi River flood hazard amplified by river engineering. Nature 2018, 556, 95–98. [Google Scholar] [CrossRef]
- Hamlet, A.F.; Lettenmaier, D.P. Effects of 20th century warming and climate variability on flood risk in the western U.S. Water Resour. Res. 2007, 43, W06427. [Google Scholar] [CrossRef]
- Jain, S.; Lall, U. Magnitude and timing of annual maximum floods: Trends and large-scale climatic associations for the Blacksmith Fork River, Utah. Water Resour. Res. 2000, 36, 3641–3651. [Google Scholar] [CrossRef]
- Archfield, S.A.; Hirsch, R.M.; Viglione, A.; Blöschl, G. Fragmented patterns of flood change across the United States. Geophys. Res. Lett. 2016, 43, 10,232–10,239. [Google Scholar] [CrossRef]
- Mallakpour, I.; Villarini, G. Investigating the relationship between the frequency of flooding over the central United States and large-scale climate. Adv. Water Resour. 2016, 92, 159–171. [Google Scholar] [CrossRef] [Green Version]
- Gurrapu, S.; St. Jacques, J.-M.; Sauchyn, D.J.; Hodder, K.R. The influence of the Pacific Decadal Oscillation on annual floods in the rivers of western Canada. J. Am. Water Resour. Assoc. 2016, 52, 1031–1045. [Google Scholar] [CrossRef]
- Burn, D.H.; Cunderlik, J.M.; Pietroniro, A. Hydrological trends and variability in the Liard River basin. Hydrol. Sci. J. 2004, 49, 53–67. [Google Scholar] [CrossRef] [Green Version]
- Fortier, C.; Assani, A.; Mesfioui, M.; Roy, A.G. Comparison of the interannual and interdecadal variability of heavy flood characteristics upstream and downstream from dams in inversed hydrologic regime: Case study of Matawin River (Québec, Canada). River Res. Appl. 2011, 27, 1277–1289. [Google Scholar] [CrossRef]
- Assani, A.A.; Charron, S.; Matteau, M.; Mesfioui, M.; Quessy, J.-F. Temporal variability modes of floods for catchments in the St. Lawrence watershed (Quebec, Canada). J. Hydrol. 2010, 385, 292–299. [Google Scholar] [CrossRef]
- Gobena, A.K.; Gan, T.Y. Low-frequency variability in southwestern Canadian streamflow: Links to large-scale climate anomalies. Int. J. Climatol. 2006, 26, 1843–1869. [Google Scholar] [CrossRef]
- Mazouz, R.; Assani, A.A.; Quessy, J.-F.; Légaré, G. Comparison of the interannual variability of spring heavy floods characteristics of tributaries of the St. Lawrence river in Quebec (Canada). Adv. Water Resour. 2012, 35, 110–120. [Google Scholar] [CrossRef]
- Zanardo, S.; Nicotina, L.; Hilberts, A.G.J.; Jewson, S.P. Modulation of economic losses from European floods by the North Atlantic Oscillation. Geophys. Res. Lett. 2019, 46, 2563–2572. [Google Scholar] [CrossRef]
- Huntingford, C.; Marsh, T.; Scaife, A.A.; Kendon, E.J.; Hannaford, J.; Kay, A.L.; Lockwood, M.; Prudhomme, C.; Reynard, N.S.; Parry, S.; et al. Potential influences on the United Kingdom’s floods of winter 2013/14. Nat. Clim. Chang. 2014, 4, 769–777. [Google Scholar] [CrossRef]
- Hannaford, J.; Marsh, T.J. High-flow and flood trends in a network of undisturbed catchments in the UK. Int. J. Climatol. 2008, 28, 1325–1338. [Google Scholar] [CrossRef] [Green Version]
- Toonen, W.H.J.; Middelkoop, H.; Konijnendijk, T.Y.M.; Macklin, M.G.; Cohen, K.M. The influence of hydroclimatic variability on flood frequency in the Lower Rhine. Earth Surf. Process. Landf. 2016, 41, 1266–1275. [Google Scholar] [CrossRef]
- Nobre, G.G.; Jongman, B.; Aerts, J.; Ward, P.J. The role of climate variability in extreme floods in Europe. Environ. Res. Lett. 2017, 12, 084012. [Google Scholar] [CrossRef]
- Rimbu, N.; Dima, M.; Lohmann, G.; Stefan, S. Impacts of the North Atlantic Oscillation and the El Niño–Southern Oscillation on Danube river flow variability. Geophys. Res. Lett. 2004, 31, 1035. [Google Scholar] [CrossRef]
- Ionita, M.; Lohmann, G.; Rimbu, N.; Chelcea, S. Interannual variability of Rhine River streamflow and its relationship with large-scale anomaly patterns in spring and autumn. J. Hydrometeorol. 2012, 13, 172–188. [Google Scholar] [CrossRef]
- Ionita, M.; Rimbu, N.; Lohmann, G. Decadal variability of the Elbe River streamflow. Int. J. Climatol. 2011, 31, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Micevski, T.; Franks, S.W.; Kuczera, G. Multidecadal variability in coastal eastern Australian flood data. J. Hydrol. 2006, 327, 219–225. [Google Scholar] [CrossRef]
- Franks, S.W.; Kuczera, G. Flood frequency analysis: Evidence and implications of secular climate variability, New South Wales. Water Resour. Res. 2002, 38, 1062. [Google Scholar] [CrossRef]
- Verdon, D.C.; Wyatt, A.M.; Kiem, A.S.; Franks, S.W. Multidecadal variability of rainfall and streamflow: Eastern Australia. Water Resour. Res. 2004, 40, W10201. [Google Scholar] [CrossRef]
- Kiem, A.S.; Franks, S.W.; Kuczera, G. Multi-decadal variability of flood risk. Geophys. Res. Lett. 2003, 30, 1035. [Google Scholar] [CrossRef]
- Franks, S.W. Identification of a change in climate state using regional flood data. Hydrol. Earth Syst. Sci. 2002, 6, 11–16. [Google Scholar] [CrossRef]
- Pascolini-Campbella, M.; Seagerb, R.; Pinsonc, A.; Cook, B.I. Covariability of climate and streamflow in the Upper Rio Grande from interannual to interdecadal timescales. J. Hydrol. Reg. Stud. 2017, 13, 58–71. [Google Scholar] [CrossRef]
- Isla, F.I. ENSO-triggered floods in South America: Correlation between maximum monthly discharges during strong events. Hydrol. Earth Syst. Sci. Discuss. 2018, 1–13. [Google Scholar] [CrossRef]
- Isla, F.I.; Junior, E.E.T. ENSO impacts on Atlantic watersheds of South America. Quat. Environ. Geosci. 2013, 4, 34–41. [Google Scholar] [CrossRef] [Green Version]
- Depetris, P.J. The Parana River under extreme flooding: A hydrological and hydro-geochemical insight. Interciencia 2007, 32, 656–662. [Google Scholar]
- Siderius, C.; Gannon, K.E.; Ndiyoi, M.; Opere, A.; Batisani, N.; Olago, D.; Pardoe, J.; Conway, D. Hydrological response and complex impact pathways of the 2015/2016 El Niño in Eastern and Southern Africa. Earth’s Future 2018, 6, 2–22. [Google Scholar] [CrossRef]
- Alemaw, B.F.; Chaoka, T.R. The 1950–1998 warm ENSO events and regional implications to river flow variability in Southern Africa. Water 2006, 32, 459–464. [Google Scholar]
- Siam, M.S.; Eltahir, E.A.B. Explaining and forecasting interannual variability in the flow of the Nile River. Hydrol. Earth Syst. Sci. 2015, 19, 1181–1192. Available online: www.hydrol-earth-syst-sci.net/19/1181/2015 (accessed on 22 April 2021). [CrossRef] [Green Version]
- Brigadier, L.; Ogwang, B.A.; Ongoma, V.; Ngonga, C.; Nyasa, L. Diagnosis of the 2010 DJF flood over Zambia. Nat. Hazards 2016, 81, 189–201. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Szwed, M.; Pinskwar, I. Climate Variability and Floods-A Global Review. Water 2019, 11, 1399. [Google Scholar] [CrossRef] [Green Version]
- Kundzewicz, Z.W.; Huang, J.; Pinskwar, I.; Su, B.; Szwed, M.; Jiang, T. Climate variability and floods in China-A review. Earth Sci. Rev. 2020, 211, 103434. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; Rao, A.R. (Eds.) Artificial Neural Networks in Hydrology; Water Science and Technology Library book series (WSTL); Springer: Dordrecht, The Netherlands, 2000; Volume 36. [Google Scholar] [CrossRef] [Green Version]
- Barnes, E.A.; Hurrell, J.W.; Ebert-Uphoff, I.; Anderson, C.; Anderson, D. Viewing forced climate patterns through an AI lens. Geoph. Res. Lett. 2019, 46, 13389–13398. [Google Scholar] [CrossRef] [Green Version]
- Coulibaly, P.; Anctil, F.; Rasmussen, P.; Bobée, B. A recurrent neural networks approach using indices of low-frequency climatic variability to forecast regional annual runoff. Special Issue: Canadian Geophysical Union—Hydrology Section. Hydrol. Proc. 2000, 14, 2755–2777. [Google Scholar] [CrossRef]
- Song, C.M.; Kim, D.Y. Developing a discharge estimation model for ungauged watershed using CNN and hydrological image. Water 2020, 12, 3534. [Google Scholar] [CrossRef]
- Song, C.M. Application of convolution neural networks and hydrological images for the estimation of pollutant loads in ungauged watersheds. Water 2021, 13, 239. [Google Scholar] [CrossRef]
- Chaudhuri, C.; Robertson, C. CliGAN: A structurally sensitive convolutional neural network model for statistical downscaling of precipitation from multi-model ensembles. Water 2020, 12, 3353. [Google Scholar] [CrossRef]
- Baek, S.-S.; Pyo, J.; Chun, J.A. Prediction of water level and water quality using a CNN-LSTM combined Deep learning approach. Water 2020, 12, 3399. [Google Scholar] [CrossRef]
- Raghavendra, S.; Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- Rasouli, K.; Hsieh, W.W.; Cannon, A.J. Daily streamflow forecasting by machine learning methods with weather and climate inputs. J. Hydrol. 2012, 414–415, 284–293. [Google Scholar] [CrossRef]
- Chakraborty, D.; Basagaoglu, H.; Winterle, J. Interpretable vs. noninterpretable machine learning models for data-driven hydro-climatological process modeling. Expert Syst. Appl. 2021, 170, 114498. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Shukla, S. Support vector machine based modeling of evapotranspiration using hydro-climatic variables in a sub-tropical environment. Agric. For. Meteorol. 2015, 200, 172–184. [Google Scholar] [CrossRef]
- Tongal, H.; Booij, M.J. Simulation and forecasting of streamflows using machine learning models coupled with base flow separation. J. Hydrol. 2018, 564, 266–282. [Google Scholar] [CrossRef]
- Park, J.H.; Yoo, S.; Nadiga, B. Machine learning climate variability. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Norel, M.; Kałczynski, M.; Pinskwar, I.; Krawiec, K.; Kundzewicz, Z.W. Climate variability indices–a guided tour. Geosciences 2021, 11, 128. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 22 April 2021).
- van den Oord, A.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. Wavenet: A generative model for raw audio. arXiv 2016, arXiv:1609.03499v2. [Google Scholar]
- Berndt, D.J.; Clifford, J. Using dynamic time warping to find patterns in time series. KDD Workshop 1994, 10, 359–370. [Google Scholar]
- Gorgino, T. Computing and visualizing dynamic time warping alignments in R: The dtw package. J. Stat. Softw. 2009, 31, 1–24. Available online: https://www.jstatsoft.org/article/view/v031i07 (accessed on 22 April 2021). [CrossRef] [Green Version]










| Multivariate | Univariate | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ID | Lat. | Long. | # of Alid Cells | PER(MAE) | PER(DTW) | PER(TEEE) | PER(MAE) | PER(DTW) | PER(TEEE) |
| 1 | 30° N–36° N | 86.5° W–79° W | 140 | 20.37 ± 1.24 | 14.28 ± 0.67 | 31.08 ± 1.36 | 18.28 ± 0.10 | 12.19 ± 0.13 | 27.65 ± 0.22 |
| 2 | 17° N–25.5° N | 85.5° W–73.5° W | 49 | 3.36 ± 0.21 | 3.62 ± 0.16 | 1.54 ± 0.33 | 2.23 ± 0.30 | 3.05 ± 0.28 | 4.80 ± 0.51 |
| 3 | 13.5° S–4.5° S | 80.5° W–71.5° W | 233 | −0.02 ± 1.24 | −2.63 ± 1.15 | 4.36 ± 0.89 | 0.06 ± 0.16 | −2.47 ± 0.19 | 3.41 ± 0.16 |
| 4 | 37° N–44° N | 10° W–0.5° E | 235 | 3.39 ± 0.32 | 1.94 ± 0.29 | 2.66 ± 1.72 | 2.45 ± 0.12 | 1.52 ± 0.02 | 4.26 ± 0.57 |
| 5 | 50° N–63° N | 1° E–12.5° E | 287 | 1.67 ± 0.74 | 0.95 ± 0.52 | – | 3.30 ± 0.06 | 2.13 ± 0.05 | – |
| 6 | 48.5° N–55° N | 5.5° E–16.5° E | 237 | 4.8 ± 0.43 | 2.72 ± 0.35 | 4.63 ± 0.76 | 6.83 ± 0.05 | 4.01 ± 0.05 | 6.15 ± 0.55 |
| 7 | 42° N–47.5° N | 11.5° E–19.5° E | 118 | 0.85 ± 0.48 | 0.97 ± 0.26 | 0.8 ± 0.58 | 0.56 ± 0.08 | 1.07 ± 0.24 | 0.85 ± 0.23 |
| 8 | 48° N–56° N | 13.5° E–24.5° E | 290 | 7.14 ± 0.94 | 5.09 ± 0.56 | 7.17 ± 1.05 | 9.08 ± 0.09 | 6.45 ± 0.04 | 10.84 ± 0.33 |
| 9 | 42° N–49° N | 20° E–31.5° E | 256 | 3.04 ± 0.57 | 1.98 ± 0.38 | 6.05 ± 0.89 | 2.52 ± 0.08 | 1.53 ± 0.17 | 7.20 ± 0.77 |
| 10 | 27.5° S–35° S | 17.5° E–32° E | 313 | 5.75 ± 0.27 | 2.71 ± 0.19 | 3.28 ± 0.4 | 5.54 ± 0.12 | 2.66 ± 0.11 | 2.29 ± 0.34 |
| 11 | 9° N–20° N | 96° E–104.5° E | 224 | −1.3 ± 0.26 | −0.73 ± 0.14 | −0.21 ± 0.31 | −2.62 ± 0.17 | −2.34 ± 0.10 | −0.88 ± 0.44 |
| 12 | 3° S–7° N | 95.5° E–103.5° E | 187 | 11.06 ± 0.73 | 5.58 ± 0.37 | 10.58 ± 1.31 | 11.30 ± 0.08 | 5.54 ± 0.15 | 9.92 ± 0.56 |
| 13 | 8° N–18.5° N | 101° E–111.5° E | 237 | 0.96 ± 0.38 | 0.86 ± 0.2 | 3.57 ± 0.63 | −1.41 ± 0.13 | −1.38 ± 0.06 | 2.57 ± 0.51 |
| 14 | 19° N–26° N | 109.5° E–116.5° E | 108 | 2.84 ± 0.85 | 0.61 ± 0.6 | −0.78 ± 0.48 | 0.92 ± 0.08 | −0.88 ± 0.12 | −1.16 ± 0.69 |
| 15 | 5° S–13.5° N | 114.5° E–128° E | 273 | 21.27 ± 0.32 | 20.89 ± 0.19 | 17.03 ± 0.49 | 19.30 ± 0.12 | 19.68 ± 0.16 | 14.83 ± 0.61 |
| 16 | 29° N–41° N | 123.5° E–144.5° E | 241 | −0.15 ± 0.46 | 0.71 ± 0.34 | 1.58 ± 1.48 | −1.17 ± 0.08 | 0.55 ± 0.05 | 0.68 ± 0.43 |
| 17 | 10.5° S–15.5° S | 128.5° E–136.5° E | 94 | 8.76 ± 0.81 | 4.29 ± 0.82 | 12.3 ± 1.25 | 5.92 ± 0.21 | 2.70 ± 0.26 | 9.00 ± 0.60 |
| 18 | 21° S–30.5° S | 145.5° E–154.5° E | 263 | 9.18 ± 1.41 | 11.55 ± 2.11 | 9.62 ± 3.85 | 8.46 ± 0.14 | 11.71 ± 0.20 | 10.01 ± 0.19 |
| Mean | 210.3 | 5.72 | 4.18 | 6.78 | 5.09 | 3.76 | 2.06 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Norel, M.; Krawiec, K.; Kundzewicz, Z.W. Machine Learning Modeling of Climate Variability Impact on River Runoff. Water 2021, 13, 1177. https://doi.org/10.3390/w13091177
Norel M, Krawiec K, Kundzewicz ZW. Machine Learning Modeling of Climate Variability Impact on River Runoff. Water. 2021; 13(9):1177. https://doi.org/10.3390/w13091177
Chicago/Turabian StyleNorel, Mateusz, Krzysztof Krawiec, and Zbigniew W. Kundzewicz. 2021. "Machine Learning Modeling of Climate Variability Impact on River Runoff" Water 13, no. 9: 1177. https://doi.org/10.3390/w13091177
APA StyleNorel, M., Krawiec, K., & Kundzewicz, Z. W. (2021). Machine Learning Modeling of Climate Variability Impact on River Runoff. Water, 13(9), 1177. https://doi.org/10.3390/w13091177






