Evaluation of InVEST’s Water Ecosystem Service Models in a Brazilian Subtropical Basin
Abstract
:1. Introduction
2. Materials and Methods
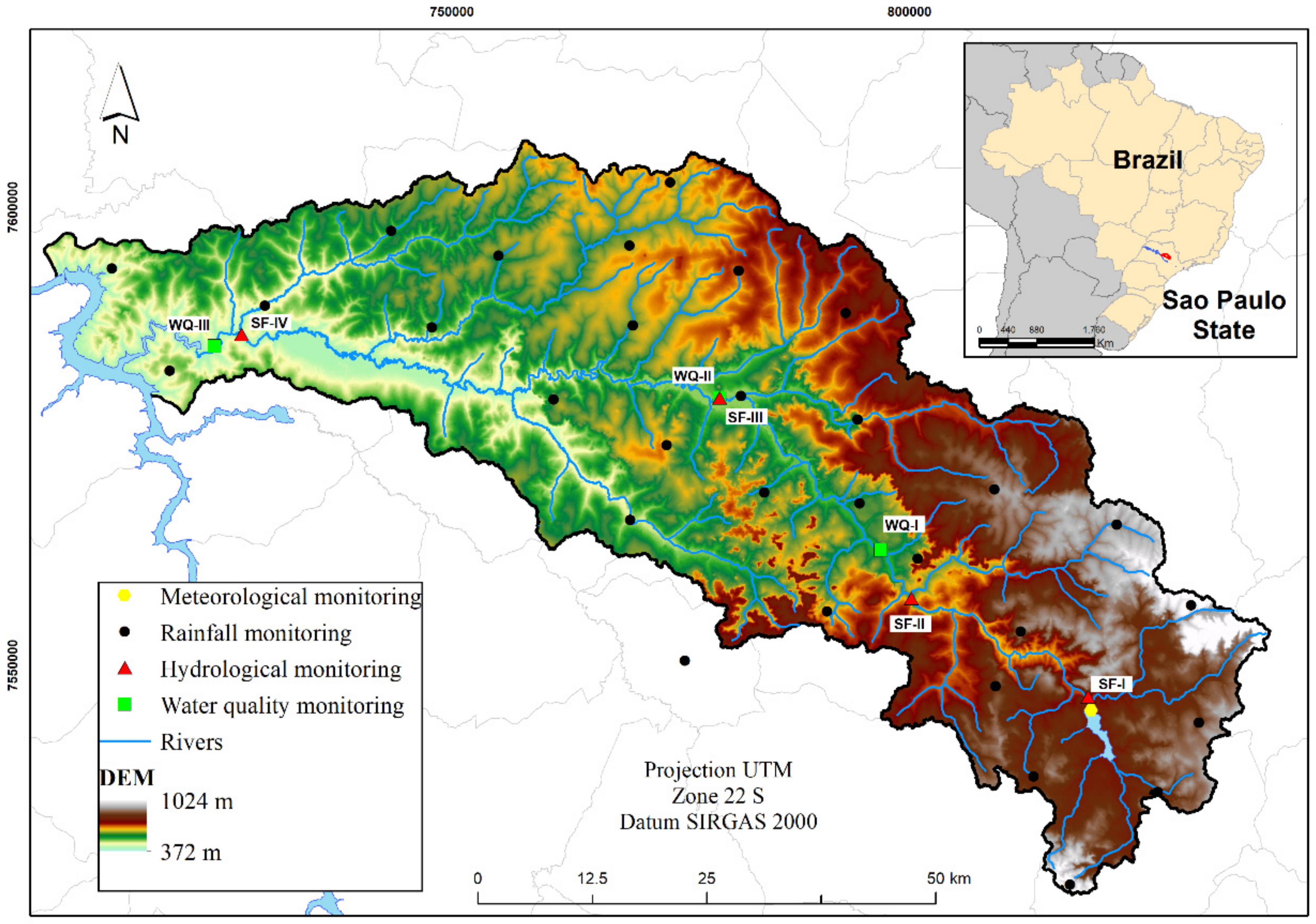
2.1. Study Area
2.2. Databases
2.3. Water Ecosystem Service Models
2.3.1. Seasonal Water Yield Model
2.3.2. Sediment Delivery Ratio Model
2.3.3. Nutrient Delivery Ratio Model
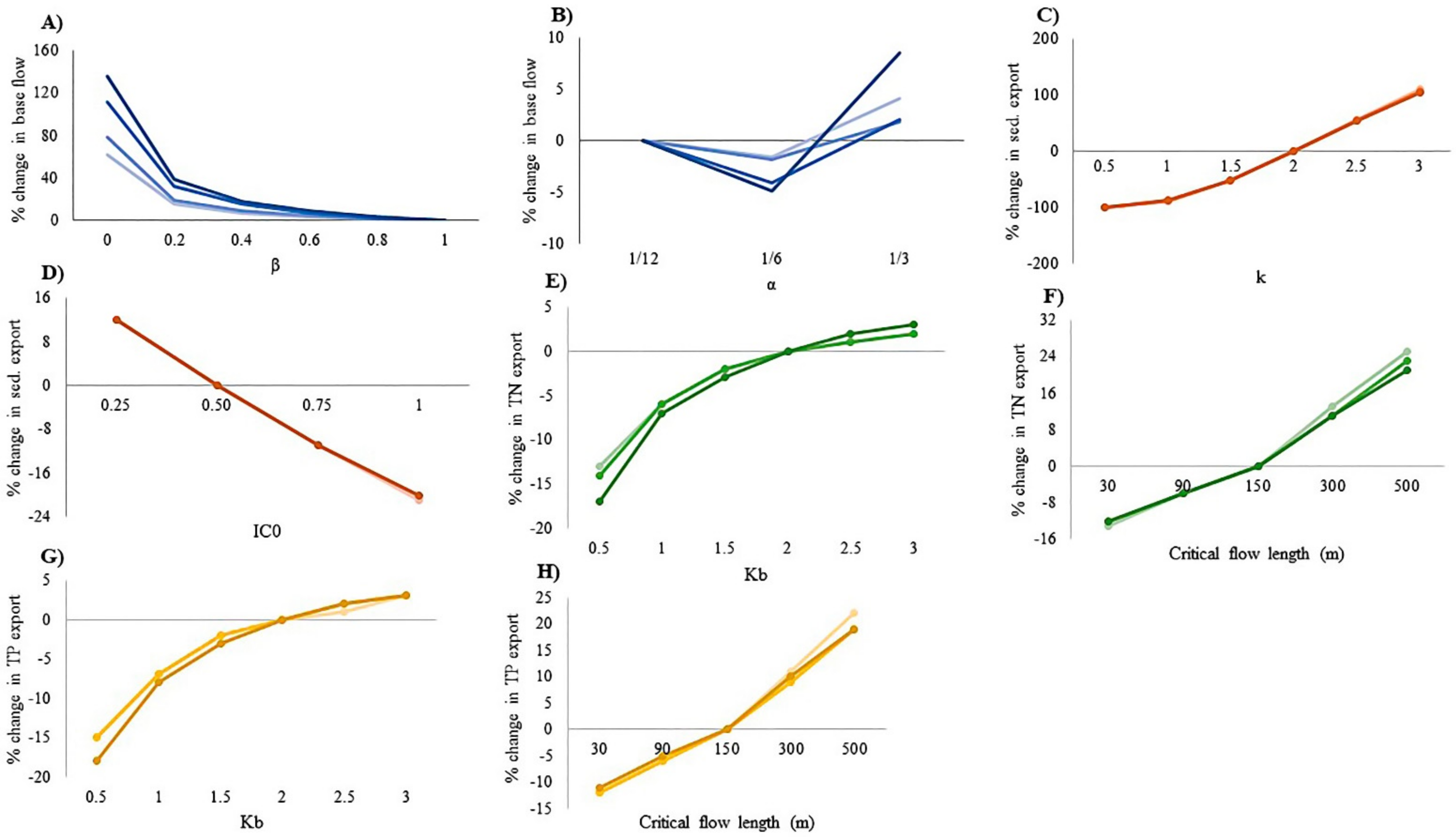
2.4. Sensitivity Analysis
2.5. Model Calibration and Validation
2.6. Model Performance Analysis
3. Results
3.1. WES Models Sensitivity Analysis
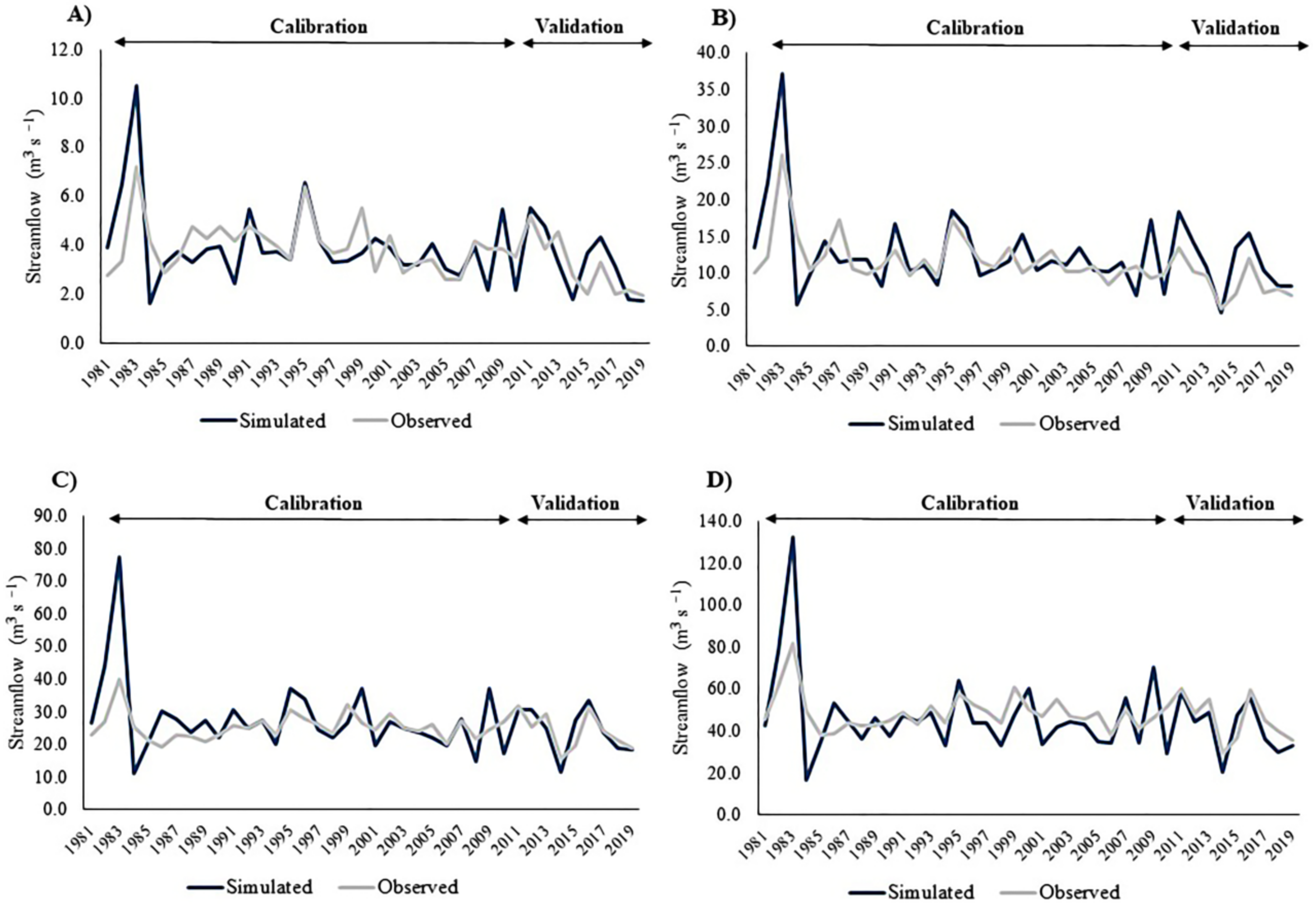
3.2. Calibration and Validation of WES Temporal Variability
3.3. WES Spatial Performance Analysis
4. Discussion
4.1. WES Sensitivity Analysis
4.2. InVEST WES Model Performance
4.3. InVEST WES Model Potentials and Limitations
4.4. Potential, Uncertainties, and Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Grizzetti, B.; Lanzanova, D.; Liquete, C.; Reynaud, A.; Cardoso, A.C. Assessing Water Ecosystem Services for Water Resource Management. Environ. Sci. Policy 2016, 61, 194–203. [Google Scholar] [CrossRef]
- Brauman, K.A.; Daily, G.C.; Duarte, T.K.E.; Mooney, H.A. The Nature and Value of Ecosystem Services: An Overview High-Lighting Hydrologic Services. Annu. Rev. Environ. Resour. 2007, 32, 67–98. [Google Scholar] [CrossRef]
- Palomo, I.; Bagstad, J.K.; Nedkov, S.; Klug, H.; Adamescu, M.; Cazacu, C. Tools for Mapping Ecosystem Services. In Mapping Ecosystem Services; Pensoft Publishers: Sofia, Bulgaria, 2017; p. 70. [Google Scholar]
- Bucak, T.; Trolle, D.; Tavşanoğlu, Ü.N.; Çakıroğlu, A.İ.; Özen, A.; Jeppesen, E.; Beklioğlu, M. Modeling the Effects of Climatic and Land Use Changes on Phytoplankton and Water Quality of the Largest Turkish Freshwater Lake: Lake Beyşehir. Sci. Total Environ. 2018, 621, 802–816. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Ochuodho, T.O.; Yang, J. Impact of Land Use and Climate Change on Water-Related Ecosystem Services in Kentucky, USA. Ecol. Indic. 2019, 102, 51–64. [Google Scholar] [CrossRef]
- Ferreira, P.; van Soesbergen, A.; Mulligan, M.; Freitas, M.; Vale, M.M. Can Forests Buffer Negative Impacts of Land-Use and Climate Changes on Water Ecosystem Services? The Case of a Brazilian Megalopolis. Sci. Total Environ. 2019, 685, 248–258. [Google Scholar] [CrossRef]
- Kadaverugu, A.; Rao, C.N.; Viswanadh, G.K. Quantification of Flood Mitigation Services by Urban Green Spaces using InVEST Model: A Case Study of Hyderabad City, India. Modeling Earth Syst. Environ. 2021, 7, 589–602. [Google Scholar] [CrossRef]
- Feld, C.K.; Birk, S.; Bradley, D.C.; Hering, D.; Kail, J.; Marzin, A.; Pont, D. From Natural to Degraded Rivers and Back Again: A 1248 Test of Restoration Ecology Theory and Practice. Adv. Ecol. Res. 2011, 44, 119–209. [Google Scholar] [CrossRef]
- Li, T.; Lü, Y.; Fu, B.; Hu, W.; Comber, A.J. Bundling Ecosystem Services for Detecting Their Interactions Driven by Large-Scale Vegetation Restoration: Enhanced Services While Depressed Synergies. Ecol. Indic. 2019, 99, 332–342. [Google Scholar] [CrossRef] [Green Version]
- Lara, A.; Jones, J.; Little, C.; Vergara, N. Streamflow Response to Native Forest Restoration in Former Eucalyptus Plantations in South Central Chile. Hydrol. Processes 2021, 35, e14270. [Google Scholar] [CrossRef]
- Souza, A.R.; Dupas, F.A.; da Silva, I.A. Spatial Targeting Approach for a Payment for Ecosystem Services Scheme in a Peri-Urban Wellhead Area in Southeastern Brazil. Environ. Chall. 2021, 5, 100206. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Savenije, H.H.G.; Blöschl, G.; McDonnell, J.J.; Sivapalan, M.; Pomeroy, J.W.; Cudennec, C. A Decade of Predictions in Ungauged Basins (PUB)—A Review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar] [CrossRef]
- Benra, F.; De Frutos, A.; Gaglio, M.; Álvarez-Garretón, C.; Felipe-Lucia, M.; Bonn, A. Mapping Water Ecosystem Services: Evaluating InVEST Model Predictions in Data Scarce Regions. Environ. Model. Softw. 2021, 138, 104982. [Google Scholar] [CrossRef]
- Villa, F.; Ceroni, M.; Bagstad, K.; Johnson, G.; Krivov, S. ARIES (Artificial Intelligence for Ecosystem Services): A New Tool for Ecosystem Services Assessment, Planning, and Valuation. In Proceedings of the 11th Annual BIOECON Conference on Economic Instruments to Enhance the Conservation and Sustainable Use of Biodiversity, Venice, Italy, 21–22 September 2009; pp. 21–22. [Google Scholar]
- Boumans, R.; Roman, J.; Altman, I.; Kaufman, L. The Multiscale Integrated Model of Ecosystem Services (MIMES): Simulating the Interactions of Coupled Human and Natural Systems. Ecosyst. Serv. 2015, 12, 30–41. [Google Scholar] [CrossRef]
- Sharp, R.; Douglass, J.; Wolny, S.; Arkema, K.; Bernhardt, J.; Bierbower, W.; Chaumont, N.; Denu, D.; Fisher, D.; Glowinski, K.; et al. InVEST 3.9.0. User’s Guide. The Natural Capital Project; Stanford University: Stanford, CA, USA, 2020. [Google Scholar]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Kannan, N. SWAT: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A Simple Hydrologically Based Model of Land Surface Water and Energy Fluxes for General Circulation Models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Tague, C.L.; Band, L.E. Regional Hydro-Ecologic Simulation System—An Object-Oriented Approach to Spatially Distributed Modeling of Carbon, Water, and Nutrient Cycling. Earth Interact. 2004, 8, 1–42. [Google Scholar] [CrossRef]
- Keeler, B.L.; Polasky, S.; Brauman, K.A.; Johnson, K.A.; Finlay, J.C.; O’Neill, A.; Dalzell, B. Linking Water Quality and Well-Being for Improved Assessment and Valuation of Ecosystem Services. Proc. Natl. Acad. Sci. USA 2012, 109, 18619–18624. [Google Scholar] [CrossRef] [Green Version]
- Vigerstol, K.L.; Aukema, J.E. A Comparison of Tools for Modeling Freshwater Ecosystem Services. J. Environ. Manag. 2011, 92, 2403–2409. [Google Scholar] [CrossRef]
- Jorda-Capdevila, D.; Gampe, D.; García, V.H.; Ludwig, R.; Sabater, S.; Vergoñós, L.; Acuña, V. Impact and Mitigation of Global Change on Freshwater-Related Ecosystem Services in Southern Europe. Sci. Total Environ. 2019, 651, 895–908. [Google Scholar] [CrossRef]
- Yang, S.; Zhao, W.; Liu, Y.; Wang, S.; Wang, J.; Zhai, R. Influence of Land Use Change on the Ecosystem Service Trade-Offs in the Ecological Restoration Area: Dynamics and Scenarios in the Yanhe Watershed, China. Sci. Total Environ. 2018, 644, 556–566. [Google Scholar] [CrossRef] [PubMed]
- Terrado, M.; Acuña, V.; Ennaanay, D.; Tallis, H.; Sabater, S. Impact of Climate Extremes on Hydrological Ecosystem Services in a Heavily Humanized Mediterranean Basin. Ecol. Indic. 2014, 37, 199–209. [Google Scholar] [CrossRef]
- Hamel, P.; Chaplin-Kramer, R.; Sim, S.; Mueller, C. A New Approach to Modeling the Sediment Retention Service (InVEST 3.0): Case Study of the Cape Fear Catchment, North Carolina, USA. Sci. Total Environ. 2015, 524, 166–177. [Google Scholar] [CrossRef]
- Redhead, J.W.; Stratford, C.; Sharps, K.; Jones, L.; Ziv, G.; Clarke, D.; Bullock, J.M. Empirical Validation of the InVEST Wateryield Ecosystem Service Model at a National Scale. Sci. Total Environ. 2016, 569, 1418–1426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Redhead, J.W.; May, L.; Oliver, T.H.; Hamel, P.; Sharp, R.; Bullock, J.M. National Scale Evaluation of the InVEST Nutrient Retention Model in the United Kingdom. Sci. Total Environ. 2018, 610, 666–677. [Google Scholar] [CrossRef] [PubMed]
- Hamel, P.; Valencia, J.; Schmitt, R.; Shrestha, M.; Piman, T.; Sharp, R.P.; Guswa, A.J. Modeling Seasonal Water Yield for Landscape Management: Applications in Peru and Myanmar. J. Environ. Manag. 2020, 270, 110792. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Yan, Y.; Zhu, J.; Jin, T.; Liu, G.; Wu, G.; Stringer, L.C.; Dallimer, M. Spatiotemporal Water Yield Variations and Influencing Factors in the Lhasa River Basin, Tibetan Plateau. Water 2020, 12, 1498. [Google Scholar] [CrossRef]
- Hackbart, V.C.; De Lima, G.T.; Dos Santos, R.F. Theory and Practice of Water Ecosystem Services Valuation: Where Are We Going? Ecosyst. Serv. 2017, 23, 218–227. [Google Scholar] [CrossRef]
- Willcock, S.; Hooftman, D.; Sitas, N.; O’Farrell, P.; Hudson, M.D.; Reyers, B.; Bullock, J.M. Do Ecosystem Service Maps and Models Meet Stakeholders’ Needs? A Preliminary Survey across Sub-Saharan Africa. Ecosyst. Serv. 2016, 18, 110–117. [Google Scholar] [CrossRef] [Green Version]
- Manhães, A.P.; Mazzochini, G.G.; Oliveira-Filho, A.T.; Ganade, G.; Carvalho, A.R. Spatial Associations of Ecosystem Services and Biodiversity as a Baseline for Systematic Conservation Planning. Divers. Distrib. 2016, 22, 932–943. [Google Scholar] [CrossRef]
- Saad, S.I.; Mota da Silva, J.; Silva, M.L.N.; Guimarães, J.L.B.; Sousa, W.C., Jr.; Figueiredo, R.D.O.; Rocha, H.R.D. Analyzing Ecological Restoration Strategies for Water and Soil Conservation. PLoS ONE 2018, 13, e0192325. [Google Scholar] [CrossRef] [Green Version]
- Resende, F.M.; Cimon-Morin, J.; Poulin, M.; Meyer, L.; Loyola, R. Consequences of Delaying Actions for Safeguarding Ecosystem Services in the Brazilian Cerrado. Biol. Conserv. 2019, 234, 90–99. [Google Scholar] [CrossRef]
- Rosário, V.A.; Guimarães, J.C.; Viani, R.A. How Changes in Legally Demanded Forest Restoration Impact Ecosystem Services: A Case Study in the Atlantic Forest, Brazil. Trop. Conserv. Sci. 2019, 12, 1940082919882885. [Google Scholar] [CrossRef]
- Gomes, L.C.; Bianchi, F.J.; Cardoso, I.M.; Fernandes Filho, E.I.; Schulte, R.P. Land Use Change Drives the Spatio-Temporal Variation of Ecosystem Services and Their Interactions along an Altitudinal Gradient in Brazil. Landsc. Ecol. 2020, 35, 1571–1586. [Google Scholar] [CrossRef]
- Hamel, P.; Bremer, L.L.; Ponette-González, A.G.; Acosta, E.; Fisher, J.R.; Steele, B.; Brauman, K.A. The Value of Hydrologic Information for Watershed Management Programs: The Case of Camboriú, Brazil. Sci. Total Environ. 2020, 705, 135871. [Google Scholar] [CrossRef] [PubMed]
- Saad, S.I.; da Silva, J.M.; Ponette-González, A.G.; Silva ML, N.; da Rocha, H.R. Modeling the On-Site and Off-Site Benefits of Atlantic Forest Conservation in a Brazilian Watershed. Ecosyst. Serv. 2021, 48, 101260. [Google Scholar] [CrossRef]
- CBH-TJ. Tietê Jacaré River Hydrographic Basin Committee. UGRHI 13 River Basin Plan. Technical Document, São Paulo, Brazil. 2016. Available online: https://sigrh.sp.gov.br/ (accessed on 22 July 2021).
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated World Map of the Köppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- Costa, C.W.; Lorandi, R.; Lollo, J.A.; Santos, V.S. Potential for Aquifer Contamination of Anthropogenic Activity in the Recharge Area of the Guarani Aquifer System, Southeast of Brazil. Groundw. Sustain. Dev. 2019, 8, 10–23. [Google Scholar] [CrossRef]
- Lucas, M.; Wendland, E. Recharge Estimates for Various Land Uses in the Guarani Aquifer System Outcrop Area. Hydrol. Sci. J. 2016, 61, 1253–1262. [Google Scholar] [CrossRef]
- Rossi, M. Mapa Pedológico do Estado de São Paulo: Revisado e Ampliado; Instituto Florestal: São Paulo, Brasil, 2017; Volume 1, p. 118. [Google Scholar]
- Trevisan, D.P.; Ruggiero, M.H.; Bispo PD, C.; Almeida, D.; Imani, M.; Balzter, H.; Moschini, L.E. Evaluation of Environmental Naturalness: A Case Study in the Tietê-Jacaré Hydrographic Basin, São Paulo, Brazil. Sustainability 2021, 13, 3021. [Google Scholar] [CrossRef]
- MapBiomas. Brazil Land Use Data Series. Collection 5, Brazil. 2021. Available online: https://mapbiomas.org/colecoes-mapbiomas-1?cama_set_language=pt-BR (accessed on 13 July 2021).
- ASF. Alaska Satellite Facility. ALOS-PALSAR Images. 2021. Available online: https://vertex.daac.asf.alaska.edu (accessed on 5 May 2021).
- ANA. National Water and Sanitation Agency. Hydrological Information System (HidroWeb), Brasilia, Brazil. 2021. Available online: https://www.snirh.gov.br/hidroweb/apresentacao (accessed on 15 August 2021).
- DAEE. Department of Water and Electric Energy. Hydrological database, Sao Paulo, Brazil. 2021. Available online: http://www.daee.sp.gov.br/site/ (accessed on 22 August 2021).
- CETESB. São Paulo State Environmental Company. Information System InfoÁGUAS, Sao Paulo, Brazil. 2021. Available online: https://sistemainfoaguas.cetesb.sp.gov.br/ (accessed on 20 August 2021).
- NRCS. Urban Hydrology for Small Watersheds-Technical Release 55; US Department of Agriculture Natural Resources Conservation: Washington, DC, USA, 1986. [Google Scholar]
- Borselli, L.; Cassi, P.; Torri, D. Prolegomena to Sediment and Flow Connectivity in the Landscape: A GIS and Field Numerical Assessment. Catena 2008, 75, 268–277. [Google Scholar] [CrossRef]
- Mannigel, A.R.; de Passos, M.; Moreti, D.; da Rosa Medeiros, L. Fator Erodibilidade e Tolerância de Perda dos Solos do Estado de São Paulo. Acta Scientiarum. Agron. 2002, 24, 1335–1340. [Google Scholar] [CrossRef]
- Vigiak, O.; Borselli, L.; Newham, L.T.H.; McInnes, J.; Roberts, A.M. Comparison of Conceptual Landscape Metrics to Define Hillslope-Scale Sediment Delivery Ratio. Geomorphology 2012, 138, 74–88. [Google Scholar] [CrossRef]
- SMA. Secretariat for the Environment of the State of São Paulo. Billings Reservoir Watershed Development and Environmental Protection Plan, Sao Paulo, Brazil. 2010. Available online: https://www.infraestruturameioambiente.sp.gov.br/cpla/2013/03/aprm-billings/ (accessed on 23 August 2021).
- IBGE. Brazilian Institute of Geography and Statistics. Metadados. 2021. Available online: https://metadados.geo.ibge.gov.br/ (accessed on 27 July 2021).
- Anjinho, P.S.; Barbosa MA, G.A.; Neves, G.L.; Dos Santos, A.R.; Mauad, F.F. Integrated Empirical Models to Assess Nutrient Concentration in Water Resources: Case Study of a Small Basin in Southeastern Brazil. Environ. Sci. Pollut. Res. 2021, 28, 23349–23367. [Google Scholar] [CrossRef] [PubMed]
- Anjinho, P.S. Distributed Modeling of Point and Diffuse Pollution of the Water Systems of the Lobo Stream Watershed, Itirapina-SP. Master’s Thesis, University of Sao Paulo, São Carlos, São Paulo, Brazil, 2019. Available online: https://teses.usp.br/teses/disponiveis/18/18139/tde-13052019-164214/pt-br.php (accessed on 27 July 2021).
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Rauf, A.; Ghumman, A.R. Impact Assessment of Rainfall-Runoffsimulations on the Flow Duration Curve of the Upper Indus River—A Comparison of Data-Driven and Hydrologic Models. Water 2018, 10, 876. [Google Scholar] [CrossRef] [Green Version]
- Bagstad, K.J.; Cohen, E.; Ancona, Z.H.; McNulty, S.G.; Sun, G. The Sensitivity of Ecosystem Service Models to Choices of Input Data and Spatial Resolution. Appl. Geogr. 2018, 93, 25–36. [Google Scholar] [CrossRef]
- Wang, Z.; Lechner, A.M.; Baumgartl, T. Ecosystem Services Mapping Uncertainty Assessment: A Case Study in the Fitzroy Basin Mining Region. Water 2018, 10, 88. [Google Scholar] [CrossRef] [Green Version]
- Han, B.; Reidy, A.; Li, A. Modeling Nutrient Release with Compiled Data in a Typical Midwest Watershed. Ecol. Indic. 2021, 121, 107213. [Google Scholar] [CrossRef]
- Santos, F.M.; de Oliveira, R.P.; Mauad, F.F. Evaluating a Parsimonious Watershed Model Versus SWAT to Estimate Streamflow, Soil Loss and River Contamination in Two Case Studies in Tietê River Basin, São Paulo, Brazil. J. Hydrol. Reg. Stud. 2020, 29, 100685. [Google Scholar] [CrossRef]
- Benez-Secanho, F.J.; Dwivedi, P. Does Quantification of Ecosystem Services Depend Upon Scale (Resolution and Extent)? A Case Study Using the InVEST Nutrient Delivery Ratio Model in Georgia, United States. Environments 2019, 6, 52. [Google Scholar] [CrossRef] [Green Version]
- Sahle, M.; Saito, O.; Fürst, C.; Yeshitela, K. Quantifying and Mapping of Water-Related Ecosystem Services for Enhancing the Security of the Food-Water-Energy Nexus in Tropical Data–Sparse Catchment. Sci. Total Environ. 2019, 646, 573–586. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Canales, M.; López-Benito, A.; Acuña, V.; Ziv, G.; Hamel, P.; Chaplin-Kramer, R.; Elorza, F.J. Sensitivity Analysis of a Sediment Dynamics Model Applied in a Mediterranean River Basin: Global Change and Management Implications. Sci. Total Environ. 2015, 502, 602–610. [Google Scholar] [CrossRef] [PubMed]
- Costa, C.W.; Lorandi, R.; de Lollo, J.A.; Imani, M.; Dupas, F.A. Surface Runoff and Accelerated Erosion in a Peri-Urban Wellhead Area in Southeastern Brazil. Environ. Earth Sci. 2018, 77, 160. [Google Scholar] [CrossRef] [Green Version]
- Brooks, P.D.; Chorover, J.; Fan, Y.; Godsey, S.E.; Maxwell, R.M.; McNamara, J.P.; Tague, C. Hydrological Partitioning in the Critical Zone: Recent Advances and Opportunities for Developing Transferable Understanding of Water Cycle Dynamics. Water Resour. Res. 2015, 51, 6973–6987. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Clark, M.; Lawrence, D.M.; Swenson, S.; Band, L.E.; Brantley, S.L.; Yamazaki, D. Hillslope Hydrology in Global Change Research and Earth System Modeling. Water Resour. Res. 2019, 55, 1737–1772. [Google Scholar] [CrossRef] [Green Version]
- Scordo, F.; Lavender, T.M.; Seitz, C.; Perillo, V.L.; Rusak, J.A.; Piccolo, M.; Perillo, G.M. Modeling Water Yield: Assessing the Role of Site and Region-Specific Attributes in Determining Model Performance of the InVEST Seasonal Water Yield Model. Water 2018, 10, 1496. [Google Scholar] [CrossRef] [Green Version]
- Neves, G.L.; Barbosa, M.A.G.A.; Anjinho, P.S.; Guimarães, T.T.; das Virgens Filho, J.S.; Mauad, F.F. Evaluation of the Impacts of Climate Change on Streamflow through Hydrological Simulation and under Downscaling Scenarios: Case Study in a Watershed in Southeastern Brazil. Environ. Monit. Assess. 2020, 192, 707. [Google Scholar] [CrossRef]
- Wassen, M.J.; de Boer, H.J.; Fleischer, K.; Rebel, K.T.; Dekker, S.C. Vegetation-Mediated Feedback in Water, Carbon, Nitrogen and Phosphorus Cycles. Landsc. Ecol. 2013, 28, 599–614. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Batista, P.V.G.; Silva, M.L.N.; Silva, B.P.C.; Curi, N.; Bueno, I.T.; Júnior, F.W.A.; Quinton, J. Modelling spatially distributed soil losses and sediment yield in the upper Grande River Basin-Brazil. Catena 2017, 157, 139–150. [Google Scholar] [CrossRef]
- Bertol, I.; Schick, J.; Batistela, O. Razão de perdas de solo e fator C para as culturas de soja e trigo em três sistemas de preparo em um Cambissolo Húmico alumínico. Rev. Bras. Ciência Solo 2001, 25, 451–461. [Google Scholar] [CrossRef] [Green Version]
- Bertoni, J.; Lombardi Neto, F. Conservação do Solo, 4th ed.; Ícone: São Paulo, Brazil, 1990. [Google Scholar]
- Camargo, A.D.; Marin, F.R.; Sentelhas, P.C.; Picini, A.G. Ajuste da equação de Thornthwaite para estimar a evapotranspiração potencial em climas áridos e superúmidos, com base na amplitude térmica diária. Rev. Bras. Agrometeorol. 1990, 7, 251–257. [Google Scholar]
- Cunha, E.R.; Bacani, V.M.; Panachuki, E. Modeling soil erosion using RUSLE and GIS in a watershed occupied by rural settlement in the Brazilian Cerrado. Nat. Hazards 2017, 85, 851–868. [Google Scholar] [CrossRef]
- Desmet, P.J.J.; Govers, G. A GIS procedure for automatically calculating the USLE LS factor on topographically complex landscape units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar]
- Gomes, L.; Simões, S.J.; Dalla Nora, E.L.; de Sousa-Neto, E.R.; Forti, M.C.; Ometto, J.P.H. Agricultural expansion in the Brazilian Cerrado: Increased soil and nutrient losses and decreased agricultural productivity. Land 2019, 8, 12. [Google Scholar] [CrossRef] [Green Version]
- Lombardi Neto, F.; Moldenhauer, W.C. Erosividade da chuva: Sua distribuição e relação com as perdas de solo em Campinas (SP). Bragantia 1992, 51, 189–196. [Google Scholar] [CrossRef] [Green Version]
- Marin, F.R.; Angelocci, L.R. Irrigation requirements and transpiration coupling to the atmosphere of a citrus orchard in Southern Brazil. Agric. Water Manag. 2011, 98, 1091–1096. [Google Scholar] [CrossRef]
- Marin, F.R.; Angelocci, L.R.; Nassif, D.S.; Vianna, M.S.; Pilau, F.G.; da Silva, E.H.; Carvalho, K.S. Revisiting the crop coefficient–reference /10.1002/esp.37management. Theor. Appl. Climatol. 2019, 138, 1785–1793. [Google Scholar] [CrossRef]
- Oliveira, P.T.S.; Nearing, M.A.; Wendland, E. Orders of magnitude increase in soil erosion associated with land use change from native to cultivated vegetation in a Brazilian savannah environment. Earth Surf. Processes Landf. 2015, 40, 1524–1532. [Google Scholar] [CrossRef]
- Silva, F.D.G.B.D.; Minotti, R.T.; Lombardi Neto, F.; Primavesi, O.; Crestana, S. Previsão da perda de solo na Fazenda Canchim-SP (EMBRAPA) utilizando geoprocessamento e o USLE 2D. Eng. Sanitária Ambient. 2010, 15, 141–148. [Google Scholar] [CrossRef] [Green Version]
- Von Sperling, M. Introdução à Qualidade das Águas e ao Tratamento de Esgotos; Federal University of Minas Gerais: Minas Gerais, Brazil, 2005. [Google Scholar]
- USDA. Urban Hydrology for Small Watersheds; Technical Release, No 55 (TR-55); Soil Conservation Service: Washigton, DC, USA, 1986. [Google Scholar]


| Classes | NSE | R2 | PBIAS |
|---|---|---|---|
| Very good | 0.75 > NSE ≤ 1.00 | 0.85 > R2 ≤ 1.00 | <|5| |
| Good | 0.65 > NSE ≤ 0.75 | 0.70 > R2 ≤ 0.85 | |5| − |10| |
| Satisfactory | 0.50 > NSE ≤ 0.65 | 0.60 > R2 ≤ 0.70 | |10| − |15| |
| Acceptable | 0.40 > NSE ≤ 0.50 | 0.40 > R2 ≤ 0.60 | |
| Unsatisfactory | NSE ≤ 0.40 | ≤0.40 | ≥|15| |
| Calibration | Validation | |||||||
|---|---|---|---|---|---|---|---|---|
| Monitoring Station | Model | Indicator | R2 | PBIAS (%) | NSE | R2 | PBIAS (%) | NSE |
| SF-I | SWY | Streamflow | 0.4 | −0.6 | −0.6 | 0.5 | 8.1 | 0.6 |
| SF-II | SWY | Streamflow | 0.5 | 6.6 | −0.6 | 0.8 | 30.3 | 0.6 |
| SF-III | SWY | Streamflow | 0.5 | 8.8 | −4.6 | 0.7 | 0.9 | 0.5 |
| SF-IV | SWY | Streamflow | 0.6 | −3.4 | −2 | 0.7 | −8.5 | 0.6 |
| WQ-I | SDR | Exported sediment | 0.3 | 0.2 | 0.2 | - | - | - |
| WQ-II | SDR | Exported sediment | 0 | 0.6 | −0.1 | 0.2 | −14.6 | −0.1 |
| WQ-III | SDR | Exported sediment | 0 | 6.6 | −0.3 | 0.1 * | 5.6 | −0.4 |
| WQ-I | NDR | Exported TP | 0.2 | 50 | −4.5 | - | - | - |
| WQ-II | NDR | Exported TP | 0.6 * | −23 | −1.1 | 0.4 | 1.7 | 0.2 |
| WQ-III | NDR | Exported TP | 0.3 | −10 | 0.1 | 0.3 * | 2.2 | −0.3 |
| WQ-I | NDR | Exported TN | 0.3 | −18.6 | −0.8 | − | − | − |
| WQ-II | NDR | Exported TN | 0.4 * | 2 | −0.2 | 0.4 * | 12.3 | −0.6 |
| WQ-III | NDR | Exported TN | 0.1 | 27 | −1.5 | 0.6 * | 44 | −3.4 |
| Model | R2 | PBIAS | NSE |
|---|---|---|---|
| SWY | 0.47 | 3.50 | −0.39 |
| SDR | −0.10 | −6.25 | −0.13 |
| NDR-TN | 0.30 | 11.00 | 0.13 |
| NDR-TP | 0.00 | −3.31 | −0.23 |
| Sub-Basin | Period | QF (m³ s−1) | BF (m³ s−1) | Simulated Streaflow (m³ s−1) | Observed Streamflow (m³ s−1) | Discrepancy (%) |
|---|---|---|---|---|---|---|
| SF-I | 1981–2019 | 1.2 | 2.6 | 3.8 | 3.8 | 1 |
| SF-II | 1981–2019 | 3.1 | 9.4 | 12.5 | 11.3 | 11 |
| SF-III | 1981–2019 | 8.9 | 18.0 | 26.9 | 25.1 | 7 |
| SF-IV | 1981–2019 | 13.1 | 32.6 | 45.8 | 47.9 | −5 |
| Sub-basin | Period | Simulated exported sediment (kt.yr−1) | Observed exported sediment (kt.yr−1) | Discrepancy(%) | ||
| WQ-I | 2011–2019 | 8.350 | 7.759 | 8 | ||
| WQ-II | 2001–2019 | 14.843 | 15.533 | −4 | ||
| WQ-IIII | 2000–2019 | 27.557 | 31.757 | −13 | ||
| Sub-basin | Period | Nonpoint TN load (t.yr1) | Point TN load (t.yr1) | Simulated TN (t.yr1) | Observed TN (t.yr1) | Discrepancy(%) |
| WQ-I | 2011–2019 | 136.4 | 280.4 | 416.8 | 512.0 | −19 |
| WQ-II | 2001–2019 | 242.3 | 331.4 | 573.6 | 542.4 | 6 |
| WQ-IIII | 2000–2019 | 485.9 | 707.2 | 1193.0 | 900.0 | 32 |
| Sub-basin | Period | Nonpoint TP load (t.yr1) | Point TP load (t.yr1) | Simulated TP (t.yr1) | Observed TP (t.yr1) | Discrepancy(%) |
| WQ-I | 2011–2019 | 16.2 | 27.0 | 43.2 | 28.8 | 50 |
| WQ-II | 2001–2019 | 29.6 | 32.6 | 62.2 | 73.2 | −15 |
| WQ-IIII | 2000–2019 | 63.0 | 71.7 | 134.8 | 143.9 | −6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anjinho, P.d.S.; Barbosa, M.A.G.A.; Mauad, F.F. Evaluation of InVEST’s Water Ecosystem Service Models in a Brazilian Subtropical Basin. Water 2022, 14, 1559. https://doi.org/10.3390/w14101559
Anjinho PdS, Barbosa MAGA, Mauad FF. Evaluation of InVEST’s Water Ecosystem Service Models in a Brazilian Subtropical Basin. Water. 2022; 14(10):1559. https://doi.org/10.3390/w14101559
Chicago/Turabian StyleAnjinho, Phelipe da Silva, Mariana Abibi Guimarães Araujo Barbosa, and Frederico Fábio Mauad. 2022. "Evaluation of InVEST’s Water Ecosystem Service Models in a Brazilian Subtropical Basin" Water 14, no. 10: 1559. https://doi.org/10.3390/w14101559
APA StyleAnjinho, P. d. S., Barbosa, M. A. G. A., & Mauad, F. F. (2022). Evaluation of InVEST’s Water Ecosystem Service Models in a Brazilian Subtropical Basin. Water, 14(10), 1559. https://doi.org/10.3390/w14101559






