An Equivalent Pipe Network Modeling Approach for Characterizing Fluid Flow through Three-Dimensional Fracture Networks: Verification and Applications
Abstract
:1. Introduction
2. Generation of DFN and EPN Models
2.1. Generation of 3D DFN Models
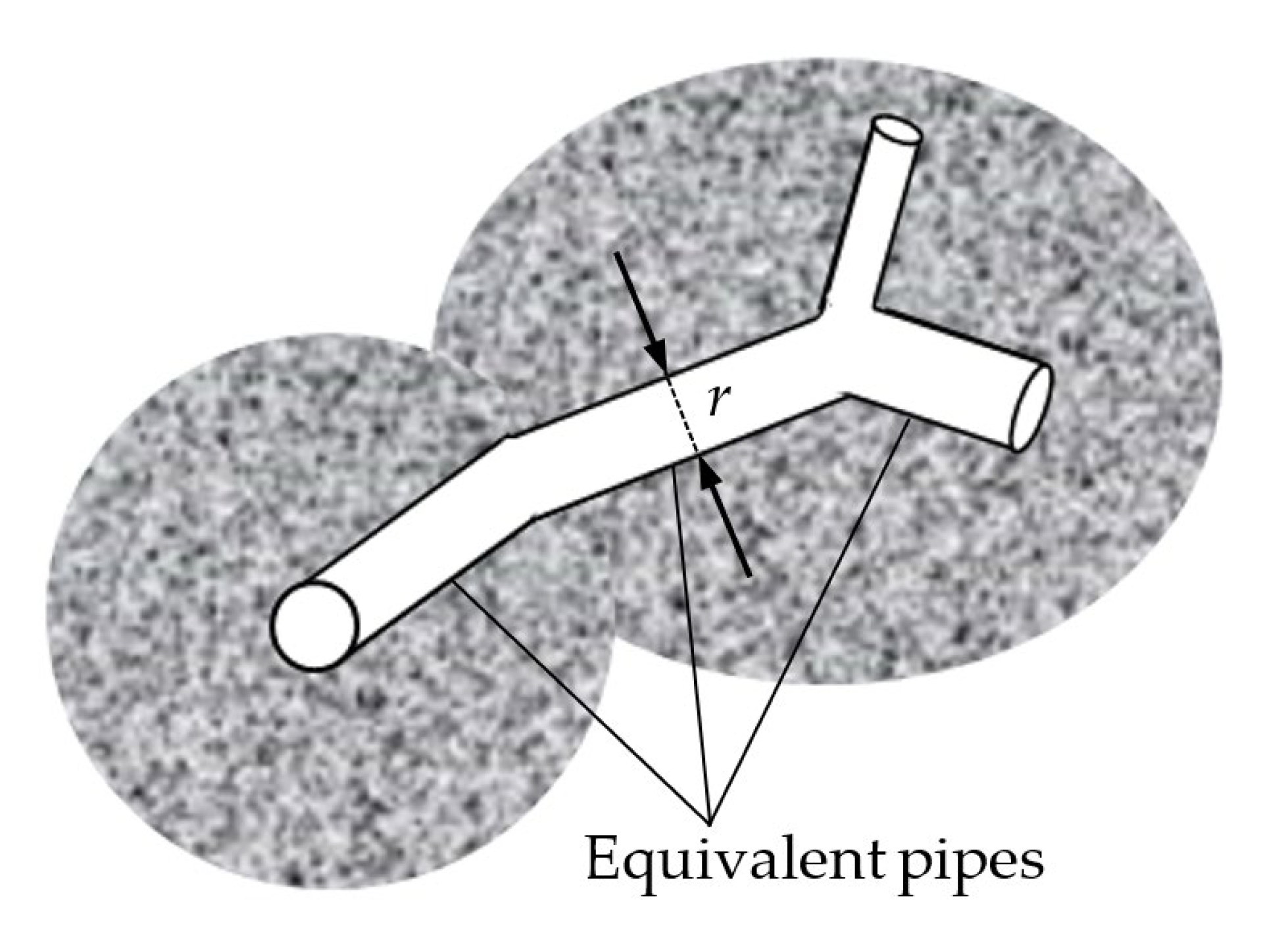
2.2. Generation of 3D EPN Models
3. Verification of the EPN Model
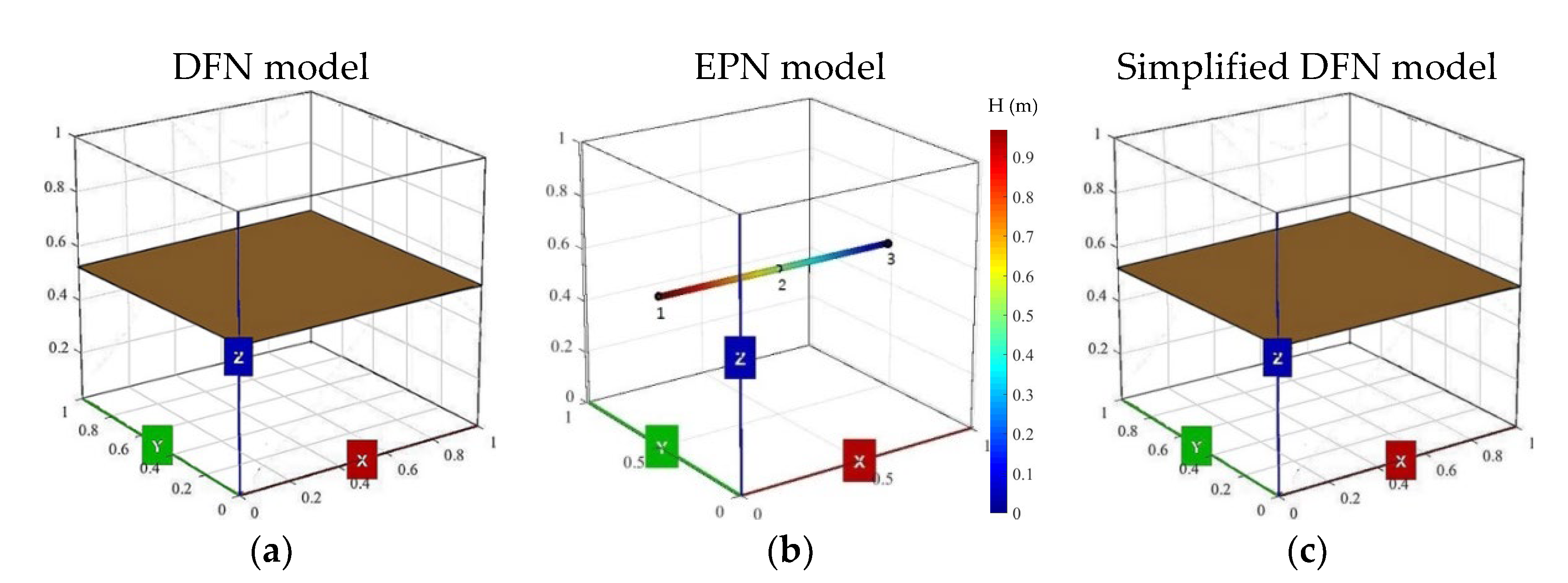
3.1. Validation of the Simple EPN Models
3.2. Validation of the Complex EPN Models
4. The Evolution of Seepage Properties with Various Geometry Characteristics
4.1. Effect of Fracture Length Distribution
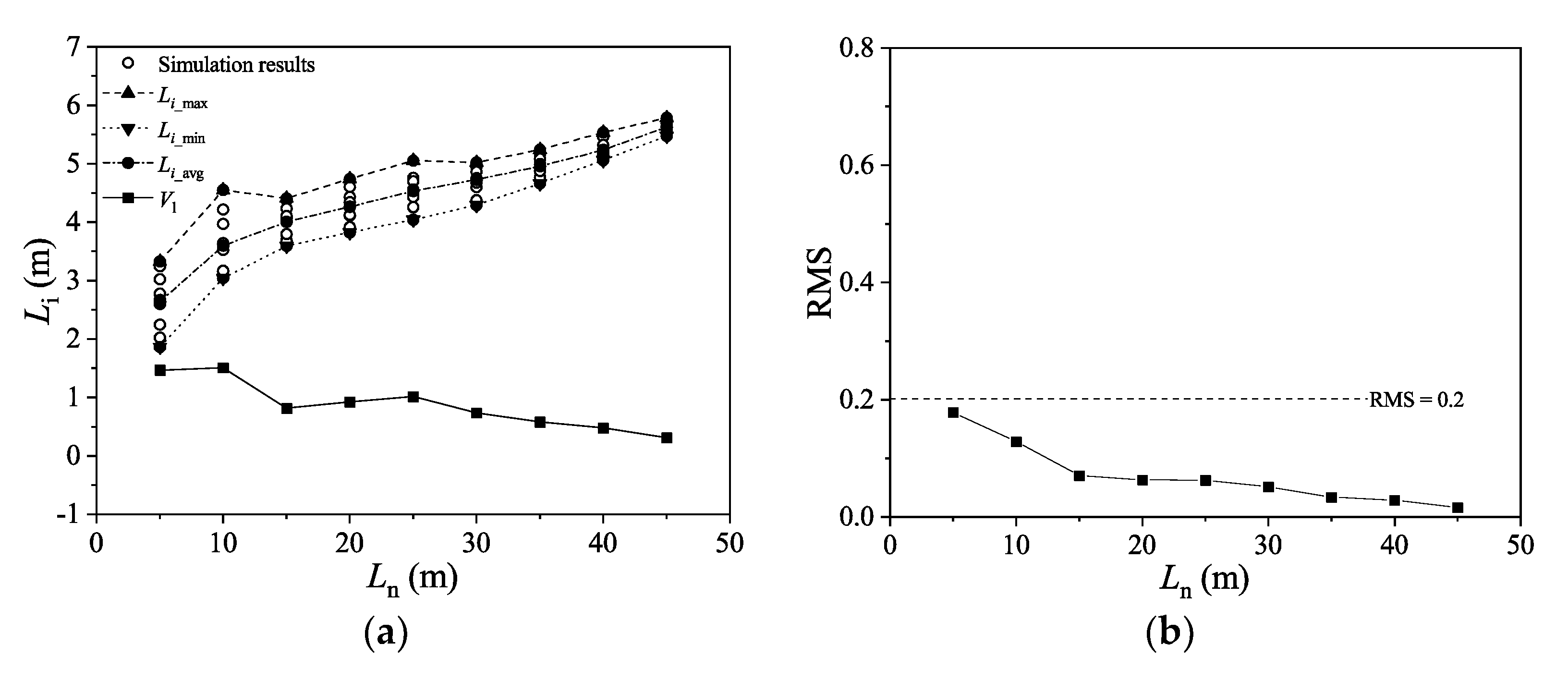
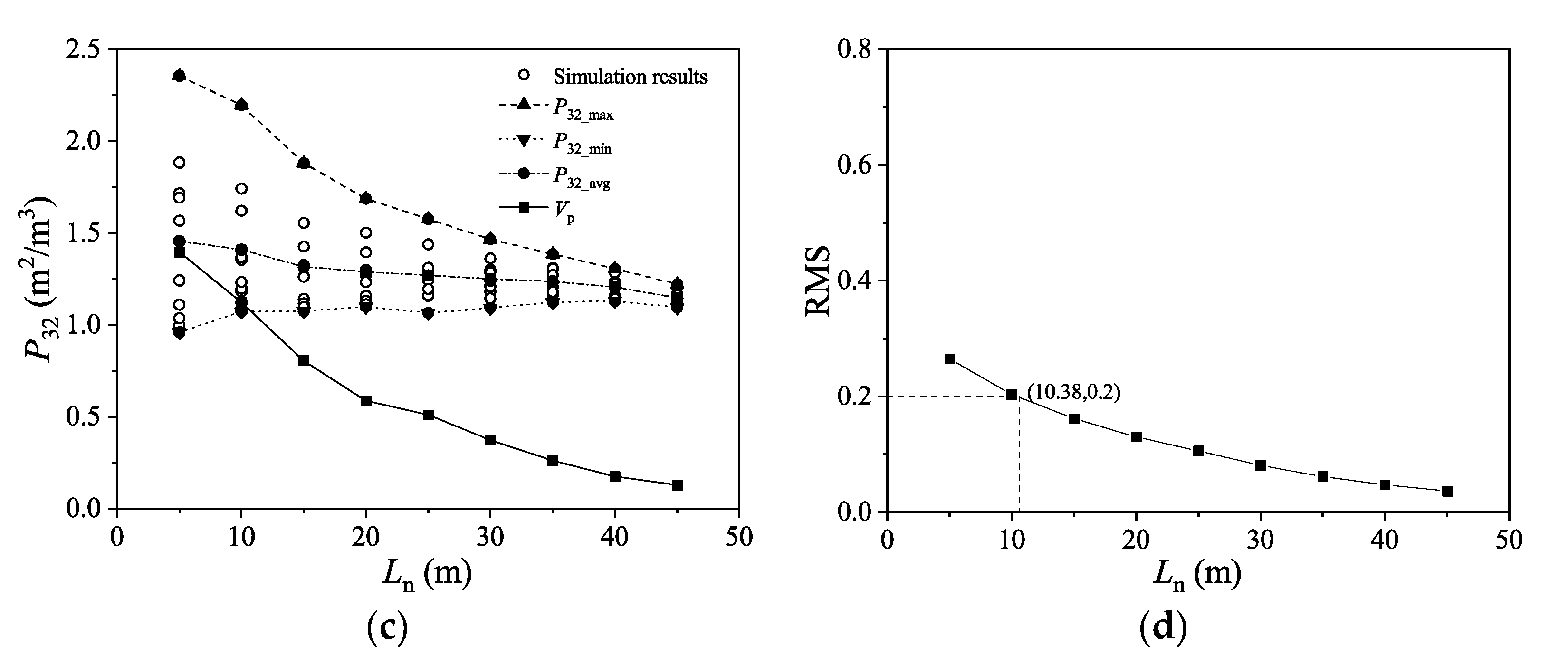
4.2. Estimation of REV Size
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol | Meaning and Unit |
|---|---|
| Q | The total flow rate through single fracture or fracture network (m3/s) |
| g | The gravity acceleration (m/s2) |
| v | The kinematic viscosity of the fluid (m2/s) |
| a | Fracture aperture (m) |
| w | The section width (m) |
| J | Hydraulic gradient |
| Hin | The water head applied on the inlet boundary (m) |
| Hout | The water head applied on the outlet boundary (m) |
| Ldis | The distance between the opposite boundaries of fracture network models (m) |
| Cij | The equivalent conductance of the pipe between node i and node j (m2/s) |
| Lij | The length of the pipe between node i and node j (m) |
| Qij | The flow rate through the pipe between node i and node j (m3/s) |
| Hi | The water head of node i (m) |
| Hj | The water head of node j (m) |
| △H | Water head difference between adjacent nodes (m) |
| k | Equivalent permeability (m2) |
| ks | The equivalent permeability of the equivalent pipe network model (m2) |
| kt | The equivalent permeability of the simplified discrete fracture network model (m2) |
| ε | The relative error between kt and ks (%) |
| u | The average value of fracture length (m) |
| Li | The average value of intersection length between fractures (m) |
| P32 | The total area of fracture surface per unit volume (m2/m3) |
References
- Gangi, A.F. Variation of whole and fractured porous rock permeability with confining pressure. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 249–257. [Google Scholar] [CrossRef]
- Brown, S.R.; Scholz, C.H. Closure of random elastic surfaces in contact. J. Geophys. Res. Solid Earth 1985, 90, 5531–5545. [Google Scholar] [CrossRef]
- Brown, S.R. Fluid flow through rock joints: The effect of surface roughness. J. Geophys. Res. Solid Earth 1987, 92, 1337–1347. [Google Scholar] [CrossRef]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Min, K.; Jing, L.; Stephansson, O. Determining the equivalent permeability tensor for fractured rock masses using a stochastic REV approach: Method and application to the field data from Sellafield, UK. Hydrogeol. J. 2004, 12, 497–510. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L. Hydraulic properties of fractured rock masses with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2007, 44, 704–719. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L. Stress effects on permeability in a fractured rock mass with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2008, 45, 1320–1334. [Google Scholar] [CrossRef]
- Gale, J.F.W.; Laubach, S.E.; Olson, J.E.; Eichhuble, P.; Fall, A. Natural fractures in shale: A review and new observations. AAPG Bull. 2014, 98, 2165–2216. [Google Scholar] [CrossRef]
- Huang, N.; Jiang, Y.; Li, B.; Liu, R. A numerical method for simulating fluid flow through 3-D fracture networks. J. Nat. Gas Sci. Eng. 2016, 33, 1271–1281. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Qin, X.; Han, D.; Liu, Z. Study on seepage and deformation characteristics of coal microstructure by 3D reconstruction of CT images at high temperatures. Int. J. Min. Sci. Technol. 2021, 31, 175–185. [Google Scholar] [CrossRef]
- Thanh, H.V.; Sugai, Y.; Nguele, R.; Sasaki, K. Integrated workflow in 3D geological model construction for evaluation of CO2 storage capacity of a fractured basement reservoir in Cuu Long Basin, Vietnam. Int. J. Greenh. Gas Control 2019, 90, 102826. [Google Scholar] [CrossRef]
- Neuman, S.P. Trends, prospects and challenges in quantifying flow and transport through fractured rocks. Hydrogeol. J. 2005, 13, 124–147. [Google Scholar] [CrossRef]
- Rothert, E.; Shapiro, S. Statistics of fracture strength and fluid-induced microseismicity. J. Geophys. Res. 2007, 112, 1–16. [Google Scholar] [CrossRef]
- De Dreuzy, J.R.; Méheust, Y.; Pichot, G. Influence of fracture scale heterogeneity on the flow properties of three-dimensional discrete fracture networks (DFN). J. Geophys. Res. Solid Earth 2012, 117, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Fitch, P.J.R.; Lovell, M.A.; Davies, S.J.; Pritchard, T.; Harvey, P.K. An integrated and quantitative approach to petrophysical heterogeneity. Mar. Pet. Geol. 2015, 63, 82–96. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Zhan, S.; Huang, T. Determining transmissivity of fracture sets with statistical significance using single-borehole hydraulic tests: Methodology and implementation at Heshe well site in central Taiwan. Eng. Geol. 2015, 198, 1–15. [Google Scholar] [CrossRef]
- Zhang, F.; Damjanac, B.; Maxwell, S. Investigating hydraulic fracturing complexity in naturally fractured rock masses using fully coupled multiscale numerical modeling. Rock Mech. Rock Eng. 2019, 52, 5137–5160. [Google Scholar] [CrossRef]
- Liu, R.; He, M.; Huang, N.; Jiang, Y.; Yu, L. Three-dimensional double-rough-walled modeling of fluid flow through self-affine shear fractures. J. Rock Mech. Geotech. Eng. 2020, 12, 41–49. [Google Scholar] [CrossRef]
- Hu, M.; Rutqvist, J. Multi-scale coupled processes modeling of fractures as porous, interfacial and granular systems from rock images with the numerical manifold method. Rock Mech. Rock Eng. 2021, 1–19. [Google Scholar] [CrossRef]
- Dershowitz, W.S.; Fidelibus, C. Derivation of equivalent pipe network analogues for three-dimensional discrete fracture networks by the boundary element method. Water Resour. Res. 1999, 35, 2685–2691. [Google Scholar] [CrossRef]
- Maillot, J.; Davy, P.; Le Goc, R.; Darcel, C.; De Dreuzy, J.R. Connectivity, permeability, and channeling in randomly distributed and kinematically defined discrete fracture network models. Water Resour. Res. 2016, 52, 8526–8545. [Google Scholar] [CrossRef] [Green Version]
- Viswanathan, H.S.; Hyman, J.D.; Karra, S.; O’Malley, D.; Srinivasan, S.; Hagberg, A.; Srinivasan, G. Advancing graph-based algorithms for predicting flow and transport in fractured rock. Water Resour. Res. 2018, 54, 6085–6099. [Google Scholar] [CrossRef]
- Ashraf, U.; Zhang, H.; Anees, A.; Mangi, H.N.; Zhang, X. Application of unconventional seismic attributes and unsupervised machine learning for the identification of fault and fracture network. Appl. Sci. 2020, 10, 3864. [Google Scholar] [CrossRef]
- Jiang, R.; Zhao, L.; Xu, A.; Ashraf, U.; Yin, J.; Song, H.; Su, N.; Du, B.; Anees, A. Sweet spots prediction through fracture genesis using multi-scale geological and geophysical data in the karst reservoirs of Cambrian Longwangmiao Carbonate Formation, Moxi-Gaoshiti area in Sichuan Basin, South China. J. Pet. Explor. Prod. Technol. 2021, 12, 1313–1328. [Google Scholar] [CrossRef]
- Doolaeghe, D.; Davy, P.; Hyman, J.D.; Darcel, C. Graph-based flow modeling approach adapted to multiscale discrete-fracture-network models. Phys. Rev. E 2020, 102, 53312. [Google Scholar] [CrossRef]
- De Dreuzy, J.R.; Davy, P.; Bour, O. Percolation parameter and percolation-threshold estimates for three-dimensional random ellipses with widely scattered distributions of eccentricity and size. Phys. Rev. E 2000, 62, 5948–5952. [Google Scholar] [CrossRef] [Green Version]
- Cruden, D.M. Describing the size of discontinuities. Int. J. Rock Mech. Min. Sci. 1977, 14, 133–137. [Google Scholar] [CrossRef]
- Hudson, J.A.; Priest, S.D. Discontinuities and rock mass geometry. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 339–362. [Google Scholar] [CrossRef]
- Priest, S.D.; Hudson, J.A. Estimation of discontinuity spacing and trace length using scanline surveys. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 183–197. [Google Scholar] [CrossRef]
- Cowie, P.A.; Scholz, C.H.; Edwards, M.; Malinverno, A. Fault strain and seismic coupling on mid-ocean ridges. J. Geophys. Res. Solid Earth 1993, 98, 17911–17920. [Google Scholar] [CrossRef]
- Carbotte, S.M.; Macdonald, K.C. Comparison of seafloor tectonic fabric at intermediate, fast, and super fast spreading ridges: Influence of spreading rate, plate motions, and ridge segmentation on fault patterns. J. Geophys. Res. Solid Earth 1994, 99, 13609–13631. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of fracture systems in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Einstein, H.H.; Dershowitz, W.S. Stereological relationship between trace length and size distribution of elliptical discontinuities. Géotechnique 2002, 52, 419–433. [Google Scholar] [CrossRef]
- Agosta, F.; Alessandroni, M.; Antonellini, M.; Tondi, E.; Giorgioni, M. From fractures to flow: A field-based quantitative analysis of an outcropping carbonate reservoir. Tectonophysics 2010, 490, 197–213. [Google Scholar] [CrossRef]
- Bustin, A.M.M.; Bustin, R.M. Importance of rock properties on the producibility of gas shales. Int. J. Coal Geol. 2012, 103, 132–147. [Google Scholar] [CrossRef]
- Cowie, P.A.; Sornette, D.; Vanneste, C. Multifractal scaling properties of a growing fault population. Geophys. J. R. Astron. Soc. 2010, 122, 457–469. [Google Scholar] [CrossRef] [Green Version]
- Long, J.C.S.; Remer, J.S.; Wilson, C.R.; Witherspoon, P.A. Porous media equivalents for networks of discontinuous fractures. Water Resour. Res. 1982, 18, 645–658. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Tang, Z. Discrete fracture network modelling in a naturally fractured carbonate reservoir in the Jingbei oilfield, China. Energies 2017, 10, 183. [Google Scholar]
- Priest, S.D. Discontinuity Analysis for Rock Engineering; Chapman & Hall: London, UK, 1993. [Google Scholar] [CrossRef]
- Hyman, J.D.; Karra, S.; Makedonska, N.; Gable, C.W.; Painter, S.L.; Viswanathan, H.S. dfnWorks: A discrete fracture network framework for modeling subsurface flow and transport. Comput. Geosci. 2015, 84, 10–19. [Google Scholar] [CrossRef] [Green Version]
- Cacas, M.C.; Ledoux, E.; De Marsily, G.; Tillie, B.; Durand, E.; Feuga, B.; Peaudecerf, P. Modeling fracture flow with a stochastic discrete fracture network: Calibration and validation: 1. The flow model. Water Resour. Res. 1990, 26, 479–489. [Google Scholar] [CrossRef]
- Nordqvist, A.W.; Tsang, Y.W.; Tsang, C.F.; Dverstorp, B.; Andersson, J. A variable aperture fracture network model for flow and transport in fractured rocks. Water Resour. Res. 1992, 28, 1703–1713. [Google Scholar] [CrossRef]
- Xu, C.; Fidelibus, C.; Dowd, P. Realistic Pipe Models for Flow Modelling in Discrete Fracture Networks. In Proceedings of the First International Discrete Fracture Network Engineering Conference, Vancouver, BC, Canada, 19–22 October 2014. [Google Scholar]
- Alghalandis, Y.F. ADFNE: Open source software for discrete fracture network engineering, two and three dimensional applications. Comput. Geosci. 2017, 102, 1–11. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, Y.; Li, X.; Wang, X.; Zhang, P. Study on three-dimensional fracture network connectivity path of rock mass and seepage characteristics based on equivalent pipe network. Environ. Earth Sci. 2019, 78, 516. [Google Scholar] [CrossRef]
- Dverstorp, B.; Andersson, J.; Nordqvist, W. Discrete fracture network interpretation of field tracer migration in sparsely fractured rock. Water Resour. Res. 1992, 28, 2327–2343. [Google Scholar] [CrossRef]
- Davy, P.; Darcel, C.; Bour, O.; Munier, R.; De Dreuzy, J.R. A note on the angular correction applied to fracture intensity profiles along drill core. J. Geophys. Res. Solid Earth 2006, 111, B11408. [Google Scholar] [CrossRef] [Green Version]
- Panda, B.B.; Kulatilake, P. Effect of joint geometry and transmissivity on jointed rock hydraulics. J. Eng. Mech. 1999, 125, 41–50. [Google Scholar] [CrossRef]
- Kulatilake, P.; Panda, B.B. Effect of block size and joint geometry on jointed rock hydraulics and REV. J. Eng. Mech. 2000, 126, 850–858. [Google Scholar] [CrossRef]
- Ohman, J.; Niemi, A. Upscaling of fracture hydraulics by means of an oriented correlated stochastic continuum model. Water Resour. Res. 2003, 39, 71. [Google Scholar] [CrossRef] [Green Version]
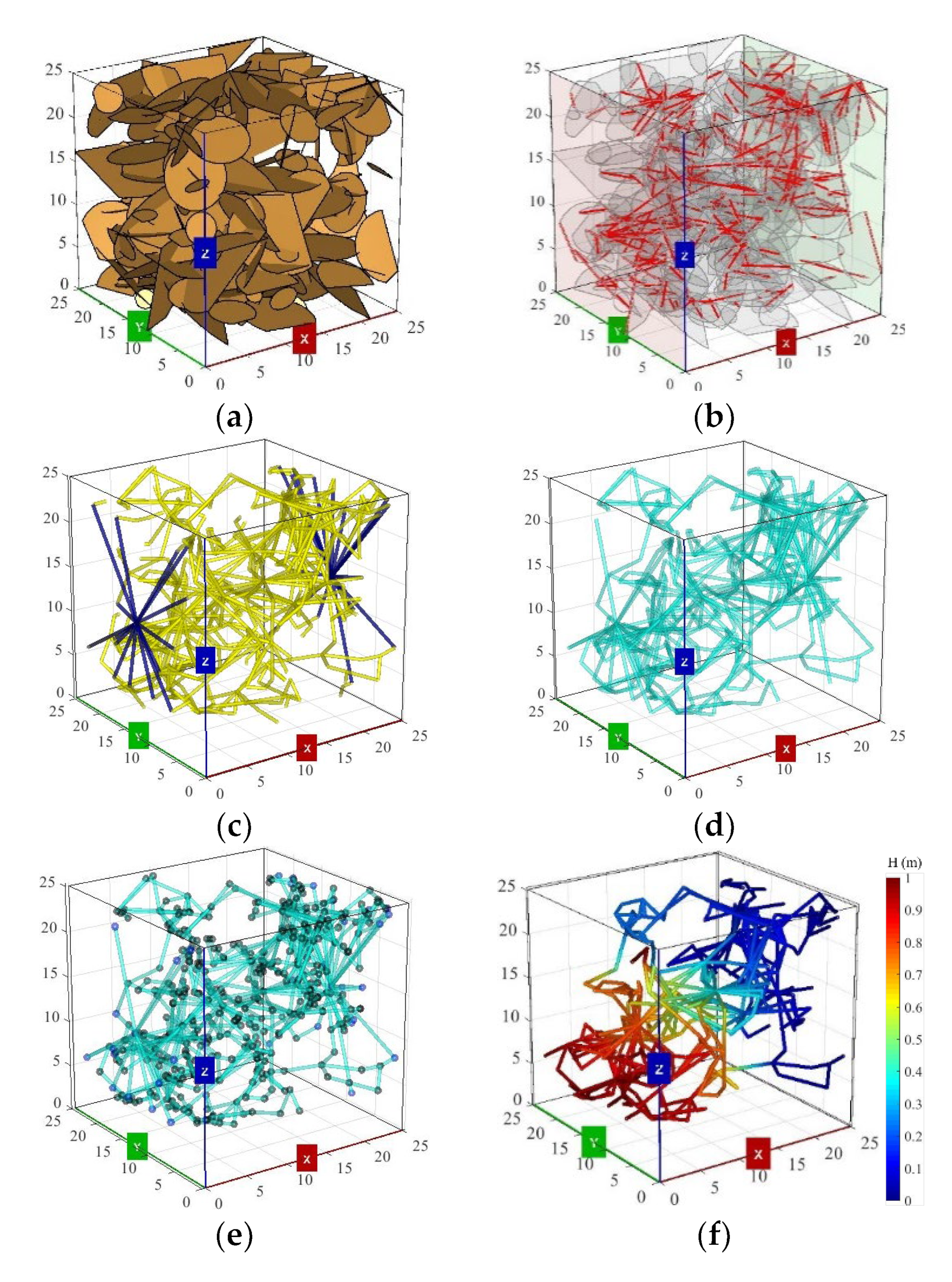
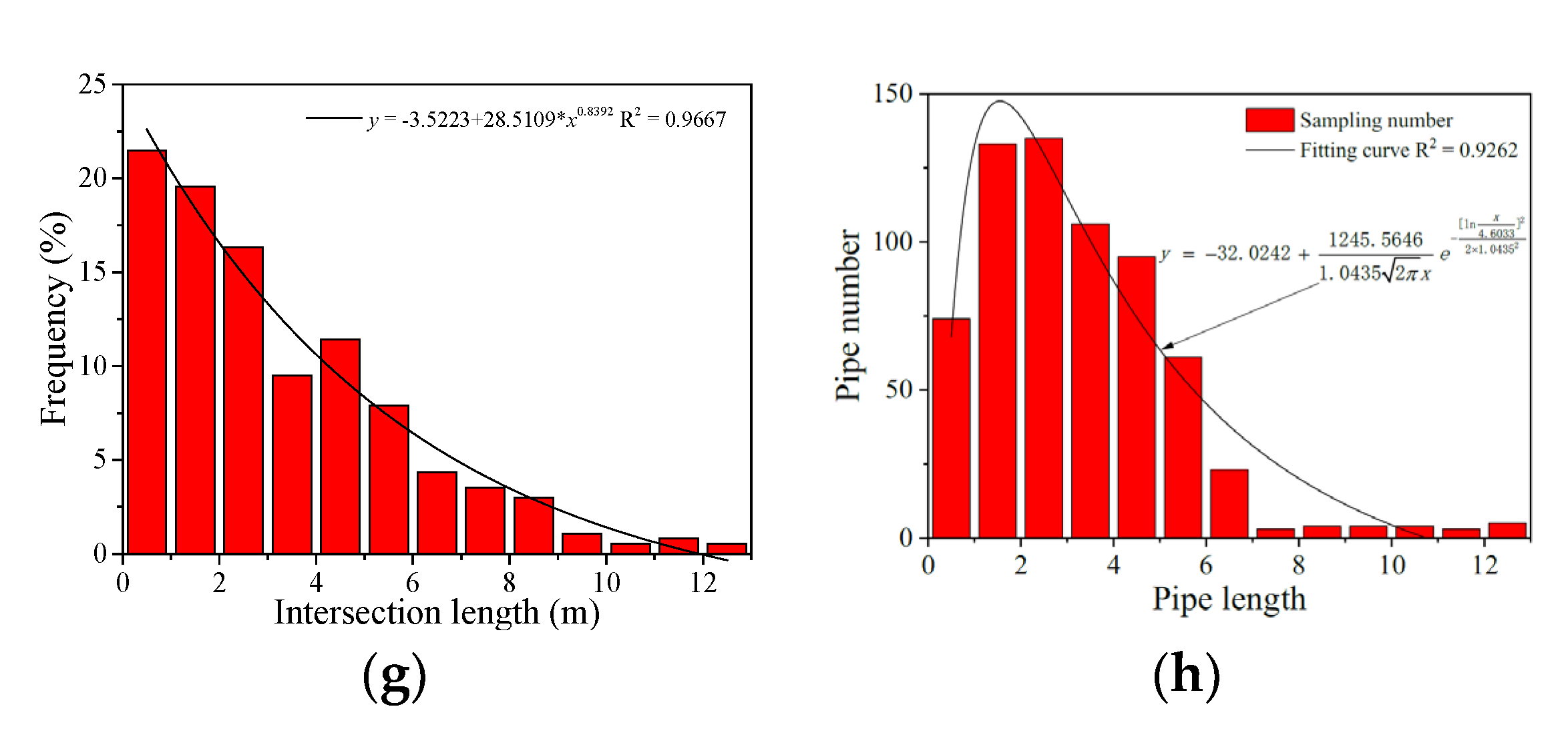


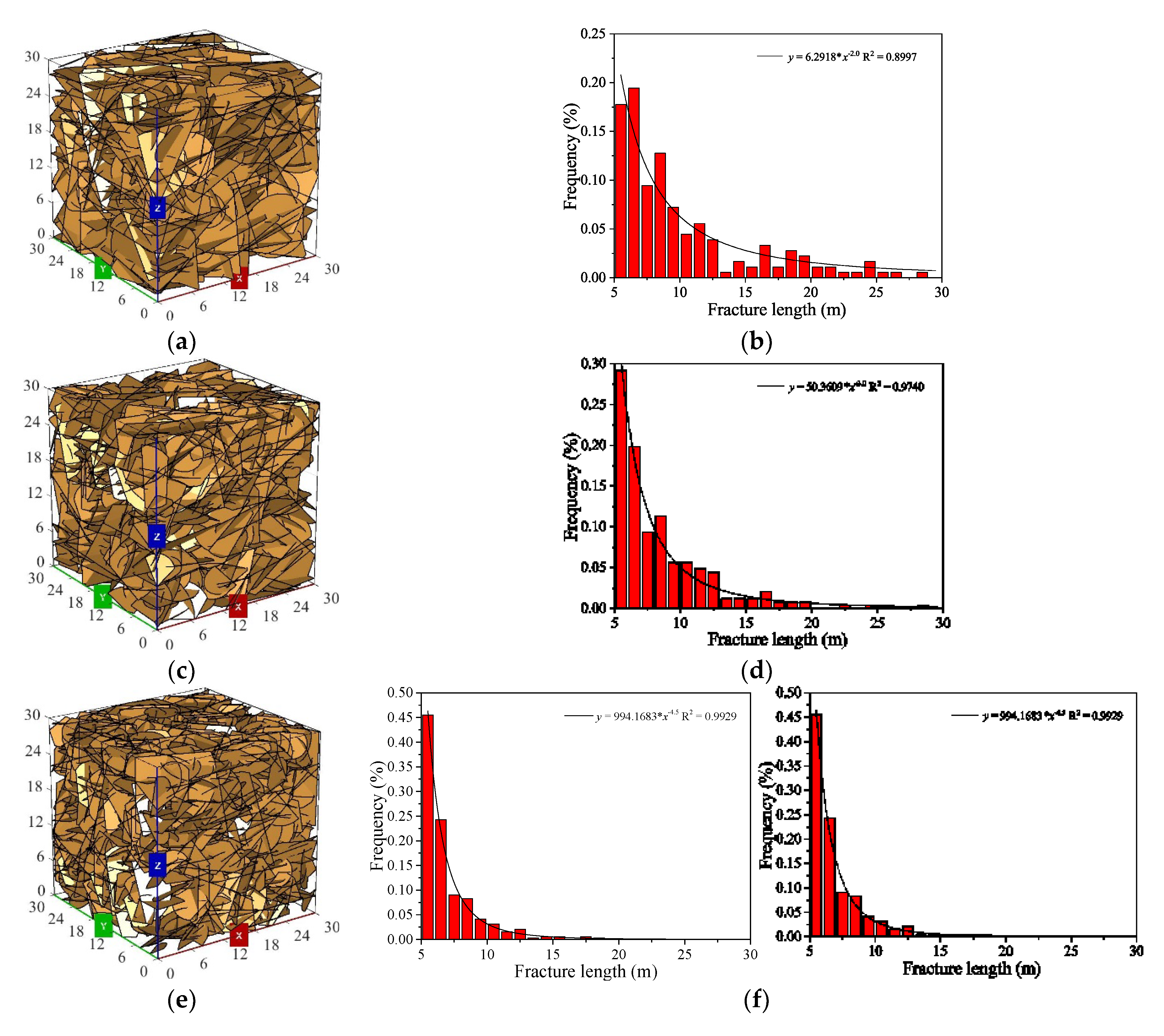
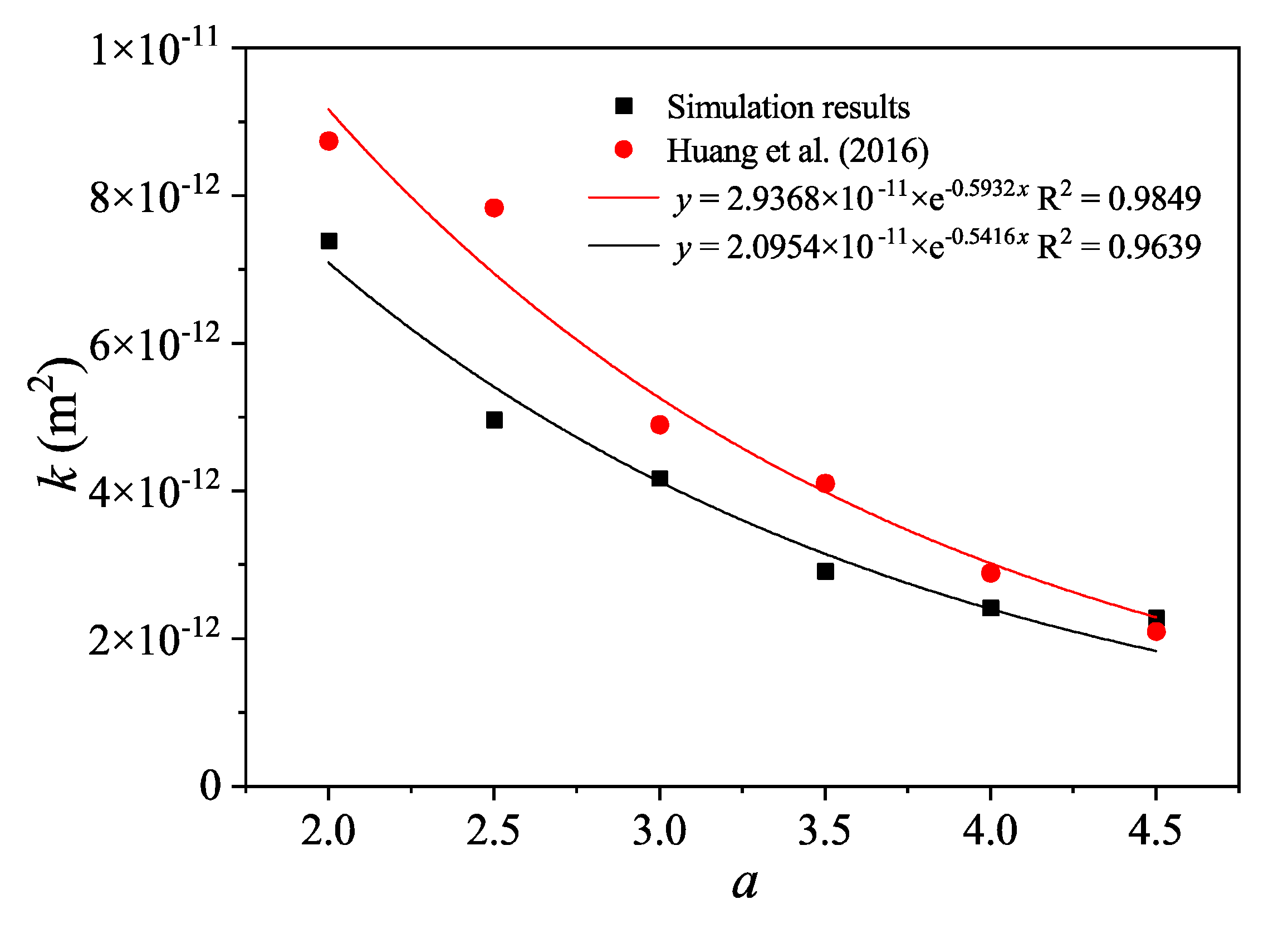





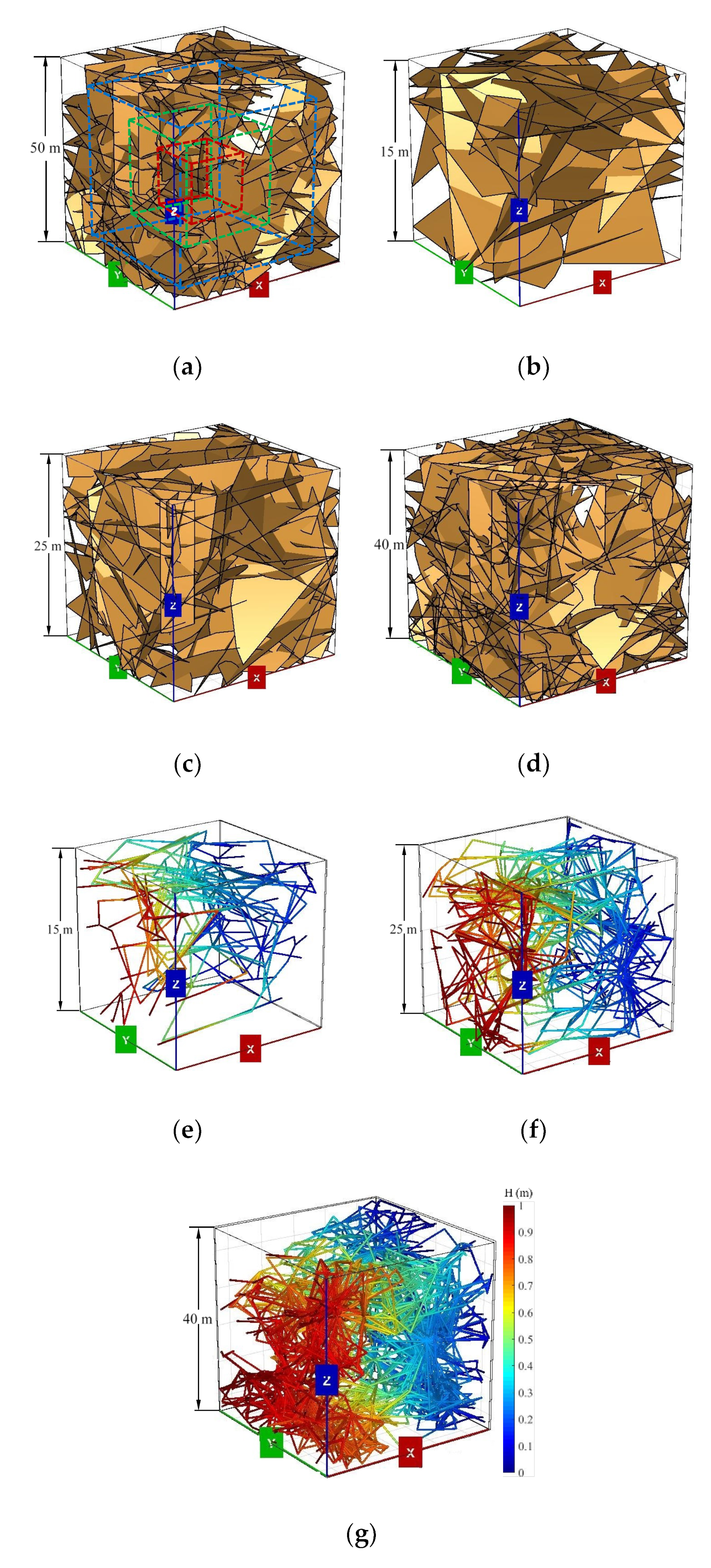


| Parameters | Distribution | Parameters |
|---|---|---|
| Domain size (m) | Constant | L = 30 (m) |
| Positions | Uniform random | |
| Orientations (°) | Fisher | Set 1: DA = 90, DD = 10, κ = 200 Set 1: DA = 40, DD = 120, κ = 200 Set 1: DA = 60, DD = 70, κ = 200 Set 1: DA = 80, DD = 320, κ = 200 |
| Length (m) | Power law | 2 < a < 4.5, 5 < Lf < 30 |
| Density (m2/m3) | Constant | P32 = 0.4 |
| u (m) | c | d | h | R2 |
|---|---|---|---|---|
| 3 | −1.2557 | −47.1492 | 0.7142 | 0.9860 |
| 4 | −1.2333 | −39.4450 | 0.7509 | 0.9797 |
| 5 | −3.0247 | −33.2154 | 0.8193 | 0.9533 |
| 6 | −2.9572 | −32.6267 | 0.8611 | 0.9764 |
| 7 | −0.7913 | −34.2912 | 0.7688 | 0.9701 |
| 8 | −3.7502 | −31.3042 | 0.8412 | 0.9641 |
| 9 | −4.0304 | −30.3075 | 0.8516 | 0.9767 |
| 10 | −13.6517 | −34.8342 | 0.9271 | 0.9197 |
| 11 | −12.5329 | −33.6306 | 0.9242 | 0.9567 |
| 12 | −3.4822 | −28.4039 | 0.8546 | 0.9540 |
| 13 | −3.8291 | −28.1998 | 0.8611 | 0.9472 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Liu, R.; Yu, L.; Li, S.; Wang, X.; Liu, D. An Equivalent Pipe Network Modeling Approach for Characterizing Fluid Flow through Three-Dimensional Fracture Networks: Verification and Applications. Water 2022, 14, 1582. https://doi.org/10.3390/w14101582
Zhang J, Liu R, Yu L, Li S, Wang X, Liu D. An Equivalent Pipe Network Modeling Approach for Characterizing Fluid Flow through Three-Dimensional Fracture Networks: Verification and Applications. Water. 2022; 14(10):1582. https://doi.org/10.3390/w14101582
Chicago/Turabian StyleZhang, Jing, Richeng Liu, Liyuan Yu, Shuchen Li, Xiaolin Wang, and Ding Liu. 2022. "An Equivalent Pipe Network Modeling Approach for Characterizing Fluid Flow through Three-Dimensional Fracture Networks: Verification and Applications" Water 14, no. 10: 1582. https://doi.org/10.3390/w14101582







