Study of the Behavior of Alkalinities Predicted by the AM2 Model
Abstract
:1. Introduction
2. Modifications to the AM2 System
Physicochemical Relationships
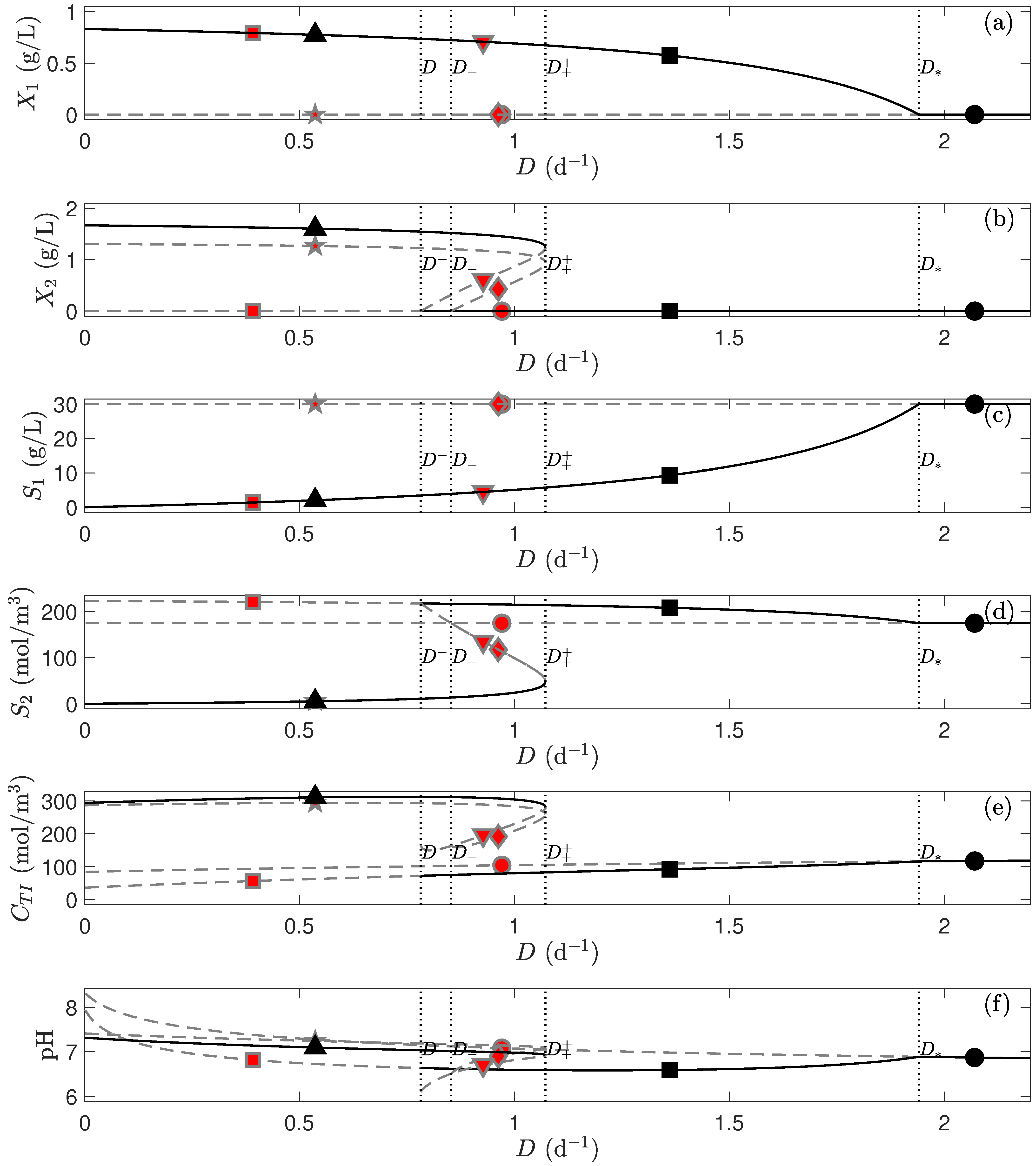
3. Bifurcation Analysis
- EP1
- The washout of both biomasses, for .
- EP2
- The washout only of the methanogenic biomass, for , with .
- EP3
- The washout of the acidogenic biomass only (with two possible equilibrium points):
- EP3a
- for , withand ,
- EP3b
- for .
- EP4
- The survival of both biomasses (with two possible equilibrium points):
- EP4a
- for withand ,
- EP4b
- for .
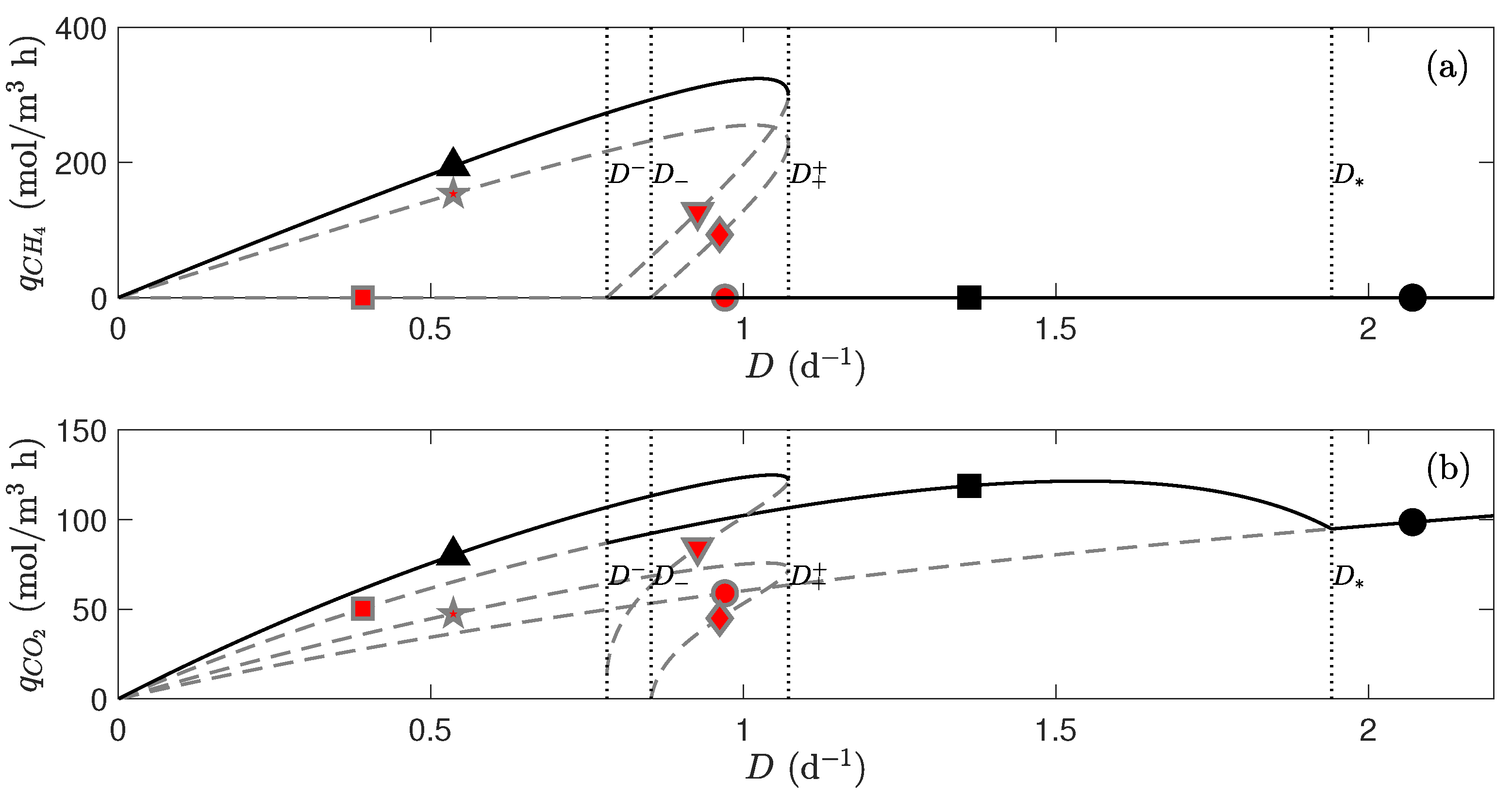
4. Discussion
4.1. Bifurcation of an Analytical Case Study
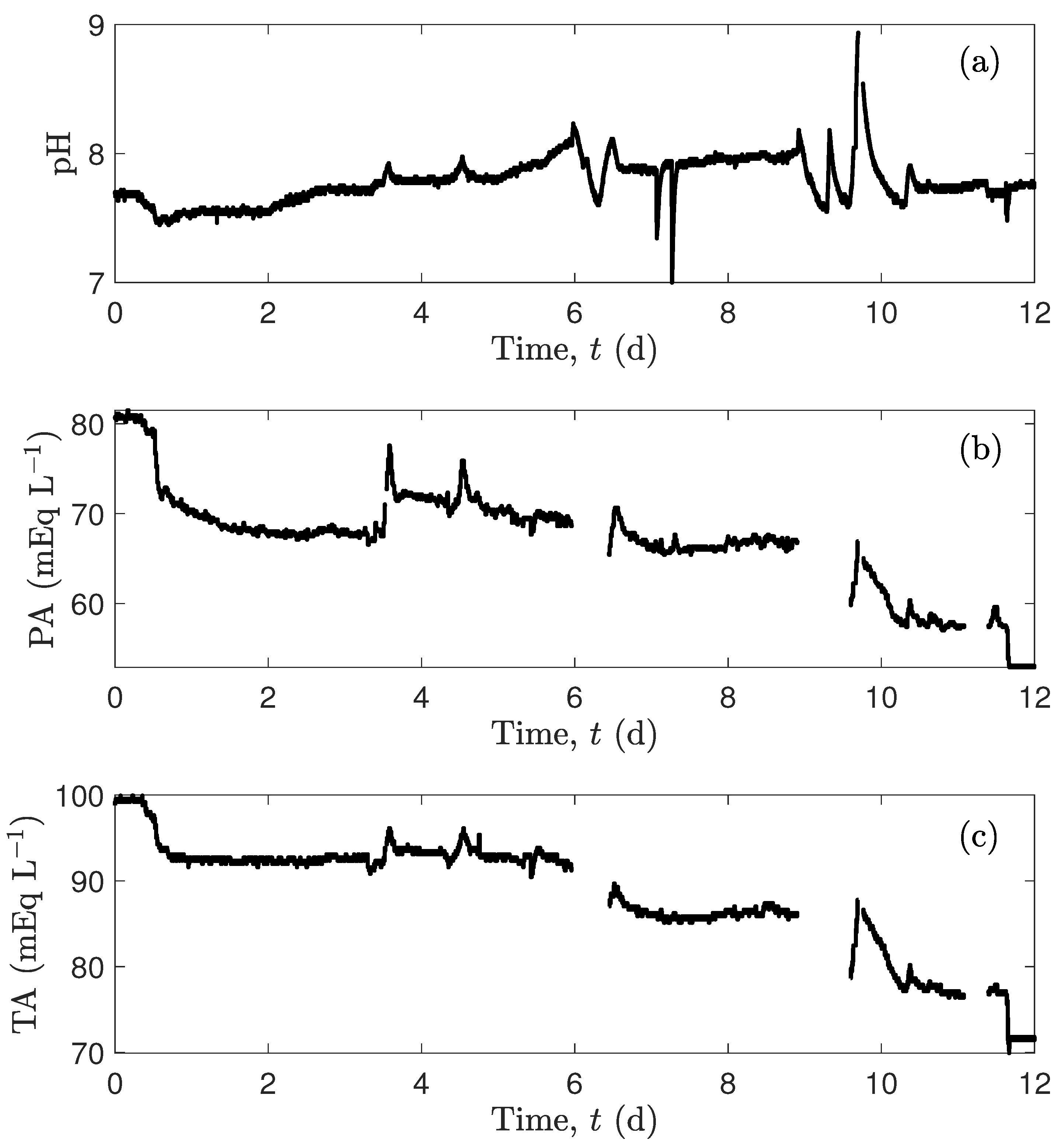
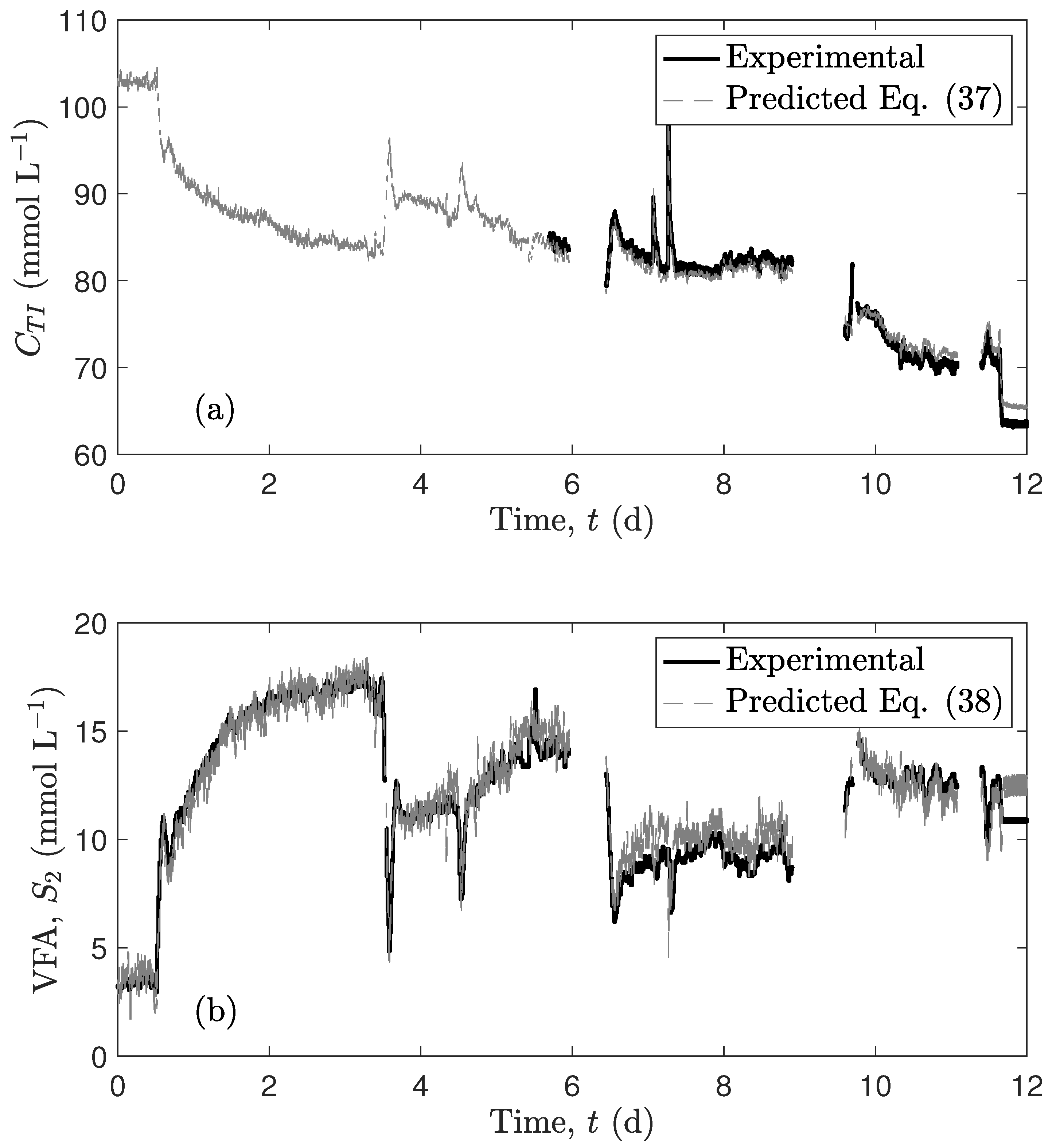
4.2. Predictions of an Experimental Case Study
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | Anaerobic digestion |
| AM2 | Anaerobic digestion model 2 |
| AMOCO | Automatic monitoring and control project |
| COD | Chemical oxygen demand |
| VFA | Volatile fatty acids |
| PA | Partial alkalinity |
| IA | Intermediate alkalinity |
| TA | Total alkalinity |
| TIC | Total inorganic carbon |
| EP | Equilibrium point |
References
- Alcaraz-González, V.; Fregoso-Sánchez, F.A.; González-Alvarez, V.; Steyer, J.P. Multivariable robust regulation of alkalinities in continuous anaerobic digestion processes: Experimental validation. Processes 2021, 9, 1153. [Google Scholar] [CrossRef]
- Santana Junior, A.E.; Duda, R.M.; de Oliveira, R.A. Improving the energy balance of ethanol industry with methane production from vinasse and molasses in two-stage anaerobic reactors. J. Clean. Prod. 2019, 238, 117577. [Google Scholar] [CrossRef]
- Meegoda, J.N.; Li, B.; Patel, K.; Wang, L.B. A review of the processes, parameters, and optimization of anaerobic digestion. Int. J. Environ. Res. Public Health 2018, 15, 2224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, H.; Zhu, N. Progress in inhibition mechanisms and process control of intermediates and by-products in sewage sludge anaerobic digestion. Renew. Sustain. Energy Rev. 2016, 58, 429–438. [Google Scholar] [CrossRef]
- Molino, A.; Nanna, F.; Ding, Y.; Bikson, B.; Braccio, G. Biomethane production by anaerobic digestion of organic waste. Fuel 2013, 103, 1003–1009. [Google Scholar] [CrossRef]
- Suhartini, S.; Heaven, S.; Banks, C.J. Comparison of mesophilic and thermophilic anaerobic digestion of sugar beet pulp: Performance, dewaterability and foam control. Bioresour. Technol. 2014, 152, 202–211. [Google Scholar] [CrossRef] [Green Version]
- Abbasi, T.; Tauseef, S.M.; Abbasi, S.A. A brief history of anaerobic digestion and “biogas”. In Biogas Energy; Springer Briefs in Environmental Science; Springer: New York, NY, USA, 2012; Volume 2, pp. 11–23. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, J.J.; Creamer, K.S. Inhibition of anaerobic digestion process: A review. Bioresour. Technol. 2008, 99, 4044–4064. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, J.; Wang, X. Effects of alkalinity sources on the stability of anaerobic digestion from food waste. Waste Manag. Res. 2015, 33, 1033–1040. [Google Scholar] [CrossRef]
- Ripley, L.E.; Boyle, W.C.; Converse, J.C. Improved alkalimetric monitoring for anaerobic digestion of high-strength waste. J. Water Pollut. Control Fed. 1986, 58, 406–411. [Google Scholar]
- Tian, Z.; Zhang, Y.; Li, Y.; Chi, Y.; Yang, M. Rapid establishment of thermophilic anaerobic microbial community during the one-step startup of thermophilic anaerobic digestion from a mesophilic digester. Water Res. 2015, 69, 9–19. [Google Scholar] [CrossRef]
- Björnsson, L.; Mattiasson, B.; Henrysson, T. Effects of support material on the pattern of volatile fatty acid accumulation at overload in anaerobic digestion of semi-solid waste. Appl. Microbiol. Biotechnol. 1997, 47, 640–644. [Google Scholar] [CrossRef]
- Piceno-Díaz, E.R.; Ricardez-Sandoval, L.A.; Gutierrez-Limon, M.A.; Méndez-Acosta, H.O.; Puebla, H. Robust nonlinear model predictive control for two-stage anaerobic digesters. Ind. Eng. Chem. Res. 2020, 59, 22559–22572. [Google Scholar] [CrossRef]
- Sun, C.; Guo, L.; Zheng, Y.; Yu, D.; Jin, C.; Zhao, Y.; Yao, Z.; Gao, M.; She, Z. Effect of mixed primary and secondary sludge for two-stage anaerobic digestion (AD). Bioresour. Technol. 2022, 343, 126160. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Ocampo, U.E.; Santiago, S.G.; Vargas, A.; Moreno-Andrade, I. Feedback control strategy for optimizing biohydrogen production from organic solid waste in a discontinuous process. Int. J. Hydrogen Energy 2021, 46, 35831–35839. [Google Scholar] [CrossRef]
- Méndez-Acosta, H.; Campos-Rodríguez, A.; González-Álvarez, V.; García-Sandoval, J.; Snell-Castro, R.; Latrille, E. A hybrid cascade control scheme for the VFA and COD regulation in two-stage anaerobic digestion processes. Bioresour. Technol. 2016, 218, 1195–1202. [Google Scholar] [CrossRef]
- Aguilar-Garnica, E.; Dochain, D.; Alcaraz-González, V.; González-Álvarez, V. A multivariable control scheme in a two-stage anaerobic digestion system described by partial differential equations. J. Process Control 2009, 19, 1324–1332. [Google Scholar] [CrossRef]
- Hernández, M.; Rodríguez, M. Hydrogen production by anaerobic digestion of pig manure: Effect of operating conditions. Renew. Energy 2013, 53, 187–192. [Google Scholar] [CrossRef]
- Schievano, A.; D’Imporzano, G.; Adani, F. Substituting energy crops with organic wastes and agro-industrial residues for biogas production. J. Environ. Manag. 2009, 90, 2537–2541. [Google Scholar] [CrossRef]
- Parawira, W.; Read, J.; Mattiasson, B.; Björnsson, L. Energy production from agricultural residues: High methane yields in pilot-scale two-stage anaerobic digestion. Biomass Bioenergy 2008, 32, 44–50. [Google Scholar] [CrossRef]
- Moosbrugger, R.E.; Wentzel, M.C.; Ekama, G.A.; Marais, G.V. Weak acid/bases and pH control in anaerobic systems—A review. Water SA 1993, 19, 1–10. [Google Scholar]
- Palacios-Ruiz, B.; Méndez-Acosta, H.; Alcaraz-González, V.; González-Álvarez, V.; Pelayo-Ortiz, C. Modelo dinámico para un proceso de digestión anaerobia en dos etapas. In Proceedings of the XXIX Encuentro Nacional de la AMIDIQ, Puerto Vallarta, Jalisco, Mexico, 13–16 May 2008. [Google Scholar]
- Lahav, O.; Morgan, B. Titration methodologies for monitoring of anaerobic digestion in developing countries—A review. J. Chem. Technol. Biotechnol 2004, 79, 1331–1341. [Google Scholar] [CrossRef] [Green Version]
- Barampouti, E.M.P.; Mai, S.T.; Vlyssides, A.G. Dynamic Modeling of the Ratio Volatile Fatty Acids/Bicarbonate Alkalinity in a UASB Reactor for Potato Processing Wastewater Treatment. Environ. Monit. Assess. 2005, 110, 121–128. [Google Scholar] [CrossRef] [PubMed]
- Keshtkar, A.; Meyssami, B.; Abolhamd, G.; Ghaforian, H.; Khalagi Asadi, M. Mathematical modeling of non-ideal mixing continuous flow reactors for anaerobic digestion of cattle manure. Bioresour. Technol. 2003, 87, 113–124. [Google Scholar] [CrossRef]
- Saravanan, V.; Sreekrishnan, T. Modelling anaerobic biofilm reactors—A review. J. Environ. Manag. 2006, 81, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Haag, J.; Vande Wouwer, A.; Queinnec, I. Macroscopic modelling and identification of an anaerobic waste treatment process. Chem. Eng. Sci. 2003, 58, 4307–4316. [Google Scholar] [CrossRef]
- Tomei, M.; Bragugloa, C.; Cento, G.; Mininni, G. Modeling of Anaerobic Digestion of Sludge. Crit. Rev. Environ. Sci. Technol. 2009, 39, 1003–1051. [Google Scholar] [CrossRef]
- Florencio, L.; Field, J.; Van Langerak, A.; Lettinga, G. pH-stability in anaerobic bioreactors treating methanolic wastewaters. Water Sci. Technol. 1996, 33, 177–184. [Google Scholar] [CrossRef]
- Liu, B.Y.; Pfeffer, J.T.; Suidan, M.T. Equilibrium Model of Anaerobic Reactors. Environ. Eng. 1995, 121, 56–65. [Google Scholar] [CrossRef]
- Bastone, D.; Keller, J.; Angelidaki, I.; Kalyuzhnyl, S.; Pavlostathis, S.; Rozzi, A.; Sanders, W.T.M.; Siegrist, H.A. The IWA anaerobic digestion model no. 1 (ADM1). Wat. Sci. Tech. 2002, 45, 65–73. [Google Scholar] [CrossRef]
- Blumensaat, F.; Keller, J. Modelling of two-stage anaerobic digestion using the IWA Anaerobic Digestion Model No. 1 (ADM1). Water Res. 2005, 39, 171–183. [Google Scholar] [CrossRef]
- Bernard, O.; Hadj-Sadok, Z.; Dochain, D.; Genovesi, A.; Steyer, J. Dynamical model development and parameter identification of an anaerobic wastewater treatment process. Biotech. Bioeng. 2001, 75, 424–438. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Bai, X.; Li, Z.; Zhou, X.; Cheng, S.; Sun, J.; Liu, T. Evaluation of artificial neural network models for online monitoring of alkalinity in anaerobic co-digestion system. Biochem. Eng. J. 2018, 140, 85–92. [Google Scholar] [CrossRef]
- Alcaraz-González, V.; Fregoso-Sanchez, F.A.; Mendez-Acosta, H.O.; Gonzalez-Alvarez, V. Robust regulation of alkalinity in highly uncertain continuous anaerobic digestion processes. CLEAN–Soil Air Water 2013, 41, 1157–1164. [Google Scholar] [CrossRef]
- Benyahia, B.; Sari, T.; Cherki, B.; Harmand, J. Bifurcation and stability analysis of a two step model for monitoring anaerobic digestion processes. J. Process Control 2012, 22, 1008–1019. [Google Scholar] [CrossRef] [Green Version]
- Hess, J.; Bernard, O. Design and study of a risk management criterion for an unstable anaerobic wastewater treatment process. J. Process Control 2008, 18, 71–79. [Google Scholar] [CrossRef]
- Shen, S.; Premier, G.C.; Guwy, A.; Dinsdale, R. Bifurcation and stability analysis of an anaerobic digestion model. Nonlinear Dyn. 2007, 48, 391–408. [Google Scholar] [CrossRef]
- Méndez-Acosta, H.; Palacios-Ruiz, B.; Alcaraz-González, V.; González-Álvarez, V.; García-Sandoval, J. A robust control scheme to improve the stability of anaerobic digestion processes. J. Process Control 2010, 20, 375–383. [Google Scholar] [CrossRef]
- Seydel, R. Practical Bifurcation and Stability Analysis. In Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2009; Volume 5. [Google Scholar] [CrossRef]
- Harris, D.C. Quantitative Chemical Analysis; Macmillan: New York, NY, USA, 1995. [Google Scholar]
- Schaum, A.; Alvarez, J.; Garcia-Sandoval, J.P.; Gonzalez-Alvarez, V.M. On the dynamics and control of a class of continuous digesters. J. Process Control 2015, 34, 82–96. [Google Scholar] [CrossRef]


| Total | Only | Only Acidogenic Washout | Without Washout | |||
|---|---|---|---|---|---|---|
| Variable | Washout | Methanogenic | Root 1 | Root 2 | Root 1 | Root 2 |
| Washout | ||||||
| EP1 | EP2 | EP3a | EP3b | EP4a | EP4b | |
| Conditions | ||||||
| 0 | 0 | |||||
| 0 | 0 | |||||
| Solution of: | ||||||
| Solution of: | ||||||
| 0 | 0 | |||||
| with | ||||||
| 0 | 0 | |||||
| Parameter | Value | Parameter | Value |
|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campos-Rodríguez, A.; Zárate-Navarro, M.A.; Aguilar-Garnica, E.; Alcaraz-González, V.; García-Sandoval, J.P. Study of the Behavior of Alkalinities Predicted by the AM2 Model. Water 2022, 14, 1634. https://doi.org/10.3390/w14101634
Campos-Rodríguez A, Zárate-Navarro MA, Aguilar-Garnica E, Alcaraz-González V, García-Sandoval JP. Study of the Behavior of Alkalinities Predicted by the AM2 Model. Water. 2022; 14(10):1634. https://doi.org/10.3390/w14101634
Chicago/Turabian StyleCampos-Rodríguez, Armando, Marco A. Zárate-Navarro, Efrén Aguilar-Garnica, Víctor Alcaraz-González, and Juan Paulo García-Sandoval. 2022. "Study of the Behavior of Alkalinities Predicted by the AM2 Model" Water 14, no. 10: 1634. https://doi.org/10.3390/w14101634






