An Adaptive Surrogate-Assisted Simulation-Optimization Method for Identifying Release History of Groundwater Contaminant Sources
Abstract
:1. Introduction
- Unlike most surrogate-assisted simulation-optimization methods using pre-determined surrogates, an adaptive surrogate technique was proposed to construct the most appropriate surrogate model. The high performance and reliability of the technique were confirmed in this study.
- Detailed comparisons of the proposed and traditional methods were conducted on two representative cases about the inversion of contaminant sources. The results clearly indicated that the proposed method had higher accuracy and shorter computation time than the traditional method.
- A solving framework that is able to apply any evolutionary algorithm and numerical model was presented. The flexibility and feasibility of the framework were verified in our study.
2. Methodology
2.1. Mathematical Description of the Inverse Contaminant Source Identification Problems
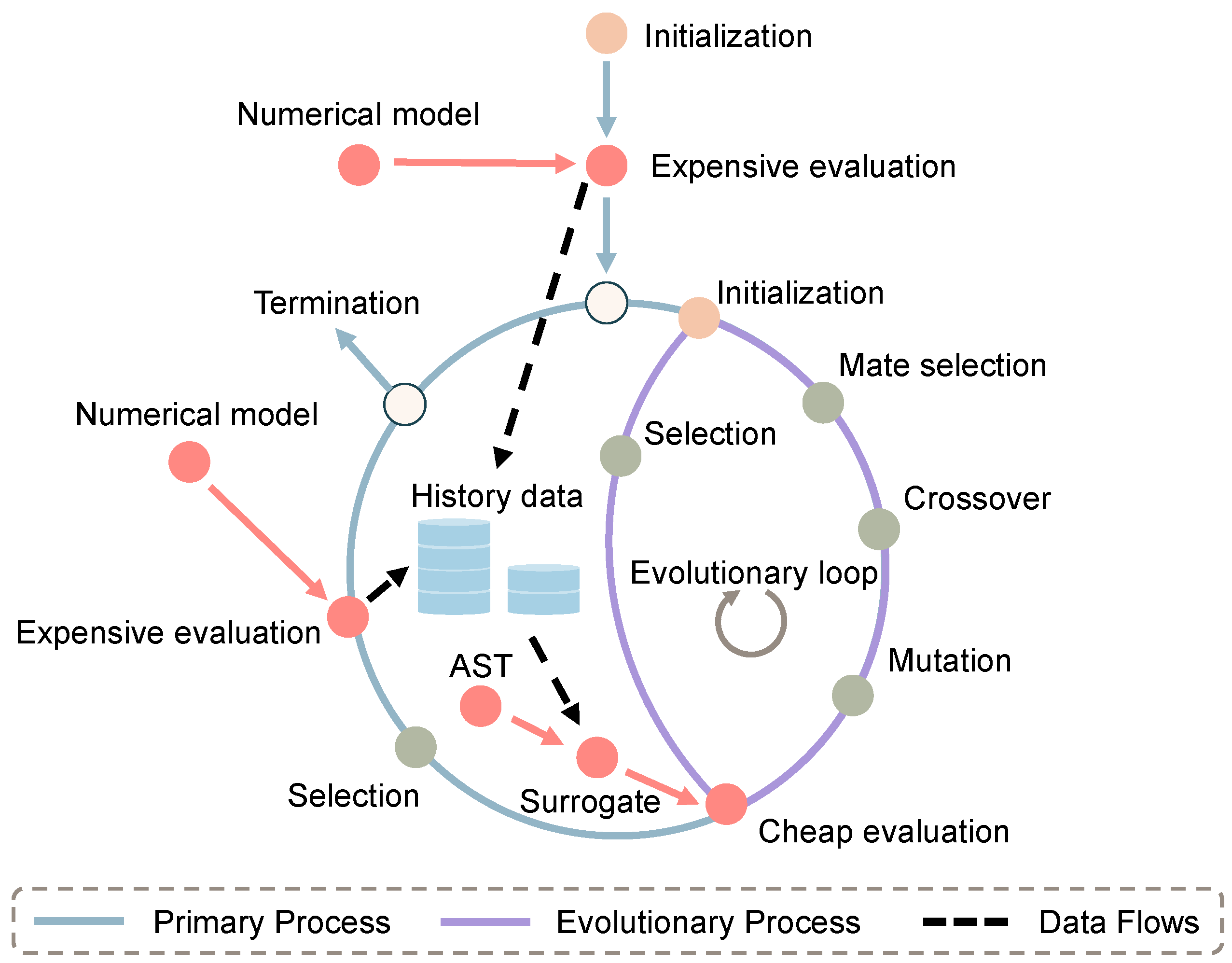
2.2. Proposed Surrogate-Assisted Simulation-Optimization Method
2.3. Simulation Model
2.4. Radial Basis Function
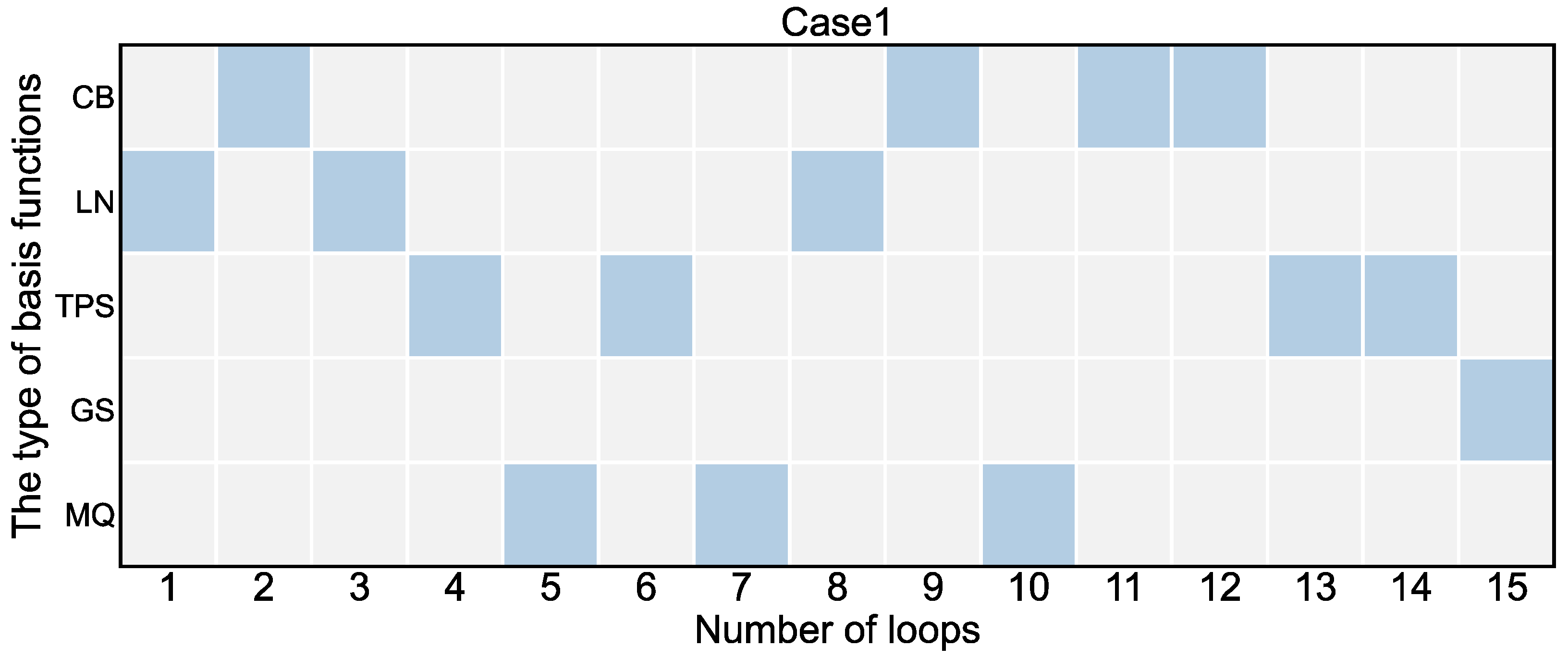
2.5. Adaptive Surrogate Technique
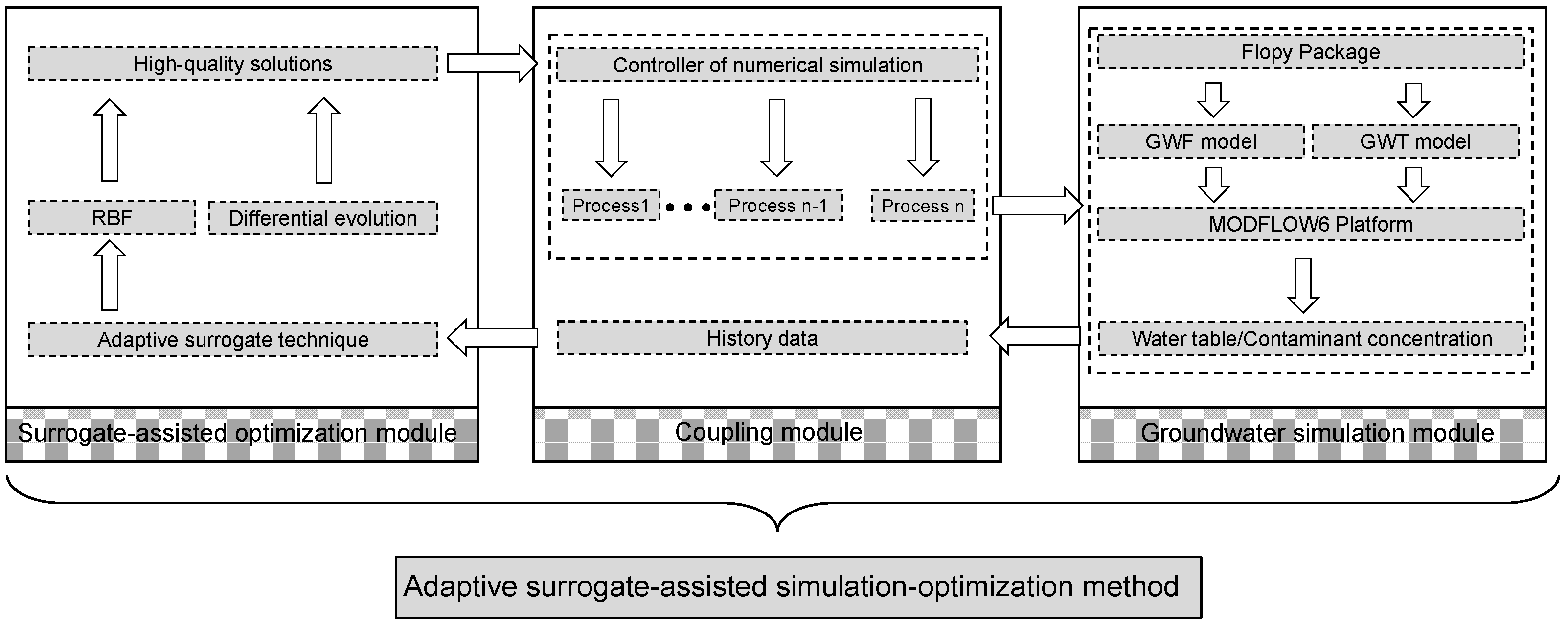
2.6. Procedure Framework of the Proposed Method
- Surrogate-assisted optimization module. This module aims to provide high-quality solutions to be precisely evaluated by simulation. In this paper, differential evolution (DE) is used as the evolutionary algorithm.
- Coupling module, used as an auxiliary module. The function of this module is to link the other two modules, such as invoking a parallel simulation, converting simulation results into response values, representing the performance metric of one solution, and storing history data.
- Groundwater simulation module. This module aims to automatically run the simulation and extract necessary data, including the water table and contaminant concentration.
3. Empirical Study
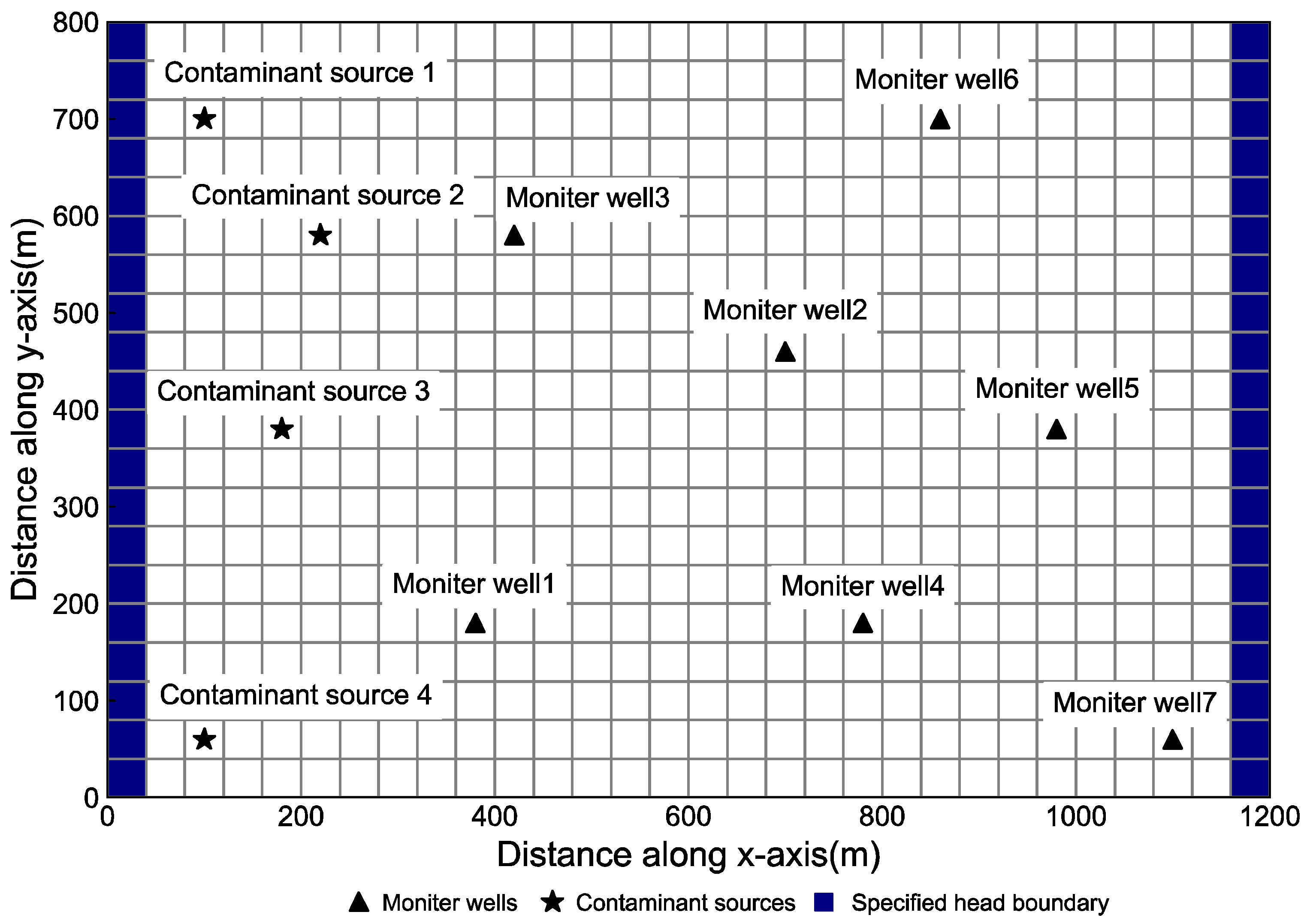
3.1. Experimental Setup
- The size of the initial population in the evolutionary loop was set to 50.
- The maximum number of expensive evaluation FEmax was set to 200 for case 1 and 1000 for case 2.
- For the simulated binary crossover, the pc and ηc were set to 1 and 20, respectively; For the polynomial mutation, the pm and ηm were set to 1/D and 20, respectively.
- For PSO, based on the previous literature, the inertia weight w was set to 0.4.
- The value of k for cross-validation was set to 30.
- The value of Ntop was set to 10, which meant that the rank top 10 of the population based on the surrogate model would be precisely evaluated by the numerical model at the end of the evolutionary loop.
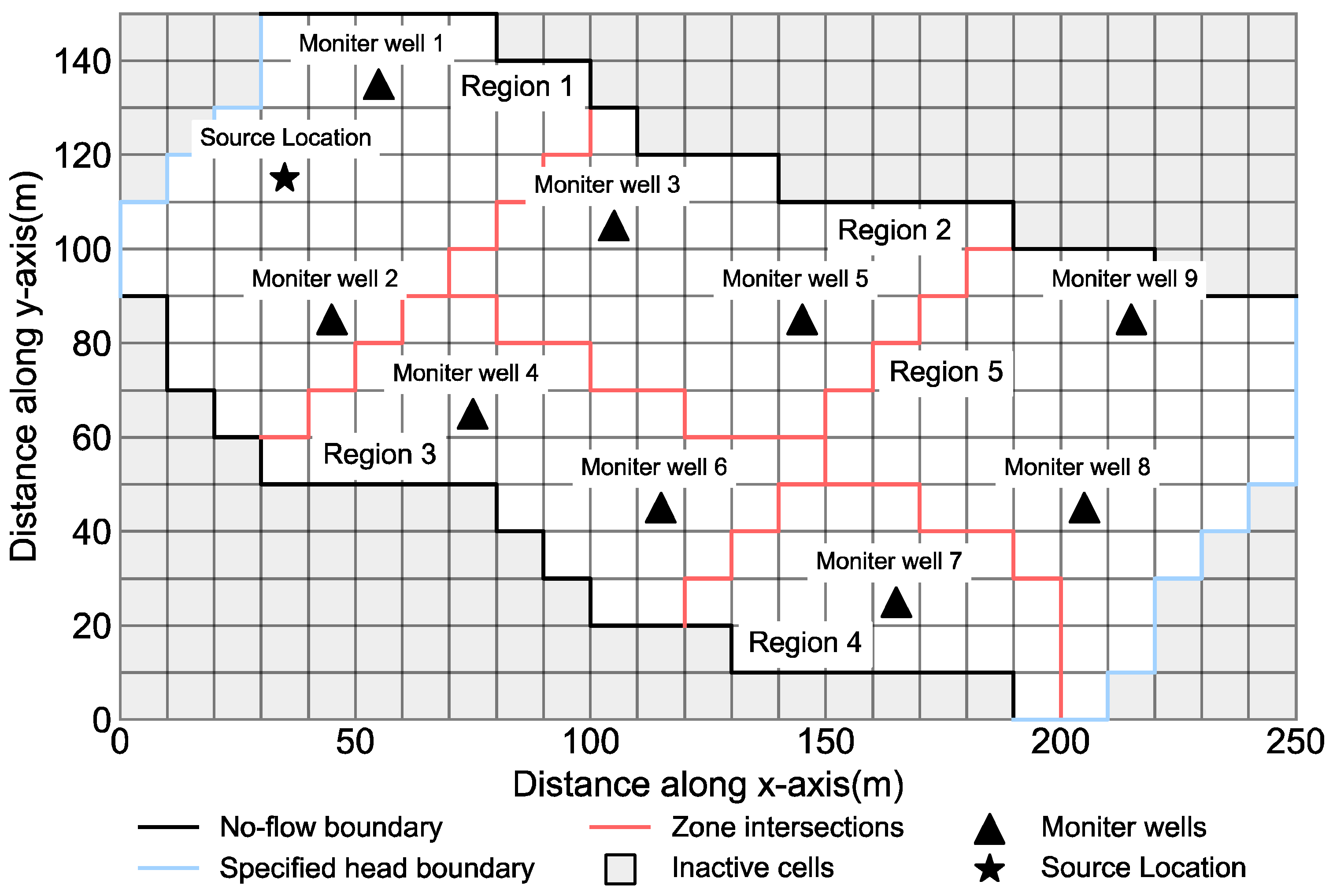
3.2. Case 1: Identification of Release History of a Single Contaminant Source
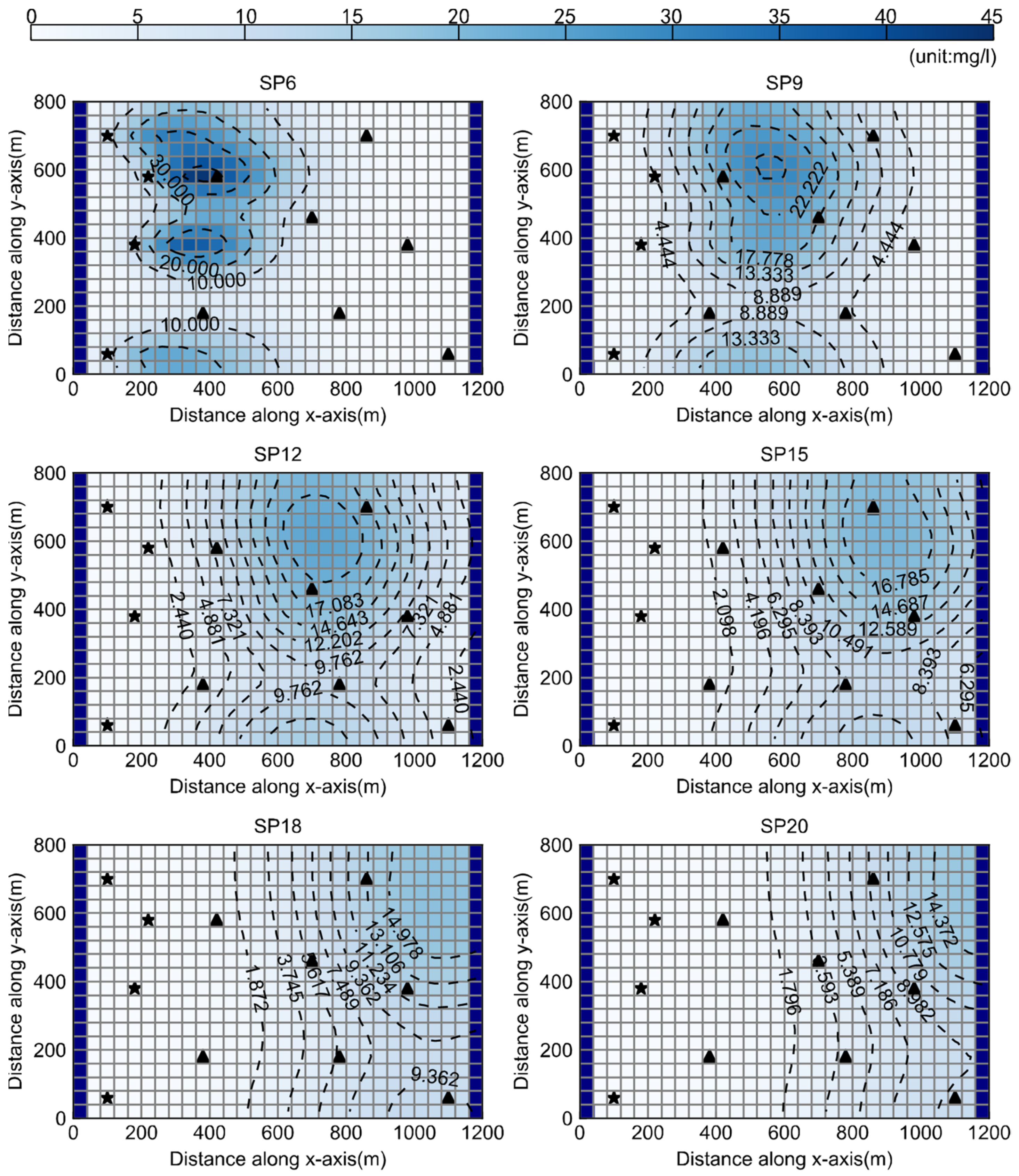
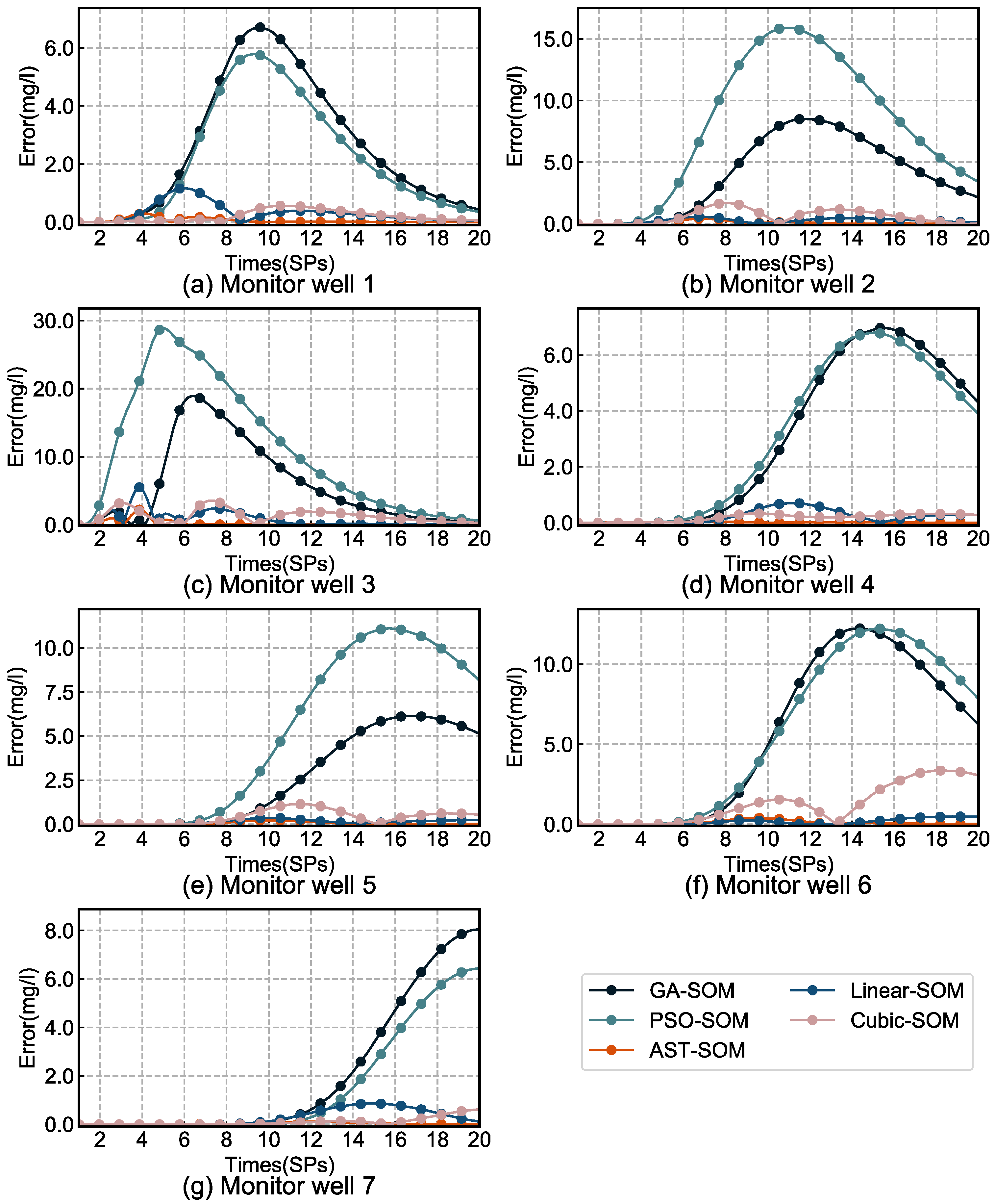
3.3. Case 2: Identification of Release History of Multiple Contaminant Sources
3.4. Additional Discussion
- Under the limited expensive evaluations, the proposed method could significantly improve the accuracy of solving the inverse contaminant source identification problems.
- Under the same solving precision, the proposed method could save about 80% to 90% of the computation.
- All experiments were successfully run on our proposed simulation-optimization framework.
- The feasibility and flexibility of our simulation-optimization framework are confirmed.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Atmadja, J.; Bagtzoglou, A.C. State of the Art Report on Mathematical Methods for Groundwater Pollution Source Identification. Environ. Forensics 2001, 2, 205–214. [Google Scholar] [CrossRef]
- Singh, R.M.; Datta, B. Identification of Groundwater Pollution Sources Using GA-Based Linked Simulation Optimization Model. J. Hydrol. Eng. 2006, 11, 101–109. [Google Scholar] [CrossRef]
- Sreekanth, J.; Datta, B. Review: Simulation-Optimization Models for the Management and Monitoring of Coastal Aquifers. Hydrogeol. J. 2015, 23, 1155–1166. [Google Scholar] [CrossRef]
- Amaran, S.; Sahinidis, N.V.; Sharda, B.; Bury, S.J. Simulation Optimization: A Review of Algorithms and Applications. Ann. Oper. Res. 2016, 240, 351–380. [Google Scholar] [CrossRef] [Green Version]
- Harbaugh, A.W. MODFLOW-2005, the US Geological Survey Modular Groundwater Model-the Groundwater Flow Process; Center for Integrated Data Analytics Wisconsin Science Center: Madison, WI, USA, 2005. [Google Scholar]
- Zheng, C.; Wang, P. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection; Engineer Research and Development Center: Vicksburg, MS, USA, 1999. [Google Scholar]
- Hughes, J.D.; Langevin, C.D.; Banta, E.R. Documentation for the MODFLOW 6 Framework; US Geological Survey: Reston, VA, USA, 2017. [CrossRef] [Green Version]
- Eissa, M.A.; de Dreuzy, J.-R.; Parker, B. Integrative Management of Saltwater Intrusion in Poorly-Constrained Semi-Arid Coastal Aquifer at Ras El-Hekma, Northwestern Coast, Egypt. Groundw. Sustain. Dev. 2018, 6, 57–70. [Google Scholar] [CrossRef] [Green Version]
- Mualem, Y.; Bear, J. The Shape of the Interface in Steady Flow in a Stratified Aquifer. Water Resour. Res. 1974, 10, 1207–1215. [Google Scholar] [CrossRef]
- Mahinthakumar, G.K.; Sayeed, M. Hybrid Genetic Algorithm—Local Search Methods for Solving Groundwater Source Identification Inverse Problems. J. Water Resour. Plan. Manage.-ASCE 2005, 131, 45–57. [Google Scholar] [CrossRef]
- Chen, M.; Izady, A.; Abdalla, O.A. An Efficient Surrogate-Based Simulation-Optimization Method for Calibrating a Regional MODFLOW Model. J. Hydrol. 2017, 544, 591–603. [Google Scholar] [CrossRef]
- Hou, Z.; Lu, W. Comparative Study of Surrogate Models for Groundwater Contamination Source Identification at DNAPL-Contaminated Sites. Hydrogeol. J. 2018, 26, 923–932. [Google Scholar] [CrossRef]
- Han, Z.; Lu, W.; Fan, Y.; Lin, J.; Yuan, Q. A Surrogate-Based Simulation-Optimization Approach for Coastal Aquifer Management. Water Supply 2020, 20, 3404–3418. [Google Scholar] [CrossRef]
- Asher, M.J.; Croke, B.F.W.; Jakeman, A.J.; Peeters, L.J.M. A Review of Surrogate Models and Their Application to Groundwater Modeling. Water Resour. Res. 2015, 51, 5957–5973. [Google Scholar] [CrossRef]
- Razavi, S.; Tolson, B.A.; Burn, D.H. Review of Surrogate Modeling in Water Resources. Water Resour. Res. 2012, 48, W07401. [Google Scholar] [CrossRef]
- Jin, Y. Surrogate-Assisted Evolutionary Computation: Recent Advances and Future Challenges. Swarm Evol. Comput. 2011, 1, 61–70. [Google Scholar] [CrossRef]
- Zhao, Y.; Lu, W.; An, Y. Surrogate Model-Based Simulation-Optimization Approach for Groundwater Source Identification Problems. Environ. Forensics 2015, 16, 296–303. [Google Scholar] [CrossRef]
- Li, J.; Lu, W.; Wang, H.; Fan, Y.; Chang, Z. Groundwater Contamination Source Identification Based on a Hybrid Particle Swarm Optimization-Extreme Learning Machine. J. Hydrol. 2020, 584, 124657. [Google Scholar] [CrossRef]
- Song, Z.; Wang, H.; He, C.; Jin, Y. A Kriging-Assisted Two-Archive Evolutionary Algorithm for Expensive Many-Objective Optimization. IEEE Trans. Evol. Comput. 2021, 25, 1013–1027. [Google Scholar] [CrossRef]
- Kang, F.; Xu, Q.; Li, J. Slope Reliability Analysis Using Surrogate Models via New Support Vector Machines with Swarm Intelligence. Appl. Math. Model. 2016, 40, 6105–6120. [Google Scholar] [CrossRef]
- Huh, J.; Haldar, A.; Doan, N.S.; Dang, P.V.; Mac, V.H. Efficient Approach for Calibration of Load and Resistance Factors in the Limit State Design of a Breakwater Foundation. Ocean Eng. 2022, 251, 111170. [Google Scholar] [CrossRef]
- Garcia Kerdan, I.; Morillon Galvez, D. Artificial Neural Network Structure Optimisation for Accurately Prediction of Exergy, Comfort and Life Cycle Cost Performance of a Low Energy Building. Appl. Energy 2020, 280, 115862. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, K.; Xue, X.; Zhang, L.; Yao, C.; Wang, J.; Yao, J. A Radial Basis Function Surrogate Model Assisted Evolutionary Algorithm for High-Dimensional Expensive Optimization Problems. Appl. Soft. Comput. 2022, 116, 108353. [Google Scholar] [CrossRef]
- Luo, J.; Lu, W. Comparison of Surrogate Models with Different Methods in Groundwater Remediation Process. J. Earth Syst. Sci. 2014, 123, 1579–1589. [Google Scholar] [CrossRef]
- Majumder, P.; Eldho, T.I. Artificial Neural Network and Grey Wolf Optimizer Based Surrogate Simulation-Optimization Model for Groundwater Remediation. Water Resour. Manag. 2020, 34, 763–783. [Google Scholar] [CrossRef]
- Vali, M.; Zare, M.; Razavi, S. Automatic Clustering-Based Surrogate-Assisted Genetic Algorithm for Groundwater Remediation System Design. J. Hydrol. 2021, 598, 125752. [Google Scholar] [CrossRef]
- Yin, J.; Tsai, F.T.-C. Saltwater Scavenging Optimization under Surrogate Uncertainty for a Multi-Aquifer System. J. Hydrol. 2018, 565, 698–710. [Google Scholar] [CrossRef]
- Fen, C.-S.; Chan, C.; Cheng, H.-C. Assessing a Response Surface-Based Optimization Approach for Soil Vapor Extraction System Design. J. Water Resour. Plan. Manag.-ASCE 2009, 135, 198–207. [Google Scholar] [CrossRef]
- Guo, J.; Lu, W.; Yang, Q.; Miao, T. The Application of 0-1 Mixed Integer Nonlinear Programming Optimization Model Based on a Surrogate Model to Identify the Groundwater Pollution Source. J. Contam. Hydrol. 2019, 220, 18–25. [Google Scholar] [CrossRef]
- Khu, S.T.; Werner, M.G.F. Reduction of Monte-Carlo Simulation Runs for Uncertainty Estimation in Hydrological Modelling. Hydrol. Earth Syst. Sci. 2003, 7, 680–692. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Srinivasan, R.; Van Liew, M. Approximating Swat Model Using Artificial Neural Network and Support Vector Machine. J. Am. Water Resour. Assoc. 2009, 45, 460–474. [Google Scholar] [CrossRef]
- Zhao, Y.; Qu, R.; Xing, Z.; Lu, W. Identifying Groundwater Contaminant Sources Based on a KELM Surrogate Model Together with Four Heuristic Optimization Algorithms. Adv. Water Resour. 2020, 138, 103540. [Google Scholar] [CrossRef]
- Xing, Z.; Qu, R.; Zhao, Y.; Fu, Q.; Ji, Y.; Lu, W. Identifying the Release History of a Groundwater Contaminant Source Based on an Ensemble Surrogate Model. J. Hydrol. 2019, 572, 501–516. [Google Scholar] [CrossRef]
- Ouyang, Q.; Lu, W.; Miao, T.; Deng, W.; Jiang, C.; Luo, J. Application of Ensemble Surrogates and Adaptive Sequential Sampling to Optimal Groundwater Remediation Design at DNAPLs-Contaminated Sites. J. Contam. Hydrol. 2017, 207, 31–38. [Google Scholar] [CrossRef] [PubMed]
- Müller, J.; Shoemaker, C.A. Influence of Ensemble Surrogate Models and Sampling Strategy on the Solution Quality of Algorithms for Computationally Expensive Black-Box Global Optimization Problems. J. Glob. Optim. 2014, 60, 123–144. [Google Scholar] [CrossRef]
- Sreekanth, J.; Datta, B. Coupled Simulation-Optimization Model for Coastal Aquifer Management Using Genetic Programming-Based Ensemble Surrogate Models and Multiple-Realization Optimization: Ensemble surrogates for optimal coastal aquifers. Water Resour. Res. 2011, 47, W04516. [Google Scholar] [CrossRef] [Green Version]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Forrester, A.I.; Keane, A.J. Recent Advances in Surrogate-Based Optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Stork, J.; Friese, M.; Zaefferer, M.; Bartz-Beielstein, T.; Fischbach, A.; Breiderhoff, B.; Naujoks, B.; Tušar, T. Open Issues in Surrogate-Assisted Optimization. In High-Performance Simulation-Based Optimization; Springer: Berlin/Heidelberg, Germany, 2020; pp. 225–244. [Google Scholar]
- Langevin, C.D.; Hughes, J.D.; Banta, E.R.; Niswonger, R.G.; Panday, S.; Provost, A.M. Documentation for the MODFLOW 6 Groundwater Flow Model; Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2017; Volume 6-A55.
- Langevin, C.D.; Provost, A.M.; Panday, S.; Hughes, J.D. Documentation for the MODFLOW 6 Groundwater Transport Model; Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2022; Volume 6-A61, p. 56.
- Gutmann, H.-M. A Radial Basis Function Method for Global Optimization. J. Glob. Optim. 2001, 19, 201–227. [Google Scholar] [CrossRef]
- Ayvaz, M.T. A Linked Simulation–Optimization Model for Solving the Unknown Groundwater Pollution Source Identification Problems. J. Contam. Hydrol. 2010, 117, 46–59. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volumes 1–6, pp. 1942–1948. [Google Scholar]




| Abbreviation of Methods | Usage of Surrogate | Usage of Evolutionary Algorithm |
|---|---|---|
| AST-SOM | All RBFs + AST | Differential Evolution Algorithm |
| Cubic-SOM | Cubic RBF | Differential Evolution Algorithm |
| Linear-SOM | Linear RBF | Differential Evolution Algorithm |
| GA-SOM | / | Genetic Algorithm |
| PSO-SOM | / | Particle Swarm Optimization |
| Parameters | Values |
|---|---|
| Effective porosity, θ | 0.25 |
| Longitudinal dispersity, αL (m) | 40 |
| Transverse dispersity, αT (m) | 5 |
| Saturated thickness, b (m) | 10 |
| Storage coefficient, Ss | 0.0001 |
| Locations | Region 1 | Region 2 | Region 3 | Region 4 | Region 5 |
|---|---|---|---|---|---|
| Values (m/day) | 18 | 24 | 26 | 12 | 20 |
| Release fluxes (kg/day) | SP1 | SP2 | SP3 | SP4 | SP5 |
| 5.00 | 1.10 | 1.50 | 2.60 | 7.30 |
| Algorithm | Mean Value | Best Value | Median Value | Deviation |
|---|---|---|---|---|
| AST-SOM | 0.000 | 0.000 | 0.000 | 0.000 |
| Cubic-SOM | 49.762 | 36.725 | 49.105 | 12.225 |
| Linear-SOM | 36.092 | 23.271 | 34.274 | 14.745 |
| GA-SOM | 593.499 | 360.631 | 562.468 | 325.479 |
| PSO-SOM | 632.572 | 486.199 | 654.167 | 286.619 |
| Methods | Optimization Result (Unit: kg/day) | Objective Value | ||||
|---|---|---|---|---|---|---|
| SP1 (5.00) | SP2 (1.10) | SP3 (1.50) | SP4 (2.60) | SP5 (7.30) | ||
| AST-SOM | 5.00 (0.0%) | 1.10 (0.0%) | 1.50 (0.0%) | 2.60 (0.0%) | 7.30 (0.0%) | 0.000 |
| Cubic-SOM | 5.406 (8.1%) | 0.500 (54.5%) | 2.052 (36.9%) | 1.809 (30.4%) | 7.733 (5.9%) | 49.105 |
| Linear-SOM | 4.773 (4.5%) | 1.137 (3.4%) | 1.778 (18.5%) | 2.965 (14.1%) | 6.869 (5.9%) | 34.274 |
| GA-SOM | 3.878 (22.4%) | 2.611 (137.4%) | 2.525 (68.3%) | 3.425 (31.7%) | 5.395 (26.1%) | 562.468 |
| PSO-SOM | 3.733 (25.3%) | 1.015 (7.7%) | 1.030 (33.2%) | 6.700 (157.7%) | 5.225 (28.4%) | 654.167 |
| Parameters | Values |
|---|---|
| Effective porosity, θ | 0.25 |
| Longitudinal dispersity, αL (m) | 40 |
| Transverse dispersity, αT (m) | 15 |
| Saturated thickness, b (m) | 30 |
| Storage coefficient, Ss | 0.0001 |
| Sources | Release Fluxes (kg/day) | ||||
|---|---|---|---|---|---|
| SP1 | SP2 | SP3 | SP4 | SP5 | |
| S1 | 67.00 | 0.00 | 22.00 | 51.00 | 14.00 |
| S2 | 21.00 | 82.00 | 0.00 | 50.00 | 32.00 |
| S3 | 14.00 | 0.00 | 100.00 | 33.00 | 25.00 |
| S4 | 62.00 | 25.00 | 0.00 | 13.00 | 24.00 |
| Algorithm | Mean Value | Best Value | Median Value | Deviation |
|---|---|---|---|---|
| AST-SOM | 9.741 | 7.381 | 10.730 | 5.842 |
| Cubic-SOM | 67.594 | 56.049 | 65.308 | 17.732 |
| Linear-SOM | 150.949 | 133.084 | 137.311 | 15.407 |
| GA-SOM | 8707.862 | 4457.061 | 8136.775 | 4339.845 |
| PSO-SOM | 10,657.852 | 6658.126 | 9955.026 | 4892.449 |
| Algorithm | AST-SOM | Cubic-SOM | Linear-SOM | GA-SOM | PSO-SOM |
|---|---|---|---|---|---|
| CPU time (minutes) | 392.77 | 324.96 | 320.85 | 231.52 | 225.68 |
| Algorithm | Response Value | Times of Expensive Evaluation | CPU Time |
|---|---|---|---|
| GA | 8.074 | 13,250 | 2891.47 min (48.19 h) |
| PSO | 7.988 | 14,650 | 3198.67 min (53.31 h) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, M.; Xu, J.; Hu, P.; Lu, Q.; Xu, P.; Chen, H.; Wang, L. An Adaptive Surrogate-Assisted Simulation-Optimization Method for Identifying Release History of Groundwater Contaminant Sources. Water 2022, 14, 1659. https://doi.org/10.3390/w14101659
Wu M, Xu J, Hu P, Lu Q, Xu P, Chen H, Wang L. An Adaptive Surrogate-Assisted Simulation-Optimization Method for Identifying Release History of Groundwater Contaminant Sources. Water. 2022; 14(10):1659. https://doi.org/10.3390/w14101659
Chicago/Turabian StyleWu, Mengtian, Jin Xu, Pengjie Hu, Qianyi Lu, Pengcheng Xu, Han Chen, and Lingling Wang. 2022. "An Adaptive Surrogate-Assisted Simulation-Optimization Method for Identifying Release History of Groundwater Contaminant Sources" Water 14, no. 10: 1659. https://doi.org/10.3390/w14101659
APA StyleWu, M., Xu, J., Hu, P., Lu, Q., Xu, P., Chen, H., & Wang, L. (2022). An Adaptive Surrogate-Assisted Simulation-Optimization Method for Identifying Release History of Groundwater Contaminant Sources. Water, 14(10), 1659. https://doi.org/10.3390/w14101659





