A GPU-Based δ-Plus-SPH Model for Non-Newtonian Multiphase Flows
Abstract
:1. Introduction
2. Governing Equations
3. Multiphase δ-Plus-SPH Model
3.1. The Basics of SPH
3.2. SPH Description of Governing Equations
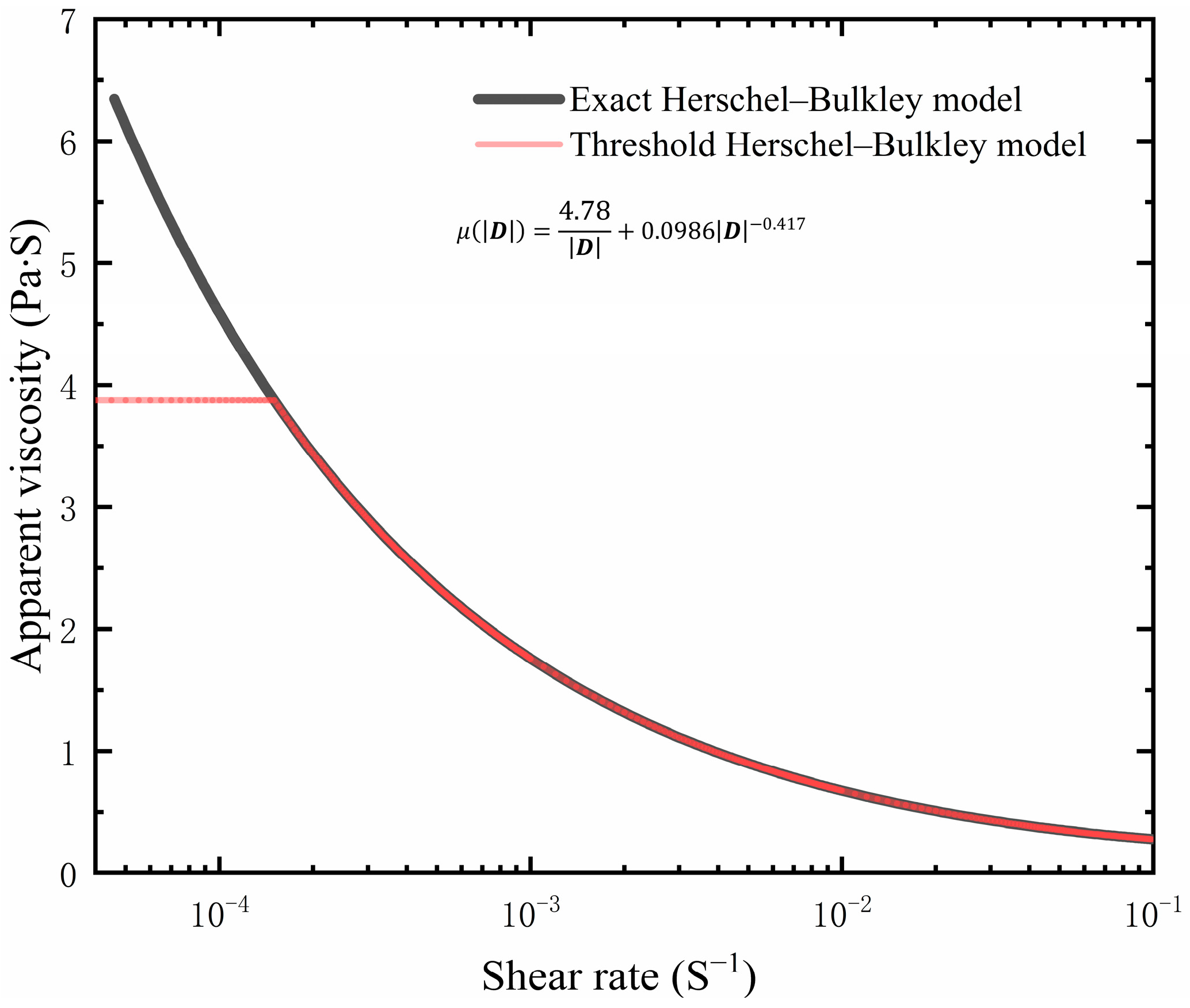
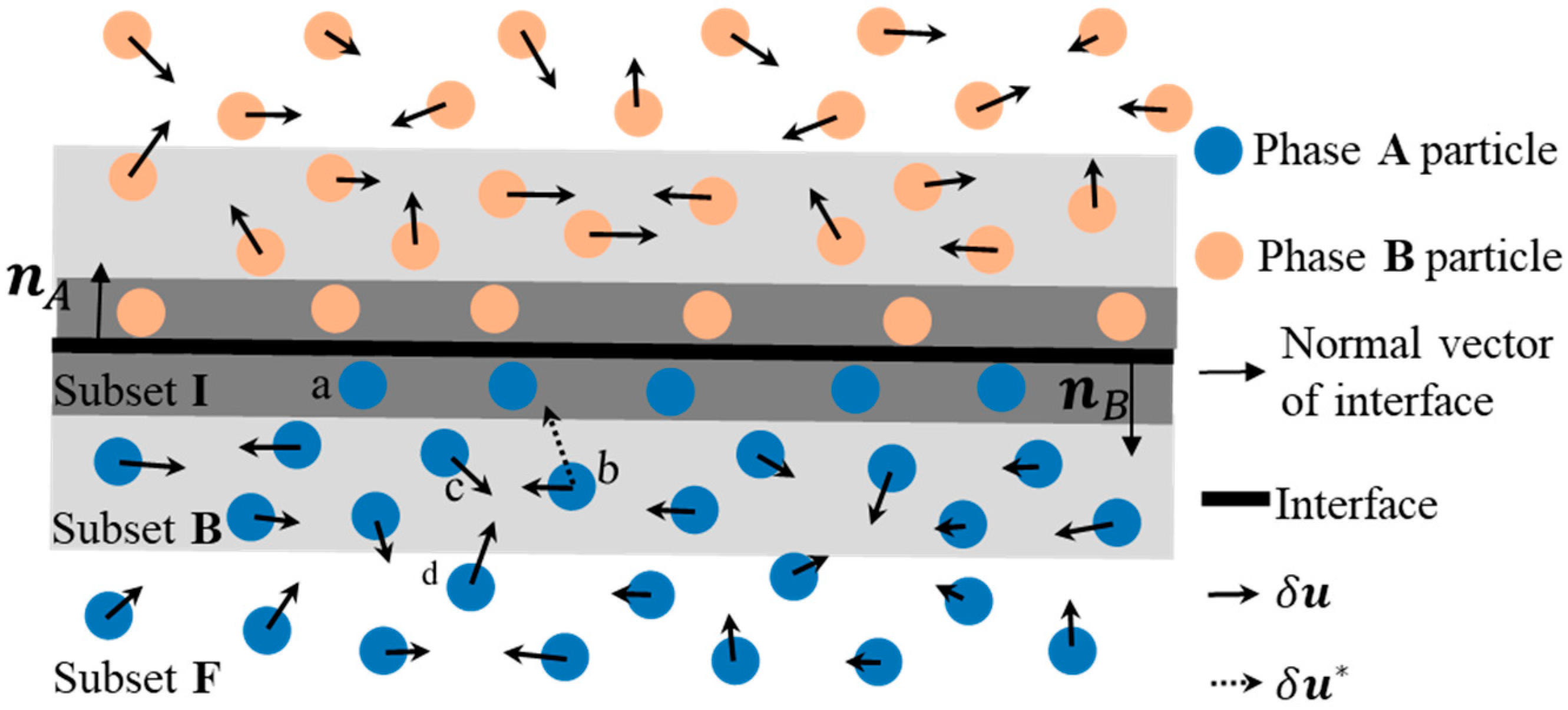
3.3. Particle Shifting Velocity
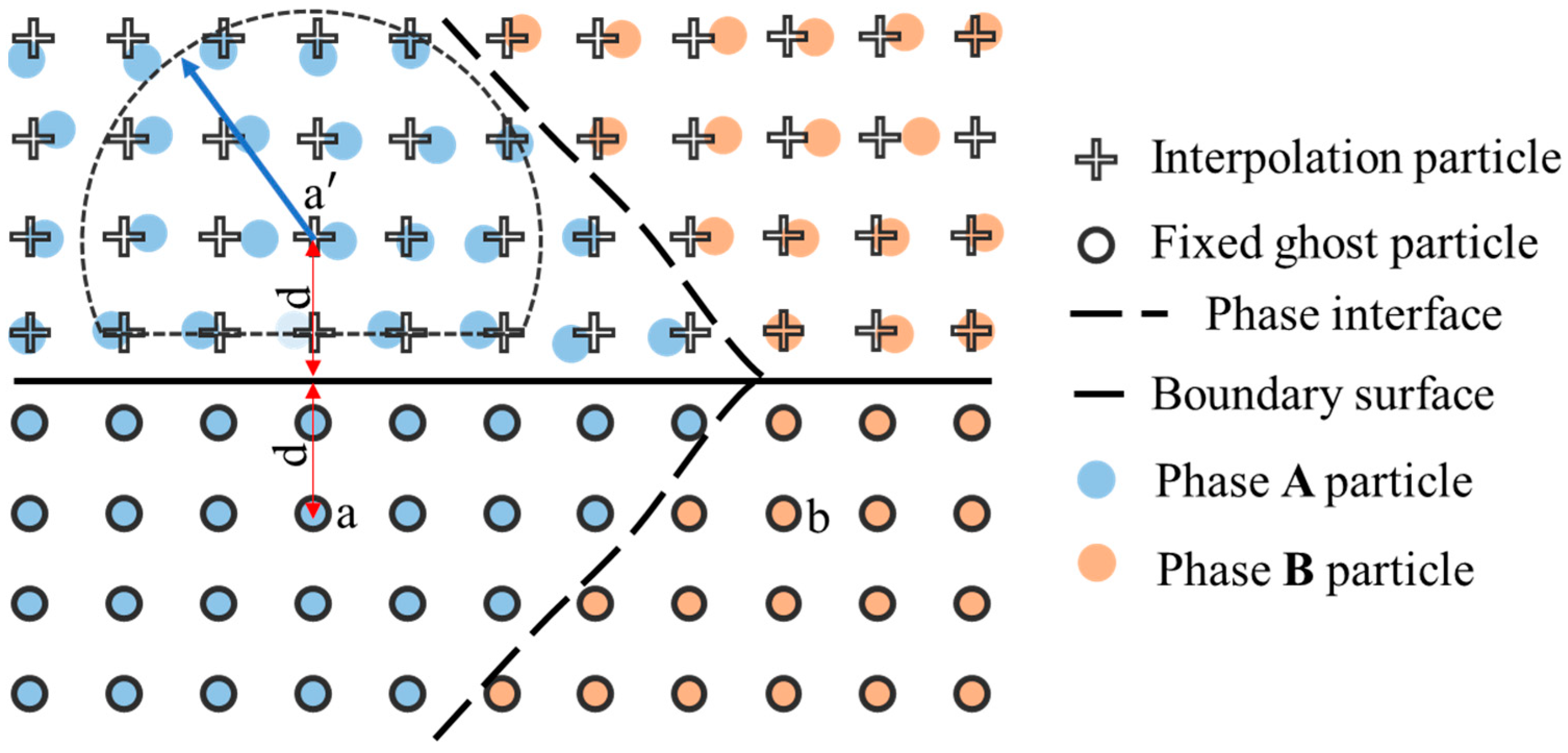
3.4. Boundary Condition
3.5. Time-Step Scheme
4. GPU Implementation
5. Numerical Results
5.1. Static Tank
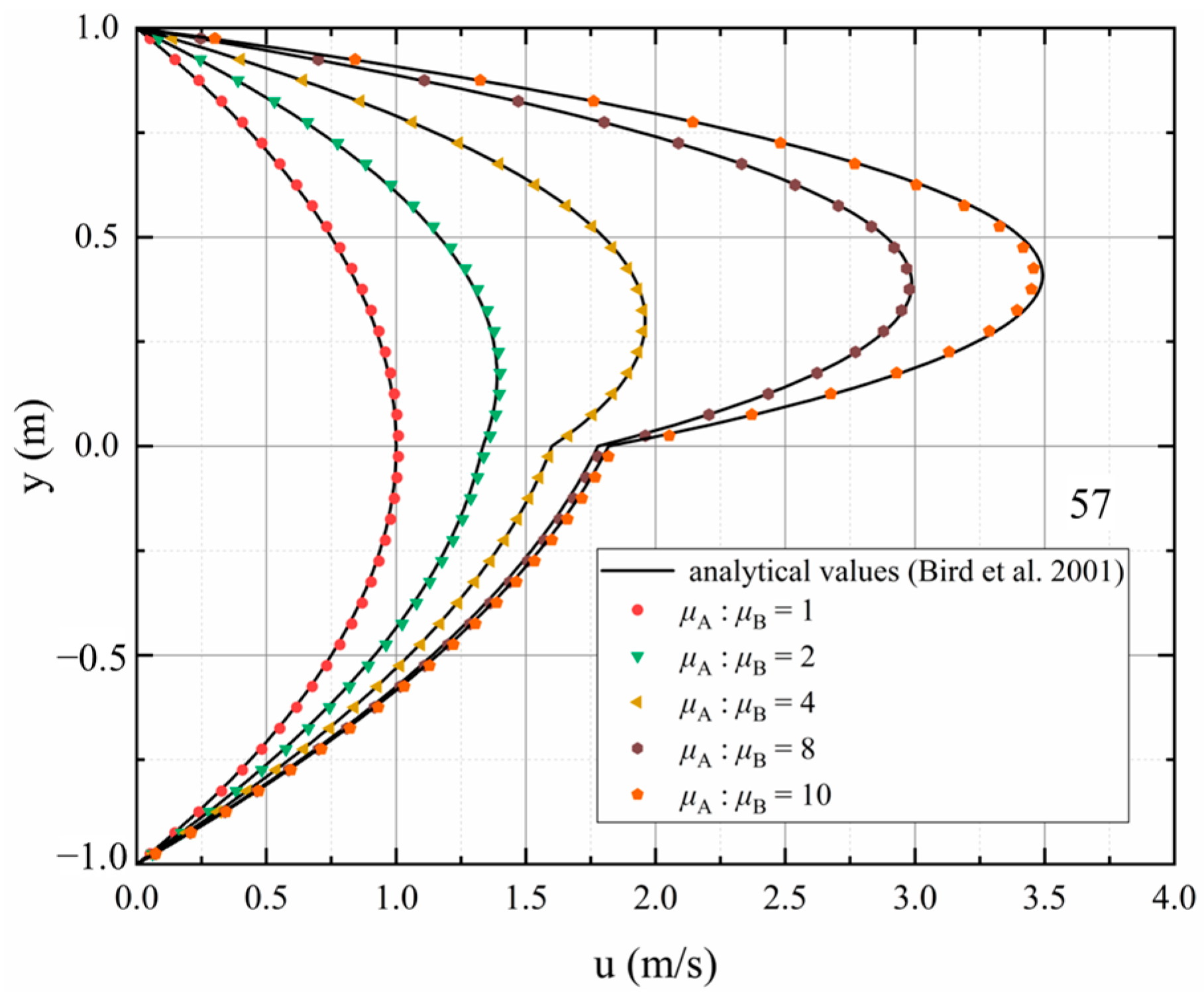
5.2. Two-Phase Poiseuille Flow
5.3. Submarine Debris Flow
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ouda, M.; Toorman, E.A. Development of a new multiphase sediment transport model for free surface flows. Int. J. Multiph. Flow 2019, 117, 81–102. [Google Scholar] [CrossRef]
- Ratkovich, N.; Majumder, S.K.; Bentzen, T.R. Empirical correlations and CFD simulations of vertical two-phase gas-liquid (Newtonian and non-Newtonian) slug flow compared against experimental data of void fraction. Chem. Eng. Res. Des. 2013, 91, 988–998. [Google Scholar] [CrossRef]
- Biscarini, C. Computational fluid dynamics modelling of landslide generated water waves. Landslides 2010, 7, 117–124. [Google Scholar] [CrossRef]
- Hao, Y.; Prosperetti, A. A numerical method for three-dimensional gas-liquid flow computations. J. Comput. Phys. 2004, 196, 126–144. [Google Scholar] [CrossRef]
- Dias, F.; Dutykh, D.; Ghidaglia, J.M. A two-fluid model for violent aerated flows. Comput. Fluids 2010, 39, 283–293. [Google Scholar] [CrossRef] [Green Version]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Gu, H.B.; Causon, D.M.; Mingham, C.G.; Qian, L. Development of a free surface flow solver for the simulation of wave/body interactions. Eur. J. Mech. B Fluids 2013, 38, 1–17. [Google Scholar] [CrossRef]
- Yang, J.; Jeong, D.; Kim, J. A fast and practical adaptive finite difference method for the conservative Allen–Cahn model in two-phase flow system. Int. J. Multiph. Flow 2021, 137, 103561. [Google Scholar] [CrossRef]
- Garoosi, F.; Hooman, K. Numerical simulation of multiphase flows using an enhanced Volume-of-Fluid (VOF) method. Int. J. Mech. Sci. 2022, 215, 106956. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Hu, X.Y.; Adams, N.A. A multi-phase SPH method for macroscopic and mesoscopic flows. J. Comput. Phys. 2006, 213, 844–861. [Google Scholar] [CrossRef]
- Hammani, I.; Marrone, S.; Colagrossi, A.; Oger, G.; Le Touzé, D. Detailed study on the extension of the δ-SPH model to multi-phase flow. Comput. Methods Appl. Mech. Eng. 2020, 368, 113189. [Google Scholar] [CrossRef]
- Grenier, N.; Antuono, M.; Colagrossi, A.; Le Touzé, D.; Alessandrini, B. An Hamiltonian interface SPH formulation for multi-fluid and free surface flows. J. Comput. Phys. 2009, 228, 8380–8393. [Google Scholar] [CrossRef]
- Chen, Z.; Zong, Z.; Liu, M.B.; Zou, L.; Li, H.T.; Shu, C. An SPH model for multiphase flows with complex interfaces and large density differences. J. Comput. Phys. 2015, 283, 169–188. [Google Scholar] [CrossRef]
- Zainali, A.; Tofighi, N.; Shadloo, M.S.; Yildiz, M. Numerical investigation of Newtonian and non-Newtonian multiphase flows using ISPH method. Comput. Methods Appl. Mech. Eng. 2013, 254, 99–113. [Google Scholar] [CrossRef]
- Xenakis, A.M.; Lind, S.J.; Stansby, P.K.; Rogers, B.D. An incompressible smoothed particle hydrodynamics scheme for Newtonian/non-Newtonian multiphase flows including semi-analytical solutions for two-phase inelastic Poiseuille flows. Int. J. Numer. Methods Fluids 2020, 92, 703–726. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S.; Molteni, D. Free-surface flows solved by means of SPH schemes with numerical diffusive terms. Comput. Phys. Commun. 2010, 181, 532–549. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical diffusive terms in weakly-compressible SPH schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Antuono, M.; Bouscasse, B.; Colagrossi, A.; Marrone, S. A measure of spatial disorder in particle methods. Comput. Phys. Commun. 2014, 185, 2609–2621. [Google Scholar] [CrossRef]
- Wang, P.P.; Meng, Z.F.; Zhang, A.M.; Ming, F.R.; Sun, P.N. Improved particle shifting technology and optimized free-surface detection method for free-surface flows in smoothed particle hydrodynamics. Comput. Methods Appl. Mech. Eng. 2019, 357, 112580. [Google Scholar] [CrossRef]
- Sun, P.N.; Colagrossi, A.; Marrone, S.; Zhang, A.M. The δplus-SPH model: Simple procedures for a further improvement of the SPH scheme. Comput. Methods Appl. Mech. Eng. 2017, 315, 25–49. [Google Scholar] [CrossRef]
- Sun, P.N.; Colagrossi, A.; Marrone, S.; Antuono, M.; Zhang, A.M. A consistent approach to particle shifting in the δ-Plus-SPH model. Comput. Methods Appl. Mech. Eng. 2019, 348, 912–934. [Google Scholar] [CrossRef]
- Wang, Z.B.; Chen, R.; Wang, H.; Liao, Q.; Zhu, X.; Li, S.Z. An overview of smoothed particle hydrodynamics for simulating multiphase flow. Appl. Math. Model. 2016, 40, 9625–9655. [Google Scholar] [CrossRef]
- Song, Y.; Huang, D.; Zeng, B. GPU-based parallel computation for discontinuous deformation analysis (DDA) method and its application to modelling earthquake-induced landslide. Comput. Geotech. 2017, 86, 80–94. [Google Scholar] [CrossRef]
- Zhang, A.; Sun, P.; Ming, F. An SPH modeling of bubble rising and coalescing in three dimensions. Comput. Methods Appl. Mech. Eng. 2015, 294, 189–209. [Google Scholar] [CrossRef]
- Wu, Y.; Tian, L.; Rubinato, M.; Gu, S.; Yu, T.; Xu, Z.; Cao, P.; Wang, X.; Zhao, Q. A new parallel framework of SPH-SWE for dam break simulation based on OpenMP. Water 2020, 50, 1395. [Google Scholar] [CrossRef]
- Oger, G.; Le Touzé, D.; Guibert, D.; De Leffe, M.; Biddiscombe, J.; Soumagne, J.; Piccinali, J.G. On distributed memory MPI-based parallelization of SPH codes in massive HPC context. Comput. Phys. Commun. 2016, 200, 1–14. [Google Scholar] [CrossRef]
- Cui, X.; Habashi, W.G.; Casseau, V. MPI Parallelisation of 3D Multiphase Smoothed Particle Hydrodynamics. Int. J. Comut. Fluid Dyn. 2020, 34, 610–621. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Rakhsha, M.; Hu, W.; Negrut, D. A consistent multiphase flow model with a generalized particle shifting scheme resolved via incompressible SPH. J. Comput. Phys. 2022, 458, 111079. [Google Scholar] [CrossRef]
- Xu, R.; Stansby, P.; Laurence, D. Accuracy and stability in incompressible SPH (ISPH) based on the projection method and a new approach. J. Comput. Phys. 2009, 228, 6703–6725. [Google Scholar] [CrossRef]
- Lind, S.J.; Xu, R.; Stansby, P.K.; Rogers, B.D. Incompressible smoothed particle hydrodynamics for free-surface flows: A generalised diffusion-based algorithm for stability and validations for impulsive flows and propagating waves. J. Comput. Phys. 2012, 231, 1499–1523. [Google Scholar] [CrossRef]
- Antuono, M.; Marrone, S.; Di Mascio, A.; Colagrossi, A. Smoothed particle hydrodynamics method from a large eddy simulation perspective. Generalization to a quasi-Lagrangian model. Phys. Fluids 2021, 33, 015102. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, J.; Qi, Y.; Li, J.; Xu, Q. Numerical simulation of landslide generated impulse waves using a δ+-LES-SPH model. Adv. Water Resour. 2021, 151, 103890. [Google Scholar] [CrossRef]
- Kaitna, R.; Rickenmann, D.; Schatzmann, M. Experimental study on rheologic behaviour of debris flow material. Acta Geotech. 2007, 2, 71–85. [Google Scholar] [CrossRef]
- Burger, J.; Haldenwang, R.; Alderman, N. Experimental database for non-Newtonian flow in four channel shapes. J. Hydraul. Res. 2010, 48, 363–370. [Google Scholar] [CrossRef]
- Vajravelu, K.; Sreenadh, S.; Devaki, P.; Prasad, K.V. Peristaltic Transport of a Herschel-Bulkley Fluid in an Elastic Tube. Heat Transf. Asian Res. 2015, 44, 585–598. [Google Scholar] [CrossRef]
- Guo, T.; Zhao, K.; Zhang, Z.; Gao, X.; Qi, X. Rheology Study on Low-Sugar Apple Jam by a New Nonlinear Regression Method of Herschel-Bulkley Model. J. Food Process. Preserv. 2017, 41, e12810. [Google Scholar] [CrossRef]
- Di Mascio, A.; Antuono, M.; Colagrossi, A.; Marrone, S. Smoothed particle hydrodynamics method from a large eddy simulation perspective. Phys. Fluids 2017, 29, 035102. [Google Scholar] [CrossRef]
- Gotoh, H.; Shao, S.; Memita, T. SPH-LES model for numerical investigation of wave interaction with partially immersed breakwater. Coast. Eng. J. 2004, 46, 39–63. [Google Scholar] [CrossRef]
- Molteni, D.; Colagrossi, A. A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH. Comput. Phys. Commun. 2009, 180, 861–872. [Google Scholar] [CrossRef]
- Qi, Y.; Chen, J.; Zhang, G.; Xu, Q.; Li, J. An improved multi-phase weakly-compressible SPH model for modeling various landslides. Powder Technol. 2022, 397, 117120. [Google Scholar] [CrossRef]
- Randles, P.W.; Libersky, L.D. Smoothed particle hydrodynamics: Some recent improvements and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 375–408. [Google Scholar] [CrossRef]
- Hu, X.Y.; Adams, N.A. An incompressible multi-phase SPH method. J. Comput. Phys. 2007, 227, 264–278. [Google Scholar] [CrossRef]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touzé, D.; Graziani, G. δ-SPH model for simulating violent impact flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Fan, X.J.; Tanner, R.I.; Zheng, R. Smoothed particle hydrodynamics simulation of non-Newtonian moulding flow. J. Nonnewton. Fluid Mech. 2010, 165, 219–226. [Google Scholar] [CrossRef]
- Vacondio, R.; Altomare, C.; De Leffe, M.; Hu, X.; Le Touzé, D.; Lind, S.; Marongiu, J.C.; Marrone, S.; Rogers, B.D.; Souto-Iglesias, A. Grand challenges for Smoothed Particle Hydrodynamics numerical schemes. Comput. Part. Mech. 2021, 8, 575–588. [Google Scholar] [CrossRef]
- Yashiro, S. Application of particle simulation methods to composite materials: A review. Adv. Compos. Mater. 2017, 26, 1–22. [Google Scholar] [CrossRef]
- Dai, Z.; Huang, Y.; Cheng, H.; Xu, Q. 3D numerical modeling using smoothed particle hydrodynamics of flow-like landslide propagation triggered by the 2008 Wenchuan earthquake. Eng. Geol. 2014, 180, 21–33. [Google Scholar] [CrossRef]
- Cercos-Pita, J.L. AQUAgpusph, a new free 3D SPH solver accelerated with OpenCL. Comput. Phys. Commun. 2015, 192, 295–312. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Domínguez, J.M.; Rogers, B.D.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Zheng, D.; Wu, P.; Shang, W.; Cao, X. Nearest neighbor search algorithm based on multiple background grids for fluid simulation. J. Shanghai Univ. 2011, 15, 405–408. [Google Scholar] [CrossRef]
- Awile, O.; Büyükkeçeci, F.; Reboux, S.; Sbalzarini, I.F. Fast neighbor lists for adaptive-resolution particle simulations. Comput. Phys. Commun. 2012, 183, 1073–1081. [Google Scholar] [CrossRef]
- Viccione, G.; Bovolin, V.; Carratelli, E.P. Defining and optimizing algorithms for neighbouring particle identification in SPH fluid simulations. Int. J. Numer. Methods Fluids 2008, 58, 625–638. [Google Scholar] [CrossRef]
- Green, S. Particle Simulation using CUDA; NVIDIA Whitepaper; NVIDIA: Santa Clara, CA, USA, 2013; pp. 1–12. [Google Scholar]
- Chen, J.Y.; Lien, F.S.; Peng, C.; Yee, E. GPU-accelerated smoothed particle hydrodynamics modeling of granular flow. Powder Technol. 2020, 359, 94–106. [Google Scholar] [CrossRef]
- Byron Bird, R.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; Anderson, W., Ed.; Wiley: Hoboken, NJ, USA, 2001; Volume 1, ISBN 0471410772. [Google Scholar]
- Rzadkiewicz, S.A.; Mariotti, C.; Heinrich, P. Numerical Simulation of Submarine Landslides and Their Hydraulic Effects. J. Waterw. Port Coastal Ocean Eng. 1997, 123, 149–157. [Google Scholar] [CrossRef]
- Zakeri, A.; Høeg, K.; Nadim, F. Submarine debris flow impact on pipelines—Part I: Experimental investigation. Coast. Eng. 2008, 55, 1209–1218. [Google Scholar] [CrossRef]
- Yin, M.; Rui, Y. Laboratory study on submarine debris flow. Mar. Georesources Geotechnol. 2018, 36, 950–958. [Google Scholar] [CrossRef] [Green Version]
- Takabatake, T.; Mäll, M.; Han, D.C.; Inagaki, N.; Kisizaki, D.; Esteban, M.; Shibayama, T. Physical modeling of tsunamis generated by subaerial, partially submerged, and submarine landslides. Coast. Eng. J. 2020, 62, 582–601. [Google Scholar] [CrossRef]
- Zakeri, A.; Høeg, K.; Nadim, F. Submarine debris flow impact on pipelines—Part II: Numerical analysis. Coast. Eng. 2009, 56, 1–10. [Google Scholar] [CrossRef]
- Ren, Z.; Zhao, X.; Liu, H. Numerical study of the landslide tsunami in the South China Sea using Herschel-Bulkley rheological theory. Phys. Fluids 2019, 31, 056601. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, L.; Wei, X.; Jiang, M.; Liao, C.; Kou, H. Simulation of runout behavior of submarine debris flows over regional natural terrain considering material softening. Mar. Georesources Geotechnol. 2021, 1–20. [Google Scholar] [CrossRef]
- Capone, T.; Panizzo, A.; Monaghan, J.J. SPH modelling of water waves generated by submarine landslides. J. Hydraul. Res. 2010, 48, 80–84. [Google Scholar] [CrossRef]














| Parameter | Phase A | Phase B |
|---|---|---|
| (kg/m3) | 2000 | 1000 |
| (N/m2) | 10 | 0 |
| K (Pa∙sN) | 100 | 0.001 |
| N | 0.8 | 1 |
| Parameter | Phase A | Phase B |
|---|---|---|
| (kg/m3) | 1000.0 | 1950.0 |
| (N/m2) | 0 | 1000.0 |
| K (Pa∙sN) | 0.001 | 1.0 |
| N | 1.0 | 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, H.; Huang, Y. A GPU-Based δ-Plus-SPH Model for Non-Newtonian Multiphase Flows. Water 2022, 14, 1734. https://doi.org/10.3390/w14111734
Shi H, Huang Y. A GPU-Based δ-Plus-SPH Model for Non-Newtonian Multiphase Flows. Water. 2022; 14(11):1734. https://doi.org/10.3390/w14111734
Chicago/Turabian StyleShi, Hao, and Yu Huang. 2022. "A GPU-Based δ-Plus-SPH Model for Non-Newtonian Multiphase Flows" Water 14, no. 11: 1734. https://doi.org/10.3390/w14111734
APA StyleShi, H., & Huang, Y. (2022). A GPU-Based δ-Plus-SPH Model for Non-Newtonian Multiphase Flows. Water, 14(11), 1734. https://doi.org/10.3390/w14111734







