Numerical Study of Vertical Slot Fishway Flow with Supplementary Cylinders
Abstract
:1. Introduction
2. Methods
2.1. Numerical Framework
2.2. Computational Setup and Boundary Conditions
2.3. Model Validation
3. Results and Discussion
3.1. Time-Averaged Flow and Fish Swimming
3.2. Second-Order Turbulence Statistics
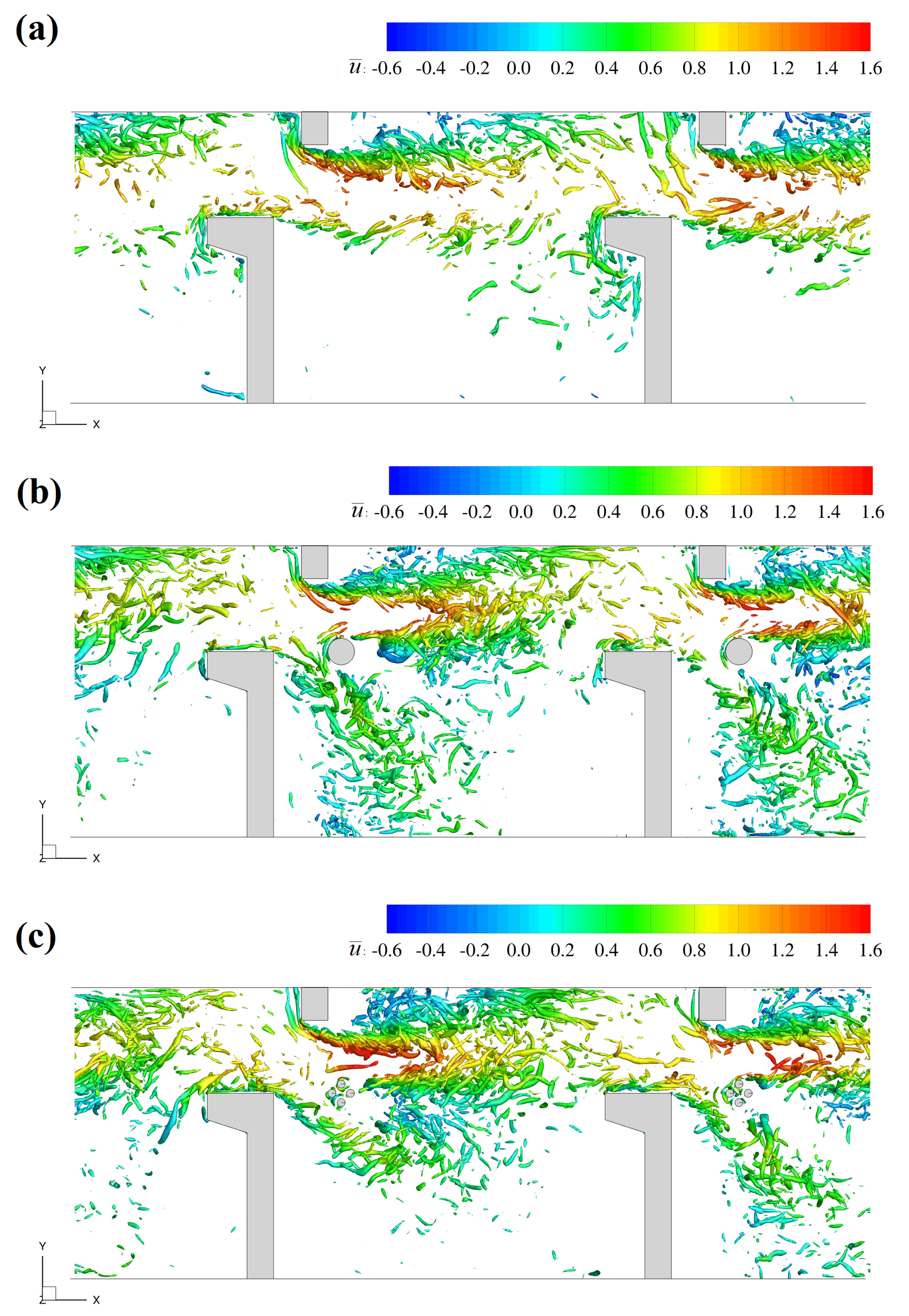
3.3. Instantaneous Flow Features
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| filtered velocity vectors | |
| time-averaged streamwise, spanwise and vertical velocity | |
| fluctuated streamwise, spanwise and vertical velocity | |
| primary shear stress | |
| p | filtered pressure |
| k | turbulent kinetic energy |
| vertical vorticity | |
| kinematic viscosity | |
| sub-grid scale eddy viscosity | |
| subgrid scale stresses | |
| anisotropic subgrid stresses | |
| strain rate | |
| Kronecker delta | |
| residual kinetic energy | |
| Smagorinsky constant | |
| L | pool length |
| W | pool width |
| H | water depth |
| Q | discharge |
| bed slope | |
| mean velocity | |
| Reynolds number | |
| Froude number |
References
- Nilsson, C.; Reidy, C.A.; Dynesius, M.; Revenga, C. Fragmentation and Flow Regulation of the World’s Large River Systems. Science 2005, 308, 405–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zarfl, C.; Lumsdon, A.E.; Berlekamp, J.; Tydecks, L.; Tockner, K. A global boom in hydropower dam construction. Aquat. Sci. 2015, 77, 161–170. [Google Scholar] [CrossRef]
- Chen, S.; Chen, B.; Fath, B.D. Assessing the cumulative environmental impact of hydropower construction on river systems based on energy network model. Renew. Sustain. Energy Rev. 2015, 42, 78–92. [Google Scholar] [CrossRef]
- Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Garrote, L. Influence of hydrologically based environmental flow methods on flow alteration and energy production in a run-of-river hydropower plant. J. Clean. Prod. 2019, 232, 1028–1042. [Google Scholar] [CrossRef]
- Radinger, J.; Wolter, C. Patterns and predictors of fish dispersal in rivers. Fish Fish. 2014, 15, 456–473. [Google Scholar] [CrossRef]
- Lynch, A.J.; Cooke, S.J.; Deines, A.M.; Bower, S.D.; Bunnell, D.B.; Cowx, I.G.; Nguyen, V.M.; Nohner, J.; Phouthavong, K.; Riley, B.; et al. The social, economic, and environmental importance of inland fish and fisheries. Environ. Rev. 2016, 24, 115–121. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Rajaratnam, N.; Katopodis, C. Structure of Flow in Vertical Slot Fishway. J. Hydraul. Eng. 1999, 125, 351–360. [Google Scholar] [CrossRef]
- Rodriguez, T.T.; Agudo, J.P.; Mosquera, L.P.; González, E.P. Evaluating vertical-slot fishway designs in terms of fish swimming capabilities. Ecol. Eng. 2006, 27, 37–48. [Google Scholar] [CrossRef]
- Thiem, J.; Binder, T.; Dumont, P.; Hatin, D.; Hatry, C.; Katopodis, C.; Stamplecoskie, K.; Cooke, S.J. Multispecies fish passage behaviour in a vertical slot fishway on the Richelieu River, Quebec, Canada. River Res. Appl. 2013, 29, 582–592. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Katopodis, C.; Solanki, S. New designs for vertical slot fishways. Can. J. Civ. Eng. 1992, 19, 402–414. [Google Scholar] [CrossRef]
- Li, G.; Sun, S.; Liu, H.; Zheng, T. Schizothorax prenanti swimming behavior in response to different flow patterns in vertical slot fishways with different slot positions. Sci. Total Environ. 2021, 754, 142142. [Google Scholar] [CrossRef]
- An, R.d.; Li, J.; Yi, W.m.; Mao, X. Hydraulics and swimming behavior of schizothorax prenanti in vertical slot fishways. J. Hydrodyn. 2019, 31, 169–176. [Google Scholar] [CrossRef]
- Roscoe, D.W.; Hinch, S.G. Effectiveness monitoring of fish passage facilities: Historical trends, geographic patterns and future directions. Fish Fish. 2010, 11, 12–33. [Google Scholar] [CrossRef]
- Tarrade, L.; Pineau, G.; Calluaud, D.; Texier, A.; David, L.; Larinier, M. Detailed experimental study of hydrodynamic turbulent flows generated in vertical slot fishways. Environ. Fluid Mech. 2011, 11, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Katopodis, C.; Williams, J.G. The development of fish passage research in a historical context. Ecol. Eng. 2012, 48, 8–18. [Google Scholar] [CrossRef]
- Noonan, M.J.; Grant, J.W.A.; Jackson, C.D. A quantitative assessment of fish passage efficiency: Effectiveness of fish passage facilities. Fish Fish. 2012, 13, 450–464. [Google Scholar] [CrossRef]
- Chorda, J.; Maubourguet, M.M.; Roux, H.; Larinier, M.; Tarrade, L.; David, L. Two-dimensional free surface flow numerical model for vertical slot fishways. J. Hydraul. Res. 2010, 48, 141–151. [Google Scholar] [CrossRef] [Green Version]
- Tran, T.D.; Chorda, J.; Laurens, P.; Cassan, L. Modelling nature-like fishway flow around unsubmerged obstacles using a 2D shallow water model. Environ. Fluid Mech. 2016, 16, 413–428. [Google Scholar] [CrossRef] [Green Version]
- Bombač, M.; Četina, M.; Novak, G. Study on flow characteristics in vertical slot fishways regarding slot layout optimization. Ecol. Eng. 2017, 107, 126–136. [Google Scholar] [CrossRef]
- Quaresma, A.L.; Romão, F.; Branco, P.; Ferreira, M.T.; Pinheiro, A.N. Multi slot versus single slot pool-type fishways: A modelling approach to compare hydrodynamics. Ecol. Eng. 2018, 122, 197–206. [Google Scholar] [CrossRef]
- Ahmadi, M.; Ghaderi, A.; MohammadNezhad, H.; Kuriqi, A.; Di Francesco, S. Numerical investigation of hydraulics in a vertical slot fishway with upgraded configurations. Water 2021, 13, 2711. [Google Scholar] [CrossRef]
- Mitsopoulos, G.; Theodoropoulos, C.; Papadaki, C.; Dimitriou, E.; Santos, J.M.; Zogaris, S.; Stamou, A. Model-based ecological optimization of vertical slot fishways using macroinvertebrates and multispecies fish indicators. Ecol. Eng. 2020, 158, 106081. [Google Scholar] [CrossRef]
- Calluaud, D.; Pineau, G.; Texier, A.; David, L. Modification of vertical slot fishway flow with a supplementary cylinder. J. Hydraul. Res. 2014, 52, 614–629. [Google Scholar] [CrossRef]
- Fuentes-Pérez, J.F.; Silva, A.T.; Tuhtan, J.A.; García-Vega, A.; Carbonell-Baeza, R.; Musall, M.; Kruusmaa, M. 3D modelling of non-uniform and turbulent flow in vertical slot fishways. Environ. Model. Softw. 2018, 99, 156–169. [Google Scholar] [CrossRef]
- Chanson, H. Utilising the boundary layer to help restore the connectivity of fish habitats and populations. An engineering discussion. Ecol. Eng. 2019, 141, 105613. [Google Scholar] [CrossRef]
- Bombač, M.; Novak, G.; Mlačnik, J.; Četina, M. Extensive field measurements of flow in vertical slot fishway as data for validation of numerical simulations. Ecol. Eng. 2015, 84, 476–484. [Google Scholar] [CrossRef]
- Stoesser, T.; Kim, S.J.; Diplas, P. Turbulent flow through idealized emergent vegetation. J. Hydraul. Eng. 2010, 136, 1003–1017. [Google Scholar] [CrossRef]
- Stoesser, T.; McSherry, R.; Fraga, B. Secondary currents and turbulence over a non-uniformly roughened open-channel bed. Water 2015, 7, 4896–4913. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.; Stoesser, T.; Mao, J.; McSherry, R. LES of flow through and around a finite patch of thin plates. Water Resour. Res. 2019, 55, 7587–7605. [Google Scholar] [CrossRef] [Green Version]
- Vui Chua, K.; Fraga, B.; Stoesser, T.; Ho Hong, S.; Sturm, T. Effect of bridge abutment length on turbulence structure and flow through the opening. J. Hydraul. Eng. 2019, 145, 04019024. [Google Scholar] [CrossRef]
- Liu, Y.; Stoesser, T.; Fang, H. Effect of secondary currents on the flow and turbulence in partially filled pipes. J. Fluid Mech. 2022, 938. [Google Scholar] [CrossRef]
- Liu, Y.; Stoesser, T.; Fang, H. Impact of turbulence and secondary flow on the water surface in partially filled pipes. Phys. Fluids 2022, 34, 035123. [Google Scholar] [CrossRef]
- Uhlmann, M. An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 2005, 209, 448–476. [Google Scholar] [CrossRef] [Green Version]
- Cristallo, A.; Verzicco, R. Combined immersed boundary/large-eddy-simulations of incompressible three dimensional complex flows. Flow Turbul. Combust. 2006, 77, 3–26. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Bomminayuni, S.; Stoesser, T. Turbulence statistics in an open-channel flow over a rough bed. J. Hydraul. Eng. 2011, 137, 1347–1358. [Google Scholar] [CrossRef]
- Ouro, P.; Wilson, C.A.M.E.; Evans, P.; Angeloudis, A. Large-eddy simulation of shallow turbulent wakes behind a conical island. Phys. Fluids 2017, 29, 126601. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez, J.F.; García, M.H. Laboratory measurements of 3-D flow patterns and turbulence in straight open channel with rough bed. J. Hydraul. Res. 2008, 46, 454–465. [Google Scholar] [CrossRef]
- Thorstad, E.B.; ØKland, F.; Finstad, B. Effects of telemetry transmitters on swimming performance of adult Atlantic salmon. J. Fish Biol. 2000, 57, 531–535. [Google Scholar] [CrossRef]
- Watson, J.R.; Goodrich, H.R.; Cramp, R.L.; Gordos, M.A.; Franklin, C.E. Utilising the boundary layer to help restore the connectivity of fish habitats and populations. Ecol. Eng. 2018, 122, 286–294. [Google Scholar] [CrossRef]
- Lacroix, G.L.; Knox, D.; McCurdy, P. Effects of implanted acoustic transmitters on juvenile Atlantic salmon. Trans. Am. Fish. Soc. 2004, 133, 211–220. [Google Scholar] [CrossRef]
- Bleckmann, H.; Zelick, R. Lateral line system of fish. Integr. Zool. 2009, 4, 13–25. [Google Scholar] [CrossRef]
- Lacey, R.J.; Neary, V.S.; Liao, J.C.; Enders, E.C.; Tritico, H.M. The IPOS framework: Linking fish swimming performance in altered flows from laboratory experiments to rivers. River Res. Appl. 2012, 28, 429–443. [Google Scholar] [CrossRef]
- Wilkes, M.; Enders, E.; Silva, A.; Acreman, M.; Maddock, I. Position choice and swimming costs of juvenile Atlantic salmon salmo salar in turbulent flow. J. Ecohydraulics 2017, 2, 16–27. [Google Scholar] [CrossRef]
- Cote, A.J.; Webb, P.W. Living in a Turbulent World—A New Conceptual Framework for the Interactions of Fish and Eddies. Integr. Comp. Biol. 2015, 55, 662–672. [Google Scholar] [CrossRef] [Green Version]
- Tritico, H.M.; Cotel, A.J. The effects of turbulent eddies on the stability and critical swimming speed of creek chub (Semotilus atromaculatus). J. Exp. Biol. 2010, 213, 2284–2293. [Google Scholar] [CrossRef] [Green Version]
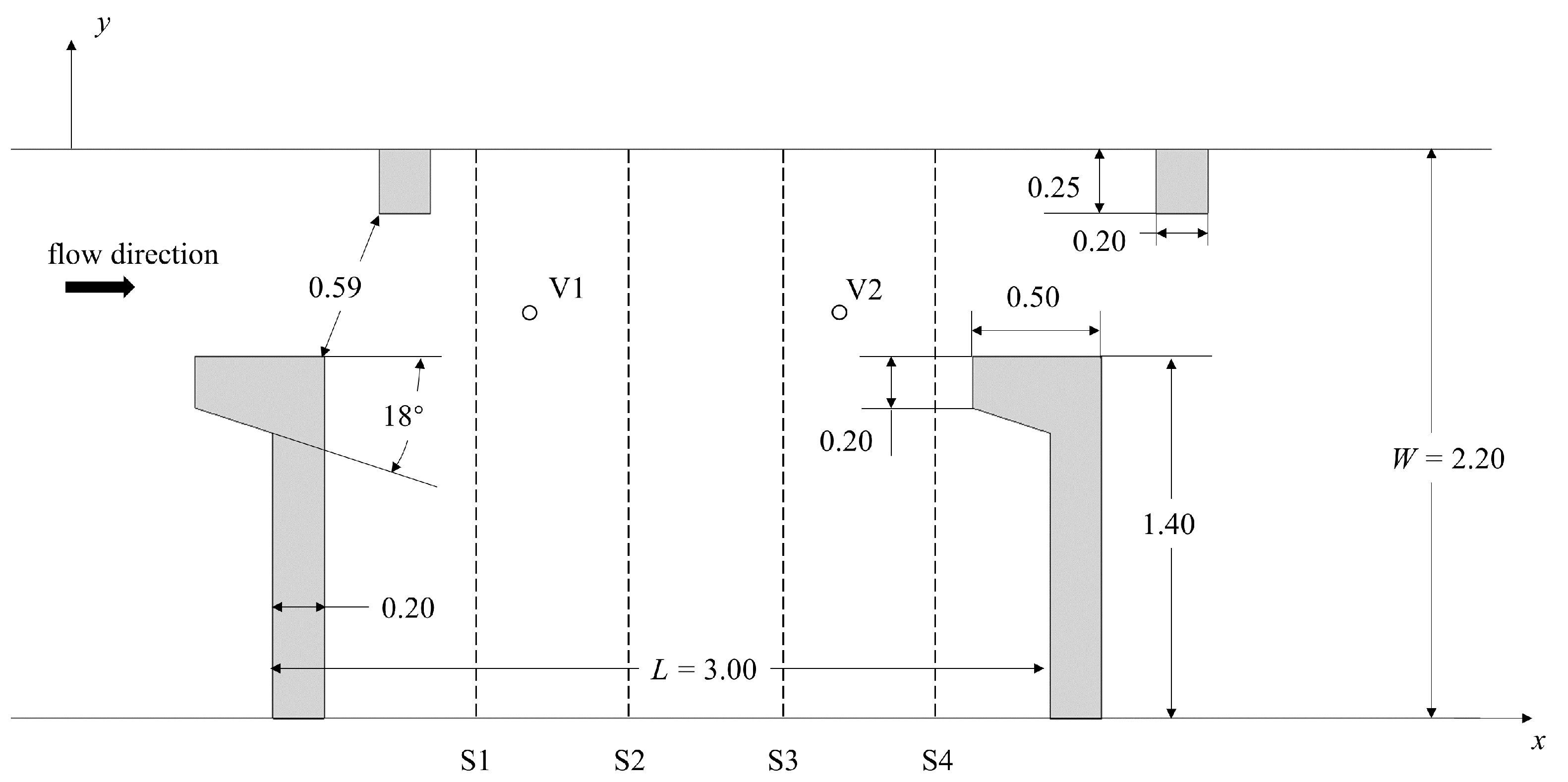







| Case | (m/s) | Re | Fr | No. of Cylinders | No. of IB Points |
|---|---|---|---|---|---|
| 1 | 0.3497 | 349,700 | 0.098 | 0 | 1,013,004 |
| 2 | 0.3497 | 349,700 | 0.098 | 2 | 1,141,488 |
| 3 | 0.3497 | 349,700 | 0.098 | 8 | 1,052,220 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Xu, Y.; Lu, Y.; Lu, S.; Dai, J.; Meng, D. Numerical Study of Vertical Slot Fishway Flow with Supplementary Cylinders. Water 2022, 14, 1772. https://doi.org/10.3390/w14111772
Zhao H, Xu Y, Lu Y, Lu S, Dai J, Meng D. Numerical Study of Vertical Slot Fishway Flow with Supplementary Cylinders. Water. 2022; 14(11):1772. https://doi.org/10.3390/w14111772
Chicago/Turabian StyleZhao, Hanqing, Yun Xu, Yang Lu, Shanshan Lu, Jie Dai, and Dinghua Meng. 2022. "Numerical Study of Vertical Slot Fishway Flow with Supplementary Cylinders" Water 14, no. 11: 1772. https://doi.org/10.3390/w14111772
APA StyleZhao, H., Xu, Y., Lu, Y., Lu, S., Dai, J., & Meng, D. (2022). Numerical Study of Vertical Slot Fishway Flow with Supplementary Cylinders. Water, 14(11), 1772. https://doi.org/10.3390/w14111772





