Trend Detection in Annual Streamflow Extremes in Brazil
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Streamflow Data
2.3. Streamflow Indices
2.4. Presence of Reservoirs
2.5. Trend Detection Framework
2.5.1. Mann–Kendall Trend Test
2.5.2. Theil–Sen Slope Estimator
2.5.3. Adjustment for Autocorrelated Data
- Estimate the magnitude of the trend, , using Equation (7).
- Obtain a detrended series, , by removing the estimated trend from of the original series, , where t is the time interval.
- Estimate an unbiased sample autocorrelation (r1) of the detrended series, .
- If r1 is not statistically different from zero, then the MK test is applied to the original series, . Otherwise, the PW procedure is applied to the original series, , to obtain a prewhitened series, .
- Apply the MK test to to check the significance of the trend.
2.5.4. The Multiplicity Problem
3. Results and Discussion
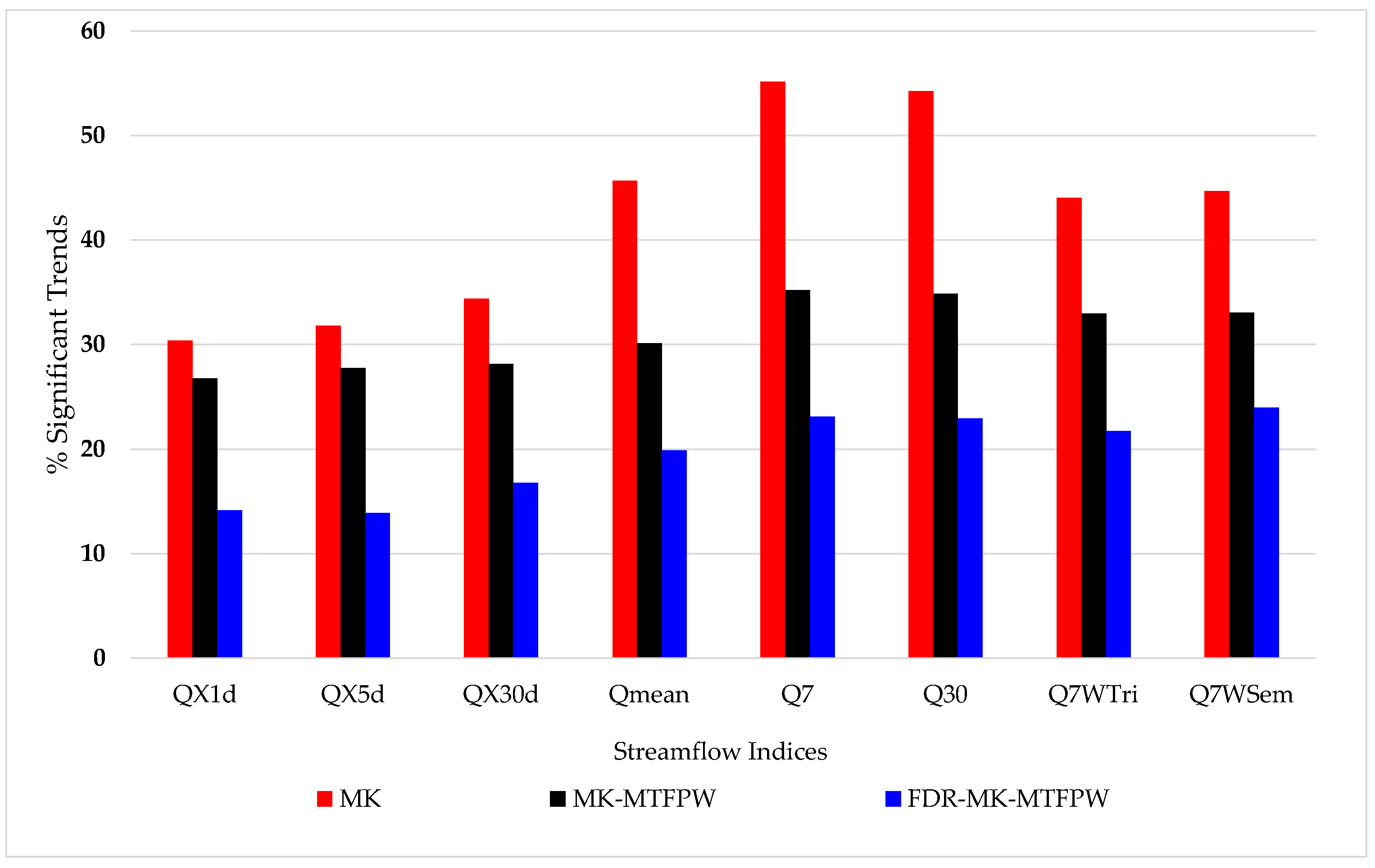
3.1. Impacts of Serial Correlation and Multiplicity of Tests
3.2. Trend Analysis in Hydrographic Regions
3.3. Analysis with Gauges Unaffected by Reservoirs
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- National Academies of Sciences, Engineering, and Medicine. Future Water Priorities for the Nation: Directions for the U.S. Geological Survey Water Mission Area; National Academies Press: Washington, DC, USA, 2018; ISBN 9780309477093. [Google Scholar]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Climate change—Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Serinaldi, F.; Kilsby, C.G. Stationarity is undead: Uncertainty dominates the distribution of extremes. Adv. Water Resour. 2015, 77, 17–36. [Google Scholar] [CrossRef] [Green Version]
- Serinaldi, F.; Kilsby, C.G.; Lombardo, F. Untenable nonstationarity: An assessment of the fitness for purpose of trend tests in hydrology. Adv. Water Resour. 2018, 111, 132–155. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J.; Vogel, R.M. Techniques for assessing water infrastructure for nonstationary extreme events: A review. Hydrol. Sci. J. 2018, 63, 325–352. [Google Scholar] [CrossRef]
- IPCC. IPCC, 2021: Summary for policymakers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Conn, S.L., Eds.; IPCC: Geneva, Switzerland, 2021. [Google Scholar]
- Su, L.; Miao, C.; Kong, D.; Duan, Q.; Lei, X.; Hou, Q.; Li, H. Long-term trends in global river flow and the causal relationships between river flow and ocean signals. J. Hydrol. 2018, 563, 818–833. [Google Scholar] [CrossRef]
- Zhao, W.; Du, H.; Wang, L.; He, H.S.; Wu, Z.; Liu, K.; Guo, X.; Yang, Y. A Comparison of recent trends in precipitation and temperature over western and eastern eurasia: Differences of climate change between western and eastern eurasia. Q. J. R. Meteorol. Soc. 2018, 144, 604–613. [Google Scholar] [CrossRef]
- Wang, W.; Zhu, Y.; Liu, B.; Chen, Y.; Zhao, X. Innovative variance corrected sen’s trend test on persistent hydrometeorological data. Water 2019, 11, 2119. [Google Scholar] [CrossRef] [Green Version]
- Luke, A.; Vrugt, J.A.; AghaKouchak, A.; Matthew, R.; Sanders, B.F. Predicting nonstationary flood frequencies: Evidence supports an updated stationarity thesis in the United States. Water Resour. Res. 2017, 53, 5469–5494. [Google Scholar] [CrossRef]
- Vogel, R.M.; Rosner, A.; Kirshen, P.H. Brief Communication: Likelihood of Societal preparedness for global change: Trend detection. Nat. Hazards Earth Syst. Sci. 2013, 13, 1773–1778. [Google Scholar] [CrossRef] [Green Version]
- Rosner, A.; Vogel, R.M.; Kirshen, P.H. A Risk-based approach to flood management decisions in a nonstationary world. Water Resour. Res 2014, 50, 1928–1942. [Google Scholar] [CrossRef]
- Doocy, S.; Daniels, A.; Murray, S.; Kirsch, T.D. The human impact of floods: A historical review of events 1980–2009 and systematic literature review. PLoS Curr. 2013. [Google Scholar] [CrossRef]
- Read, L.K.; Vogel, R.M. Reliability, return periods, and risk under nonstationarity. Water Resour. Res. 2015, 51, 6381–6398. [Google Scholar] [CrossRef]
- Svensson, C.; Kundzewicz, W.Z.; Maurer, T. Trend detection in river flow series: 2. Flood and low-flow index series/Détection de tendance dans des séries de débit fluvial: 2. Séries d’indices de crue et d’étiage. Hydrol. Sci. J. 2005, 50, 824. [Google Scholar] [CrossRef] [Green Version]
- Kundzewicz, Z.W.; Mata, L.J.; Arnell, N.W.; Döll, P.; Jimenez, B.; Miller, K.; Oki, T.; Şen, Z.; Shiklomanov, I. The implications of projected climate change for freshwater resources and their management. Hydrol. Sci. J. 2008, 53, 3–10. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Robson, A.J. Change detection in hydrological records—A review of the methodology/revue méthodologique de la détection de changements dans les chroniques hydrologiques. Hydrol. Sci. J. 2004, 49, 7–19. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Serinaldi, F.; Bales, J.; Bates, P.D.; Krajewski, W.F. Flood frequency analysis for nonstationary annual peak records in an urban drainage basin. Adv. Water Resour. 2009, 32, 1255–1266. [Google Scholar] [CrossRef]
- Rice, J.S.; Emanuel, R.E.; Vose, J.M.; Nelson, S.A.C. Continental US streamflow trends from 1940 to 2009 and their relationships with watershed spatial characteristics. Water Resour. Res. 2015, 51, 6262–6275. [Google Scholar] [CrossRef]
- Rodgers, K.; Roland, V.; Hoos, A.; Crowley-Ornelas, E.; Knight, R. An analysis of streamflow trends in the southern and southeastern US from 1950–2015. Water 2020, 12, 3345. [Google Scholar] [CrossRef]
- Mastin, M.C.; Konrad, C.P.; Veilleux, A.G.; Tecca, A.E. Magnitude, frequency, and trends of floods at gaged and ungaged sites in Washington, based on data through water year 2014. Sci. Investig. Rep. 2016. [Google Scholar] [CrossRef] [Green Version]
- Tamaddun, K.; Kalra, A.; Ahmad, S. Identification of streamflow changes across the continental united states using variable record lengths. Hydrology 2016, 3, 24. [Google Scholar] [CrossRef] [Green Version]
- Ishak, E.H.; Rahman, A.; Westra, S.; Sharma, A.; Kuczera, G. Evaluating the non-stationarity of australian annual maximum flood. J. Hydrol. 2013, 494, 134–145. [Google Scholar] [CrossRef]
- Zhang, X.S.; Amirthanathan, G.E.; Bari, M.A.; Laugesen, R.M.; Shin, D.; Kent, D.M.; MacDonald, A.M.; Turner, M.E.; Tuteja, N.K. How streamflow has changed across australia since the 1950s: Evidence from the network of hydrologic reference stations. Hydrol. Earth Syst. Sci. 2016, 20, 3947–3965. [Google Scholar] [CrossRef] [Green Version]
- Potter, N.J.; Chiew, F.H.S.; Frost, A.J. An assessment of the severity of recent reductions in rainfall and runoff in the murray—Darling Basin. J. Hydrol. 2010, 381, 52–64. [Google Scholar] [CrossRef]
- Zhang, X.; Cong, Z. Trends of precipitation intensity and frequency in hydrological regions of China from 1956 to 2005. Glob. Planet. Chang. 2014, 117, 40–51. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, X.; Singh, V.P.; Xiao, M.; Chen, X. Evaluation of flood frequency under non-stationarity resulting from climate indices and reservoir indices in the East River Basin, China. J. Hydrol. 2015, 527, 565–575. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, C.; Xu, C.-Y.; Xu, Y.; Jiang, T. Observed trends of annual maximum water level and streamflow during past 130 years in the Yangtze River Basin, China. J. Hydrol. 2006, 324, 255–265. [Google Scholar] [CrossRef]
- Miao, C.Y.; Shi, W.; Chen, X.H.; Yang, L. Spatio-temporal variability of streamflow in the yellow river: Possible causes and implications. Hydrol. Sci. J. 2012, 57, 1355–1367. [Google Scholar] [CrossRef] [Green Version]
- Giuntoli, I.; Maugis, P.; Renard, B. Observed Trends in River Flow Rates in France; ONEMA: Paris, France, 2012; 8p. [Google Scholar]
- Renard, B.; Lang, M.; Bois, P.; Dupeyrat, A.; Mestre, O.; Niel, H.; Sauquet, E.; Prudhomme, C.; Parey, S.; Paquet, E.; et al. Regional methods for trend detection: Assessing field significance and regional consistency. Water Resour. Res. 2008, 44, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Dixon, H.; Lawler, D.M.; Shamseldin, A.Y. Streamflow trends in western britain. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Harrigan, S.; Hannaford, J.; Muchan, K.; Marsh, T.J. Designation and trend analysis of the updated UK benchmark network of river flow stations: The UKBN2 dataset. Hydrol. Res. 2018, 49, 552–567. [Google Scholar] [CrossRef] [Green Version]
- Petrow, T.; Merz, B. Trends in flood magnitude, frequency and seasonality in Germany in the period 1951–2002. J. Hydrol. 2009, 371, 129–141. [Google Scholar] [CrossRef] [Green Version]
- Yeste, P.; Dorador, J.; Martin-Rosales, W.; Molero, E.; Esteban-Parra, M.J.; Rueda, F.J. Climate-driven trends in the streamflow records of a reference hydrologic network in Southern Spain. J. Hydrol. 2018, 566, 55–72. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; Sanchez, N.; Herrero-Jimenez, C.M. Recent trends in rivers with near-natural flow regime: The case of the river headwaters in Spain. Prog. Phys. Geogr. 2013, 37, 685–700. [Google Scholar] [CrossRef]
- Cigizoglu, H.K.; Bayazit, M.; Önöz, B. Trends in the maximum, mean, and low flows of turkish rivers. J. Hydrometeorol. 2005, 6, 280–290. [Google Scholar] [CrossRef]
- Murphy, C.; Harrigan, S.; Hall, J.; Wilby, R.L. Climate-driven trends in mean and high flows from a network of reference stations in Ireland. Hydrol. Sci. J. 2013, 58, 755–772. [Google Scholar] [CrossRef]
- Piniewski, M.; Marcinkowski Pawełand Kundzewicz, Z.W. Trend detection in river flow indices in Poland. Acta Geophys. 2018, 66, 347–360. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Harvey, K.D.; Hogg, W.D.; Yuzyk, T.R. Trends in canadian streamflow. Water Resour. Res. 2001, 37, 987–998. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Gachon, P. Identification of temporal trends in annual and seasonal low flows occurring in canadian rivers: The effect of short- and long-term persistence. J. Hydrol. 2009, 369, 183–197. [Google Scholar] [CrossRef]
- Huziy, O.; Sushama, L.; Khaliq, M.N.; Laprise, R.; Lehner, B.; Roy, R. Analysis of streamflow characteristics over northeastern canada in a changing climate. Clim. Dyn. 2013, 40, 1879–1901. [Google Scholar] [CrossRef] [Green Version]
- Dethier, E.N.; Sartain, S.L.; Renshaw, C.E.; Magilligan, F.J. Spatially coherent regional changes in seasonal extreme streamflow events in the united states and Canada since 1950. Sci. Adv. 2020, 6, eaba5939. [Google Scholar] [CrossRef]
- Wang, W.; Van Gelder, P.H.A.J.M.; Vrijling, J.K. Detection of changes in streamflow series in Western Europe over 1901–2000. Water Sci. Technol. Water Supply 2005, 5, 289–299. [Google Scholar] [CrossRef]
- Hannaford, J.; Buys, G.; Stahl, K.; Tallaksen, L.M. The influence of decadal-scale variability on trends in long European streamflow records. Hydrol. Earth Syst. Sci. 2013, 17, 2717–2733. [Google Scholar] [CrossRef] [Green Version]
- Stahl, K.; Hisdal, H.; Hannaford, J.; Tallaksen, L.M.; van Lanen, H.A.J.; Sauquet, E.; Demuth, S.; Fendekova, M.; Jódar, J. Streamflow trends in Europe: Evidence from a dataset of near-natural catchments. Hydrol. Earth Syst. Sci. 2010, 14, 2367–2382. [Google Scholar] [CrossRef] [Green Version]
- Hall, J.; Arheimer, B.; Borga, M.; Brázdil, R.; Claps, P.; Kiss, A.; Kjeldsen, T.R.; Kriaučiūnienė, J.; Kundzewicz, Z.W.; Lang, M.; et al. Understanding flood regime changes in europe: A state-of-the-art assessment. Hydrol. Earth Syst. Sci. 2014, 18, 2735–2772. [Google Scholar] [CrossRef] [Green Version]
- Madsen, H.; Lawrence, D.; Lang, M.; Martinkova, M.; Kjeldsen, T.R. Review of trend analysis and climate change projections of extreme precipitation and floods in Europe. J. Hydrol. 2014, 519, 3634–3650. [Google Scholar] [CrossRef] [Green Version]
- Kundzewicz, Z.W.; Graczyk, D.; Maurer, T.; Pińskwar, I.; Radziejewski, M.; Svensson, C.; Szwed, M. Trend detection in river flow series: 1. Annual maximum flow/Détection de tendance dans des séries de débit fluvial: 1. Débit maximum annuel. Hydrol. Sci. J. 2005, 50, 810. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, K.A.; Vecchia, A.V. Global pattern of trends in streamflow and water availability in a changing climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef]
- Do, H.X.; Westra, S.; Leonard, M. A global-scale investigation of trends in annual maximum streamflow. J. Hydrol. 2017, 552, 28–43. [Google Scholar] [CrossRef]
- Bürger, G. On trend detection. Hydrol. Process. 2017, 31, 4039–4042. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. The importance of prewhitening in change point analysis under persistence. Stoch. Environ. Res. Risk Assess. 2016, 30, 763–777. [Google Scholar] [CrossRef] [Green Version]
- Serinaldi, F.; Kilsby, C. Understanding persistence to avoid underestimation of collective flood risk. Water 2016, 8, 152. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Chen, Y.; Becker, S.; Liu, B. Variance correction prewhitening method for trend detection in autocorrelated data. J. Hydrol. Eng. 2015, 20, 4015033. [Google Scholar] [CrossRef]
- Cox, D.R.; Stuart, A. Some quick sign tests for trend in location and dispersion. Biometrika 1955, 42, 80. [Google Scholar] [CrossRef] [Green Version]
- Lettenmaier, D.P. Detection of trends in water quality data from records with dependent observations. Water Resour. Res. 1976, 12, 1037–1046. [Google Scholar] [CrossRef]
- von Storch, H. Misuses of statistical analysis in climate research. In Analysis of Climate Variability; Springer: Berlin, Heidelberg, 1995; pp. 11–26. [Google Scholar]
- Douglas, E.M.; Vogel, R.M.; Kroll, C.N. Trends in floods and low flows in the united states: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The influence of serial correlation on the mann-whitney test for detecting a shift in median. Adv. Water Resour. 2002, 25, 325–333. [Google Scholar] [CrossRef]
- Bayazit, M.; Önöz, B. To prewhiten or not to prewhiten in trend analysis? Hydrol. Sci. J. 2007, 52, 611–624. [Google Scholar] [CrossRef]
- Hamed, K.H. Enhancing the effectiveness of prewhitening in trend analysis of hydrologic data. J. Hydrol. 2009, 368, 143–155. [Google Scholar] [CrossRef]
- Önöz, B.; Bayazit, M. Block bootstrap for mann-kendall trend test of serially dependent data: Block bootstrap for mann-kendall trend test of serially dependent data. Hydrol. Process. 2012, 26, 3552–3560. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Hamed, K.H.; Ramachandra Rao, A. A modified mann-kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Wilks, D.S. On “field Significance” and the false discovery rate. J. Appl. Meteorol. Clim. 2006, 45, 1181–1189. [Google Scholar] [CrossRef]
- Wilks, D.S. “The stippling shows statistically significant grid points”: How research results are routinely overstated and overinterpreted, and what to do about It. Bull. Am. Meteorol. Soc. 2016, 97, 2263–2273. [Google Scholar] [CrossRef]
- Holm, S. A simple sequentially rejective multiple test procedure. Scand. Stat. Theory Appl. 1979, 6, 65–70. [Google Scholar]
- Hochberg, Y. A sharper bonferroni procedure for multiple tests of significance. Biometrika 1988, 75, 800. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Alpert, P. The paradoxical increase of mediterranean extreme daily rainfall in spite of decrease in total values. Geophys. Res. Lett. 2002, 29, 31-1–31-4. [Google Scholar] [CrossRef] [Green Version]
- Ventura, V.; Paciorek, C.J.; Risbey, J.S. Controlling the proportion of falsely rejected hypotheses when conducting multiple tests with climatological data. J. Clim. 2004, 17, 4343–4356. [Google Scholar] [CrossRef] [Green Version]
- Fatichi, S.; Caporali, E. A comprehensive analysis of changes in precipitation regime in tuscany. Int. J. Clim. 2009, 29, 1883–1893. [Google Scholar] [CrossRef]
- Anderson, B.T.; Gianotti, D.J.; Salvucci, G.D. Detectability of historical trends in station-based precipitation characteristics over the continental United States: Station-based precipitation trends. J. Geophys. Res. 2015, 120, 4842–4859. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Seneviratne, S.I. European drought trends. Proc. Int. Assoc. Hydrol. Sci. 2015, 369, 75–79. [Google Scholar] [CrossRef] [Green Version]
- Mallya, G.; Mishra, V.; Niyogi, D.; Tripathi, S.; Govindaraju, R.S. Trends and variability of droughts over the indian monsoon region. Weather Clim. Extrem. 2016, 12, 43–68. [Google Scholar] [CrossRef] [Green Version]
- Genta, J.; Perez-Iribarren, G.; Mechoso, C.R. A recent increasing trend in the streamflow of rivers in Southeastern South America. J. Clim. 1998, 11, 2858–2862. [Google Scholar] [CrossRef]
- Marengo, J.A.; Tomasella, J.; Uvo, C.R. Trends in streamflow and rainfall in Tropical South America: Amazonia, Eastern Brazil, and Northwestern Peru. J. Geophys. Res. 1998, 103, 1775–1783. [Google Scholar] [CrossRef]
- Collischonn, W.; Tucci, C.E.M.; Clarke, R.T. Further evidence of changes in the hydrological regime of the river paraguay: Part of a wider phenomenon of climate change? J. Hydrol. 2001, 245, 218–238. [Google Scholar] [CrossRef]
- Detzel, D.; Bessa, M.; Vallejos, C.; Santos, A.; Thomsen, L.; Mine, M.; Bloot, M.; Estrocio, J. Estacionariedade das afluências às usinas hidrelétricas brasileiras. RBRH 2011, 16, 95–111. [Google Scholar] [CrossRef]
- Doyle, M.E.; Barros, V.R. Attribution of the river flow growth in the Plata Basin. Int. J. Clim. 2011, 31, 2234–2248. [Google Scholar] [CrossRef]
- Alves, B.; Filho, F. Análise de tendências e padrões de variação das séries históricas de vazões do operador nacional do sistema (ONS). RBRH 2013, 18, 19–34. [Google Scholar] [CrossRef]
- Bartiko, D.; Chaffe, P.L.B.; Bonumá, N.B. Nonstationarity in maximum annual daily streamflow series from Southern Brazil. RBRH 2017, 22. [Google Scholar] [CrossRef] [Green Version]
- Chagas, V.B.P.; Chaffe, P.L.B. The role of land cover in the propagation of rainfall into streamflow trends. Water Resour. Res. 2018, 54, 5986–6004. [Google Scholar] [CrossRef]
- Luiz Silva, W.; Xavier, L.N.R.; Maceira, M.E.P.; Rotunno, O.C. Climatological and hydrological patterns and verified trends in precipitation and streamflow in the basins of brazilian hydroelectric plants. Theor. Appl. Clim. 2019, 137, 353–371. [Google Scholar] [CrossRef]
- Agência Nacional de Águas. Conjuntura dos Recursos Hídricos no Brasil 2017: Relatório Pleno; Agência Nacional de Águas: Brasilia, Brazil, 2017; 169p. [Google Scholar]
- Vörösmarty, C.J.; Sharma, K.P.; Fekete, B.M.; Copeland, A.H.; Holden, J.; Marble, J.; Lough, J.A. Lough the storage and aging of continental runoff in large reservoir systems of the world. Ambio 1997, 26, 210–219. [Google Scholar]
- Nilsson, C.; Reidy, C.A.; Dynesius, M.; Revenga, C. Fragmentation and flow regulation of the world’s large river systems. Science 2005, 308, 405–408. [Google Scholar] [CrossRef] [Green Version]
- Lehner, B.; Liermann, C.R.; Revenga, C.; Vörösmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. High-resolution mapping of the world’s reservoirs and dams for sustainable river-flow management. Front. Ecol. Environ. 2011, 9, 494–502. [Google Scholar] [CrossRef] [Green Version]
- Dynesius, M.; Nilsson, C. Fragmentation and flow regulation of river systems in the northern third of the world. Science 1994, 266, 753–762. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Kendall, M.G. Time Series, 2nd ed.; Hefner: New York, NY, USA, 1975; 40p. [Google Scholar]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the mann-kendall and spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Sonali, P.; Nagesh Kumar, D. Review of trend detection methods and their application to detect temperature changes in India. J. Hydrol. 2013, 476, 212–227. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The mann-kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. Applicability of prewhitening to eliminate the influence of serial correlation on the mann-kendall test: Technical note. Water Resour. Res. 2002, 38, 4–7. [Google Scholar] [CrossRef]
- Anderson, R.L. Distribution of the serial correlation coefficient. Ann. Math. Stat. 1942, 13, 1–13. [Google Scholar] [CrossRef]
- Yevjevich, V. Probability Statistics in Hydrology; Water Resources Publication: Fort Collins, CO, USA, 1972. [Google Scholar]
- Salas, J.D.; Delleur, J.W.; Yevjevich, V. Applied Modeling of Hydrologic Time Series; Water Resources Publications: Littleton, CO, USA, 1985. [Google Scholar]
- van Giersbergen, N.P.A. On the effect of deterministic terms on the bias in stable AR models. Econ. Lett. 2005, 89, 75–82. [Google Scholar] [CrossRef] [Green Version]
- Yue, S.; Pilon, P.; Phinney, B. Canadian streamflow trend detection: Impacts of serial and cross-correlation. Hydrol. Sci. J. 2003, 48, 51–63. [Google Scholar] [CrossRef]
- Sun, X.; Thyer, M.; Renard, B.; Lang, M. A general regional frequency analysis framework for quantifying local-scale climate effects: A case study of ENSO effects on southeast queensland rainfall. J. Hydrol. 2014, 512, 53–68. [Google Scholar] [CrossRef] [Green Version]
- Amorim, R.S. Detecção de Tendências em Séries de Extremos Hidrológicos Considerando Efeitos de Autocorrelação Temporal e Multiplicidade de Testes. Master’s Dissertation, Universidade de Brasília, Brasília, Brazil, 2018. [Google Scholar]
- Gelman, A.; Stern, H. The difference between “Significant” and “Not Significant” is not itself statistically significant. Am. Stat. 2006, 60, 328–331. [Google Scholar] [CrossRef] [Green Version]
- Sullivan, G.M.; Feinn, R. Using effect size—Or why the p value is not enough. J. Grad. Med. Educ. 2012, 4, 279–282. [Google Scholar] [CrossRef] [Green Version]
- Peeters, M.J. Practical significance: Moving beyond statistical significance. Curr. Pharm. Teach. Learn. 2016, 8, 83–89. [Google Scholar] [CrossRef]
- Clarke, R.T. On the (mis) use of statistical methods in hydro-climatological research. Hydrol. Sci. J. 2010, 55, 139–144. [Google Scholar] [CrossRef]
- Clarke, R.T. How should trends in hydrological extremes be estimated? Trends in hydrological extremes. Water Resour. Res. 2013, 49, 6756–6764. [Google Scholar] [CrossRef]
- Bartiko, D.; Oliveira, D.Y.; Bonumá, N.B.; Chaffe, P.L.B. Spatial and seasonal patterns of flood change across Brazil. Hydrol. Sci. J. 2019, 64, 1071–1079. [Google Scholar] [CrossRef]









| Index | Definition |
|---|---|
| QX1d | Annual maximum daily flow |
| QX5d | Annual maximum 5-day consecutive average flow |
| QX30d | Annual maximum 30-day consecutive average flow |
| Qmean | Mean annual streamflow |
| Q7 | Annual minimum 7-day consecutive average flow |
| Q30 | Annual minimum 30-day consecutive average flow |
| Q7Wtri | Annual minimum 7-day consecutive average flow (wettest trimester) |
| Q7Wsem | Annual minimum 7-day consecutive average flow (wettest semester) |
| Indice | Res | Tot | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30–44 years | 45–59 years | >60 years | 30–44 years | 45–59 years | >60 years | 30–44 years | 45–59 years | >60 years | 30–44 years | 45–59 years | >60 years | 30–44 years | 45–59 years | >60 years | 30–44 years | 45–59 years | >60 years | |||
| QX1d | NS | 6% | 1% | 0% | 2% | 0% | 0% | 86% | 2% | 1% | 5% | 3% | 2% | 12% | 6% | 9% | 11% | 7% | 10% | 86% |
| 7% | 3% | 11% | 9% | 27% | 28% | |||||||||||||||
| S | 4% | 1% | 1% | 1% | 0% | 1% | 0% | 0% | 1% | 1% | 1% | 2% | 0% | 0% | 0% | 0% | 0% | 0% | 14% | |
| 6% | 2% | 2% | 3% | 0% | 1% | |||||||||||||||
| QX5d | NS | 7% | 1% | 0% | 2% | 0% | 0% | 9% | 3% | 1% | 5% | 3% | 2% | 10% | 6% | 9% | 11% | 6% | 10% | 87% |
| 8% | 2% | 13% | 10% | 26% | 27% | |||||||||||||||
| S | 4% | 2% | 1% | 0% | 1% | 0% | 0% | 0% | 1% | 1% | 0% | 2% | 0% | 0% | 0% | 0% | 0% | 1% | 13% | |
| 6% | 1% | 2% | 3% | 1% | 1% | |||||||||||||||
| QX30d | NS | 6% | 1% | 0% | 2% | 0% | 0% | 9% | 3% | 2% | 5% | 3% | 2% | 10% | 6% | 11% | 11% | 6% | 8% | 84% |
| 8% | 2% | 13% | 9% | 27% | 25% | |||||||||||||||
| S | 5% | 2% | 1% | 0% | 0% | 0% | 1% | 0% | 2% | 1% | 0% | 3% | 0% | 0% | 0% | 0% | 0% | 0% | 16% | |
| 7% | 1% | 3% | 4% | 1% | 0% | |||||||||||||||
| Qmean | NS | 8% | 2% | 0% | 2% | 0% | 0% | 7% | 3% | 2% | 6% | 2% | 1% | 10% | 8% | 10% | 9% | 5% | 7% | 81% |
| 11% | 2% | 11% | 8% | 28% | 21% | |||||||||||||||
| S | 6% | 2% | 0% | 0% | 0% | 0% | 1% | 1% | 2% | 1% | 1% | 4% | 0% | 0% | 0% | 0% | 0% | 0% | 19% | |
| 8% | 1% | 3% | 6% | 0% | 0% | |||||||||||||||
| Q7 | NS | 10% | 3% | 1% | 4% | 0% | 0% | 7% | 3% | 2% | 3% | 3% | 1% | 8% | 6% | 8% | 7% | 3% | 7% | 77% |
| 14% | 5% | 12% | 7% | 22% | 16% | |||||||||||||||
| S | 7% | 2% | 1% | 2% | 1% | 2% | 1% | 1% | 1% | 0% | 0% | 3% | 0% | 0% | 0% | 0% | 0% | 0% | 23% | |
| 11% | 4% | 3% | 3% | 1% | 0% | |||||||||||||||
| Q30 | NS | 8% | 3% | 0% | 4% | 1% | 0% | 7% | 4% | 2% | 4% | 2% | 1% | 9% | 6% | 9% | 6% | 3% | 6% | 77% |
| 12% | 5% | 13% | 7% | 24% | 16% | |||||||||||||||
| S | 8% | 2% | 1% | 2% | 1% | 1% | 2% | 1% | 1% | 0% | 1% | 3% | 0% | 0% | 0% | 0% | 0% | 0% | 23% | |
| 11% | 4% | 4% | 4% | 0% | 0% | |||||||||||||||
| Q7WTri | NS | 8% | 3% | 0% | 2% | 0% | 0% | 5% | 4% | 2% | 3% | 2% | 1% | 8% | 7% | 9% | 9% | 5% | 8% | 78% |
| 11% | 2% | 12% | 7% | 24% | 21% | |||||||||||||||
| S | 7% | 5% | 2% | 1% | 0% | 0% | 0% | 1% | 2% | 0% | 0% | 2% | 0% | 0% | 0% | 0% | 0% | 0% | 22% | |
| 14% | 1% | 3% | 2% | 1% | 0% | |||||||||||||||
| Q7WSem | NS | 7% | 2% | 0% | 3% | 0% | 0% | 8% | 4% | 2% | 5% | 2% | 2% | 9% | 5% | 8% | 7% | 4% | 7% | 76% |
| 9% | 3% | 13% | 9% | 23% | 19% | |||||||||||||||
| S | 7% | 4% | 1% | 1% | 1% | 1% | 1% | 2% | 2% | 0% | 0% | 2% | 0% | 0% | 1% | 0% | 0% | 0% | 24% | |
| 13% | 2% | 5% | 3% | 1% | 0% | |||||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souza, S.A.d.; Reis, Jr., D.S. Trend Detection in Annual Streamflow Extremes in Brazil. Water 2022, 14, 1805. https://doi.org/10.3390/w14111805
Souza SAd, Reis, Jr. DS. Trend Detection in Annual Streamflow Extremes in Brazil. Water. 2022; 14(11):1805. https://doi.org/10.3390/w14111805
Chicago/Turabian StyleSouza, Saulo A. de, and Dirceu S. Reis, Jr. 2022. "Trend Detection in Annual Streamflow Extremes in Brazil" Water 14, no. 11: 1805. https://doi.org/10.3390/w14111805
APA StyleSouza, S. A. d., & Reis, Jr., D. S. (2022). Trend Detection in Annual Streamflow Extremes in Brazil. Water, 14(11), 1805. https://doi.org/10.3390/w14111805






