Impact of Rainfall Movement on Flash Flood Response: A Synthetic Study of a Semi-Arid Mountainous Catchment
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Catchment
2.2. Hydraulic Model
2.3. Study Setup
2.3.1. Model Setup
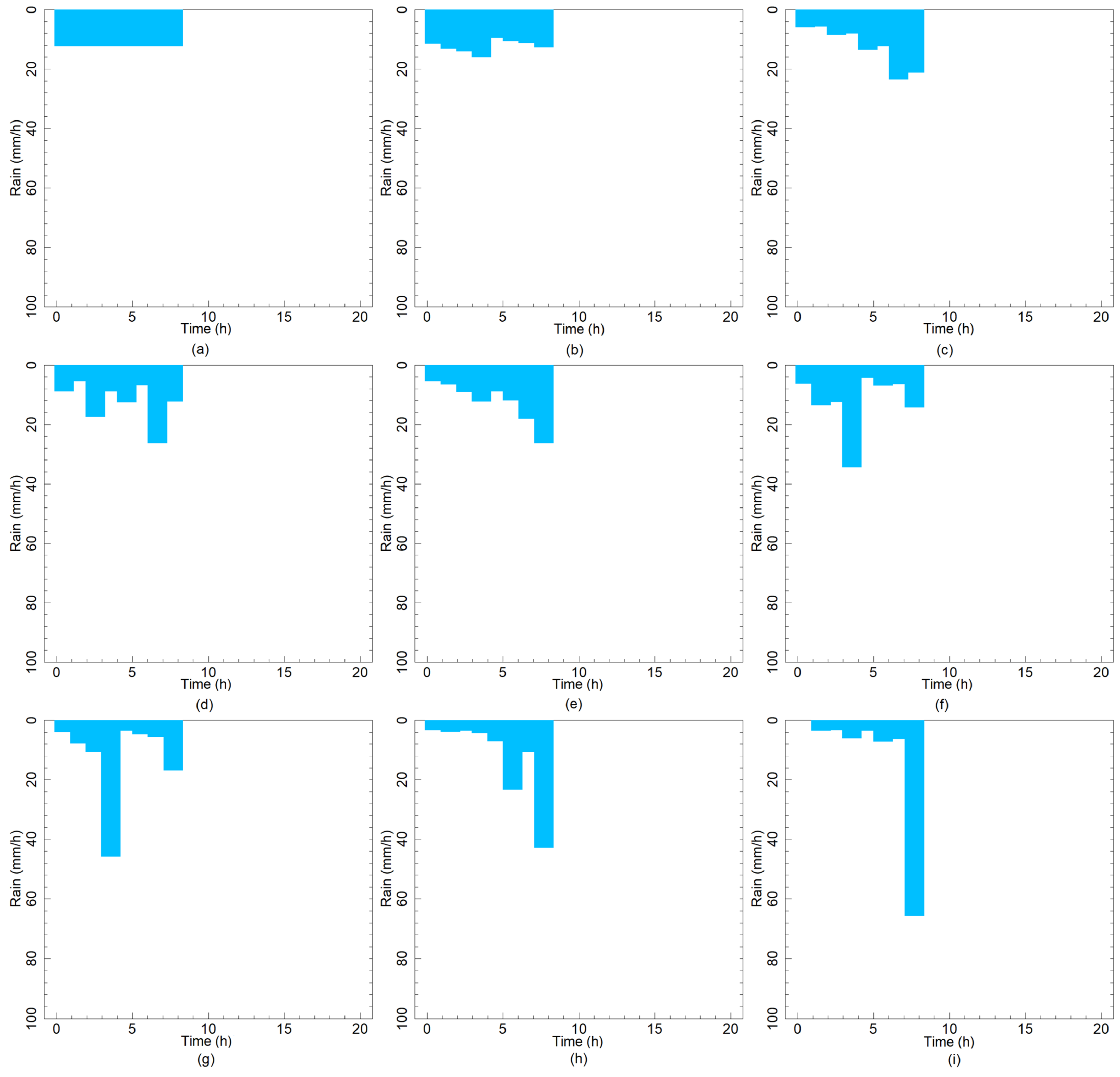
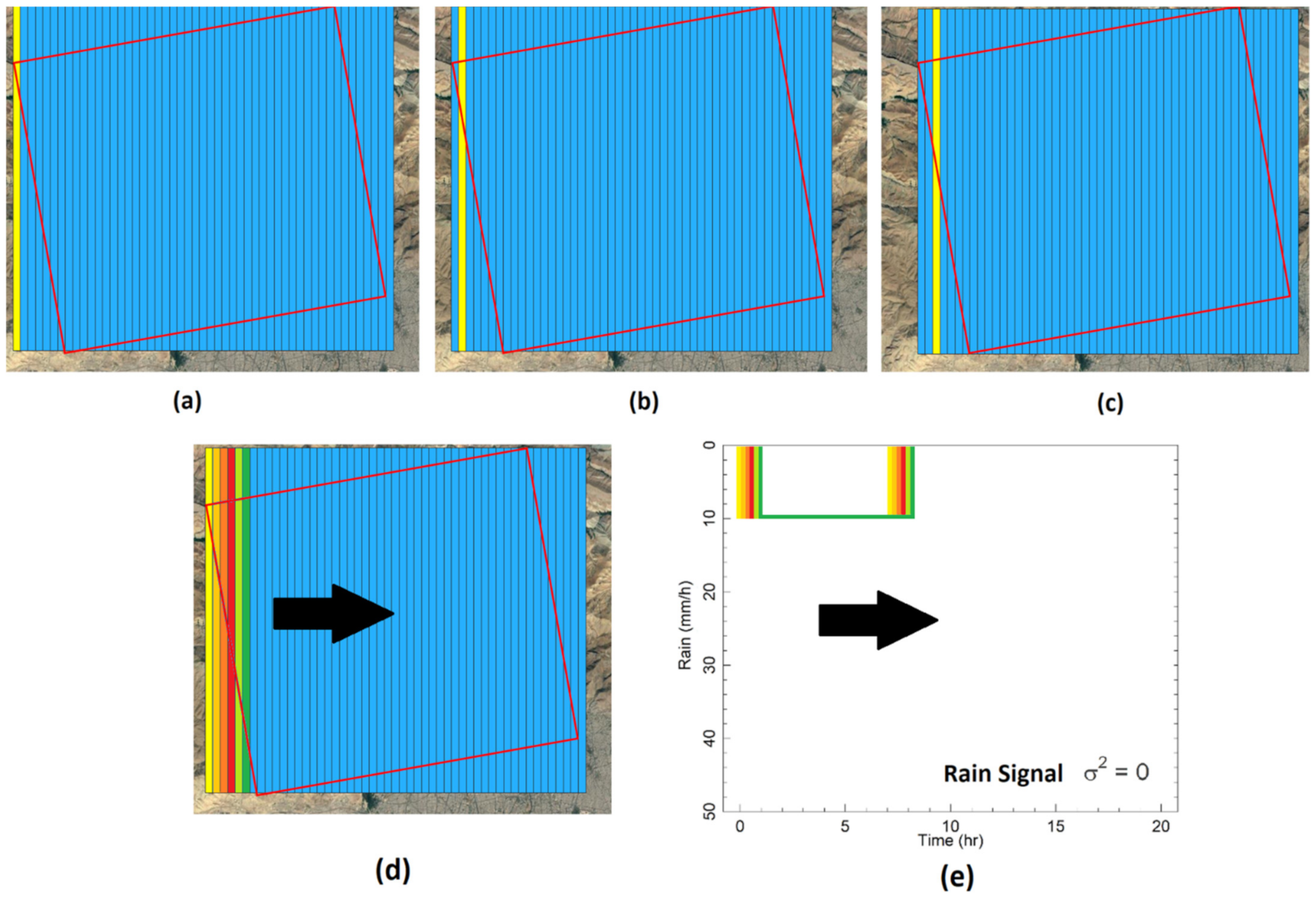
2.3.2. Rain Modeling
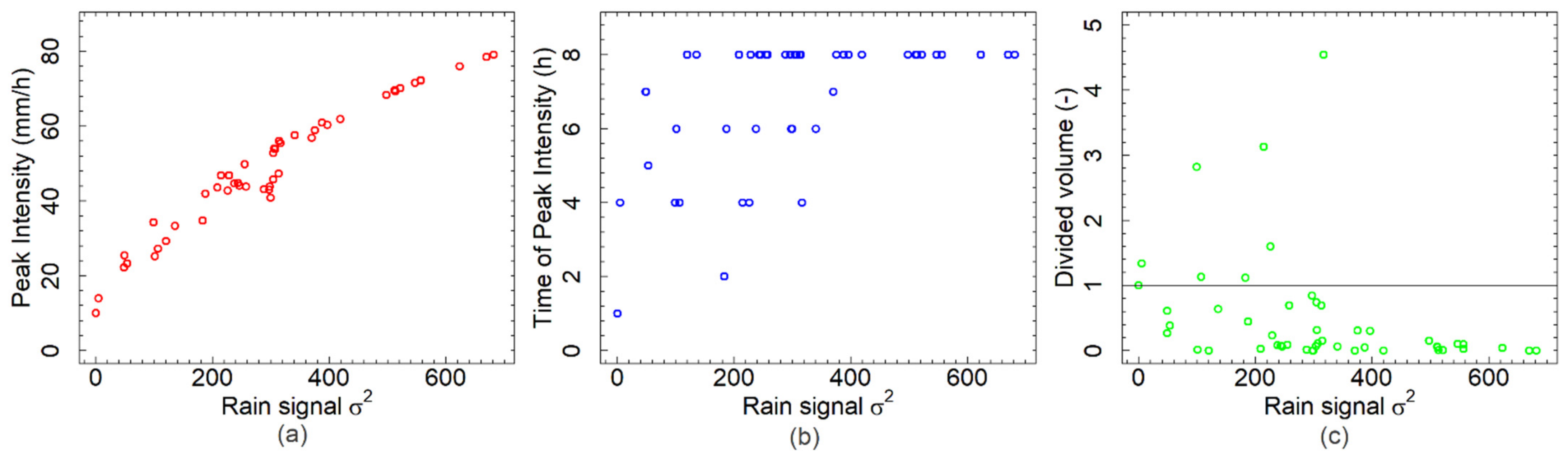
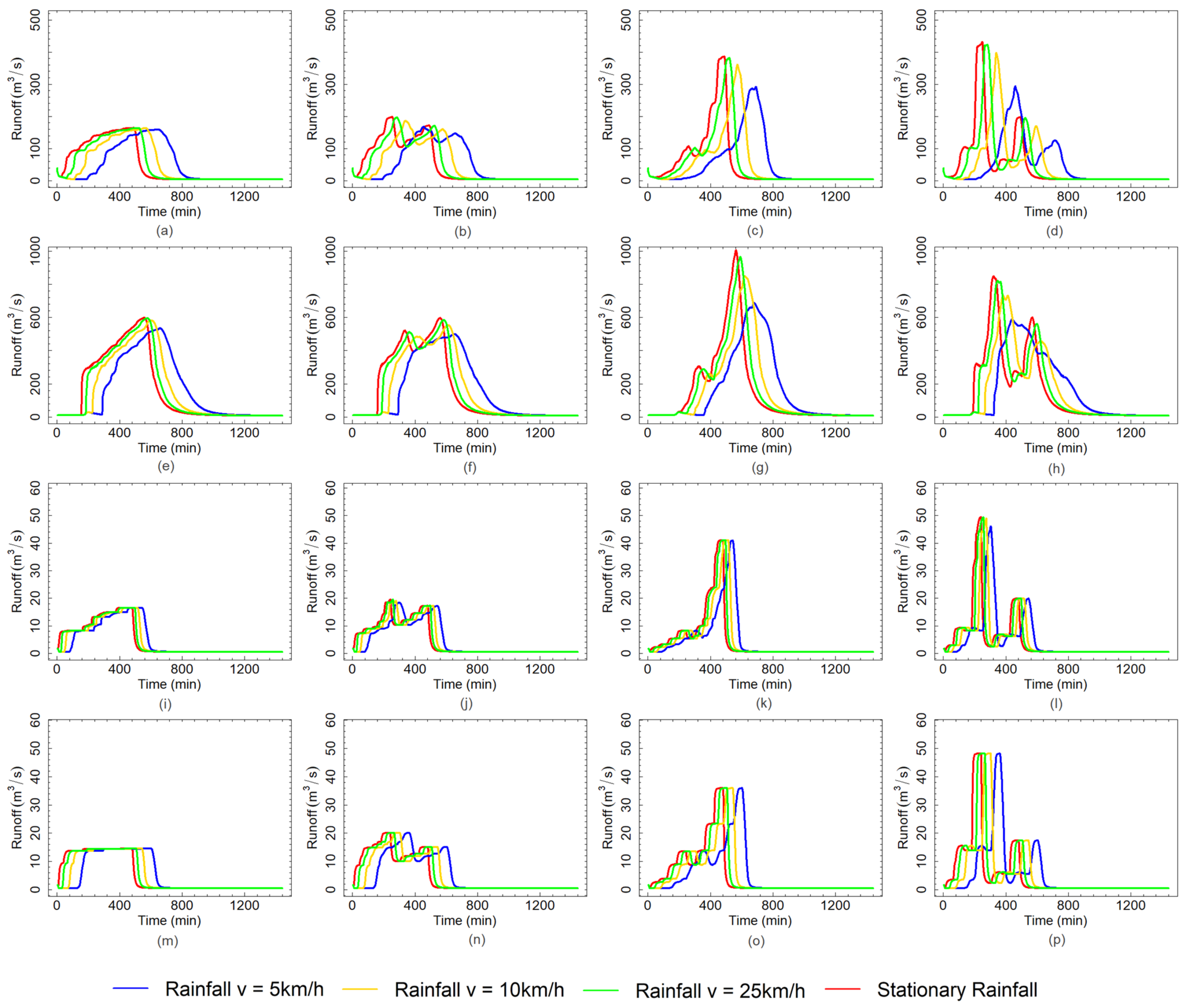
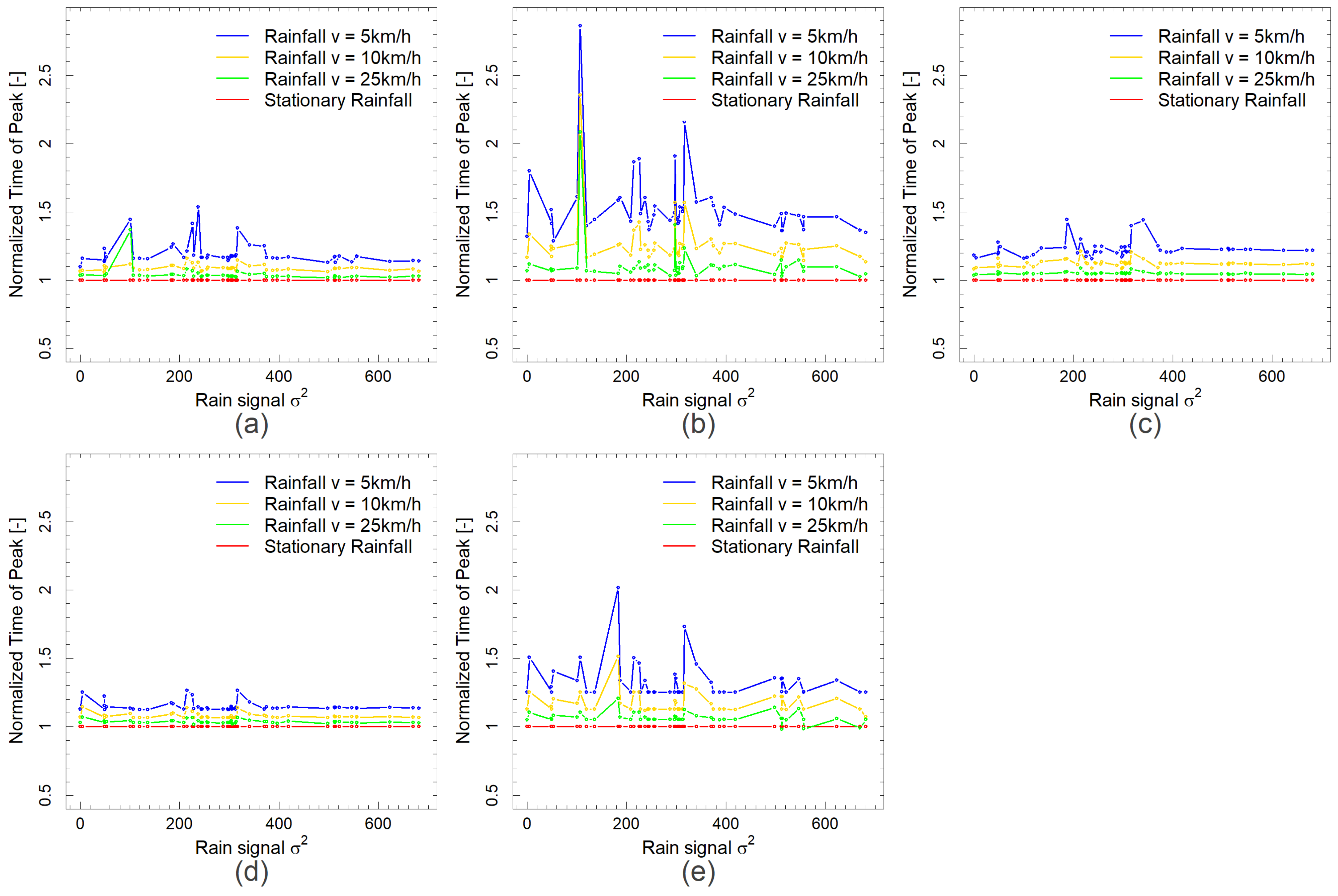
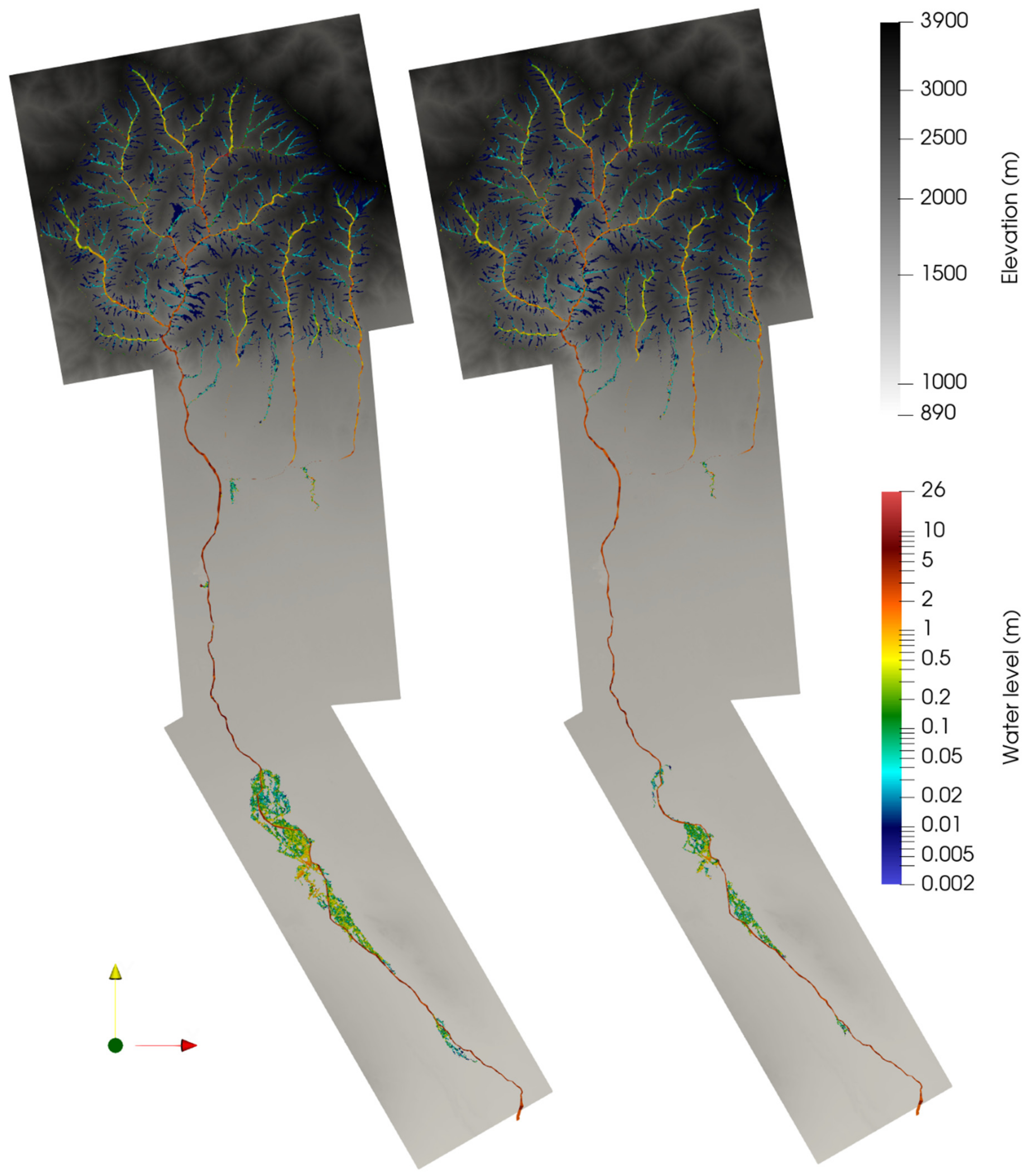
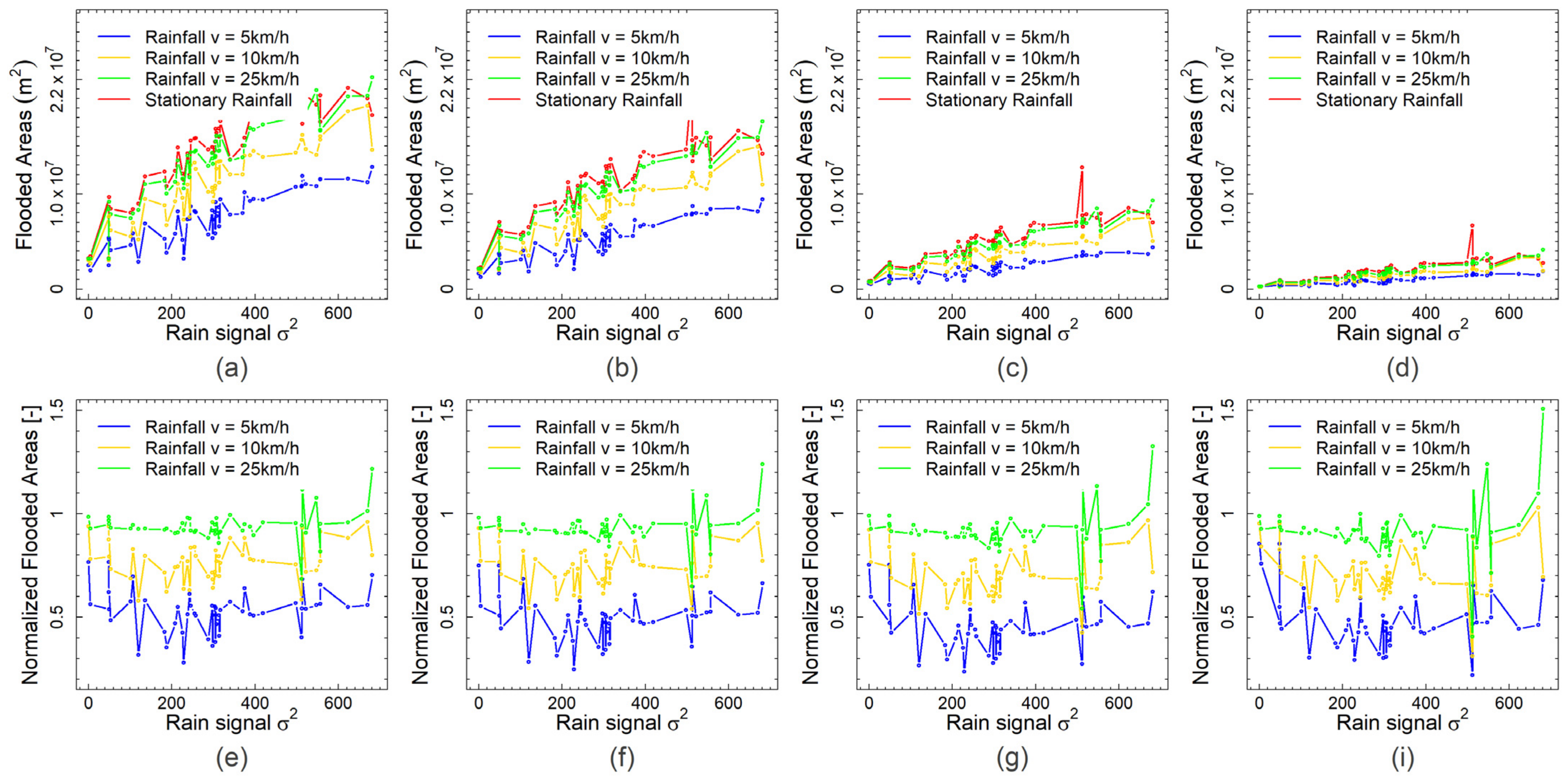
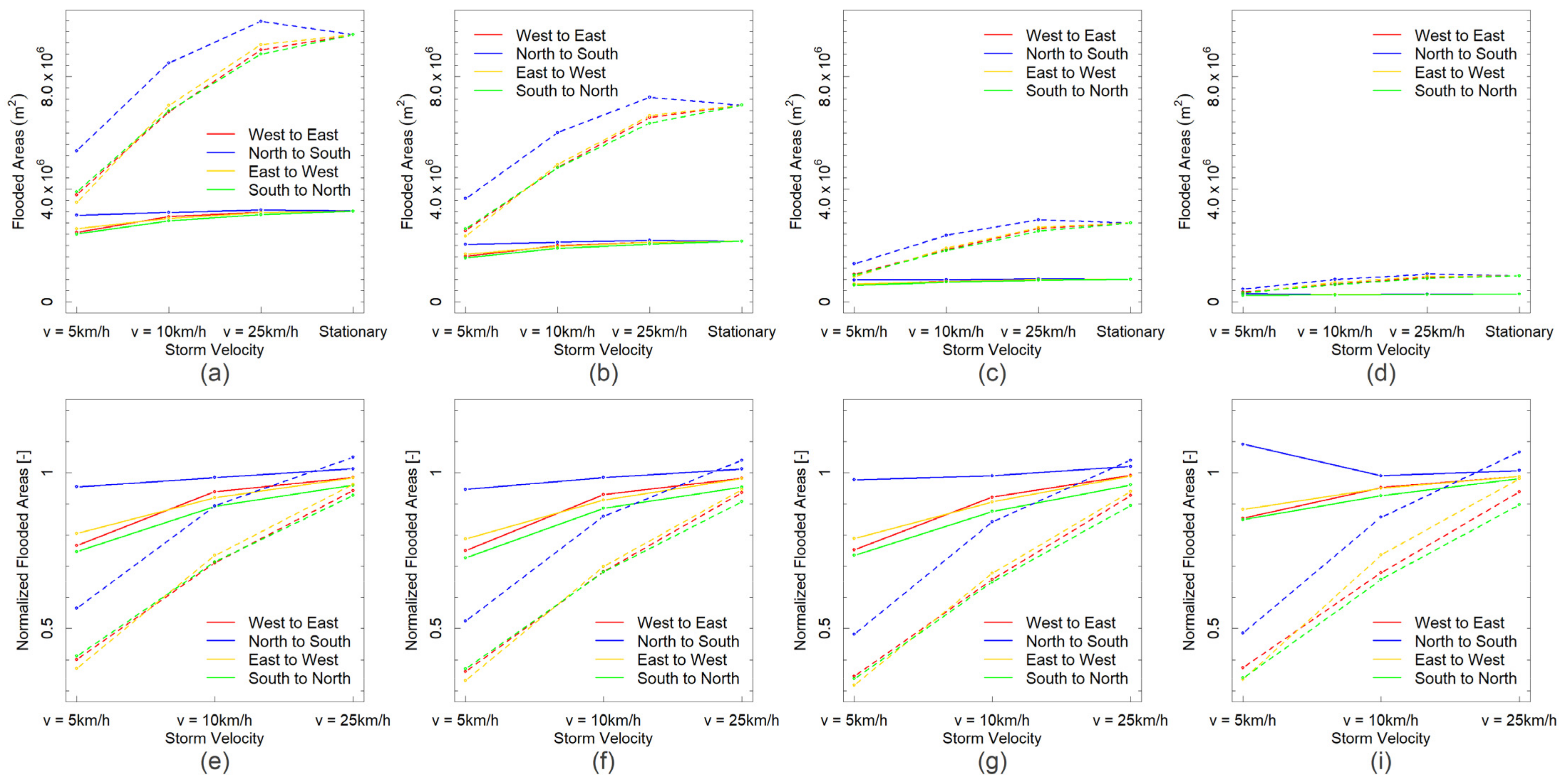
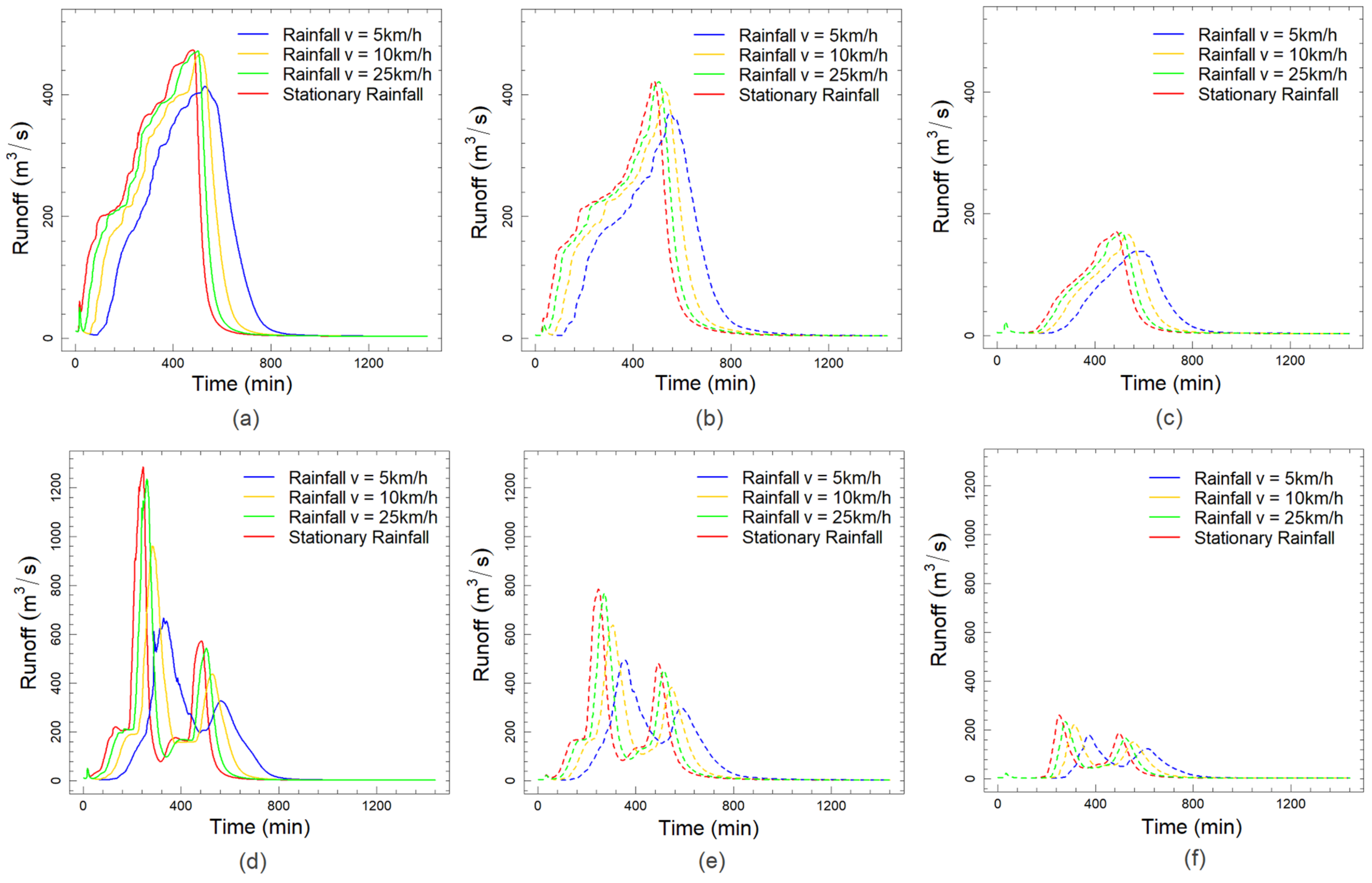
3. Results and Discussion
Limitations and Outlook
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marani, M. Non-power-law scale properties of rainfall in space and time. Water Resour. Res. 2005, 41, W08413. [Google Scholar] [CrossRef]
- Huff, F.A. Hydrometeorological Characteristics of Severe Rainstorms in Illinois; Illinois State Water Survey: Urbana, IL, USA, 1979; 18p. [Google Scholar]
- Marshall, R.J. The estimation and distribution of storm movement and storm structure, using a correlation-analysis technique and rain-gauge data. J. Hydrol. 1980, 48, 19–39. [Google Scholar] [CrossRef]
- Upton, G.J.G. A correlation-regression method for tracking rainstorms using rain-gauge data. J. Hydrol. 2002, 261, 60–73. [Google Scholar] [CrossRef]
- Yen, B.C.; Chow, V.T. A Study of Surface Runoff Due to Moving Rainstorms; Hydraulic Engineering Series; University of Illinois: Urbana, IL, USA, 1968; Volume 17. [Google Scholar]
- Jensen, M. Runoff pattern and peak flows from moving block rains based on linear time-area curve. Hydrol. Res. 1984, 15, 155–168. [Google Scholar] [CrossRef]
- Seo, Y.; Schmidt, A.R.; Sivapalan, M. Effect of storm movement on flood peaks: Analysis framework based on characteristic time scales. Water Resour. Res. 2012, 48, W05532. [Google Scholar] [CrossRef]
- Singh, V.P.; de Lima, J.L.M.P. One-dimensional linear kinematic wave solution for overland flow under moving storms using the method of characteristics. J. Hydrol. Eng. 2018, 23, 04018029. [Google Scholar] [CrossRef]
- Yao, Q.; Xie, J.; Guo, L.; Zhang, X.; Liu, R. Analysis and evaluation of flash flood disasters: A case of Lingbao County of Henan province in China. Procedia Eng. 2016, 154, 835–843. [Google Scholar] [CrossRef] [Green Version]
- Papaioannou, G.; Efstratiadis, A.; Vasiliades, L.; Loukas, A.; Papalexiou, S.M.; Koukouvinos, A.; Tsoukalas, I.; Kossieris, P. An operational method for flood directive implementation in ungauged urban areas. Hydrology 2018, 5, 24. [Google Scholar] [CrossRef] [Green Version]
- Doswell, C.A. Hydrology, floods and droughts|Flooding. In Encyclopedia of Atmospheric Sciences, 2nd ed.; North, G.R., Pyle, J.A., Zhang, F., Eds.; Academic Press: Cambridge, MA, USA, 2015; pp. 201–208. [Google Scholar] [CrossRef]
- Doocy, S.; Daniels, A.; Murray, S.; Kirsch, T.D. The human impact of floods: A historical review of events 1980–2009 and systematic literature review. PLoS Curr. 2013, 5, 23857425. [Google Scholar] [CrossRef]
- Zhong, M.; Jiang, T.; Li, K.; Lu, Q.; Wang, J.; Zhu, J. Multiple environmental factors analysis of flash flood risk in Upper Hanjiang River, southern China. Environ. Sci. Pollut. Res. 2020, 27, 37218–37228. [Google Scholar] [CrossRef]
- Kelsch, M. Hydrometeorological characteristics of flash floods. In Coping with Flash Floods; NATO Science Series; Gruntfest, E., Handmer, J., Eds.; Springer: Dordrecht, The Netherlands, 2001; Volume 77. [Google Scholar] [CrossRef]
- Hu, X.; Song, L. Hydrodynamic modeling of flash flood in mountain watersheds based on high-performance GPU computing. Nat. Hazards 2018, 91, 567–586. [Google Scholar] [CrossRef]
- Chang, T.-Y.; Chen, H.; Fu, H.-S.; Chen, W.-B.; Yu, Y.-C.; Su, W.-R.; Lin, L.-Y. An operational high-performance forecasting system for city-scale pluvial flash floods in the southwestern plain areas of Taiwan. Water 2021, 13, 405. [Google Scholar] [CrossRef]
- Chen, Y.-M.; Liu, C.-H.; Shih, H.-J.; Chang, C.-H.; Chen, W.-B.; Yu, Y.-C.; Su, W.-R.; Lin, L.-Y. An operational forecasting system for flash floods in mountainous areas in Taiwan. Water 2019, 11, 2100. [Google Scholar] [CrossRef] [Green Version]
- Abderrezzak, K.E.K.; Paquier, A.; Mignot, E. Modelling flash flood propagation in urban areas using a two-dimensional numerical model. Nat. Hazards 2009, 50, 433–460. [Google Scholar] [CrossRef]
- Xing, Y.; Liang, Q.; Wang, G.; Ming, X.; Xia, X. City-scale hydrodynamic modelling of urban flash floods: The issues of scale and resolution. Nat. Hazards 2019, 96, 473–496. [Google Scholar] [CrossRef] [Green Version]
- Deodhar, L.A.; Kale, V.S. Downstream adjustments in allochthonous rivers: Western Deccan Trap upland region, India. In Varieties of Fluvial Form; Miller, A.J., Gupta, A., Eds.; John Wiley and Sons: New York, NY, USA, 1999; pp. 295–315. [Google Scholar]
- Wrzesiński, D.; Sobkowiak, L. Transformation of the flow regime of a large allochthonous river in central Europe—An example of the Vistula River in Poland. Water 2020, 12, 507. [Google Scholar] [CrossRef] [Green Version]
- Deutsches Komitee Katastrophenvorsorge e.V. Das Hochwasser im Juni 2013: Bewährungsprobe für das Hochwasserrisikomanagement in Deutschland (Schriftenreihe des DKKV). 2015. Available online: https://www.dkkv.org/fileadmin/user_upload/Veroeffentlichungen/Publikationen/DKKV_53_Hochwasser_Juni_2013.pdf (accessed on 4 February 2022).
- Blöschl, G.; Gaál, L.; Hall, J.; Kiss, A.; Komma, J.; Nester, T.; Parajka, J.; Perdigão, R.A.P.; Plavcová, L.; Rogger, M.; et al. Increasing river floods: Fiction or reality? WIREs Water 2015, 2, 329–344. [Google Scholar] [CrossRef]
- Black, P.E. Hydrograph response to geomorphic model watershed characteristics and precipitation variables. J. Hydrol. 1972, 17, 309–329. [Google Scholar] [CrossRef]
- Yen, B.C.; Chow, V.T. A laboratory study of surface runoff due to moving rainstorms. Water Resour. Res. 1969, 5, 989–1006. [Google Scholar] [CrossRef]
- De Lima, J.; Singh, V. The influence of the pattern of moving rainstorms on overland flow. Adv. Water Resour. 2002, 25, 817–828. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.-H.; Seo, Y. Hydrodynamic analysis of storm movement effects on runoff hydrographs and loop-rating curves of a V-shaped watershed. Water Resour. Res. 2013, 49, 6613–6623. [Google Scholar] [CrossRef]
- Volpi, E.; Lazzaro, M.D.; Fiori, A. Analytical modeling of the hydrologic response under moving rainstorms: Storm–catchment interaction and resonance. J. Hydrol. 2013, 493, 132–139. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Borga, M.; Zoccatelli, D.; Anagnostou, E.N. Catchment-scale storm velocity: Quantification, scale dependence and effect on flood response. Hydrol. Sci. J. 2014, 59, 1363–1376. [Google Scholar] [CrossRef] [Green Version]
- Amengual, A.; Borga, M.; Ravazzani, G.; Crema, S. The role of storm movement in controlling flash flood response: An analysis of the 28 September 2012 extreme event in Murcia, southeastern Spain. J. Hydrometeorol. 2021, 22, 2379–2392. [Google Scholar] [CrossRef]
- Perez, G.; Gomez-Velez, J.D.; Mantilla, R.; Wright, D.B.; Li, Z. The effect of storm direction on flood frequency analysis. Geophys. Res. Lett. 2021, 48, e2020GL091918. [Google Scholar] [CrossRef]
- Sigaroodi, S.K.; Chen, Q. Effects and consideration of storm movement in rainfall–runoff modelling at the basin scale. Hydrol. Earth Syst. Sci. 2016, 20, 5063–5071. [Google Scholar] [CrossRef] [Green Version]
- Nunes, J.P.; de Lima, J.L.M.P.; Singh, V.P.; de Lima, M.I.P.; Vieira, G.N. Numerical modeling of surface runoff and erosion due to moving rainstorms at the drainage basin scale. J. Hydrol. 2006, 330, 709–720. [Google Scholar] [CrossRef] [Green Version]
- Heng, B.C.P.; Sander, G.C.; Armstrong, A.; Quinton, J.N.; Chandler, J.H.; Scott, C.F. Modeling the dynamics of soil erosion and size-selective sediment transport over nonuniform topography in flume-scale experiments. Water Resour. Res. 2011, 47, W02513. [Google Scholar] [CrossRef] [Green Version]
- De Lima, J.; Dinis, P.; Souza, C.; de Lima, M.; Cunha, P.; Azevedo, J.; Singh, V.; Abreu, J. Patterns of grainsize temporal variation of sediment transported by overland flow associated with moving storms: Interpreting soil flume experiments. Nat. Hazards Earth Syst. Sci. 2011, 11, 2605–2615. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.-P.; Gires, A.; Pina, R.D.; Reinoso-Rondinel, R.; Bruni, G.; Ichiba, A.; Gaitan, S.; Cristiano, E.; van Assel, J.; et al. Impact of spatial and temporal resolution of rainfall inputs on urban hydrodynamic modelling outputs: A multi-catchment investigation. J. Hydrol. 2015, 531, 389–407. [Google Scholar] [CrossRef]
- Jongman, B.; Kreibich, H.; Apel, H.; Barredo, J.I.; Bates, P.D.; Feyen, L.; Gericke, A.; Neal, J.; Aerts, J.C.J.H.; Ward, P.J. Comparative flood damage model assessment: Towards a European approach. Nat. Hazards Earth Syst. Sci. 2012, 12, 3733–3752. [Google Scholar] [CrossRef] [Green Version]
- Krvavica, N.; Rubinić, J. Evaluation of design storms and critical rainfall durations for flood prediction in partially urbanized catchments. Water 2020, 12, 2044. [Google Scholar] [CrossRef]
- Jencso, K.G.; McGlynn, B.L. Hierarchical controls on runoff generation: Topographically driven hydrologic connectivity, geology, and vegetation. Water Resour. Res. 2011, 47, W11527. [Google Scholar] [CrossRef] [Green Version]
- Sivapalan, M.; Blöschl, G.; Zhang, L.; Vertessy, R. Downward approach to hydrological prediction. Hydrol. Process. 2003, 17, 2101–2111. [Google Scholar] [CrossRef]
- Struthers, I.; Hinz, C.; Sivapalan, M.; Deutschmann, G.; Beese, F.; Meissner, R. Modelling the water balance of a free-draining lysimeter using the downward approach. Hydrol. Process. 2003, 17, 2151–2169. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; García-Navarro, P.; Murillo, J. Influence of mesh structure on 2D full shallow water equations and SCS curve number simulation of rainfall/runoff events. J. Hydrol. 2012, 448–449, 39–59. [Google Scholar] [CrossRef]
- Khosh Bin Ghomash, S.; Caviedes-Voullieme, D.; Hinz, C. Effects of erosion-induced changes to topography on runoff dynamics. J. Hydrol. 2019, 573, 811–828. [Google Scholar] [CrossRef]
- Ghahroudi Tali, M.; Nezammahalleh, M.A. Urban flooding management using the natural drainage system case study: Tehran, capital of Iran. In Floods: From Risk to Opportunity; International Association of Hydrological Science: Wallingford, UK, 2013; Volume 357, pp. 174–180. [Google Scholar]
- Saghafian, B.; Haghnegahdar, A.; Dehghani, M. Effect of ENSO on annual maximum floods and volume over threshold in the southwestern region of Iran. Hydrol. Sci. J. 2017, 62, 1039–1049. [Google Scholar] [CrossRef]
- Yazdi, J.; Salehi Neyshabouri, S.A.A.; Niksokhan, M.H.; Sheshangosht, S.; Elmi, M. Optimal prioritisation of watershed management measures for flood risk mitigation on a watershed scale. J. Flood Risk Manag. 2013, 6, 372–384. [Google Scholar] [CrossRef]
- Jahangir, M.H.; Reineh, S.M.M.; Abolghasemi, M. Spatial predication of flood zonation mapping in Kan River Basin, Iran, using artificial neural network algorithm. Weather Clim. Extrem. 2019, 25, 100215. [Google Scholar] [CrossRef]
- Saleh, A.; Ghobad, R.; Noredin, R. Evaluation of HEC-HMS methods in surface runoff simulation (Case study: Kan watershed, Iran). Adv. Environ. Biol. 2011, 5, 1316–1322. [Google Scholar]
- Habibi, M.; Hourcade, B. Atlas of Tehran Metropolis; Tehran Geographic Information Center: Teheran, Iran; CNRS: Paris, France, 2005; Volume 1. [Google Scholar]
- Ramos, M.C.; Martinez-Casasnovas, J.A. Trends in precipitation concentration and extremes in the Mediterranean Penedes-Anoia region, NE Spain. Clim. Change 2006, 74, 457–474. [Google Scholar] [CrossRef]
- Batisani, N.; Yarnal, B. Rainfall variability and trends in semi-arid Botswana: Implications for climate change adaptation policy. Appl. Geogr. 2010, 30, 483–489. [Google Scholar] [CrossRef]
- Bokaie, M.; Zarkesh, M.K.; Peyman, A.D. Assessment of Urban Heat Island based on the relationship between land surface temperature and land use/land cover in Tehran. Sustain. Cities Soc. 2016, 23, 94–104. [Google Scholar] [CrossRef]
- Hooshyaripor, F.; Faraji-Ashkavar, S.; Koohyian, F.; Tang, Q.; Noori, R. Evaluation of the probable annual flood damage influenced by El-Niño in the Kan River Basin, Iran. Nat. Hazards Earth Syst. Sci. Discuss. 2019, 2019, 2739–2751. [Google Scholar]
- Roshan, G.; Shahraki, S.Z.; Sauri, D. Urban sprawl and climate changes in Tehran. J. Environ. Health Sci. Eng. 2010, 7, 43–52. [Google Scholar]
- Azizi, M.M.; Javanmardi, K. The effects of urban block forms on the patterns of wind and natural ventilation. Procedia Eng. 2017, 180, 541–549. [Google Scholar] [CrossRef]
- Weatherspark, Climate and Average Weather Year Round in Tehran. 2022. Available online: https://weatherspark.com/y/105125/Average-Weather-in-Tehran-Iran-Year-Round (accessed on 2 February 2022).
- Bachmann, D.; Khosh Bin Ghomash, S.; Schotten, R. Neue entwicklungen in der hochwasserrisikoanalyse: Niederschlagsgeneratoren und kritische infrastrukturen. WasserWirtschaft 2021, 111, 32–38. [Google Scholar] [CrossRef]
- Bachmann, D. Beitrag zur Entwicklung eines Entscheidungsunterstützungssystems zur Bewertung und Planung von Hochwasserschutzmaßnahmen. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2012. [Google Scholar]
- Caviedes-Voullième, D.; Fernández-Pato, J.; Hinz, C. Cellular automata and finite volume solvers converge for 2D shallow flow modelling for hydrological modelling. J. Hydrol. 2018, 563, 411–417. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; Fernández-Pato, J.; Hinz, C. Performance assessment of 2D Zero-inertia and shallow water models for simulating rainfall-runoff processes. J. Hydrol. 2020, 584, 124663. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; Macchione, F. Performances and limitations of the diffusive approximation of the 2-d shallow water equations for flood simulation in urban and rural areas. Appl. Numer. Math. 2017, 116, 141–156. [Google Scholar] [CrossRef]
- Bates, P.; Roo, A.D. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Cea, L.; Garrido, M.; Puertas, J. Experimental validation of two-dimensional depth-averaged models for forecasting rainfall–runoff from precipitation data in urban areas. J. Hydrol. 2010, 382, 88–102. [Google Scholar] [CrossRef]
- Echeverribar, I.; Morales-Hernández, M.; Brufau, P.; García-Navarro, P. Analysis of the performance of a hybrid CPU/GPU 1D2D coupled model for real flood cases. J. Hydroinform. 2020, 22, 1198–1216. [Google Scholar] [CrossRef]
- Noh, S.J.; Lee, J.-H.; Lee, S.; Kawaike, K.; Seo, D.-J. Hyper-resolution 1D-2D urban flood modelling using LiDAR data and hybrid parallelization. Environ. Model. Softw. 2018, 103, 131–145. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; García-Navarro, P.; Burguete, J.; Brufau, P. A conservative strategy to couple 1D and 2D models for shallow water flow simulation. Comput. Fluids 2013, 81, 26–44. [Google Scholar] [CrossRef] [Green Version]
- Chen, A.S.; Djordjević, S.; Leandro, J.; Savic, D. The urban inundation model with bidirectional flow interaction between 2D overland surface and 1D sewer networks. In Proceedings of the Novatech 2007, 6th International Conference on Sustainable Techniques and Strategies in Urban Water Management, Lyon, France, 25–28 June 2007. [Google Scholar]
- Brown, J.D.; Spencer, T.; Moeller, I. Modeling storm surge flooding of an urban area with particular reference to modeling uncertainties: A case study of Canvey Island. Water Resour. Res. 2007, 43, W06402. [Google Scholar] [CrossRef] [Green Version]
- Sampson, C.C.; Bates, P.D.; Neal, J.C.; Horritt, M.S. An automated routing methodology to enable direct rainfall in high resolution shallow water models. Hydrol. Process. 2013, 27, 467–476. [Google Scholar] [CrossRef]
- Russo, B.; Sunyer, D.; Velasco, M.; Djordjević, S. Analysis of extreme flooding events through a calibrated 1D/2D coupled model: The case of Barcelona (Spain). J. Hydroinform. 2015, 17, 473–491. [Google Scholar] [CrossRef]
- Chang, T.-J.; Wang, C.-H.; Chen, A.S. A novel approach to model dynamic flow interactions between storm sewer system and overland surface for different land covers in urban areas. J. Hydrol. 2015, 524, 662–679. [Google Scholar] [CrossRef] [Green Version]
- Yin, J.; Yu, D.; Yin, Z.; Liu, M.; He, Q. Evaluating the impact and risk of pluvial flash flood on intra-urban road network: A case study in the city center of Shanghai, China. J. Hydrol. 2016, 537, 138–145. [Google Scholar] [CrossRef] [Green Version]
- Yu, D.; Coulthard, T.J. Evaluating the importance of catchment hydrological parameters for urban surface water flood modelling using a simple hydro-inundation model. J. Hydrol. 2015, 524, 385–400. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Pato, J.; Caviedes-Voullième, D.; García-Navarro, P. Rainfall/runoff simulation with 2D full shallow water equations: Sensitivity analysis and calibration of infiltration parameters. J. Hydrol. 2016, 536, 496–513. [Google Scholar] [CrossRef]
- Löwe, R.; Urich, C.; Domingo, N.S.; Mark, O.; Deletic, A.; Arnbjerg-Nielsen, K. Assessment of urban pluvial flood risk and efficiency of adaptation options through simulations—A new generation of urban planning tools. J. Hydrol. 2017, 550, 355–367. [Google Scholar] [CrossRef] [Green Version]
- Skougaard Kaspersen, P.; Høegh Ravn, N.; Arnbjerg-Nielsen, K.; Madsen, H.; Drews, M. Comparison of the impacts of urban development and climate change on ex-posing European cities to pluvial flooding. Hydrol. Earth Syst. Sci. 2017, 21, 4131–4147. [Google Scholar] [CrossRef] [Green Version]
- Ghorbanian, A.; Kakooei, M.; Amani, M.; Mahdavi, S.; Mohammadzadeh, A.; Hasanlou, M. Improved land cover map of Iran using sentinel imagery within Google Earth engine and a novel automatic workflow for land cover classification using migrated training samples. ISPRS J. Photogramm. Remote Sens. 2020, 167, 276–288. [Google Scholar] [CrossRef]
- Chaplot, V.; Khampaseuth, X.; Valentin, C.; le Bissonais, Y. Interrill erosion in the sloping lands of northern Laos subjected to shift in cultivation. Earth Surf. Process. Landf. 2007, 32, 415–428. [Google Scholar] [CrossRef]
- Pohle, I.; Niebisch, M.; Müller, H.; Schümberg, S.; Zha, T.; Maurer, T.; Hinz, C. Coupling Poisson rectangular pulse and multiplicative microcanonical random cascade models to generate sub-daily precipitation timeseries. J. Hydrol. 2018, 562, 50–70. [Google Scholar] [CrossRef] [Green Version]
- Yazdi, J.; Mohammadiun, S.; Sadiq, R.; Salehi Neyshabouri, S.A.A.; Alavi Gharahbagh, A. Assessment of different MOEAs for rehabilitation evaluation of Urban Stormwater Drainage Systems—Case study: Eastern catchment of Tehran. J. Hydro-Environ. Res. 2018, 21, 76–85. [Google Scholar] [CrossRef]
- Tetzlaff, D.; Uhlenbrook, S. Significance of spatial variability in precipitation for process-oriented modelling: Results from two nested catchments using radar and ground station data. Hydrol. Earth Syst. Sci. 2005, 9, 29–41. [Google Scholar] [CrossRef] [Green Version]
- Ogden, F.L.; Richardson, J.R.; Julien, P.Y. Similarity in catchment response: 2. Moving rainstorms. Water Resour. Res. 1995, 31, 1543–1547. [Google Scholar] [CrossRef]
- Natural Resources Conservation Service, United States Department of Agriculture (NRCS, USDA). National Engineering Handbook: Part 630—Hydrology; USDA Soil Conservation Service: Washington, DC, USA, 2004.
- HEC-HMS Technical Reference Manual, CN Tables. 2022. Available online: https://www.hec.usace.army.mil/confluence/hmsdocs/hmstrm/cn-tables (accessed on 4 February 2022).
- Fernández-Pato, J.; Gracia, J.L.; García-Navarro, P. A fractional-order infiltration model to improve the simulation of rainfall/runoff in combination with a 2D shallow water model. J. Hydroinform. 2018, 20, 898–916. [Google Scholar] [CrossRef]
- Thompson, S.; Katul, G.; Konings, A.; Ridolfi, L. Unsteady overland flow on flat surfaces induced by spatial permeability con-trasts. Adv. Water Resour. 2011, 34, 1049–1058. [Google Scholar] [CrossRef]
- Thomas, I.; Jordan, P.; Shine, O.; Fenton, O.; Mellander, P.-E.; Dunlop, P.; Murphy, P. Defining optimal DEM resolutions and point densities for modelling hydrologically sensitive areas in agricultural catchments dominated by microtopography. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 38–52. [Google Scholar] [CrossRef] [Green Version]
- Helming, K.; Römkens, M.J.M.; Prasad, S.N. Surface roughness related processes of runoff and soil loss: A flume study. Soil Sci. Soc. Am. J. 1998, 62, 243–250. [Google Scholar] [CrossRef]
- Luo, J.; Zheng, Z.; Li, T.; He, S. Spatial heterogeneity of microtopography and its influence on the flow convergence of slopes under different rainfall patterns. J. Hydrol. 2017, 545, 88–99. [Google Scholar] [CrossRef]
- Donohue, R.J.; Roderick, M.L.; McVicar, T.R. On the importance of including vegetation dynamics in Budyko’s hydrological model. Hydrol. Earth Syst. Sci. 2007, 11, 983–995. [Google Scholar] [CrossRef] [Green Version]
- Birkel, C.; Soulsby, C.; Tetzlaff, D. Modelling the impacts of land-cover change onstreamflow dynamics of a tropical rainforest head-water catchment. Hydrol. Sci. J. 2012, 57, 1543–1561. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zhang, Y.; Vaze, J.; Wang, B. Separating effects of vegetation change and climate variability using hydrological modelling and sensitivity-based approaches. J. Hydrol. 2012, 420, 403–418. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; Ahmadinia, E.; Hinz, C. Interactions of microtopography, slope and infiltration cause complex rainfall-runoff behavior at the hillslope scale for single rainfall events. Water Resour. Res. 2021, 57, e2020WR028127. [Google Scholar] [CrossRef]
- Bellen, J. Conservative vs. optimum: Perspective on process design. In Proceedings of the ASEAN’s 16th Regional Symposium on Chemical Engineering, Manila, Philippines, 1–2 December 2009. [Google Scholar] [CrossRef]
- Molinari, D.; Dazzi, S.; Gattai, E.; Minucci, G.; Pesaro, G.; Radice, A.; Vacondio, R. Cost–benefit analysis of flood mitigation measures: A case study employing high-performance hydraulic and damage modelling. Nat. Hazards 2021, 108, 3061–3084. [Google Scholar] [CrossRef]
- Ventimiglia, U.; Candela, A.; Aronica, G.T. A cost efficiency analysis of flood proofing measures for hydraulic risk mitigation in an urbanized riverine area. Water 2020, 12, 2395. [Google Scholar] [CrossRef]
- Beven, K.J. Uniqueness of place and process representations in hydrological modelling. Hydrol. Earth Syst. Sci. 2000, 4, 203–213. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khosh Bin Ghomash, S.; Bachmann, D.; Caviedes-Voullième, D.; Hinz, C. Impact of Rainfall Movement on Flash Flood Response: A Synthetic Study of a Semi-Arid Mountainous Catchment. Water 2022, 14, 1844. https://doi.org/10.3390/w14121844
Khosh Bin Ghomash S, Bachmann D, Caviedes-Voullième D, Hinz C. Impact of Rainfall Movement on Flash Flood Response: A Synthetic Study of a Semi-Arid Mountainous Catchment. Water. 2022; 14(12):1844. https://doi.org/10.3390/w14121844
Chicago/Turabian StyleKhosh Bin Ghomash, Shahin, Daniel Bachmann, Daniel Caviedes-Voullième, and Christoph Hinz. 2022. "Impact of Rainfall Movement on Flash Flood Response: A Synthetic Study of a Semi-Arid Mountainous Catchment" Water 14, no. 12: 1844. https://doi.org/10.3390/w14121844
APA StyleKhosh Bin Ghomash, S., Bachmann, D., Caviedes-Voullième, D., & Hinz, C. (2022). Impact of Rainfall Movement on Flash Flood Response: A Synthetic Study of a Semi-Arid Mountainous Catchment. Water, 14(12), 1844. https://doi.org/10.3390/w14121844






