Three-Dimensional Hole Size (3DHS) Approach for Water Flow Turbulence Analysis over Emerging Sand Bars: Flume-Scale Experiments
Abstract
:1. Introduction
2. Materials and Methods
2.1. Laboratory Experiments
2.2. Experimental TKE Analysis
2.3. Analysis of Octagonal Bursting Events
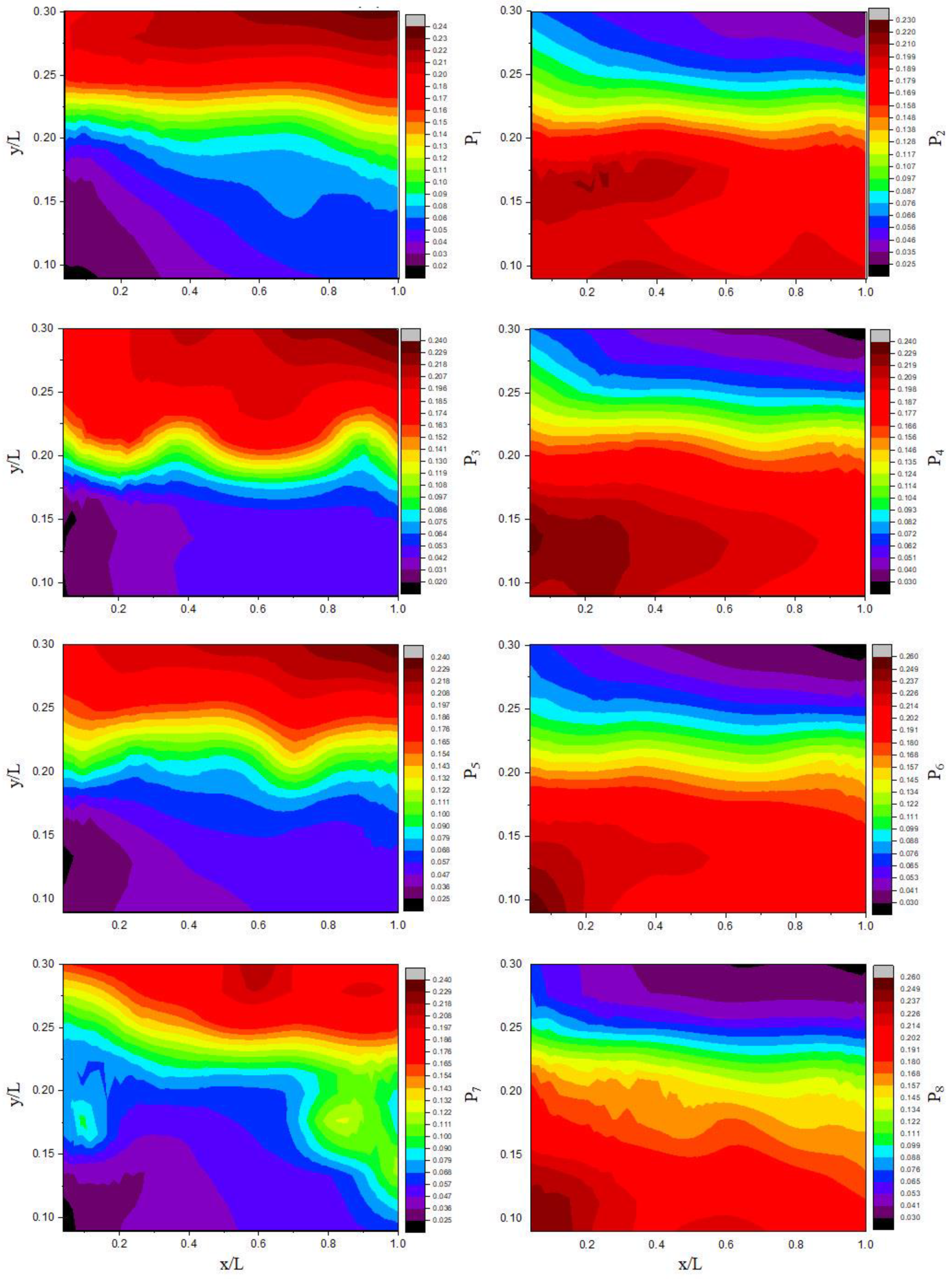
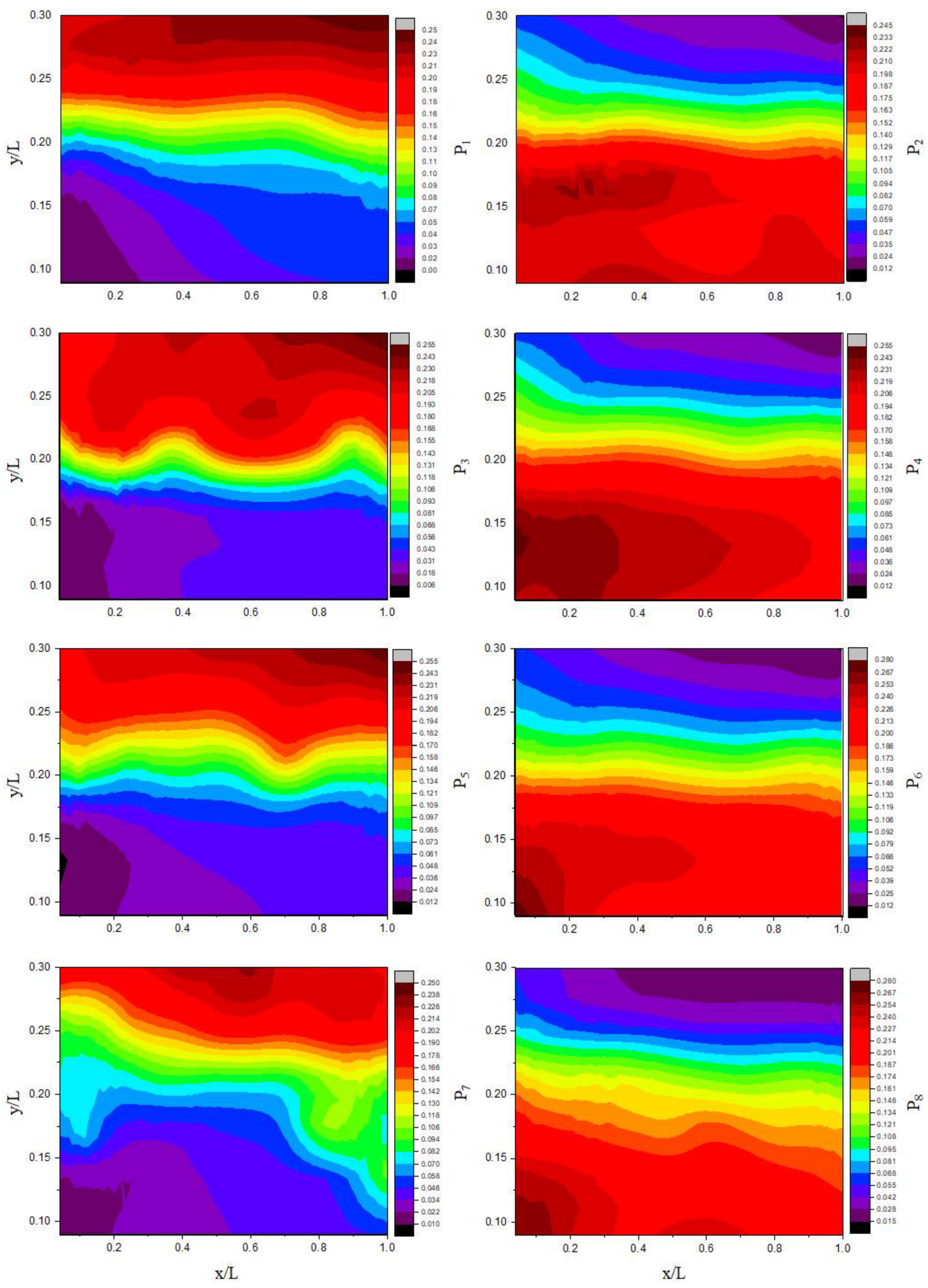
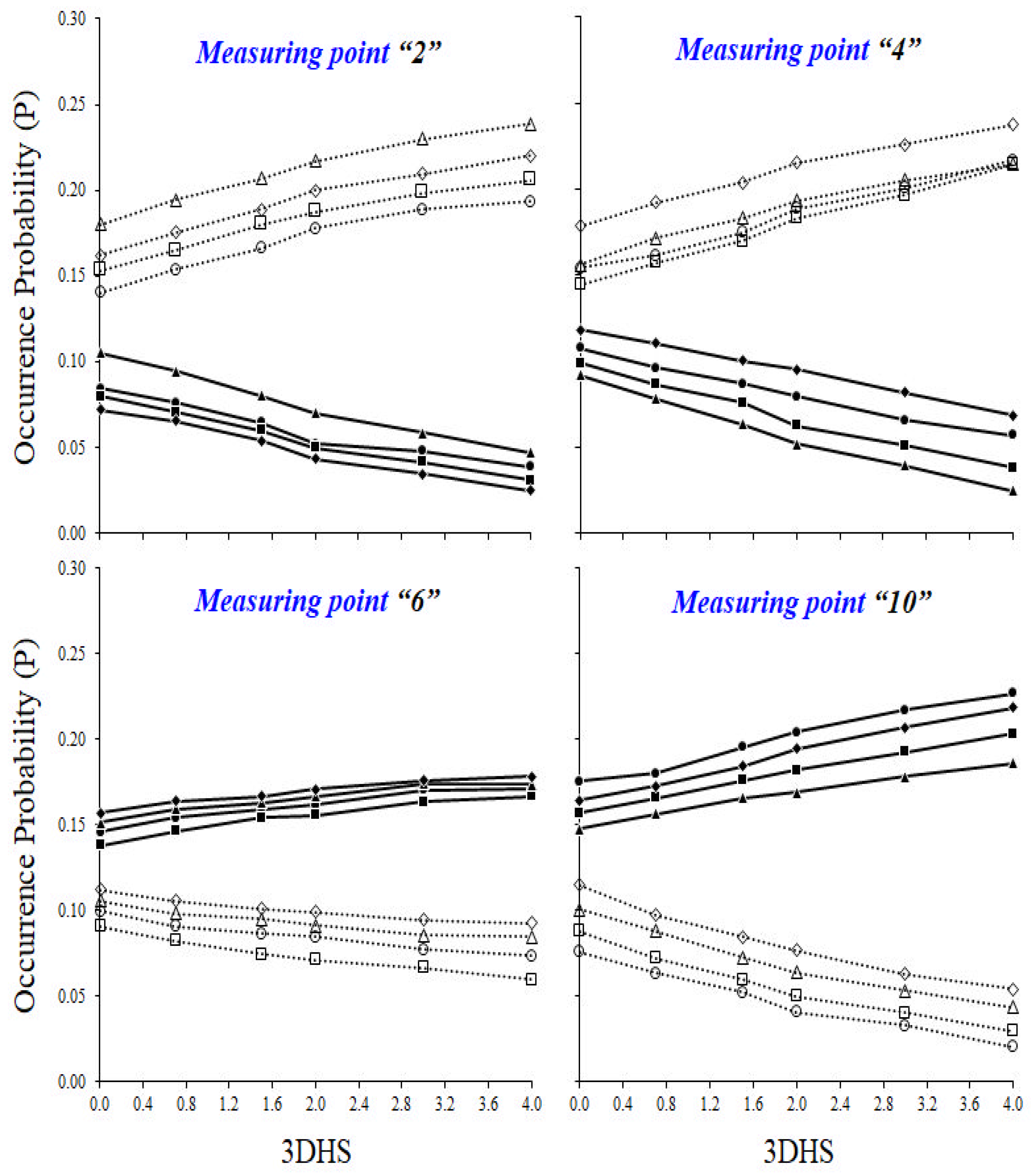
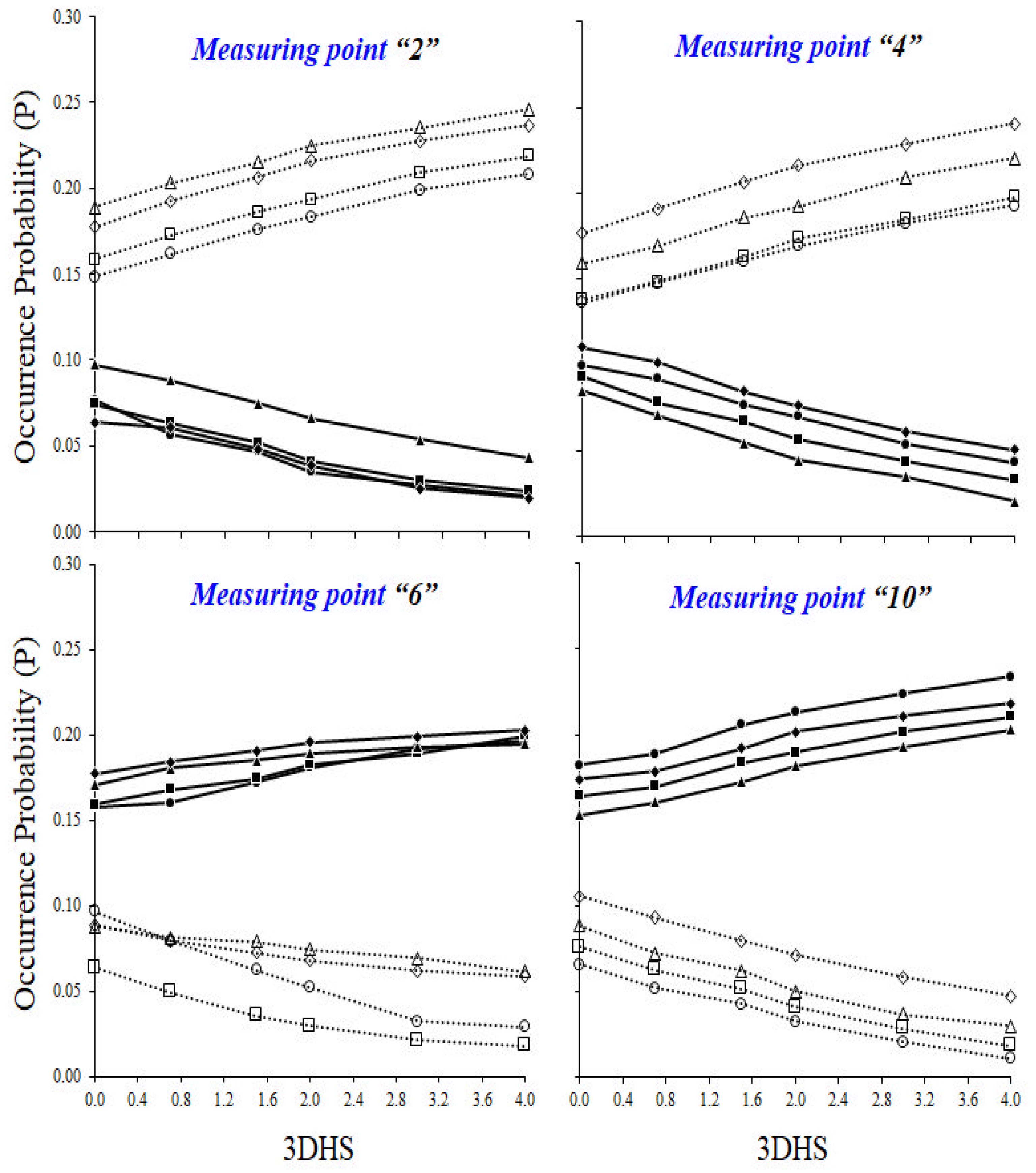
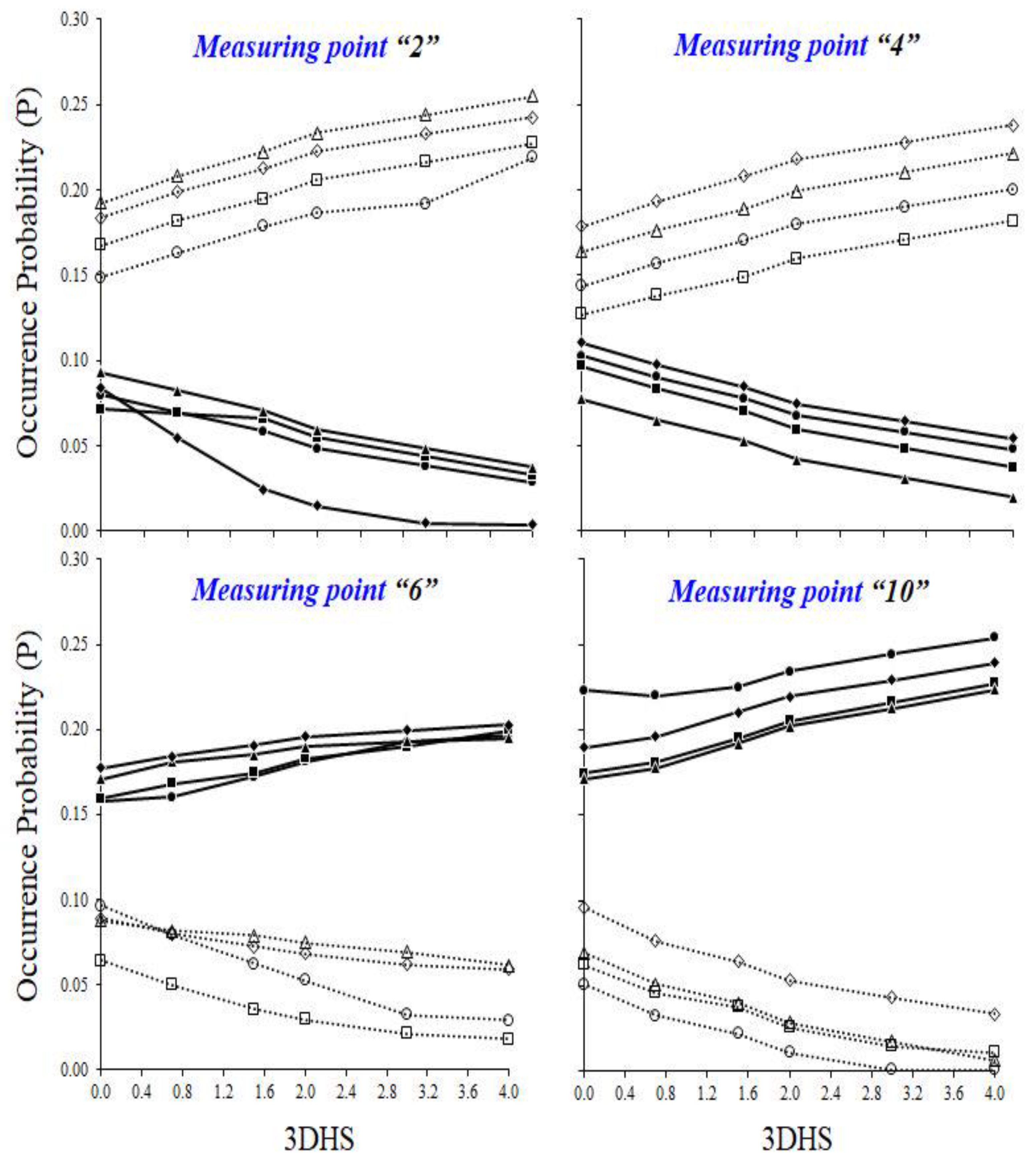
2.4. Analysis of Three-Dimensional Hole Size (3DHS)
3. Results and Discussion
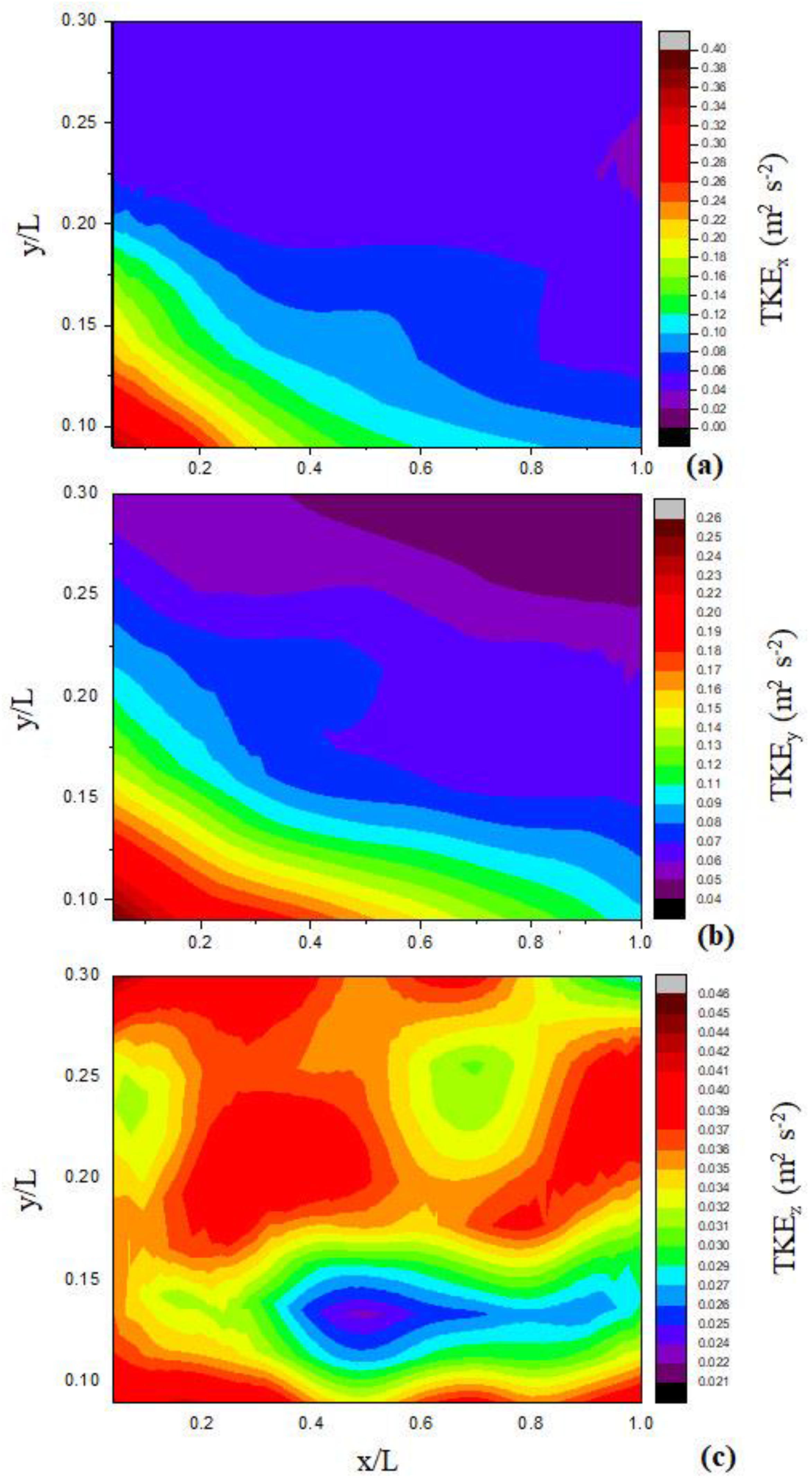
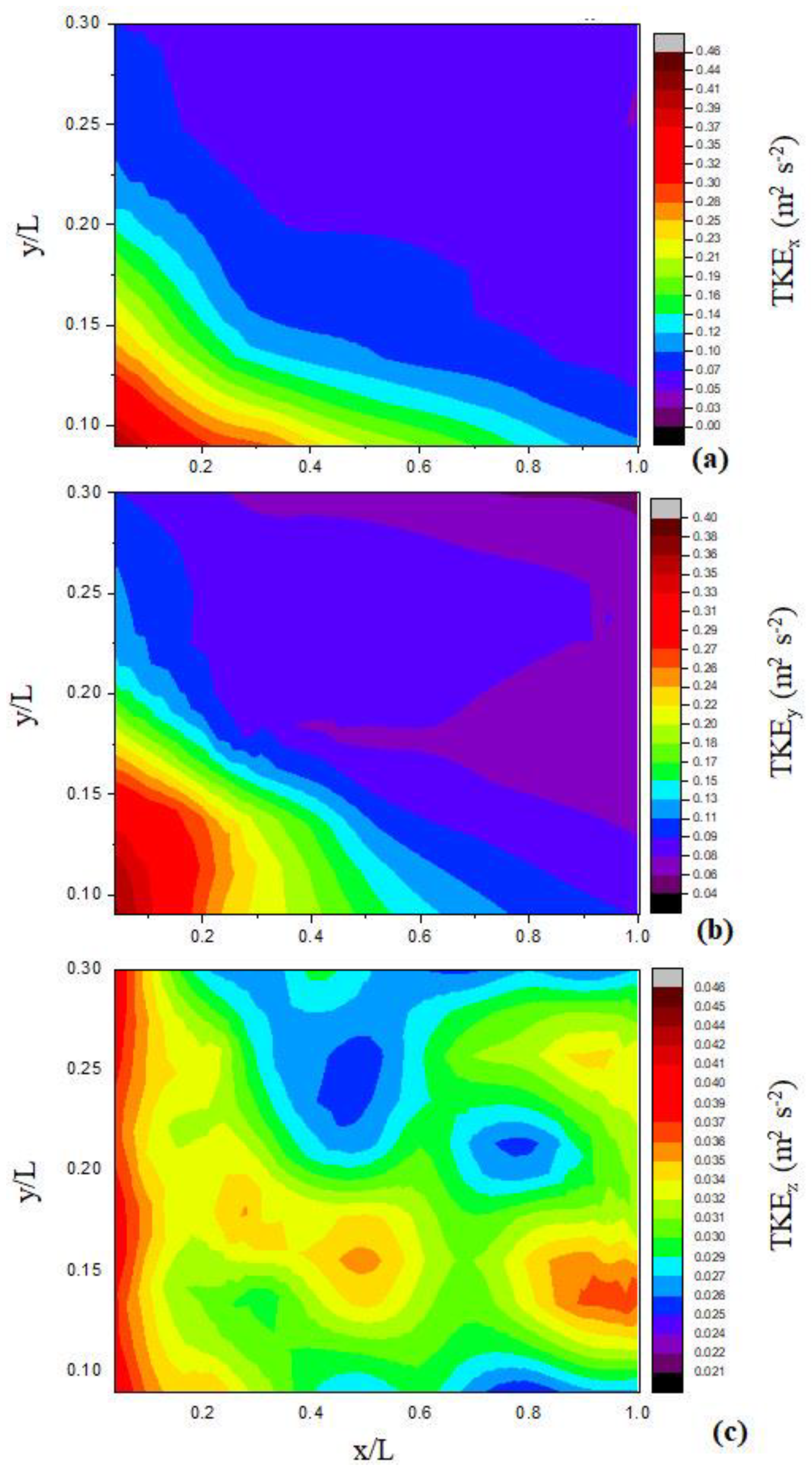
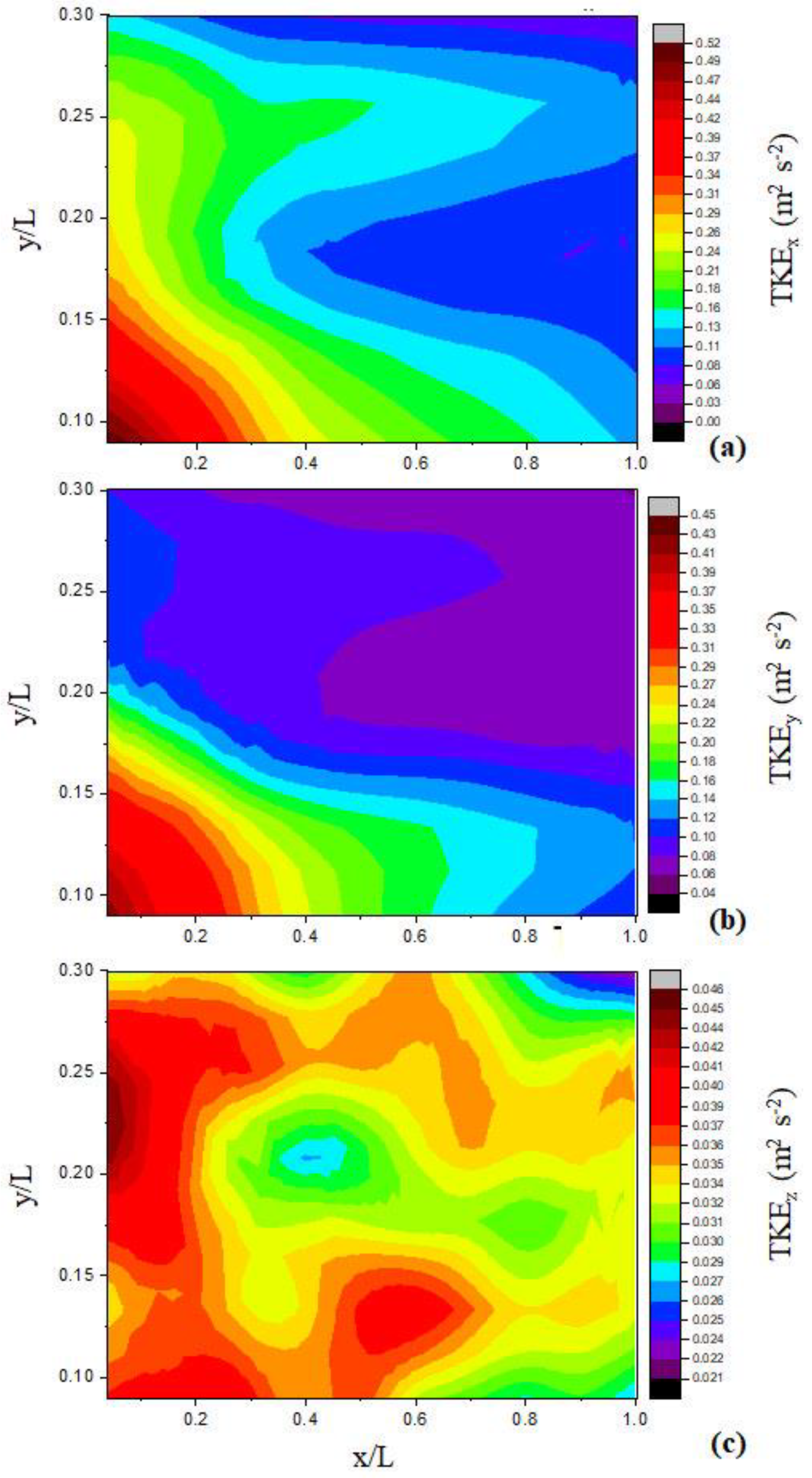
3.1. Experimental TKE Analysis
3.2. Analysis of Octagonal Bursting Events
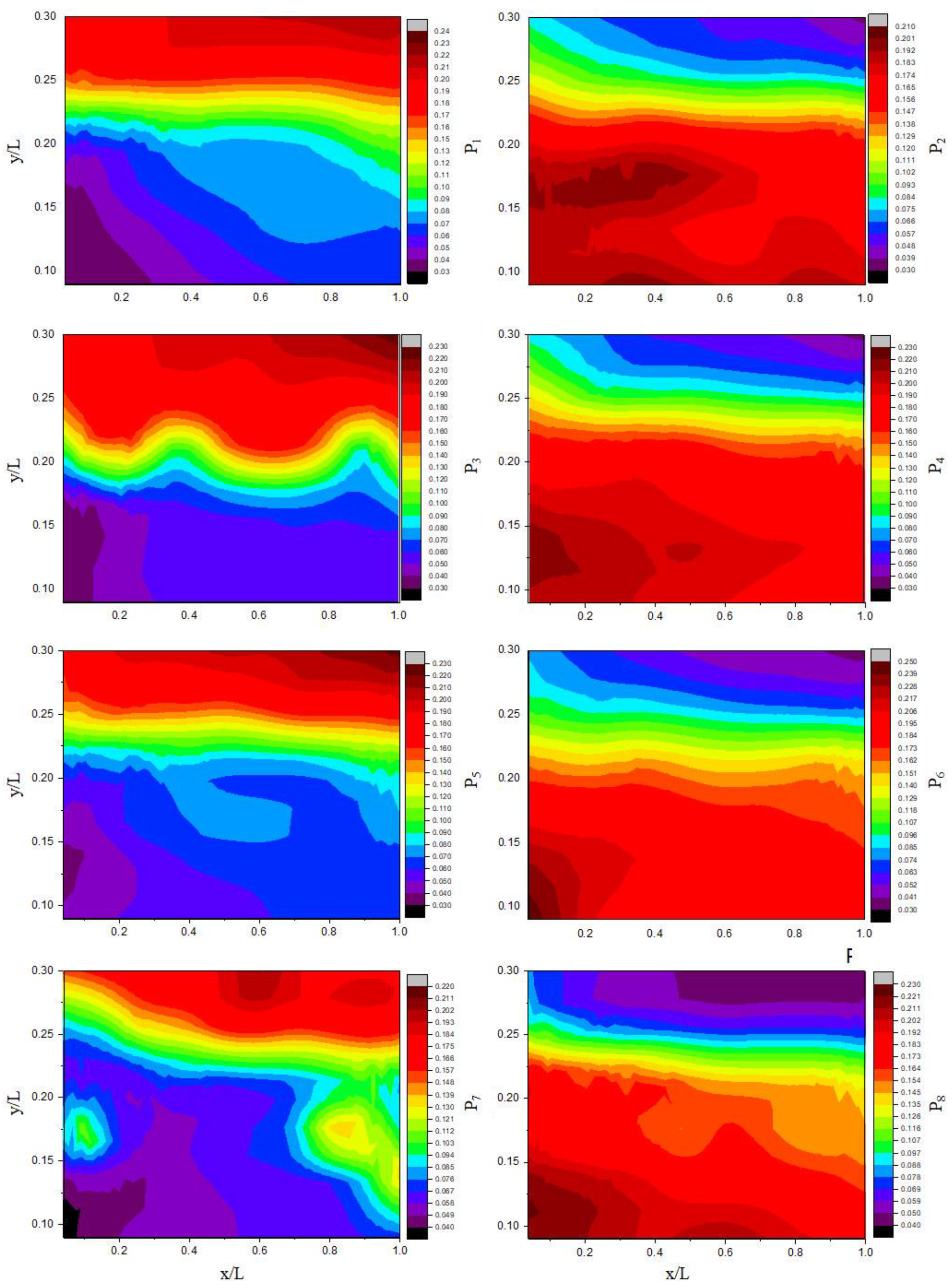
3.3. Analysis of Three-Dimensional Hole Size (3DHS)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, B.; Xu, Y.J. Sediment Trapping by Emerged Channel Bars in the Lowermost Mississippi River during a Major Flood. Water 2015, 7, 6079–6096. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Xu, Y.J.; Wang, B.; Cheng, H. Riverbed dune morphology of the Lowermost Mississippi River – Implications of leeside slope, flow resistance and bedload transport in a large alluvial river. Geomorphology 2021, 385, 107733. [Google Scholar] [CrossRef]
- Garambois, P.-A.; Calmant, S.; Roux, H.; Paris, A.; Monnier, J.; Finaud-Guyot, P.; Samine Montazem, A.; Santos da Silva, J. Hydraulic visibility: Using satellite altimetry to parameterize a hydraulic model of an ungauged reach of a braided river. Hydrol. Process. 2017, 31, 756–767. [Google Scholar] [CrossRef] [Green Version]
- Lama, G.F.C.; Crimaldi, M.; De Vivo, A.; Chirico, G.B.; Sarghini, F. Eco-hydrodynamic characterization of vegetated flows derived by UAV-based imagery. In Proceedings of the 2021 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Trento-Bolzano, Italy, 3–5 November 2021; pp. 273–278. [Google Scholar] [CrossRef]
- Javernick, L.; Redolfi, M.; Bertoldi, W. Evaluation of a numerical model’s ability to predict bed load transport observed in braided river experiments. Adv. Water Resour. 2018, 115, 207–218. [Google Scholar] [CrossRef]
- Donadio, C.; Brescia, M.; Riccardo, A.; Angora, G.; Delli Veneri, M.; Riccio, G. A novel approach to the classification of terrestrial drainage networks based on deep learning and preliminary results on solar system bodies. Sci. Rep. 2021, 11, 5875. [Google Scholar] [CrossRef] [PubMed]
- Gurnell, A.M.; Bertoldi, W.; Francis, R.A.; Gurnell, J.; Mardhiah, U. Understanding processes of island development on an island braided river over timescales from days to decades. Earth Surf. Process. Landf. 2019, 44, 624–640. [Google Scholar] [CrossRef]
- Tauro, F. River basins on the edge of change. Science 2021, 372, 680–681. [Google Scholar] [CrossRef] [PubMed]
- Lama, G.F.C.; Crimaldi, M.; Pasquino, V.; Padulano, R.; Chirico, G.B. Bulk Drag Predictions of Riparian Arundo donax Stands through UAV-acquired Multispectral Images. Water 2021, 13, 1333. [Google Scholar] [CrossRef]
- Yücesan, S.; Schobesberger, J.; Sindelar, C.; Hauer, C.; Habersack, H.; Tritthart, M. Large Eddy Simulation of a sediment particle under entrainment conditions. J. Hydraul. Res. 2022, 60, 568–587. [Google Scholar] [CrossRef]
- Tang, C.; Li, Y.; Acharya, K.; Du, W.; Gao, X.; Luo, L.; Yu, Z. Impact of intermittent turbulent bursts on sediment resuspension and internal nutrient release in Lake Taihu, China. Environ. Sci. Pollut. Res. 2019, 26, 16519–16528. [Google Scholar] [CrossRef]
- Zordan, J.; Juez, C.; Schleiss, A.J.; Franca, M.J. Entrainment, transport and deposition of sediment by saline gravity currents. Adv. Water Resour. 2018, 115, 17–32. [Google Scholar] [CrossRef]
- McSherry, R.; Chua, K.; Stoesser, T.; Mulahasan, S. Free surface flow over square bars at intermediate relative submergence. J. Hydraul. Res. 2018, 56, 825–843. [Google Scholar] [CrossRef] [Green Version]
- Jalalabadi, R.; Stoesser, T.; Ouro, P.; Luo, Q.; Xie, Z. Free surface flow over square bars at different Reynolds numbers. J. Hydro-environ. Res. 2021, 36, 67–76. [Google Scholar] [CrossRef]
- González, C.; Richter, D.H.; Bolster, D.; Bateman, S.; Calantoni, J.; Escauriaza, C. Characterization of bedload intermittency near the threshold of motion using a Lagrangian sediment transport model. Environ. Fluid Mech. 2017, 17, 111–137. [Google Scholar] [CrossRef]
- Branß, T.; Núñez-González, F.; Aberle, J. Fluvial levees in compound channels: A review on formation processes and the impact of bedforms and vegetation. Environ. Fluid Mech. 2022, 22, 559–585. [Google Scholar] [CrossRef]
- Hamidouche, S.; Calluaud, D.; Pineau, G.; Texier, A. Study of instantaneous flow behind a single fixed ripple. J. Hydro-environ. Res. 2018, 19, 117–127. [Google Scholar] [CrossRef]
- Guillén Ludeña, S.; Cheng, Z.; Constantinescu, G.; Franca, M.J. Hydrodynamics of mountain-river confluences and its relationship to sediment transport. J. Geophys. Res. Earth Surf. 2017, 122, 901–924. [Google Scholar] [CrossRef]
- Peruzzi, C.; Poggi, D.; Ridolfi, L.; Manes, C. On the scaling of large-scale structures in smooth-bed turbulent open-channel flows. J. Fluid Mech. 2020, 889, A1. [Google Scholar] [CrossRef]
- Cheng, Z.; Koken, M.; Constantinescu, G. Approximate methodology to account for effects of coherent structures on sediment entrainment in RANS simulations with a movable bed and applications to pier scour. Adv. Water Resour. 2018, 120, 65–82. [Google Scholar] [CrossRef]
- Peruzzi, C.; Vettori, D.; Poggi, D.; Blondeaux, P.; Ridolfi, L.; Manes, C. On the influence of collinear surface waves on turbulence in smooth-bed open-channel flows. J. Fluid Mech. 2021, 924, A6. [Google Scholar] [CrossRef]
- Tsai, C.W.; Huang, S.-H.; Hung, S.Y. Incorporating the memory effect of turbulence structures into suspended sediment transport modeling. Water Resour. Res. 2021, 57, e2020WR028475. [Google Scholar] [CrossRef]
- Sharma, A. Velocity Distribution and the Moments of Turbulent Flow over a Sand-Gravel Mixture Bed. Water Resour. 2021, 49, 81–87. [Google Scholar] [CrossRef]
- Nakagawa, H.; Nezu, I. Prediction of the contributions to the Reynolds stress from bursting events in open-channel flows. J. Fluid Mech. 1977, 80, 99. [Google Scholar] [CrossRef]
- Lu, S.S.; Willmarth, W.W. Measurements of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 1973, 60, 481–511. [Google Scholar] [CrossRef]
- Gualtieri, P.; De Felice, S.; Pasquino, V.; Pulci Doria, G. Use of conventional flow resistance equations and a model for the Nikuradse roughness in vegetated flows at high submergence. JOHH 2018, 66, 107–120. [Google Scholar] [CrossRef] [Green Version]
- Lama, G.F.C.; Errico, A.; Francalanci, S.; Solari, L.; Preti, F.; Chirico, G.B. Evaluation of Flow Resistance Models Based on Field Experiments in a Partly Vegetated Reclamation Channel. Geosciences 2020, 10, 47. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Balachandar, R.; Barron, R. Generation and characterization of fully developed state in open channel flow. J. Fluid Mech. 2022, 934, A35. [Google Scholar] [CrossRef]
- Carbonari, C.; Recking, A.; Solari, L. Morphology, Bedload, and Sorting Process Variability in Response to Lateral Confinement: Results From Physical Models of Gravel-bed Rivers. J. Geophys. Res. Earth Surf. 2020, 125, e2020JF005773. [Google Scholar] [CrossRef]
- Leary, K.C.P.; Schmeeckle, M.W. The importance of splat events to the spatiotemporal structure of near-bed fluid velocity and bed load motion over bed forms: Laboratory experiments downstream of a backward facing step. J. Geophys. Res. Earth Surf. 2017, 122, 2411–2430. [Google Scholar] [CrossRef] [Green Version]
- Schobesberger, J.; Lichtneger, P.; Hauer, C.; Habersack, H.; Sindelar, C. Three-dimensional coherent flow structures during incipient particle motion. J. Hydraul. Eng. 2020, 146, 04020027. [Google Scholar] [CrossRef]
- Volino, R.J.; Simon, T.W. An Application of Octant Analysis to Turbulent and Transitional Flow Data. ASME J. Turbomach. 1994, 116, 752–758. [Google Scholar] [CrossRef]
- Ninto, Y.; Garcia, M.H. Experiments on particle-turbulence interactions in the near-wall region of an open channel flow: Implications for sediment transport. J. Fluid Mech. 1996, 326, 285–319. [Google Scholar] [CrossRef]
- Liu, C.; Gao, Y.; Dong, X.; Liu, C.; Gao, Y.S.; Dong, X.R.; Wang, Y.Q.; Liu, J.M.; Zhang, Y.N.; Cai, X.S.; et al. Third generation of vortex identification methods: Omega and Liutex/Rortex based systems. J. Hydrodyn. 2019, 31, 205–223. [Google Scholar] [CrossRef]
- Elsas, J.H.; Moriconi, L. Vortex identification from local properties of the vorticity field. Phys. Fluids 2017, 29, 015101. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Zhong, W.; Tang, Y. On the relationships between different vortex identification methods based on local trace criterion. Phys. Fluids 2021, 33, 105116. [Google Scholar] [CrossRef]
- Guan, D.; Melville, B.W.; Friedrich, H. Flow patterns and turbulence structures in a scour hole downstream of a submerged weir. J. Hydraul Eng. 2014, 140, 68–76. [Google Scholar] [CrossRef]
- Khan, M.A.; Sharma, N.; Pu, J.H.; Alfaisal, F.M.; Alam, S.; Garg, R.; Qamar, M.O. Mid-Channel Braid-Bar-Induced Turbulent Bursts: Analysis Using Octant Events Approach. Water 2022, 14, 450. [Google Scholar] [CrossRef]
- Borisova, T.D.; Blagoveshchenska, N.F.; Moskvin, I.V.; Rietveld, M.T.; Kosch, M.J.; Thidé, B. Doppler shift simulation of scattered HF signals during the Tromsø HF pumping experiment on 16 February. Ann. Geophys. 2002, 20, 1479–1486. [Google Scholar] [CrossRef] [Green Version]
- Chang, K.A.; Ariyarathne, K.; Mercier, R. Three-dimensional green water velocity on a model structure. Exp. Fluids 2011, 51, 327–345. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Chirico, G.B. Effects of reed beds management on the hydrodynamic behaviour of vegetated open channels. In Proceedings of the 2020 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Trento, Italy, 4–6 November 2020; pp. 149–154. [Google Scholar] [CrossRef]
- Johnson, K.R.; Ting, F.C. Measurements of water surface profile and velocity field at a circular pier. J. Eng. Mech. 2003, 129, 502–513. [Google Scholar] [CrossRef]
- Durgesh, V.; Thomson, J.; Richmond, M.C.; Polagye, B.L. Noise correction of turbulent spectra obtained from acoustic doppler velocimeters. Flow. Meas. Instrum. 2014, 37, 29–41. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Rillo Migliorini Giovannini, M.; Errico, A.; Mirzaei, S.; Padulano, R.; Chirico, G.B.; Preti, F. Hydraulic Efficiency of Green-Blue Flood Control Scenarios for Vegetated Rivers: 1D and 2D Unsteady Simulations. Water 2021, 13, 2620. [Google Scholar] [CrossRef]
- Huang, Y.N.; Cheng, K.; Chen, S.W. On the detection of acoustic-gravity waves generated by typhoon by use of real time HF Doppler frequency shift sounding system. Radio sci. 1985, 20, 897–906. [Google Scholar] [CrossRef]
- Xie, J.; Hu, P.; Pähtz, T.; He, Z.; Cheng, N. Fluid-particle interaction regimes during the evolution of turbidity currents from a coupled LES/DEM model. Adv. Water Res. 2022, 104171. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Giovannini, M.R.M.; Errico, A.; Mirzaei, S.; Chirico, G.B.; Preti, F. The impacts of Nature Based Solutions (NBS) on vegetated flows’ dynamics in urban areas. In Proceedings of the 2021 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Trento-Bolzano, Italy, 3–5 November 2021; pp. 58–63. [Google Scholar] [CrossRef]
- Calvo, L.; De Padova, D.; Mossa, M.; Rosman, P. Non-Hydrostatic Discontinuous/Continuous Galerkin Model for Wave Propagation, Breaking and Runup. Computation 2021, 9, 47. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Melville, B.; Ball, J. Three-dimensional analysis of coherent turbulent flow structure around a single circular bridge pier. Environ. Fluid Mech. 2014, 14, 821–847. [Google Scholar] [CrossRef]
- Lee, S.O.; Abid, I.; Hong, S.H. Effect of complex shape of pier foundation exposure on time development of scour. Environ. Fluid Mech. 2021, 21, 103–127. [Google Scholar] [CrossRef]
- Nikou, N.R.; Ziaei, A.N.; Ansary, H.; McDonough, J.M. Flow field investigation in a vortex settling basin using Acoustic Doppler Velocimetry and large eddy simulation. Water Environ. J. 2021, 35, 865–883. [Google Scholar] [CrossRef]
- Li, D.; Yang, Z.; Guo, M. Study of Suspended Sediment Diffusion Coefficients in Submerged Vegetation Flow. Water Resour. Res. 2022, 58, e2021WR031155. [Google Scholar] [CrossRef]
- Mali, M.; De Serio, F.; Dell’Anna, M.M.; Mastrorilli, P.; Damiani, L.; Mossa, M. Enhancing the performance of hazard indexes in assessing hot spots of harbour areas by considering hydrodynamic parameters. Ecol. Indic. 2017, 73, 38–45. [Google Scholar] [CrossRef]
- Bianco, F.; Race, M.; Papirio, S.; Esposito, G. Removal of polycyclic aromatic hydrocarbons during anaerobic biostimulation of marine sediments. Sci. Tot. Environ. 2020, 709, 136141. [Google Scholar] [CrossRef] [PubMed]
- Thompson, J.; Sattar, A.M.A.; Gharabaghi, B.; Warner, R.C. Event-based total suspended sediment particle size distribution model. J. Hydrol. 2016, 536, 236–246. [Google Scholar] [CrossRef]
- Chavan, R.; Gualtieri, P.; Kumar, B. Turbulent Flow Structures and Scour Hole Characteristics around Circular Bridge Piers over Non-Uniform Sand Bed Channels with Downward Seepage. Water 2019, 11, 1580. [Google Scholar] [CrossRef] [Green Version]
- Bianco, F.; Monteverde, G.; Race, M.; Papirio, S.; Esposito, G. Comparing performances, costs and energy balance of ex situ remediation processes for PAH-contaminated marine sediments. Environ. Sci. Pollut. Res. 2020, 27, 19363–19374. [Google Scholar] [CrossRef]
- Palermo, M.; Bombardelli, F.A.; Pagliara, S.; Kuroiwa, J. Time-dependent scour processes on granular beds at large scale. Environ. Fluid Mech. 2021, 21, 791–816. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Crimaldi, M. Remote Sensing of Ecohydrological, Ecohydraulic, and Ecohydrodynamic Phenomena in Vegetated Waterways: The Role of Leaf Area Index (LAI). Biol. Life Sci. Forum 2021, 3, 54. [Google Scholar] [CrossRef]
- Waldschläger, K.; Brückner, M.Z.M.; Almroth, B.C.; Hackney, C.R.; Adyel, T.M.; Alimi, S.O.; Belontz, S.L.; Cowger, W.; Doyle, D.; Gray, A.; et al. Learning from natural sediments to tackle microplastics challenges: A multidisciplinary perspective. Earth-Sci. Rev. 2022, 228, 104021. [Google Scholar] [CrossRef]
- Huang, A.; Liu, X.; Peng, W.; Dong, F.; Ma, B.; Li, J.; Wang, W. Spatiotemporal Characteristics, Influencing Factors and Evolution Laws of Water Exchange Capacity of Poyang Lake. J. Hydrol. 2022, 609, 127717. [Google Scholar] [CrossRef]
- Qi, M.; Li, J.; Chen, Q.; Zhang, Q. Roughness effects on near-wall turbulence modelling for open-channel flows. J. Hydraul. Res. 2018, 56, 648–661. [Google Scholar] [CrossRef]
- Ali, N.; Hamilton, N.; Calaf, M.; Cal, R.B. Turbulence kinetic energy budget and conditional sampling of momentum, scalar, and intermittency fluxes in thermally stratified wind farms. J. Turbul. 2019, 20, 32–63. [Google Scholar] [CrossRef] [Green Version]
- Przyborowski, L.; Łoboda, A.M. Identification of coherent structures downstream of patches of aquatic vegetation in a natural environment. J. Hydrol. 2021, 596, 126123. [Google Scholar] [CrossRef]
- Zhang, X.; Nepf, H.M. Reconfiguration of and drag on marsh plants in combined waves and current. J. Fluids Struct. 2022, 110, 103539. [Google Scholar] [CrossRef]
- Park, G.I.; Wallace, J.M.; Wu, X.; Moin, P. Boundary layer turbulence in transitional and developed states. Phys. Fluids 2012, 24, 035105. [Google Scholar] [CrossRef] [Green Version]
- Bauri, K.P.; Sarkar, A. Turbulent bursting events within equilibrium scour holes around aligned submerged cylinder. J. Turbul. 2020, 21, 53–83. [Google Scholar] [CrossRef]
- Yuan, S.; Tang, H.; Li, K.; Xu, L.; Xiao, Y.; Gualtieri, C.; Rennie, C.; Melville, B. Hydrodynamics, sediment transport and morphological features at the confluence between the Yangtze River and the Poyang Lake. Water Resour. Res. 2021, 57, e2020WR028284. [Google Scholar] [CrossRef]
- Yuan, S.; Zhu, Y.; Tang, H.; Xu, L.; Li, K.; Xiao, Y.; Gualtieri, C. Planform evolution and hydrodynamics near the multi-channel confluence between the Yarlung Zangbo River and the delta of the Niyang River. Geomorphology 2022, 402, 108157. [Google Scholar] [CrossRef]
- Ölçmen, S.M.; Simpson, R.L.; Newby, J.W. Octant analysis based structural relations for three-dimensional turbulent boundary layers. Phys. Fluids 2006, 18, 02510. [Google Scholar] [CrossRef] [Green Version]
- Keylock, C.J.; Lane, S.N.; Richards, K.S. Quadrant/octant sequencing and the role of coherent structures in bed load sediment entrainment. J. Geophys. Res. Earth Surf. 2014, 119, 264–286. [Google Scholar] [CrossRef]
- Shi, Y.; Xia, Z.; Chen, S. A new identification method in sampled quadrant analysis for wall-bounded turbulence. Phys. Fluids 2016, 28, 061702. [Google Scholar] [CrossRef]
- Wallace, J.M. Quadrant analysis in turbulence research: History and evolution. Annu. Rev. Fluid Mech. 2016, 48, 131–158. [Google Scholar] [CrossRef]
- Xu, F.; Zhong, S.; Zhang, S. Experimental study on secondary flow in turbulent boundary layer over spanwise heterogeneous microgrooves. Phys. Fluids 2020, 32, 035109. [Google Scholar] [CrossRef]
- Hou, J.; Babak, L.; Hokmabad, V.; Ghaemi, S. Three-dimensional measurement of turbulent flow over a riblet surface. Exp. Therm. Fluid Sci. 2017, 85, 229–239. [Google Scholar] [CrossRef]
- Di Bernardino, A.; Monti, P.; Leuzzi, G.; Querzoli, G. Turbulent Schmidt Number Measurements Over Three-Dimensional Cubic Arrays. Boundary-Layer Meteorol. 2020, 174, 231–250. [Google Scholar] [CrossRef] [Green Version]
- De Serio, F.; Mossa, M. Analysis of mean velocity and turbulence measurements with ADCPs. Adv. Water Resour. 2015, 81, 172–185. [Google Scholar] [CrossRef]
- Errico, A.; Lama, G.F.C.; Francalanci, S.; Chirico, G.B.; Solari, L.; Preti, F. Flow dynamics and turbulence patterns in a drainage channel colonized by common reed (Phragmites australis) under different scenarios of vegetation management. Ecol. Eng. 2019, 133, 39–52. [Google Scholar] [CrossRef]
- De Padova, D.; Meftah, M.B.; Mossa, M.; Sibilla, S. A multi-phase SPH simulation of hydraulic jump oscillations and local scouring processes downstream of bed sills. Adv. Water Resour. 2022, 159, 104097. [Google Scholar] [CrossRef]
- Deshpande, V.; Kumar, B. Turbulent flow structures in alluvial channels with curved cross-sections under conditions of downward seepage. Earth Surf. Process. Landf. 2016, 41, 1073–1087. [Google Scholar] [CrossRef]
- Agarwal, M.; Deshpande, V.; Katoshevski, D.; Kumar, B. A novel Python module for statistical analysis of turbulence (P-SAT) in geophysical flows. Sci. Rep. 2021, 11, 3998. [Google Scholar] [CrossRef]
- Dey, S.; Sakar, S.; Solari, L. Near-bed turbulence characteristics at the entrainment threshold of sediment beds. J. Hydraul. Eng. 2011, 137, 945–958. [Google Scholar] [CrossRef]
- Poggi, D.; Katul, G.G.; Albertson, J.D. Momentum Transfer and Turbulent Kinetic Energy Budgets within a Dense Model Canopy. Boundary-Layer Meteorol. 2004, 111, 589–614. [Google Scholar] [CrossRef]
- Franca, M.J.; Lemmin, U. Eliminating velocity aliasing in acoustic Doppler velocity profiler data. Meas. Sci. Technol. 2006, 17, 313. [Google Scholar] [CrossRef]
- James, C.N.; Houze, R.A., Jr. A real-time four-dimensional Doppler dealiasing scheme. J. Atmos. Ocean. Technol. 2001, 18, 1674–1683. [Google Scholar] [CrossRef]
- Gong, J.D.; Wang, L.L.; Xu, Q. A three-step dealiasing method for Doppler velocity data quality control. J. Atmos. Ocean. Technol. 2003, 20, 1738–1748. [Google Scholar] [CrossRef]
- Lemmin, U.; Rolland, T. Acoustic velocity profiler for laboratory and field studies. J. Hydraul. Eng. 1997, 123, 1089–1098. [Google Scholar] [CrossRef]
- Rinoshika, H.; Rinoshika, A.; Wang, J.J.; Zheng, Y. 3D flow structures behind a wall-mounted short cylinder. Ocean Eng. 2021, 221, 108535. [Google Scholar] [CrossRef]
- Sadeghifar, T.; Lama, G.F.C.; Sihag, P.; Bayram, A.; Kisi, O. Wave height predictions in complex sea flows through soft computing models: Case study of Persian gulf. Ocean Eng. 2022, 245, 110467. [Google Scholar] [CrossRef]
- Tang, Z.; Jiang, N. The effect of a synthetic input on small-scale intermittent bursting events in near-wall turbulence. Phys. Fluids 2020, 32, 015110. [Google Scholar] [CrossRef]
- Morani, M.C.; Simão, M.; Gazur, I.; Santos, R.S.; Carravetta, A.; Fecarotta, O.; Ramos, H.M. Pressure Drop and Energy Recovery with a New Centrifugal Micro-Turbine: Fundamentals and Application in a Real WDN. Energies 2022, 15, 1528. [Google Scholar] [CrossRef]
- Busico, G.; Alessandrino, L.; Mastrocicco, M. Denitrification in Intrinsic and Specific Groundwater Vulnerability Assessment: A Review. Appl. Sci. 2021, 11, 10657. [Google Scholar] [CrossRef]
- Guan, D.; Agarwal, P.; Chiew, Y.M. Quadrant analysis of turbulence in a rectangular cavity with large aspect ratios. J. Hydraul. Eng. 2018, 144, 04018035. [Google Scholar] [CrossRef]
- Busico, G.; Colombani, N.; Fronzi, D.; Pellegrini, M.; Tazioli, A.; Mastrocicco, M. Evaluating SWAT model performance, considering different soils data input, to quantify actual and future runoff susceptibility in a highly urbanized basin. J. Environ. Manage. 2020, 266, 110625. [Google Scholar] [CrossRef] [PubMed]
- Lama, G.F.C.; Sadeghifar, T.; Azad, M.T.; Sihag, P.; Kisi, O. On the Indirect Estimation of Wind Wave Heights over the Southern Coasts of Caspian Sea: A Comparative Analysis. Water 2022, 14, 843. [Google Scholar] [CrossRef]
- Ramos, H.M.; Morani, M.C.; Carravetta, A.; Fecarrotta, O.; Adeyeye, K.; López-Jiménez, P.A.; Pérez-Sánchez, M. New Challenges towards Smart Systems’ Efficiency by Digital Twin in Water Distribution Networks. Water 2022, 14, 1304. [Google Scholar] [CrossRef]
- Peng, W.; Yuan, Z.; Wang, J. Attention-enhanced neural network models for turbulence simulation. Phys Fluids 2022, 34, 025111. [Google Scholar] [CrossRef]
- Khan, A.M.; Sharma, N.; Pandey, M.; Qamar, O. Turbulent characteristics of flow in the vicinity of mid-channel braid bar. Can. J. Civ. Eng. 2021, 48, 879–887. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Errico, A.; Francalanci, S.; Solari, L.; Preti, F.; Chirico, G.B. Comparative analysis of modeled and measured vegetative Chézy’s flow resistance coefficients in a drainage channel vegetated by dormant riparian reed. In Proceedings of the International IEEE Workshop on Metrology for Agriculture and Forestry, Portici, Italy, 4–6 November 2020; pp. 180–184. [Google Scholar] [CrossRef]
- Yunping, Y.; Jinhai, Z.; Mingjin, Z.; Lingling, Z.; Yude, Z.; Jianjun, W.; Weiyang, Z. Sandy riverbed shoal under anthropogenic activities: The sandy reach of the Yangtze River, China. J. Hydrol. 2021, 603, 126861. [Google Scholar] [CrossRef]
- Khan, M.A.; Sharma, N.; Singhal, G.D. Experimental study on bursting events around a bar in physical model of a braided channel. ISH J. Hydraul. Eng. 2017, 23, 63–70. [Google Scholar] [CrossRef]
- Manna, M.; Vacca, A.; Verzicco, R. Reverse transition of a turbulent spiral Poiseuille flow at $Ta=1500$. J. Fluid Mech. 2022, 941, A6. [Google Scholar] [CrossRef]
- Yunping, Y.; Jinhai, Z.; Huaqing, Z.; Yuanfang, C.; Yude, Z.; Chenyang, W. Impact of the Three Gorges Dam on riverbed scour and siltation of the middle reaches of the Yangtze River. Earth Surf. Process. Landf. 2022, 209, 1514–1531. [Google Scholar] [CrossRef]
- Khan, M.A.; Sharma, N.; Garg, R.; Biswas, T. Contribution of quadrant bursting events to the turbulent flow structure at region close to the mid-channel bar. ISH J. Hydraul. Eng. 2021, 1–10. [Google Scholar] [CrossRef]
- Hasan, M.S.U.; Rai, A.K.; Ahmad, Z.; Alfaisal, F.M.; Khan, M.A.; Alam, S.; Sahana, M. Hydrometeorological consequences on the water balance in the ganga river system under changing climatic conditions using land surface model. J. King Saud Univ. Sci. 2022, 34, 102065. [Google Scholar] [CrossRef]
- Khan, M.D.; Sharma, N. Analysis of turbulent flow characteristics around bar using the conditional bursting technique for varying discharge conditions. KSCE J. Civ. Eng. 2018, 22, 2315–2324. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Cantero-Chinchilla, F.N.; Hager, W.H. High-order shallow water expansions in free surface flows: Application to steady overflow processes. Ocean Eng. 2022, 250, 110717. [Google Scholar] [CrossRef]
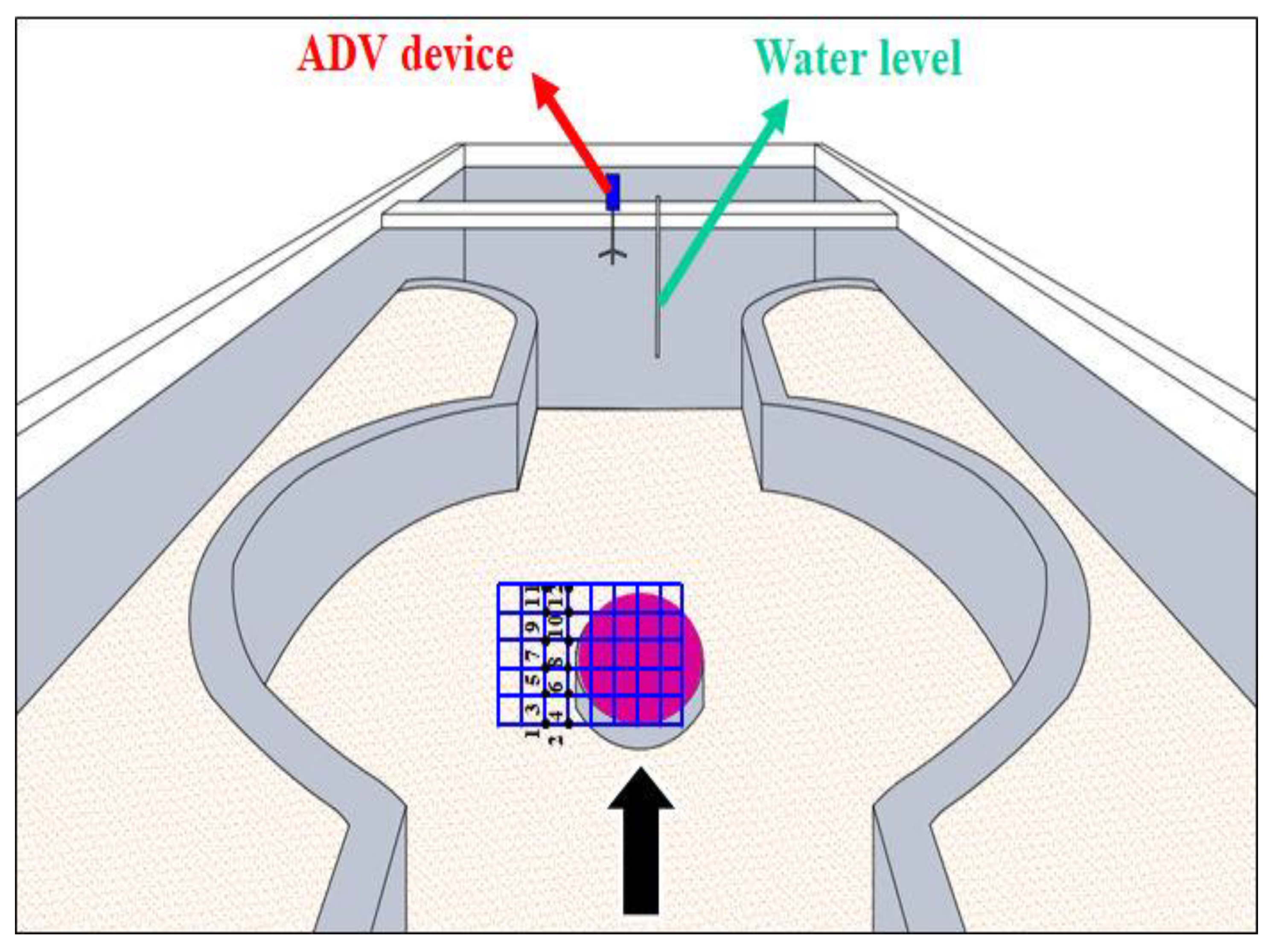
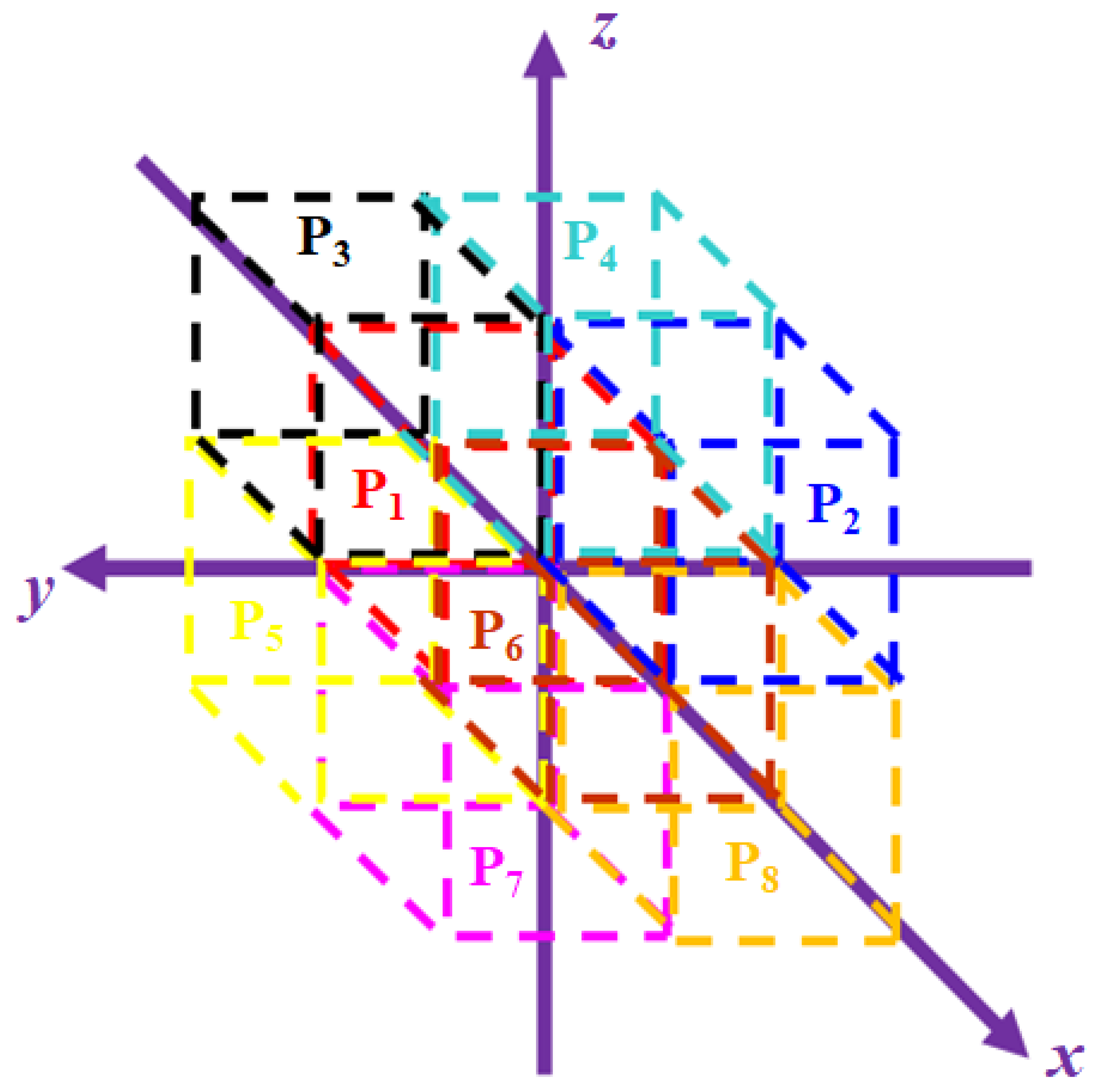
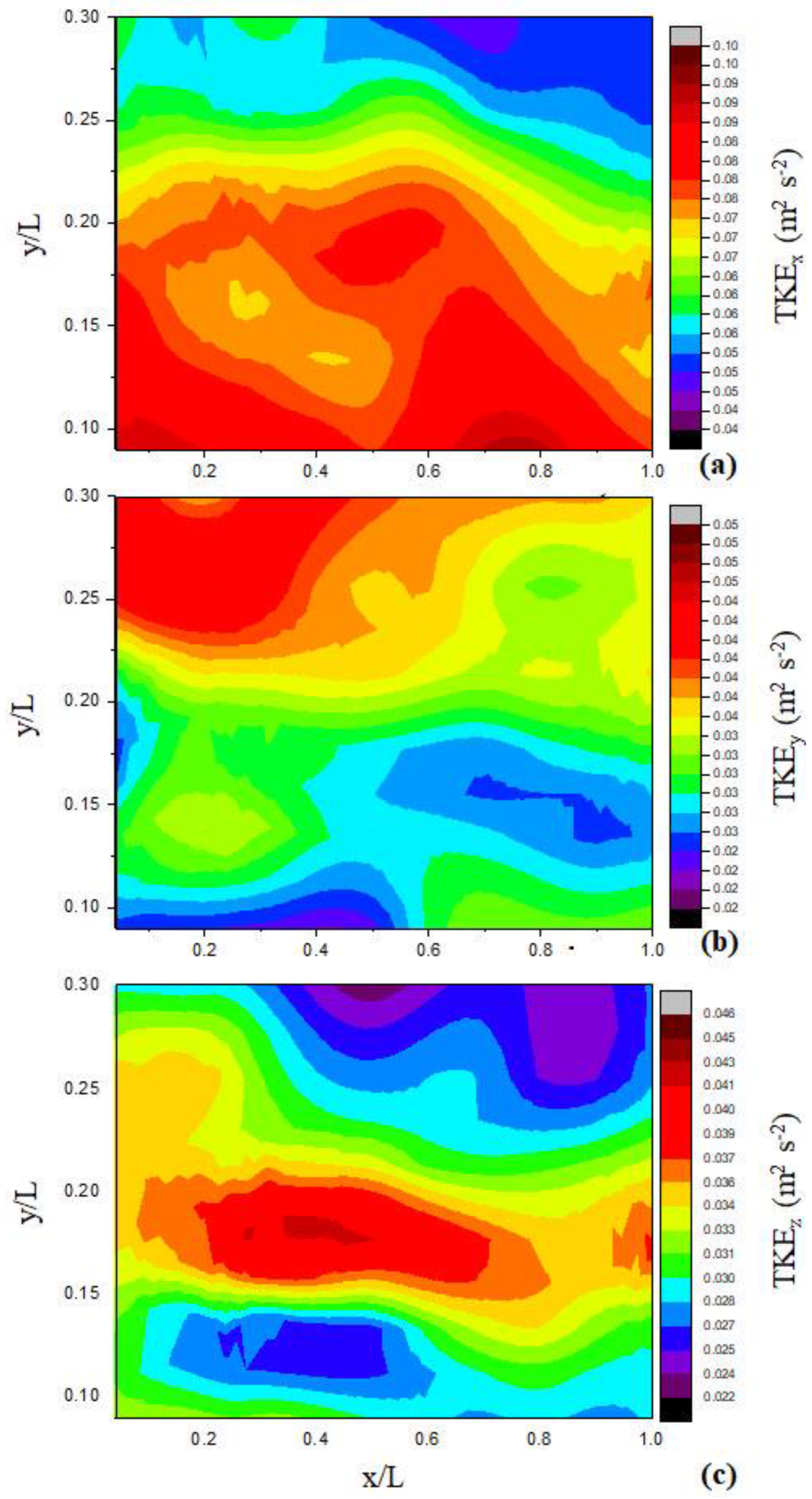
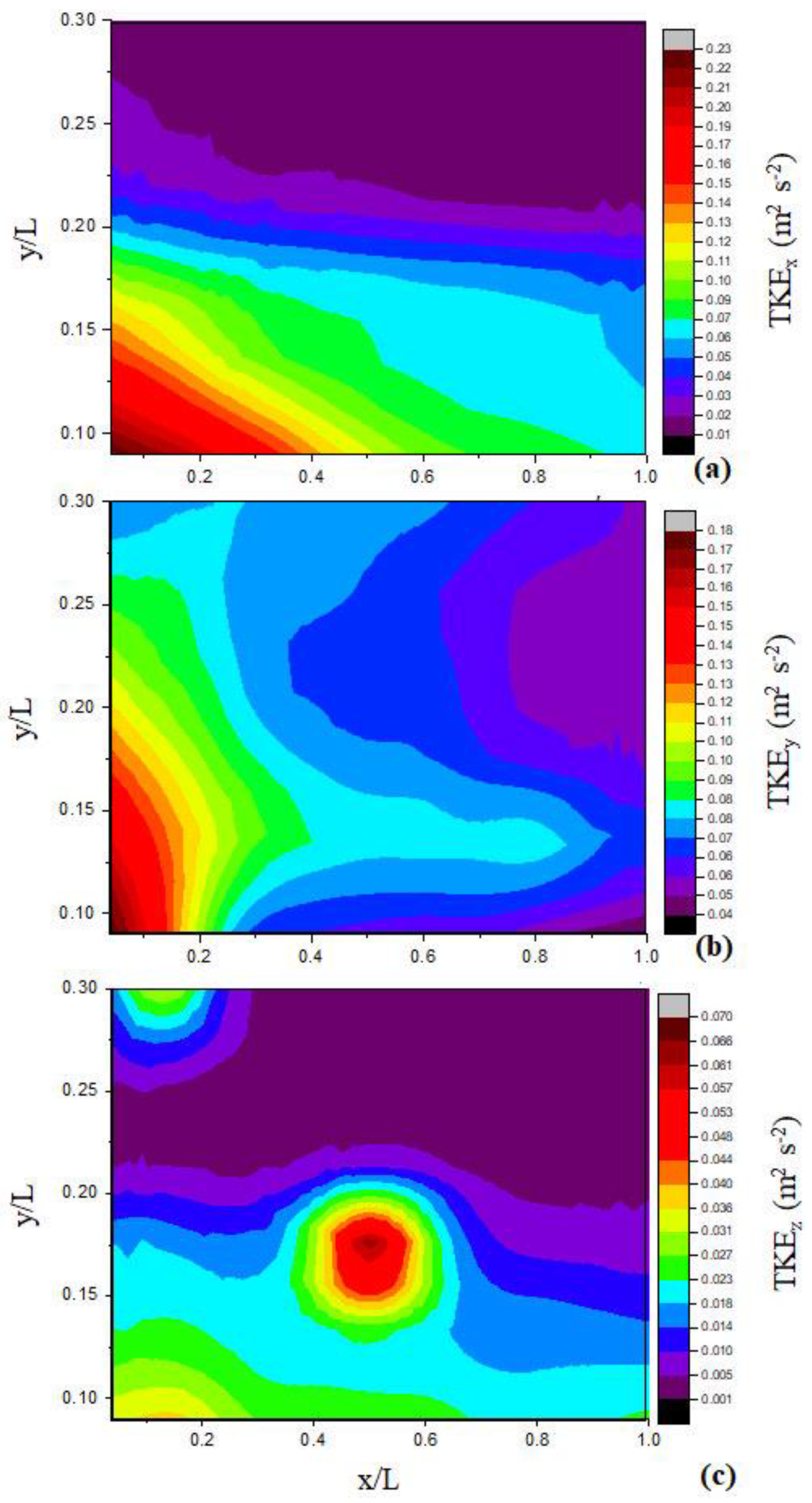


| Flow Velocity Range (mm s−1) | ADV Error Range (mm s−1) |
|---|---|
| ±50 | ±0.88 |
| ±100 | ±0.83 |
| ±200 | ±1.01 |
| Experimental Run | hb/h | b × l × hb |
|---|---|---|
| 1R | - | - |
| 2R | 0.25 | 80 × 130 × 8 |
| 3R | 0.31 | 80 × 130 × 10 |
| 4R | 0.41 | 80 × 130 × 13 |
| 5R | 0.47 | 80 × 130 × 15 |
| 6R | 0.53 | 80 × 130 × 17 |
| 7R | 0.59 | 80 × 130 × 19 |
| 8R | 0.66 | 80 × 130 × 21 |
| 9R | 0.72 | 80 × 130 × 23 |
| 10R | 0.81 | 80 × 130 × 26 |
| 11R | 0.88 | 80 × 130 × 28 |
| 12R | 0.90 | 80 × 130 × 29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.A.; Sharma, N.; Lama, G.F.C.; Hasan, M.; Garg, R.; Busico, G.; Alharbi, R.S. Three-Dimensional Hole Size (3DHS) Approach for Water Flow Turbulence Analysis over Emerging Sand Bars: Flume-Scale Experiments. Water 2022, 14, 1889. https://doi.org/10.3390/w14121889
Khan MA, Sharma N, Lama GFC, Hasan M, Garg R, Busico G, Alharbi RS. Three-Dimensional Hole Size (3DHS) Approach for Water Flow Turbulence Analysis over Emerging Sand Bars: Flume-Scale Experiments. Water. 2022; 14(12):1889. https://doi.org/10.3390/w14121889
Chicago/Turabian StyleKhan, Mohammad Amir, Nayan Sharma, Giuseppe Francesco Cesare Lama, Murtaza Hasan, Rishav Garg, Gianluigi Busico, and Raied Saad Alharbi. 2022. "Three-Dimensional Hole Size (3DHS) Approach for Water Flow Turbulence Analysis over Emerging Sand Bars: Flume-Scale Experiments" Water 14, no. 12: 1889. https://doi.org/10.3390/w14121889
APA StyleKhan, M. A., Sharma, N., Lama, G. F. C., Hasan, M., Garg, R., Busico, G., & Alharbi, R. S. (2022). Three-Dimensional Hole Size (3DHS) Approach for Water Flow Turbulence Analysis over Emerging Sand Bars: Flume-Scale Experiments. Water, 14(12), 1889. https://doi.org/10.3390/w14121889








