Application of Image Technique to Obtain Surface Velocity and Bed Elevation in Open-Channel Flow
Abstract
:1. Introduction
2. Mathematical Formulation
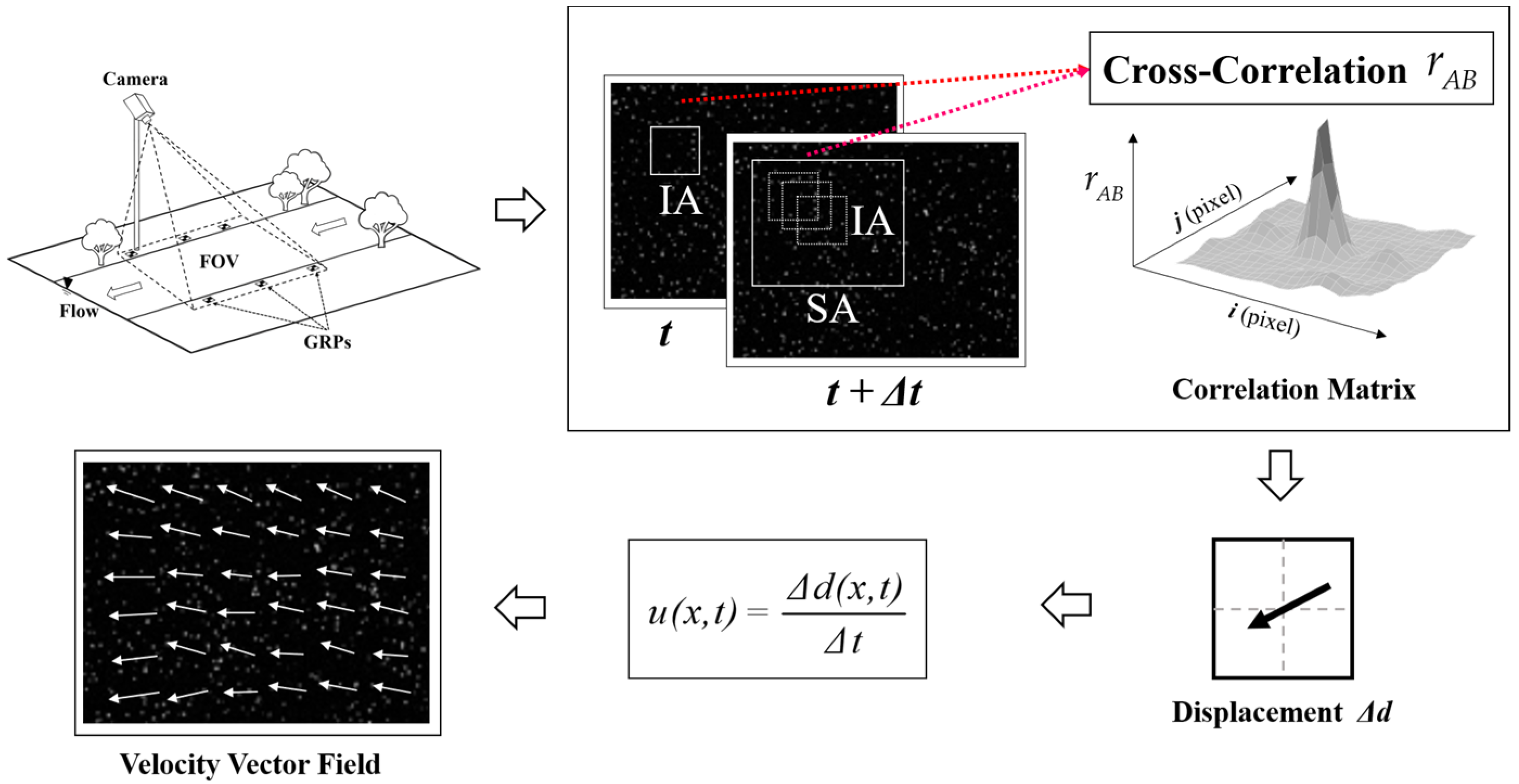
2.1. LSPIV Algorithm
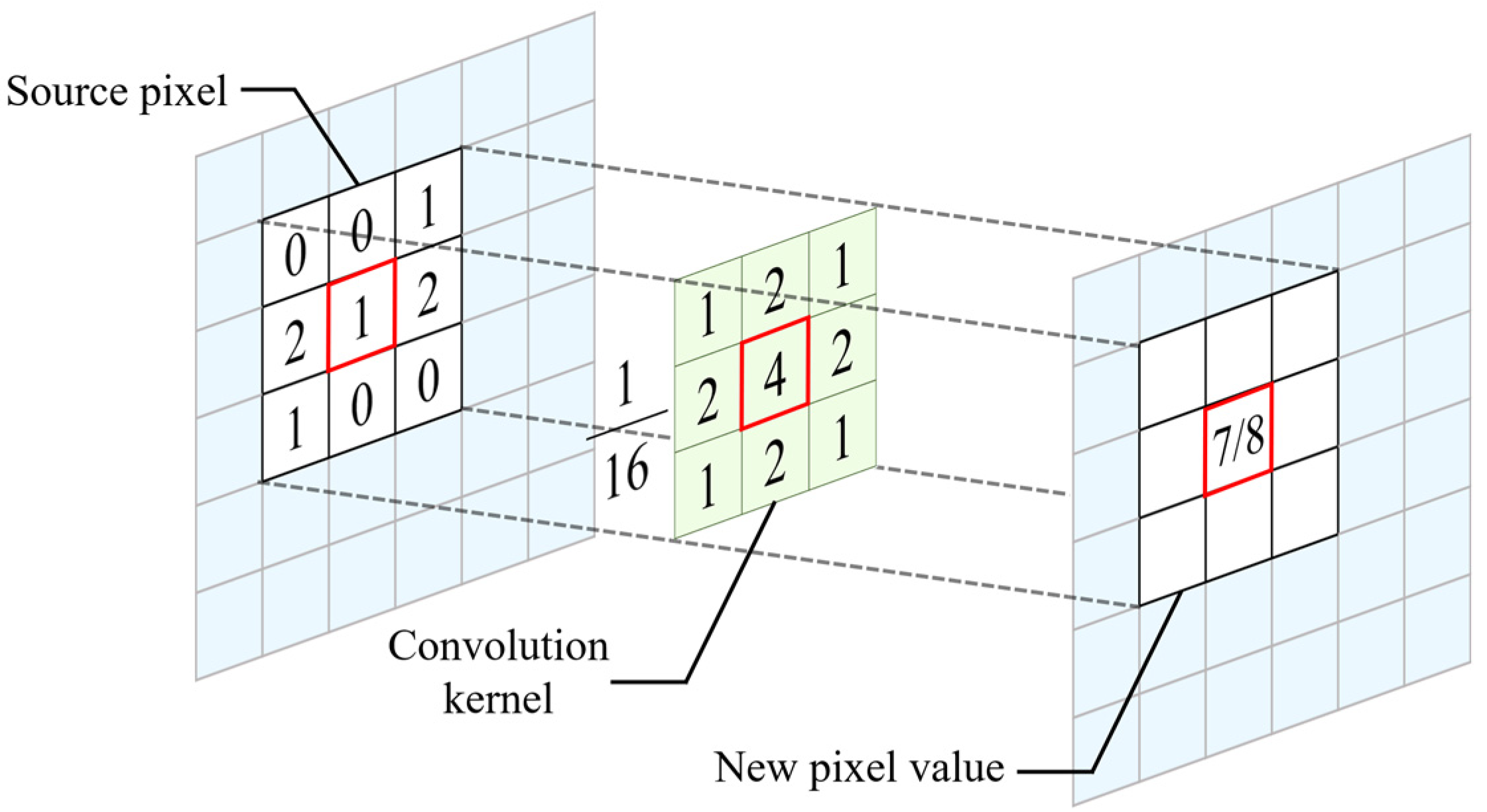
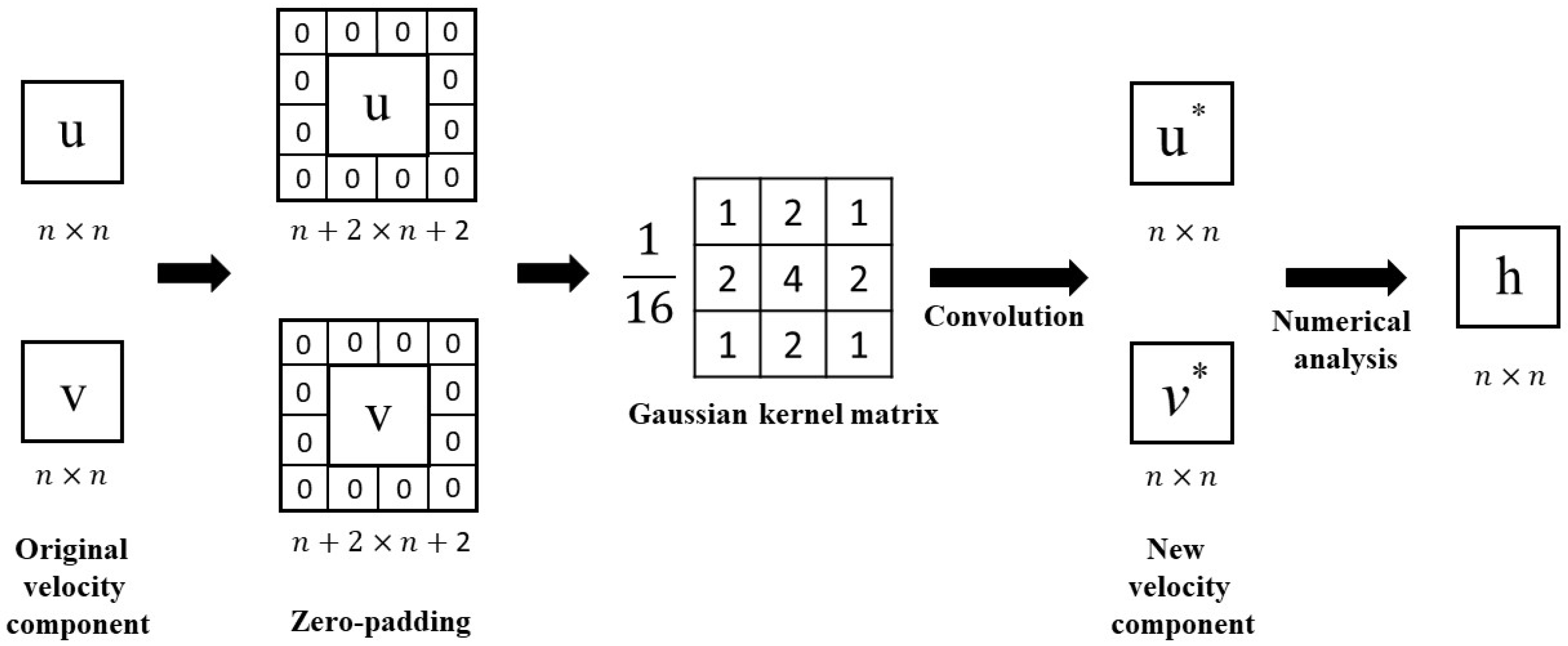
2.2. Combined with the Differental Equation
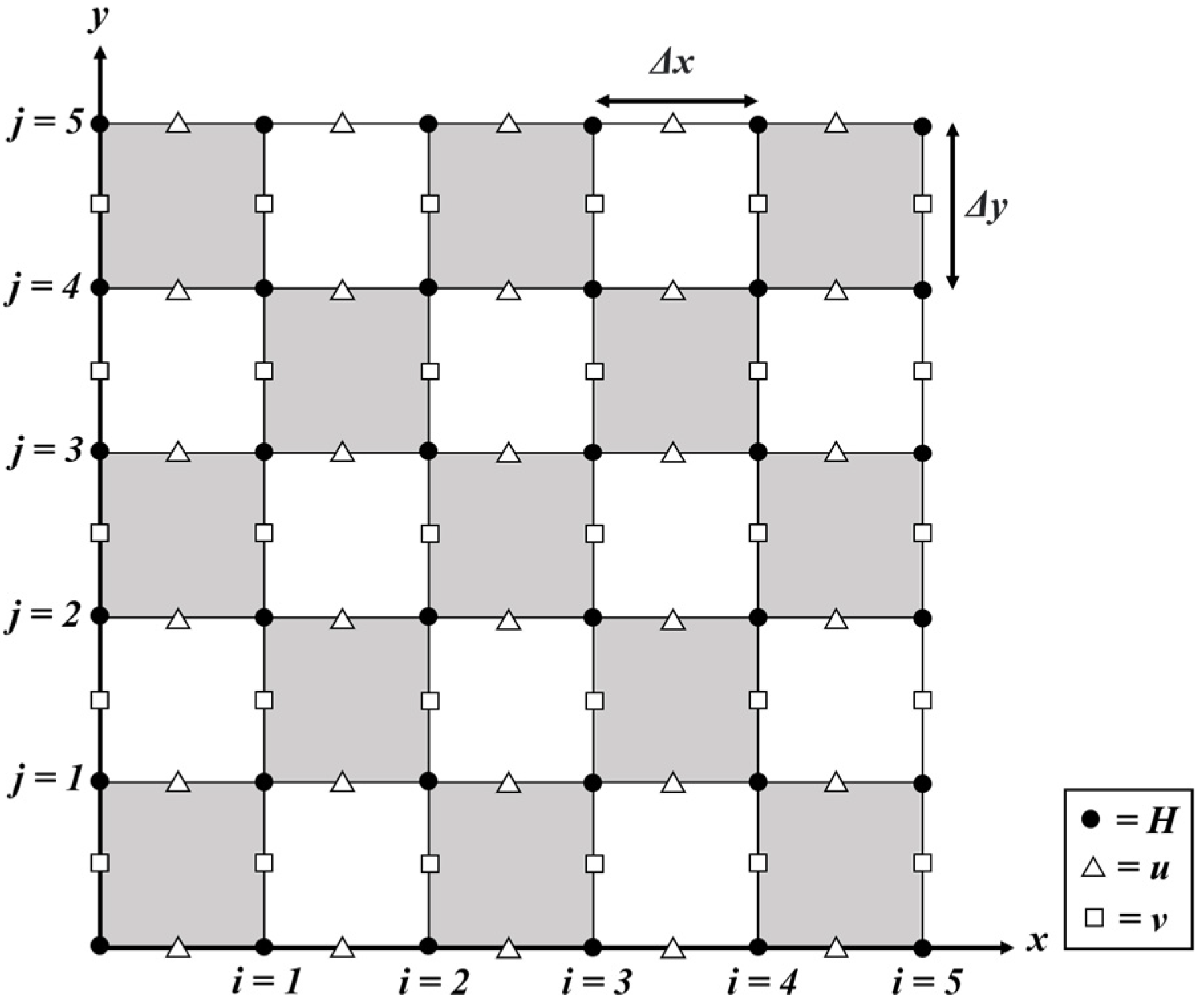
2.3. Leapfrog Method
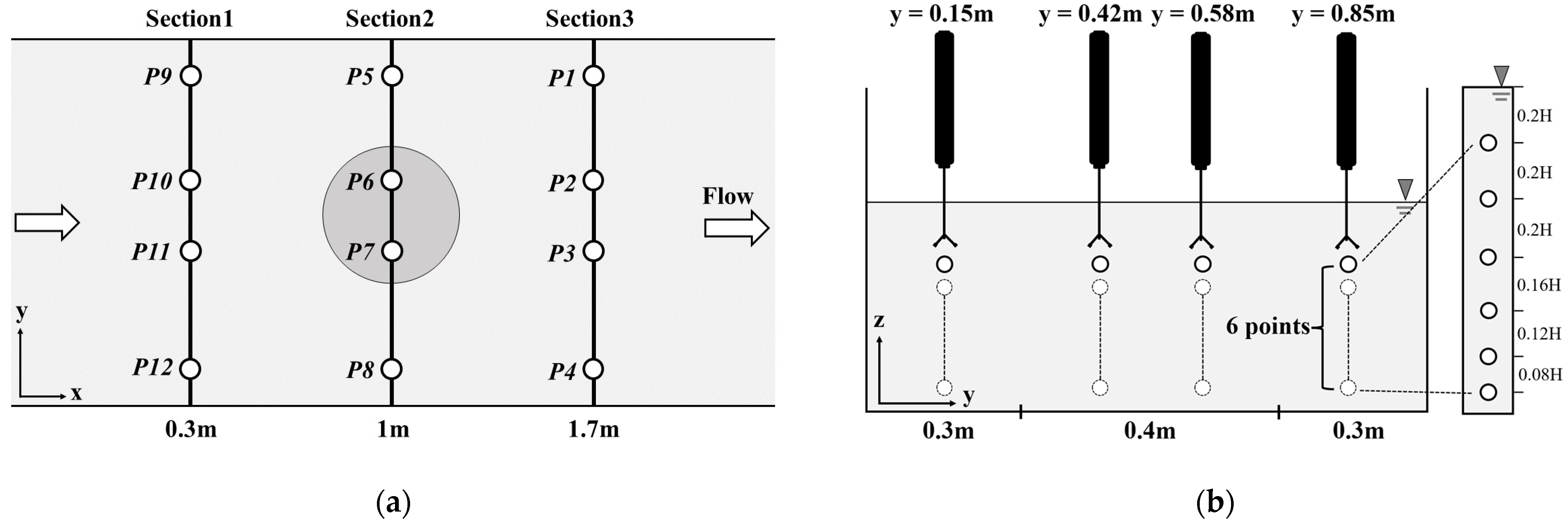
3. Experimental Setup
4. Results and Discussion
4.1. ADV Results
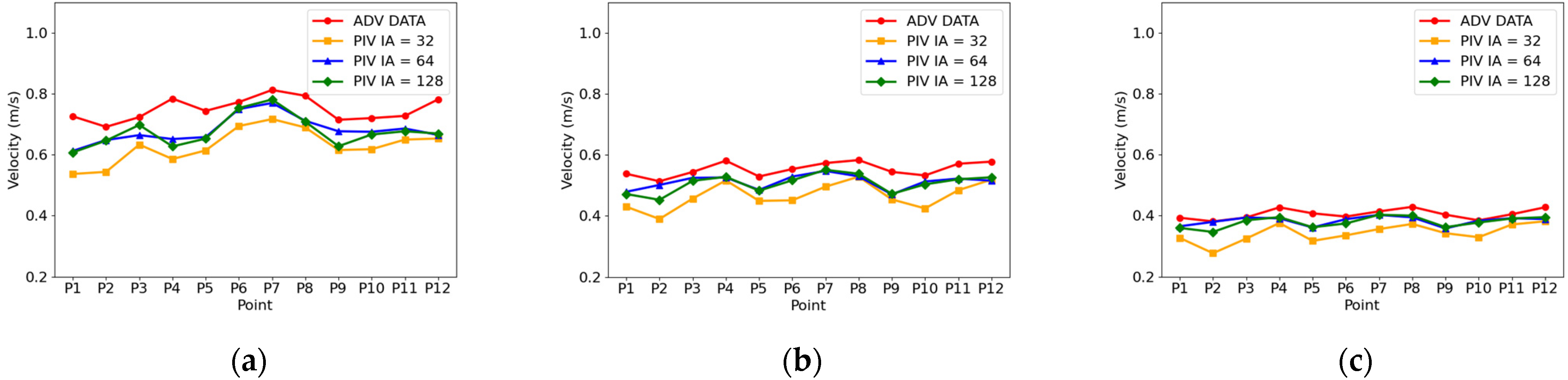
4.2. Comparison with Different Interrogation Areas
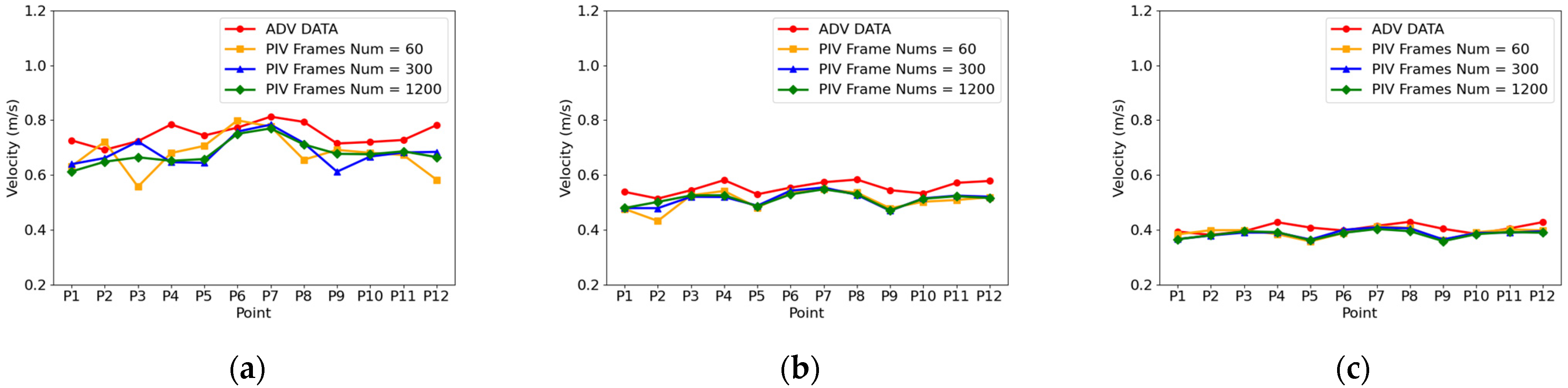
4.3. Comparison with Different Frame Rates
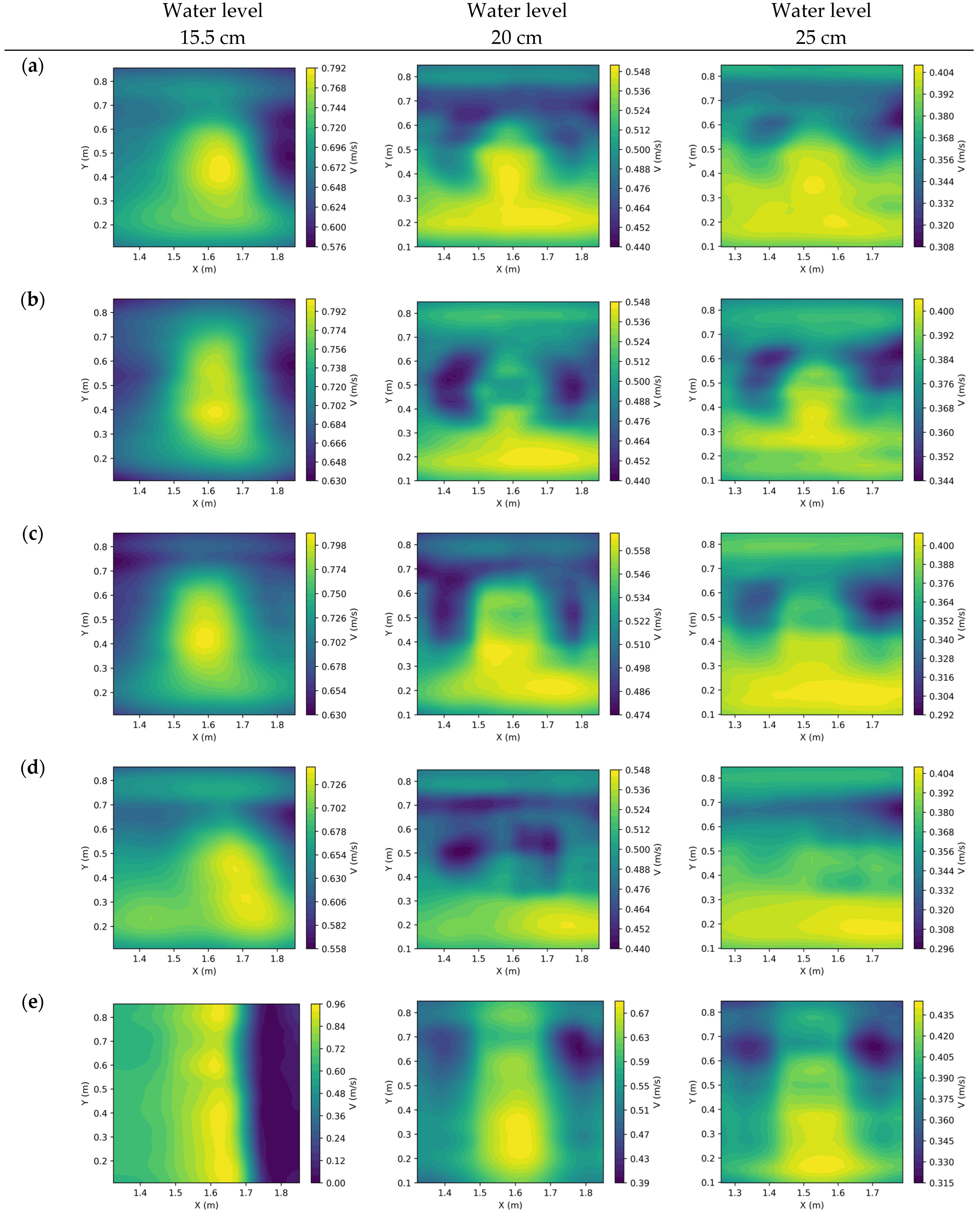
4.4. LSPIV Surface Velocity
4.5. Comparison of Different Mesh Settings
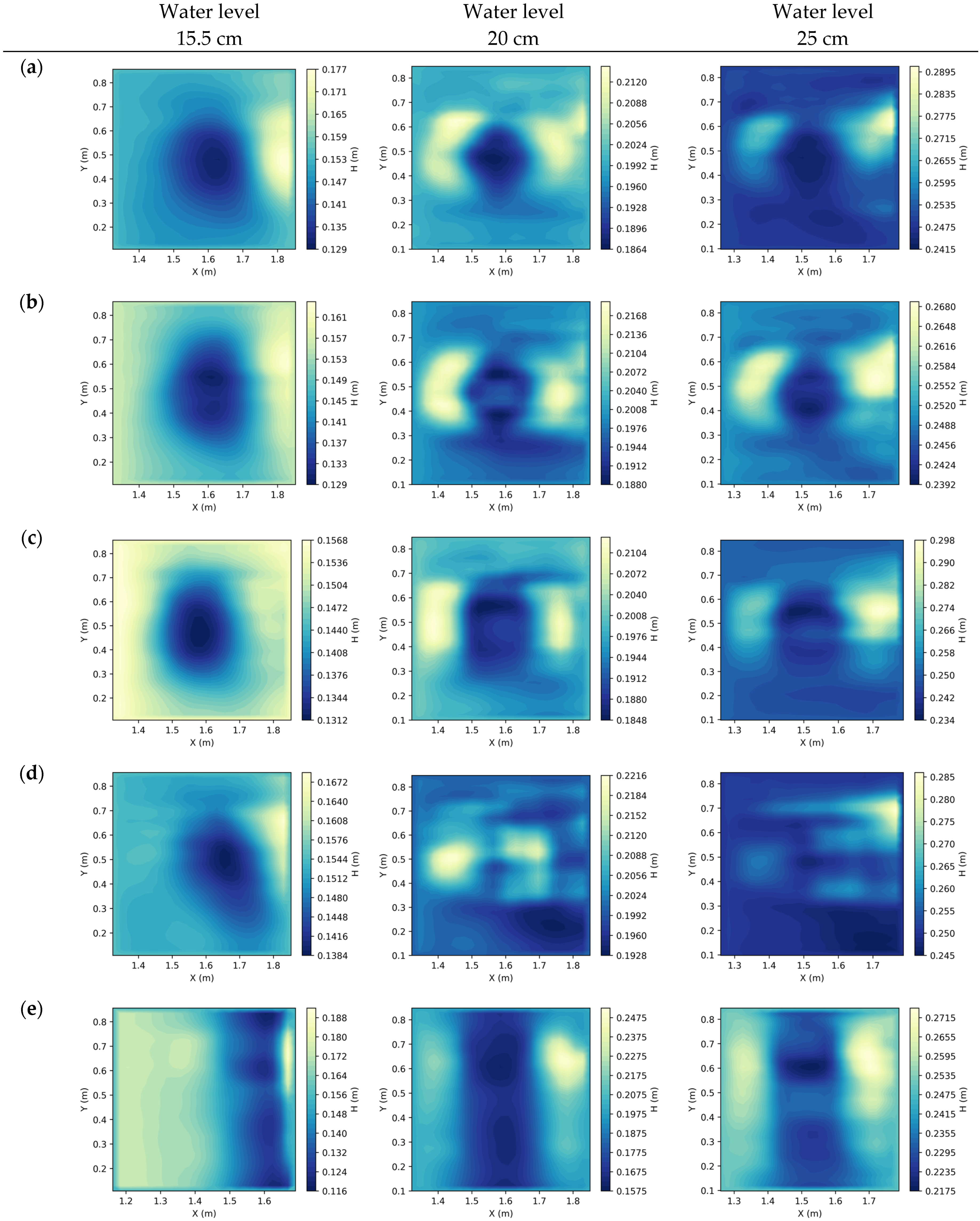
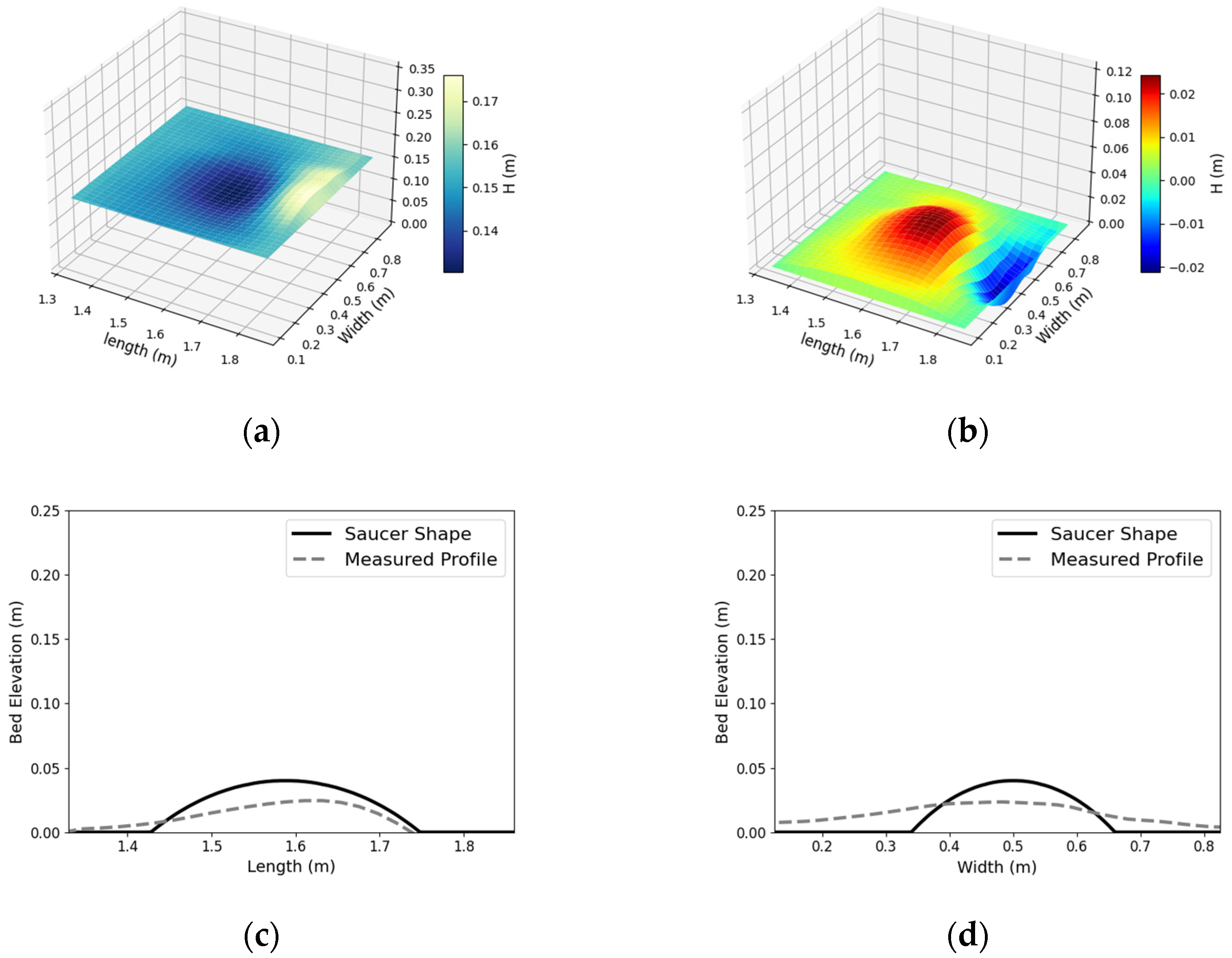
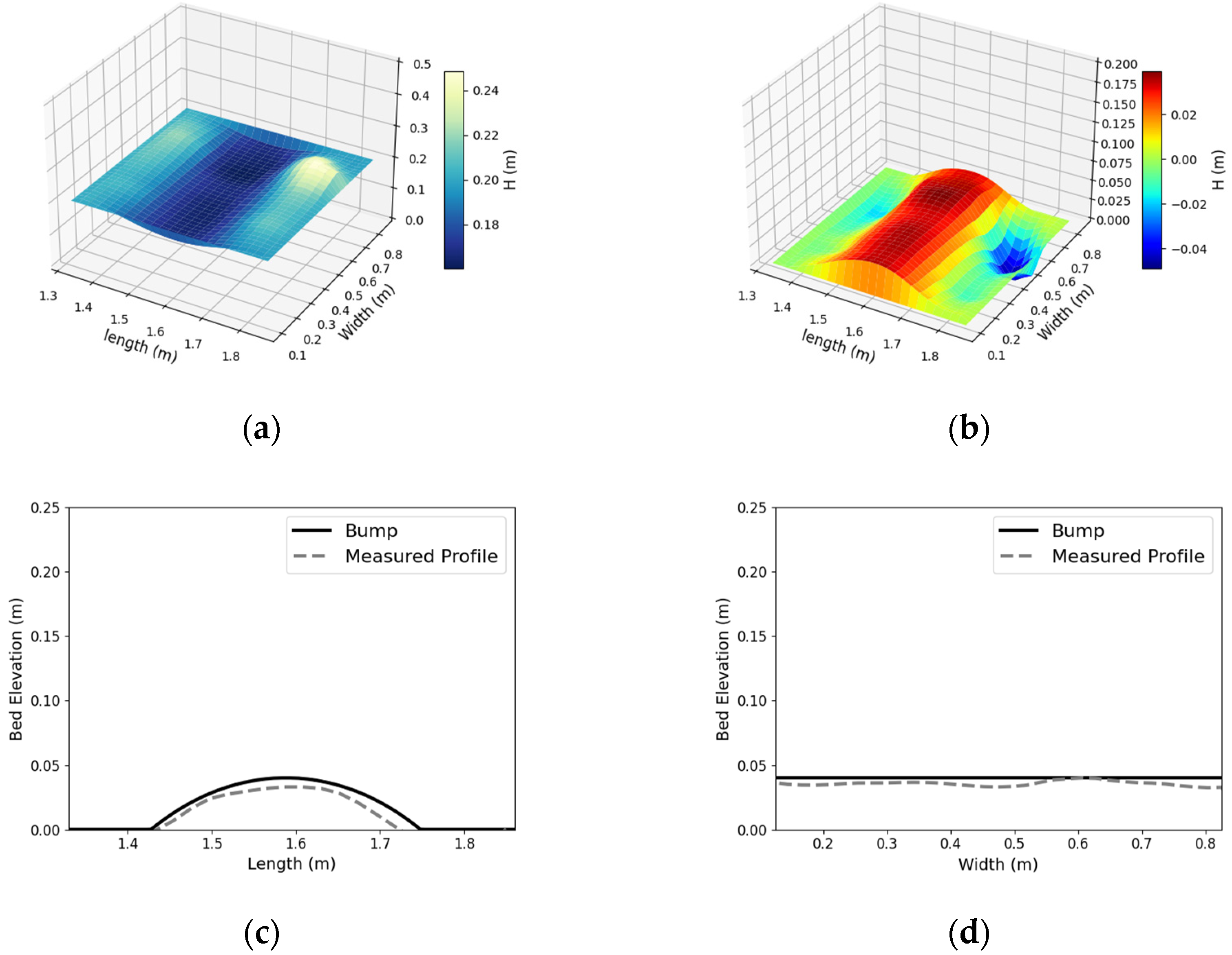
4.6. Bathymetry Measurements
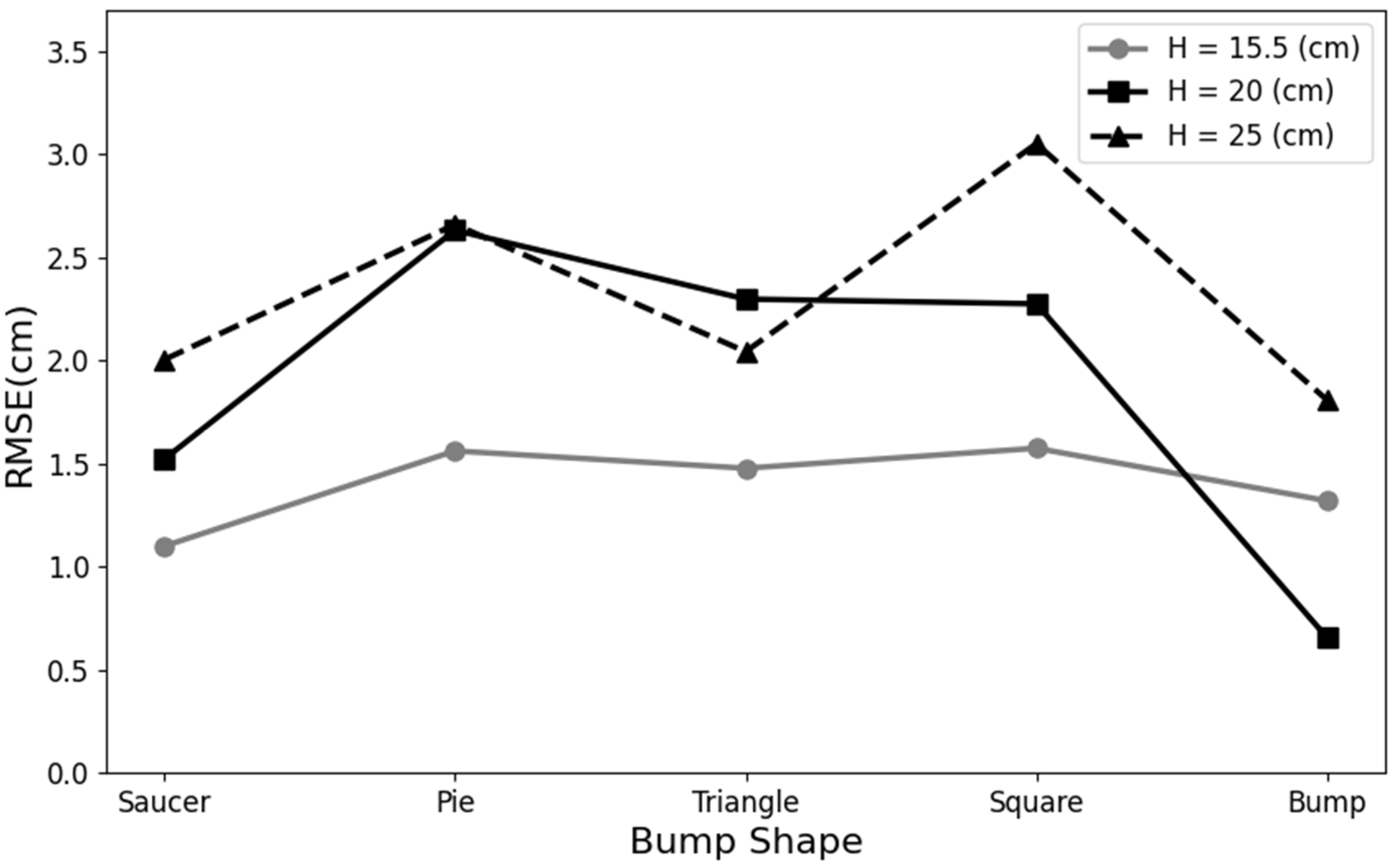
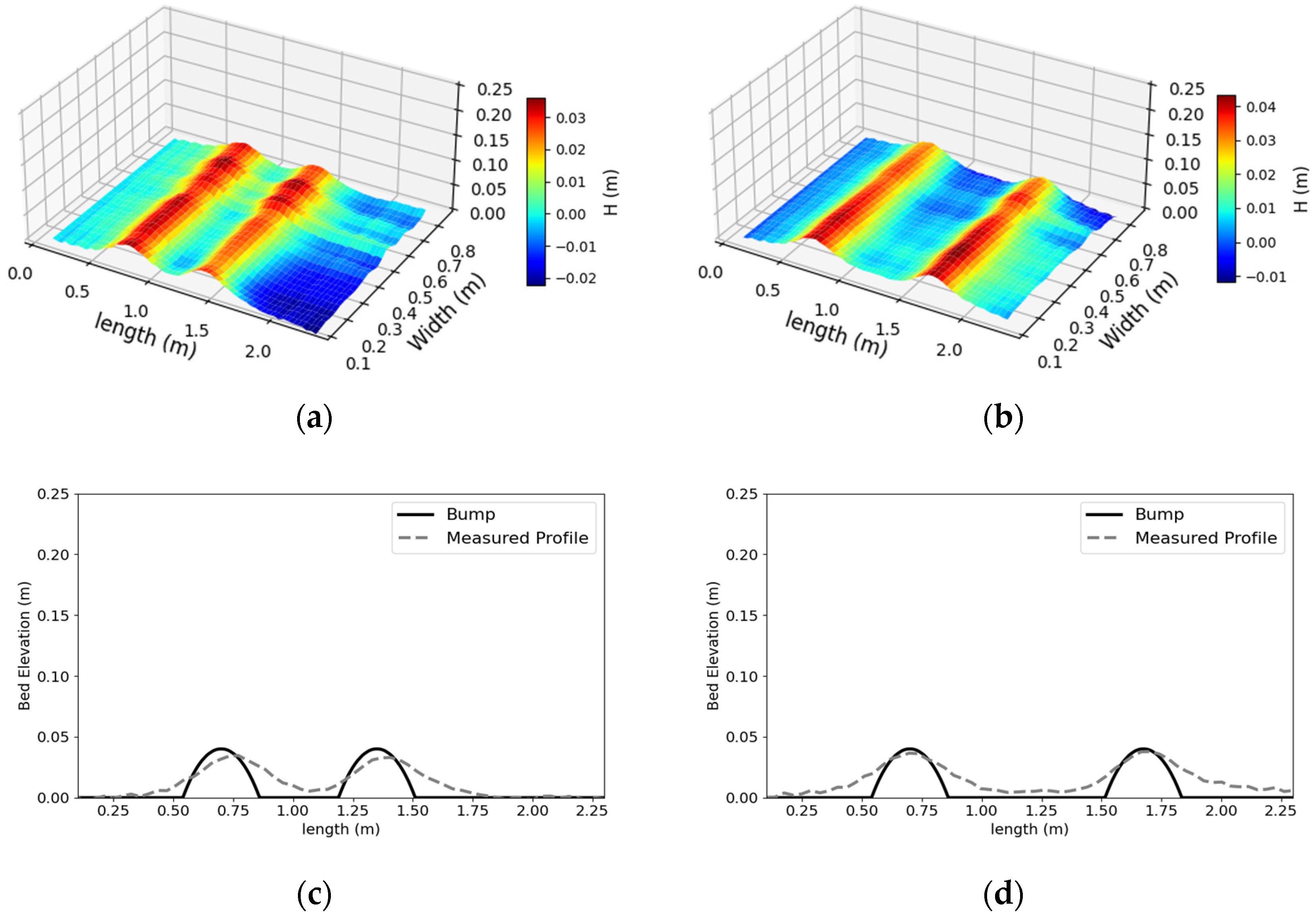
4.7. Comparison with Composite Bed Structures
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviation
| Symbol | Description |
| moving distance about distinct pattern | |
| time difference between each frame | |
| , | image coordinates |
| , | width and height for subimages |
| , | pixel intensity at location (, ) for subimage A and B |
| , | average pixel intensity |
| standard divination of the Gaussian kernel | |
| size of Gaussian kernel | |
| total water depth () | |
| height deviation of its mean height | |
| mean height of the horizontal pressure surface | |
| , | depth-averaged velocity in the length and width direction |
| upstream boundary water depth | |
| initial water depth | |
| sidewall water depth | |
| length of the grid | |
| width of the grid | |
| average relative error | |
| measured locations | |
| surface velocity from LSPIV | |
| surface velocity from ADV | |
| elevation of model | |
| elevation estimated with proposed method | |
| total number of grids | |
| position of z-direction | |
| x-directional velocity value of z-position | |
| shear velocity | |
| shear stress | |
| von Kármán constant | |
| constant |
References
- Loucks, D.P.; Beek, E.V. Water resources planning and management: An overview. In Water Resource Systems Planning and Management; Springer: Cham, Switzerland, 2017; pp. 1–49. [Google Scholar]
- Wu, S.-J.; Lien, H.-C.; Chang, C.-H. Modeling risk analysis for forecasting peak discharge during flooding prevention and warning operation. Stoch. Environ. Res. Risk Assess. 2010, 24, 1175–1191. [Google Scholar] [CrossRef]
- Rantz, S.E. Measurement and Computation of Streamflow; US Department of the Interior, Geological Survey: Reston, VA, USA, 1982; Volume 2175.
- Lee, C.-J.; Kim, W.; Kim, C.-Y.; Kim, D.-G. Velocity and discharge measurement using ADCP. J. Korea Water Resour. Assoc. 2005, 38, 811–824. [Google Scholar] [CrossRef] [Green Version]
- Sassi, M.; Hoitink, A.; Vermeulen, B. Discharge estimation from H-ADCP measurements in a tidal river subject to sidewall effects and a mobile bed. Water Resour. Res. 2011, 47, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Kuczera, G. Correlated rating curve error in flood frequency inference. Water Resour. Res. 1996, 32, 2119–2127. [Google Scholar] [CrossRef]
- Sivapragasam, C.; Muttil, N. Discharge rating curve extension—A new approach. Water Resour. Manag. 2005, 19, 505–520. [Google Scholar] [CrossRef]
- Clarke, R.T.; Mendiondo, E.; Brusa, L. Uncertainties in mean discharges from two large South American rivers due to rating curve variability. Hydrol. Sci. J. 2000, 45, 221–236. [Google Scholar] [CrossRef]
- Westerberg, I.; Guerrero, J.L.; Seibert, J.; Beven, K.; Halldin, S. Stage-discharge uncertainty derived with a non-stationary rating curve in the Choluteca River, Honduras. Hydrol. Processes 2011, 25, 603–613. [Google Scholar] [CrossRef]
- Fujita, I.; Komura, S. Application of video image analysis for measurements of river-surface flows. Proc. Hydraul. Eng. 1994, 38, 733–738. [Google Scholar] [CrossRef]
- Bradley, A.A.; Kruger, A.; Meselhe, E.A.; Muste, M.V. Flow measurement in streams using video imagery. Water Resour. Res. 2002, 38, 51-1–51-8. [Google Scholar] [CrossRef]
- Takehara, K.; Fujita, I.; Takano, Y.; Etoh, G.T.; Aya, S.; Tamai, M.; Miyamoto, H.; Sakai, N. An atempt of field measurements of surface flow on a river by using a helicopter aided image velocimetry. Proc. Hydraul. Eng. 2002, 46, 809–814. [Google Scholar] [CrossRef] [Green Version]
- Meselhe, E.; Peeva, T.; Muste, M. Large scale particle image velocimetry for low velocity and shallow water flows. J. Hydraul. Eng. 2004, 130, 937–940. [Google Scholar] [CrossRef]
- Dermisis, D.; Papanicolaou, A. Determining the 2-D surface velocity field around hydraulic structures with the use of a large scale particle image velocimetry (LSPIV) technique. In Impacts of Global Climate Change; ASCE Library: Reston, VA, USA, 2005; pp. 1–12. [Google Scholar]
- Kim, Y. Uncertainty Analysis for Non-Intrusive Measurement of River Discharge Using Image Velocimetry; The University of Iowa: Iowa City, IA, USA, 2006. [Google Scholar]
- Lewis, Q.W.; Lindroth, E.M.; Rhoads, B.L. Integrating unmanned aerial systems and LSPIV for rapid, cost-effective stream gauging. J. Hydrol. 2018, 560, 230–246. [Google Scholar] [CrossRef]
- Tauro, F.; Pagano, C.; Phamduy, P.; Grimaldi, S.; Porfiri, M. Large-scale particle image velocimetry from an unmanned aerial vehicle. IEEE/ASME Trans. Mechatron. 2015, 20, 3269–3275. [Google Scholar] [CrossRef]
- Fujita, I. Discharge measurements of snowmelt flood by space-time image velocimetry during the night using far-infrared camera. Water 2017, 9, 269. [Google Scholar] [CrossRef]
- Gerritsen, G. Flood Wave Monitoring Using LSPIV: A Methodology for Monitoring Flood Waves in an Equatorial Urban Stream with Fast Response Time; Delft University of Technology: Delft, The Netherlands, 2020; pp. 37–47. [Google Scholar]
- Le Coz, J.; Hauet, A.; Pierrefeu, G.; Dramais, G.; Camenen, B. Performance of image-based velocimetry (LSPIV) applied to flash-flood discharge measurements in Mediterranean rivers. J. Hydrol. 2010, 394, 42–52. [Google Scholar] [CrossRef] [Green Version]
- Theule, J.I.; Crema, S.; Marchi, L.; Cavalli, M.; Comiti, F. Exploiting LSPIV to assess debris-flow velocities in the field. Nat. Hazards Earth Syst. Sci. 2018, 18, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Johnson, E.; Cowen, E. Remote monitoring of volumetric discharge employing bathymetry determined from surface turbulence metrics. Water Resour. Res. 2016, 52, 2178–2193. [Google Scholar] [CrossRef] [Green Version]
- García-Navarro, P.; Murillo, J.; Fernández-Pato, J.; Echeverribar, I.; Morales-Hernández, M. The shallow water equations and their application to realistic cases. Environ. Fluid Mech. 2019, 19, 1235–1252. [Google Scholar] [CrossRef] [Green Version]
- Kinnmark, I. The Shallow Water Wave Equations: Formulation, Analysis and Application; Springer: Berlin/Heidelberg, Germany, 1986; Volume 15, pp. 159–171. [Google Scholar]
- Fraccarollo, L.; Toro, E.F. Experimental and numerical assessment of the shallow water model for two-dimensional dam-break type problems. J. Hydraul. Res. 1995, 33, 843–864. [Google Scholar] [CrossRef]
- Kocaman, S.; Güzel, H.; Evangelista, S.; Ozmen-Cagatay, H.; Viccione, G. Experimental and numerical analysis of a dam-break flow through different contraction geometries of the channel. Water 2020, 12, 1124. [Google Scholar] [CrossRef] [Green Version]
- Bao, Y.; Chen, J.; Sun, X.; Han, X.; Li, Y.; Zhang, Y.; Gu, F.; Wang, J. Debris flow prediction and prevention in reservoir area based on finite volume type shallow-water model: A case study of pumped-storage hydroelectric power station site in Yi County, Hebei, China. Environ. Earth Sci. 2019, 78, 1–16. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, L.M.; Chen, H.; Shen, P. Simulating debris flow mobility in urban settings. Eng. Geol. 2016, 214, 67–78. [Google Scholar] [CrossRef]
- Ferrolino, A.; Mendoza, R.; Magdalena, I.; Lope, J.E. Application of particle swarm optimization in optimal placement of tsunami sensors. PeerJ Comput. Sci. 2020, 6, e333. [Google Scholar] [CrossRef] [PubMed]
- Ha, T.; Cho, Y.-S. Tsunami propagation over varying water depths. Ocean. Eng. 2015, 101, 67–77. [Google Scholar] [CrossRef]
- Mesinger, F.; Arakawa, A. Numerical methods used in atmospheric models. Glob. Atmos. Res. Programme 1976, 1, 9–21. [Google Scholar]
- Zhou, W. An alternative leapfrog scheme for surface gravity wave equations. J. Atmos. Ocean. Technol. 2002, 19, 1415–1423. [Google Scholar] [CrossRef]
- Pudjaprasetya, S.R. Transport Phenomena, Equations and Numerical Methods; Wiley: Hoboken, NJ, USA, 2018; pp. 101–106. [Google Scholar]
- Stelling, G.S.; Duinmeijer, S.A. A staggered conservative scheme for every Froude number in rapidly varied shallow water flows. Int. J. Numer. Methods Fluids 2003, 43, 1329–1354. [Google Scholar] [CrossRef]
- Hauet, A.; Morlot, T.; Daubagnan, L. Velocity Profile and Depth-Averaged to Surface Velocity in Natural Streams: A Review over Alarge Sample of Rivers, E3s Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 40, p. 06015. [Google Scholar]
- Muste, M.; Fujita, I.; Hauet, A. Large-scale particle image velocimetry for measurements in riverine environments. Water Resour. Res. 2008, 44, 4–6. [Google Scholar] [CrossRef] [Green Version]
- Muste, M.; Ho, H.-C.; Kim, D. Considerations on direct stream flow measurements using video imagery: Outlook and research needs. J. Hydro-Environ. Res. 2011, 5, 289–300. [Google Scholar] [CrossRef]
- Welber, M.; Le Coz, J.; Laronne, J.B.; Zolezzi, G.; Zamler, D.; Dramais, G.; Hauet, A.; Salvaro, M. Field assessment of noncontact stream gauging using portable surface velocity radars (SVR). Water Resour. Res. 2016, 52, 1108–1126. [Google Scholar] [CrossRef] [Green Version]
- Fujita, I.; Aya, S. Refinement of LSPIV technique for monitoring river surface flows. In Building Partnerships; ASCE Library: Reston, VA, USA, 2000; pp. 1–9. [Google Scholar]
- Kantoush, S.A.; Schleiss, A.J.; Sumi, T.; Murasaki, M. LSPIV implementation for environmental flow in various laboratory and field cases. J. Hydro-Environ. Res. 2011, 5, 263–276. [Google Scholar] [CrossRef] [Green Version]
- Fujita, I.; Muste, M.; Kruger, A. Large-scale particle image velocimetry for flow analysis in hydraulic engineering applications. J. Hydraul. Res. 1998, 36, 397–414. [Google Scholar] [CrossRef]
- Delis, A.I.; Nikolos, I.K. Shallow Water Equations in Hydraulics: Modeling, Numerics and Applications; Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2021; Volume 13, p. 3598. [Google Scholar]
- Altaie, H.; Dreyfuss, P. Numerical Solutions for 2D Depth-Averaged Shallow Water Equations; International Mathematical Forum: Ruse, Bulgaria, 2018; pp. 79–90. [Google Scholar]
- Goto, C.; Ogawa, Y.; Shuto, N.; Imamura, F. IUGG/IOC time project: Numerical method of tsunami simulation with the leapfrog scheme. Intergov. Oceanogr. Comm. UNESCO Man. Guides 1997, 35, 130. [Google Scholar]
- Griffiths, S.D. Kelvin wave propagation along straight boundaries in C-grid finite-difference models. J. Comput. Phys. 2013, 255, 639–659. [Google Scholar] [CrossRef] [Green Version]
- Kleptsova, O.; Pietrzak, J.; Stelling, G. On the accurate and stable reconstruction of tangential velocities in C-grid ocean models. Ocean. Model. 2009, 28, 118–126. [Google Scholar] [CrossRef]
- Cebeci, T. Analysis of Turbulent Boundary Layers; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- White, F.M.; Majdalani, J. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 2006; Volume 3. [Google Scholar]






| Water Level | 15.5 cm | 20 cm | 25 cm | |||
|---|---|---|---|---|---|---|
| Point | ADV [m/s] | IA (64 × 64) [m/s] | ADV [m/s] | IA (64 × 64) [m/s] | ADV [m/s] | IA (64 × 64) [m/s] |
| P1 | 0.7259 | 0.6125 | 0.5380 | 0.4791 | 0.3930 | 0.3650 |
| P2 | 0.6915 | 0.6482 | 0.5135 | 0.5014 | 0.3810 | 0.3796 |
| P3 | 0.7233 | 0.6643 | 0.5440 | 0.5248 | 0.3939 | 0.3937 |
| P4 | 0.7843 | 0.6514 | 0.5810 | 0.5258 | 0.4271 | 0.3910 |
| P5 | 0.7439 | 0.6578 | 0.5292 | 0.4851 | 0.4076 | 0.3611 |
| P6 | 0.7727 | 0.7499 | 0.5536 | 0.5289 | 0.3969 | 0.3884 |
| P7 | 0.8126 | 0.7698 | 0.5733 | 0.5475 | 0.4139 | 0.4025 |
| P8 | 0.7935 | 0.7112 | 0.5830 | 0.5297 | 0.4288 | 0.3945 |
| P9 | 0.7147 | 0.6769 | 0.5443 | 0.4705 | 0.4031 | 0.3581 |
| P10 | 0.7202 | 0.6753 | 0.5327 | 0.5129 | 0.3846 | 0.3836 |
| P11 | 0.7275 | 0.6859 | 0.5710 | 0.5222 | 0.4046 | 0.3914 |
| P12 | 0.7817 | 0.6650 | 0.5778 | 0.5157 | 0.4274 | 0.3889 |
| (%) | 9.11% | 7.44% | 5.34% | |||
| Water Level | 15.5 cm | 20 cm | 25 cm | |||
|---|---|---|---|---|---|---|
| Point | ADV [m/s] | IA (64 × 64) [m/s] | ADV [m/s] | IA (64 × 64) [m/s] | ADV [m/s] | IA (64 × 64) [m/s] |
| P1 | 0.7259 | 0.6393 | 0.5380 | 0.4787 | 0.3930 | 0.3654 |
| P2 | 0.6915 | 0.6617 | 0.5135 | 0.4785 | 0.3810 | 0.3789 |
| P3 | 0.7233 | 0.7219 | 0.5440 | 0.5202 | 0.3939 | 0.3895 |
| P4 | 0.7843 | 0.6463 | 0.5810 | 0.5194 | 0.4271 | 0.3897 |
| P5 | 0.7439 | 0.6440 | 0.5292 | 0.4875 | 0.4076 | 0.3637 |
| P6 | 0.7727 | 0.7583 | 0.5536 | 0.5425 | 0.3969 | 0.3994 |
| P7 | 0.8126 | 0.7835 | 0.5733 | 0.5539 | 0.4139 | 0.4082 |
| P8 | 0.7935 | 0.7163 | 0.5830 | 0.5270 | 0.4288 | 0.4047 |
| P9 | 0.7147 | 0.6118 | 0.5443 | 0.4692 | 0.4031 | 0.3642 |
| P10 | 0.7202 | 0.6672 | 0.5327 | 0.5144 | 0.3846 | 0.3877 |
| P11 | 0.7275 | 0.6819 | 0.5710 | 0.5243 | 0.4046 | 0.3894 |
| P12 | 0.7817 | 0.6841 | 0.5778 | 0.5204 | 0.4274 | 0.3941 |
| (%) | 8.60% | 7.58% | 4.82% | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.-C.; Ho, H.-C.; Lee, T.-A.; Chen, H.-Y. Application of Image Technique to Obtain Surface Velocity and Bed Elevation in Open-Channel Flow. Water 2022, 14, 1895. https://doi.org/10.3390/w14121895
Lin Y-C, Ho H-C, Lee T-A, Chen H-Y. Application of Image Technique to Obtain Surface Velocity and Bed Elevation in Open-Channel Flow. Water. 2022; 14(12):1895. https://doi.org/10.3390/w14121895
Chicago/Turabian StyleLin, Yen-Cheng, Hao-Che Ho, Tzu-An Lee, and Hsin-Yu Chen. 2022. "Application of Image Technique to Obtain Surface Velocity and Bed Elevation in Open-Channel Flow" Water 14, no. 12: 1895. https://doi.org/10.3390/w14121895
APA StyleLin, Y.-C., Ho, H.-C., Lee, T.-A., & Chen, H.-Y. (2022). Application of Image Technique to Obtain Surface Velocity and Bed Elevation in Open-Channel Flow. Water, 14(12), 1895. https://doi.org/10.3390/w14121895






