The Effect of Spatial Input Data Quality on the Performance of the SWAT Model
Abstract
:1. Introduction
2. Materials and Methods
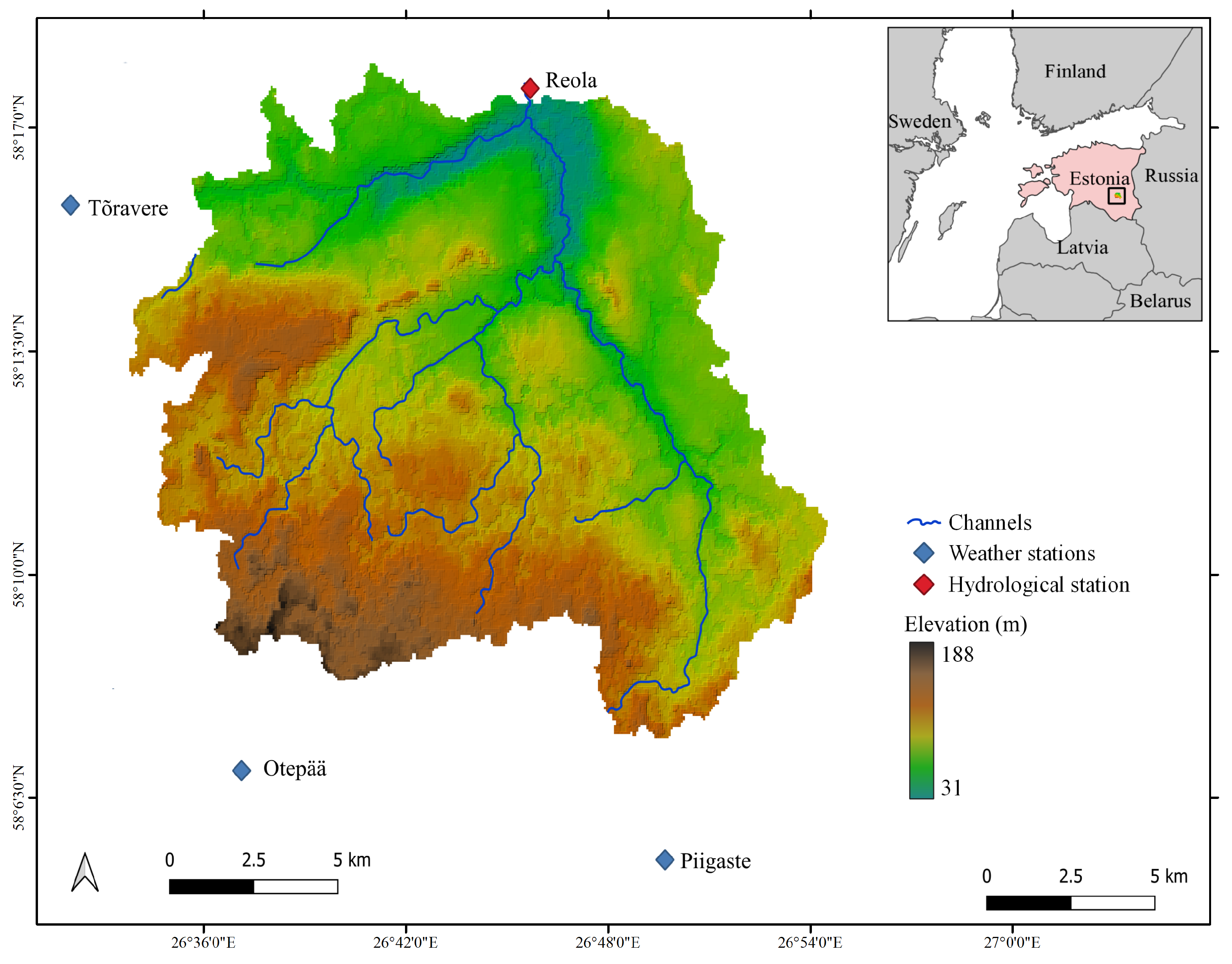
2.1. Description of the Study Area
2.2. Input Data
2.3. Model Setup
- First, each of the four models is calibrated and validated individually to understand and assess their capability to predict streamflow in the catchment by itself.
- Secondly, we collate the calibrated parameter ranges from each individual model into an encompassing range for each originally selected parameter. With this parameter configuration, we run a sensitivity analysis for each model.
- Finally, we reduce the list of parameters from the previous step to only the sensitive parameters and their ranges, run a final uncertainty analysis again, and extract the results.
2.4. Calibration and Validation
2.5. Sensitivity Analysis
2.6. Joint Parameter-Based Evaluation of Differences in Model Performance
3. Results
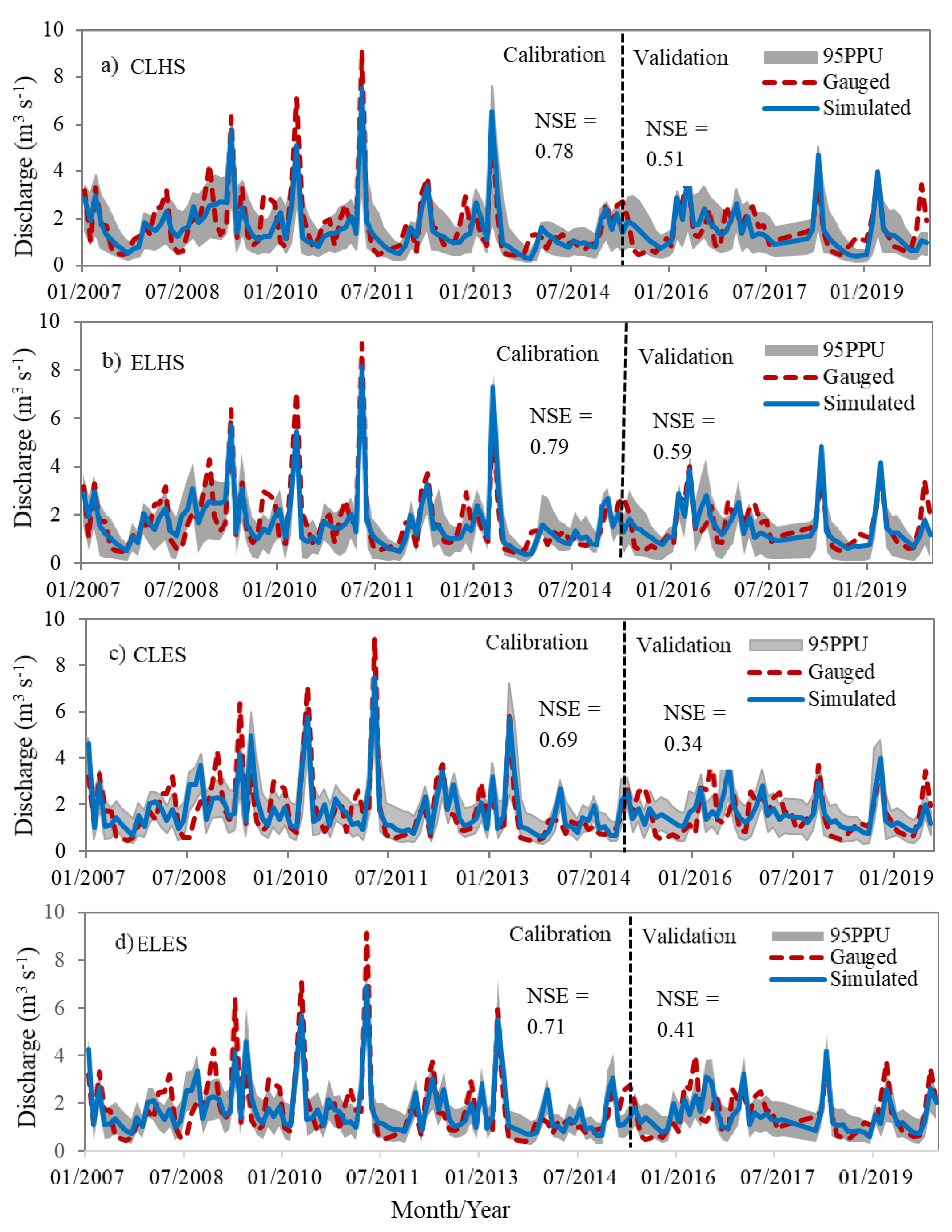
3.1. General Model Performance
3.2. Joint Parameter Level Performance Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ETAK | Estonian Topographic Database |
| HRU | Hydrologic Response Unit |
| HWSD | Harmonized World Soil Database |
| NSE | Nash–Sutcliffe Efficiency |
| SWAT | Soil and Water Assessment Tool |
| USDA | United States Department of Agriculture |
Appendix A

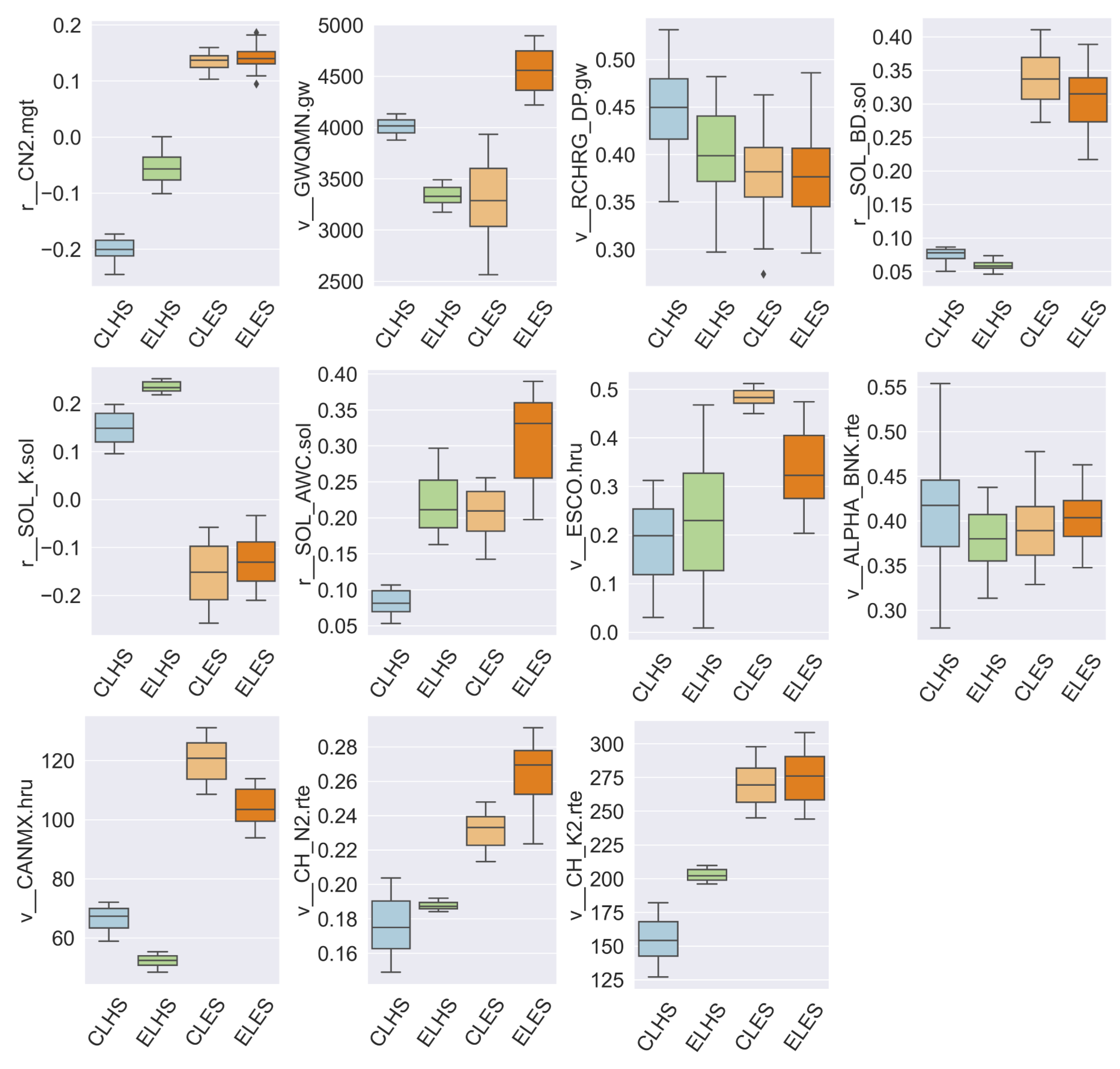
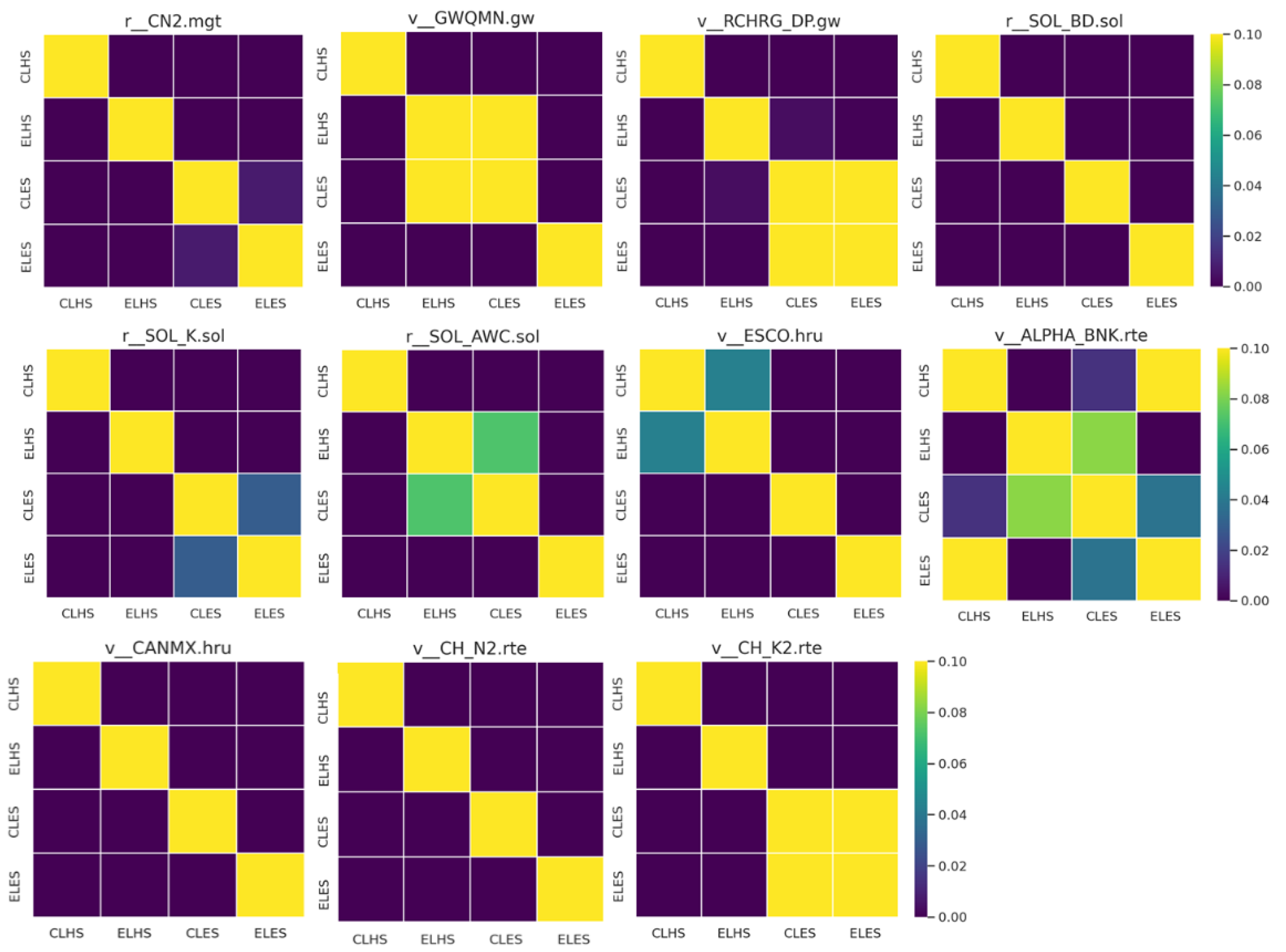
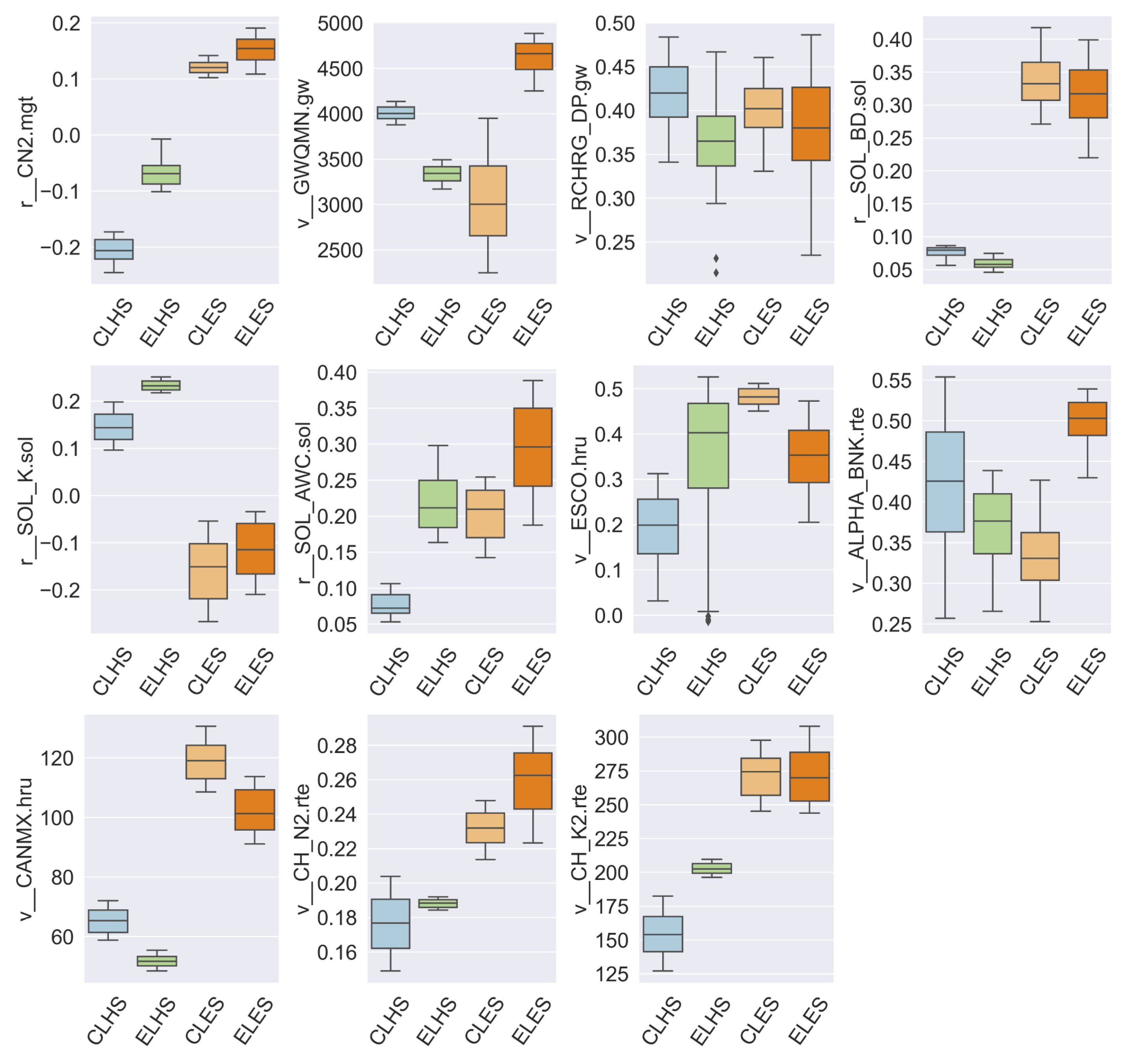
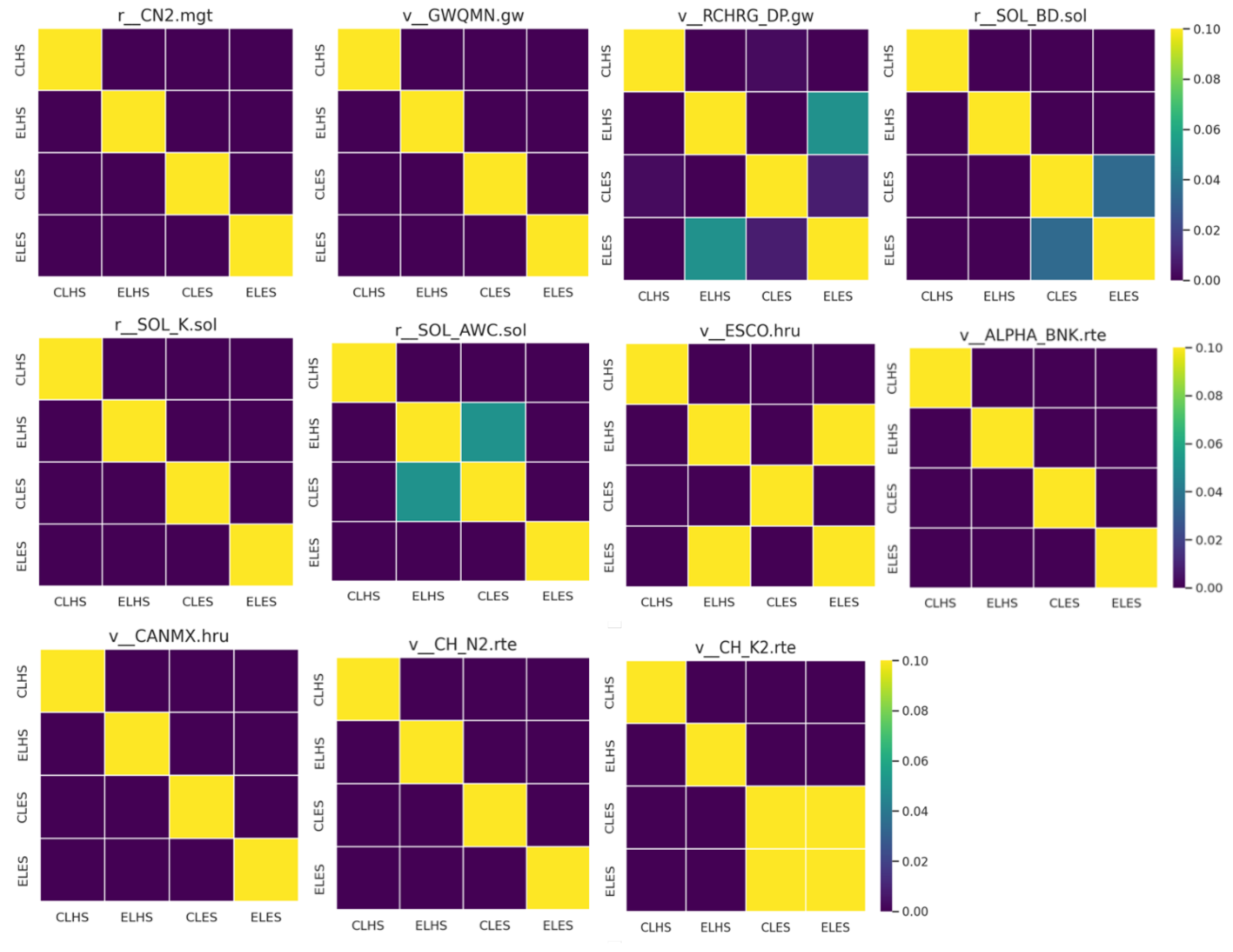

References
- Ghaith, M.; Li, Z. Propagation of parameter uncertainty in SWAT: A probabilistic forecasting method based on polynomial chaos expansion and machine learning. J. Hydrol. 2020, 586, 124854. [Google Scholar] [CrossRef]
- Beven, K.J.; Lirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- Abbott, M.; Bathurst, J.; Cunge, J.; O’Connell, P.; Rasmussen, J. An introduction to the European Hydrological System—Systeme Hydrologique Europeen, “SHE”, 1: History and philosophy of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Lin, Q.; Zhang, D. A scalable distributed parallel simulation tool for the SWAT model. Environ. Model. Softw. 2021, 144, 105133. [Google Scholar] [CrossRef]
- Camargos, C.; Julich, S.; Houska, T.; Bach, M.; Breuer, L. Effects of Input Data Content on the Uncertainty of Simulating Water Resources. Water 2018, 10, 621. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Tiwari, K. A comparative appraisal of hydrological behavior of SRTM DEM at catchment level. J. Hydrol. 2014, 519, 1394–1404. [Google Scholar] [CrossRef]
- Hoang, L.; Mukundan, R.; Moore, K.E.B.; Owens, E.M.; Steenhuis, T.S. The effect of input data resolution and complexity on the uncertainty of hydrological predictions in a humid vegetated watershed. Hydrol. Earth Syst. Sci. 2018, 22, 5947–5965. [Google Scholar] [CrossRef] [Green Version]
- Dakhlalla, A.O.; Parajuli, P.B. Assessing model parameters sensitivity and uncertainty of streamflow, sediment, and nutrient transport using SWAT. Inf. Process. Agric. 2019, 6, 61–72. [Google Scholar] [CrossRef]
- McMillan, H.; Seibert, J.; Petersen-Overleir, A.; Lang, M.; White, P.; Snelder, T.; Rutherford, K.; Krueger, T.; Mason, R.; Kiang, J. How uncertainty analysis of streamflow data can reduce costs and promote robust decisions in water management applications. Water Resour. Res. 2017, 53, 5220–5228. [Google Scholar] [CrossRef] [Green Version]
- Asante, K.; Leh, M.D.; Cothren, J.D.; Luzio, M.D.; Brahana, J.V. Effects of land-use land-cover data resolution and classification methods on SWAT model flow predictive reliability. Int. J. Hydrol. Sci. Technol. 2017, 7, 39. [Google Scholar] [CrossRef]
- Al-Khafaji, M.; Saeed, F.H.; Al-Ansari, N. The Interactive Impact of Land Cover and DEM Resolution on the Accuracy of Computed Streamflow Using the SWAT Model. Water Air Soil Pollut. 2020, 231, 416. [Google Scholar] [CrossRef]
- Moges, D.M.; Kmoch, A.; Uuemaa, E. Application of satellite and reanalysis precipitation products for hydrological modeling in the data-scarce Porijõgi catchment, Estonia. J. Hydrol. Reg. Stud. 2022, 41, 1–21. [Google Scholar] [CrossRef]
- Geza, M.; McCray, J.E. Effects of soil data resolution on SWAT model stream flow and water quality predictions. J. Environ. Manag. 2008, 88, 393–406. [Google Scholar] [CrossRef]
- Chaplot, V. Impact of spatial input data resolution on hydrological and erosion modeling: Recommendations from a global assessment. Phys. Chem. Earth Parts A/B/C 2014, 67–69, 23–35. [Google Scholar] [CrossRef]
- Mander, Ü.; Uuemaa, E.; Roosaare, J.; Aunap, R.; Antrop, M. Coherence and fragmentation of landscape patterns as characterized by correlograms: A case study of Estonia. Landsc. Urban Plan. 2010, 94, 31–37. [Google Scholar] [CrossRef]
- Varep, E. The landscape regions of Estonia. In Publications on Geography, 156 ed.; IV. Acta Commerstationes Univ. Tartu.: Tartu, Estonia, 1964; pp. 3–28. [Google Scholar]
- Mander, Ü.; Kuusemets, V.; Ivask, M. Nutrient dynamics of riparian ecotones: A case study from the Porijõgi River catchment, Estonia. Landsc. Urban Plan. 1995, 31, 333–348. [Google Scholar] [CrossRef]
- Mander, Ü.; Kull, A.; Kuusemets, V.; Tamm, T. Nutrient runoff dynamics in a rural catchment: Influence of land-use changes, climatic fluctuations and ecotechnological measures. Ecol. Eng. 2000, 14, 405–417. [Google Scholar] [CrossRef]
- Pärn, J.; Henine, H.; Kasak, K.; Kauer, K.; Sohar, K.; Tournebize, J.; Uuemaa, E.; Välik, K.; Mander, Ü. Nitrogen and phosphorus discharge from small agricultural catchments predicted from land use and hydroclimate. Land Use Policy 2018, 75, 260–268. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Sosa, J.; Bates, P.D.; Allen, G.H.; Pavelsky, T.M. MERIT Hydro: A High-Resolution Global Hydrography Map Based on Latest Topography Dataset. Water Resour. Res. 2019, 55, 5053–5073. [Google Scholar] [CrossRef] [Green Version]
- Fischer, G.; Nachtergaele, F.; Prieler, S.; van Velthuizen, H.; Verelst, L.; Wiberg, D. Global Agro-ecological Zones Assessment for Agriculture (GAEZ 2008); FAO: Rome, Italy, 2008. [Google Scholar]
- Kmoch, A.; Kanal, A.; Astover, A.; Kull, A.; Virro, H.; Helm, A.; Pärtel, M.; Ostonen, I.; Uuemaa, E. EstSoil-EH: A high-resolution eco-hydrological modelling parameters dataset for Estonia. Earth Syst. Sci. Data 2021, 13, 83–97. [Google Scholar] [CrossRef]
- European Environment Agency. CORINE Land Cover (CLC) Inventory. Available online: https://land.copernicus.eu/pan-european/corine-land-cover/clc2012 (accessed on 18 February 2022).
- Estonian Land Board. Estonian Topographic Database. Available online: https://geoportaal.maaamet.ee/eng/Spatial-Data/Estonian-Topographic-Database-p305.html (accessed on 18 February 2022).
- Dile, Y.T.; Daggupati, P.; George, C.; Srinivasan, R.; Arnold, J. Introducing a new open source GIS user interface for the SWAT model. Environ. Model. Softw. 2016, 85, 129–138. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; van Genuchten, M.T.; Schulin, R.; Schläppi, E. A sequential uncertainty domain inverse procedure for estimating subsurface flow and transport parameters. Water Resour. Res. 1997, 33, 1879–1892. [Google Scholar] [CrossRef] [Green Version]
- Arnold, J.; Kiniry, J.; Srinivasan, R.; Williams, J.; Haney, E.; Neitsch, S. SWAT 2012 Input/Output Documentation. Available online: https://swat.tamu.edu/docs/ (accessed on 18 February 2022).
- Abbaspour, K.; Vaghefi, S.; Srinivasan, R. A Guideline for Successful Calibration and Uncertainty Analysis for Soil and Water Assessment: A Review of Papers from the 2016 International SWAT Conference. Water 2017, 10, 6. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Kmoch, A. Swatpy: A Set of Python Modules to Work with SWAT2012 Models (v0.2). Available online: https://doi.org/10.5281/zenodo.6322023 (accessed on 2 March 2022).
- Mann, H.B.; Whitney, D.R. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Abbaspour, K.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L.; Binger, R.; Harmel, R.D.; Veith, T.L.; Bingner, R.L.; et al. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Attinger, S. Multiscale parameter regionalization of a grid-based hydrologic model at the mesoscale. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- Koch, J.; Demirel, M.C.; Stisen, S. The SPAtial EFficiency metric (SPAEF): Multiple-component evaluation of spatial patterns for optimization of hydrological models. Geosci. Model Dev. 2018, 11, 1873–1886. [Google Scholar] [CrossRef] [Green Version]
- Moges, D.M.; Kmoch, A. Effect of Spatial Input Data Quality on SWAT Modelling in the Porijõgi Catchment (v1.0). Available online: https://doi.org/10.5281/zenodo.6321991 (accessed on 2 March 2022).
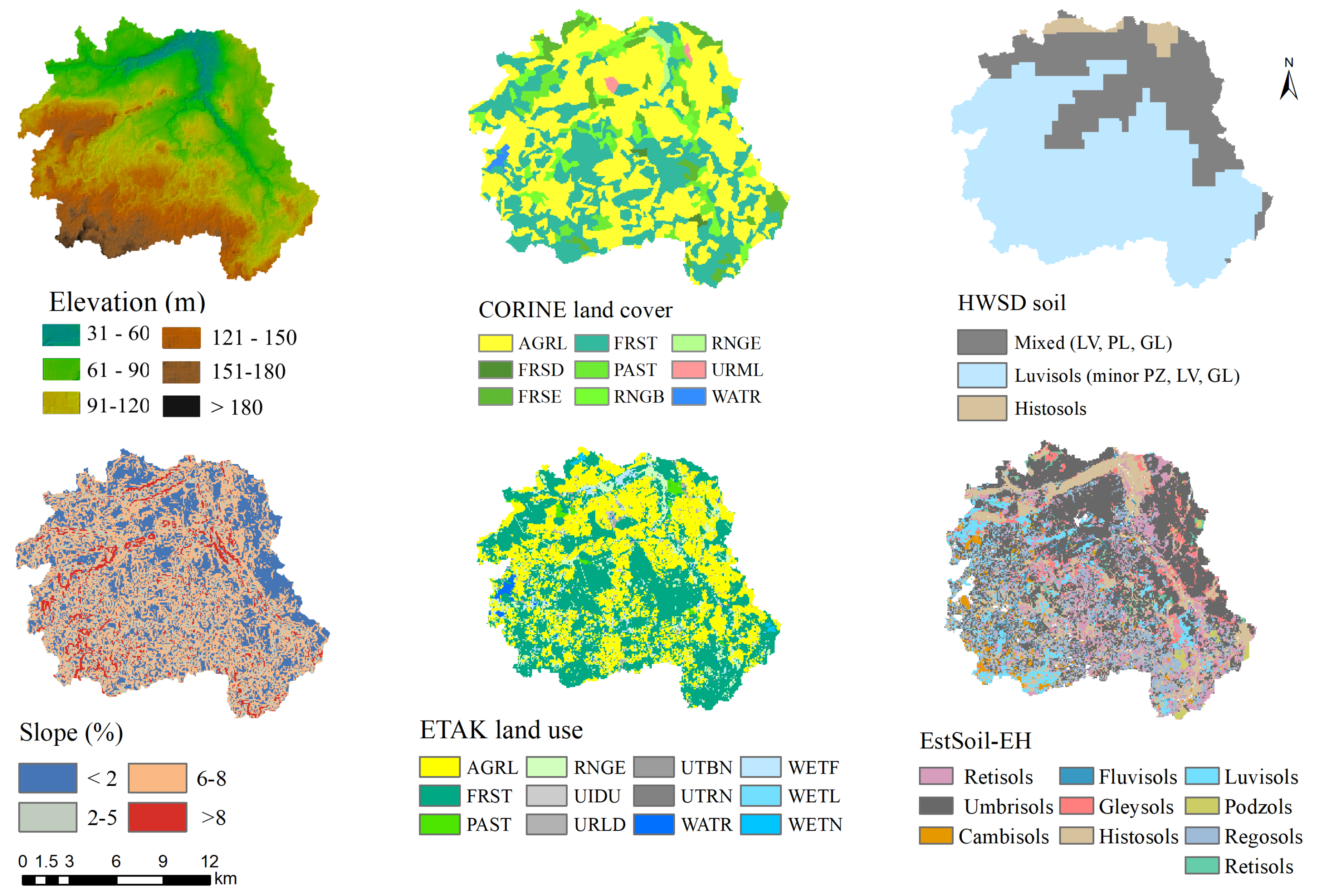


| ETAK Reclassied | CORINE Reclassified | ||||
|---|---|---|---|---|---|
| SWAT Types | SWAT Code | % | SWAT Types | SWAT Code | % |
| Generic-Agriculture | AGRL | 38.0 | Generic-Agriculture | AGRL | 49.8 |
| Mixed Forest | FRST | 45.8 | Mixed Forest | FRST | 37.3 |
| Deciduous Forest | FRSD | 0.4 | |||
| Coniferous Forest | FRSE | 4.9 | |||
| Pasture/Hay | PAST | 8.7 | Pasture/Hay | PAST | 4.9 |
| Range Shrubland | RNGB | 0.9 | Range Shrubland | RNGB | 6.1 |
| Grasslands/ Herbaceous | RNGE | 0.01 | Grasslands/ Herbaceous | RNGE | 0.7 |
| Urban Transportation | UTRN | 0.5 | Urban Medium Density | URML | 0.4 |
| Urban Industrial | UIDU | 0.3 | |||
| Residential / Public building | UTBN | 0.3 | |||
| Private yard | URLD | 2.2 | |||
| Wetland | WETL | 0.01 | |||
| Herbaceous Wetlands | WETN | 0.1 | |||
| Woody Wetlands | WETF | 2.2 | |||
| Water | WATR | 0.9 | Water | WATR | 0.4 |
| Model Abbreviation | Data Combination | No. of Subbasins | No. of HRUs (10% Threshold) | No. of HRUs (Unconstrained) |
|---|---|---|---|---|
| CLHS | CORINE land cover and HWSD global soil | 37 | 293 | 616 |
| ELHS | ETAK land use and HWSD global soil | 37 | 300 | 936 |
| CLES | CORINE land cover and EstSoil-EH | 37 | 573 | 2999 |
| ELES | ETAK Estonian land use and EstSoil-EH | 37 | 575 | 4448 |
| Parameter | Description (Unit) | Initial Range |
|---|---|---|
| CN2 | SCS runoff curve number (-) | −20% to 20% |
| GWQMN | Threshold depth of water in the shallow aquifer required for return flow to occur (mm H2O) | 500 to 4500 |
| RCHRG_DP | Deep aquifer percolation function (-) | 0 to 1 |
| GW_REVAP | Groundwater revap coefficient (-) | 0.02 to 0.2 |
| GW_DELAY | Groundwater delay (day) | 30 to 450 |
| SOL_BD | Moist soil bulk density (g/cm3) | −20% to 20% |
| SOL_K | Soil hydraulic conductivity in the main channel (mm/h) | −20% to 20% |
| SOL_AWC | Soil available water storage capacity (mm H2O/mm soil) | −20% to 20% |
| ALPHA_BF | Baseflow alpha factor (day) | 0 to 1 |
| ESCO | Soil evaporation compensation factor (-) | 0 to 1 |
| ALPHA_BNK | Baseflow alpha factor for bank storage (day) | 0 to 1 |
| CANMX | Maximum canopy storage (mm H2O) | 50 to 100 |
| CH_N2 | Manning coefficient for main channel (-) | 0 to 0.3 |
| CH_K2 | Effective hydraulic conductivity in the main channel (mm/h) | 5 to 250 |
| Indices | CLHS | ELHS | CLES | ELES | ||||
|---|---|---|---|---|---|---|---|---|
| cal | val | cal | val | cal | val | cal | val | |
| NSE | 0.78 | 0.51 | 0.79 | 0.59 | 0.69 | 0.34 | 0.71 | 0.41 |
| P-factor | 0.72 | 0.8 | 0.83 | 0.27 | 0.72 | 0.76 | 0.86 | 0.36 |
| R-factor | 0.87 | 1.75 | 0.99 | 0.1 | 0.88 | 1.45 | 1.02 | 0.41 |
| PBIAS | −3.0 | 0.4 | 5.7 | 4.7 | −0.4 | 4.2 | 3.9 | 3.6 |
| Parameter | CLHS | ELHS | CLES | ELES | |
|---|---|---|---|---|---|
| CN2 | 83.57 | 82.63 | 66.42 | 64.37 | |
| GWQMN | 1000 | 1000 | 1000 | 1000 | |
| SOL_BD | 1.58 | 1.58 | 1.05 | 1.03 | |
| CANMX | 0 | 0 | 0 | 0 | |
| SAND | 41.51 | 41.52 | 55.6 | 54.16 | |
| SILT | 27.57 | 27.57 | 17.42 | 17.45 | |
| CLAY | 30.92 | 30.92 | 26.97 | 28.4 | |
| ROCK | 5.82 | 5.83 | 2.99 | 2.4 | |
| SOL_CBN | 1.2 | 1.27 | 9.75 | 10.34 | |
| Hydrologic Soil Group, | A | 0 | 0 | 141.21 | 130.88 |
| Area in km2 | B | 0 | 0 | 0 | 0 |
| (of total 241.53 km2) | C | 0 | 0 | 99.85 | 109.01 |
| D | 241.53 | 241.53 | 0.46 | 1.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kmoch, A.; Moges, D.M.; Sepehrar, M.; Narasimhan, B.; Uuemaa, E. The Effect of Spatial Input Data Quality on the Performance of the SWAT Model. Water 2022, 14, 1988. https://doi.org/10.3390/w14131988
Kmoch A, Moges DM, Sepehrar M, Narasimhan B, Uuemaa E. The Effect of Spatial Input Data Quality on the Performance of the SWAT Model. Water. 2022; 14(13):1988. https://doi.org/10.3390/w14131988
Chicago/Turabian StyleKmoch, Alexander, Desalew Meseret Moges, Mahdiyeh Sepehrar, Balaji Narasimhan, and Evelyn Uuemaa. 2022. "The Effect of Spatial Input Data Quality on the Performance of the SWAT Model" Water 14, no. 13: 1988. https://doi.org/10.3390/w14131988
APA StyleKmoch, A., Moges, D. M., Sepehrar, M., Narasimhan, B., & Uuemaa, E. (2022). The Effect of Spatial Input Data Quality on the Performance of the SWAT Model. Water, 14(13), 1988. https://doi.org/10.3390/w14131988








