Quantifying the UDS Hydraulic and Social Resilience to Flooding: An Index-Based Approach vs. a Parameter-Based MCDM Method

Abstract

Various approaches to quantifying resilience have sparked debate in past years. This study measures the social and hydraulic resilience of an Urban Drainage System (UDS) using two methodologies, i.e., a proposed index-based framework and a parametric-based Multi-Criteria Decision Making (MCDM) method. The former positions flexibility as a key property of the resilience concept, and after quantifying four characteristics of a flexible system, measures the flood resilience based on quantifying the two resilience components, i.e., flexibility and resistance; while. The latter calculates the resilience through a linear combination of the actual values and relative weights for different UDS sub-characteristics which best describe the resiliency of the system. The methodologies were applied to a basin, focusing on flooding as a disaster, to quantitatively evaluate the behavior of UDS under both single-event and long-term precipitation. The results of both methods were indicative of a relatively low level of flood resiliency for the UDS in the studied area. Among different scenarios examined for the studied region, using Best Management Practices (BMPs) was turned out to be an effective adaptive measure to enhance the UDS resilience to a higher level.

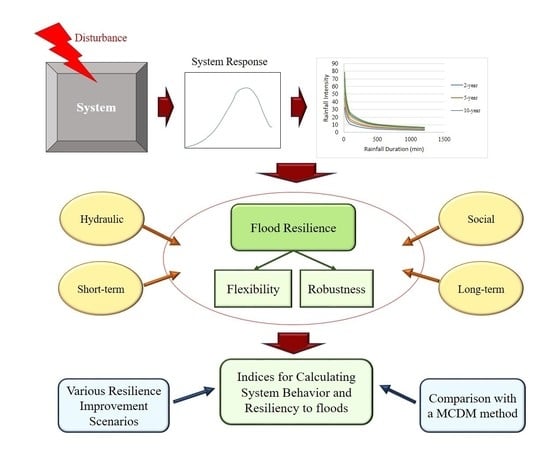
1. Introduction

Building resilience into urban critical infrastructures is essential to have the urban daily functions continue as normal in the face of various disasters. Measuring resilience is a crucial step in gaining such an achievement. It is known that resilience is the ability of a system to revert to its previous state after being disturbed by a perturbation. Flexibility, on the other hand, is sometimes used in the same meaning as resilience [1], which means there is a lack of focus on this concept as a different notion from resilience. Although- in some of the past studies and particularly in the field of psychology- flexibility has been mentioned as a close concept to resilience and related to it, it has not been characterized as an element under resilience structure. In other words, the concept of flexibility has not been well placed within the resilience mechanism. Only a few studies have focused on the notion of flexibility in detail, while the quantification of this concept has been missing in most cases. Some studies believe that a flexible system has the main capabilities of resilience.

However, most studies agree that robustness (as an attribute of the resistance concept) could be at least a part of resilience. Restemeyer et al. [2] argue that resistance can be one important aspect of resilience. In line with this, Tempels and Hartmann [3] believe that prioritizing resistance or flexibility over each other does not seem to be true and state that there should be a balanced approach towards flexibility and robustness [4]. Asokan et al. [5] defined flexibility as the representative of two main resilience parameters, i.e., robustness and transformation, but not as a factor inside the resilience configuration. In the current study, we have a new definition of resilience based on system flexibility. In the proposed definition, flexibility is nearly the same as resilience, excluding one metric (the robustness), which is the only term that resilience has more than flexibility. In fact, flexibility is most of the resilience concept. Such an approach seems to agree with the idea represented by Husdal [6], who believes robustness and flexibility are essential tools for handling risks and uncertainties.

It could be said that despite the frequent use of the term flexibility, very little work has been accomplished to quantify this term, especially regarding the urban drainage system. Some studies focused on flexibility measurements concerning the other meanings of flexibility suitable for the other types of systems and provided with the quantification methods are not necessarily applicable to the UDS. For example, Stinner et al. [7] proposed a quantification method of flexibility specific to the Building Energy Systems with Heat Pumps. Fletcher [8] addressed flexibility in Water Supply Infrastructure Planning. However, the purpose was not to quantify the flexibility or resilience of the system. Sidqi et al. [9] defined flexibility in the household as the capacity to increase, decrease, or shift the consumption of domestic appliances over time and quantified the consumed power in 194 households, and computed the share of both heating needs, i.e., space heating and hot water heating.

Almost all previous studies agreed on the measuring method of UDS robustness in the face of extreme rainfall (which is accepted by this paper and is explained later). But the question arises: how is the system flexibility measured? This study mainly focuses on this part of quantifying the resilience concept. In the proposed approach, finding the answer to the seven following questions is necessary: (1) how much of the disturbance can be tolerated by the system? (2) how fast does the system degrade in facing the disturbance? (3) how big is the response by the system when hit by an external disturbance? (4) how long does it take for the system to be able to survive from the minimum failure state? (5) how fast is the process of regaining stability and restoration to an acceptable performance level? (6) how much improvement is obtained after the recovery process? And (7) how well has the system been adapted to the new condition? The index-based framework discussed in the following sections is proposed to answer the above questions.

The results of the proposed index-based method will be compared with results from a parametric-based methodology, which has an emphasis on the multi-dimensional nature of resilience and is developed based on a Multi-Criteria Decision Making (MCDM) method.

This study attempts to fill in the gaps in previous works by concentrating on an urban drainage system resilience and flexibility from various viewpoints, i.e., hydraulic and social aspects, and instant and long-term evaluation of the system. Tahmasebi Birgani and Yazdandoost [10] proposed a framework to quantify resilience in the case of a drainage system facing a single-event rainfall based on three indicators of “reaction magnitude”, “graduality”, and “recovery capacity”. They suggested that future studies evaluate the long-term performance of UDS while going under long-term rainfall events. This has been focused on as a part of the current study. Most other studies, such as the works done by Mugume and Butler [11] and Bakhshipour et al. [12], quantified the UDS functional/structural resilience; however, they didn’t consider the quantification of resilience indicators and, instead, defined direct formulas for calculating the system resiliency. This is while the current study introduces indicator-based methodologies for UDS resilience quantification in the face of extreme rainfall events.

2. Literature Review

To provide a framework for quantifying the resilience of a disturbed system based on the notions of robustness and flexibility, after reviewing some of the most well-known definitions provided in recent years, it should be clarified what is meant exactly by these three concepts to be able to clarify how they are related to each other.

2.1. Definition of Resilience Based on “Robustness” and “Flexibility”

Resilience is defined as the system’s capacity to cope, adapt, and improve in response to both chronic stresses and acute shocks applied to it [13,14]. Before explaining how such a definition could be expressed based on two elements of “robustness” and “flexibility”, we had better have a comparison between the two components.

Robustness points to the ability of a system to “stay on course” and absorb unforeseen and uncertain future disturbances [6]. A Robust system accommodates the perturbations and resists the disturbance so that it continues its pre-defined path without functional degradation. This is why flexibility means the capacity to accommodate unforeseen disturbances “by changing tracks and being open to temporarily deviate from the initial course to reach the desired goal” [6]. A flexible system can gracefully degrade while exposed to a disturbance and restructure itself rapidly with an adaptive approach and by learning from past experiences. It seems that concerning the flexibility concept, what is important is the final goal without being hurt, no matter how the path has to be paced during a disaster, whereas robustness focuses on the capacity of the system to endure such changes [15]. Totally, as Husdal [6] states, “robustness reduces uncertainty and flexibility adapts to it”.

According to resilience’s general definition and descriptions of system robustness and flexibility presented above, the resilience of a system is highly dependent on these two concepts. Thus, measuring the system resilience requires quantifying the subset components, i.e., robustness and flexibility. Walker et al. [16] define flexibility as “dynamic robustness”, which enables a plan to change in response to changing conditions over time.

A literature review indicates that flexibility has been viewed from two different angles based on where on the system functionality curve (Figure 1) it will be considered: in the response phase or within the recovery phase and after that. In the first meaning, flexibility refers to the degree of proportionality in response to distribution and means not having an abrupt failure due to a sudden shock. In this meaning, a system is flexible if the applied perturbation is mostly absorbed, and therefore, consequences or damages emerge little by little. Based on such a definition, with a flexible system, there is enough time to mobilize the equipment and resources and cope with the impacts of the shock while the damages are not too large. This meaning of flexibility has been expressed in the current study as “braking capacity”, which has a close relationship with the notion of “graduality” introduced by De Bruijn [17]. Graduality refers to the increase in damage with increased disturbance magnitude [18]. This is why braking capacity represents the trend of system degradation with time. (For more information on the difference between the two concepts of graduality and braking capacity, see Supplementary Materials, Figure S1).

In the second meaning, flexibility is related to uncertainties in future conditions and, thus, uncertainties in estimations for future planning. In this meaning, flexibility refers to the willingness and ability to adopt alternative strategies in response to changing circumstances or sudden crises [13]. In other words, despite the primary estimations for future conditions and planned implementations, a flexible system could still be stable and welcome such unforeseen changes. Heggarty et al. [19] considered this meaning of flexibility for power systems and defined it as “the ability to cope with variability and uncertainty in demand”. This translation of flexibility has been referred to as “adaptive capacity” in the current study.

However, some other descriptions of flexibility can be found in the literature covering both above-mentioned definitions, according to which flexibility is described as system change, evolution, and adaptation in response to changing circumstances. This definition matches the most to what the current study means by flexibility. The current definition encompasses a wide range of system behavior in the face of an external perturbation and involves both the meanings pointed out above. This study believes that flexibility is composed of four metrics of response, survivability, recovery, and adaptability, and defines flexibility as the ability of a disturbed system to have (1) a soft response (i.e., with a small response-magnitude and a graceful degradation), (2) a short stay in the failure mode and ability to immediate rise-up, (3) a rapid restoration to an acceptable level of performance or ideally, an improved one, and (4) adapt to the new conditions after changing the surrounding environment or the system condition.

2.2. System Behavior in Response to a Disturbance

Before quantifying the resilience components, it is necessary to explain the system performance and behavior as well as the critical thresholds in response to an external perturbation. The behavior of a disturbed system vs. time has been presented in Figure 1. Three types of critical thresholds can be recognized in such a performance curve. The first one is the “reaction threshold”, which is located at the end of the resistance domain. After that, the system is no longer able to endure the applied perturbation and thus, starts responding to it and degrades. Concerning urban flooding, the reaction threshold occurs when we have the largest load on the system (i.e., the largest amount of extreme rainfall), which is not supposed to create flooding [20,21,22]. At the end of the response process, when the system performance reaches its minimum level possible, the “tolerance threshold” occurs, which means a threshold where the system cannot bear the disturbance anymore. This is why before this threshold, a part of the disturbance could be absorbed by the system alongside the performance degradation. In fact, the “tolerance threshold” is located before the maximum failure of the system. Apart from the two mentioned thresholds, a third could be identified in the system behavior curve, which is called the “non-recovery” threshold and is not determined in Figure 1 since it occurs only in certain conditions. The “non-recovery” threshold happens when the system is no longer able to return to its previous status and enters a new attraction basin and new stability domain. A regime change happens in system performance and status, which may occur when the failure time duration and system stagnation is too long. If the magnitude of the system response to a disturbance is so large that it causes the system to spend a long time at its minimum level of performance, or if the disturbance magnitude is too large and goes beyond certain limits, the system is no longer able to return to its previous stability status, which is where the “non-recovery” threshold makes sense [23,24].

As shown in Figure 1, the system behavior curve experiences five different stages when exposed to an external disturbance (i.e., resistance, response, rise-up, recovery, and adaptability phases). Quantifying these phases means measuring the components of a disaster cycle, from resistance against a disaster to recovery, mitigation, and preparedness for future similar hazards. Figure 2 demonstrates the components of system resilience in the proposed framework.

3. Introduction to the Case Study

A semi-urbanized basin in the northern areas of Tehran, Iran, was considered the case study in which the proposed methodology (explained in the following section) would be applied. Three major rivers—Darakeh, Farahzad, and Hesarak—are located in this basin whose waters discharge to a constructed diversion channel west of Tehran, which ultimately joins the Kan River. In the current study, we call the basin the “West Flood Diversion (WFD)” catchment. The basin covers an area of more than 140 Km² and involves both urban and suburban mountainous areas upstream of the urbanized region. Figure 3 depicts the situation of the catchment in Tehran and Iran. The blue and gray areas in the basin represent the urban and suburban areas, respectively. Black lines represent the sub-basins’ boundaries. In addition,

Table 1. The sub-basins’ physiographic characteristics in WFD catchment [25].

The Parameter		Area (Km2)	Perimeter (m)	Length (m)	Min height (m)	Max height (m)	Time of Concentration (min)	Average Slope (%)
The Sub-Basin
Hesarak (Suburb)		14	17,516	7052	1550	2750	35	50
Hesarak (Urban)	Main Channel	8	14,763.7	6840	1243	1570	56	5.3
	Shahin & Shaghayegh Channels	17	24,942	8484	1243	1985	53	7.2
Farahzad (Suburb)		23	24,412.7	9909	1600	3400	45	57.4
Farahzad (Urban)	Main Channel	20	27,337.6	9450	1269	2224	54	9.4
	Moradabad channel	3	9141.3	4027	1565	2520	20	36.9
	Behroud channel	4	10,833.5	4887	1628	2790	23	36.8
Darakeh (Suburb)		25	24,121.8	9376	1700	3800	39	59
Darakeh (Urban)	Main channel	12	29,472.7	9384	1320	2200	55	13.2
	Tappeh-Neizar channel	13	19,239.8	637	1300	1800	54	7.9
	Khoshkeh channel	2	9151.3	3750	1650	2700	18	46.7

represents the physiographic characteristics of the sub-basins.

4. Materials and Methods

Figure 4 represents the flowchart of the works accomplished in the current study. This flowchart gives a total view of the process of measuring resilience and flexibility, comparing the results with an MCDM method and choosing the best solutions for improving the resilience index of the system, which are discussed in detail in the following sections.

4.1. Index-Based Measurement of Resilience

4.1.1. System Definition and Characterizing the Disturbance and the System Response

To use the framework, the system boundaries should first be defined, and the type of disturbance applied to the system and its main characteristics should be determined. The system under investigation in the current study is Urban Drainage Infrastructure (UDI), embedded in the surrounding urban complex environment and is in mutual dependency with it through social feedback. Since this study will examine the resilience of UDS to flooding, any cases of extreme rainfall, pluvial flooding, rapid urbanization, or climatic changes (as the source of extreme events) could be considered the disturbance. Herein, the precipitation was chosen as the applied perturbation for the drainage system, and therefore, the surcharges from the UDS would be the response to such a disturbance. The response magnitude would be the surcharged depth, while the response trend would be determined through the increase in inundation depth with time.

To determine the characteristics of the extreme rainfalls (as the perturbation) and the system surcharges (as a consequence), the Intensity-Duration-Frequency (IDF) curves alongside the Stormwater Management Model (SWMM) were utilized (Sensitivity analysis and calibration of the rainfall-runoff model are presented in Supplementary Material, Tables S1–S3). The total rainfall depth was extracted from IDF curves, and parameters such as the volume/depth of the surcharged runoff and flood duration were obtained from the simulation results in EPA SWMM (as well as PCSWMM). SWMM is a dynamic hydrology-hydraulic water quality simulation model often used for a single event or continuous simulation of runoff quantity and quality in urban areas [26,27].

It should be noted that what is meant by flood in the current study is any surcharging from the drainage network, which inundates the surrounding area. And what is meant by extreme rainfall is the precipitation that results in a surcharge from UDS and thus causes inundation in the surrounding area.

4.1.2. Developing IDF Curves for the Region

The Equations (1) and (2) have been proposed by Ghahreman [28] for the condition of Iran—based on the relation offered by Bell [29]—which calculate the rainfall with a duration of 15 min to 20 hrs and a return period of 2 to 100 years [30].

$$P_T^t=\left(0.4524+0.2471\ln \left(T-0.6000\right)\right)\left(0.3710+0.6184t^{0.4484}\right)P_{10}^{60}$$

(1)

In Equation (1), t represents the time (min), T is the return period (year), $P_{10}^{60}$ is the amount of 10-year, 1-h rainfall, which is obtained through Equation (2) [31,32]:

$$P_{10}^{60}=e^{0.291}\times {\left(P_{24h}\right)}^{0.694}$$

(2)

where $P_{24h}$ is the maximum average of daily rainfall (mm).

To develop IDF curves for the studied region, Equations (1) and (2) were modified and calibrated based on the IDF equation presented for Tehran by Mahab-e-Ghods Consulting Engineers [33] (Equation (3)).

$$P=(C_{\mathrm{Alt}.\mathrm{RP}}{D}^{-0.645})·\left(D/60\right)$$

(3)

In which P is the rainfall value and D is the rainfall duration in minutes ($D\le 360 \min$). $C_{\mathrm{Alt}.\mathrm{RP}}$ is a coefficient that is calculated from Equation (4) and is dependent on the two factors of the return period (T, year) and average ground level (H, MASL).

$$C_{\mathrm{Alt}.\mathrm{RP}}=108\times \left(0.0008\times H+0.2\right)\times \left(0.304\times \mathrm{Ln}\left(T\right)+0.78928\right)$$

(4)

After calibration and verification, the IDF curve for the WFD catchment could be obtained as Equation (5).

$$P_T^t=\left(0.3+0.114\ln \left(T-0.57\right)\right)\left(0.3+0.6t^{0.4692}\right)P_{10}^{60}$$

(5)

where:

$$P_{10}^{60}=e^{0.2}\times {\left(P_{24h}\right)}^{0.6}$$

(6)

4.1.3. Calculating the System Robustness

Robustness could be evaluated as the resistance phase in the system’s behavior curve, during which the disturbance is endured by the system, and no reaction is shown. This characteristic represents the tolerance capacity of the system under perturbation. On the system behavior curve, resistance refers to the duration from when the disturbance is applied to the system until the system can fully resist it (where no performance degradation occurs anymore), which is representative of “full absorption” of the disturbance by the system. For instance, in a normal system undergoing precipitation less than the designed rainfall (for which the system is designed), no response or reaction is made by the system. In such a situation, it could be said that the system behavior is in the resistance phase. In most previous studies [10,23,34,35], the resistance capacity (RC) has been quantified as a quota of the magnitude of the disturbance, which could be absorbed by the system without performance degradation and with no essential change in the system structure.

According to what was mentioned, two terms of Hydraulic Resistance Capacity (HRC) and Social Resistance Capacity (SRC) can be extracted for the current study. Hydraulic Resistance Capacity for Single-event rainfalls (HRC_S) can be measured as the largest rainfall depth that could be tolerated by the system without any failures (Equation (7)). The amount of such rainfall with a certain return period could be extracted from the IDF curves of the studied region. The focus of the current study is on a 6-h design rainfall, which is common in the study site [36], and therefore, the largest amount of such a rainfall depth could be obtained through IDF curves for different return periods, and the surcharge from the system was calculated using the rainfall-runoff modeling in SWMM. However, it is better to normalize the system resistance to be comparable with the other cases and, simultaneously, apply it to the current study. To do this, the maximum rainfall depth that would not result in a surcharge from the UDS ($Max(R_{D_i})),$ is divided by Probable Maximum Precipitation (PMP) for the region.

$$Max(R_{D_i})<R_{D_S}\hspace{1em}\hspace{1em}\to \hspace{1em}\hspace{1em}HR{C}_S=\frac{Max(R_{D_i})}{PMP}$$

(7)

In Equation (7), $R_{D_S}$ is the smallest depth of rainfall which results in a surcharge from the system, $Max(R_{D_i})$ is the largest rainfall which does not cause a surcharge from UDS, and i is counter of the rainfall-induced runoff depths during the simulation process.

For long-term events, the basis for the calculation of the HRC would be the same as single event rainfall in general. However, since the return periods may not be known in a long-term continuous precipitation time series, HRC against a long-term rainfall disturbance (HRC_L) can be defined as the quotient of the largest rainfall depth in the time series, which causes no surcharge from the UDS to the amount of PMP for the basin.

In the social context, quantifying the UDS robustness may be somehow different. When we are focusing on social problems regarding floods, not every inundation depth is going to be considered a hazard; therefore, we need to, first, have a threshold for that. Such a threshold may depend on the community under investigation. Herein, a 60 mm depth was considered a critical depth in the social context, and it is assumed that the flowing water with a depth of less than 60 mm could not make serious problems for the residents and commuters in the region [37]. On this basis, the largest rainfall value, which does not result in surface runoff of more than 60 mm in depth, is considered the Social Resistance Capacity against single-event rainfall (SRC_S). For long-term precipitation, Social Resistance Capacity (SRC_L) could be obtained as the quotient of the largest rainfall depth in the time series for which the surcharges from the drainage system do not exceed 60 mm to the PMP minus the given inundation threshold causing societal problems (herein 60 mm).

$$Max(R_{D_{i60}})<R_{D=60 \mathrm{mm}}\hspace{1em}\hspace{1em}\to \hspace{1em}\hspace{1em}HR{C}_S=Max(R_{D_{i60}})$$

(8)

$$HR{C}_L=\frac{Max(R_{D_{i60}})}{PMP-60\mathrm{mm}}$$

(9)

4.1.4. Quantifying the System Flexibility

System Response

What is meant by the response is the system’s reaction to the disturbance. The response of the system can be argued from two viewpoints: response magnitude (i.e., degradation capacity, $DC$) and response trend (i.e., braking capacity, $BrC$). Before addressing the two components of the response phase, the quantification of absorptive capacity must be explained.

Absorptive Capacity

Absorptive capacity refers to that part of the behavior of a disturbed system that is resisting transformation under a disturbance. According to this definition, absorptive capacity is determined as the sum of the resistance domain and the quota of the response phase during which a part of the disturbance is absorbed by the system. Looking at a system behavior curve (Figure 1), the system may absorb the disturbance for a certain time duration and remain unchanged (i.e., resistance domain), but after reaching the reaction threshold, it is no longer able to endure the disturbance and, therefore, its track change (i.e., performance degradation) commences. In this phase (response domain), only a part of the disturbance is absorbed until the system reaches its minimum performance regarding the applied perturbation. This partial absorption in the response phase plus the total absorption happening during the resistance domain forms the “absorptive capacity” of a system. To quantify the absorptive capacity, the following equation is suggested:

$$AbC=RC+BrC+1/DC$$

(10)

where $RC$ is the resistance capacity.

Degradation Capacity

The degradation capacity of a system is indicative of the fact as to what degree the system is impacted by the disturbance. In some previous works [1,17], the Expected Annual Damage (EAD) has been utilized to measure the response magnitude of a disturbed system, which is a commonly used index representing the expenses related to damages resulting from the perturbation applied to a system [38]. However, in the current study, the system response is described as the inundation depth considering the extreme rainfall as the disturbance on the UDS. (See Figure S2 (Supplementary Material) for more available approaches towards a system response to a disturbance). Therefore, the simulation results by SWMM can be utilized to determine this indicator for the system. In the current study, the Hydraulic Degradation Capacity (HDC) could be measured as the average surcharged runoff depth from the UDS. Social Degradation Capacity (SDC) is approximately the same other than subtracting the 60 mm surface runoff depth, which does not create significant social problems. This can be described as the following equation:

$$SDC=HDC-60(\mathrm{If}\hspace{1em}SDC<0\hspace{1em}\hspace{1em}\to \hspace{1em}\hspace{1em}SDC=0)$$

(11)

where SDC and HDC are the values of social and hydraulic degradation capacities in mm.

For long-term time series, the average of surcharged runoff depths could represent the HDC, and accordingly, SDC can be calculated using Equation (9). In addition, SDC could be measured by considering the number of casualties and deaths during floods, the average delay time in reaching the destination, and increased traffic jams due to inundation problems. However, such a measurement requires having enough reliable data across the region. It is not the case in the current study since most of this kind of information is qualitative and not reliably documented.

Braking Capacity

Braking capacity (i.e., response trend) is described as the extent covering the onset point of performance reduction to the minimum performance level of the system (Figure 1). The longer the time duration is within this extent, or the gentler the performance reduction, the higher the braking capacity of the system.

This indicator is quite dependent on the “absorptive capacity” of the system, as the more the system absorption is, the less the probability of abrupt failure is, and the system degrades more gracefully—due to the absorption of a part of the disturbance by the system. According to the behavior of a disturbed system (Figure 3), the UDS braking capacity (BrC) is the inverse slope of the functionality degradation line. It can be calculated as described in Equation (10).

$$BrC=\frac{1}{\frac{{{\displaystyle \sum }}_{i=1}^N\left(\frac{D{C}_i}{(T_{Pi})}\right)}{N}}=\frac{N}{{{\displaystyle \sum }}_{i=1}^N\left(\frac{D{C}_i}{(T_{Pi})}\right)}$$

(12)

In the above equation, DC_i is the degradation capacity of the i^th flooded node (practically the surcharged flow-depth for that node), N is the total number of flooded nodes, and i is the counter. T_P is time to peak, calculated as $(T_M-T_0)$ where T₀ and T_M are representative of the flooding start-time and peak-flood time, respectively. The higher the value of BrC is, the higher the system braking capacity (and consequently, resilience) is.

For calculating social braking capacity, T_P would be the difference between $T_M$ and the time the surcharged runoff depth exceeds 60 mm (T₆₀). Equation (10), which calculates the inverse slope of the response curve in Figure 1, can be utilized for both hydraulic and social braking capacities for single-event rainfall. To have the index for the long-term time series, Equation (11) can be used instead.

$$Br{C}_L=\frac{N}{{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^M\left(\frac{D{C}_{ij}}{(T_{Pij})}\right)}$$

(13)

where M is the number of single rainfalls in the precipitation time series. Supplementary Material (Figure S2) explains the difference in a system’s behavior (i.e., response and recovery phases) under a similar disturbance.

4.1.5. Rise-Up Capacity

This study introduces an indicator describing a part of the system’s behavior, hereafter called “survivability”, which means the ability of the system to rise after a minimum failure state. In other words, the degree of the system agility in restoration after reaching the minimum possible performance under a specific disturbance. This system property has an inverse proportionality to the time duration during which the system remains in minimum failure mode. Considering the important parameter of flood depth as the multiplying weight for each node, the rise-up capacity (i.e., survivability) can be defined as follows:

$$SRV={\displaystyle \sum }_{i=1}^N\frac{1}{T_{St}}=\frac{{{\displaystyle \sum }}_{i=1}^N{D}_i}{{{\displaystyle \sum }}_{i=1}^N(T_{S1i}-T_{Mi})D_i}$$

(14)

where $T_{St}$ is the stagnation time, i.e., the time duration the system remains in the minimum failure mode, which is the time between maximum inundation ($T_M$) and the time of flood subsidence in at least one node of the drainage system $(T_{S1})$. For the social aspect, $T_{S1}$ represents the time the flooding subsides below the 60 mm threshold at least in one node of the UDS. $D_i$ indicates the flood depth above the i^th node of UDS, and therefore, SRV for the social aspect is meaningful only when the inundation depth reaches 60 mm. For long-term precipitation time series, this indicator should be calculated by averaging the obtained SRV for all extreme rainfall events (resulting in surcharges from the UDS). SRV values have been expressed with the unit 1/hr. A high value of SRV represents a system highly resilient to the given disturbance.

4.1.6. Restorative Capacity

By investigating the recovery phase in the system behavioral curve (Figure 1), we know the speed and the trend of the system in bouncing back to its previous (or acceptable) level of performance. Thus, recovery (i.e., restorative capacity) encompasses two characteristics of the system in response to disturbances: (1) system rapidity and (2) system improvability.

Rapidity

The Rapidity (RPD) indicator explains how fast the disturbed system returns to normal (or acceptable) performance after its functionality has reached the minimum possible level.

The recovery time (T_R) is defined as the time duration the largest value of runoff depth starts to subside in one node ($T_{S1}$) until it is 100% finished in all UDS nodes ($T_{SS}$). To formulate UDS rapidity, the inversely weighted average of the recovery time is calculated. Inundation depth is the multiplying weight for each flooded node as the flood depth well represents the severity of the disaster. Accordingly, rapidity is formulated as the inverse of the weighted average of flood duration above the drainage nodes (Equation (15)).

$$RPD=\frac{{{\displaystyle \sum }}_{i=1}^N{D}_i}{{{\displaystyle \sum }}_{i=1}^N{T}_{Ri}{D}_i}=\frac{{{\displaystyle \sum }}_{i=1}^N{D}_i}{{{\displaystyle \sum }}_{i=1}^N(T_{SSi}-T_{S1i})D_i}$$

(15)

Equation (15) can obtain both hydraulic and social rapidity. To calculate social rapidity, $T_{SS}$ represents the time the flood depth reaches less than 60 mm in all UDS nodes ($T_{SS}$), and like the SRV indicator, it is meaningless if the surcharged runoff from the system is below 60 mm. For long-term precipitation time-series, the rapidity would be the average of calculated RPD for any of the rainfall events.

Improvability

Improvability refers to the increase in the performance level (after resuming the normal functioning) compared to the pre-disaster level of functionality. Improvability is important for moving towards sustainability, which means the same disturbance with the same characteristics would not be able to disrupt the system efficiency for a second time. It is in agreement with the idea of some other researchers [14], who believe that a recovered system is expected to reach a higher resilience than the pre-disaster condition, and a “new normal” state is required at the end of this process, so that the system may even enter a new stability state and attraction basin.

To measure the improvability of the system, we use a modified version of the relationships proposed in the study by Binesh et al. [39] and calculate this system property as the difference between the UDS performances before and after implementing the adaptive solutions. The whole system’s improvability is obtained by averaging the calculated index for every single conduit, according to Equation (16) (provided that the modeling time steps are equal for all conduits’ simulations before and after implementing the adaptive strategies).

$$IMP=\frac{{{\displaystyle \sum }}_{j=1}^{N_s}\frac{\left(V_{sbj}-V_{saj}\right)}{V_{sbj}}}{N_c}$$

(16)

In Equation (16), V_sbj and V_saj are representative of the surcharge volume in j^th surcharged conduit in the UDS before the disaster and after the recovery process of the disturbed system, respectively; N_s is the number of surcharged conduits in the simulating process, and N_c is the whole number of UDS conduits. The IMP indicator varies between zero and one.

Equation (16) applies to single-event precipitation and long-term rainfall time series. Regarding the social aspect, a surcharged runoff depth equal to 60 mm (or less) plays the role of “no runoff” for the hydraulic improvability of UDS, which means only those surcharges from the system are accounted for that exceed 60 mm depth.

Herein, the improvability index was defined from a “volumetric” viewpoint. It could also be described from a “temporal” or “number of occurrence” point of view, which means how much improvability has been gained in terms of reduction in inundation duration time or frequency of surcharges from the system.

4.1.7. Adaptive Capacity

The factor of adaptability is of the most important components of resiliency as some studies consider the whole resiliency of a system mainly within this single property and define resiliency as “the ability of the system to adapt” [40]. It could be said that adaptability is considered a basic property and a key measure of resiliency [41,42]. An adaptive system changes its behavior in response to the change in the environment, reducing uncertainty. For example, using some adaptive solutions may accommodate different volumes of rainfall-induced runoff, and therefore, up to a certain threshold, no inundation (or little inundation) occurs. To calculate the adaptability of UDS (after considering the adaptive solutions alongside the drainage system), the following equation is used herein:

$$ADP=\frac{R{D}_{LR}}{D_{LR}}-\frac{R{D}_{SR}}{R{D}_{SR}}$$

(17)

where $R{D}_{LR}$ and $R{D}_{SR}$ represent the inundation depth following the largest and smallest rainfalls that occurred in a rainfall time series or a certain period, while $D_{LR}$ and $R{D}_{SR}$ are the rainfall depths for the largest and smallest rainfall events in the time series or a certain period, respectively. The ADP index is expected to be a number less than one. An ADP closer to zero represents a highly adaptive system. For addressing the social aspect for all indicators, 60 mm of inundation depth is ignored during the calculation, as expressed in the previous sections.

4.1.8. Calculating the System Flexibility and Resilience

After estimating the quantities mentioned above, the system flexibility is calculated by averaging the normalized values of its components. It is worth noting that among all flexibility components, the system degradation capacity is inversely proportional to flexibility; therefore, before using this component in calculating the final flexibility index, it should be modified as Equation (18).

$$D{C}_m=1-DC$$

(18)

where $D{C}_m$ is the modified degradation capacity.

The Flexibility Index (FLX) is then obtained using Equation (19) for both single-event and long-term events in both hydraulic and social dimensions.

$$FLX=\left(D{C}_m+BrC+SRV+RPD+IMP+ADP\right)/6$$

(19)

Afterward, having the flexibility value and the resistance capacity, the UDS resilience index (RI) can be obtained by averaging the two components (Equation (20)), which could be interpreted as Table S4 (Supplementary Material). The classification of resiliency levels is suggested with equal intervals as proposed in some similar previous studies [43].

$$RI=\left(FLX+RC\right)/2$$

(20)

4.2. Evaluating Different Scenarios for Improving the UDS Resiliency

The index-based methodology was applied to the WFD catchment using four types of drainage scenarios, including the existing condition of UDS, installing the BMPs, increasing the system capacity, and adding an auxiliary channel to a section of UDS where most inundation problems usually occur.

4.2.1. Scenario No. 1: The Existing Condition of UDS

The first scenario is considered the current situation of UDS without any changes to the existing system or using any adaptive measures. This scenario is required to be included to compare the degree of improvement achieved by other scenarios to see if they are helpful in comparison with the existing situation.

A primary simulation of UDS and rainfall-runoff modeling represent that the system encounters some flooded nodes and surcharged conduits when it goes under a 10-year, 6-h design rainfall. Figure S3 (Supplementary Material) shows the simulated drainage network in PCSWMM.

4.2.2. Scenario No. 2: Increasing the UDS Capacity

A proposed scenario could be the enlargement of the drainage channels in critical points to make up for the lack of hydraulic capacity in conveying the stormwater runoff. To apply this scenario, the flow conveyance capacity of the channel was increased up to 30 percent.

4.2.3. Scenario No. 3: Using Auxiliary Channels (Parallel Channels)

Given the discharge of all drainage channels of the area to the WFD channel in the south of the catchment, the probability of emerging bottlenecks alongside the main WFD channel is high [44]. Therefore, a scenario of adding a rectangular closed-channel to the location indicated in Figure S3 (Supplementary Material) is proposed. The auxiliary channel’s depth, width, and length are 2 m, 3 m, and 5 km, respectively. By adding this channel, it is expected that the system redundancy will increase, and the inundation points and surcharges from the system will decrease as a result.

4.2.4. Scenario No. 4: BMP Implementation alongside the Drainage System

The BMP installation scenario includes two sub-scenarios of (1) installing BMPs merely in the urban sub-basin and (2) installing BMPs in urban and upstream suburban areas. Two types of BMPs were determined for the catchment- i.e., Porous Pavement (PP) and Detention Pond (DP) according to the previous studies performed for the basin and some areas in the neighborhood [39,45]. Tahmasebi Birgani et al. [45] ranked eight BMPs according to the managers’ preferences in four areas of hydraulic, environmental, social, and economic aspects for an urban part of northern Tehran. The results (Table S5, Supplementary Material) indicated that some BMPs, including PP and DP, are among the most suitable for the studied area in various priorities considering the four studied aspects. Both selected BMPs were simulated in urban parts of the catchment. However, since PP is mostly suitable for urbanized areas, only DP was considered for the suburban areas of the basin.

4.3. Parametric-Based Resilience Calculation Using an MCDM Method

The second proposed method for calculating the system resilience index is a parametric MCDM methodology, namely IMPRESS (i.e., an Integrated Methodology for Parametric-based quantification of RESilience). In this approach, different characteristics of the system which play a role in accelerating/alleviating the urban flooding and inundation problems are first identified (i.e., the number and severity of rainfalls and inundations, average annual precipitation, UDS materials’ deterioration and aging, the drainage system density per unit area, etc.). These characteristics were chosen considering both single-event and continuous rainfalls/flooding. In addition, some characteristics of resilience (some accepted from previous works and some are proposed here in this study) are considered, including robustness, amplitude (i.e., the magnitude of the system response to a disturbance), graduality (i.e., the response trend), redundancy (i.e., representing an excess capacity and the extent to which system components are substitutable), modularity (i.e., the ability of each part of the system to perform independently and on its own), survivability (i.e., the degree of agility for bouncing back towards the previous functionality after reaching the minimum failure state), and rapidity (i.e., the speed of recovery in a disturbed system).

In the next step, the actual values (v_obs) for each system’s characteristics are acquired based on several databases, including historical data, official reports, and data recorded in the Iranian Meteorological Organization (IMO), Iranian Water Resources Management Company, Iranian Red Crescent and Disaster Management Organizations, Environmental Conservation agencies, Tehran Municipality as well as doing interviews and field observations. In addition, the corresponding minimum and maximum values (V_min and V_max) are furthermore obtained according to the available data and observations.

Since the identified system characteristics do not have the same importance regarding resilience to floods, the relative importance of each factor should be determined by a weight given to it by experts. The actual values and weights were normalized to be used as a non-dimensional number between 0 and 1.

In the next stage, a matrix approach is utilized, and the resilience matrix is developed. For this purpose, the system characteristics are categorized under relevant domains and resilience properties, as indicated in Figure 5. Finally, PROMETHEE (i.e., preference ranking organization method for Enrichment of Evaluations) was utilized to quantify the resilience index based on an MCDM approach. (For more information on the PROMETHEE method, refer to Brans et al. [46] and Brans and Vincke [47]).

5. Results and Discussion

5.1. Data Collection

The map of the studied region, as well as the UDS configuration and the conduits’ characteristics, were obtained from Yekom Consulting Engineers [48] and some past studies performed on the basin [49]. The data required for rainfall-runoff modeling—such as sub-basins’ curve number (CN), manning coefficient, UDS characteristics, and land properties—were extracted from relevant sources [33,50,51]. Wherever needed, information on the catchment was gained through recorded data in the Tehran Municipality Database and interviews with informed individuals and authorities.

Rainfall data was mainly extracted from two stations inside the WFD catchment, Mehrabad and Darakeh (Haft-Howz), whose characteristics are listed in

Table 2. The characteristics of two main stations in the basin for rainfall data extraction.

Station Name	Station Type	Latitude	Longitude	Height (MASL)
Darakeh (Haft-howz)	Hydrometer	35°48′ N	51°23′ E	1700
Mehrabad	Synoptic	35°41′ N	51°19′ E	1190.8

. For long-term precipitation as the disturbance, a 30-year rainfall time series from 1985 to 2015 was utilized.

5.2. Estimating the Resilience Indicators

To estimate UDS robustness to a 6-h rainfall, it is first required that total rainfall depth is calculated through IDF curves obtained for the studied region. Figure S4 (Supplementary Material) shows the catchment’s IDF curves for different return periods, and Table S6 (Supplementary Material) represents the values of total rainfall depths for different return periods of a 6-h rainfall.

By introducing the total rainfalls for any return periods presented in Table S6 (Supplementary Material) to the rainfall-runoff model, one can have the stormwater runoff surcharged from the UDS.

Table 3. Average surcharge (mm) from the UDS (i.e., degradation capacity) calculated for various scenarios.

	Return Period	2-year	5-year	10-year	25-year	50-year	100-year	Continuous Rainfall
Scenario
Channel enlargement		0	10	23	39	58	92	19
Auxiliary channel		0	15	29	47	66	103	23
BMP in urban areas		0	0	8	16	25	33	9
BMP in both urban and non-urban sub-basins		0	0	0	4	11	19	3
Existing UDS		16	37	49	68	129	337	54

has listed the average runoff depth surcharged from the whole drainage network in the face of rainfalls with different return periods while using various scenarios. Since stormwater runoff depth directly correlates with the consequent damages [10,52,53,54,55,56], it seems to be a good indicator representing the UDS response to the disturbance (i.e., extreme rainfall). As can be seen in Table 3, the Response Magnitude (RM) values for the current situation of UDS in the study region are significantly larger than RM for the proposed adaptive measures for both single-event and continuous rainfall. Among all scenarios, BMP implementation in both urban and non-urban parts of the basin reduces the average surcharged runoff from the UDS the most.

Robustness, which is representative of UDS resistance capacity, was estimated according to what was explained in the Methods section and is similar to the previous works [10]. In this viewpoint, the threshold to which the drainage network can bear the disturbance- no surcharge occurs- is considered as the reaction threshold, shown by a unique number, which is the rainfall value for the corresponding return period (presented in Table S6, Supplementary Material). For instance, using the first scenario (channel enlargement), a 2-year, 6-h rainfall can be tolerated, whose value is 32.62 mm according to Table S6 (Supplementary Material). For the second scenario, the resistance capacity is the same. BMP installation has the most impact on improving the system’s robustness, particularly if BMPs are installed in both urbanized and upstream suburban areas. This is while the resistance capacity for the current condition of UDS is nearly zero. On this basis, the values of UDS robustness to a 6-h rainfall could be represented as indicated in

Table 4. The value of UDS resistance capacity (RC) under different scenarios.

Scenario	Single-Event Rainfall		Continuous Rainfall
	Hydraulic Robustness	Social Robustness	Hydraulic Robustness	Social Robustness
Channel enlargement	32.62	78.9	11.4	23.2
Auxiliary channel	32.62	63.59	7.31	16.6
BMP in urban areas	44.96	(more than) 78.9	32.5	49.4
BMP in both urban and non-urban sub-basins	53.2	(more than) 78.9	44.8	76
Existing UDS	0	53.2	1.88	9.34

. Such values represent the capacity of adapted UDS to absorb the disturbance and withstand it.

A similar procedure was accomplished for a continuous rainfall time series in both social and hydraulic domains. The long-term system robustness was obtained by estimating the surcharges from the UDS and the rate of rainfalls in the time series the system can tolerate. It can be concluded that for both single-event and continuous rainfalls, the resistance domain would become larger under the given adaptive scenarios.

Based on the average degradation capacity obtained for UDS, the braking capacity is estimated using Equations (10) and (11).

Table 5. Braking capacity (BrC) for various scenarios (mm/min).

	Return Period	2-year	5-year	10-year	25-year	50-year	100-year	Continuous Rainfall
Scenario
Channel enlargement		-	4.8	2.3	0.94	0.78	0.34	4.4
Auxiliary channel		-	4	1.6	0.7	0.5	0.2	3.9
BMP in urban areas		-	-	5.3	4.9	3.3	2.8	5.7
BMP in both urban and non-urban sub-basins		-	-	-	7.4	6.9	5.6	6.9
Existing UDS		8	2.9	1.1	0.55	0.36	0.11	2.6

indicates that the system braking capacity is the largest in the case of BMP installation and is the lowest for the existing condition of UDS, which leads to lower resilience.

To summarize the evaluation briefly and rapidly, the rest of the indicators are calculated only for the 100-year, 6-hr rainfall. A 100-year rainfall could represent an extreme event, and a 6-h rainfall is the typical duration of design rainfall in the study area. The calculation results have been presented in

Table 6. The quantified (normalized) sub-factors of UDS flexibility for various scenarios for the hydraulic aspect.

Scenarios	Type of Disturbance	AbC	SRV	RPD	IMP	ADP
Channel enlargement	Single-event rainfall	32.97	0.51	0.16	0.54	0.54
	Continuous rainfall	15.85	0.48	0.15	0.49	0.5
auxiliary channel	Single-event rainfall	32.83	0.38	0.11	0.51	0.53
	Continuous rainfall	11.25	0.37	0.09	0.45	0.47
BMP in urban areas	Single-event rainfall	47.79	30	4.1	0.79	0.77
	Continuous rainfall	38.31	26	3.8	0.74	0.75
BMP in both urban and non-urban sub-basins	Single-event rainfall	58.85	4000	7	0.83	0.84
	Continuous rainfall	52.03	90	6.7	0.8	0.79
Existing condition of UDS	Single-event rainfall	0.11	0.19	0.04	-	-
	Continuous rainfall	4.50	0.17	0.03	-	-

and Table S7 (Supplementary Material) for the hydraulic and social domains, respectively. It can be observed that nearly in all cases, BMP installation in upstream non-urban areas as long as the urbanized parts of the basin would be the best adaptive scenario, both for single-event and continuous rainfall. Absorptive capacity, as well as survivability and rapidity, are the least for the current state of UDS while possessing the highest values for BMP implementation scenarios. Among two other management scenarios, channel enlargement is mostly more successful than using an auxiliary channel. This may be due to the local effectiveness of the auxiliary channel while inundated locations are expanded through the entire drainage system. Regarding social resilience, according to the obtained results, there is no serious problem even with the existing condition of the drainage system in the studied area. However, even in the social context, utilizing the management strategies could help improve system sustainability.

It should be noted that to estimate the total flexibility and resilience, the calculated indices would be normalized considering the maximum possible value for the given indicator.

5.3. Final Resilience of the System

Table 7. The calculated resilience (percent) by different scenarios.

	Resilience	Single-Event Rainfall		Continuous Rainfall
Scenario		Hydraulic Resilience	Social Resilience	Hydraulic Resilience	Social Resilience
Enlarging the channels		0.64	0.66	0.61	0.62
Adding an auxiliary channel		0.53	0.59	0.5	0.55
BMPs in Urban sub-basin		0.79	0.83	0.75	0.78
BMPs in both Urban and Suburban areas		0.87	0.92	0.83	0.89
Existing UDS		0.39	0.44	0.35	0.39

represents the results of estimating UDS future resilience calculated under various scenarios for hydraulic and social aspects and two types of disturbances, i.e., single-event and continuous rainfall. The table shows that in the system in both single event and long-term rainfall cases, social resistance values are higher than hydraulic ones, resulting from the methodology that considers a 60 mm surcharged runoff in the social domain the same as zero runoff in the hydraulic domain. In addition, for continuous rainfall time series, the resilience values—as well as the values of its components—are near the ones for single-event rainfall, though a little bit smaller, which again is a consequence of the proposed methodology and formula for gaining the value of such indicators.

According to the results and considering Table S4 (Supplementary Material), the UDS resilience for the studied area in its current condition is evaluated as “low” except for social resilience, which hardly enters the “medium” level. Using adaptive scenarios, the resilience level of the drainage system would improve significantly (Table 7). So that by implementing the scenarios of “adding an auxiliary channel to the system”, the resilience level falls into one level higher, i.e., “medium level”. For both scenarios of “enlarging the UDS channels” and “BMP installation only in the urban part of the catchment”, the UDS resilience would mostly reach the “acceptable level”; and the scenario of “BMP installation in both urban and upstream non-urban areas” would result in a system with “high” resilience. Such findings indicate the importance of utilizing various adaptive measures in urbanized catchments and would help urban planners find the best solutions for reducing urban inundation problems. The results are in agreement with some similar previous works, including the one performed by Tahmasebi Birgani and Yazdandoot [10], which was accomplished for a region near the WFD catchment, and emphasizes the fact that, considering most of the resilience indicators, using BMPs are more effective than channels’ enlargement for improving the UDS resiliency to inundation and flooding.

5.4. Comparison of the Resilience Calculated from the two Methodologies

Table 8. The calculated resilience index by IMPRESS methodology for various resilience domains.

	Resilience Domains	Single-Event Rainfall		Continuous Rainfall
Scenario		Hydraulic Resilience	Social Resilience	Hydraulic Resilience	Social Resilience
Existing UDS		0.41	0.39	0.37	0.35

represents the resilience calculated for social and hydraulic aspects of the drainage system by the IMPRESS method for the existing condition of the UDS. Comparing the results with the index-based method shows that the calculated index from both methodologies is almost the same and relatively low (below 50%) for the studied region. Therefore, using adaptive measures such as BMPs (which, in the previous section, were proved to be the best solutions for the studied region) seems to be of great necessity in this semi-urbanized basin.

According to the results of the IMPRESS framework, the social resilience index shows a lower value than the hydraulic resilience index. This is why when using the index-based methodology the social aspects have an almost better condition compared to hydraulic issues of the drainage system. It can be related to the formulas used for calculating the social resilience, considering the water depths below 6 cm as no threat to social disorder and community safety. This is while the calculated index in the parameter-based method is based on previous events, observations, and interviews, which is more probable to be coincident with reality.

6. Conclusions

Unlike the traditional risk management of urban critical infrastructures, which makes an effort to resist the system in the face of all types of perturbations (as much as possible), the resilience-based approach emphasizes the system’s ability to restore from the unexpected disturbances given the fact that not all disasters can be predicted or even recognized. The flexibility of a system has recently gained attention as an important factor related to resilience. However, their relative position to each other is still a matter of discussion. The current study focused mainly on providing a framework for quantifying the UDS resilience to disasters (flooding, in particular) based on a main resilience component, i.e., flexibility, and aimed to cover the gap in previous research by accounting for recovery from long-term precipitation considering both hydraulic and social aspects.

The resilience of a drainage system in a semi-urbanized basin was calculated considering four different scenarios to find the best solution for improving the UDS functionality and resilience to flooding. Within this proposed framework, seven indicators representing the system behavior in the face of a disaster were quantified. The resilience indices were obtained and discussed from both hydraulic and social viewpoints under both single-event and continuous precipitation, and compared with the results from an MCDM approach. The findings of this study suggested a relatively low level of flood resiliency for the study site, and it was revealed that BMPs as structural adaptive solutions are among the best choices for improving the system’s resilience to flooding.

By focusing on resilience measurement to quantify its components, this study can be considered the first step to the sustainable management and planning of the drainage infrastructure in urban areas. Resilience quantification for UDSs is a crucial task for evaluating the system as it can provide a better view of the direction the system functionality is moving toward. This could help the urban managers and practitioners evaluate the performance of such critical infrastructures as a primary step to managing them more efficiently and making more realistic decisions.

In the current study, the social resilience indicators were mostly obtained considering the fact that a 6 cm inundation depth is tolerable for the residents and commuters in the region (based on the information from reliable sources). This amount of inundation depth may differ for other societies based on other sources of information. Besides, in future works, other social parameters could be added to such a methodology to evaluate the social resilience of UDS to flooding in the context of the complicated urban society. The proposed framework in the current study can be utilized in predicting the UDS resilience in future periods and, therefore, can be used as a method to estimate the design criteria of UDS in the face of future climatic changes and urban development.

However, performing this methodology has its limitations and difficulties. Gathering data from reliable sources is the most important challenge for having accurate results, and this can be more challenging when using this methodology for estimating infrastructure resilience in the future. Nevertheless, if reliable data are available, this proposed framework can act as a helpful tool for the primary assessment of UDS performance which covers the gaps in some similar tools developed in the past. The other issue, which is suggested to be considered in similar studies, is the need to examine if the final solutions to solve the UDS problems are economically and environmentally feasible and sustainable. In the current study, the focus was mainly on quantifying social and hydraulic aspects of UDS resilience. However, a cost-benefit analysis could be added to identify the best compromise between increasing resilience and investments based on the probability of rainfall events and the impacts on UDS. It should be emphasized that the proposed methodology and the indicators could be modified to be usable for resilience assessment from other viewpoints, such as economic and environmental aspects.