Artificial Neural Networks for the Prediction of the Reference Evapotranspiration of the Peloponnese Peninsula, Greece

Abstract

The aim of the study was to investigate the utility of artificial neural networks (ANNs) for the estimation of reference evapotranspiration (ETo) on the Peloponnese Peninsula in Greece for two representative months of wintertime and summertime during 2016–2019 and to test if using fewer inputs could lead to satisfactory predictions. Datasets from sixty-two meteorological stations were employed. The available inputs were mean temperature (Tmean), sunshine (N), solar radiation (Rs), net radiation (Rn), vapour pressure deficit (es-ea), wind speed (u₂) and altitude (Z). Nineteen Multi-layer Perceptron (MLP) and Radial Basis Function (RBF) models were tested and compared against the corresponding FAO-56 Penman Monteith (FAO PM) estimates of a previous study, via statistical indices. The MLP1 7-2 model with all the variables as inputs outperformed the rest of the models (RMSE = 0.290 mm d⁻¹, R² = 98%). The results indicate that even ANNs with simple architecture can be very good predictive models of ETo for the Peloponnese, based on the literature standards. The MLP1 model determined Tmean, followed by u_2, as the two most influential factors for ETo. Moreover, when one input was used (Tmean, Rn), RBFs slightly outperformed MLPs (RMSE < 0.385 mm d⁻¹, R² ≥ 96%), which means that even a sole-input ANN resulted in satisfactory predictions of ETo.

1. Introduction

Reference Evapotranspiration (ETo) is a key climate parameter investigated in the frame of climate crisis and water resources management [1,2,3,4]. Moreover, ETo has an effect on the productive sector of agriculture [5]. In particular, the precision irrigation techniques and the decision-making irrigation systems demand accurate ETo values [6]. Therefore, the importance of effective estimation and prediction methods of ETo is crucial [7,8].

The necessity of acquiring ETo values led to the development of several methods of estimation, ranging from simple empirical or physically based models [9,10] to complex neuro-fuzzy and machine learning algorithms [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47]. The methods incorporate data from meteorological stations or, due to the scarcity of the former, remotely sensed data [48,49,50,51,52,53,54,55,56,57,58]. The FAO-56 Penman Monteith (FAO PM) equation requires numerous meteorological variables for effective application [59,60]. Even the more refined empirical methods of ETo, such as Valiantzas’ equations [61], share a common denominator; the more meteorological inputs, the higher the accuracy of ETo [62]. On the other hand, there are empirical methods requiring limited climatic variables (e.g., the Hargreaves’-Samani equation). However, the accuracy of these methods, compared to FAO PM, is limited and performance in some cases has been reported to be season-dependent [63]. The unavailability of input data is a global issue, due to the high cost of equipping and running meteorological stations, especially for developing countries. Thus, reducing the number of inputs for the predicting models to only trivial parameters is highly recommended [64]. Those parameters can be air temperature (minimum, maximum and mean values) plus parameters that can be either measured or easily computed based on latitude and Julian day (e.g., sunshine, solar radiation, net radiation, vapor pressure deficit and wind speed) [59]. Computing the missing parameters is a commonly used practice in ETo research [61,65]. However, even if input parameters are trivial, their inner relationships are non-linear and complex. Among different methods, Artificial Neural Networks (ANNs) stand out for their capability to model complex non-linear relationships. ANNs demand short real-time control and computational effort [66]. Hence, they are considered as a suitable approach to model ETo.

Artificial neural networks are utilized in a broad spectrum of applications. ANN architectures consist of one input layer (including several input variables), multiple hidden layers and one output layer. The hidden layers consist of several neurons (or nodes) and each neuron can have multiple inputs and one output. The output of each neuron is connected to a neuron of the successive layer via a synapse. Each synapse is a link which has a particular weight to represent the strength of the connection between two successive neurons. After computing the sum of all weighted inputs, neurons transfer this sum into an output via an activation function. This output is fed to the next layer. The output of the network is computed by the last neuron of the network [67]. Multi-layer Perceptron (MLP) and Radial Basis Function (RBF) are common ANNs with capabilities in ETo forecasting [68,69,70,71,72].

Trajkovic (2009) [68], based on Trajkovic et al. (2003) [69], demonstrated that an RBF model with only two input variables is able to predict ETo with greater accuracy than FAO PM, amongst other equations. Kumar et al. (2020) [70] tested two models with five and two input variables, respectively, for the Himalayan region, employing ground-based data from forty-seven stations. They found that MLP could satisfactorily predict ETo even with limited inputs. Tabari et al. (2012) [71] investigated four MLP models with four, three and two input variables, for a semi-arid region in Iran. They concluded that the model with the most inputs resulted in the most accurate predictions of ETo and that tanh was the best activation function in all cases. Sattari et al. (2021) tried ten combinations of input variables (from eight to one inputs) [72]. The best performance yielded an R² = 0.978. Shamshirband et al. (2016) [73] used data from twelve meteorological stations in Serbia for optimizing an ANN with very low error levels, but an R² below 0.97. Gavili et al. (2017) [74] tested soft computing methods versus empirical ones and deduced that the former exhibited better performance in modeling ETo. Amongst these methods, the ANN had the best performance. As far as Greece is concerned, Diamantopoulou et al. (2011) [75] tested two ANNs to estimate daily ETo with limited meteorological data, separately for four meteorological stations in the Northern Greece. The best results obtained an RMSE = 0.545 mm d⁻¹ and an R² = 95.7%. Antonopoulos et al. (2016) [76] applied ANNs also in the Northern Greece (Lake Vegoritis) to predict ETo. For years 2003 and 2004, they obtained: RMSE = 0.69 mm d⁻¹, R² = 79.2% and RMSE = 1.09 mm d⁻¹, R² = 82.8%, respectively. Antonopoulos and Antonopoulos (2017) [77], in consecutive research in the same study area, trained ANNs with datasets from one meteorological station (Amyntaio) over the period 2009–2013 to estimate ETo. Their best results yielded an RMSE = 0.574 mm d⁻¹ and an R² around 97.2%, while the indices’ values were slightly deteriorated for lesser (i.e., three and two) inputs.

Although ANN is considered a suitable method to model ETo, the literature lacks in studies of areas with interchangeable land use/land cover (LU/LC) and relief characteristics over short distances. In those areas the performance of a model predicting ETo would be challenging in terms of accuracy and seasonal consistency. Moreover, the number of meteorological stations employed in the literature is usually low compared to the corresponding study area, which leads to a coarser spatial representation of the climate variables. Lastly, as shown above, there are only a few applications of ANNs for ETo prediction in Greece in the literature.

The aim of the study was to investigate whether ANNs could predict ETo satisfactorily close to the reference method (FAO PM) in the Peloponnese, Greece, for the selected period. The study also aimed to determine the model that best fits the data, based on the literature standards, and to indicate the most influential factors on ETo. This study examines nineteen MLP and RGB (ANN) models utilizing sixty-two meteorological stations in the Peloponnese peninsula in Southwestern Greece (

Table A1. Meteorological stations (62) used (source: https://meteosearch.meteo.gr (accessed on 15 April 2022)).

ID	Station	X	Y	Elevation (m)	Municipality	ID	Station	X	Y	Elevation (m)	Municipality
Meteorological Stations for the 3 Empirical Methods (ETo)						Meteorological Stations for the 3 Empirical Methods (ETo)
1	Kalavrita	334349.9	4210128	781	Achaia	32	Oleni	282783.4	4177872	61	Ilia
2	Kato Vlassia	317683.4	4208558	773	Achaia	33	Pineia	285425.3	4191240	184	Ilia
3	Lappa	273550	4218928	15	Achaia	34	Pirgos	273886.9	4171891	22	Ilia
4	Olenia	288845.1	4221654	34	Achaia	35	Vartholomio	253773.8	4193127	15	Ilia
5	Panachaiko	313491.4	4235800	1588	Achaia	36	Zacharo	290302.6	4150806	5	Ilia
6	Panagopoula	318709.5	4243842	15	Achaia	37	Amoni Sofikou	424227.5	4186898	55	Korinthia
7	Panepistimio	305972.3	4239289	66	Achaia	38	Derveni	362057.1	4221737	5	Korinthia
8	Patra	301697.8	4236694	6	Achaia	39	Isthmos	408645.4	4200499	6	Korinthia
9	Rio	305898.1	4242177	2	Achaia	40	Kiato	389163.5	4207722	15	Korinthia
10	Romanos	313476.1	4235744	228	Achaia	41	Krioneri	378491.9	4203310	887	Korinthia
11	Sageika	280638.4	4219575	26	Achaia	42	Loutraki	410248.7	4202636	30	Korinthia
12	Argos	386329.1	4165059	38	Argolida	43	Nemea	381197.9	4188976	290	Korinthia
13	Didima	426936.9	4146702	175	Argolida	44	Perigiali	397303.1	4199344	38	Korinthia
14	Kranidi	424615.7	4137411	110	Argolida	45	Trikala Korinthias	365493.7	4206835	1077	Korinthia
15	Lagadia	326139.9	4172057	970	Arkadia	46	Agioi Theodoroi	423533.6	4198395	37	Korinthia
16	Levidi	349386.5	4171330	853	Arkadia	47	Apidia	392819.7	4082655	230	Lakonia
17	Lykochia	337772.6	4151113	870	Arkadia	48	Asteri	386527.1	4076757	8	Lakonia
18	Magouliana	334497.7	4171275	1256	Arkadia	49	Geraki	384706.6	4094508	330	Lakonia
19	Megalopoli	335363	4140782	432	Arkadia	50	Krokees	371576.2	4082640	241	Lakonia
20	Stemnitsa	330377.8	4157967	1094	Arkadia	51	Molaoi	397984.6	4072957	128	Lakonia
21	Tripoli	359989.3	4152250	650	Arkadia	52	Monemvasia	413811.4	4059051	17	Lakonia
22	Vytina	339989.8	4170409	1013	Arkadia	53	Sparti	360929.9	4101670	204	Lakonia
23	Spetses	424919.5	4124662	3	Attiki	54	Alagonia	343840.9	4107863	765	Messinia
24	Taktikoupoli Troizinias	443373.2	4152374	15	Attiki	55	Arfara	326299.4	4113666	96	Messinia
25	Ydra	452645.8	4133727	2	Attiki	56	Filiatra	285439.9	4115175	65	Messinia
26	Amaliada	264604.9	4186923	26	Ilia	57	Kalamata	331127	4098974	5	Messinia
27	Andritsaina	314220.3	4152125	731	Ilia	58	Kalamata Dytika	329347.3	4100001	10	Messinia
28	Archaia Olympia	287981.3	4163856	45	Ilia	59	Kardamili	347857.7	4074651	13	Messinia
29	Foloi	297082.7	4174732	600	Ilia	60	Kopanaki	306288.6	4128741	184	Messinia
30	Katakolo	263537.2	4169327	2	Ilia	61	Kyparissia	291691	4123584	36	Messinia
31	Lampeia	306840.3	4192041	840	Ilia	62	Pylos	294556.8	4087590	5	Messinia

). The Peloponnese peninsula is a study area with distinguished differences over short distances. Empirical methods applied across the area in a previous study [63] showed inferior performance in terms of accuracy, especially for August (summertime). A further objective was to examine whether fewer input variables would produce satisfactory predictions of ETo in terms of accuracy. Therefore, the number of inputs of the models were consecutively reduced to examine whether fewer than the seven available inputs, or even a sole input, could predict ETo acceptably. The novelty of the study is twofold: it is the first time that ANNs are used to predict the ETo across a large area of Southern Greece, which includes elevation, relief and LU/LC interchanges that are challenging in terms of the consistency of model performance. Even more challenging is the usage of continuous climate datasets over a recent four-year period, instead of datasets for individual days or short intervals. In addition, the exploitation of a dense meteorological station network, instead of a couple of stations, enhances the significance of the results. A good performance from ANNs, despite the aforementioned difficulties, would prove the flexibility and the potential of ANNs in ETo modeling. The latter would be useful in cases where there is a shortage of climate data. Moreover, it could save time and decrease computational load for interdisciplinary research purposes.

2. Materials and Methods

2.1. The Study Area

The Peloponnese is a peninsula in Southwestern Greece that occupies about 1/6th of the Greek territory (21,439 km²), with a population of 1086.935 (census 2011; https://www.statistics.gr/el/statistics/-/publication/SAM03/2011 (accessed on 10 March 2022). A large part is covered by high hills and mountains, running NW to SE, with an elevation up to 2407 m. Lithology, tectonic activity and climate conditions have resulted in the relief formation of the study area. A well-developed hydrographic network, though with few large rivers, has formed [78]. Based on the latest Copernicus LU/LC classification, the widest urban area is located at the northmost edge [79]. In addition to urban areas, the main LU/LC types are forest and transitional vegetation, as well as crop plots covering the plains (Figure 1). The broadest plain lies over the western coastal part. According to Köppen-Geiger’s classification, the climate of the Peloponnese is Mediterranean warm temperate with dry summers and mild winters (Csa) [80]. The annual normal measurements (1971–2000) of air temperature, precipitation and sunshine range between 8–20 °C, 400 to over 2000 mm and 1900–3100 h, respectively (http://climatlas.hnms.gr/sdi/?lang=EN (accessed on 27 April 2022).

2.2. Methods

Meteorological datasets of daily measurements from sixty-two stations under the National Observatory of Athens, for the months August and December of 2016–2019, were utilized (Table A1). These months and years were selected for the application of ANNs in methodological consistency with our previous study [63], where ETo was computed for the Peloponnese by FAO PM, our reference method. In that study, August and December had been selected as typical months of summer and winter, respectively. FAO PM has been widely used as a reference method to estimate ETo in studies investigating ANNs, either as the only reference method [10,70,81] or combined with direct methods [82]. Multi-Layer Perceptron (MLP) and Radial Basis Function (RBF) ANN models were examined in this study. Nineteen combinations of input variables were tested (from seven inputs to one input) with both MLP and RBF models. The inputs included climate and non-climate (such as altitude) variables that affect ETo [83], namely, solar radiation (Rs), net radiation (Rn), sunshine hours (N), mean air temperature (Tmean), vapour pressure deficit (es-ea), wind speed at 2 m from the surface (u₂) and altitude (Z). The first three were previously calculated as functions of the station latitude and the Julian day, as in Zanetti et al. (2008) [36]. Based on Rahimikhoob (2020) [84], the input combinations were subsequently limited, aiming to explore the possibility of producing acceptably accurate predictions of ETo with fewer variables than the available seven or even with a sole input variable (such as Tmean or Rn). About three fifths of the sample data were used for training and the other two fifths were used for testing and validation (about one fifth each) [40]. The tested architecture was based on the trial-and-error method and the ANNs were trained using the Levenberg-Marquardt algorithm [40,41]. Hyperbolic tangent (Equation (1); [85]) was the utilized activation function, based on the literature [71,86]. The hyperbolic tangent, along with the sigmoid function, is a non-linear function widely used as an activation function in ANNs [85]. The hyperbolic tangent exhibits the advantage of giving higher enhancement to the negative values. The output of the former spans in [−1, 1] while the sigmoid outputs are only half of the previous ([0, 1]) [87].

$$Tanh\left(x\right)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

(1)

The values predicted by the ANN models were then compared against the values by FAO PM via statistical indices that were computed during the training, testing and validation phases (SSE, RE) (

Table 1. Formulae of the indices utilized to evaluate the performance of the examined ANN models.

Performance Evaluating Indices
$\mathrm{RMSE}\sqrt{\raisebox{1ex}{${{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{p}}_{\mathrm{i}}-{\mathrm{o}}_{\mathrm{i}}\right)}^2$}\!\left/ \!\raisebox{-1ex}{$\mathrm{n}$}\right.}$	$\mathrm{NRMSE}=\frac{\sqrt{\raisebox{1ex}{${{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{p}}_{\mathrm{i}}-{\mathrm{o}}_{\mathrm{i}}\right)}^2$}\!\left/ \!\raisebox{-1ex}{$\mathrm{n}$}\right.}}{\bar{\mathrm{o}}}$	$\mathrm{{\rm I}}\mathrm{o}\mathrm{{\rm A}}=1-\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{p}}_{\mathrm{i}}-{\mathrm{o}}_{\mathrm{i}}\right)}^2}{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}(\left|{\mathrm{p}}_{\mathrm{i}}-\bar{\mathrm{o}}\right|-{\left|{\mathrm{o}}_{\mathrm{i}}-\bar{\mathrm{o}}\right|}^2}$
$\mathrm{MAE}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}\left|{\mathrm{p}}_{\mathrm{i}}-{\mathrm{o}}_{\mathrm{i}}\right|}{\mathrm{n}}$	$\mathrm{MB}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{p}}_{\mathrm{i}}-{\mathrm{o}}_{\mathrm{i}}\right)}{\mathrm{n}}$	$\mathrm{r}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{p}}_{\mathrm{i}}-\bar{\mathrm{p}}\right)\left({\mathrm{o}}_{\mathrm{i}}-\bar{\mathrm{o}}\right)}{\sqrt{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{p}}_{\mathrm{i}}-\bar{\mathrm{p}}\right)}^2{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{o}}_{\mathrm{i}}-\bar{\mathrm{o}}\right)}^2}}$
$\mathrm{SSE}={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{p}}_{\mathrm{i}}-{\mathrm{o}}_{\mathrm{i}}\right)}^2$	$\mathrm{RE}=\left|\frac{{\mathrm{p}}_{\mathrm{i}}-{\mathrm{o}}_{\mathrm{i}}}{{\mathrm{o}}_{\mathrm{i}}}\right|$	${\mathrm{R}}^2={\left(\frac{\mathrm{n}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{p}}_{\mathrm{i} }{\mathrm{o}}_{\mathrm{i}}-{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{p}}_{\mathrm{i} }{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{o}}_{\mathrm{i}}}{\sqrt{\mathrm{n}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{p}}_{\mathrm{i} }{}^2-{\left({{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{p}}_{\mathrm{i} }\right)}^2}\ast \sqrt{\mathrm{n}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{o}}_{\mathrm{i} }{}^2-{\left({{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{p}}_{\mathrm{i} }\right)}^2}}\right)}^2$

). Furthermore, the error levels between predicted and reference values have been computed via measures such as Root Mean Square Error (RMSE, mm d⁻¹), Normalized Root Mean Square Error (NRMSE, %), Mean Absolute Error (MAE, mm d⁻¹), Mean Bias (MB, mm d⁻¹) and Sum of Squares Error (SSE, mm² d⁻¹) (Table 1). The error values depict the magnitude of the computed ETo values, except from NRMSE, which is expressed in *100%. Mean Bias is a signed measure so that, in addition to producing the Mean Bias Error (MBE = |MB|), it provides some extra information; the minus sign depicts that the reference ETo value (by FAO PM) is greater than the model predicted value and vice versa. Moreover, three measures that express correlation, strength of fit or agreement were used, namely, Pearson correlation coefficient (Pearson’s r), coefficient of determination (R²) and Index of Agreement (IoA) (Table 1).

In Table 1, p_i stands for the ith predicted value by an ANN, o_i stands for the ith observed value, which in this study is the ith reference value estimated by FAO PM, $\bar{o}$ is the mean of the observed (reference) values and n = 290 is the sample size.

3. Results

In total, nineteen models with different input combinations were tested. The results are presented in

Table 2. The examined ANN models (19) and the corresponding indices of performance.

ANN	Architecture	RMSE	NRMSE	MAE	MBE	R2	Pearson’s r	IoA	SSE Testing	RE Testing	RE Holdout
7 inputs: N, Rs, Rn, u2, es-ea, Tmean, Z
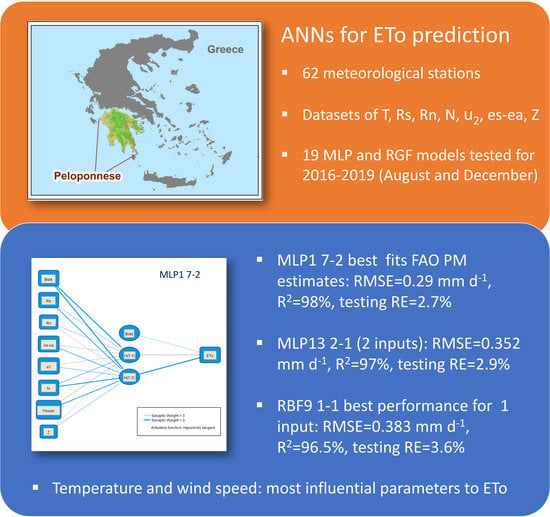
MLP1	7-2	0.290	0.086	0.217	0.017	0.980	0.990	0.995	0.695	0.027	0.022
MLP2	7-4-3	0.305	0.090	0.230	0.024	0.978	0.989	0.994	0.573	0.021	0.029
RBF1	7-5	0.423	0.125	0.267	0.004	0.957	0.978	0.989	0.948	0.027	0.100
RBF2	7-9	0.333	0.098	0.246	−0.032	0.974	0.987	0.993	1.547	0.045	0.028
6 inputs: Rs, Rn, u2, es-ea, Tmean, Z
MLP8	6-4	0.311	0.092	0.240	0.005	0.977	0.988	0.994	0.827	0.024	0.025
MLP9	6-4-3	0.296	0.088	0.218	−0.008	0.979	0.989	0.995	1.188	0.035	0.024
RBF3	6-9	0.318	0.094	0.232	0.016	0.976	0.988	0.994	0.623	0.026	0.022
4 inputs: Rs, u2, es-ea, Tmean and 4’ inputs: Rn, u2, es-ea, Tmean
MLP7	4-3	0.309	0.091	0.233	−0.002	0.977	0.989	0.994	0.543	0.020	0.027
MLP10	4-3-2	0.300	0.089	0.221	0.001	0.978	0.989	0.995	0.541	0.020	0.028
RBF4	4-10	0.406	0.120	0.263	−0.042	0.961	0.980	0.990	1.044	0.031	0.092
MLP3	4’-1	0.319	0.094	0.245	−0.025	0.976	0.988	0.994	0.459	0.160	0.300
3 inputs: Rn, u2, Tmean
MLP5	3-1	0.314	0.093	0.244	−0.019	0.976	0.988	0.994	1.101	0.032	0.030
2 inputs: Rn, Tmean; 2’ inputs: Rn, u2; 2’’ inputs: u2, Tmean
MLP4	2-1	0.377	0.111	0.268	−0.023	0.966	0.983	0.991	1.443	0.042	0.034
MLP6	2’-1	0.343	0.101	0.268	0.026	0.972	0.986	0.093	0.961	0.037	0.028
MLP13	2’’-1	0.352	0.104	0.267	−0.008	0.970	0.985	0.992	0.819	0.029	0.029
1 input: Tmean; 1’ input: Rn
MLP14	1-1	0.360	0.106	0.258	0.014	0.969	0.984	0.992	0.747	0.027	0.041
MLP16	1’-1	0.404	0.119	0.313	−0.014	0.961	0.980	0.990	0.594	0.030	0.042
RBF6	1-1	0.363	0.107	0.259	0.006	0.968	0.984	0.992	0.710	0.028	0.033
RBF9	1’-1	0.383	0.113	0.298	−0.005	0.965	0.982	0.991	1.109	0.036	0.033

Note: The values in italics (RE holdout column) indicate overtraining of the corresponding model. The models in bold exhibit performance that is discussed in detail. RMSE, MAE, MB are in mm d⁻¹ and SSE in mm² d⁻¹.

.

As presented in Table 2, MLP1 7-2, with all the available parameters as inputs, appears to provide the best performance, expressed via the minimum error values in the testing and validation data and the maximum correlation and agreement indices (R², Pearson’s r and IoA) between prediction and reference values. The architecture is simple, consisting of one hidden layer with two neurons (Figure 2).

The parameter-estimates of the MLP1 model are displayed in

Table 3. Parameter estimates of the model with the best performance (MLP1).

Predictor		Predicted
		Hidden Layer 1		Output Layer
		H (1:1)	H (1:2)	ETο
Input Layer	(Bias)	−0.616	−0.638
	Rs	−0.010	−0.355
	Rn	0.397	0.173
	es-ea	0.224	−0.181
	u2	0.214	−0.049
	N	−0.100	−0.520
	Tmean	0.461	−0.394
	Z	0.059	−0.040
Hidden Layer 1	(Bias)			−0.009
	H (1:1)			0.578
	H (1:2)			−0.867

. As presented, the values of both the nodes and the hidden layers are not negligible values, a fact that constitutes one of the desirable characteristics of an ANN model.

As presented in Table 2, MLP9 6-4-3 follows closely the model with the superior performance (MLP1), except for the testing SSE value, which is almost double the corresponding MLP1 value. It is interesting that the MLP10 4-3-2 model, with only four inputs and two hidden layers, exhibits a performance very close to that of MLP1, with a couple of values (MBE and SSE) even better than those of MLP1. The added value is that it produces almost the same values with only four basic parameters as inputs, specifically, Rs, es-ea, u₂ and Tmean. The data of the aforementioned parameters are usually available either from meteorological stations or via remote sensing. Moreover, in the event of any missing data, the parameters can be easily computed [59]. It is obvious that the RBF network displays inferior performance to MLP for our data. RBF3 6-9 is the best among the RBF networks and fourth in the total rank of model performance. The relative errors of MLPs in the validation phase were between 2.2–4.2% for all trials, whereas for RBFs the relative errors lay between 2.8–10%. For the majority of the models, the holdout RE values were greater than the testing RE values, despite the satisfactory error levels (2.8–4.5%). This indicates that those models were overtrained towards the testing data.

The cases where only a sole basic parameter (Tmean or Rn) was set as input seem noteworthy. In those cases, the RBF models exhibited better performance than the MLP ones. RBF9 (Rn as input) obtained RMSE = 0.383 mm d⁻¹ and R² = 96.5% with RE = 3.3%. In the case of Tmean as the sole input, the RMSE was around 0.360 mm d⁻¹ and the R² was above 96.7%. However, as previously commented, there was evidence of overtraining of some models (Table 2). Therefore, those models are not recommended. The influence of each climatic variable on ETo presented is considered important in respect of the ANN that best fits the data and bears interesting determination [14]. As shown in Figure 3, the most influential factor is Tmean followed by u₂. The third factor in the rank is vapour pressure deficit (es-ea). Those results are aligned with the ETo estimates by FAO PM of the same period for the Peloponnese [63].

4. Discussion

The determination of ETo is crucial for climate crisis research, hydrological cycle, water resources management and irrigation precision techniques. The available methods of estimation require the knowledge of numerous climate parameters, which means an increased cost. Since ETo includes complex and nonlinear relationships, ANNs have been proven to be a suitable modeling choice. In this study, ETo has been estimated via nineteen MLP and RBF ANN architectures, with different combination and number of inputs (from seven to one).

This period is interesting in the frame of the climate crisis, since it is recent and includes the first (2016) and second (2019) warmest years since the preindustrial era, which challenges the performance of ANNs.

For the majority of the trials, the RMSE was below 0.4 mm d⁻¹ and the relative error of the testing phase was below 4%. MLPs performed generally better than RBFs for multiple inputs, whereas RBFs performed slightly better when only one input (Rn or Tmean) was set. The model that best fits the reference values was that with the most input parameters and only one hidden layer (MLP1 7-2), bearing RMSE = 0.290 mm d⁻¹, R² = 98% and RE of testing and validation phases equal to 2.7% and 2.2%, respectively. The different runs with the same input combination, but different model architecture, showed that any increase in the number of hidden layers and the number of neurons in the hidden layer exhibited negligible improvement in prediction accuracy. Those conclusions are in line with the findings by Tabari et al. (2012) [71]. The data of the seven used inputs can be easily derived, either by meteorological stations or via remote sensing, or can be easily computed as missing data by FAO guidelines [59]. However, during the trials, the number of the inputs was gradually limited in order to examine whether ANNs can provide satisfactory estimates of ETo, when incorporating only the most commonly available climate data. It is interesting that the MLP10 with four climate parameters as inputs exhibited results very close to the best model (MLP1). Moreover, models with two basic parameters as inputs, exhibited RMSE up to 0.352 mm d⁻¹, testing RE below 3% and R² at least equal to 97% (MLP6, MLP13). When only one input was used (i.e., Tmean or Rn) in RBF models, the RMSE was below 0.385 mm d⁻¹, testing RE was below 3.6% and R² was at least equal to 96%. According to the literature, those values are considered very good to excellent. For example, Rahimikhoob (2010) recommended an ANN for the coastal area of the Caspian Sea in Northern Iran, which used only air temperature as an input, with an RMSE = 0.41 mm d⁻¹ and R² = 95% [84], whereas in this study MLP14 with Tmean as an input has better accuracy (RMSE = 0.360 mm d⁻¹ and R² = 96.9%). In the same vein, Zanetti et al. (2008) used MLP ANN with only temperature and radiation inputs to predict ETo for Campos dos Goytacazes, Brazil [66], while Ravindran et al. (2021) deduced that Rs was the most influential parameter to ETo and used it as a sole input in ANNs for California (R² up to 95.4%) [14]. This proves that ANNs with simple architecture can be good predictive models of ETo over the Peloponnese for the examined period. In addition, based on the best ANN model (MLP1), we found that Tmean and u₂ were the two most influential factors on ETo, out of the seven examined. This is in line with the findings of a previous study of the same period for the Peloponnese, where ETo had been computed by FAO PM [63]. Tmean, as a proxy of the energy state of the system, is one of the most influential factors on ETo. This depicts the altitude and land cover difference over short distances across the Peloponnese. Probably, due to the fact that the Peloponnese has a very low variance in latitude, the radiation factors were not that influential for the determination of the ETo. Regarding the second most influential factor (u₂), in contrast with December (winter), increased values of u₂ are not frequent in Greece during August (summer). Therefore, where increased u₂ values occurred in August, they affected the determination of the local ETo values. In conclusion, ANNs resulted in predictions very close to FAO PM, which is the most established reference method, for the examined period for the Peloponnese. Therefore, ANNs present the potential of general usage in modeling ETo across Greece, after further investigation.

This study proves that ANNs can be useful alternatives for predicting ETo, requiring limited climate data as input. The former is of considerable usefulness in cases where climate data are in shortage or the cost of the meteorological stations is not affordable, such as in developing countries. Despite the cost, ANNs provide a time saving and a computational effort-decreasing alternative to the complex algorithms currently used, which is applicable for interdisciplinary research purposes.

5. Conclusions

Among the tested ANNs, MLPs performed generally better than RBFs for multiple inputs, whereas RBFs performed slightly better when one sole input (Rn or Tmean) was set. The results revealed better performance of the MLP1 7-2 model, with all the available variables as inputs and only one hidden layer, bearing an RMSE = 0.290 mm d⁻¹, R² = 98% and RE values of testing and validation phases equal to 2.7% and 2.2%, respectively. The former proves that even simple ANN architectures can constitute very satisfactory predicting models. Models with only two parameters as inputs exhibited RMSE values up to 0.352 mm d⁻¹ and R² values at least equal to 97% (MLP6, MLP13). When one sole input was used (Tmean or Rn) in RBF models, RMSE was below 0.385 mm d⁻¹ and R² was at least equal to 96%. The results in both cases are very satisfactory. The MLP1, which outperformed the rest of the ANNs, determined the order of importance of parameters that affect ETo. The first two most influential parameters were Tmean and u₂. Tmean is commonly a parameter to which ETo variances are attributed, as it depicts the overall energy state of the system. For the Peloponnese, where the variance of the latitude (and consequently of solar radiation) values is minor, Tmean variances occur mostly due to distinguished differences in relief, LU/LC types and proximity to the coast over short distances. Wind speed (u₂) plays a substantial role, especially in August, when any increased u₂ values directly affect the ETo values, since those are not frequent in summertime. Future research could test the MLP1 performance for a larger period and across different areas of Greece that differentiate in micro-climatic conditions and regimes. Moreover, direct measurements such as pan evaporation measurements employing ANNs could be investigated on a local scale. Another interesting idea, based on the satisfactory results of this study regarding a sole input variable, would be to explore the potential of multilinear regression analysis, which is a simpler method and comprehensible by a wider interdisciplinary audience.