The Role of Citrus Groves in Rainfall-Triggered Landslide Hazards in Uwajima, Japan
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Descriptions
2.2. The Rainfall Event in July 2018
2.3. Data Preparation
2.4. Analysis
3. Results
3.1. Landslide Area Density on Each Conditioning Factor
3.2. Landslide Area Density Based on Rainfall Indices
3.3. Land Use Effect to Landslide Density Distribution
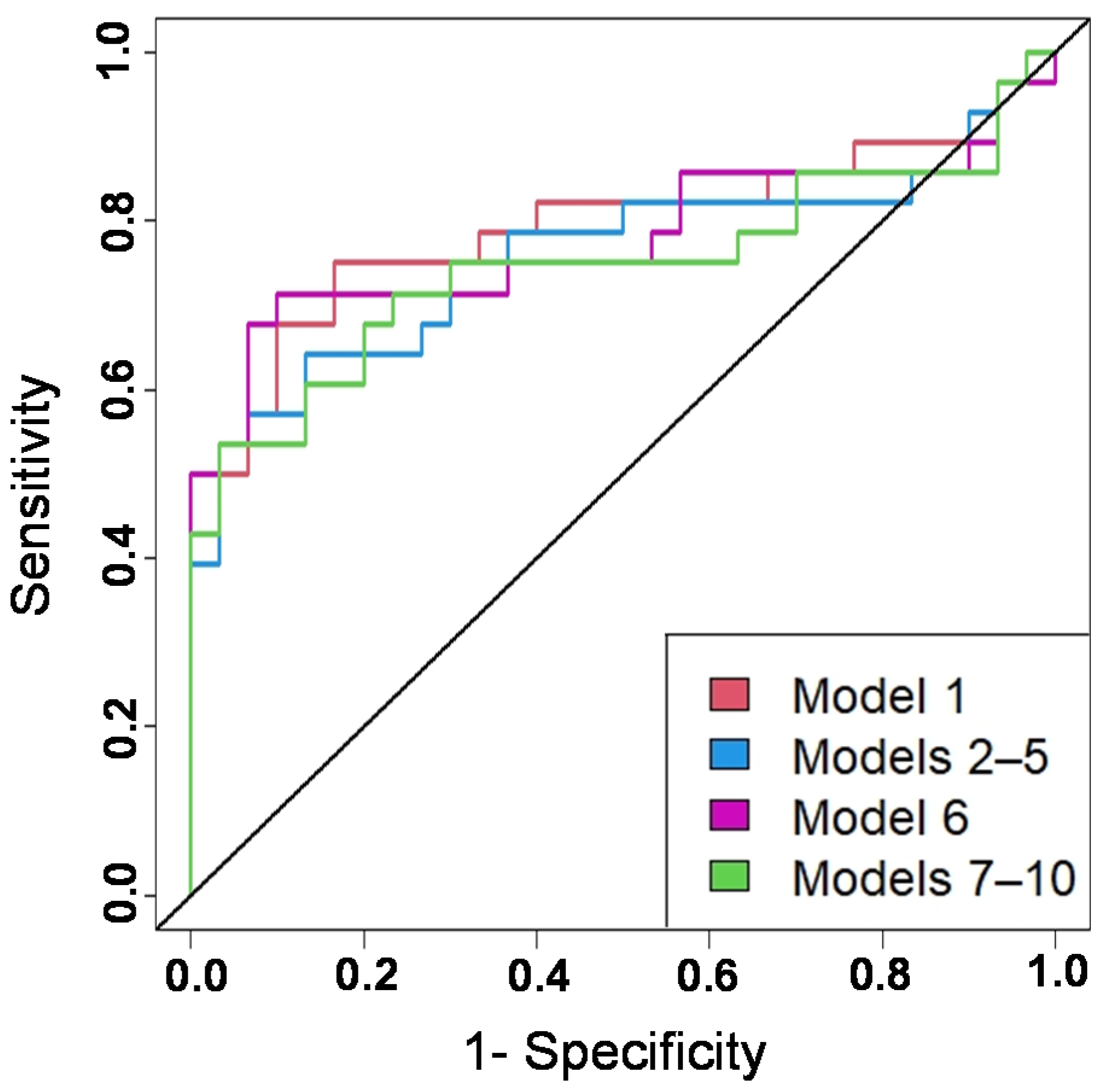
3.4. Significant Effects of Landslide Conditioning Factors
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Forest | Citrus Grove | Others | |
|---|---|---|---|
| Dummy 1 | 1 | 0 | 0 |
| Dummy 2 | 0 | 1 | 0 |
| Sandy Turbidite | Muddy Turbidite | Others | |
|---|---|---|---|
| Dummy 3 | 1 | 0 | 0 |
| Dummy 4 | 0 | 1 | 0 |
| Model | Factor | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Slope Gradient | Slope Aspect | NDVI | Forest | Citrus Grove | Geology | 1h-Max Rainfall | 3h-Max Rainfall | 12h-Max Rainfall | 24h-Max Rainfall | Total Rainfall | |
| 1 | √ | √ | √ | √ | √ | √ | |||||
| 2 | √ | √ | √ | √ | √ | √ | |||||
| 3 | √ | √ | √ | √ | √ | √ | |||||
| 4 | √ | √ | √ | √ | √ | √ | |||||
| 5 | √ | √ | √ | √ | √ | √ | |||||
| 6 | √ | √ | √ | √ | √ | √ | |||||
| 7 | √ | √ | √ | √ | √ | √ | |||||
| 8 | √ | √ | √ | √ | √ | √ | |||||
| 9 | √ | √ | √ | √ | √ | √ | |||||
| 10 | √ | √ | √ | √ | √ | √ | |||||
| Landslide Conditioning Factors | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 |
|---|---|---|---|---|---|
| Slope gradient | 1.27 | 1.08 | 1.11 | 1.11 | 1.10 |
| Slope aspect | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| NDVI | 1.23 | 1.14 | 1.18 | 1.18 | 1.18 |
| Dummy 1 | 1.10 | 1.13 | 1.15 | 1.15 | 1.15 |
| Dummy 3 | 1.83 | 1.83 | 1.83 | 1.83 | 1.83 |
| Dummy 4 | 1.77 | 1.78 | 1.77 | 1.77 | 1.77 |
| Rainfall | 1.37 | 1.05 | 1.18 | 1.18 | 1.16 |
| Landslide Conditioning Factors | Model 6 | Model 7 | Model 8 | Model 9 | Model 10 |
|---|---|---|---|---|---|
| Slope gradient | 1.27 | 1.09 | 1.11 | 1.11 | 1.10 |
| Slope aspect | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| NDVI | 1.23 | 1.15 | 1.18 | 1.18 | 1.18 |
| Dummy 2 | 1.11 | 1.16 | 1.20 | 1.20 | 1.77 |
| Dummy 3 | 1.81 | 1.80 | 1.80 | 1.80 | 1.80 |
| Dummy 4 | 1.77 | 1.78 | 1.77 | 1.77 | 1.77 |
| Rainfall | 1.38 | 1.08 | 1.22 | 1.22 | 1.20 |
References
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef] [Green Version]
- Petley, D.N.; Hearn, G.J.; Hart, A.; Rosser, N.J.; Dunning, S.A.; Oven, K.; Mitchell, W.A. Trends in landslide occurrence in Nepal. Nat. Hazards 2007, 43, 23–44. [Google Scholar] [CrossRef]
- Carrión-Mero, P.; Montalván-Burbano, N.; Morante-Carballo, F.; Quesada-Román, A.; Apolo-Masache, B. Worldwide research trends in landslide science. Int. J. Environ. Res. Public Health 2021, 18, 9445. [Google Scholar] [CrossRef] [PubMed]
- UNDRR/CRED. Human Cost of Disasters. In An Overview of the Last 20 Years 2000–2019; UN Office for Disaster Risk Reduction: Geneva, Switzerland, 2020; pp. 6–7. [Google Scholar]
- Dahal, B.K.; Dahal, R.K. Landslide hazard map: Tool for optimization of low-cost mitigation. Geoenvironmental Disasters 2017, 4, 8. [Google Scholar] [CrossRef] [Green Version]
- Van Westen, C.J.; Castellanos, E.; Kuriakose, S.L. Spatial data for landslide susceptibility, hazard, and vulnerability assessment: An Overview. Eng. Geol. 2008, 102, 112–131. [Google Scholar] [CrossRef]
- Wu, W.; Sidle, R.C. A Distributed slope stability model for steep forested basins. Water Resour. Res. 1995, 31, 2097–2110. [Google Scholar] [CrossRef]
- Schwarz, M.; Lehmann, P.; Or, D. Quantifying lateral root reinforcement in steep slopes—From a bundle of roots to tree stands. Earth Surf. Process. Landforms 2010, 35, 354–367. [Google Scholar] [CrossRef]
- Schmaltz, E.M.; Steger, S.; Glade, T. The influence of forest cover on landslide occurrence explored with spatio-temporal information. Geomorphology 2017, 290, 250–264. [Google Scholar] [CrossRef]
- Shu, H.; Hürlimann, M.; Molowny-Horas, R.; González, M.; Pinyol, J.; Abancó, C.; Ma, J. Relation between land cover and landslide susceptibility in Val d’Aran, Pyrenees (Spain): Historical aspects, present situation and forward prediction. Sci. Total Environ. 2019, 693, 133557. [Google Scholar] [CrossRef]
- Joybari, J.; Kavian, A.A.; Mosaffaie, J. Effect of land use on landslide movement in the Tavan District, Qazvin. Watershed Manag. Res. J. 2017, 30, 29–39. [Google Scholar]
- Jia, Q.; Wang, Y.P. Relationships between leaf area index and evapotranspiration and crop coefficient of hilly apple orchard in the Loess Plateau. Water 2021, 13, 1957. [Google Scholar] [CrossRef]
- Shi, D.; Tan, H.; Rao, W.; Liu, Z.; Elenga, H.I. Variations in water content of soil in apricot orchards in the western hilly regions of the Chinese Loess Plateau. Vadose Zone J. 2020, 19, e20034. [Google Scholar] [CrossRef]
- Mousavi, S.Z.; Kavian, A.; Soleimani, K.; Mousavi, S.R.; Shirzadi, A. GIS-based spatial prediction of landslide susceptibility using logistic regression model. Geomatics Nat. Hazards Risk 2011, 2, 33–50. [Google Scholar] [CrossRef] [Green Version]
- Sangrawee, P.; Rangsipanich, A.; Suvachananonda, T. Analyzing the effects of land use changes for landslide susceptibility assessment: A case study of LabLae District, Uttradit Province, Thailand. In Proceedings of the 38th Asian Conference on Remote Sensing in Space Applications Touching Human Lives, ACRS, New Delhi, India, 3–7 October 2017. [Google Scholar]
- Boonyanuphap, J. Cost-benefit analysis of vetiver system-based rehabilitation measures for landslide-damaged mountainous agricultural lands in the Lower Northern Thailand. Nat. Hazards 2013, 69, 599–629. [Google Scholar] [CrossRef]
- Miyagi, T.; Prasad, G.B.; Tanavud, C.; Potichan, A.; Hamasaki, E. Landslide risk evaluation and mapping—Manual of aerial photo interpretation for landslide topography and risk management. Rep. Natl. Res. Inst. Earth Sci. Disaster Prev. 2004, 66, 75–137. [Google Scholar]
- World Meteorological Organization. Integrated Flood Management Tools Series-Management of Sediment-Related Risks; Issue 12; 2011. Available online: https://library.wmo.int/doc_num.php?explnum_id=4274) (accessed on 10 April 2022).
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef] [Green Version]
- Saito, H.; Uchiyama, S.; Hayakawa, Y.S.; Obanawa, H. Landslides triggered by an earthquake and heavy rainfalls at Aso Volcano, Japan, Detected by UAS and SfM-MVS photogrammetry. Prog. Earth Planet. Sci. 2018, 5, 1–10. [Google Scholar] [CrossRef]
- Chang, K.T.; Chiang, S.H. An integrated model for predicting rainfall-induced landslides. Geomorphology 2009, 105, 366–373. [Google Scholar] [CrossRef]
- Chang, K.; Chiang, S.-H.; Lei, F. Analysing the relationship between typhoon-triggered landslides and critical rainfall conditions. Earth Surf. Process. Landforms 2008, 33, 1261–1271. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- Karger, D.N.; Wilson, A.M.; Mahony, C.; Zimmermann, N.E.; Jetz, W. Global daily 1 km land surface precipitation based on cloud cover-informed downscaling. Sci. Data 2021, 8, 307. [Google Scholar] [CrossRef] [PubMed]
- Mori, S.; Ono, K. Landslide disasters in Ehime prefecture resulting from the july 2018 heavy rain event in Japan. Soils Found. 2019, 59, 2396–2409. [Google Scholar] [CrossRef]
- Lee, C.T.; Huang, C.C.; Lee, J.F.; Pan, K.L.; Lin, M.L.; Dong, J.J. Statistical approach to storm event-induced landslides susceptibility. Nat. Hazards Earth Syst. Sci. 2008, 8, 941–960. [Google Scholar] [CrossRef] [Green Version]
- Dou, J.; Yamagishi, H.; Pourghasemi, H.R.; Yunus, A.P.; Song, X.; Xu, Y.; Zhu, Z. An Integrated artificial neural network model for the landslide susceptibility assessment of Osado Island, Japan. Nat. Hazards 2015, 78, 1749–1776. [Google Scholar] [CrossRef]
- Geospatial Information Authority of Japan (GSI). Map/Aerial Photo Viewing Display. 2022. Available online: https://mapps.gsi.go.jp/maplibSearch.do;jsessionid=DAD5878D8589927635F982E6AAFE3A9F#1 (accessed on 10 April 2022).
- Tachikawa, I.T.; Hato, M.; Kaku, M.; Iwasaki, A. The Characteristics of ASTER GDEM Version 2. IGRASS 2011. Available online: https://www.jspacesystems.or.jp/ersdac/GDEM/J/ (accessed on 10 April 2022).
- United State Geological Survey (USGS). Earth Explorer. 2022. Available online: https://earthexplorer.usgs.gov/ (accessed on 10 April 2022).
- Pinto, C.T.; Jing, X.; Leigh, L. Evaluation analysis of landsat level-1 and level-2 data products using in situ measurements. Remote Sens. 2020, 12, 2597. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure, Transport and Tourism (MLIT) of Japan. National Land Numerical Information Download Service. 2022. Available online: https://nlftp.mlit.go.jp/ksj/ (accessed on 10 April 2022).
- Ministry of Land, Infrastructure, Transport and Tourism (MLIT) of Japan. X/C Band MP Radar (XRAIN) Real-Time Rainfall Information by Data Integration and Analysis System Program (DIAS). 2022. Available online: http://apps.diasjp.net/xband/ (accessed on 10 April 2022).
- Dai, F.C.; Xu, C.; Yao, X.; Xu, L.; Tu, X.B.; Gong, Q.M. Spatial distribution of landslides triggered by the 2008 ms 8.0 Wenchuan earthquake, China. J. Asian Earth Sci. 2011, 40, 883–895. [Google Scholar] [CrossRef]
- Keefer, D.K. Statiscal analysis of an earthquake-induced landslide distribution—The 1989 Loma Prieta, California event. Eng. Geol. 2000, 58, 231–249. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Bai, S.B.; Wang, J.; Lü, G.N.; Zhou, P.G.; Hou, S.S.; Xu, S.N. GIS-based logistic regression for landslide susceptibility mapping of the Zhongxian segment in the Three Gorges Area, China. Geomorphology 2010, 115, 23–31. [Google Scholar] [CrossRef]
- Danjo, T.; Ishizawa, T.; Kimura, T. Spatial analysis of the landslide characteristics caused by heavy rainfall in the Northern Kyushu District in July 2017 using topography, geology, and rainfall levels. J. Disaster Res. 2018, 13, 832–845. [Google Scholar] [CrossRef]
- Di Napoli, M.; Di Martire, D.; Bausilio, G.; Calcaterra, D.; Confuorto, P.; Firpo, M.; Pepe, G.; Cevasco, A. Rainfall-induced shallow landslide detachment, transit and runout susceptibility mapping by integrating machine learning techniques and gis-based approaches. Water 2021, 13, 488. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I. Landslide susceptibility assessment in Vietnam using support vector machines, decision tree, and nave bayes models. Math. Probl. Eng. 2012, 2012, 974638. [Google Scholar] [CrossRef] [Green Version]
- Nefeslioglu, H.A.; Gokceoglu, C.; Sonmez, H. An assessment on the use of logistic regression and artificial neural networks with different sampling strategies for the preparation of landslide susceptibility maps. Eng. Geol. 2008, 97, 171–191. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Delineation of landslide hazard areas on Penang Island, Malaysia, by using frequency ratio, logistic regression, and artificial neural network models. Environ. Earth Sci. 2010, 60, 1037–1054. [Google Scholar] [CrossRef]
- Gautam, P.; Kubota, T.; Aditian, A. Evaluating underlying causative factors for earthquake-induced landslides and landslide susceptibility mapping in upper Indrawati watershed, Nepal. Geoenviron. Disasters 2021, 8, 30. [Google Scholar] [CrossRef]
- Gujarati, D.N.; Porter, D.C. Multicollinearity: What Happens If the Regressor Are Correlated? Basic Econometrics, 5th ed.; McGraw-Hill Irwin: New York, NY, USA, 2013; pp. 328–330. [Google Scholar]
- Corsini, A.; Mulas, M. Use of ROC curves for early warning of landslide displacement rates in response to precipitation (Piagneto Landslide, Northern Apennines, Italy). Landslides 2017, 14, 1241–1252. [Google Scholar] [CrossRef]
- Midi, H.; Sarkar, S.K.; Rana, S. Collinearity diagnostics of binary logistic regression model. J. Interdiscip. Math. 2010, 13, 253–267. [Google Scholar] [CrossRef]
- Johnston, R.; Jones, K.; Manley, D. Confounding and collinearity in regression analysis: A cautionary tale and an alternative procedure, illustrated by studies of british voting behaviour. Qual. Quant. 2018, 52, 1957–1976. [Google Scholar] [CrossRef] [Green Version]
- Hengl, T.; Heuvelink, G.B.M.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef] [Green Version]
- Hand, D.J.; Christen, P.; Kirielle, N. F*: An interpretable transformation of the F-measure. Mach. Learn. 2021, 110, 451–456. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef] [Green Version]
- Xing, Y.; Yue, Y.; Guo, Z.; Chen, Y.; Hu, J.; Travé, A. Large-Scale landslide susceptibility mapping using an integrated machine learning model: A case study in the Lvliang Mountains of China. Front. Earth Sci. 2021, 9, 622. [Google Scholar] [CrossRef]
- Rupke, J.; Huisman, M.; Kruse, H.M.G. Stability of man-made slopes. Eng. Geol. 2007, 91, 16–24. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, G.; Chen, W.; Liang, S.; Chen, R.; Han, W. Human-induced landslide on a high cut slope: A case of repeated failures due to multi-excavation. J. Rock Mech. Geotech. Eng. 2012, 4, 367–374. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.M.; Zhang, K.B. Case study of cutting slope with progressive failure due to continuous excavation. In Proceedings of the 8th Japan-China Geotechnical Symposium Challenges to Breakthrough Geotechnics, Kyoto, Japan, 28–29 September 2020; pp. 436–440. [Google Scholar]
- Ayalew, L.; Moeller, D.; Reik, G. Geotechnical aspects and stability of road cuts in the Blue Nile Basin, Ethiopia. Geotech. Geol. Eng. 2009, 27, 713–728. [Google Scholar] [CrossRef]
- Ziegler, A.D.; Bruun, T.B.; Guardiola-Claramonte, M.; Giambelluca, T.W.; Lawrence, D.; Thanh Lam, N. Environmental consequences of the Demise in Swidden cultivation in Montane Mainland Southeast Asia: Hydrology and geomorphology. Hum. Ecol. 2009, 37, 361–373. [Google Scholar] [CrossRef]
- Shakti, P.C.; Misumi, R.; Nakatani, T.; Iwanami, K.; Maki, M.; Maesaka, T.; Hirano, K. Accuracy of quantitative precipitation estimation using operational weather radars: A case study of heavy rainfall on 9–10 September 2015 in the east Kanto region, Japan. J. Disaster Res. 2016, 11, 1003–1016. [Google Scholar] [CrossRef]
- Bernardie, S.; Vandromme, R.; Thiery, Y.; Houet, T.; Grémont, M.; Masson, F.; Grandjean, G.; Bouroullec, I. Modelling landslide hazards under global changes: The case of a Pyrenean Valley. Nat. Hazards Earth Syst. Sci. 2021, 21, 147–169. [Google Scholar] [CrossRef]
- Tyagi, A.; Tiwari, R.K.; James, N. GIS-Based Landslide Hazard Zonation and Risk Studies using MCDM BT—Local Site Effects and Ground Failures; Springer: Singapore, 2021; pp. 251–266. [Google Scholar]



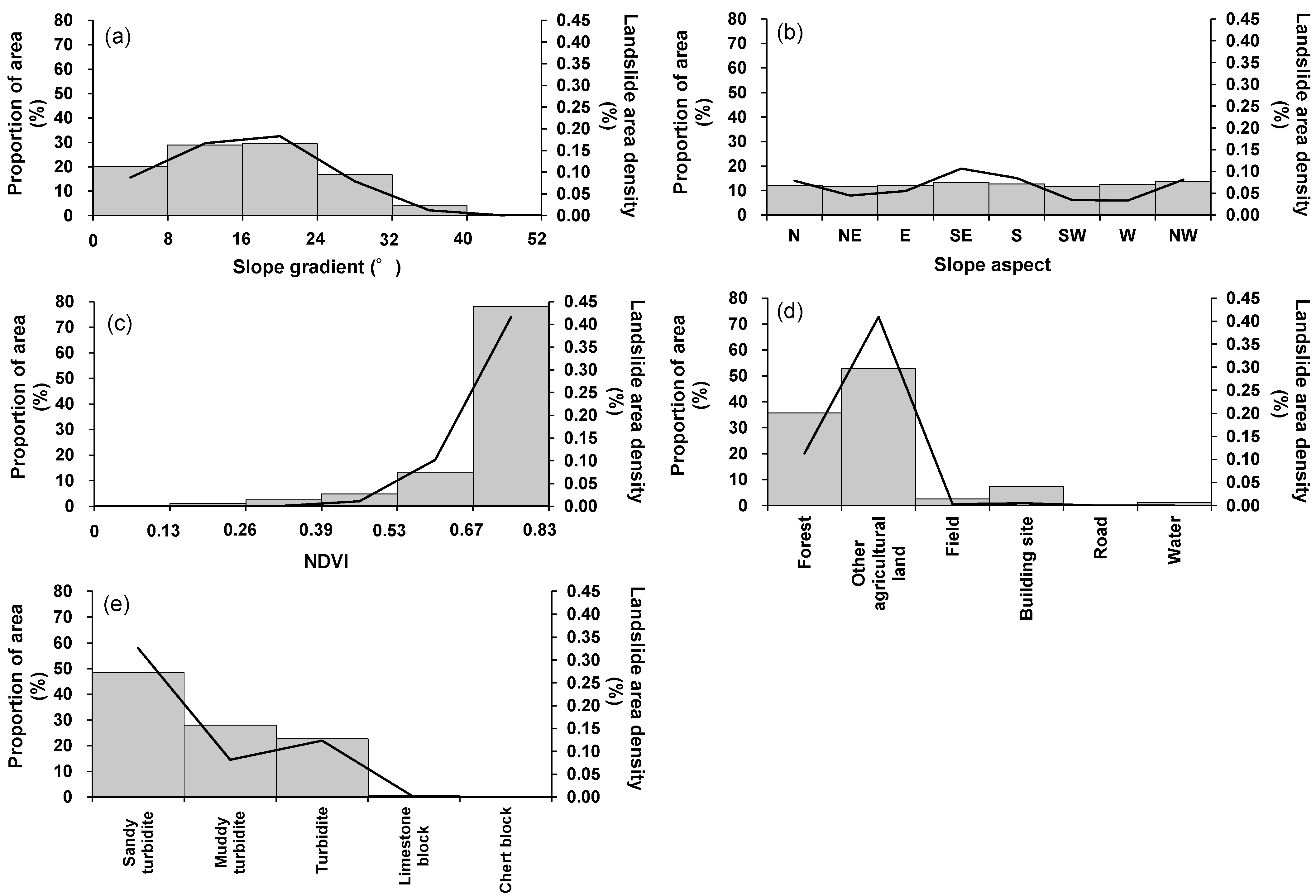
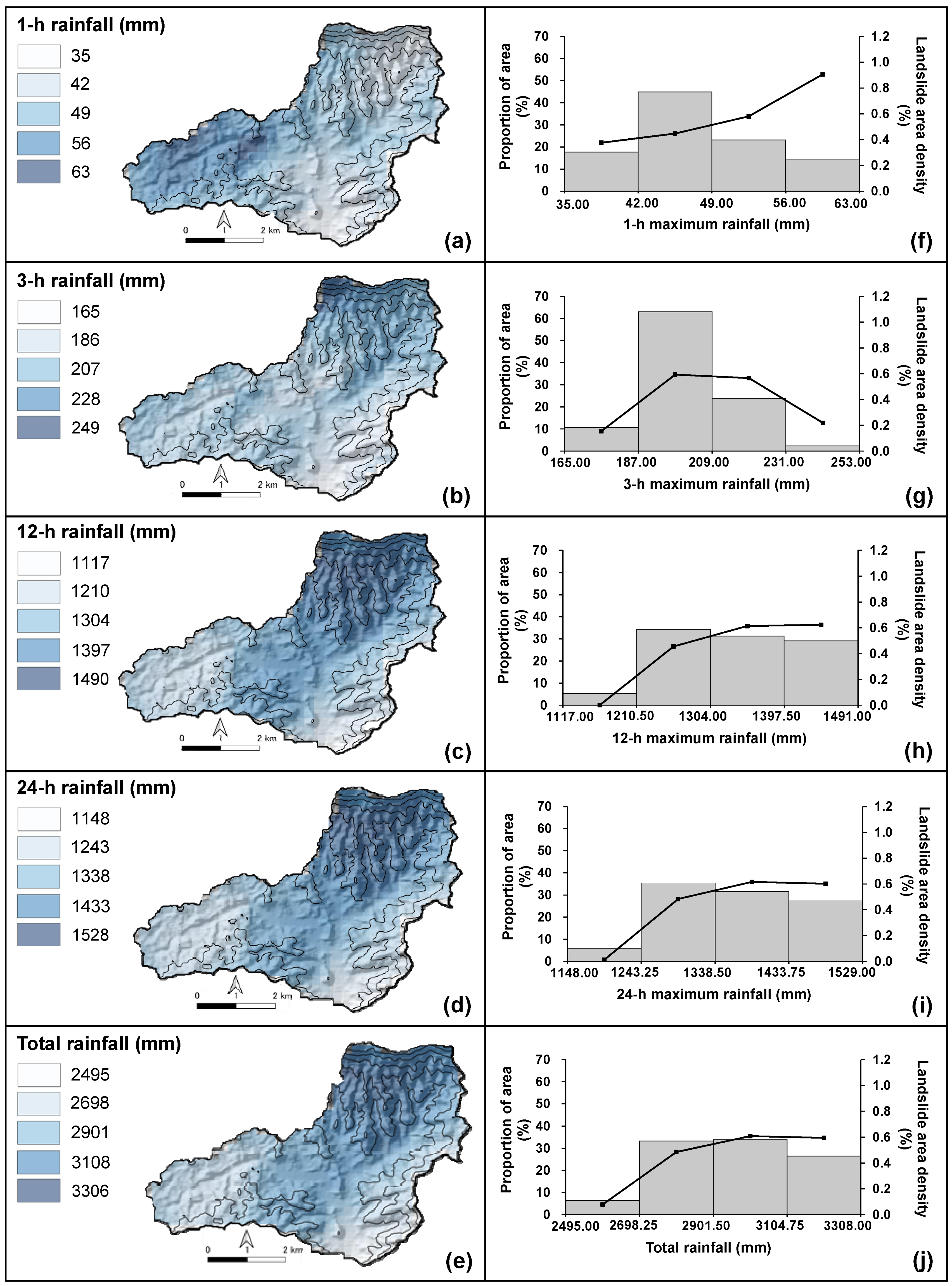
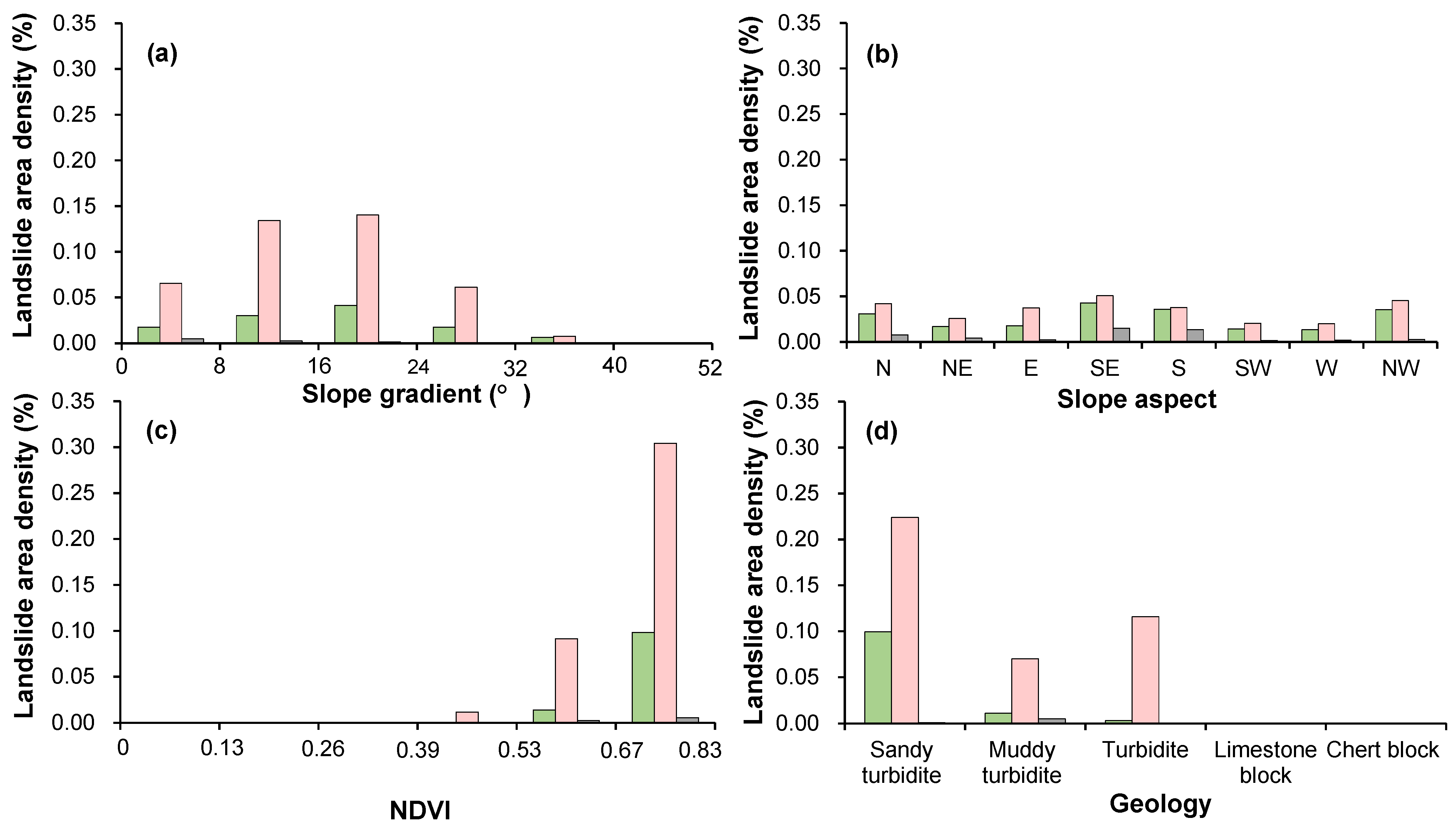
| Datasets | Data Type | Scale/ Resolution | Source |
|---|---|---|---|
| Landslide inventory maps (LIM) | Polygon coverage | 1:25,000 | [29] |
| Digital Elevation Model (DEM) | Raster | 30 × 30 m | [30] |
| Normalized Difference Vegetation Index (NDVI) | Raster | 30 × 30 m | [31] |
| Land use | Polygon coverage | 1:200,000 | [33] |
| Geology | Polygon coverage | 1:200,000 | [33] |
| Rainfall | Raster | 258 × 258 m | [34] |
| Variable | Coefficient | Variable | Coefficient | ||
|---|---|---|---|---|---|
| Model 1 | Models 2–5 | Model 6 | Models 7–10 | ||
| Slope gradient | – | –0.01 | Slope gradient | – | –0.005 |
| Slope aspect | – | – | Slope aspect | – | – |
| NDVI | –3.27 *** | –3.48 *** | NDVI | –3.10 *** | –3.29 *** |
| Dummy 1 | –0.14 * | –0.15 * | Dummy 2 | 0.22 *** | 0.23 *** |
| Dummy 3 | 0.13 | 0.12 | Dummy 3 | 0.13 | 0.13 |
| Dummy 4 | – | – | Dummy 4 | – | – |
| Rainfall | 0.01 | – | Rainfall | 0.01 | – |
| Method | Model 1 | Models 2–5 | Model 6 | Models 7–10 |
|---|---|---|---|---|
| AUC | 79.40 | 75.95 | 77.86 | 74.64 |
| F1 score | 77.78 | 67.92 | 72.73 | 72.73 |
| Overall accuracy | 79.31 | 70.69 | 74.14 | 74.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lusiana, N.; Shinohara, Y. The Role of Citrus Groves in Rainfall-Triggered Landslide Hazards in Uwajima, Japan. Water 2022, 14, 2113. https://doi.org/10.3390/w14132113
Lusiana N, Shinohara Y. The Role of Citrus Groves in Rainfall-Triggered Landslide Hazards in Uwajima, Japan. Water. 2022; 14(13):2113. https://doi.org/10.3390/w14132113
Chicago/Turabian StyleLusiana, Novia, and Yoshinori Shinohara. 2022. "The Role of Citrus Groves in Rainfall-Triggered Landslide Hazards in Uwajima, Japan" Water 14, no. 13: 2113. https://doi.org/10.3390/w14132113
APA StyleLusiana, N., & Shinohara, Y. (2022). The Role of Citrus Groves in Rainfall-Triggered Landslide Hazards in Uwajima, Japan. Water, 14(13), 2113. https://doi.org/10.3390/w14132113






