Robust Multi-Objective Design Optimization of Water Distribution System under Uncertainty
Abstract
:1. Introduction
1.1. Optimization under Uncertainty
1.2. Multi-Objective Optimization of WDS Design under Uncertainty
2. Methodology
2.1. Robust Optimization
2.2. Ellipsoidal Uncertainty Set
2.3. Two-Objective Cost vs. Resilience Design of Water Distribution System
2.4. Robust Optimization Formulation Considering Demand(q) as an Uncertain Variable
3. Case Study
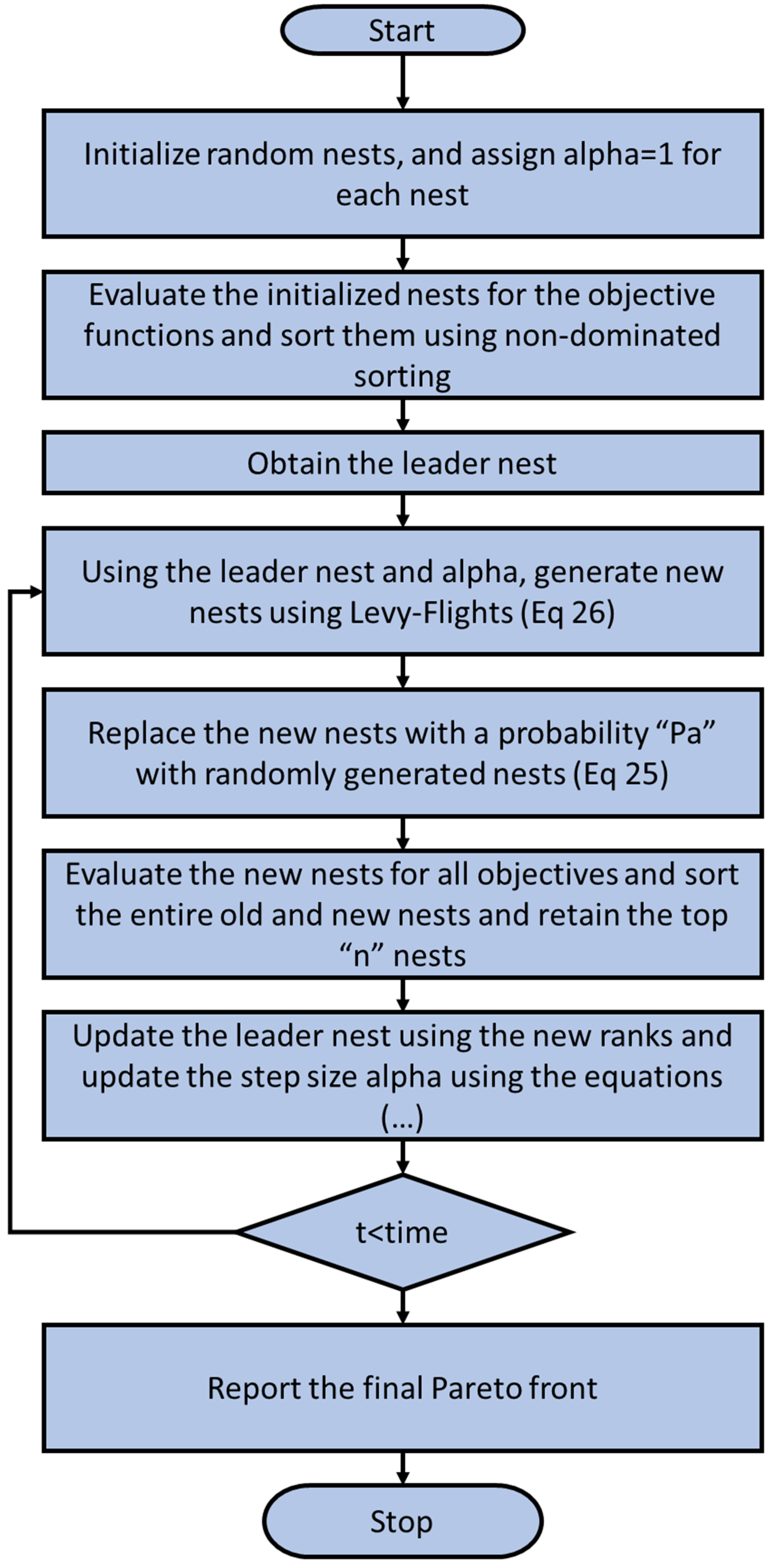
3.1. Multi-Objective Optimization Method
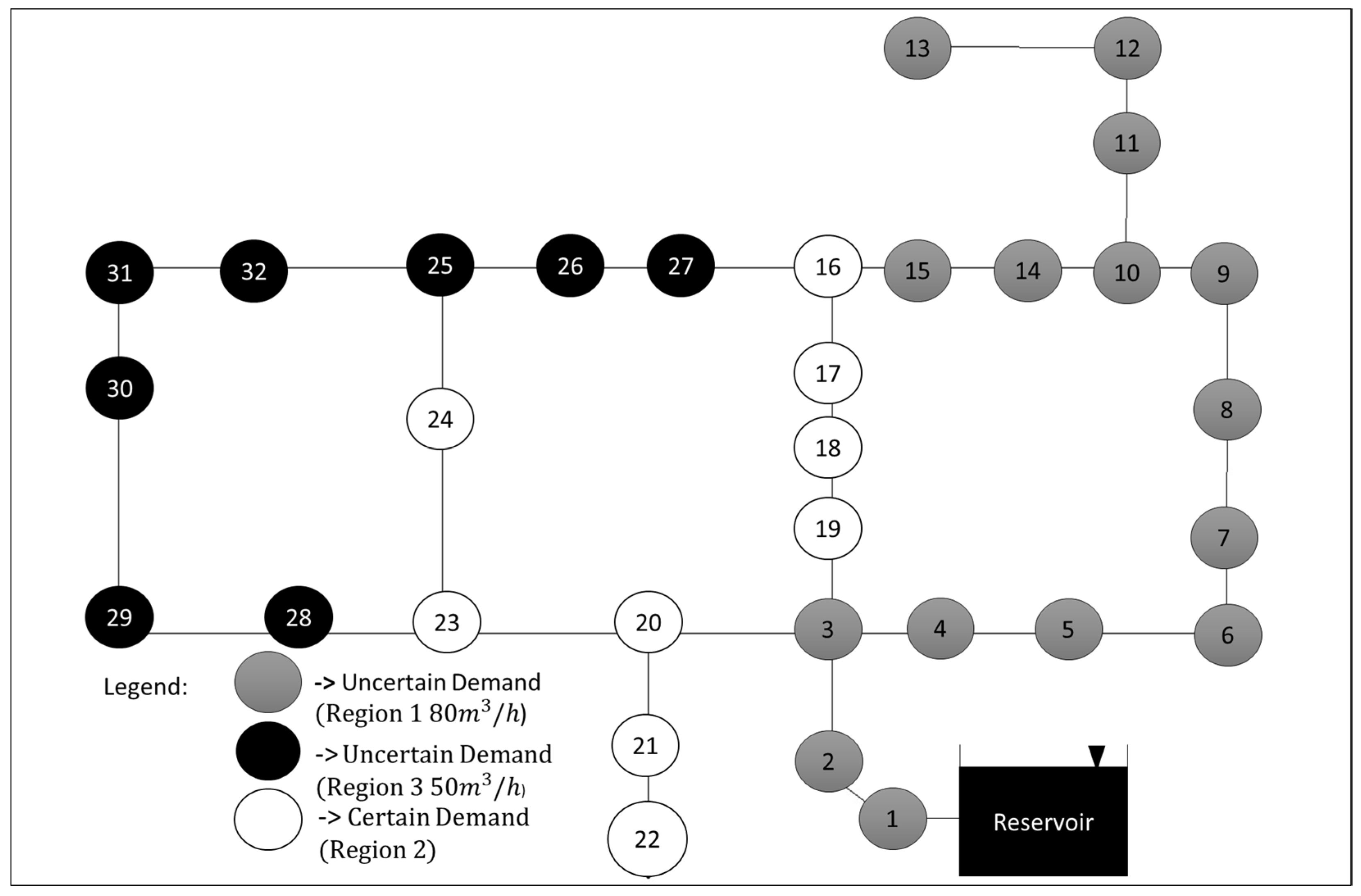
3.2. Case Study 1-Hanoi WDS
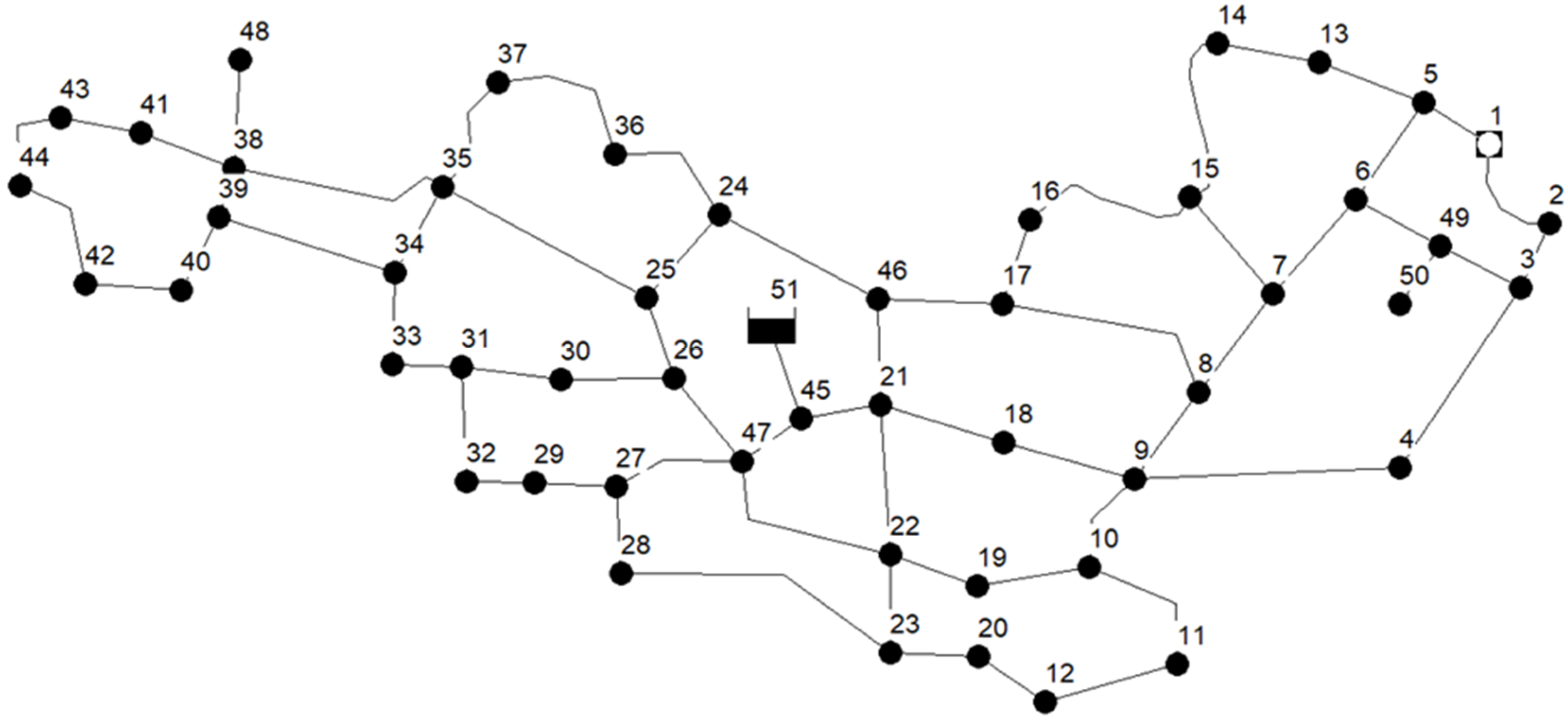
3.3. Case Study 2-Large Network
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Prasad, T.D.; Park, N.-S. Multiobjective Genetic Algorithms for Design of Water Distribution Networks. J. Water Resour. Plan. Manag. 2004, 130, 73–82. [Google Scholar] [CrossRef]
- Farmani, R.; Walters, G.A.; Savic, D.A. Trade-off between Total Cost and Reliability for Anytown Water Distribution Network. J. Water Resour. Plan. Manag. 2005, 131, 161–171. [Google Scholar] [CrossRef]
- Kapelan, Z.; Babayan, A.V.; Savic, D.A.; Walters, G.A.; Khu, S.T. Two new approaches for the stochastic least cost design of water distribution systems. Water Sci. Technol. Water Supply 2004, 4, 355–363. [Google Scholar] [CrossRef]
- Moosavian, N.; Lence, B.J. Nondominated Sorting Differential Evolution Algorithms for Multiobjective Optimization of Water Distribution Systems. J. Water Resour. Plan. Manag. 2017, 143, 04016082. [Google Scholar] [CrossRef]
- Naveen Naidu, M.; Boindala, P.S.; Vasan, A.; Varma, M.R.R. Optimization of Water Distribution Networks Using Cuckoo Search Algorithm; Springer: Singapore, 2020; Volume 949, ISBN 9789811381959. [Google Scholar]
- Ostfeld, A. Uncertainty and Risk Inclusions in Water Distribution Systems Management: Review and Challenges. In Proceedings of the Second International Conference on Vulnerability and Risk Analysis and Management (ICVRAM) and the Sixth International Symposium on Uncertainty, Modeling, and Analysis (ISUMA), Liverpool, UK, 13–16 July 2014; pp. 1980–1985. [Google Scholar]
- Pankaj, B.S.; Naidu, M.N.; Vasan, A.; Varma, M.R. Self-Adaptive Cuckoo Search Algorithm for Optimal Design of Water Distribution Systems. Water Resour. Manag. 2020, 34, 3129–3146. [Google Scholar] [CrossRef]
- Patil, M.B.; Naveen Naidu, M.; Vasan, A.; Varma, M.R.R. Water Distribution System Design Using Multi-Objective Genetic Algorithm with External Archive and Local Search. arXiv 2019, arXiv:1905.08105. [Google Scholar]
- Wang, Q.; Guidolin, M.; Savic, D.; Kapelan, Z. Two-Objective Design of Benchmark Problems of a Water Distribution System via MOEAs: Towards the Best-Known Approximation of the True Pareto Front. J. Water Resour. Plan. Manag. 2014, 141, 04014060. [Google Scholar] [CrossRef] [Green Version]
- Bargiela, A.; Hainsworth, G.D. Pressure and flow uncertainty in water systems. J. Water Resour. Plan. Manag. 1989, 115, 212–229. [Google Scholar] [CrossRef]
- Kretzmann, H.A.; van Zyl, J.E. Stochastic Analysis of Water Distribution Systems. In Critical Transitions in Water and Environmental Resources Management; American Society of Civil Engineers: Reston, VA, USA, 2004; pp. 1–10. [Google Scholar]
- Pasha, M.F.K.; Lansey, K. Effect of parameter uncertainty on water quality predictions in distribution systems-case study. J. Hydroinformatics 2010, 12, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Pasha, M.F.K.; Lansey, K. Analysis of uncertainty on water distribution hydraulics and water quality. In Proceedings of the World Water and Environmental Resources Congress 2005, Anchorage, AL, USA, 15–19 May 2005. [Google Scholar]
- Sumer, D.; Lansey, K. Effect of uncertainty on water distribution system model design decisions. J. Water Resour. Plan. Manag. 2009, 135, 38–47. [Google Scholar] [CrossRef]
- Lansey, K.E.; Duan, N.; Mays, L.W.; Tung, Y. Water Distribution System Design Under Uncertainties. J. Water Resour. Plan. Manag. 1989, 115, 630–645. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Goulter, I.C. Reliability-based optimal design of water distribution networks. J. Water Resour. Plan. Manag. 1999, 125, 352–362. [Google Scholar] [CrossRef] [Green Version]
- Babayan, A.V.; Kapelan, Z.S.; Savic, D.A.; Walters, G.A. Comparison of two approaches for the least cost design of water distribution systems under uncertain demands. In Critical Transitions in Water and Environmental Resources Management; American Society of Civil Engineers: Reston, VA, USA, 2004; Volume 38, pp. 1–10. [Google Scholar]
- Babayan, A.V.; Savic, D.A.; Walters, G.A.; Kapelan, Z.S. Robust Least-Cost Design of Water Distribution Networks Using Redundancy and Integration-Based Methodologies. J. Water Resour. Plan. Manag. 2007, 133, 67–77. [Google Scholar] [CrossRef]
- Perelman, L.; Housh, M.; Ostfeld, A. Robust optimization for water distribution systems least cost design. Water Resour. Res. 2013, 49, 6795–6809. [Google Scholar] [CrossRef]
- Perelman, L.; Housh, M.; Ostfeld, A. Least-cost design of water distribution systems under demand uncertainty: The robust counterpart approach. J. Hydroinformatics 2013, 15, 737–750. [Google Scholar] [CrossRef] [Green Version]
- Kapelan, Z.S.; Savic, D.A.; Walters, G.A. Multiobjective design of water distribution systems under uncertainty. Water Resour. Res. 2005, 41, 1–15. [Google Scholar] [CrossRef]
- Giustolisi, O.; Laucelli, D.; Colombo, A.F. Deterministic versus Stochastic Design of Water Distribution Networks. J. Water Resour. Plan. Manag. 2009, 135, 117–127. [Google Scholar] [CrossRef]
- Jung, D.; Kang, D.; Kim, J.H.; Lansey, K. Robustness-Based Design of Water Distribution Systems. J. Water Resour. Plan. Manag. 2014, 140, 04014033. [Google Scholar] [CrossRef]
- Seifollahi-Aghmiuni, S.; Bozorg Haddad, O.; Mariño, M.A. Water Distribution Network Risk Analysis Under Simultaneous Consumption and Roughness Uncertainties. Water Resour. Manag. 2013, 27, 2595–2610. [Google Scholar] [CrossRef]
- Hwang, H.; Lansey, K.; Jung, D. Accuracy of First-Order Second-Moment Approximation for Uncertainty Analysis of Water Distribution Systems. J. Water Resour. Plan. Manag. 2018, 144, 04017087. [Google Scholar] [CrossRef]
- Tolson, B.A.; Maier, H.R.; Simpson, A.R.; Lence, B.J. Genetic Algorithms for Reliability-Based Optimization of Water Distribution Systems. J. Water Resour. Plan. Manag. 2004, 130, 63–72. [Google Scholar] [CrossRef] [Green Version]
- Housh, M.; Ostfeld, A.; Shamir, U. Optimal multiyear management of a water supply system under uncertainty: Robust counterpart approach. Water Resour. Res. 2011, 47, 1–15. [Google Scholar] [CrossRef]
- Matrosov, E.S.; Woods, A.M.; Harou, J.J. Robust Decision Making and Info-Gap Decision Theory for water resource system planning. J. Hydrol. 2013, 494, 43–58. [Google Scholar] [CrossRef]
- Korteling, B.; Dessai, S.; Kapelan, Z. Using Information-Gap Decision Theory for Water Resources Planning Under Severe Uncertainty. Water Resour. Manag. 2013, 27, 1149–1172. [Google Scholar] [CrossRef] [Green Version]
- Pankaj, B.S.; Jaykrishnan, G.; Ostfeld, A. Optimizing Water Quality Treatment Levels for Water Distribution Systems under Mixing Uncertainty at Junctions. J. Water Resour. Plan. Manag. 2022, 148, 04022013. [Google Scholar] [CrossRef]
- Roach, T.; Kapelan, Z.; Ledbetter, R. Comparison of info-gap and robust optimisation methods for integrated water resource management under severe uncertainty. Procedia Eng. 2015, 119, 874–883. [Google Scholar] [CrossRef] [Green Version]
- Schwartz, R.; Housh, M.; Ostfeld, A. Limited multistage stochastic programming for water distribution systems optimal operation. J. Water Resour. Plan. Manag. 2016, 142, 06016003. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust Convex Optimization. Math. Oper. Res. 1998, 23, 769–805. [Google Scholar] [CrossRef] [Green Version]
- Engelhardt, M.O.; Skipworth, P.J.; Savic, D.A.; Saul, A.J.; Walters, G.A. Rehabilitation strategies for water distribution networks: A literature review with a UK perspective. Urban Water 2000, 2, 153–170. [Google Scholar] [CrossRef]
- Walski, T.M. The Wrong Paradigm—Why Water Distribution Optimization Doesn’t Work. J. Water Resour. Plan. Manag. 2001, 127, 203–205. [Google Scholar] [CrossRef]
- Fu, G.; Kapelan, Z.; Reed, P. Reducing the Complexity of Multiobjective Water Distribution System Optimization through Global Sensitivity Analysis. J. Water Resour. Plan. Manag. 2012, 138, 196–207. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Todini, E. Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Gheisi, A.; Forsyth, M.; Naser, G. Water Distribution Systems Reliability: A Review of Research Literature. J. Water Resour. Plan. Manag. 2016, 142, 04016047. [Google Scholar] [CrossRef]
- Dziedzic, R.; Karney, B.W. Performance Index for Water Distribution Networks under Multiple Loading Conditions. J. Water Resour. Plan. Manag. 2016, 142, 04015040. [Google Scholar] [CrossRef]
- Geem, Z.W. Multiobjective optimization of water distribution networks using fuzzy theory and harmony search. Water (Switzerland) 2015, 7, 3613–3625. [Google Scholar] [CrossRef]
- Fujiwara, O.; Khang, D.B. A two-phase decomposition method for optimal design of looped water distribution networks. Water Resour. Res. 1990, 26, 539–549. [Google Scholar] [CrossRef]
- Alperovits, E.; Shamir, U. Design of optimal water distribution systems. Water Resour. Res. 1977, 13, 885–900. [Google Scholar] [CrossRef]
- Design/Resiliance | Engineering | University of Exeter. Available online: https://emps.exeter.ac.uk/engineering/research/cws/resources/benchmarks/design-resiliance-pareto-fronts/ (accessed on 30 June 2022).

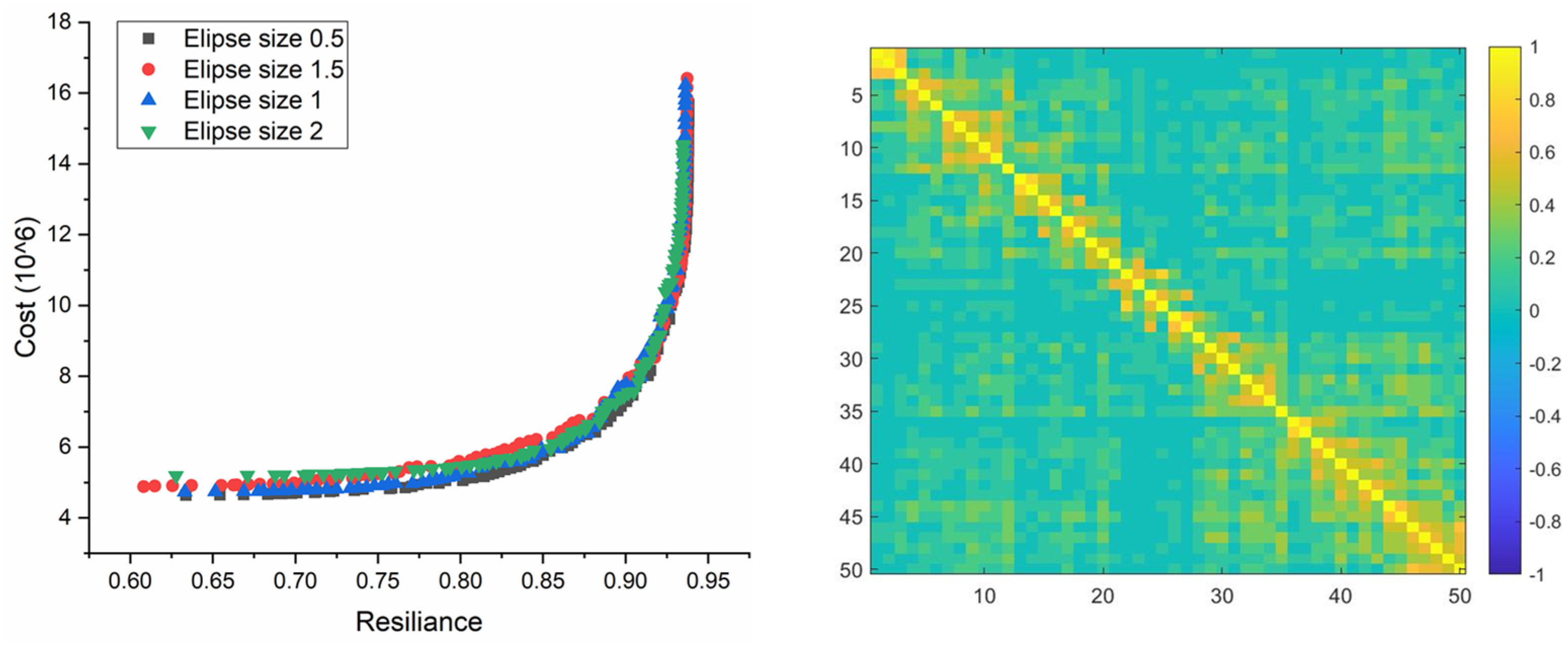
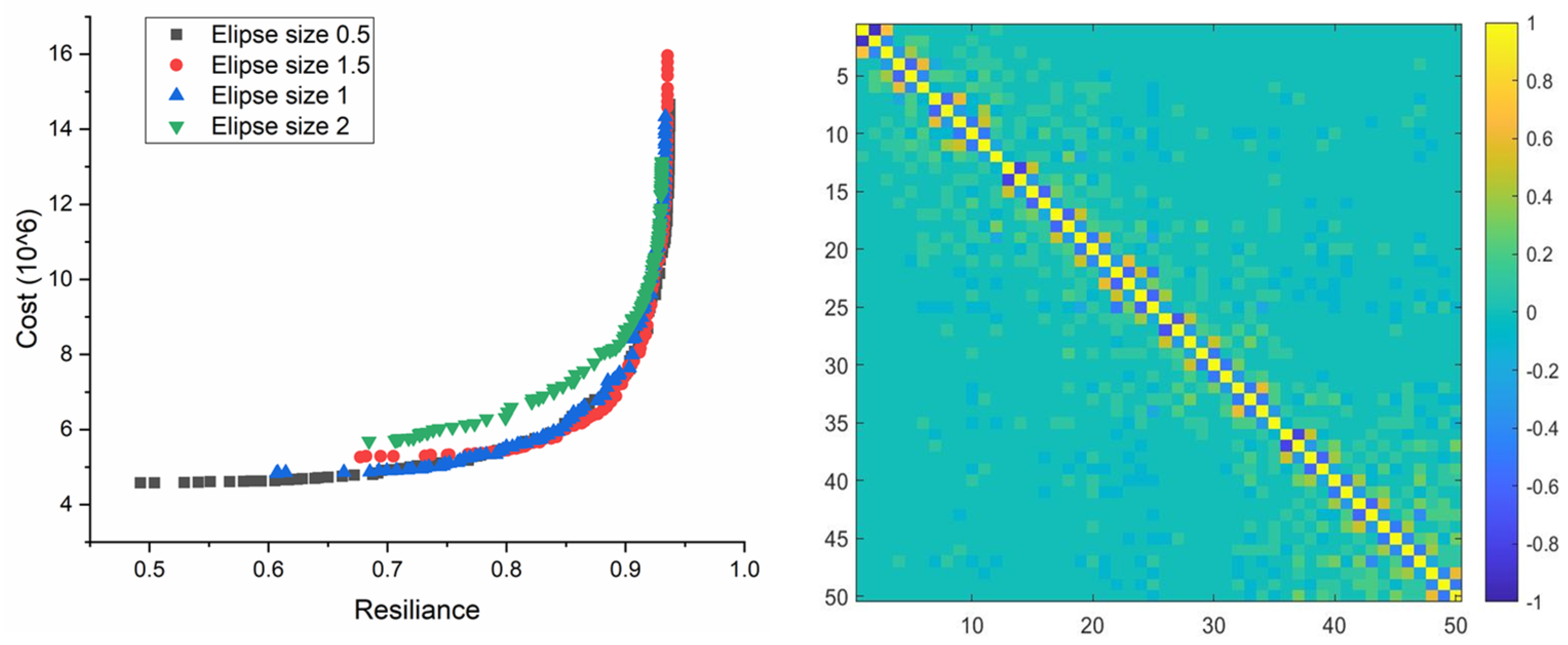
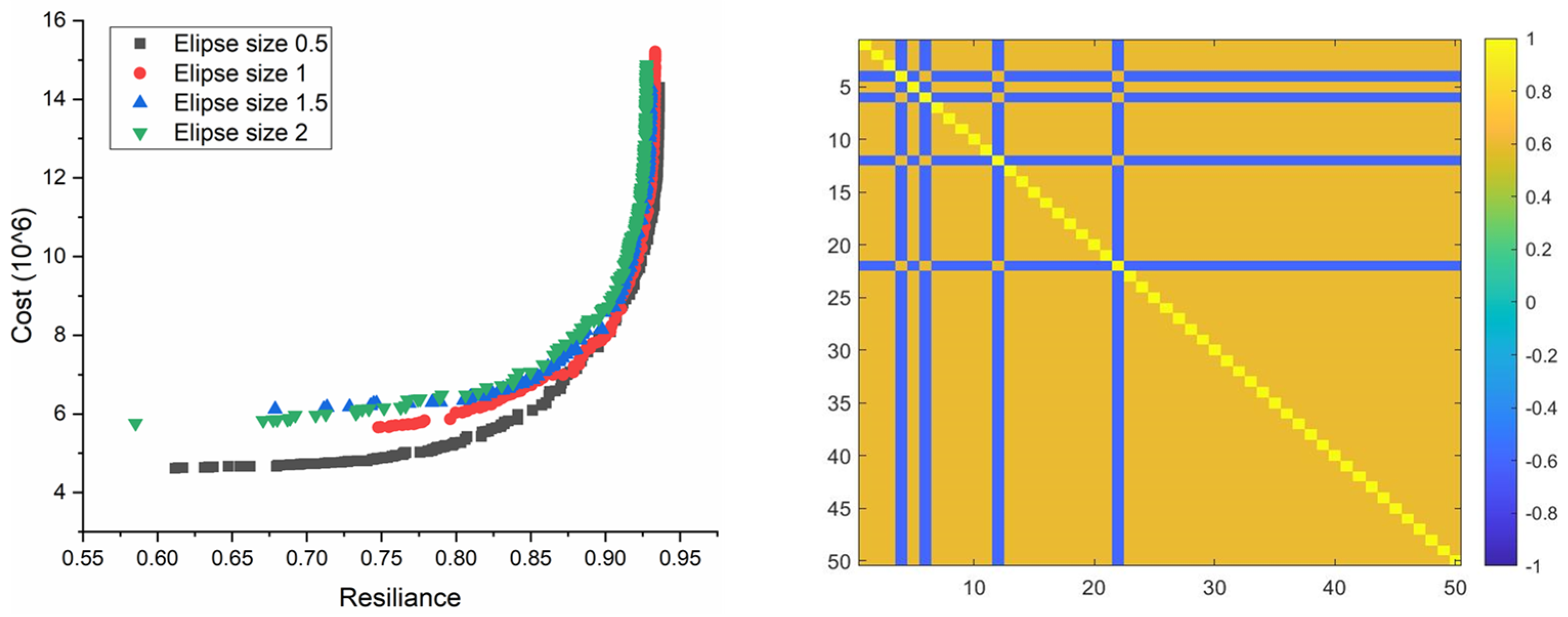
| Uncertain Parameters | PDF Assumed | Uncertainty Handling Techniques | Optimization Techniques | References | Type |
|---|---|---|---|---|---|
| q, H, RC | Normal | FORM | GRG2 | [16] | Hydraulic analysis |
| q, H, RC | Normal | MCS | GRG2 | [15] | SO Design |
| q, RC | Normal | MCS | SFLA | [24] | Hydraulic analysis |
| q, RC | Normal | FOSM and MCS | -- | [25] | Hydraulic analysis |
| q | Gaussian | LHS | GA | [17] | SO Design |
| q, RC | Normal | FORM | GA | [26] | SO Design |
| q | Gaussian | LHS | RNSGA-II | [21] | MO Design |
| q | -- | Robust optimization | cross entropy | [19,20] | SO Design |
| Diameter (in) | Unit Cost ($/m) | Diameter (in) | Unit Cost ($/m) | Diameter (in) | Unit Cost ($/m) |
|---|---|---|---|---|---|
| 12.0 | 45.73 | 20 | 98.39 | 30 | 180.75 |
| 16.0 | 70.4 | 24 | 129.33 | 40 | 278.28 |
| Correlation | Uncertainty Set Size | Extreme Point-1 | Extreme Point-2 | ||
|---|---|---|---|---|---|
| Cost | Resilience | Cost | Resilience | ||
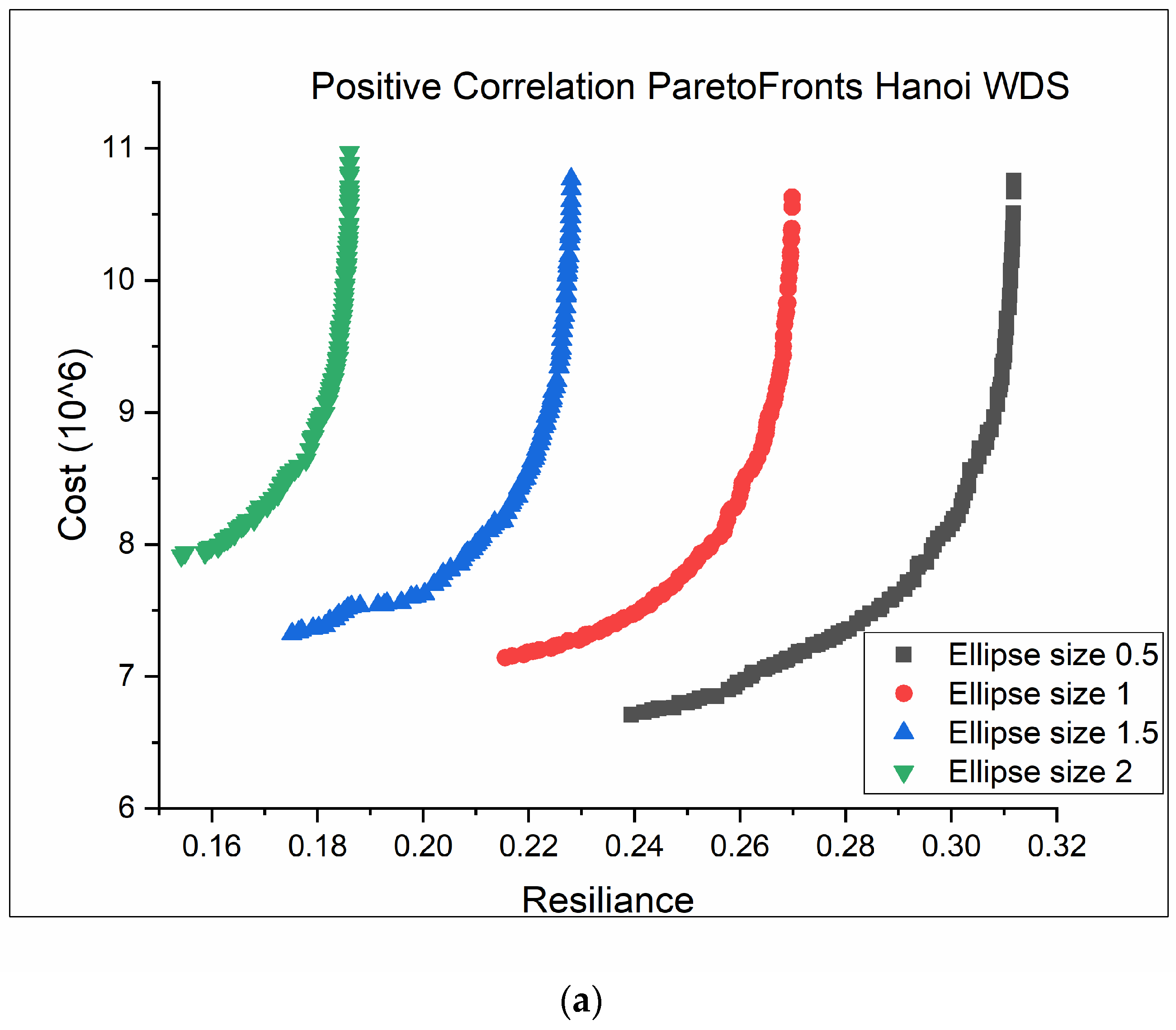
| Positive | 2 | 7.9157 | 0.154 | 10.969 | 0.186 |
| 0.5 | 6.7115 | 0.2394 | 10.755 | 0.3118 | |
| Negative | 2 | 7.154 | 0.207 | 10.121 | 0.2593 |
| 0.5 | 6.61 | 0.2516 | 10.305 | 0.3298 | |
| Zero(No) | 2 | 6.656 | 0.2211 | 10.747 | 0.308 |
| 0.5 | 6.584 | 0.2232 | 10.769 | 0.342 | |
| Diameter | 1 | 2 | 3 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| Unit Cost | 2.0 | 5.0 | 8.0 | 11.0 | 16.0 | 24.0 | 32.0 | 50.0 | 60.0 | 90.0 | 130.0 | 170.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boindala, S.P.; Ostfeld, A. Robust Multi-Objective Design Optimization of Water Distribution System under Uncertainty. Water 2022, 14, 2199. https://doi.org/10.3390/w14142199
Boindala SP, Ostfeld A. Robust Multi-Objective Design Optimization of Water Distribution System under Uncertainty. Water. 2022; 14(14):2199. https://doi.org/10.3390/w14142199
Chicago/Turabian StyleBoindala, Sriman Pankaj, and Avi Ostfeld. 2022. "Robust Multi-Objective Design Optimization of Water Distribution System under Uncertainty" Water 14, no. 14: 2199. https://doi.org/10.3390/w14142199
APA StyleBoindala, S. P., & Ostfeld, A. (2022). Robust Multi-Objective Design Optimization of Water Distribution System under Uncertainty. Water, 14(14), 2199. https://doi.org/10.3390/w14142199







