Experimental Investigation of the Earth Pressure on Horizontally Composite Breakwaters According to Different Shoulder Widths of Rubble Mounds

Abstract

A series of physical experiments were carried out to investigate the characteristics of the horizontal active earth pressure exerted by rubble stones placed in front of horizontally composite breakwaters. Typically, the shoulder width of rubble mounds is shorter than the failure wedge assumed by Rankine’s earth pressure theory; therefore, it is not appropriate to apply the theory for the estimation of the horizontal pressure of rubble stones on the caisson. Considering this, physical experiments were conducted to evaluate the horizontal earth pressure with rubble stones having different shoulder widths in front of the caisson. The experimental results showed that the horizontal pressure was considerably lower than that obtained by Rankine’s theory when the shoulder width was shorter than the failure wedge width. Even when the shoulder width was sufficiently large to apply the theory, the earth pressure was approximately 17% lower than the value calculated byRankine’s theory. Based on these analyses, an empirical equation is proposed that can estimate the earth pressure on the caisson for a wide range of shoulder widths of rubble mounds.

1. Introduction

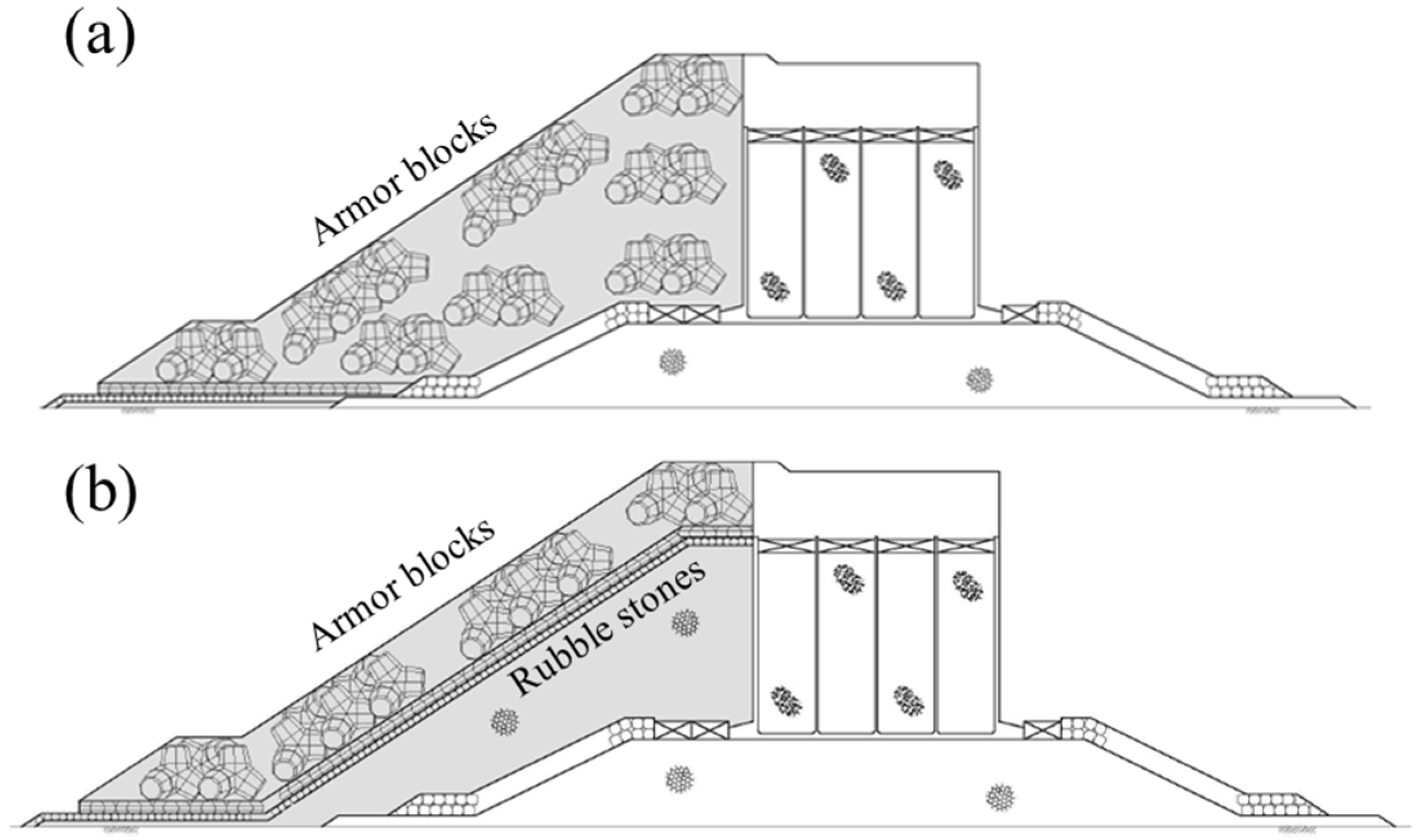
Horizontally composite breakwaters, which protect the front face of the caisson with wave-dissipating armor blocks, are known to be effective in reducing wave forces on caissons [1,2]. As shown in Figure 1, there are two different methods to construct horizontally composite breakwaters. The first method shown in Figure 1a entails covering the front of the caisson solely with concrete armor blocks. Another method is to place armor blocks on the rubble-mounted core, as shown in Figure 1b. The structure built according to the second method is similar in configuration to the front section of a rubble mound breakwater. The method of estimating the horizontal wave pressure acting on such a structure has been reported in recent research [3]. However, the lateral forces exerted by the rubble stones themselves on the front face of the caisson are not well known; in fact, few studies have been conducted on this topic, and relevant design guidelines have not been established so far.

Concerning the structure in Figure 1a, an experimental study [4] reported that the horizontal force exerted by armor blocks depends on the total height and degree of compaction of the armor blocks. It also showed that the horizontal force due to armor blocks on the caisson rapidly becomes close to zero when the wave large enough to cause the sliding of the caisson occurs because the caisson transiently swings a bit even if it does not slide in such a case. For the structure in Figure 1b, however, it is not certain that this happens, because rubble stones inherently have a much smaller interlocking effect compared to armor blocks. Hence, the lateral force on the caisson exerted by rubble stones might be to some extent different from that on the structure in Figure 1a. Although there is no formula for estimating the force on the structure in Figure 1b, it is presumed that the method of estimating the earth pressure on the retaining wall can be used because of structure similarities.

The earth pressure is the pressure exerted on a vertical wall by the soil in contact with the structure and mainly includes earth pressure at rest, active earth pressure, and passive earth pressure. The magnitude of the active and passive earth pressures is commonly estimated by the well-known Rankine’s or Coulomb’s theories [5,6]. These theories are in principle analytical methods based on the limit equilibrium approach. The main difference between the two theories is that Rankine’s theory assumes that the wall is frictionless ($\delta =0$), whereas the friction between the wall and the soil is considered in Coulomb’s theory. Therefore, the earth pressure estimated by Coulomb’s theory is slightly smaller than that obtained by Rankine’s theory. In other words, Rankine’s theory is more conservative than Coulomb’s theory.

Because Rankine’s theory does not consider wall friction, the failure wedge can be simply represented as shown in Figure 2a, where the distribution of the active pressure from this wedge is also shown. In the figure, the symbol $h_c$ is the height of the wall, $\varphi$ is the angle of internal friction of the materials used for the backfill, $G_{cR}$ is the width of the failure wedge, $h_w$ is the water depth, and ${\gamma }_{sat}$ is the saturated unit weight of the backfill materials. The width of the failure wedge, $G_{cR}$, is given as

$$G_{cR}=h_c·\cot \left({45}^{\circ }+\varphi /2\right)$$

(1)

If the width of the backfill is larger than $G_{cR}$ calculated by Equation (1), the triangular pressure distribution can be applied as shown in Figure 2a, according to which the horizontal pressure linearly increases towards the bottom of the wall. Rankine’s coefficient of active earth pressure, $K_{aR}$, is given by

$$K_{aR}=\frac{1-\sin \varphi }{1+\sin \varphi }={\tan }^2\left({45}^{\circ }-\varphi /2\right).$$

(2)

Therefore, the horizontal pressure (${\sigma }_{hR}$) and horizontal force ($F_{hR}$) at the bottom according to Rankine’s theory are expressed as follows:

$${\sigma }_{hR}=K_{aR}\gamma h_c$$

(3)

$$F_{hR}=\frac{1}{2}{K}_{aR}\gamma h_c^2$$

(4)

In case of a partially submerged wall, the still water level is located somewhere in the middle of the vertical wall. In such a case, the earth pressure below the water level should be reduced, as shown in Figure 2b.

To apply Rankine’s theory for estimating the earth pressure on the caisson exerted by the rubble stones, the shoulder width, i.e., the width of the top of the rubble mound, must be sufficiently larger than Rankine’s active wedge ($G_{cR}$). This is because Rankine’s theory was derived based on the assumption that the width of the backfill is semi-infinite. However, as shown in Figure 3, the crest width of the rubble mound mostly tends to be narrower than $G_{cR}$. Hence, it is not appropriate to use Rankine’s theory.

Various researchers have studied the active earth pressure on a wall when the backfill width is relatively narrow [7,8,9,10,11]. Taking a few examples, Fan and Fang [7] studied the active earth pressure on a retaining wall built adjacent to rock faces using the finite element method (FEM). They found that the coefficient of active earth pressure was reduced by 0.5 times compared to that calculated with Coulomb’s theory when the backfill space was confined by the rock faces. Yang and Tang [8] conducted a scale model test and measured the active earth pressure with various backfill widths under different modes of wall movement. By analyzing the measured data, they found that the earth pressure was significantly smaller than that of the Coulomb’s solution in all movement modes. Yang and Deng [9] investigated the active earth pressure on the retaining wall exerted by cohesionless soil with narrow width using limit equilibrium analysis. They also reported that the earth pressure decreased as the backfill width decreased, which was ascribed to the arching effect when the backfill width was narrower. Chen et al. [10,11] studied the active earth pressure on the retaining wall under the condition of translation mode using finite-element limit analysis (FELA). They showed that slip surfaces formed differently according to various parameters such as internal friction angle, unit weight of the soil, and width of the backfill, and concluded that the coefficient of active earth pressure in their study was approximately 0.5 to 0.7 times that of the Coulomb’s solution.

All the above-mentioned studies prove that there is a limit to applying Rankine’s or Coulomb’s theory for estimating the earth pressure in the presence of a relatively narrow backfill. However, the results in those studies are not directly applicable to evaluate the earth pressure on horizontally composite breakwater because its structural form shown in Figure 1b is quite different from the structures examined in those studies. Considering this, the horizontal loading on the caisson exerted by rubble stones was measured in this study by carrying out physical experiments by changing crest widths of rubble mound in front of the caisson. The distribution of horizontal pressure along the caisson is presented and was compared with those obtained using the classical Rankine’s or Coulomb’s theories. Finally, a modified coefficient of earth pressure is proposed that can be applied for the evaluation of the horizontal loading exerted by rubble stones on the caisson.

2. Experimental Setup

Physical experiments were performed in a wave flume 50 m long and 1.2 m wide at the Physical Experimental Building (PEB) of the Korea Institute of Ocean Science and Technology [12,13]. As shown in Figure 4, the caisson model, made of a polycarbonate plate, was installed at 31.15 m from one end of the flume. The caisson model was 0.45 m long, 0.5 m wide, and 0.6 m high. On both sides of the model, two dummy models with the same height and length but with a different width (0.35 m), were installed. Figure 5 shows the front and side views of the caisson model. The reason for conducting the experiment in the wave flume was to measure the wave pressure acting on horizontally composite breakwater, as shown in Figure 1b. Before performing such experiment, however, it was necessary to evaluate the earth pressure exerted by the rubble stones placed in front of the horizontally composite breakwater, which was the main purpose of the present study.

As shown in Figure 5, the front wall of the caisson model consisted of 10 independent transverse plates, and S-beam load cells were installed on both ends of each plate. As elucidated in Oh and Ji [14], this type of system is very effective for measuring the horizontal loading at different vertical elevations along the wall. As shown in Figure 5b, each load cell was connected to a support attachment installed on the inner side wall of the caisson model. The vertical gap between the adjacent upper and lower plates was 2 mm. Hence, each individual plate could slightly move back and forth when subjected to an external force, without being affected by adjacent upper or lower plates. To prevent the sharp edge of tiny stones from getting caught in the gaps between the plates, a thin band tape with good elasticity was attached over the gaps. Through preliminary experiments, it was confirmed that the band tape did not interfere with the movement of the plates.

Table 1. Properties of the rubble stones used in the experiments.

Type	Specific Gravity	Porosity	Cohesion (kPa)	ϕ (°)	d50 (mm)	Unit Weight (kN/m3)
Rubble stones	2.65	0.37	0	38	9.2	16.7

lists the properties of the rubble stones used in the experiment. The internal friction angle ($\varphi$) of the rubble stones was determined by measuring the angle of repose. The median size of the stones ($d_{50}$) was obtained by a sieve analysis. Using the values in the table, the width of Rankine’s active wedge presented in Equation (1) were calculated as follows

$$G_{cR}=0.6·\cot \left({45}^{\circ }+{38}^{\circ }/2\right)\approx 0.30 \mathrm{m}.$$

(5)

Based on the calculated value of $G_{cR}$, the experiment was carried out in the conditions of $G_c\ge G_{cR}$ and $G_c<G_{cR}$, where $G_c$ denotes the shoulder width of the rubble mound. For the first condition ($G_c\ge G_{cR}$), it was possible to compare the measured earth pressure with the value obtained from Rankine’s theory. The values of $G_c$ changed in the five conditions, as illustrated in Figure 6. In all the five cases, measurements were made in dry and submerged conditions while changing the water depth in three ways as shown in Figure 6. The crest level of the rubble mound was kept at the top of the caisson, and the fore slope of the mound was 1:1.5.

3. Results

3.1. Influence of the Shoulder Width of the Rubble Mound

Figure 7 shows the vertical distributions of the measured earth pressure along the front wall of the caisson for the five different shoulder widths under the dry condition. Note that the pressure on each plate was estimated by dividing the total force measured from a pair of load cells attached to both ends of the plate by the area of the plate. As shown in Figure 7a–c, the overall magnitude of the earth pressure apparently increases as the shoulder width increases. In contrast, the values in Figure 7d,e, corresponding to the condition of $G_c\ge G_{cR}$, are not significantly different from those in Figure 7c. This indicates that the earth pressure will no longer increase even if the shoulder width becomes larger than the Rankine’s failure wedge width.

In Figure 8, the earth pressure measured for five different shoulder widths is compared with the values according to Rankine’s and Coulomb’s theories. The pressures according to these theories were estimated by considering $\gamma =16.7 \mathrm{kN}/{\mathrm{m}}^3$, as listed in Table 1. The pressure distribution by Coulomb’s theory was obtained based on the assumption that the friction angle of the wall ($\delta$) was 1/3 of the internal friction angle, i.e., $\delta =\varphi /3$. This value is smaller than the value of $\delta =\varphi /2 ~ 2\varphi /3$ that is typically applied for a concrete wall [15]. The reason for this is that the model in this experiment was made of a polycarbonate plate with a smoother surface than concrete. As the friction angle of the wall was assumed to be smaller, the earth pressure estimated by Coulomb’s theory resulted in a more conservative evaluation of earth loading. On the other hand, the effect of the wall friction angle on the active earth pressure, unlike that on the passive earth pressure, is known to be not significant [16].

As shown in Figure 8a, if the shoulder width was narrower than $G_{cR}$, the pressure was considerably lower than the values estimated by both theories over the entire height of the caisson. Even when the shoulder width was greater than $G_{cR}$, as shown in Figure 8b, the pressures in the lower part of the caisson were smaller than the values obtained by the theories. Meanwhile, in the upper part of the caisson, the measurement results appeared in slightly better agreement with those obtained by Rankine’s theory than with those determined with Coulomb’s theory. Further detailed analysis in the following was carried out by comparing the measured data with those obtained with Rankine’s theory as it does not include the effects of the friction angle of the wall.

Figure 9 shows the vertical profiles of the normalized earth pressure (${\sigma }_h/\gamma z$) as a function of the normalized depth ($z/h_c$), where ${\sigma }_h$ is the horizontal earth pressure, $\gamma$ is the unit weight of the rubble stones, and $z$ is the depth measured from the top of the rubble mound. As inferred from Equation (3), the dimensionless parameter ${\sigma }_h/\gamma z$, also denoted as $K_a$ in this study, has the physical meaning of Rankine’s coefficient of active earth pressure ($K_{aR}$). As shown in Figure 9a, the values of ${\sigma }_h/\gamma z$ did not change significantly with $z/h_c$ when $G_c<G_{cR}$. In contrast, as shown in Figure 9b, the normalized pressure decreased almost linearly with the increase of the normalized depth.

In Figure 10, the vertical profiles of $K_a/K_{aR}$ are presented, illustrating the relative magnitude the normalized earth pressure with respect to Rankine’s coefficient. In the figure, the depth-averaged value of $K_a/K_{aR}$ for each $G_c$ condition is also shown as a dotted line. As shown in Figure 10a, the values of $K_a/K_{aR}$ did not change significantly in the vertical direction when the shoulder width was smaller than $G_{cR}$. The averages of $K_a/K_{aR}$ for $G_c$ = 0.05 m and 0.15 m were 0.52 and 0.66, respectively. When the shoulder width was greater or equal to $G_{cR}$, as shown in Figure 10b, the values of $K_a/K_{aR}$ gradually decreased as the depth increased. The depth-averaged values of $K_a/K_{aR}$ for the three $G_c$ conditions in Figure 10b were almost the same, and their mean value was 0.83.

Based on the results above, the depth-averaged values of $K_a/K_{aR}$ for the different shoulder widths are displayed together in Figure 11. It appears that the values of $K_a/K_{aR}$ linearly increases with $G_c/G_{cR}$ when $G_c/G_{cR}\le 1.0$, whereas it becomes flat when $G_c/G_{cR}>1.0$. In the figure, regression lines for the two ranges are also shown, from which the parameter $K_a$ can be expressed as follows:

$$K_a=\min \left\{0.37G_c/G_{cR}+0.46, 0.83\right\}\cdot K_{aR}$$

(6)

Because $K_a$ is intrinsically equivalent to Rankine’s coefficient, as elucidated in the above, Equation (6) can be interpreted as a modified coefficient of active earth pressure that considers the effect of the shoulder width of rubble stones. Hence, this equation can be applied for estimating the horizontal pressure exerted by rubble stones on the caisson, even if the shoulder width is narrow compared to the width of Rankine’s failure wedge. It is noteworthy that the value of $K_a$ given by Equation (6) is independent of the depth, as according to Rankine’s theory.

Figure 12 shows a comparison of the earth pressures evaluated by Equation (6) with the experimental data. Contrary to the results in Figure 8, where significant discrepancy was found between Rankine’s theory and the measurements, the suggested formula presents good agreement with the trend in the experimental data. In particular, the earth pressure predicted by the empirical formula was in good agreement with the pressure measured under various conditions of shoulder width. Therefore, Equation (6) can be applied regardless of the shoulder width of the rubble stones in front of the caisson.

3.2. Verification of the Formula in Submerged Conditions

When part of or all the caisson was submerged in water, as illustrated in Figure 2b, the horizontal pressure exerted by rubble stones placed in front of the caisson should be reduced due to the buoyancy effect. Figure 13 shows the change in the measured horizontal pressure in three different water level conditions illustrated in Figure 6 when $G_c/G_{cR}$ = 1 (or $G_c$ = 0.3 m). In Figure 13a, the black line represents the earth pressure in the dry condition, whereas the other three dotted lines correspond to the earth pressures when the water depth was 0.35, 0.55, and 0.70 m, respectively. As shown in the figure, the horizontal pressure below the water level apparently decreased as the water level increased. Then, as shown in Figure 13b, a comparison was made with the pressure measured with the suggested formula in Equation (6), considering the buoyancy effect according to the water depth. In other words, ${\gamma }_{sat}$ was used instead of $\gamma$ when calculating the horizontal earth pressure under the water level, as described in Figure 2b. Note that the pressure exerted by the rubble stones underneath the water level was estimated by using the submerged unit weight of stones, or the difference between the saturated unit weight of stones and the unit weight of water. Although there was a slight deviation of the measured pressures from those estimated by the suggested formula, the agreement between both quantities was generally good for all water level conditions.

4. Conclusions

This study experimentally investigated the horizontal earth pressure of rubble mound placed in a trapezoidal shape in front of the caisson, which is a form of the so-called horizontally composite breakwater. From the experiments and subsequent analysis results, it was found that when the shoulder width ($G_c$) was narrower than Rankine’s failure wedge ($G_{cR}$), the coefficient of active earth pressure ($K_a$) was constant regardless of the depth, with its value considerably smaller than Rankine’s coefficient of active earth pressure ($K_{aR}$). This suggests that the classical Rankine’s theory is not appropriate for estimating the horizontal pressure acting on the front face of the caisson in such a condition. If the shoulder width was greater than Rankine’s failure wedge, the horizontal pressure was almost constant, regardless of the magnitude of the shoulder width, being 17% smaller than Rankine’s coefficient on average. Based on these findings, a modified coefficient of active earth pressure is proposed, as presented in Equation (6). The change of horizontal pressure when the caisson was submerged in the water was also investigated in this study. The results showed that the proposed formula in Equation (6) predicted well the measured horizontal pressure if the buoyancy effect due to the water depth was properly considered.

According to a review paper on the angle of repose of granular materials [17], geometrical properties, size of particles, and friction coefficient can affect the values of the angle of repose. Hence, under conditions other than the properties of the rubbles stones shown in Table 1, the magnitude of the earth pressure may differ from the measurement results in this study. In this respect, it is desirable to verify the applicability of the proposed formula through additional experiments with different rubble stone properties.

Although not dealt with in the present study, it is expected that the earth pressure exerted by rubble stones on the caisson can be completely lost instantaneously when the wave crest in front of the caisson is extremely high, so as to cause possible sliding of the caisson. This phenomenon should be considered when designing horizontally composite breakwaters. In this respect, further investigation is required for the appropriate evaluation of the total horizontal loading caused by waves as well as by the rubble stones on the caisson, by taking such phenomenon into consideration.