Relative Energy Variation Characteristics Considering Interaction between Waves and Vegetation Structure

Abstract

Although viscous sediment environments along the coast strongly attenuate waves, the attenuation dynamics and physical mechanism governing the attenuation process remain relatively unknown. Extremely complex interactions between muddy seabed have become increasingly important for wave evolution studies pertaining to coastal areas. The coastal protection function of mangroves was confirmed during the 2004 South Asian tsunami. Nevertheless, most research has been limited to macro-qualitative analyses, including those on variations in the transmission coefficient K_t and reflection coefficient K_r, and subsequent comparisons. However, determining the micro-physical characteristics is challenging, similar to coastal vegetation analyses with respect to mangrove vegetation characteristics. This study aims to quantify the attenuation difference in the wave energy owing to the coastal vegetation structure, under different layout conditions and combinations. Particle image velocimetry (PIV) technology is used to explore the variations in the velocity field and velocity distribution during the interaction process and calculate the wave-induced kinetic energy before and after setting up the vegetation structure. The research results emphasize that the resistance and frictional effects generated by vegetation are inversely proportional to the size of the stem, and the variation of kinetic energy determined from the velocity distribution and the thickness of the vegetation stem is mainly due to the larger frictional resistance of dense vegetation, relative to the fast flow velocity above the vegetation. Different vegetation heights slightly affect the short-period waves; however, the impact on energy reduction was smaller. For long-period waves, vegetation height significantly reduces wave kinetic energy.

1. Introduction

Owing to the global warming phenomenon, sea levels around the world have risen [1]. According to [2], traditional coastal protection facilities in coastal areas have experienced increased storm intensities and increased frequencies of coastal disasters. Moreover, due to the rising sea levels, coastlines have shrunk inward. Changes in coastal dynamic conditions, such as changes in breaking wave conditions, movement of the breaking zone, and increases in the amount of bleaching sand, have been observed, which cause the shoreline to shrink inward and render the embankment relatively insufficient. Therefore, many studies have demonstrated that the energy dissipation efficiency of vegetated coastal protection facilities may not be as effective as that of various wave-absorbing breakwaters and wave-absorbing blocks. Moreover, the protection forming process is not as fast as that of rigid facilities, which was thoroughly studied in the past. However, academic study results have rarely been implemented in practical applications. The results obtained by [3] suggest that the average wave damping of breakwaters was approximately between 10% and 50%, which was proportional to the significant wave height in all simulated scenarios. The shear stress and sediment volume of the simulation results increased by 20% to 40% on average in the initial segment of the swamp area located behind the breakwater, which was proportional to the breakwater slope and its distance from the shoreline. Breakwaters are believed to help protect shorelines from wave energy; however, they may hinder sediment transport. As mentioned above, with the changes in coastal topography and recently recorded rise in sea level, such vegetation-type energy dissipation protection method has increasingly received attention. Numerous studies have been conducted to explore the properties of various rigid and flexible vegetation and wave energy dissipation ability of different vegetation structures to defend against waves. In addition to using numerical methods and on-site observations to conduct related research, numerous water tank tests were conducted to analyze the reflectivity, transmittance and energy attenuation rate. The energy attenuation rate is related to the characteristics of the energy dissipation coefficient. Thus far, many studies have used the so-called resistance or damping coefficient C_D (drag coefficient) in simulations and numerical analyses, and cited related studies on damping force and energy dissipation characteristics.

Many related studies on field observations, such as that by [4] have conducted hydraulic model experiments in large water tanks to evaluate the effects of Posidonia Oceania meadows on wave height damping and wave velocity. The parameter h/λ, which affects the wave attenuation when the wave is transmitted from the open sea to the shallow water areas, was tested with irregular waves, yielding results between 0.09 and 0.29. In addition, the wave field velocity distributions demonstrated that there was significant energy attenuation inland from the grassland and directly above the grooved bed. In contrast, in the vegetation near the edge of the grassland, energy was transferred between short waves, yielding a more evident energy attenuation mainly at longer wavelengths. Coastal conservation programs have recently increased due to the incorporation of nature-based solutions and ecosystem services. Although most previously published experiments are based on wave trough experiments using vegetation simulations, [5] provide useful guidance based on experience gained from a unique set of experiments in large wave basins, including the interaction of waves and currents with real salt marsh vegetation. They also assess the influence of different flow and vegetation parameters on the wave attenuation provided by two contrasting salt marsh species [6].

The energy dissipation characteristics of the vegetation structure were discussed using numerical and experimental verification by [7], which were conducted to evaluate the attenuation efficiency of irregular waves propagating on simulated vegetation with varying stem heights. Two vegetation types were considered in the experiments: one with uniform stem height and another with different stem heights. The height, under the condition of constant total projected area in the vertical direction, exhibited an approximately linear distribution in the vertical direction with different stem densities simultaneously. Ref. [8] compared vegetation field and laboratory research results on wave attenuation and conducted a systematic review measuring irregular energy spectra to study energy dissipation due to vegetation. They noted that wave attenuation appears to mostly depend on stem density and stem length to water depth ratio, with wave concentration decreasing slightly with wave height. The ideal vegetation bed can effectively attenuate the wave energies of unimodal and bimodal irregular wave spectra. Ref. [9] utilized both numerical and experimental methods to study the interactions among solitary waves passing through rigid vegetation. They conducted relevant experiments in a wave tank, where vegetation models of different lengths and porosities were set up. Moreover, they used the Boussinesq equation to numerically simulate vegetation with a quadratic resistance model.

In addition, the resistance and friction coefficient have been used to conduct relevant experimental research, such as research on vegetation convection and energy dissipation of waves. The roughness coefficient of channel hydraulics (such as the Manning roughness coefficient n) was introduced into the vegetation dissipation research by [10]; however, part of their research on wave energy attenuation is only based on the attenuation of water surface wave height while transitioning to the vegetation elimination area, that is, the attenuation variations with respect to the wave height. When assessing and analyzing the attenuation characteristics, it is not clear what type of motion mainly causes the velocity variations generated by the damping owing to the water molecule motion. Therefore, further research is required. The flow velocity cannot be measured; therefore, the average flow velocity of the seepage can only be calculated based on the pressure change measured by the pressure gauge. The velocity change between individual plants in the vegetation area and resistance acting on the vegetation have a significant correlation. However, few related studies focus on the interaction between water flow, wave fluctuation, and vegetation when passing through the vegetation area, and the effect of the wave flow field on the seepage velocity between vegetation. Studies using various roughness size factors to explore the wave or current resistance coefficients are more extensive, and they consider roughness coefficients such as the aforementioned Manning roughness coefficient n, as well as others, such as Chezy coefficient and Strickkler formula. Related research results can also be found based on the Nikuradse formula, Haaland formula, Ramette formula and Reynolds number. For example, [7] compared the research results obtained based on SWAN, RANS and NHWAVE with the results obtained by their laboratory hydraulic model using three different numerical models. The vegetation considered in the experiment was non-uniform, that is, the individual plant heights were different. SWAN and RANS models were utilized for estimating wave attenuation with non-uniform aboveground biomass. Using NHWAVE, a series of studies and discussions [11,12,13] were conducted on the vertical distribution changes owing to turbulent kinetic energy, eddy viscosity and energy attenuation dissipation rate caused by vegetation.

It remains unclear why the shape of the incident flow and the density, diameter and height of the plant stem approximate the hydrodynamic resistance. Ref. [14] studied the plant–flow interaction using numerical models and laboratory flume experiments, which could provide a more realistic expression of different vegetative characteristics. Leveraging various method with information on biophysical properties, a method was proposed to study the plant–flow interactions with more realistic plant representations through numerical models and laboratory sinks. Ref. [15] conducted several experimental studies in a laboratory wave tank using artificial vegetation with different flexibilities and measured the wave attenuation when the waves were affected by different rigid and flexible vegetation during the transmission process. To assess the change of water molecules velocities, an experimental process utilizing particle image velocimetry (PIV) was used to measure the temporal and spatial variations in the water particle velocities over the vertical section around vegetation. Ref. [10] proposed an engineering method to quantify the impact of common coastal wetlands on wave fields using existing wave models. They studied wave attenuation via laboratory experiments based on the modified Boussinesq equation. The numerical Cornell University long-wave and intermediate-wave model [16] derived empirical equations to estimate the most common near vegetation in marshes at different stem spacings under certain wave conditions and plant stem densities. The friction coefficient was determined under wave action caused by density and wave attenuation caused by wetland vegetation.

Ref. [17] presents a new model for waves and submerged vegetation that couples the flow motion with plant deformation (including the presence of a vegetation field) through drag force, and validated their model with small and large-scale experiments. Refs [18,19] investigated the wave dissipation caused by vegetation under a flow field because the wave dissipation of the plant canopy is closely related to the vegetation drag coefficient; they concluded that the flow field may increase or decrease wave attenuation. Ref. [20] proposed an empirical relationship between drag coefficient and Reynolds number and applied a novel method to obtain the vegetation drag coefficient based on the current–wave current combination. Ref. [21] conducted damping tests in a 310 × 5 × 7 m water tank to evaluate the water–vegetation interaction with respect to individual vegetation parameters. Accordingly, they concluded that artificial vegetation can be used to manipulate the overall stiffness and substantial occupied volume relative to the amount of vegetation. The experimental results under different arrangements demonstrated that the damping force is introduced from the dynamic frontal region owing to the phenomenon caused by bending (depending on stiffness and flexibility), which is more complex and difficult to evaluate in hydrodynamics; therefore, it needs to be determined by the frontal region. The frontal region controls the force–velocity relationship only at low orbital flow velocities, assuming that no bending occurs under these conditions.

In the offshore area, waves are transmitted from the outer sea to the coast, and after shallowing, they form waves with relatively longer wavelengths (L/H). According to the results of many experiments, whether flexible or rigid water vegetation is effective for long waves and which layout demonstrates energy dissipation benefits can be assessed. However, this approach is less effective for short waves, which affect the energy dissipation effect due to vegetation. The basic influencing factors are the density of vegetation configuration, water-free depth of the planting stem d (extremely short-valued d < ¼ h), dwarf vegetation (d < ½ h), medium vegetation (¼ h < d < ½ h), high stem vegetation (d > h, i.e., above the water surface), rigid or flexible vegetation, etc. Vegetation used in many hydraulic model tests include natural plants and artificial plastics (PVC), some of which have been neatly arranged or some chaotically arranged. Currently, it is difficult to select a specific damping coefficient under regular or irregular arrangements.

Although many studies on coastal vegetation have been published, in addition to numerical model simulation studies, many in situ observational studies and laboratory physical models have been proposed as well. The wave energy dissipation effect due to vegetation has more than 30 years of research history based on hydraulic models, most of which focus on the effects of the vegetation damping force on wave attenuation. Vegetation is considered a water-inducing coastal facility structure; therefore, many numerical studies consider vegetation as a rigid permeable structure. In the hydraulic model tests, different vegetation structures (such as natural plants, artificial leather and artificial imaginary plants) have been used to explore the effects of these vegetation structures on waves with different wave (regular, irregular, long, short, solitary waves, etc.) and attenuation characteristics (wave energy). For instance, [22] experimentally present a 1:6 scale fringe Rhizophora mangrove forest investigation, with a 26 m long forest composed of 135 mature Rhizophora mangrove trees, and with 24 prop roots, to better understand and parameterize the physical processes involved in flow–mangrove interaction, wave attenuation and drag forces.

Recently, owing to the extensive developments in PIV technology and popularization of high-speed digital cameras, many experts and scholars have started to focus their research efforts on the characteristics and variations of the flow field caused by the interaction between waves and vegetation, as well as the movement of water molecules between plant stems. Flowing water exerts resistance on vegetation. The sensitivity of vegetation to bending and fracture determines its resistance to flow and chance of survival under hydrodynamic loading. The energy loss in a vegetation field is assumed to be caused by drag. However, the general wave attenuation and vegetation scenarios are not known; thus, a “unit vegetation block” must be set up in the field or in hydraulic laboratory experiment models to quantify the energy reduction due to different vegetation structures. This study is inspired by such previous efforts. Ref. [23] proposed a technique that combined fluid dynamics, digital image processing and computer graphics to simulate a water–wave visualization simulation. The image texture analysis feedback principle was used to simulate and visualize water surface fluctuations. Subsequently, water wave images were cut from the animation to establish a simulated water wave image dataset. Ref. [24] used super-resolution PIV to analyze the waveform change characteristics of solitary waves propagating in a single downstream flow field and flow field with reverse flow. They managed to observe the velocity field changes in the wave transmission process and water molecular trajectories. Ref. [25] used PIV to investigate the energy changes in solitary waves passing through eddy currents under different submerged structures. In this study, during each testing stage, PIV was used to measure the flow and velocity fields under the various empty water tank arrangements and vegetation structures to determine the kinetic energy variations.

Regarding the practical PIV applications to the wave flow field considered in this study, owing to the recent improvements in imaging technology, many technologies that required relatively expensive precision instruments have been adopted relatively easily. Million-pixel cameras, such as 4K cameras, can be easily purchased. Moreover, many cameras on the market have 960 fps capabilities, and can be used with a variety of different visualization technologies to measure related physical properties or conduct theoretical research. In terms of microscopic research [26], conducted laboratory experiments with a glass-bottomed and glass-walled 14 × 0.25 × 0.50 m wave tank using a high-speed camera to investigate effects of an extremely steep beach. The velocity field evolution and vortex structure during solitary wave failure were assessed. A flow visualization technique was used for flow field observations.

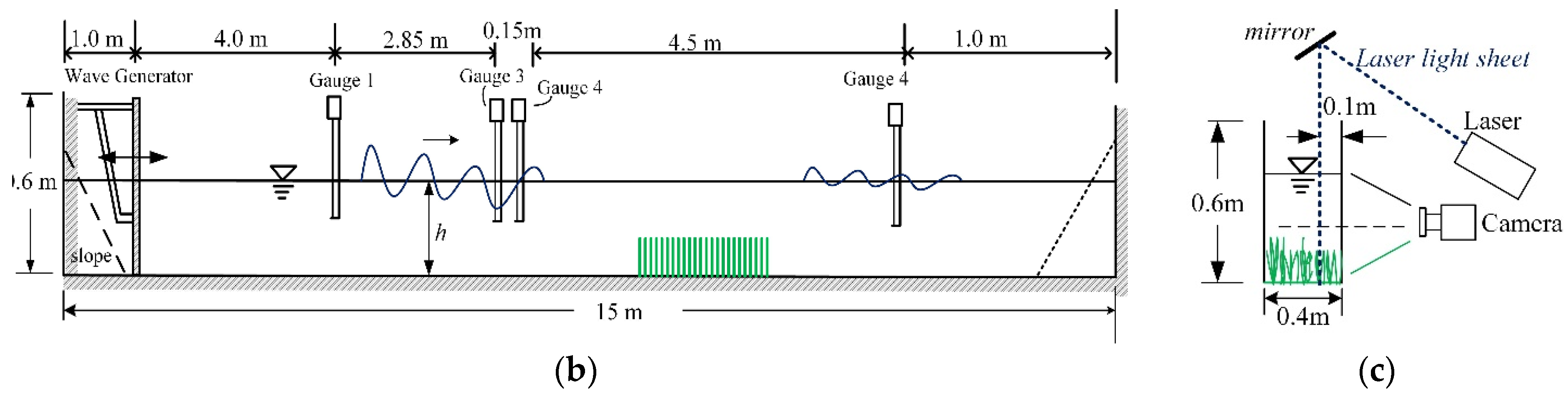
2. Experimental Set-Up and Instrumentation

As shown in Figure 1 and Figure 2, the physical model tests were conducted in a 15 × 0.4 × 0.6 m visualization wave flume made of stainless steel, with glass sidewalls for observation and visualization. The vegetation structure was fabricated using 10-mm thick transparent resin base and bamboo sticks with various diameters. The modelling water depth h was maintained at 0.15 m, and the flume was equipped with a piston-type wave generator at one end and an adjustable absorbing slope at the other. The variations in water elevation were measured using four capacitance wave gauges coupled with an adapter linked to a computer. Gauge 1 obtained incident wave height measurements, and readings from gauges 2 and 3 were used to estimate wave reflections. Gauge 4 was used to measure the water elevation variations within the chamber cause by wave transmissions.

The laser output power can reach up to 1000 mW; simple specifications are as follows: laser wave length = 532 nm, spectral linewidth < 0.1 nm and the beam diameter at aperture 5 mm, a light sheet thickness on the order of 1 mm. This laser light is in the form of a continuous light sheet. The tracer particles are hollow glass microspheres, the main component is borosilicate, the density is about 0.06–0.08 (g/cm³), and the particle size is about 100–180 μm. In order to avoid the distortion and deformation of the image during shooting, and to avoid the influence of the boundary effect of the glass surface, the laser irradiation surface (light sheet) is fixed at a position about 10 cm away from the glass. The PIVLab analysis program we adopted was released by Thielicke [27]. Accordingly, the most sensitive part of the analysis may be the cross-correlation algorithm, which is the optimization of the DPIV technique in this program, and in PIVLab, each interrogation area overlaps with one another by, for example, 50%, to calculate displacement information at every pixel via bilinear interpolation. The average number of particles on the final interrogation window depends on the interrogation area (px) setting and step (px), which in this paper were set as 32 and 16, respectively, and correlation quality set as extreme. The vegetation model was made of bamboo sticks representing the aerial roots of the mangroves (Figure 3). The lengths of the bamboo sticks were 10 and 5 cm with diameters of 0.5 cm, 0.4 cm, 0.3 cm and 0.2 cm. The bamboo sticks were fixed into a 20 cm × 8 cm × 1 cm (thickness) silicone plate; accordingly, their heights above the silicone plate were 9 cm and 4 cm, respectively. Each model was arranged as an 8 × 17 bamboo stick array along the vertical and horizontal axis with a total of 136 bamboo sticks. Finally, the experimental vegetation area was constructed using five silica gel plate with bamboo sticks, whose size was approximately 40 cm × 20 cm. The high-speed digital camera (Sony RX100 VI) used in this experiment has a built-in high frame rate (HFR) mode, ISO sensitivity was set to 5000 with auto focus, frame rate was set to 960 fps, recording quality was set to 25 p 50 M (25 frames/s; bit rate: 50 Mbps), and shooting was initiated as the start was triggered. The Image quality prerequisites for sensor read effective pixels under 480 fps is 1824 × 616. In addition, we compared the transmission coefficient variation due to waves passing through multiple sets of vegetation at once, which may have reduced the wave transmittance compared with that of a single set of vegetation scenario. The vegetation model sets were composed of bamboo sticks with a diameter of ϕ = 0.5 cm, and heights of d₁ = 10 cm and d₂ = 5 cm. The distance between each group of vegetation sets was 0, 10, 20, 30, and 40.

The relevant physical characteristic for the considered wave conditions are listed in

Table 1. Relevant physical characteristic for the considered wave conditions (incident wave height H_i = 3 cm, water depth h = 0.15 m).

Wave Period, T (s)	Wave Length, L (m)	Wave Number, k (1/m)	h/L
Transitional water wave (0.05 < h/L < 0.5)
0.50	0.384	16.354	0.390
0.56	0.471	13.326	0.318
0.63	0.574	10.941	0.261
0.71	0.690	9.105	0.217
0.83	0.859	7.314	0.174
1.00	1.090	5.765	0.138
1.11	1.235	5.086	0.121
1.25	1.417	4.433	0.106
1.43	1.648	3.812	0.091
1.67	1.951	3.220	0.077
2.00	2.364	2.658	0.063
Shallow water wave (h/L < 0.05)

, which gives the relevant physical characteristics for these conditions, relative water depth h/L (L is the wave length) varying from 0.390 to 0.063, and wave number k obtained from dispersion relation. The incident wave height H_i = 3 cm, and constant water depth h = 0.15 m.

3. Results

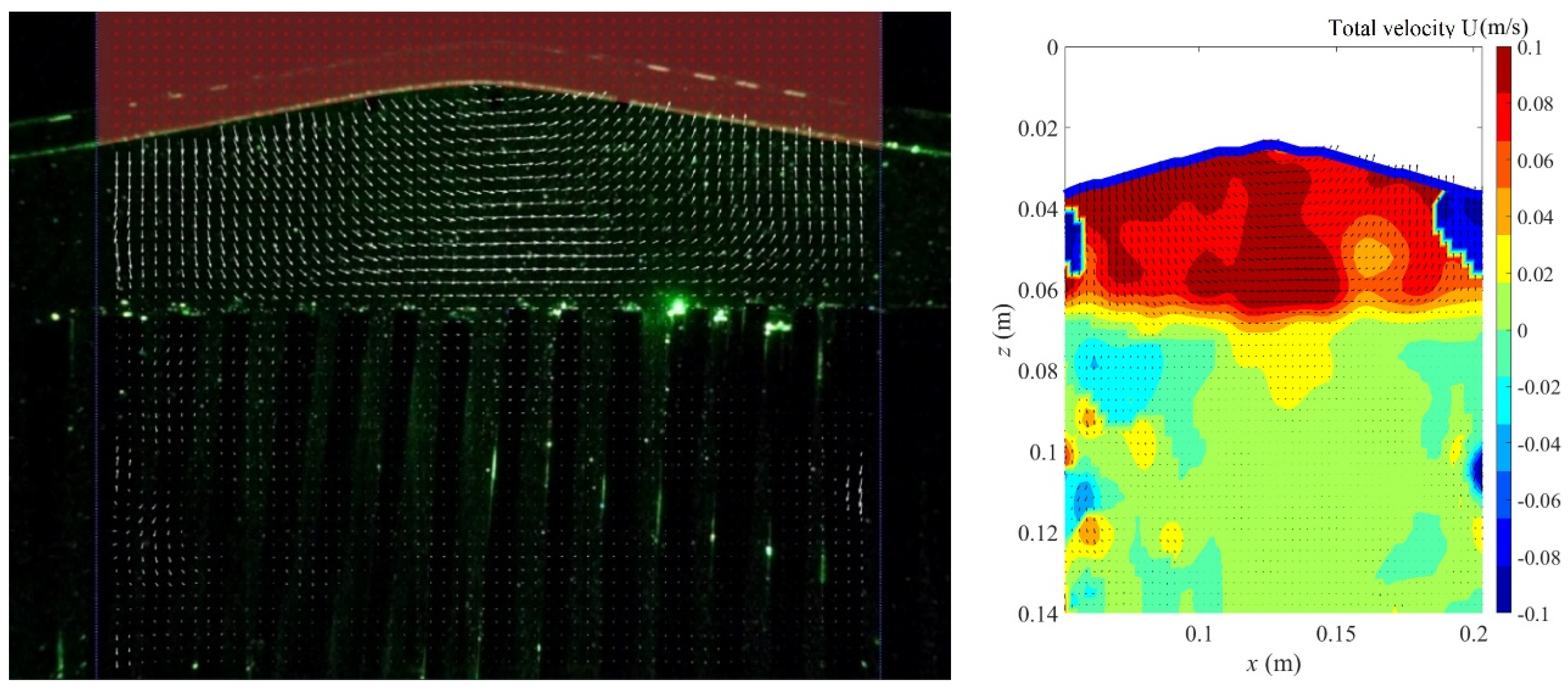
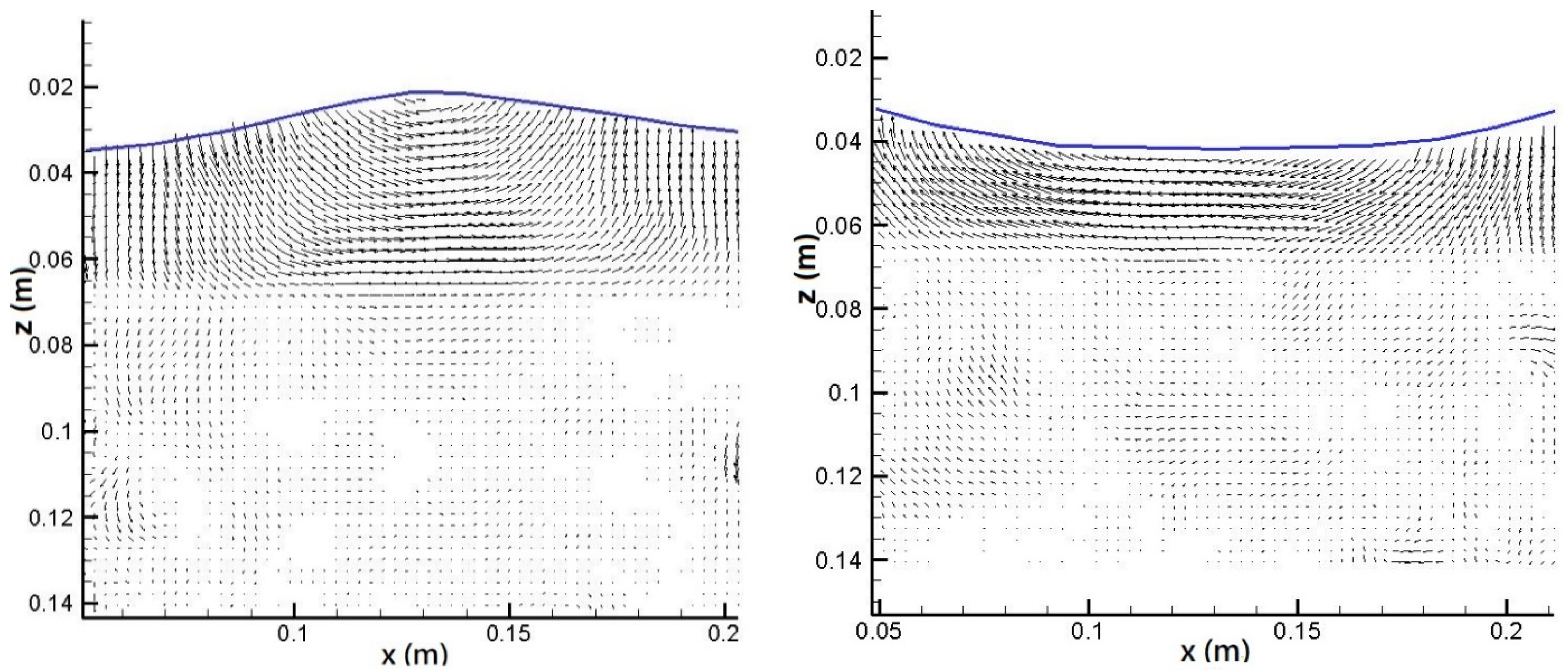
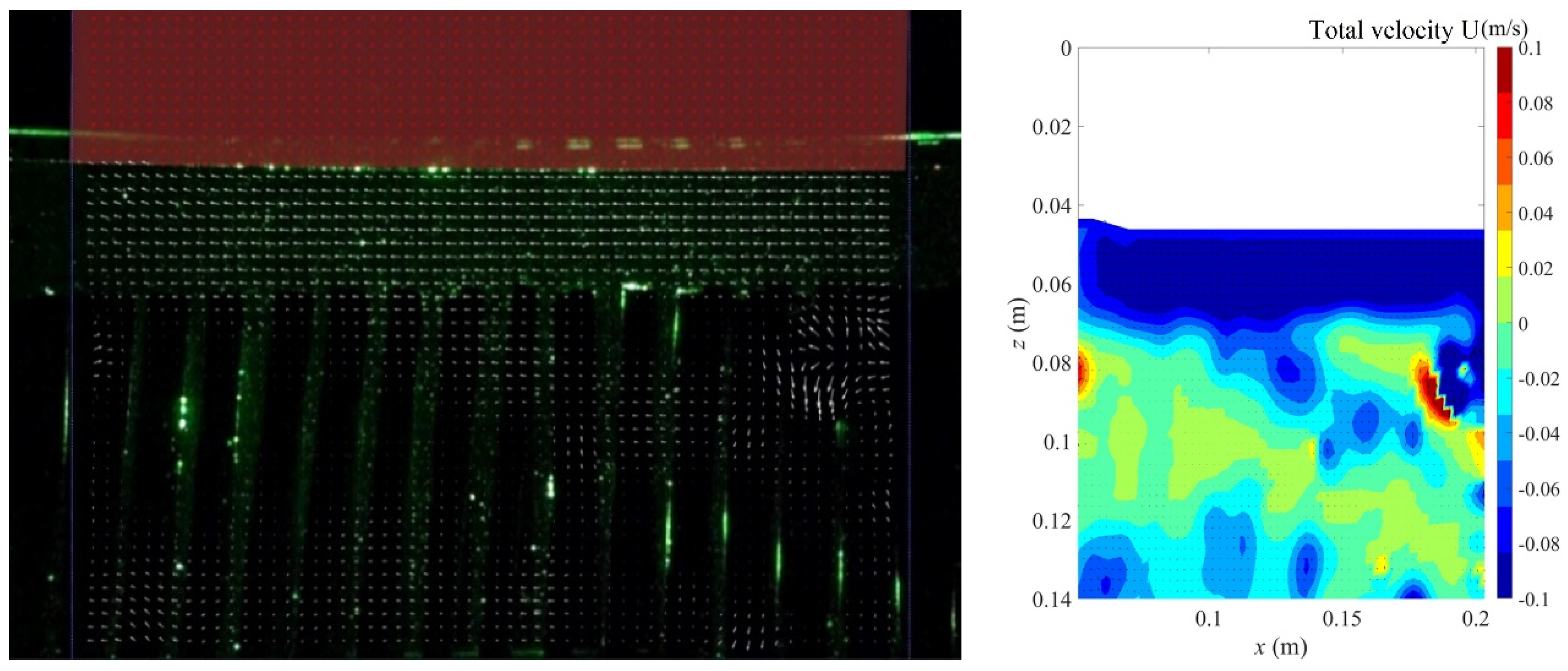
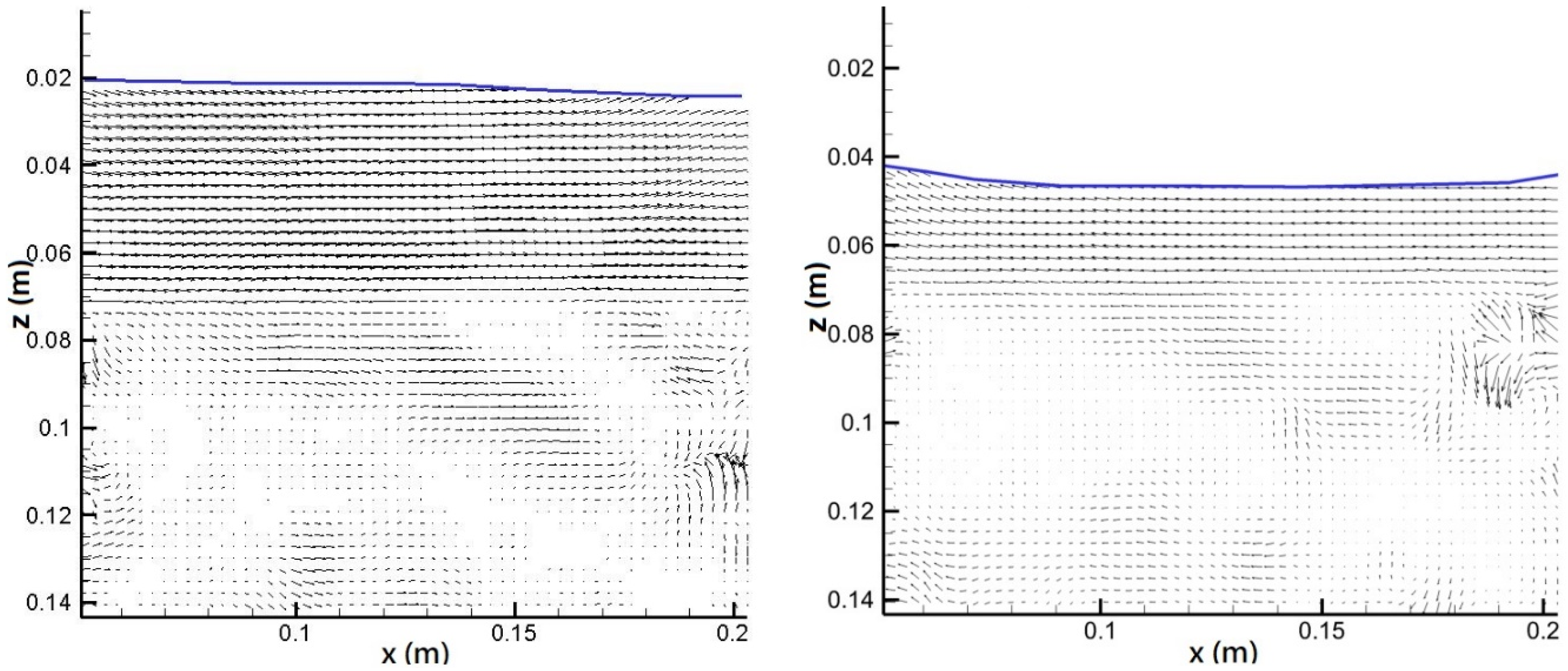
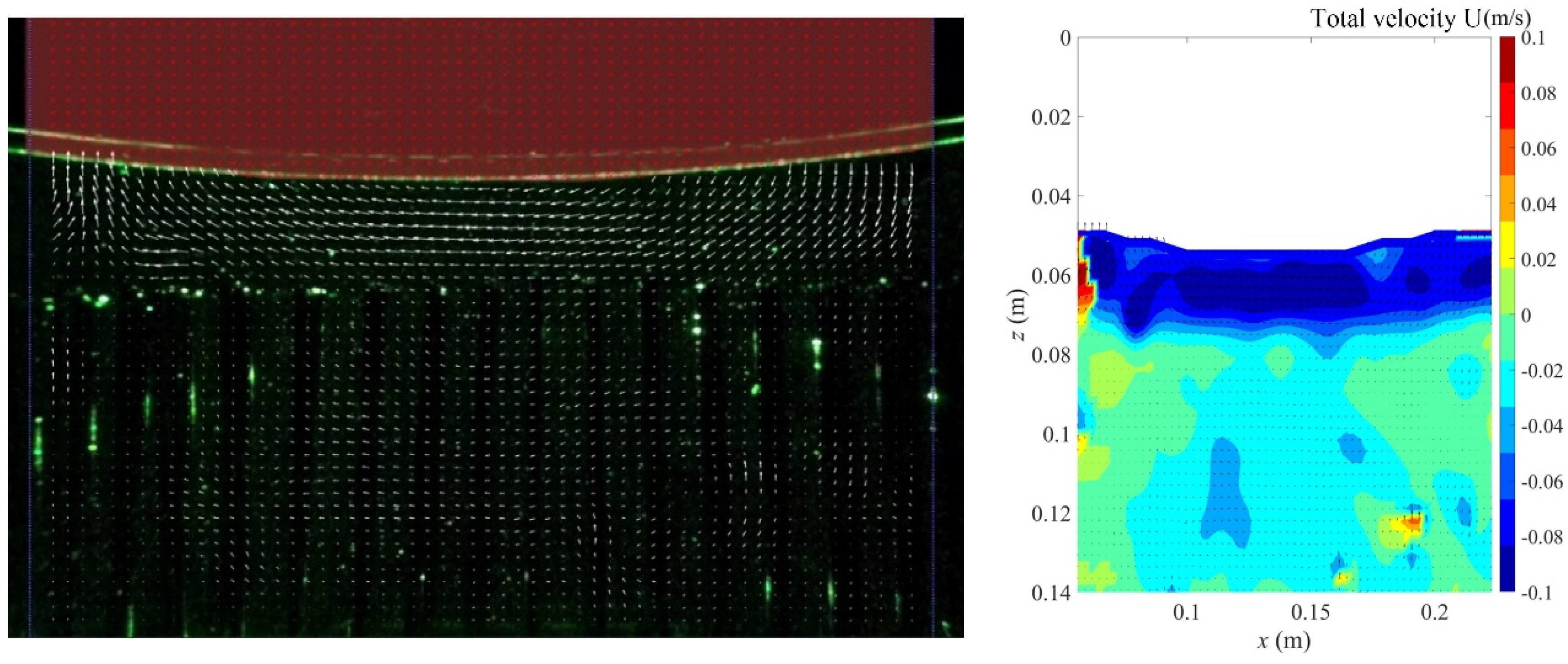
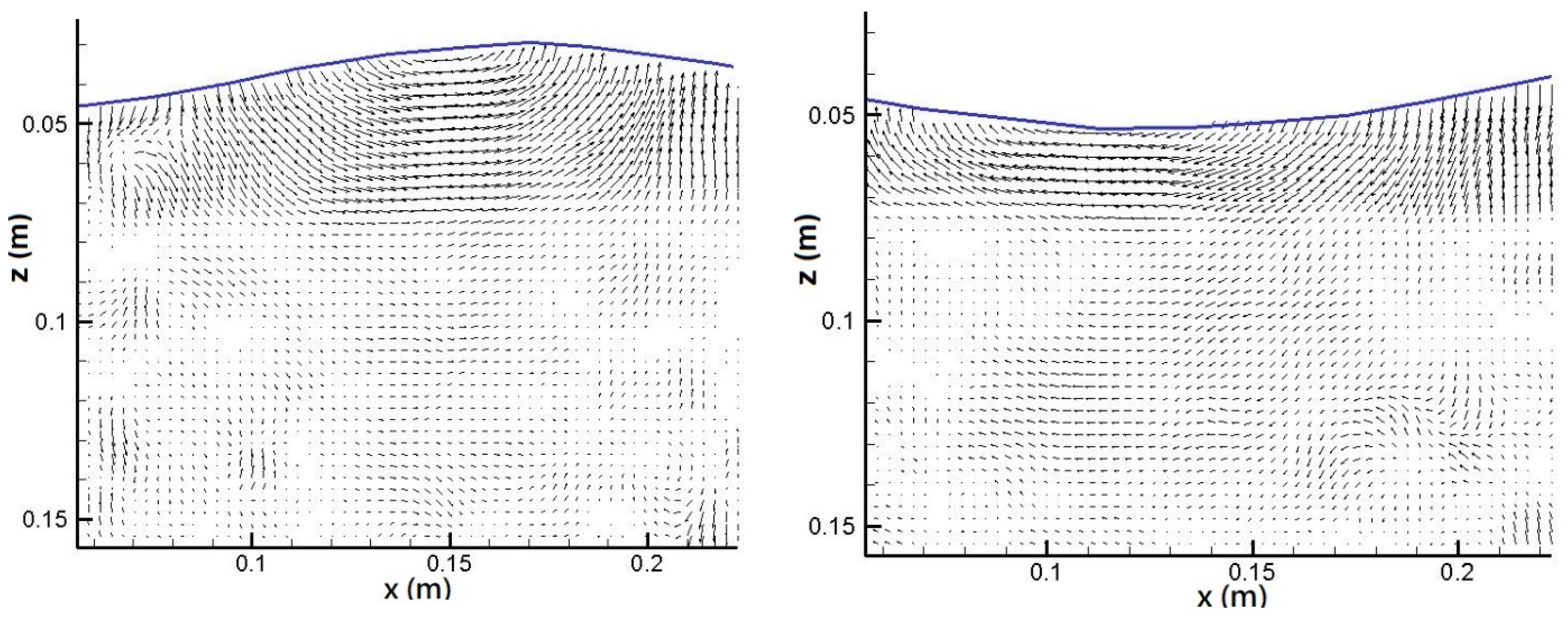
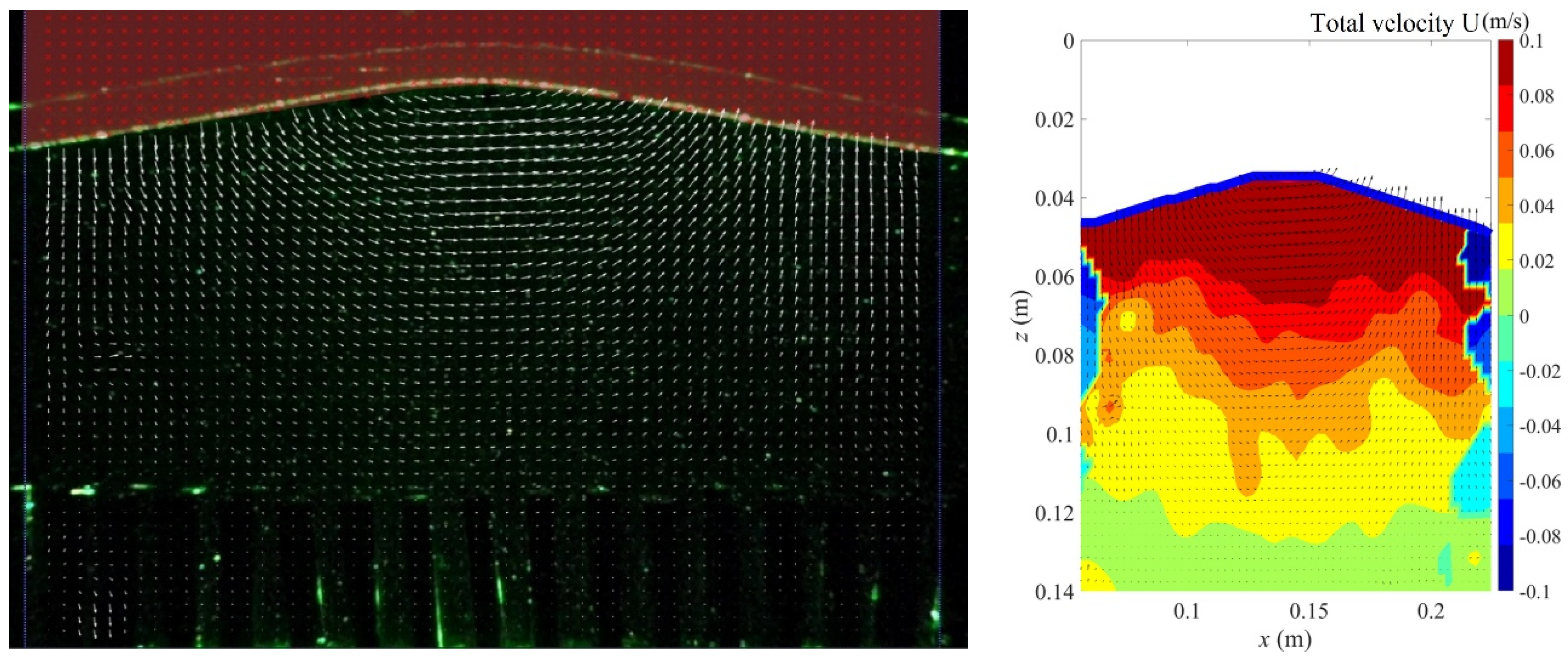
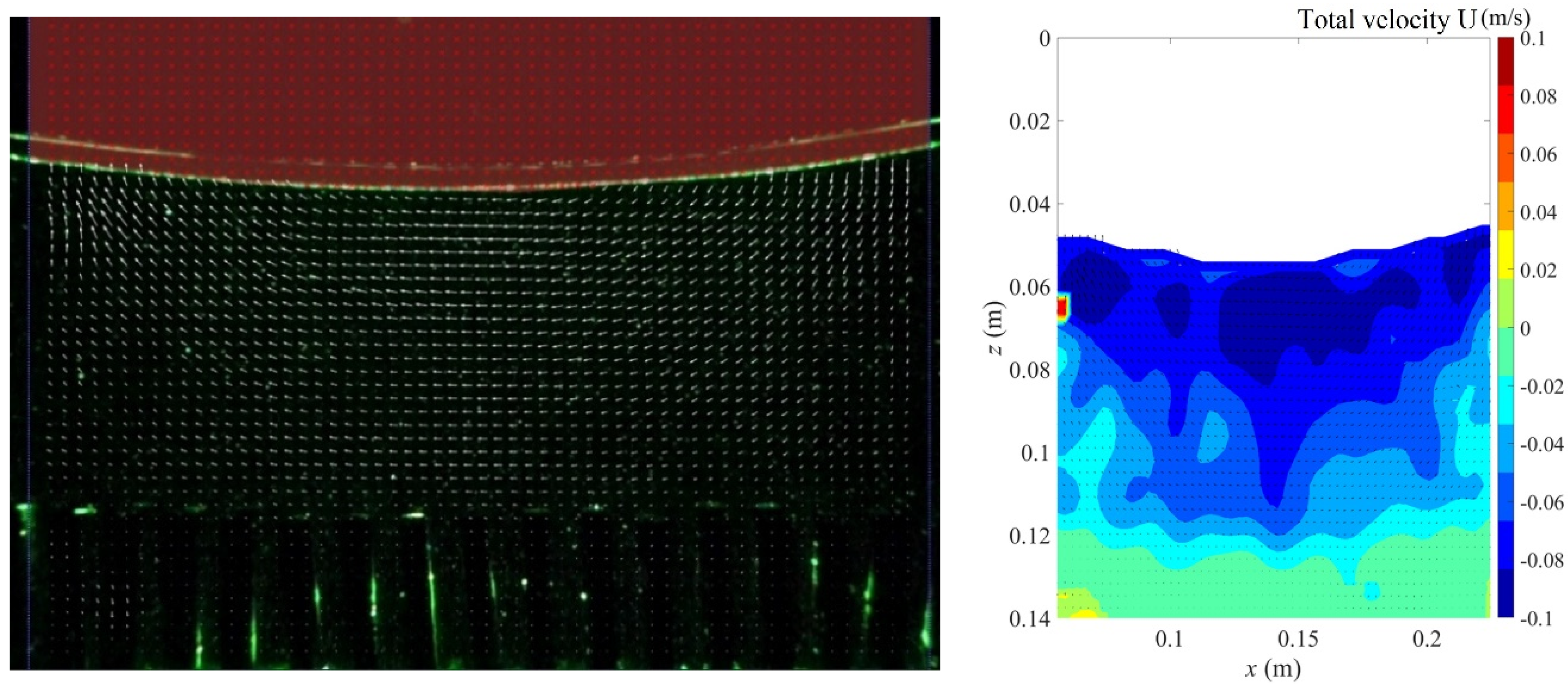
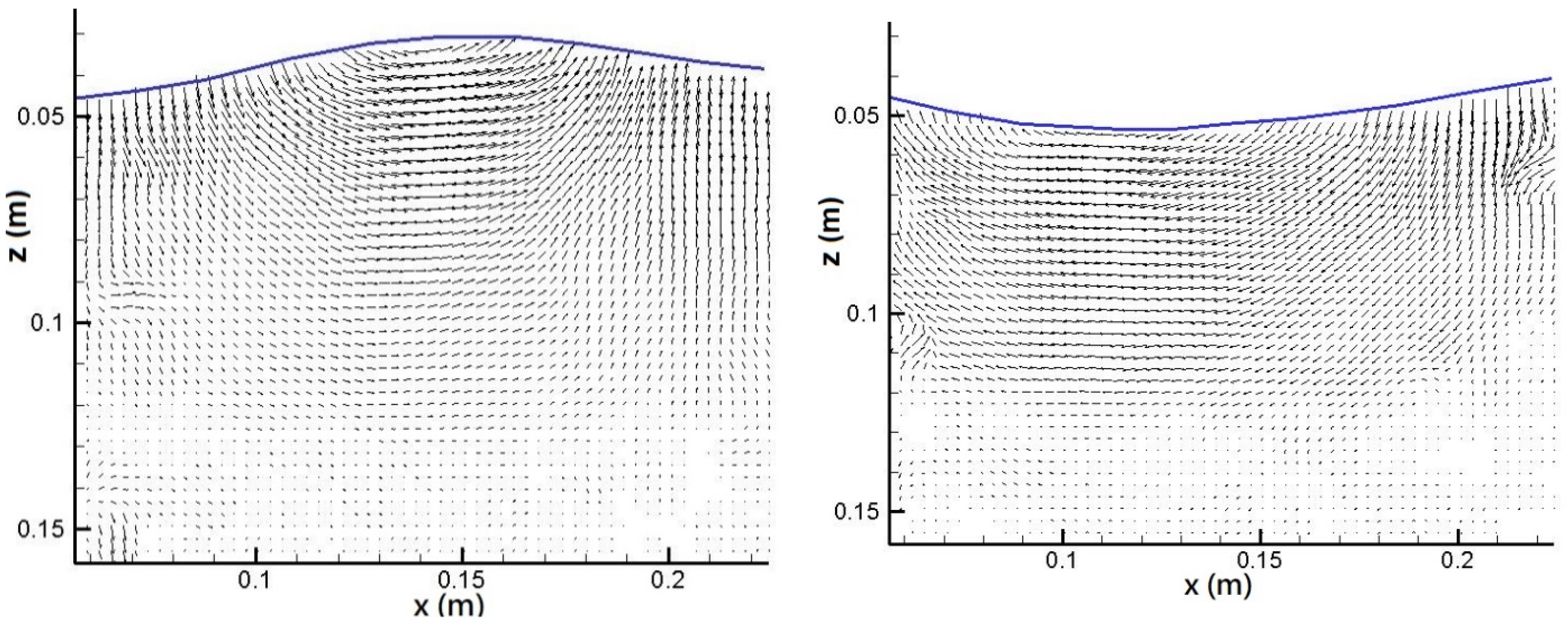
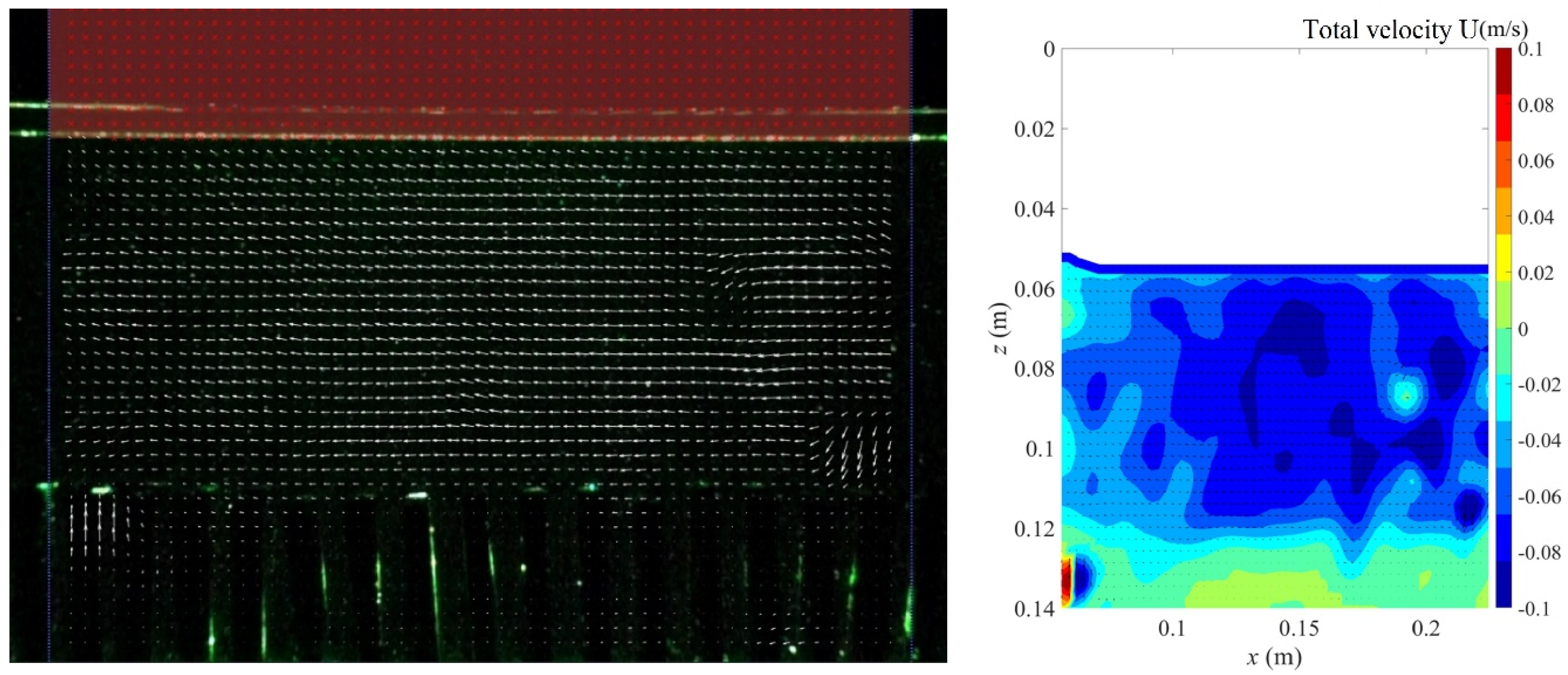
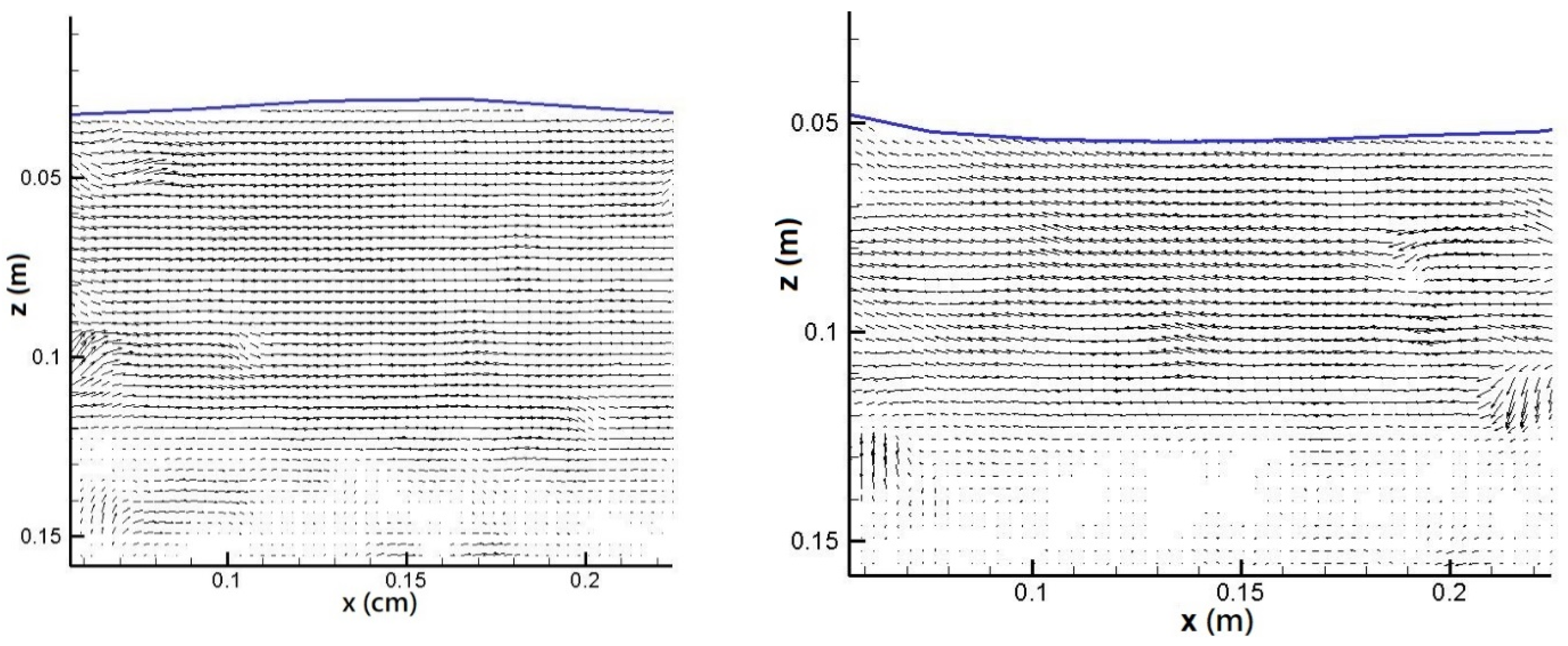
3.1. Instantaneous Velocity Field Distribution and Intensity Variation

Figure 4 shows the instantaneous velocity field distribution and variation in the vegetation structure intensity with a diameter of ϕ = 5 mm when the wave crest propagated under a wave condition of T = 0.5 s. The color depth represents the intensity distribution range, according to the motion of water particles in wave motion and to facilitate observation, for instance, red color represents the positive direction (positive x-axis direction), blue color represents the negative direction (negative x-axis direction), and the length of the arrow represents the magnitude of the total velocity. Part of the vegetation areas and the surrounding areas that are not analyzed are manually masked. In the vegetation area below, the velocity field distribution was due to the variations in the vegetation structure. Because of the shadowing effect, the measurable velocity distribution can only be evaluated based on the instantaneous velocity of the tracer particles moving through the slits between the impervious vegetation. However, the error value may be rather large; accordingly, only two-dimensional observations can be made. Therefore, the velocity field and kinetic energy variations in this part can only be used as a reference for comparing the differences among varied vegetation arrangements. To obtain more accurate assessments, the variations and differences in kinetic energy were estimated from the velocity field (movement velocity of water molecules) in the area between the top of the vegetation and water surface.

Figure 5 shows the results when the wave trough propagates over the vegetation structure under the same conditions. The velocity distribution figures demonstrated that in the vegetation area, although it is difficult to accurately measure the exact three-dimensional motion and resulting velocity field between the bamboo sticks, a partial flow field distribution could be measured. The wave field velocity was significantly affected by the vegetation structure and decreased. In this section, we focus on comparing the amplitude (scale) and characteristics of the velocity field reduction under different vegetation arrangements, rather than accurately calculating the energy at the inner vegetation region. In the past, visualization techniques to quantify the data obtained experimentally to explain the energy decay phenomena were not available.

Figure 6 shows the instantaneous velocity field recorded in the analysis area when the wave crest and trough arrived. Display vector parameters were driven by built-in smooth data function of PIVLab. The energy dissipation area formed by the vegetation was similar to that of the permeable submerged embankment; however, the so-called drag damping effect (phenomenon) occurred between the bamboo sticks. Hence, the results should vary from those of the permeable embankment.

In this study, the wave period was gradually increased from T = 0.5 s to T = 2.0 s, whereas the relative wavelength was extended from L = 0.385 m to L = 2.365 m, which was characterized by the vegetation length range (w = 20 cm) that varied from approximately w/L = 0.52 to 0.085. Figure 7, Figure 8 and Figure 9 show the results obtained with a wave period T = 2.0 s and velocity field distribution in the vegetation area when the wave crest and trough pass through. Compared with the results demonstrated in Figure 4, Figure 5 and Figure 6 when T = 0.5 s, the most evident discrepancy is that the inner vegetation area exhibits a relatively visible velocity field.

The characteristics of shallow water waves become substantially more pronounced with the increase in the wave period (wavelength). Thus, the inner vegetation area at the lower water level is affected by larger waves and currents, even if it is obstructed by vegetation structures. The velocity field can still be measured, which exhibits a wide variation range.

Under the same wave conditions, the bamboo stick vegetation model diameter was varied from ϕ = 5 mm to 4, 3 and 2 mm for subsequent experiments. When vegetation shading conditions remained constant, the flow field of the wave passing through the vegetation area varied owing to the diameter change. Figure 10, Figure 11 and Figure 12 show the analysis results with a constant height of ϕ = 2 mm and period of T = 0.5 s, which is the same as that used to plot Figure 4, Figure 5 and Figure 6 with a pipe diameter of 5 mm. Comparing the results, the velocity distribution with ϕ = 2 mm was mostly in the range of 0.08 m/s to 0.10 m/s, whereas it ranges between 0.06–0.08 m/s and 0.08–0.10 m/s when the pipe diameter was 5 mm. Comparing the results depicted in Figure 4 and Figure 10, when the pipe diameter was ϕ = 2 mm and the wave trough passed through, the reverse velocity was significantly larger than that measured when the pipe diameter was ϕ = 5 mm. However, the reverse velocity distribution on the vegetation was smaller than that measured when the pipe diameter was ϕ = 5 mm, indicating that the water flow was equal to that measured when the pipe diameter was 5 mm. At ϕ = 5 mm, the velocity above the vegetation area was relatively large because of the vegetation blockage; however, the velocity in the inner area remained relatively small. With pipe diameter ϕ = 2 mm and high water permeability, the reverse velocity above the vegetation area was relatively small; however, the relative velocity in the inner region of the vegetation was larger.

Considering the case of short vegetation, whether the long-period wave still had a relatively evident velocity field inside the vegetation area was assessed. The bamboo sticks diameter was gradually reduced from 5 to 4, 3 and 2 mm. The present model scale is assumed to be 1:10 of nature vegetation; this is a plant with a stem of approximately 2–5 cm, which is a reasonable natural stem size range, for instance, according to [28], the diameter of mangrove root approximately ranges from 15 mm (3-year-old tree) to 25 mm (11-year-old tree). Therefore, during the hydraulic model test, whose results are shown in Figure 13, Figure 14 and Figure 15, the vegetation structure dimension was 2 mm in diameter and 5 cm in length.

When the wave period was T = 0.5 s, the water depth–wavelength ratio was h/L = 0.3896, being classified as an intermediate wave with deep-water wave characteristics. The experimental results for a vegetation height of 5 cm demonstrate that the entire flow field was only slightly influenced. When the wavelength was L = 0.385 m, the length of the vegetation area was approximately w/L = 0.52. The kinetic energy was mainly distributed in the upper half, and the lower half was not considerably affected by the vegetation structure; thus, the velocity distribution exhibited a relatively uniform variation. However, when the wave period was increased to T = 2.0 s, with L = 2.365 m, the length of the vegetation area became approximately w/L = 0.085 and the water depth–wavelength ratio became h/L = 0.063. Accordingly, this wave was classified as an intermediate wave with extremely shallow water wave characteristics. Therefore, from Figure 16, Figure 17 and Figure 18, the velocity distribution near the bottom vegetation area rapidly attenuated from 0.08–0.1 m/s to 0.0–0.04 m/s, which was significantly different from those obtained with period T = 0.5 s.

In addition, compared with the case of vegetation length d = 10 cm (Figure 7, Figure 8 and Figure 9), we found that when the vegetation height was low, the velocity distribution range of the wave crest passing above the vegetation was mostly between 0.08–0.10 m/s. When the wave trough passed through the vegetation area with heights of d₁ = 5 cm and d₂ = 10 cm, the velocity distribution above the vegetation significantly varied. When d = 10 cm, the velocity distribution range was −0.08–−0.1 m/s (with larger values), whereas when d = 5 cm, the velocity range was −0.06–−0.08 m/s. Hence, under the different velocity fields, the damping effect induced by vegetation was also different.

3.2. Effects and Variation Characteristics on Kinetic Energy Induced by Various Vegetation Structures

Under constant vegetation height, d = 10 cm, when the plant stem diameter was 0.2 cm or 0.5 cm, the total energy E_k of one wavelength under different wave–structure interactions was obtained from the cumulative energy result based on the velocity distribution within the vegetation area. The wavelength of the periodic condition was divided into 16 equal parts (time stages), and the velocity field and distribution were obtained using image visualization processing according to the time interval Δt = T/16. Then, the results were analyzed using the formula E = 0.5 mV². The instantaneous kinetic energy in a section was calculated; then the kinetic energies of the 16 sections were summed to obtain the kinetic energy of a period of waves passing through the vegetation area.

The relationship between wave kinetic energy and dimensionless wave-steepness H/gT² is plotted in Figure 19, which represents the kinetic energy variations in waves passing through various vegetation stems under the arrangement of the same vegetation height structure, The figure shows that when the vegetation diameter was ϕ = 0.2 cm, the drag friction effect due to the vegetation was small; hence, the kinetic energy calculated from the velocity distribution was slightly smaller than that calculated with ϕ = 0.5 cm. In other words, when ϕ = 0.5 cm, the flow velocity above the vegetation was relatively fast, which is mainly due to the large friction drag due to the vegetation. Therefore, the overall kinetic energy was slightly larger than that calculated with ϕ = 0.2 cm. When the wavelength gradually changed from short- to long-period waves, the kinetic energy E_k increased from 0.07 N-m to approximately 0.23 N-m. However, the overall energy change trend was consistent.

In addition, from Figure 20, under the same planting conditions, evident differences in the kinetic energy changes induced by the vegetation of different heights can be observed. From the variation of the “best-fit curve”, we determined that with a decrease in H/gT², that is, when the wavelength gradually changed from short- to long- period waves, the kinetic energy E_k increased from 0.10 N-m to approximately 0.22 N-m when d = 10 cm and to 0.34 N-m when d = 5 cm. This is because the vegetation friction drag measured with ϕ = 5 mm was significantly larger than that measure with ϕ = 2 mm. In other words, under the same vegetation friction drag conditions, when ϕ = 5 mm, the total kinetic energy of the long-period wave was significantly affected by the vegetation height. However, the effect of vegetation height on short-period waves was small; hence, the effect on energy reduction was low. For long-period waves, the vegetation height can significantly reduce the kinetic energy and effectively reduce coastal erosion.

4. Discussion

The reflection coefficient varies with the different stems. Vegetation with thicker stems has a better wave-absorbing effect; vegetation with higher height has a smaller transmission coefficient, which can slow down the velocity speed of wave transmission, and shortness allows waves to pass through, resulting in a higher transmission coefficient. Although the loss coefficient varies depending on the height of the submerged plants, the energy dissipation effect of the vegetation with a higher submerged vegetation height is better than that of the vegetation with a lower height. Most of the waves pass through the vegetation, resulting in poor energy dissipation. However, it was found that the loss coefficient with the case of vegetation height d = 10 cm and diameter ϕ = 0.2 cm produces the same results as that of a case with a vegetation height of d = 5 cm and diameter ϕ = 0.2 cm. In the case of the same planting stem, but with different submerged vegetation heights, the higher the height of the submerged vegetation, the smaller the kinetic energy; on the contrary, the smaller the vegetation height, the larger the kinetic energy. The factor is that the smaller the vegetation height, waves pass easily above the vegetation, resulting in a larger wave kinetic energy; on the contrary, the higher the vegetation height, the more waves are blocked with drag force, resulting in a 10 cm vegetation with smaller kinetic energy than a 5 cm vegetation.

5. Conclusions

In this study, PIV technology was used to measure the velocity field distribution and variations of waves passing through a vegetation area to explore the attenuation characteristics and influence of vegetation on wave kinetic energy. The research results underline the following:

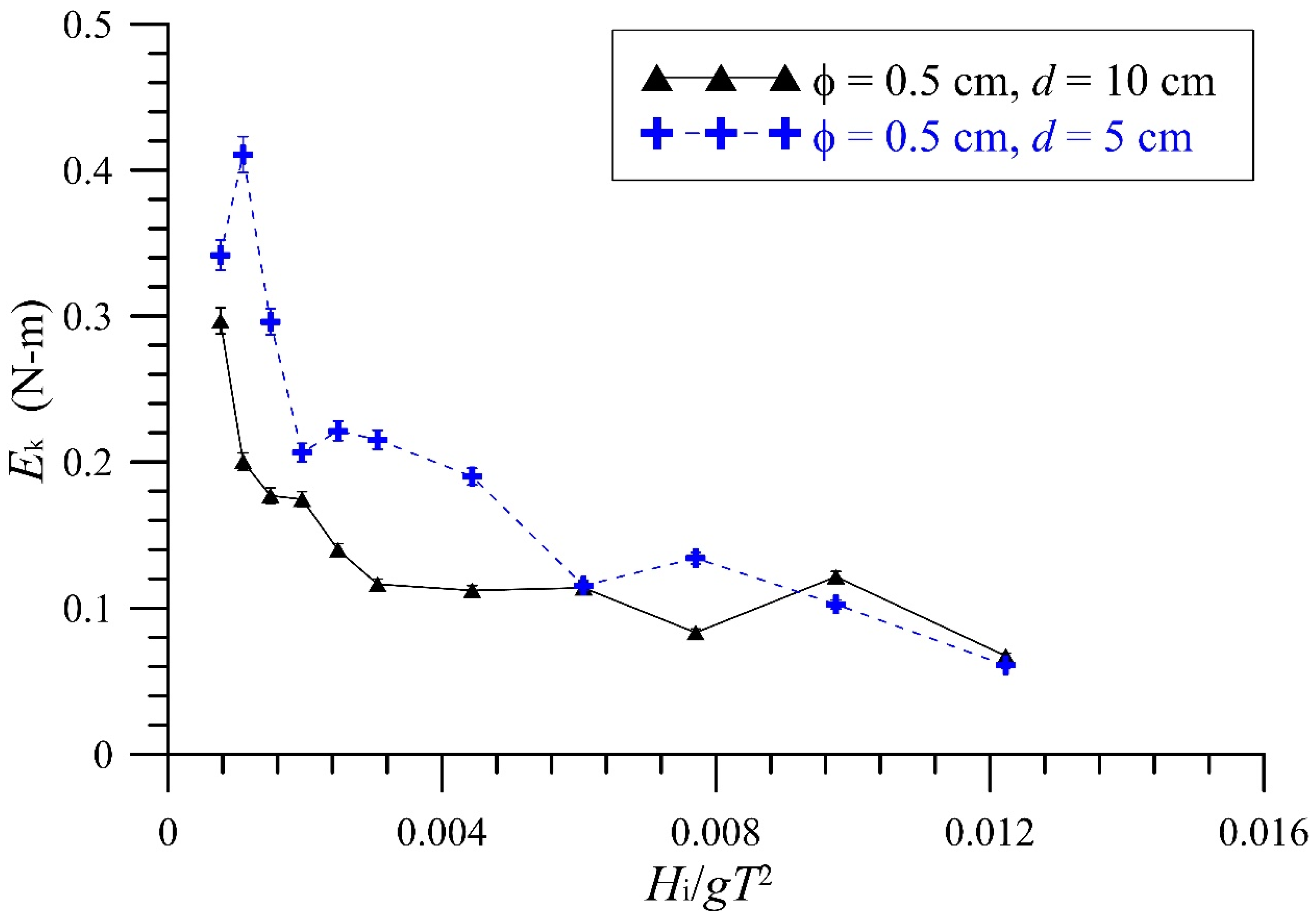
• Under constant diameter but different heights, the kinetic energy measured through the vegetation area decreased with an increase in vegetation height. The wave kinetic energy was larger within low vegetation. On the contrary, as larger vegetation structures block most waves from passing through, the kinetic energy was smaller than that measured with lower vegetation. The velocity distribution field showed that no eddy current or a chaotic flow field was observed above the vegetation. The flow field velocity inside the vegetation was relatively slow.
• Under the same wave conditions, as the bamboo diameter was reduced, which resulted in a higher water permeability, the velocity distribution on the vegetation decreased. In contrast, the velocity above the vegetation area was larger due to vegetation occlusion, and the velocity in the inner area was relatively small. Therefore, the reverse velocity above the vegetation area was relatively high.
• The resistance and friction effect due to vegetation is inversely proportional to stem size. The kinetic energy variations calculated according to the velocity distribution and vegetation stem thickness were mainly owing to the larger frictional resistance of the thick vegetation and the relatively fast flow velocity above the vegetation. Therefore, the overall kinetic energy was slightly larger than that of vegetation thinner stems. However, the overall tendency of energy changes remained consistent.
• Under the same planting conditions, evident discrepancies in kinetic energy variations were observed, which were caused by varying vegetation heights. The total kinetic energy of long-period waves under the same vegetation frictional resistance was considerably affected by vegetation height. Contrarily, the influence of different vegetation heights on short-period wave was small. However, the impact on energy reduction was smaller. For long-period waves, the vegetation height significantly reduced the kinetic energy.