Representative and Morphological Waves along the Adriatic Italian Coast in a Changing Climate
Abstract
:1. Introduction
2. Materials and Methods
2.1. Investigated Area
2.2. Wave Modeling in the Adriatic Sea
- (i)
- Historical run (HR), from 1981 to 2010;
- (ii)
- Future intermediate scenario Representative Concentration Pathway 4.5 run (RCP 4.5) from 2021 to 2050;
- (iii)
- Future worst-case scenario RCP 8.5 run (RCP 8.5) from 2021 to 2050.
2.3. Average and Extreme Value and Morphological Analyses
3. Results
3.1. Comparison between Historical and Future Average and Extreme Value Analyses
3.2. Morphological Equivalent Waves for the Historic Run
3.3. Historic and Future Morphological Equivalent Waves
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Benetazzo, A.; Davison, S.; Barbariol, F.; Mercogliano, P.; Favaretto, C.; Sclavo, M. Correction of ERA5 Wind for Regional Climate Projections of Sea Waves. Water 2022, 14, 1590. [Google Scholar] [CrossRef]
- Benetazzo, A.; Fedele, F.; Carniel, S.; Ricchi, A.; Bucchignani, E.; Sclavo, M. Wave climate of the Adriatic Sea: A future scenario simulation. Nat. Hazards Earth Syst. Sci. 2012, 12, 2065–2076. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Intergovernmental Panel on Climate Change: Fourth Assessment Report; Intergovernmental Panel on Climate Change Secretariat: Geneva, Switzerland, 2007. [Google Scholar]
- Denamiel, C.; Pranić, P.; Quentin, F.; Mihanović, H.; Vilibić, I. Pseudo-global warming projections of extreme wave storms in complex coastal regions: The case of the Adriatic Sea. Clim. Dyn. 2020, 55, 2483–2509. [Google Scholar] [CrossRef]
- De Leo, F.; Besio, G.; Mentaschi, L. Trends and variability of ocean waves under RCP8. 5 emission scenario in the Mediterranean Sea. Ocean Dyn. 2021, 71, 97–117. [Google Scholar] [CrossRef]
- Barbariol, F.; Davison, S.; Falcieri, F.M.; Ferretti, R.; Ricchi, A.; Sclavo, M.; Benetazzo, A. Wind Waves in the Mediterranean Sea: An ERA5 Reanalysis Wind-Based Climatology. Front. Mar. Sci. 2021, 8, 1–23. [Google Scholar] [CrossRef]
- Caloiero, T.; Aristodemo, F. Trend Detection of Wave Parameters along the Italian Seas. Water 2021, 13, 1634. [Google Scholar] [CrossRef]
- Caloiero, T.; Aristodemo, F.; Ferraro, D.A. Annual and seasonal trend detection of significant wave height, energy period and wave power in the Mediterranean Sea. Ocean Eng. 2022, 243, 110322. [Google Scholar] [CrossRef]
- Grases, A.; Gracia, V.; García-León, M.; Lin-Ye, J.; Sierra, J.P. Coastal flooding and erosion under a changing climate: Implications at a low-lying coast (Ebro Delta). Water 2020, 12, 346. [Google Scholar] [CrossRef]
- Bonaldo, D.; Bucchignani, E.; Pomaro, A.; Ricchi, A.; Sclavo, M.; Carniel, S. Wind waves in the Adriatic Sea under a severe climate change scenario and implications for the coasts. Int. J. Climatol. 2020, 40, 5389–5406. [Google Scholar] [CrossRef]
- Bonaldo, D.; Antonioli, F.; Archetti, R.; Bezzi, A.; Correggiari, A.; Davolio, S.; De Falco, G.; Fantini, M.; Fontolan, G.; Furlani, S.; et al. Integrating multidisciplinary instruments for assessing coastal vulnerability to erosion and sea level rise: Lessons and challenges from the Adriatic Sea, Italy. J. Coast. Conserv. 2019, 23, 19–37. [Google Scholar] [CrossRef]
- Ranasinghe, R. Assessing climate change impacts on open sandy coasts: A review. Earth-Sci. Rev. 2016, 160, 320–332. [Google Scholar] [CrossRef]
- Casas-Prat, M.; McInnes, K.L.; Hemer, M.A.; Sierra, J.P. Future wave-driven coastal sediment transport along the Catalan coast (NW Mediterranean). Reg. Environ. Chang. 2016, 16, 1739–1750. [Google Scholar] [CrossRef]
- Chonwattana, S.; Weesakul, S.; Vongvisessomjai, S. 3D Modeling of morphological changes using representative waves. Coast. Eng. J. 2005, 47, 205–229. [Google Scholar] [CrossRef]
- Plecha, S.; Sancho, F.; Silva, P.; Dias, J.M. Representative waves for morphological simulations. J. Coast. Res. 2007, 50, 995–999. [Google Scholar]
- Buccino, M.; Di Paola, G.; Ciccaglione, M.C.; Del Giudice, G.; Rosskopf, C.M. A medium-term study of Molise coast evolution based on the one-line equation and “equivalent wave” concept. Water 2020, 12, 2831. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). IPCC Workshop on Regional Climate Projections and their Use in Impacts and Risk Analysis Studies; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Eds.; IPCC Working Group I Technical Support: Bern, Switzerland, 2015. [Google Scholar]
- Ruol, P.; Martinelli, L.; Favaretto, C. Vulnerability analysis of the Venetian littoral and adopted mitigation strategy. Water 2018, 10, 984. [Google Scholar] [CrossRef]
- Capolupo, A.; Monterisi, C.; Saponieri, A.; Addona, F.; Damiani, L.; Archetti, R.; Tarantino, E. An Interactive WebGIS Framework for Coastal Erosion Risk Management. J. Mar. Sci. Eng. 2021, 9, 567. [Google Scholar] [CrossRef]
- Pasquali, D.; Marucci, A. The effects of urban and economic development on coastal zone management. Sustainability 2021, 13, 6071. [Google Scholar] [CrossRef]
- Minervino Amodio, A.; Di Paola, G.; Rosskopf, C.M. Monitoring Coastal Vulnerability by Using DEMs Based on UAV Spatial Data. ISPRS Int. J. Geo-Inf. 2022, 11, 155. [Google Scholar] [CrossRef]
- Bruno, M.F.; Saponieri, A.; Molfetta, M.G.; Damiani, L. The DPSIR approach for coastal risk assessment under climate change at regional scale: The case of Apulian coast (Italy). J. Mar. Sci. Eng. 2020, 8, 531. [Google Scholar] [CrossRef]
- Cavaleri, L.; Bajo, M.; Barbariol, F.; Bastianini, M.; Benetazzo, A.; Bertotti, L.; Chiggiato, J.; Davolio, S.; Ferrarina, C.; Magnusson, L.; et al. The October 29, 2018 storm in Northern Italy–an exceptional event and its modeling. Prog. Oceanogr. 2019, 178, 102178. [Google Scholar] [CrossRef]
- Cavaleri, L.; Bajo, M.; Barbariol, F.; Bastianini, M.; Benetazzo, A.; Bertotti, L.; Chiggiato, J.; Ferrarin, C.; Trincardi, F.; Umgiesser, G. The 2019 flooding of Venice and its implications for future predictions. Oceanography 2020, 33, 42–49. [Google Scholar] [CrossRef]
- Rockel, B.; Will, A.; Hense, A. The Regional Climate Model COSMO-CLM (CCLM). Meteorol. Z. 2008, 17, 347–348. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2021: The Physical Science Basis. In Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021. [Google Scholar]
- Schwalm, C.R.; Glendon, S.; Duffy, P.B. RCP8. 5 tracks cumulative CO2 emissions. Proc. Natl. Acad. Sci. USA 2020, 117, 19656–19657. [Google Scholar] [CrossRef] [PubMed]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic Implications of Dynamical and Statistical Approaches to Downscaling Climate Model Outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Tolman, H.L. User Manual and System Documentation of WAVEWATCH-III, version 3.14; Environmental Modeling Center Marine Modeling and Analysis Branch Research Court: College Park, MD, USA, 2009. [Google Scholar]
- MedECC. Climate and Environmental Change in the Mediterranean Basin—Current Situation and Risks for the Future; First Mediterranean Assessment Report; Cramer, W., Guiot, J., Marini, K., Eds.; Union for the Mediterranean, Plan Bleu, UNEP/MAP: Marseille, France, 2020; 632p. [Google Scholar]
- Ferreira, A.; De Haan, L. On the block maxima method in extreme value theory: PWM estimators. Ann. Stat. 2015, 43, 276–298. [Google Scholar]
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958; 201p. [Google Scholar] [CrossRef]
- US Army Corps of Engineers. Shore Protection Manual; Coastal Engineering Research Centre, Government Printing Office: Washington, DC, USA, 1984.
- Zanuttigh, B.; Palma, G.; Brizzi, G.; Bellotti, G.; Romano, A.; Suffredini, R. Design of a multi-use marine area off-shore the Mediterranean Sea. Ocean Eng. 2021, 221, 108515. [Google Scholar] [CrossRef]
- Canestrelli, P.; Mandich, M.; Pirazzoli, P.A.; Tomasin, A. Wind, Depression and Seiches: Tidal Perturbations in Venice (1951–2000); Centro Previsioni e Segnalazioni Maree: Venezia, Italy, 2001; pp. 1–104. [Google Scholar]
- Toimil, A.; Camus, P.; Losada, I.J.; Le Cozannet, G.; Nicholls, R.J.; Idier, D.; Maspataud, A. Climate change-driven coastal erosion modelling in temperate sandy beaches: Methods and uncertainty treatment. Earth-Sci. Rev. 2020, 202, 103110. [Google Scholar] [CrossRef]
- Hurdle, D.P.; Stive, R.J.H. Revision of SPM 1984 wave hindcast model to avoid inconsistencies in engineering applications. Coast. Eng. 1989, 12, 339–351. [Google Scholar] [CrossRef]






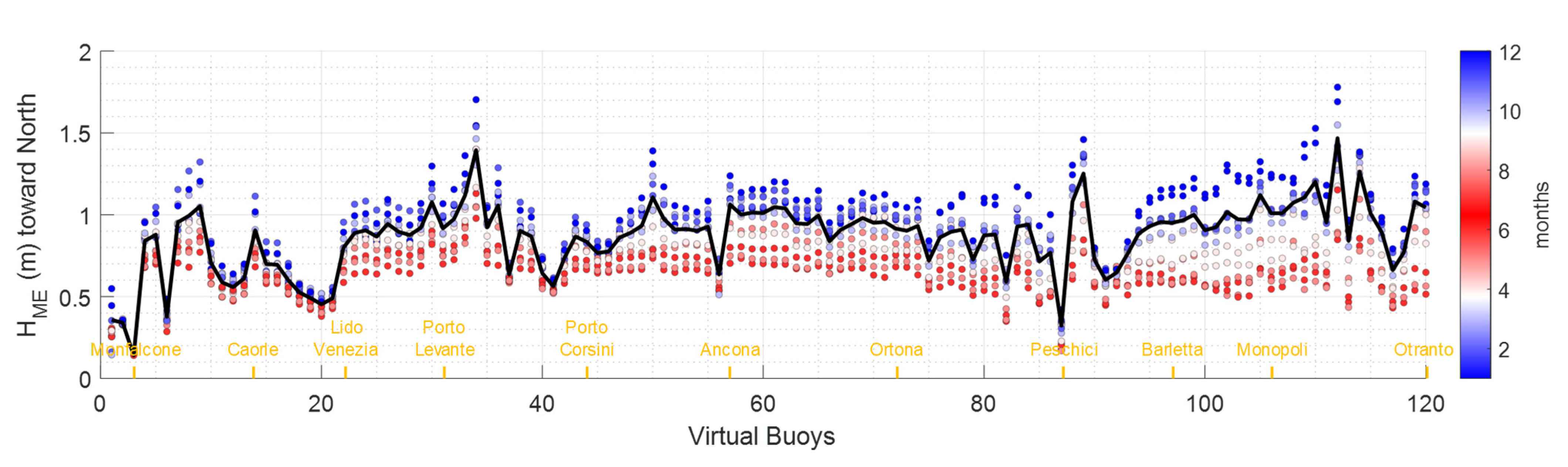

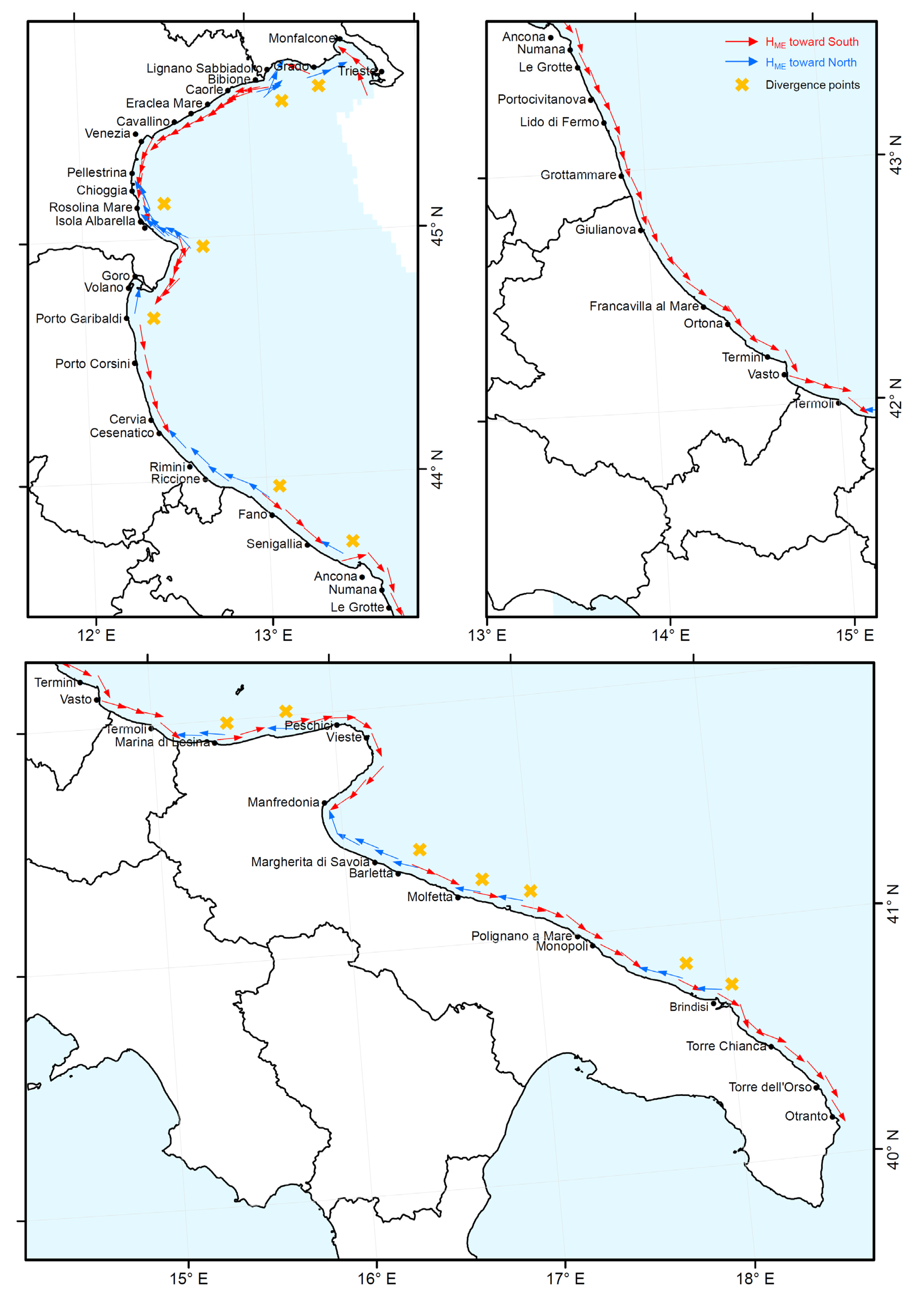


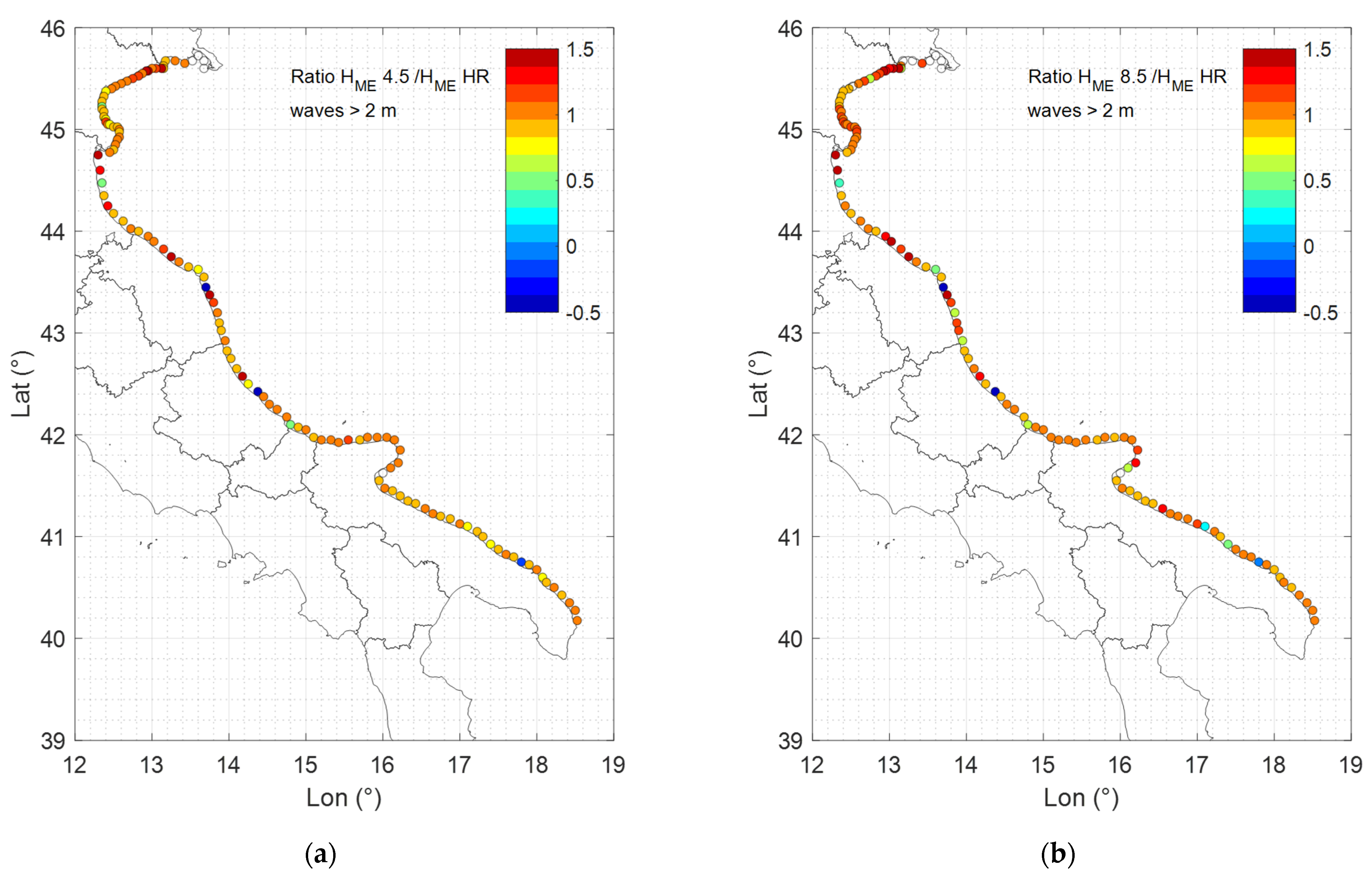
| Name | Lon (°) | Lat (°) | z (m) | Region | Name | Lon (°) | Lat (°) | z (m) | Region | Name | Lon (°) | Lat (°) | z (m) | Region |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p1 | 13.675 | 45.6 | −23 | FVG | p41 | 12.45 | 44.775 | −15 | VEN | p81 | 15.325 | 41.95 | −19 | PUG |
| p2 | 13.675 | 45.675 | −22 | FVG | p42 | 12.3 | 44.75 | −8 | ER | p82 | 15.425 | 41.925 | −13 | PUG |
| p3 | 13.6 | 45.725 | −13 | FVG | p43 | 12.325 | 44.6 | −11 | ER | p83 | 15.55 | 41.95 | −17 | PUG |
| p4 | 13.525 | 45.675 | −11 | FVG | p44 | 12.35 | 44.475 | −12 | ER | p84 | 15.7 | 41.95 | −14 | PUG |
| p5 | 13.425 | 45.65 | −10 | FVG | p45 | 12.375 | 44.35 | −10 | ER | p85 | 15.8 | 41.975 | −18 | PUG |
| p6 | 13.3 | 45.675 | −9 | FVG | p46 | 12.425 | 44.25 | −9 | ER | p86 | 15.925 | 41.975 | −18 | PUG |
| p7 | 13.175 | 45.675 | −8 | FVG | p47 | 12.5 | 44.175 | −10 | ER | p87 | 16.05 | 41.975 | −22 | PUG |
| p8 | 13.15 | 45.625 | −14 | FVG | p48 | 12.625 | 44.1 | −11 | ER | p88 | 16.15 | 41.95 | −21 | PUG |
| p9 | 13.15 | 45.6 | −16 | VEN | p49 | 12.725 | 44.025 | −11 | ER | p89 | 16.225 | 41.85 | −16 | PUG |
| p10 | 13.125 | 45.6 | −17 | VEN | p50 | 12.825 | 44 | −13 | MAR | p90 | 16.2 | 41.725 | −14 | PUG |
| p11 | 13.05 | 45.6 | −14 | VEN | p51 | 12.95 | 43.95 | −14 | MAR | p91 | 16.1 | 41.675 | −12 | PUG |
| p12 | 13 | 45.6 | −12 | VEN | p52 | 13.025 | 43.9 | −14 | MAR | p92 | 16 | 41.625 | −11 | PUG |
| p13 | 12.95 | 45.575 | −14 | VEN | p53 | 13.15 | 43.825 | −14 | MAR | p93 | 15.95 | 41.55 | −11 | PUG |
| p14 | 12.925 | 45.575 | −12 | VEN | p54 | 13.25 | 43.75 | −13 | MAR | p94 | 16.025 | 41.475 | −14 | PUG |
| p15 | 12.875 | 45.55 | −15 | VEN | p55 | 13.35 | 43.7 | −14 | MAR | p95 | 16.125 | 41.45 | −16 | PUG |
| p16 | 12.825 | 45.525 | −16 | VEN | p56 | 13.475 | 43.65 | −15 | MAR | p96 | 16.225 | 41.4 | −18 | PUG |
| p17 | 12.75 | 45.5 | −15 | VEN | p57 | 13.6 | 43.625 | −17 | MAR | p97 | 16.325 | 41.35 | −17 | PUG |
| p18 | 12.675 | 45.475 | −16 | VEN | p58 | 13.675 | 43.55 | −16 | MAR | p98 | 16.425 | 41.325 | −21 | PUG |
| p19 | 12.6 | 45.45 | −16 | VEN | p59 | 13.7 | 43.45 | −12 | MAR | p99 | 16.55 | 41.275 | −36 | PUG |
| p20 | 12.525 | 45.425 | −16 | VEN | p60 | 13.75 | 43.375 | −13 | MAR | p100 | 16.65 | 41.225 | −37 | PUG |
| p21 | 12.475 | 45.4 | −15 | VEN | p61 | 13.8 | 43.3 | −14 | MAR | p101 | 16.75 | 41.2 | −50 | PUG |
| p22 | 12.4 | 45.375 | −11 | VEN | p62 | 13.85 | 43.2 | −14 | MAR | p102 | 16.875 | 41.175 | −70 | PUG |
| p23 | 12.375 | 45.325 | −14 | VEN | p63 | 13.875 | 43.1 | −13 | MAR | p103 | 17 | 41.125 | −59 | PUG |
| p24 | 12.35 | 45.275 | −16 | VEN | p64 | 13.9 | 43.025 | −13 | MAR | p104 | 17.1 | 41.1 | −60 | PUG |
| p25 | 12.35 | 45.225 | −17 | VEN | p65 | 13.95 | 42.925 | −13 | MAR | p105 | 17.225 | 41.05 | −71 | PUG |
| p26 | 12.35 | 45.2 | −15 | VEN | p66 | 13.975 | 42.825 | −12 | ABR | p106 | 17.3 | 41 | −72 | PUG |
| p27 | 12.375 | 45.175 | −17 | VEN | p67 | 14.025 | 42.75 | −13 | ABR | p107 | 17.4 | 40.925 | −38 | PUG |
| p28 | 12.375 | 45.125 | −15 | VEN | p68 | 14.1 | 42.65 | −15 | ABR | p108 | 17.5 | 40.875 | −43 | PUG |
| p29 | 12.4 | 45.1 | −19 | VEN | p69 | 14.175 | 42.575 | −17 | ABR | p109 | 17.6 | 40.825 | −49 | PUG |
| p30 | 12.4 | 45.075 | −14 | VEN | p70 | 14.25 | 42.5 | −17 | ABR | p110 | 17.7 | 40.8 | −66 | PUG |
| p31 | 12.425 | 45.05 | −9 | VEN | p71 | 14.375 | 42.425 | −21 | ABR | p111 | 17.8 | 40.75 | −61 | PUG |
| p32 | 12.45 | 45.05 | −16 | VEN | p72 | 14.45 | 42.375 | −21 | ABR | p112 | 17.9 | 40.725 | −83 | PUG |
| p33 | 12.5 | 45.025 | −19 | VEN | p73 | 14.525 | 42.3 | −16 | ABR | p113 | 18 | 40.675 | −60 | PUG |
| p34 | 12.55 | 45.025 | −29 | VEN | p74 | 14.625 | 42.25 | −20 | ABR | p114 | 18.075 | 40.6 | −22 | PUG |
| p35 | 12.575 | 45 | −28 | VEN | p75 | 14.75 | 42.175 | −19 | ABR | p115 | 18.125 | 40.55 | −27 | PUG |
| p36 | 12.575 | 44.975 | −17 | VEN | p76 | 14.8 | 42.1 | −12 | ABR | p116 | 18.225 | 40.5 | −37 | PUG |
| p37 | 12.575 | 44.925 | −15 | VEN | p77 | 14.9 | 42.075 | −18 | MOL | p117 | 18.325 | 40.425 | −73 | PUG |
| p38 | 12.55 | 44.9 | −14 | VEN | p78 | 15 | 42.05 | −23 | MOL | p118 | 18.425 | 40.35 | −97 | PUG |
| p39 | 12.525 | 44.85 | −17 | VEN | p79 | 15.1 | 41.975 | −16 | MOL | p119 | 18.5 | 40.275 | −98 | PUG |
| p40 | 12.5 | 44.8 | −19 | VEN | p80 | 15.2 | 41.95 | −16 | PUG | p120 | 18.525 | 40.175 | −67 | PUG |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruol, P.; Martinelli, L.; Favaretto, C.; Barbariol, F.; Benetazzo, A. Representative and Morphological Waves along the Adriatic Italian Coast in a Changing Climate. Water 2022, 14, 2678. https://doi.org/10.3390/w14172678
Ruol P, Martinelli L, Favaretto C, Barbariol F, Benetazzo A. Representative and Morphological Waves along the Adriatic Italian Coast in a Changing Climate. Water. 2022; 14(17):2678. https://doi.org/10.3390/w14172678
Chicago/Turabian StyleRuol, Piero, Luca Martinelli, Chiara Favaretto, Francesco Barbariol, and Alvise Benetazzo. 2022. "Representative and Morphological Waves along the Adriatic Italian Coast in a Changing Climate" Water 14, no. 17: 2678. https://doi.org/10.3390/w14172678
APA StyleRuol, P., Martinelli, L., Favaretto, C., Barbariol, F., & Benetazzo, A. (2022). Representative and Morphological Waves along the Adriatic Italian Coast in a Changing Climate. Water, 14(17), 2678. https://doi.org/10.3390/w14172678











