The Seasonal Dynamics of Organic and Inorganic Carbon along the Tropical Usumacinta River Basin (Mexico)
Abstract
:1. Introduction
2. Materials and Methods
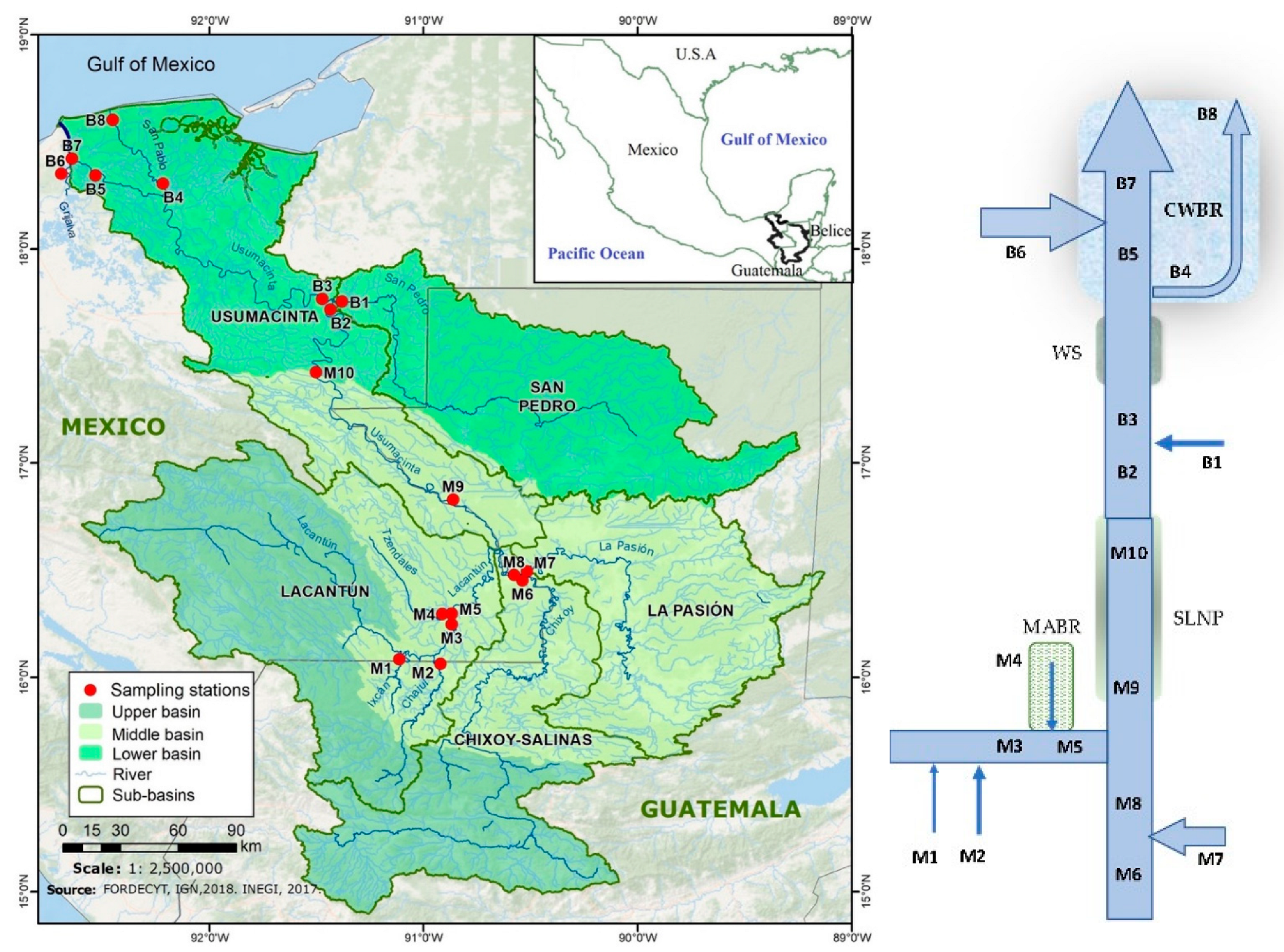
2.1. The Usumacinta River
2.2. Sampling
2.3. Analytical Methods
2.4. Data Analysis and Statistical Methods
2.5. Annual Flux Calculation
3. Results
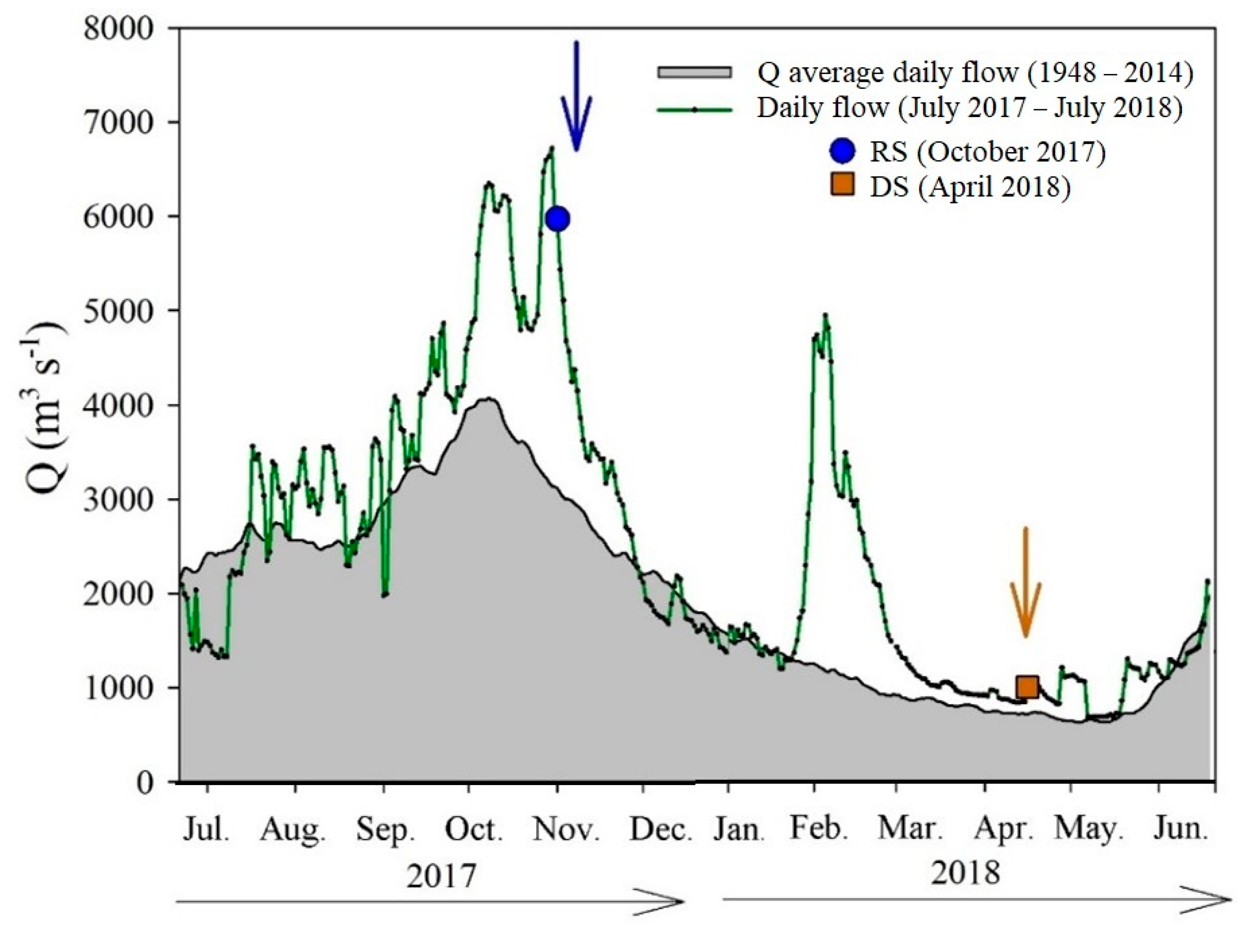
3.1. Discharge and Physical and Chemical Variables of the Usumacinta River
3.2. Temporal and Spatial Variation of Carbon Concentration
3.2.1. Dissolved Organic Carbon
3.2.2. Particulate Organic Carbon
3.2.3. Total Organic Carbon
3.2.4. Dissolved Inorganic Carbon
3.2.5. Particulate Inorganic Carbon
3.2.6. Total Carbon
3.3. Instantaneous Carbon Fluxes
3.4. C Balance in the Lower Basin of the Usumacinta River
3.5. Annual C Loads Estimates
4. Discussion
4.1. Temporal and Spatial Variation of C in the Usumacinta River
4.1.1. Comparison with Other Large Rivers
4.1.2. Correlation between DOC, POC, and DIC and Water Discharge
4.1.3. Spatial Variation of DOC, POC, and DIC Concentrations
4.2. C Balance in the Usumacinta Lower Basin
4.3. Global C Export from the Usumacinta-Grijalva River to the Gulf of Mexico
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Battin, T.J.; Luyssaert, S.; Kaplan, L.A.; Aufdenkampe, A.K.; Richter, A.; Tranvik, L.J. The boundless carbon cycle. Nat. Geosci. 2009, 2, 598–600. [Google Scholar] [CrossRef]
- Cole, J.J.; Prairie, Y.T.; Caraco, N.F.; McDowell, W.H.; Tranvik, L.J.; Striegl, R.G.; Duarte, C.M.; Kortelainen, P.; Downing, J.A.; Middelburg, J.J.; et al. Plumbing the global carbon cycle: Integrating inland waters into the terrestrial carbon budget. Ecosystems 2007, 10, 171–184. [Google Scholar] [CrossRef]
- Tranvik, L.J.; Cole, J.J.; Prairie, Y.T. The study of carbon in inland waters-from isolated ecosystems to players in the global carbon cycle. Limnol. Oceanogr. Lett. 2018, 3, 41–48. [Google Scholar] [CrossRef]
- Vachon, D.; Sponseller, R.; Karlsson, J. Integrating carbon emission, accumulation, and transport in inland waters to understand their role in the global carbon cycle. Glob. Chang. Biol. 2021, 27, 719–727. [Google Scholar] [CrossRef] [PubMed]
- Drake, T.W.; Raymond, P.A.; Spencer, R.G.M. Terrestrial carbon inputs to inland waters: A current synthesis of estimates and uncertainty. Limnol. Oceanogr. Lett. 2017, 3, 132–142. [Google Scholar] [CrossRef]
- Bertassoli, D.J.; Sawakuchi, A.O.; Sawakuchi, H.O.; Pupim, F.N.; Hartmann, G.A.; McGlue, M.M.; Chiessi, C.M.; Zabel, M.; Schefuß, E.; Pereira, T.S.; et al. The fate of carbon in sediments of the Xingu and Tapajós clearwater rivers, Eastern Amazon. Front. Mar. Sci. 2017, 4, 44. [Google Scholar] [CrossRef]
- Keller, C.K. Carbon Exports from terrestrial ecosystems: A critical-zone framework. Ecosystems 2019, 22, 1691–1705. [Google Scholar] [CrossRef]
- Raymond, P.A.; Hartmann, J.; Lauerwald, R.; Sobek, S.; McDonald, C.; Hoover, M.; Butman, D.; Striegl, R.; Mayorga, E.; Humborg, C.; et al. Global carbon dioxide emissions from inland waters. Nature 2013, 503, 355–359. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Peng, C.; Zhang, K.; Xu, L.; Wang, J.; Yang, Y.; Li, P.; Liu, Z.; He, N. Headwater stream ecosystem: An important source of greenhouse gases to the atmosphere. Water Res. 2021, 190, 116738. [Google Scholar] [CrossRef]
- Alvarez-Cobelas, M.; Angeler, D.G.; Sánchez-Carrillo, S.; Almendros, G. A worldwide view of organic carbon export from catchments. Biogeochemistry 2012, 107, 275–293. [Google Scholar] [CrossRef]
- Huang, T.-H.; Fu, Y.-H.; Pan, P.-Y. Fluvial carbon fluxes in tropical rivers. Curr. Opin. Environ. Sustain. 2012, 4, 162–169. [Google Scholar] [CrossRef]
- Meybeck, M. Origins and behaviors of carbon species in world rivers. In Soil Erosion and Carbon Dynamics; Roose, E.J., Lal, R., Feller, C., Barthes, B., Stewart, B.A., Eds.; CRC Press.: New York, NY, USA, 2005; pp. 209–238. [Google Scholar] [CrossRef]
- Aufdenkampe, A.K.; Mayorga, E.; Raymond, P.A.; Melack, J.M.; Doney, S.C.; Alin, S.R.; Aalto, R.E.; Yoo, K. Rivers and the coupling of biogeochemical cycles. Front. Ecol. Environ. 2011, 9, 53–60. [Google Scholar] [CrossRef]
- Xenopoulos, M.A.; Downing, J.A.; Kumar, M.D.; Menden-Deuer, S.; Voss, M. Headwaters to Oceans: Ecological and Biogeochemical contrasts across the aquatic continuum. Limnol. Oceanogr. 2017, 62, S3–S14. [Google Scholar] [CrossRef]
- Ward, N.D.; Bianchi, T.S.; Medeiros, P.M.; Seidel, M.; Richey, J.E.; Keil, R.G.; Sawakuchi, H.O. Where carbon goes when water flows: Carbon cycling across the Aquatic Continuum. Front. Mar. Sci. 2017, 4, 7. [Google Scholar] [CrossRef]
- Li, M.; Peng, C.; Wang, M.; Xue, W.; Zhang, K.; Wang, K.; Shi, G.; Zhu, Q. The Carbon flux of global rivers: A re-evaluation of amount and spatial patterns. Ecol. Indic. 2017, 80, 40–51. [Google Scholar] [CrossRef]
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Hauck, J.; Olsen, A.; Peters, G.P.; Peters, W.; Pongratz, J.; Sitch, S.; et al. Global carbon budget 2020. Earth Syst. Sci. Data 2020, 12, 3269–3340. [Google Scholar] [CrossRef]
- Cai, Y.; Guo, L.; Wang, X.; Aiken, G. Abundance, stable isotopic composition, and export fluxes of DOC, POC, and DIC from the Lower Mississippi River during 2006–2008. J. Geophys. Res. G Biogeosci. 2015, 120, 2273–2288. [Google Scholar] [CrossRef]
- Battin, T.J.; Kaplan, L.A.; Findlay, S.; Hopkinson, C.S.; Marti, E.; Packman, A.I.; Denis Newbold, J.; Sabater, F. Biophysical controls on organic carbon fluxes in fluvial networks. Prog. Artic. Nat. Geosci. 2008, 1, 95–100. [Google Scholar] [CrossRef]
- Schlesinger, W.H.; Bernhardt, E.S. Biogeochemistry: An Analysis of Global Change, 4th ed.; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Harrison, J.A.; Caraco, N.; Seitzinger, S.P. Global patterns and sources of Dissolved Organic Matter export to the coastal zone: Results from a spatially explicit, global model. Glob. Biogeochem. Cycles 2005, 19, GB4S04. [Google Scholar] [CrossRef]
- Tian, H.; Yang, Q.; Najjar, R.; Ren, W.; Friedrichs, M.; Hopkinson, C.; Pan, S. Anthropogenic and Climatic Influences on Carbon fluxes from eastern North America to the Atlantic Ocean: A process-based modeling study. J. Geophys. Res. Biogeosci. 2015, 120, 752–772. [Google Scholar] [CrossRef]
- Bouchez, J.; Galy, V.; Hilton, R.G.; Gaillardet, J.; Moreira-Turcq, P.; Pérez, M.A.; France-Lanord, C.; Maurice, L. Source, transport and fluxes of Amazon River particulate organic carbon: Insights from river sediment depth-profiles. Geochim. Cosmochim. Acta 2014, 133, 280–298. [Google Scholar] [CrossRef]
- Schlesinger, W.H.; Melack, J.M. Transport of organic carbon in the world’s rivers. Tellus 1981, 33, 172–187. [Google Scholar] [CrossRef]
- Seyler, P.; Coynel, A.; Moreira-Turcq, P.; Etcheber, H.; Colas, C.; Orange, D.; Bricquet, J.P.; Laraque, A.; Guyot, J.; Olivry, J.C.; et al. Organic carbon transported by the equatorial rivers: Example of Congo-Zaire and Amazon Basins. In Soil Erosion and Carbon Dynamics; Roose, E.J., Lal, R., Feller, C., Barthes, B., Stewart, B.A., Eds.; CRC Press: Boca Raton, FL, USA, 2005; pp. 255–274. [Google Scholar] [CrossRef]
- Ludwig, W.; Probst, J.L. Predicting the oceanic input of organic carbon by continental erosion. Glob. Biogeochem. Cycles 1996, 10, 23–41. [Google Scholar] [CrossRef]
- Galy, V.; Peucker-Ehrenbrink, B.; Eglinton, T. Global carbon export from the terrestrial biosphere controlled by erosion. Nature 2015, 521, 204–207. [Google Scholar] [CrossRef]
- Gaillardet, J.; Calmels, D.; Romero-Mujalli, G.; Zakharova, E.; Hartmann, J. Global climate control on carbonate weathering intensity. Chem. Geol. 2018, 527, 118762. [Google Scholar] [CrossRef]
- Meybeck, M. Global occurrence of major elements in rivers. Treatise Geochem. 2003, 5, 207–223. [Google Scholar] [CrossRef]
- Raymond, P.A.; Hamilton, S.K. Anthropogenic influences on riverine fluxes of Dissolved Inorganic Carbon to the oceans. Limnol. Oceanogr. Lett. 2018, 3, 143–155. [Google Scholar] [CrossRef]
- Raymond, P.A.; Oh, N.; Turner, R.E.; Broussard, W. Anthropogenically enhanced fluxes of water and carbon from the Mississippi River. Nature 2008, 451, 449–452. [Google Scholar] [CrossRef] [Green Version]
- Ludwig, W.; Amiotte-Suchet, P.; Munhoven, G.; Probst, J.L. Atmospheric CO2 consumption by continental erosion: Present-day controls and implications for the last glacial maximum. Glob. Planet. Chang. 1998, 16-17, 107–120. [Google Scholar] [CrossRef]
- Hope, D.; Billett, M.F.; Cresser, M.S. A Review of the export of carbon in river water: Fluxes and processes. Environ. Pollut. 1994, 84, 301–324. [Google Scholar] [CrossRef]
- Gaillardet, J.; Dupré, B.; Louvat, P.; Allègre, C.J. Global silicate weathering and CO2 consumption rates deduced from the chemistry of large rivers. Chem. Geol. 1999, 159, 3–30. [Google Scholar] [CrossRef]
- Probst, J.L.; Mortatti, J.; Tardy, Y. Carbon river fluxes and weathering CO2 consumption in the Congo and Amazon River Basins. Appl. Geochem. 1994, 9, 1–13. [Google Scholar] [CrossRef]
- Syvitski, J.; Cohen, S.; Kettner, A.J.; Brakenridge, G.R. How important and different are tropical rivers? —An overview. Geomorphology 2014, 227, 5–17. [Google Scholar] [CrossRef]
- Borges, A.V.; Darchambeau, F.; Teodoru, C.R.; Marwick, T.R.; Tamooh, F.; Geeraert, N.; Omengo, F.O.; Guérin, F.; Lambert, T.; Morana, C.; et al. Globally significant greenhouse-gas emissions from African inland waters. Nat. Geosci. 2015, 8, 637–642. [Google Scholar] [CrossRef]
- Mora, A.; Laraque, A.; Moreira-Turcq, P.; Alfonso, J.A. Temporal variation and fluxes of dissolved and particulate organic carbon in the Apure, Caura and Orinoco Rivers, Venezuela. J. S. Am. Earth Sci. 2014, 54, 47–56. [Google Scholar] [CrossRef]
- Goldsmith, S.T.; Berry Lyons, W.; Harmon, R.S.; Harmon, B.A.; Carey, A.E.; McElwee, G.T.; Berry-Lyons, W.; Harmon, R.S.; Harmon, B.A.; Carey, A.E.; et al. Organic Carbon Concentrations and Transport in Small Mountain Rivers, Panama. Appl. Geochem. 2015, 63, 540–549. [Google Scholar] [CrossRef]
- Seidel, M.; Dittmar, T.; Ward, N.D.; Krusche, A.V.; Richey, J.E.; Yager, P.L.; Medeiros, P.M. Seasonal and Spatial Variability of Dissolved Organic Matter Composition in the Lower Amazon River. Biogeochemistry 2016, 131, 281–302. [Google Scholar] [CrossRef]
- Drake, T.W.; Hemingway, J.D.; Kurek, M.R.; Peucker-Ehrenbrink, B.; Brown, K.A.; Holmes, R.M.; Galy, V.; Moura, J.M.S.; Mitsuya, M.; Wassenaar, L.I.; et al. The Pulse of the Amazon: Fluxes of Dissolved Organic Carbon, Nutrients, and Ions from the World’s Largest River. Glob. Biogeochem. Cycles 2021, 35, e2020GB006895. [Google Scholar] [CrossRef]
- Cuevas-Lara, D.; Alcocer, J.; Cortés-Guzmán, D.; Soria-Reinoso, I.F.; García-Oliva, F.; Sánchez-Carrillo, S.; Oseguera, L.A. Particulate Organic Carbon in the Tropical Usumacinta River, southeast Mexico: Concentration, Flux, and Sources. Water 2021, 13, 1561. [Google Scholar] [CrossRef]
- Richey, J.E.; Spencer, R.G.M.; Drake, T.W.; Ward, N.D. Fluvial carbon dynamics across the Land to Ocean Continuum of great tropical rivers: The Amazon and Congo. In Congo Basin Hydrology, Climate, and Biogeochemistry; Tshimanga, R.M., N’kaya, G.D.M., Alsdorf, D., Eds.; American Geophysical Union: Washington, DC, USA, 2022; pp. 393–411. [Google Scholar] [CrossRef]
- Belliard, J.P.; Hernandez, S.; Temmerman, S.; Suello, R.H.; Dominguez-Granda, L.E.; Rosado-Moncayo, A.M.; Ramos-Veliz, J.A.; Parra-Narera, R.N.; Pollete-Ramirez, K.; Govers, G.; et al. Carbon dynamics and CO2 and CH4 exchange in the mangrove dominated Guayas River delta, Ecuador. Estuar. Coast. Shelf Sci. 2022, 267, 107766. [Google Scholar] [CrossRef]
- Bird, M.I.; Robinson, R.A.J.; Oo, N.W.; Aye, M.M.; Lu, X.X.; Higgitt, D.L.; Swe, A.; Tun, T.; Lhaing Win, S.; Sandar Aye, K.; et al. A preliminary estimate of organic carbon transport by the Ayeyarwady (Irrawaddy) and Thanlwin (Salween) Rivers of Myanmar. Quat. Int. 2008, 186, 113–122. [Google Scholar] [CrossRef]
- Bouillon, S.; Yambélé, A.; Spencer, R.G.M.; Gillikin, D.P.; Hernes, P.J.; Six, J.; Merckx, R.; Borges, A.V. Organic matter sources, fluxes and greenhouse gas exchange in the Oubangui River (Congo River Basin). Biogeosciences 2012, 9, 2045–2062. [Google Scholar] [CrossRef]
- Tamooh, F.; Van Den Meersche, K.; Meysman, F.; Marwick, T.R.; Borges, A.V.; Merckx, R.; Dehairs, F.; Schmidt, S.; Nyunja, J.; Bouillon, S. Distribution and origin of suspended matter and organic carbon pools in the Tana River Basin, Kenya. Biogeosciences 2012, 9, 2905–2920. [Google Scholar] [CrossRef]
- Tamooh, F.; Borges, A.V.; Meysman, F.J.R.; Van Den Meersche, K.; Dehairs, F.; Merckx, R.; Bouillon, S. Dynamics of Dissolved Inorganic Carbon and aquatic metabolism in the Tana River Basin, Kenya. Biogeosciences 2013, 10, 6911–6928. [Google Scholar] [CrossRef]
- Tamooh, F.; Meysman, F.J.R.; Borges, A.V.; Marwick, T.R.; Van Den Meersche, K.; Dehairs, F.; Merckx, R.; Bouillon, S. Sediment and carbon fluxes along a longitudinal gradient in the lower Tana River (Kenya). J. Geophys. Res. G Biogeosci. 2014, 119, 1340–1353. [Google Scholar] [CrossRef]
- Mbaye, M.L.; Gaye, A.T.; Spitzy, A.; Dähnke, K.; Afouda, A.; Gaye, B. Seasonal and spatial variation in suspended matter, organic carbon, nitrogen, and nutrient concentrations of the Senegal River in West Africa. Limnologica 2016, 57, 1–13. [Google Scholar] [CrossRef]
- Geeraert, N.; Omengo, F.O.; Tamooh, F.; Marwick, T.R.; Borges, A.V.; Govers, G.; Bouillon, S. Seasonal and inter-annual variations in carbon fluxes in a tropical river system (Tana River, Kenya). Aquat. Sci. 2018, 80, 19. [Google Scholar] [CrossRef] [Green Version]
- Ran, L.; Lu, X.X.; Sun, H.; Han, J.; Li, R.; Zhang, J. Spatial and seasonal variability of Organic Carbon transport in the Yellow River, China. J. Hydrol. 2013, 498, 76–88. [Google Scholar] [CrossRef]
- Krishna, M.S.; Prasad, V.R.; Sarma, V.V.S.S.; Reddy, N.P.C.; Hemalatha, K.P.J.; Rao, Y.V. Fluxes of Dissolved Organic Carbon and nitrogen to the northern Indian Ocean from the Indian monsoonal rivers. J. Geophys. Res. Biogeosci. 2015, 120, 2067–2080. [Google Scholar] [CrossRef]
- Le, T.P.Q.; Phung, T.X.B.; Duong, T.T.; Le, D.; Ho, C.T. Relationship of dissolved inorganic carbon (DIC) concentrations with some Environmental variables in the Red River water in the period 2008–2015. J. Vietnam. Environ. 2016, 8, 102–106. [Google Scholar] [CrossRef]
- Le, T.P.Q.; Dao, V.N.; Rochelle-Newall, E.; Garnier, J.; Lu, X.; Billen, G.; Duong, T.T.; Ho, C.T.; Etcheber, H.; Nguyen, T.M.H.; et al. Total organic carbon fluxes of the Red River System (Vietnam). Earth Surf. Process. Landf. 2017, 42, 1329–1341. [Google Scholar] [CrossRef]
- Huang, T.-H.; Chen, C.-T.A.; Tseng, H.-C.; Lou, J.Y.; Wang, S.L.; Yang, L.; Kandasamy, S.; Gao, X.; Wang, J.T.; Aldrian, E.; et al. Riverine carbon fluxes to the south China Sea. J. Geophys. Res. Biogeosci. 2017, 122, 1239–1259. [Google Scholar] [CrossRef]
- Qin, C.; Li, S.; Yue, F.; Xu, S.; Ding, H. Spatiotemporal variations of dissolved inorganic carbon and controlling factors in a small karstic catchment, southwestern China. Earth Surf. Process. Landf. 2019, 44, 2423–2436. [Google Scholar] [CrossRef]
- Alcocer, J.; Caballero, M.; Ruiz-Fernández, A.C.; Oseguera-Pérez, L.A.; Sánchez-Cabeza, J.A.; Cuevas-Lara, D.; Soria-Reinoso, I. Ecosistemas Acuáticos Epicontinentales. In Estado del Ciclo del Carbono en México. Agenda Azul y Verde; Paz Pellat, F., Hernández Ayón, M., Sosa Ávalos, R., Velázquez, A., Eds.; Programa Mexicano del Carbono: Texcoco, Mexico, 2019; p. 716. [Google Scholar]
- Butman, D.; Striegl, R.G.; Stackpoole, S.M.; Del Giorgio, P.A.; Prairie, Y.T.; Pilcher, D.; Raymond, P.A.; Paz Pellat, F.; Alcocer, J. Inland Waters. In Second State of the Carbon Cycle Report (SOCCR2): A Sustained Assessment Report; Cavallaro, N., Shrestha, G., Birdsey, R., Mayes, M., Najar, R., Reed, S.C., Romero-Lankao, P., Zhu, Z., Eds.; U.S. Global Change Research Program: Washington, DC, USA, 2018; pp. 568–595. [Google Scholar] [CrossRef]
- Sánchez-Carrillo, S.; Alcocer, J.; Vargas-Sánchez, M.; Soria-Reinoso, I.; Rivera-Herrera, E.M.; Cortés-Guzmán, D.; Guzmán-Arias, A.P.; Merino-Ibarra, M.; Oseguera-Pérez, L.A. Greenhouse gas emissions from Mexican inland waters: First estimation and uncertainty using an upscaling approach. Inland Waters 2022, 18, 294–310. [Google Scholar] [CrossRef]
- Benke, A.C.; Cushing, C.E. Rivers of North America. In Encyclopedia of Inland Waters; Elsevier: Amsterdam, The Netherlands, 2009; pp. 425–437. [Google Scholar]
- Alcocer, J.; Bernal-Brooks, F.W. Limnology in Mexico. Hydrobiologia 2010, 644, 15–68. [Google Scholar] [CrossRef]
- Muñoz-Salinas, E.; Castillo, M. Streamflow and sediment load assessment from 1950 to 2006 in the Usumacinta and Grijalva Rivers (Southern Mexico) and the influence of ENSO. Catena 2015, 127, 270–278. [Google Scholar] [CrossRef]
- Lewis, W.; Hamilton, S.; Saunders, J. Rivers of northern South America. In Ecosystems of the World: Rivers; Cushing, C.E., Cummins, K.W., Eds.; Elsevier: New York, NY, USA, 1995; Volume III, pp. 219–256. [Google Scholar]
- Araujo, M.; Noriega, C.; Lefévre, N. Nutrients and carbon fluxes in the estuaries of major rivers flowing into the tropical Atlantic. Front. Mar. Sci. 2014, 1, 10. [Google Scholar] [CrossRef]
- Bianchi, T.S.; Wysocki, L.A.; Stewart, M.; Filley, T.R.; McKee, B.A. Temporal variability in terrestrially-derived sources of particulate organic carbon in the Lower Mississippi River and its upper tributaries. Geochim. Cosmochim. Acta 2007, 71, 4425–4437. [Google Scholar] [CrossRef]
- Duan, S.; He, Y.; Kaushal, S.S.; Bianchi, T.S. Impact of wetland decline on decreasing dissolved organic carbon concentrations along the Mississippi River continuum. Front. Mar. Sci. 2017, 3, 280. [Google Scholar] [CrossRef]
- Delduco, E.M.; Xu, Y.J. Dissolved carbon transport and processing in north America’s largest swamp river entering the northern Gulf of Mexico. Water 2019, 11, 1395. [Google Scholar] [CrossRef]
- Yáñez-Arancibia, A.; Day, J.W. Environmental sub-regions in the Gulf of Mexico coastal zone: The ecosystem approach as an integrated management tool. Ocean Coast. Manag. 2004, 47, 727–757. [Google Scholar] [CrossRef]
- Horton, A.J.; Nygren, A.; Diaz-Perera, M.A.; Kummu, M. Flood severity along the Usumacinta River, Mexico: Identifying the anthropogenic signature of tropical forest conversion. J. Hydrol. X 2021, 10, 100072. [Google Scholar] [CrossRef]
- Muñoz-Salinas, E.; Castillo, M.; Sanderson, D.; Kinnaird, T.; Cruz-Zaragoza, E. Using three different approaches of OSL for the study of young fluvial sediments at the coastal plain of the Usumacinta—Grijalva River basin, Southern Mexico. Earth Surf. Process. Landf. 2016, 41, 823–834. [Google Scholar] [CrossRef]
- Grodsky, S.A.; Carton, J.A. The Intertropical Convergence Zone in the south Atlantic and the equatorial cold tongue. Am. Meteorol. Soc. 2003, 16, 723–733. [Google Scholar] [CrossRef]
- Soares, D.; García, A. La Cuenca del Río Usumacinta desde la Perspectiva del Cambio Climático, 1st ed.; Instituto Mexicano de Tecnología del Agua: Jiutepec, México, 2017. [Google Scholar]
- Herrera-Silveira, J.A.; Lara-Domínguez, A.L.; Day, J.W.; Yáñez-Arancibia, A.; Ojeda, S.M.; Hernández, C.T.; Kemp, G.P. Ecosystem functioning and sustainable management in coastal systems with high freshwater input in the southern Gulf of Mexico and Yucatan Peninsula. In Coasts and Estuaries—The Future; Elsevier Inc.: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Magaña, V.; Vázquez, J.L.; Párez, J.L.; Pérez, J.B. Impact of El Niño on precipitation in Mexico. Geofís. Int. 2003, 42, 313–330. [Google Scholar]
- CONAGUA. Banco Nacional de Datos de Aguas Superficiales (BANDAS). Available online: http://www.conagua.gob.mx/CONAGUA07/Contenido/Documentos/PortadaBANDAS.htm (accessed on 17 May 2021).
- Meybeck, M.; Ragu, A. GEMS-GLORI World River Discharge Database. Available online: https://doi.pangaea.de/10.1594/PANGAEA.804574 (accessed on 9 March 2022).
- González-Ramírez, J.; Parés-Sierra, A. Streamflow Modeling of Five Major Rivers That Flow into the Gulf of Mexico Using SWAT. Atmosfera 2019, 32, 261–272. [Google Scholar] [CrossRef]
- March, I.; Castro, M. La cuenca del río Usumacinta: Perfil y perspectivas para su conservación y desarrollo sustentable. In Las Cuencas Hidrográficas de México: Diagnostico y Priorización; Cotler-Ávalos, E., Ed.; Pluralia Ediciones e Impresiones: Mexico City, Mexico, 2010; pp. 193–197. [Google Scholar]
- Yáñez-Arancibia, A.; Day, J.W.; Currie-Alder, B. Functioning of the Grijalva-Usumacinta River delta, Mexico: Challenges for coastal management. Ocean. Yearb. 2009, 23, 473–501. [Google Scholar] [CrossRef]
- Reyes, E.; Day, J.W.; Lara-Domínguez, A.L.; Sánchez-Gil, P.; Lomelí, D.Z.; Yáñez-Arancibia, A. Assessing coastal management plans using watershed spatial models for the Mississippi delta, USA, and the Usumacinta-Grijalva delta, Mexico. Ocean Coast. Manag. 2004, 47, 693–708. [Google Scholar] [CrossRef]
- Saavedra Guerrero, A.; López López, D.M.; Castellanos Fajardo, L.A. Descripción del medio físico de la cuenca media del Río Usumacinta en México. In Conservación y Desarrollo Sustentable en la Selva Lacandona. 25 Años de Actividades y Experiencias; Carabias, J., de La Maza, J., Cadena, R., Eds.; Natura y Ecosistemas Mexicanos A.C.: Mexico City, Mexico, 2015; pp. 19–34. [Google Scholar]
- Marshall, J.S. The geomorphology and physiographic provinces of Central America. In Central America: Geology, Resources, and Hazards; Bundschuh, J., Alvarado, G.E., Eds.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- West, R.; Psuty, N.; Thom, B. Las Tierras Bajas de Tabasco en el Sureste de México; Gobierno del Estado de Tabasco: Villahermosa, Mexico, 1985; 409p. [Google Scholar]
- Olea-Olea, S.; Alcocer, J.; Armienta, M.A.; Oseguera, L.A. Geochemical modeling unravels the water chemical changes along the largest Mexican River. Appl. Geochem. 2022, 137, 105157. [Google Scholar] [CrossRef]
- Arar, E.J.; Collins, G.B. Method 445.0—In Vitro Determination of Chlorophyll a and Pheophytin a in Marine and Freshwater Algae by Fluorescence; United States Environmental Protection Agency—Office of Research and Development, National Exposure Research Laboratory: Cincinnati, OH, USA, 1997. [Google Scholar]
- Geeraert, N.; Omengo, F.O.; Borges, A.V.; Govers, G.; Bouillon, S. Shifts in the carbon dynamics in a tropical lowland river system (Tana River, Kenya) during flooded and non-flooded conditions. Biogeochemistry 2017, 132, 141–163. [Google Scholar] [CrossRef]
- Meybeck, M. Carbon, nitrogen, and phosphorus transport by world rivers. Am. J. Sci. 1982, 282, 401–450. [Google Scholar] [CrossRef]
- Lambert, T.; Teodoru, C.R.; Nyoni, F.C.; Bouillon, S.; Darchambeau, F.; Massicotte, P.; Borges, A.V. Along-stream transport and transformation of dissolved organic matter in a large tropical river. Biogeosciences 2016, 13, 2727–2741. [Google Scholar] [CrossRef]
- Boeglin, J.-L.; Probst, J.-L.; Nyeck, B.; Ndam-Ngoupayou, J.-R.; Nyeck, B.; Etcheber, H.; Mortatti, J.; Braun, J.-J. Soil carbon stock and river carbon fluxes in humid tropical environments: The Nyong River Basin (South Cameroon). In Soil Erosion and Carbon Dynamics; Roose, E.J., Lal, R., Feller, C., Barthès, B., Stewart, B.A., Eds.; CRC Press: Boca Raton, FL, USA, 2005; pp. 275–287. [Google Scholar] [CrossRef]
- Milliman, J.D.; Farnsworth, K.L. River Discharge to the Coastal Ocean: A Global Synthesis; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Moreira-Turcq, P.; Seyler, P.; Guyot, J.L.; Etcheber, H. Exportation of organic carbon from the Amazon River and its main tributaries. Hydrol. Process. 2003, 17, 1329–1344. [Google Scholar] [CrossRef]
- Coynel, A.; Seyler, P.; Etcheber, H.; Meybeck, M.; Orange, D. Spatial and seasonal dynamics of total suspended sediment and organic carbon species in the Congo River. Glob. Biogeochem. Cycles 2005, 19, 1–17. [Google Scholar] [CrossRef]
- Balakrishna, K.; Probst, J.L. Organic carbon transport and C/N ratio variations in a large tropical river: Godavari as a case study, India. Biogeochemistry 2005, 73, 457–473. [Google Scholar] [CrossRef]
- Sarin, M.M.; Sudheer, A.K.; Balakrishna, K. Significance of riverine carbon transport: A case study of a large tropical river, Godavari (India). Sci. China 2002, 45, 97–108. [Google Scholar]
- Brunet, F.; Dubois, K.; Veizer, J.; Nkoue Ndondo, G.R.; Ndam Ngoupayou, J.R.; Boeglin, J.L.; Probst, J.L. Terrestrial and fluvial carbon fluxes in a tropical watershed: Nyong basin, Cameroon. Chem. Geol. 2009, 265, 563–572. [Google Scholar] [CrossRef]
- Gallay, M.; Mora, A.; Martinez, J.M.; Gardel, A.; Laraque, A.; Sarrazin, M.; Beaucher, E.; Doudou, J.C.; Lagane, C. Dynamics and fluxes of organic carbon and nitrogen in two Guiana shield river basins impacted by deforestation and mining activities. Hydrol. Process. 2018, 32, 17–29. [Google Scholar] [CrossRef]
- Liu, J.; Song, X.; Wang, Z.; Yang, L.; Sun, Z.; Wang, W. Variations of carbon transport in the Yellow River, China. Hydrol. Res. 2015, 46, 746–762. [Google Scholar] [CrossRef]
- Cai, W.-J.; Dai, M.; Zhang, L.; Guo, X.; Harrison, P.J.; Yin, K.; Zhai, W.; Lohrenz, S.E.; Wang, Y.; Chen, C.-T.A. A Comparative overview of weathering intensity and HCO3− flux in the world’s major rivers with emphasis on the Changjiang, Huanghe, Zhujiang (Pearl) and Mississippi Rivers. Cont. Shelf Res. 2008, 28, 1538–1549. [Google Scholar] [CrossRef]
- Depetris, P.; Kempe, S. Carbon dynamics and sources in the Parana River. Limnol. Oceanogr. 1993, 38, 382–395. [Google Scholar] [CrossRef]
- Amiotte Suchet, P.; Probst, J.-L.; Ludwig, W. Worldwide distribution of continental rock lithology: Implications for the atmospheric/Soil CO2 uptake by continental weathering and alkalinity river transport to the oceans. Glob. Biogeochem. Cycles 2003, 17, 2. [Google Scholar] [CrossRef]
- Hélie, J.-F.; Hillaire-Marcel, C.; Rondeau, B. Seasonal changes in the sources and fluxes of dissolved inorganic carbon through the St. Lawrence River—Isotopic and chemical constraint. Chem. Geol. 2002, 186, 117–138. [Google Scholar] [CrossRef]
- Degens, E.; Kempe, S.; Richey, J.E. SCOPE 42. Biogeochemistry of Major World Rivers Degens; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Meybeck, M. Riverine transport of atmospheric carbon: Sources, global typology and budget. Water Air Soil Pollut. 1993, 70, 443–463. [Google Scholar] [CrossRef]
- Bouillon, S.; Abril, G.; Borges, A.V.; Dehairs, F.; Govers, G.; Hughes, H.J.; Merckx, R.; Meysman, F.J.R.; Nyunja, J.; Osburn, C.; et al. Distribution, origin and cycling of carbon in the Tana River (Kenya): A dry season basin-scale survey from headwaters to the delta. Biogeosciences 2009, 6, 2475–2493. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Shim, M.-J.; Guo, L.; Shiller, A. Floodplain influence on carbon speciation and fluxes from the lower Pearl River, Mississippi. Geochim. Cosmochim. Acta 2016, 186, 189–206. [Google Scholar] [CrossRef]
- Aldrian, E.; Chen, T.A.; Adi, S.; Prihartanto; Sudiana, N.; Nugroho, S.P. Spatial and seasonal dynamics of riverine carbon fluxes of the Brantas catchment in East Java. J. Geophys. Res. Biogeosci. 2008, 113, G3. [Google Scholar] [CrossRef]
- Mann, P.J.; Spencer, R.G.M.; Dinga, B.J.; Poulsen, J.R.; Hernes, P.J.; Fiske, G.; Salter, M.E.; Wang, Z.A.; Hoering, K.A.; Six, J.; et al. The biogeochemistry of carbon across a gradient of streams and rivers within the Congo Basin. J. Geophys. Res. Biogeosci. 2014, 119, 687–702. [Google Scholar] [CrossRef]
- Atkins, M.L.; Santos, I.R.; Maher, D.T. Seasonal exports and drivers of dissolved inorganic and organic carbon, carbon dioxide, methane and δ13C signatures in a subtropical river network. Sci. Total Environ. 2017, 575, 545–563. [Google Scholar] [CrossRef]
- Tweed, S.; Leblanc, M.; Bass, A.; Harrington, G.A.; Munksgaard, N.; Bird, M.I. Leaky savannas: The significance of lateral carbon fluxes in the seasonal tropics. Hydrol. Process. 2016, 30, 873–887. [Google Scholar] [CrossRef]
- Mcclanahan, K.; Polk, J.; Groves, C.; Osterhoudt, L.; Grubbs, S. Dissolved inorganic carbon sourcing using δ 13C-DIC from a karst influenced river system. Earth Surf. Process Landf. 2015, 41, 392–405. [Google Scholar] [CrossRef]
- Hedges, J.I.; Mayorga, E.; Tsamakis, E.; Mcclain, M.E.; Quay, P.; Richey, J.E.; Benner, R.; Opsahl, S.; Black, B.; Quintanilla, J.; et al. Organic matter in Bolivian tributaries of the Amazon River: A comparison to the lower mainstream. Limnology 2000, 45, 1449–1466. [Google Scholar] [CrossRef]
- Dalmagro, H.J.; Johnson, M.S.; de Musis, C.R.; Lathuillière, M.J.; Graesser, J.; Pinto-Júnior, O.B.; Couto, E.G. Spatial patterns of DOC concentration and DOM optical properties in a Brazilian tropical river-wetland system. J. Geophys. Res. Biogeosci. 2017, 122, 1883–1902. [Google Scholar] [CrossRef]
- Rodiles Hernández, R.; González-Díaz, A.A.; González-Acosta, A.F. Ecosistemas acuáticos. In La Biodiversidad en Chiapas: Estudio de Estado; CONABIO: Mexico City, Mexico, 2013; pp. 45–57. [Google Scholar]
- The Ramsar Convention. Ramsar Sites Information Services. Available online: https://rsis.ramsar.org/es/ris-search/?language=es&f[0]=regionCountry_es_ss%3AGuatemala&pagetab=1 (accessed on 30 May 2019).
- CONAP. Consejo Nacional de Áreas Protegidas, Guatemala. Available online: http://www.conap.gob.gt/ (accessed on 15 July 2019).
- SEMARNAT. Secretaría de Medio Ambiente y Recursos Naturales, SEMARNAT. Available online: http://www.paot.org.mx/centro/ine-semarnat/informe02/estadisticas_2000/informe_2000/03_Suelos/3.1_Suelos/index.htm (accessed on 21 July 2019).
- INEGI. Instituto Nacional de Estadística y Geografía (INEGI). Available online: http://www.inegi.org.mx/ (accessed on 26 November 2018).
- Thurman, E.M. Organic Geochemistry of Natural Waters; Springer Science and Business Media LLC: Denver, CO, USA, 1985. [Google Scholar] [CrossRef]
- Abril, G.; Nogueira, M.; Etcheber, H.; Cabeçadas, G.; Lemaire, E.; Brogueira, M.J. Behaviour of organic carbon in nine contrasting European estuaries. Estuar. Coast. Shelf Sci. 2002, 54, 241–262. [Google Scholar] [CrossRef] [Green Version]
- Dudgeon, D. Tropical Stream Ecology; Elsevier: Amsterdam, the Netherlands, 2008. [Google Scholar]
- Wetzel, R. Limnology. Lake and River Ecosystem, 3rd ed.; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Wu, Y.; Zhang, J.; Liu, S.M.; Zhang, Z.F.; Yao, Q.Z.; Hong, G.H.; Cooper, L. Sources and distribution of carbon within the Yangtze River system. Estuar. Coast. Shelf Sci. 2007, 71, 13–25. [Google Scholar] [CrossRef]
- Carabias, J.; De la Maza, J.; Cadena, R. Caracterización de la subcuenca del Lacantún. In Conservación y Desarrollo Sustentable de la Selva Lacandona. 25 Años de Actividades y Experiencias; Carabias, J., de La Maza, J., Cadena, R., Eds.; Natura y Ecosistemas Mexicanos A.C.: Mexico City, Mexico, 2015; pp. 79–83. [Google Scholar]
- Albéric, P.; Pérez, M.A.; Moreira-Turcq, P.; Benedetti, M.F.; Bouillon, S.; Abril, G. Variation of the isotopic composition of dissolved organic carbon during the runoff cycle in the Amazon River and the floodplains. Comptes Rendus Geosci. 2018, 350, 65–75. [Google Scholar] [CrossRef]
- Aucour, A.-M.; Sheppard, S.M.F.; Guyomar, O.; Wattelet, J. Use of 13C to trace origin and cycling of inorganic carbon in the Rhône River System. Chem. Geol. 1999, 159, 87–105. [Google Scholar] [CrossRef]
- Tapia-Silva, F.-O.; Contreras-Silva, A.-I.; Rosales-Arriaga, E.-R. Hydrological characterization of the Usumacinta River basin towards the preservation of environmental services. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 1505. [Google Scholar] [CrossRef]
- Estrada Loreto, F.; Barba Macías, E.; Ramos Reyes, R. Cobertura temporal de los humedales en la cuenca el Usumacinta, Balancán, Tabasco, México. Univ. Cienc. 2013, 29, 141–151. [Google Scholar]
- Cruz-Ramírez, A.K.; Salcedo, M.; Sánchez, A.J.; Barba Macías, E.; Mendoza Palacios, J.D. Relationship among physicochemical conditions, chlorophyll-a concentration, and cater level in a tropical river–floodplain system. Int. J. Environ. Sci. Technol. 2018, 16, 3869–3876. [Google Scholar] [CrossRef]
- Castillo, M.M. Suspended sediment, nutrients, and chlorophyll in tropical floodplain lakes with different patterns of hydrological connectivity. Limnologica 2020, 82, 125767. [Google Scholar] [CrossRef]
- Sutfin, N.A.; Wohl, E.E.; Dwire, K.A. Banking Carbon: A review of organic carbon storage and physical factors influencing retention in floodplains and riparian ecosystems. Earth Surf. Process. Landf. 2016, 41, 38–60. [Google Scholar] [CrossRef]
- Sanders, L.; Taffs, K.H.; Stokes, D.J.; Sanders, C.J.; Smoak, J.M.; Enrich-Prast, A.; Macklin, P.A.; Santos, I.R.; Marotta, H. Carbon accumulation in Amazonian floodplain lakes: A significant component of Amazon budgets? Limnol. Oceanogr. Lett. 2017, 2, 29–35. [Google Scholar] [CrossRef]
- Plascencia-Vargas, H.; González-Espinosa, M.; Ramírez-Marcial, N.; Alvarez, D.; Musálem-Castillejos, K. Características físico-bióticas de la cuenca del Río Grijalva. In Montañas, Pueblos y Aguas. Dimensiones y Realidades de la Cuenca Grijalva; González-Espinosa, M., Brunel, M.C., Eds.; Ecosur: Campeche, Mexico, 2014; pp. 29–79. [Google Scholar]
- Lázaro-Vázquez, A.; Castillo, M.M.; Jarquín-Sánchez, A.; Carrillo, L.; Capps, K.A. Temporal changes in the hydrology and nutrient concentrations of a large tropical river: Anthropogenic influence in the lower Grijalva River, Mexico. River Res. Appl. 2018, 34, 649–660. [Google Scholar] [CrossRef]
- Maavara, T.; Lauerwald, R.; Regnier, P.; Van Cappellen, P. Global perturbation of organic carbon cycling by river damming. Nat. Commun. 2017, 8, 15347. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Wang, B.; Wang, F.; Peng, X. Sources and fluxes of particulate organic carbon in the Wujiang cascade reservoirs, southwest China. Inland Waters 2018, 8, 141–147. [Google Scholar] [CrossRef]
- Reiman, J.H.; Xu, Y.J. Dissolved carbon export and CO2 outgassing from the lower Mississippi River—Implications of future river carbon fluxes. J. Hydrol. 2019, 578, 124093. [Google Scholar] [CrossRef]
- Krishna, M.S.; Viswanadham, R.; Prasad, M.H.K.; Kumari, V.R.; Sarma, V.V.S.S. Export fluxes of dissolved inorganic carbon to the northern Indian Ocean from the Indian monsoonal rivers. Biogeosciences 2019, 16, 505–519. [Google Scholar] [CrossRef]
- Kumar Reddy, S.K.; Gupta, H.; Reddy, D.V. Dissolved inorganic carbon export by mountainous tropical rivers of the western Ghats, India. Chem. Geol. 2019, 530, 119316. [Google Scholar] [CrossRef]






| Code | DOC (mg L−1) | POC (mg L−1) | TOC (mg L−1) | DIC (mg L−1) | PIC (mg L−1) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| RS | DS | RS | DS | RS | DS | RS | DS | RS | DS | |
| M1 | 1.10 | 0.88 | 1.74 | 0.35 | 2.85 | 1.23 | 23.69 | 26.84 | 1.42 | 0.05 |
| 0.01 | 0.02 | 0.38 | 0.05 | 0.36 | 0.07 | 0.23 | 1.26 | 0.18 | 0.04 | |
| M2 | 1.34 | 1.44 | 2.02 | 0.21 | 3.36 | 1.64 | 22.91 | 15.59 | 1.51 | 0.12 |
| 0.34 | 0.49 | 0.63 | 0.01 | 0.29 | 0.48 | 0.11 | 0.15 | 0.38 | 0.10 | |
| M3 | 1.54 | 1.30 | 3.78 | 0.36 | 5.32 | 1.66 | 34.25 | 31.64 | 1.38 | 0.09 |
| 0.60 | 0.10 | 0.73 | 0.08 | 0.78 | 0.07 | 0.99 | 0.21 | 0.53 | 0.04 | |
| M4 | 1.39 | 1.00 | 1.27 | 0.30 | 2.67 | 1.30 | 47.19 | 35.19 | 0.27 | 0.08 |
| 0.07 | 0.18 | 0.06 | 0.02 | 0.07 | 0.15 | 0.17 | 2.85 | 0.19 | 0.01 | |
| M5 | 1.98 | 0.96 | 2.32 | 0.27 | 4.30 | 1.23 | 31.41 | 31.38 | 1.42 | 0.07 |
| 0.06 | 0.11 | 0.73 | 0.02 | 0.64 | 0.06 | 5.82 | 0.56 | 0.27 | 0.01 | |
| M6 | 2.72 | 1.82 | 1.27 | 0.97 | 3.96 | 2.79 | 23.38 | 23.83 | 1.17 | 0.24 |
| 0.15 | 0.22 | 0.26 | 0.17 | 0.34 | 0.16 | 1.54 | 3.25 | 0.25 | 0.09 | |
| M7 | 4.68 | 1.50 | 0.44 | 0.36 | 5.12 | 1.87 | 31.13 | 48.27 | 0.09 | 0.06 |
| 0.22 | 0.21 | 0.05 | 0.05 | 0.11 | 0.13 | 2.47 | 0.29 | 0.06 | 0.03 | |
| M8 | 3.72 | 1.66 | 1.02 | 0.79 | 4.74 | 2.44 | 28.63 | 36.11 | 0.71 | 0.18 |
| 0.49 | 0.23 | 0.09 | 0.17 | 0.42 | 0.16 | 0.94 | 1.51 | 0.35 | 0.14 | |
| M9 | 2.78 | 1.82 | 1.07 | 0.89 | 3.86 | 2.71 | 28.34 | 28.76 | 0.25 | 0.17 |
| 0.26 | 0.51 | 0.15 | 0.09 | 0.17 | 0.50 | 0.93 | 1.67 | 0.10 | 0.10 | |
| M10 | 3.00 | 1.45 | 0.96 | 0.61 | 3.97 | 2.06 | 31.16 | 37.58 | 0.48 | 0.26 |
| 0.13 | 0.32 | 0.05 | 0.03 | 0.19 | 0.22 | 0.28 | 1.31 | 0.42 | 0.10 | |
| B1 | 7.11 | 3.26 | 0.64 | 0.75 | 7.75 | 4.02 | 29.91 | 37.44 | 0.11 | - |
| 0.32 | 0.40 | 0.04 | 0.02 | 0.29 | 0.38 | 0.44 | 0.50 | 0.03 | - | |
| B2 | 3.02 | 1.60 | 1.09 | 0.93 | 4.14 | 2.53 | 30.16 | 38.58 | 0.48 | 0.14 |
| 0.16 | 0.08 | 0.42 | 0.12 | 0.35 | 0.22 | 0.95 | 0.05 | 0.16 | 0.15 | |
| B3 | 3.18 | 1.87 | 0.81 | 0.85 | 4.04 | 2.71 | 30.59 | 39.96 | 0.38 | 0.16 |
| 0.59 | 0.41 | 0.17 | 0.08 | 0.62 | 0.30 | 0.14 | 0.71 | 0.31 | 0.07 | |
| B4 | 3.73 | 1.94 | 1.40 | 1.18 | 5.13 | 3.12 | 30.80 | 35.61 | 0.32 | 0.40 |
| 0.06 | 0.12 | 0.02 | 0.26 | 0.08 | 0.14 | 0.0 | 1.51 | 0.09 | 0.08 | |
| B5 | 3.30 | 1.62 | 1.62 | 0.79 | 4.92 | 2.41 | 29.86 | 34.52 | 0.27 | 0.26 |
| 0.26 | 0.30 | 0.54 | 0.18 | 0.41 | 0.14 | 0.26 | 3.37 | 0.30 | 0.10 | |
| B6 | 5.23 | 2.02 | 2.42 | 0.60 | 7.65 | 2.63 | 29.04 | 31.74 | 0.37 | 0.22 |
| 0.35 | 0.29 | 0.44 | 0.07 | 0.43 | 0.30 | 1.07 | 0.06 | 0.10 | 0.05 | |
| B7 | 4.73 | 1.62 | 2.57 | 0.52 | 7.30 | 2.15 | 29.17 | 31.27 | 0.53 | 0.10 |
| 0.70 | 0.22 | 1.00 | 0.09 | 1.70 | 0.19 | 0.19 | 2.26 | 0.29 | 0.05 | |
| B8 | 6.90 | 2.86 | 2.24 | 1.45 | 9.14 | 4.31 | 30.50 | 31.61 | 0.82 | 0.21 |
| 0.87 | 0.52 | 0.46 | 0.16 | 0.50 | 0.19 | 0.13 | 1.55 | 0.41 | 0.01 | |
| Average | 3.42 | 1.70 | 1.59 | 0.68 | 5.01 | 2.38 | 30.12 | 33.11 | 0.67 | 0.17 |
| SD | 1.77 | 0.60 | 0.84 | 0.34 | 1.81 | 0.86 | 5.20 | 6.99 | 0.49 | 0.09 |
| Minimum | 1.10 | 0.88 | 0.44 | 0.21 | 2.67 | 1.23 | 22.91 | 15.59 | 0.09 | 0.05 |
| Maximum | 7.11 | 3.26 | 3.78 | 1.45 | 9.14 | 4.31 | 47.19 | 48.27 | 1.51 | 0.40 |
| Code | Q | DOC Flux | POC Flux | TOC Flux | DIC Flux | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (m3 s−1) | (t d−1) | (t d−1) | (t d−1) | (t d−1) | |||||||
| RS | DS | RS | DS | RS | DS | RS | DS | RS | DS | ||
| Input | M10 | 5970 | 998 | 1549.0 | 124.8 | 497.7 | 52.8 | 2046.8 | 177.7 | 16,073.4 | 3240.4 |
| Output | B5 | 2709 | 677 | 771.8 | 94.6 | 380.0 | 46.0 | 1151.8 | 140.6 | 6988.9 | 2018.0 |
| B8 | 368 | 146 | 219.7 | 36.0 | 71.2 | 18.3 | 290.9 | 54.3 | 970.4 | 398.5 | |
| Balance (input−output) | M10 − (B5 + B8) | 2893 | 175 | 557.5 | −5.8 | 46.5 | −11.5 | 604.1 | −17.2 | 8114.1 | 823.9 |
| Usumacinta basin export | B5 + B8 | 3077 | 823 | 991.5 | 130.6 | 451.2 | 64.3 | 1442.7 | 194.9 | 7959.3 | 2416.5 |
| Usumacinta-Grijalva | B7 | 5380 | 1048 | 2198.8 | 146.9 | 1192.9 | 47.5 | 3391.8 | 194.4 | 13,557.9 | 2830.2 |
| Usumacinta-Grijalva basin export | B7 + B8 | 5748 | 1194 | 2418.5 | 182.9 | 1264.1 | 65.8 | 3682.7 | 248.7 | 14,528.3 | 3228.7 |
| River | Watershed Area × | Q * | C (mg L−1) | Reference | ||
|---|---|---|---|---|---|---|
| 106 (km2) | (m3 s−1) | DOC | POC | DIC | ||
| Usumacinta | 0.07 | 15 to 5970 | 2.56 (0.88–7.11) | 1.14 (0.21–3.78) | 31.6 (15.6–47.2) | This study |
| Amazon | 6.30 | 209,000 | 5.65 (3.4–10.25) | 1.25 (0.44–4.46) | 1.4 | [25,92] |
| Congo/Zaire | 3.80 | 42,000 | 7.78 (3.5–11.8) | 1.57 (0.7–2.3) | 3.1 | [25,93] |
| Mississippi | 3.30 | 18,074 | 3.7 (2.9–4.1) | 4.3 (1.9–9.7) | 29.1 (19.2–41.4) | [18,31] |
| Orinoco | 1.10 | 34,880 | 2.92 (1.75–4.12) | 0.91 (0.24–2.29) | 2.0 | [38,77] |
| Irrawaddy | 0.43 | 12,049 | 1.2–2.9 | 1.2–5.2 | 23.6 | [45,77] |
| Negro | 0.68 | 28,400 | 12.7 (3–18) | 0.72 (0.26–1.09) | [92] | |
| Zambezi | 1.30 | 3171 | 1.2–4.9 | 6.3 | [77,89] | |
| Godavari | 0.31 | 2917 | 1.3–4 | 7.2 (0.3–20) | 34.8 (6–53) | [94,95] |
| Red | 0.15 | 2109 | 2.0 (0.1–8.5) | 1.5 (0.1–9.0) | 19.6 (9.1–29.9) | [54,55] |
| Senegal | 0.27 | 697 | 2.1 (1.25–3.25) | 0.2–4.0 | [50,77] | |
| Nyong | 0.03 | 193 | 16.0 (6.4–51) | 3.77 (1.6–8.1) | [96] | |
| Maroni | 0.07 | 1807 | 5.8 (2.12–11.34) | 1.8 (0.45–4.5) | [97] | |
| Tana | 0.04 | 150 | 0.2–6.9 | 0.3–120 | 13.2 (2.4–57.6) | [47,48] |
| River | Area | Q | C Flux (Tg C año−1) | Yield (t C km2 yr−1) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 106 (km2) | (km3 año−1) | DOC | POC | DIC | DOC | POC | DIC | ||
| Usumacinta-Grijalva | 0.112 | 120–147 | 0.29 (0.26–0.33) | 0.12 (0.07–0.18) | 2.44 (2.29–2.59) | 2.61 (2.36–2.99) | 1.11 (0.69–1.59) | 21.70 (20.4–23.1) | |
| [92] | Amazonas | 6.30 | 6223 | 26.9 | 13.2 | 29.4 | 5.8 | 5.5 | 4.3 |
| [25,93] | Congo | 3.80 | 1300 | 12.4 | 2.0 | 3.5 | 3.5 | 0.6 | 1.0 |
| [26,34] | Orinoco | 1.10 | 1135 | 5.0 | 1.7 | 5.7 | 4.8 | 1.6 | 5.5 |
| [18,99,137] | Mississippi | 3.30 | 570 | 3.95 | 2.3 | 12.25 | 1.4 | 2.3 | 4.2 |
| [52,99,103] | Yellow | 0.75 | 15 (43) | 0.06 | 0.41 | 1.05 | 0.1 | 0.54 | 1.632 |
| [45] | Irrawaddy | 0.43 | 380 (430) | 0.9 | 2.3–4.3 | - | 2.2 | 5.5–10.4 | - |
| [26,77] | Danube | 0.79 | 210.0 | 0.6 | - | 7.5 | 1.2 | 7.7–12.6 | 9.6 |
| [26,34,89] | Zambezi | 1.31 | 109.0 | 0.6 | 0.5 | - | 0.1–0.2 | 0.1 | 0.7 |
| [99,103] | Niger | 1.2 | 152 | 0.53 | 0.66 | 1.24 | 0.6 | 0.5 | 0.56 |
| [34,94] | Godavari | 0.31 | 92 (120) | 0.76 | 0.28 | 2.27 | - | - | 8.0 |
| [97] | Maroni | 0.07 | 63.7 | 0.34 | 0.11 | - | 5.6 | 1.9 | - |
| [50,77] | Senegal | 0.27 | 24.4 | 0.1 | 0.1 | - | 0.2 | 0.1 | - |
| [49,51,77] | Tana | 0.04 | 15 | 11.2 | 113.3 | 73.4 | 0.1 | 1.4 | 0.9 |
| [11] | Tropics | 63.8 | 25,123 | 136.0 | 131 | 210.0 | 2.05 | 2.13 | 3.3 |
| [11] | Global | 150.0 | 37,400 | 215 | 205 | 385 | 1.4 | 1.3 | 2.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soria-Reinoso, I.; Alcocer, J.; Sánchez-Carrillo, S.; García-Oliva, F.; Cuevas-Lara, D.; Cortés-Guzmán, D.; Oseguera, L.A. The Seasonal Dynamics of Organic and Inorganic Carbon along the Tropical Usumacinta River Basin (Mexico). Water 2022, 14, 2703. https://doi.org/10.3390/w14172703
Soria-Reinoso I, Alcocer J, Sánchez-Carrillo S, García-Oliva F, Cuevas-Lara D, Cortés-Guzmán D, Oseguera LA. The Seasonal Dynamics of Organic and Inorganic Carbon along the Tropical Usumacinta River Basin (Mexico). Water. 2022; 14(17):2703. https://doi.org/10.3390/w14172703
Chicago/Turabian StyleSoria-Reinoso, Ismael, Javier Alcocer, Salvador Sánchez-Carrillo, Felipe García-Oliva, Daniel Cuevas-Lara, Daniela Cortés-Guzmán, and Luis A. Oseguera. 2022. "The Seasonal Dynamics of Organic and Inorganic Carbon along the Tropical Usumacinta River Basin (Mexico)" Water 14, no. 17: 2703. https://doi.org/10.3390/w14172703
APA StyleSoria-Reinoso, I., Alcocer, J., Sánchez-Carrillo, S., García-Oliva, F., Cuevas-Lara, D., Cortés-Guzmán, D., & Oseguera, L. A. (2022). The Seasonal Dynamics of Organic and Inorganic Carbon along the Tropical Usumacinta River Basin (Mexico). Water, 14(17), 2703. https://doi.org/10.3390/w14172703











