A Coupled SWAT-AEM Modelling Framework for a Comprehensive Hydrologic Assessment
Abstract
:1. Introduction
- (a)
- How can we conserve and manage today’s SW/GW resources for the future?
- (b)
- How do we maintain the proper balance between both SW/GW systems for the long-term sustainability of water resources?
2. Materials and Methods
2.1. Development of the Integrated SWAT-AEM Model
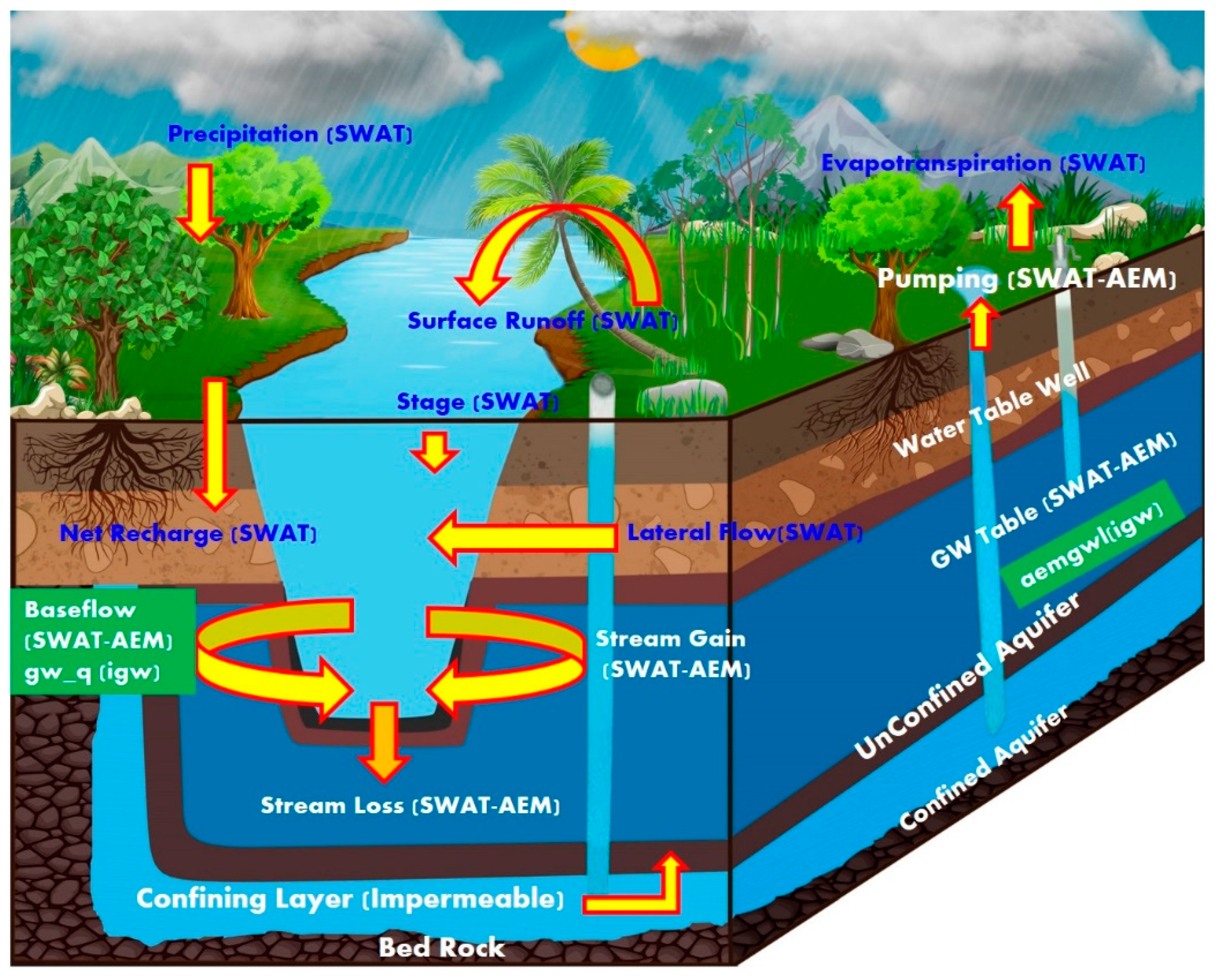
2.1.1. Brief Conceptual Overview of SWAT
2.1.2. Brief Conceptual Overview of AEM
2.2. Methodology
General GW Flow Equations and Assumptions of the AEM Model
- i.
- The two-dimensional steady-state GW model wherein the GW equations are derived from a two-dimensional mass balance of water, where the head does not vary in the vertical direction (a by-product of the Dupuit–Forchheimer assumption). Dupuit’s assumption states that groundwater moves horizontally in an unconfined aquifer and that the groundwater discharge is proportional to the saturated aquifer thickness.
- ii.
- All geologic formations are horizontal
- iii.
- The aquifer is isotropic and homogeneous
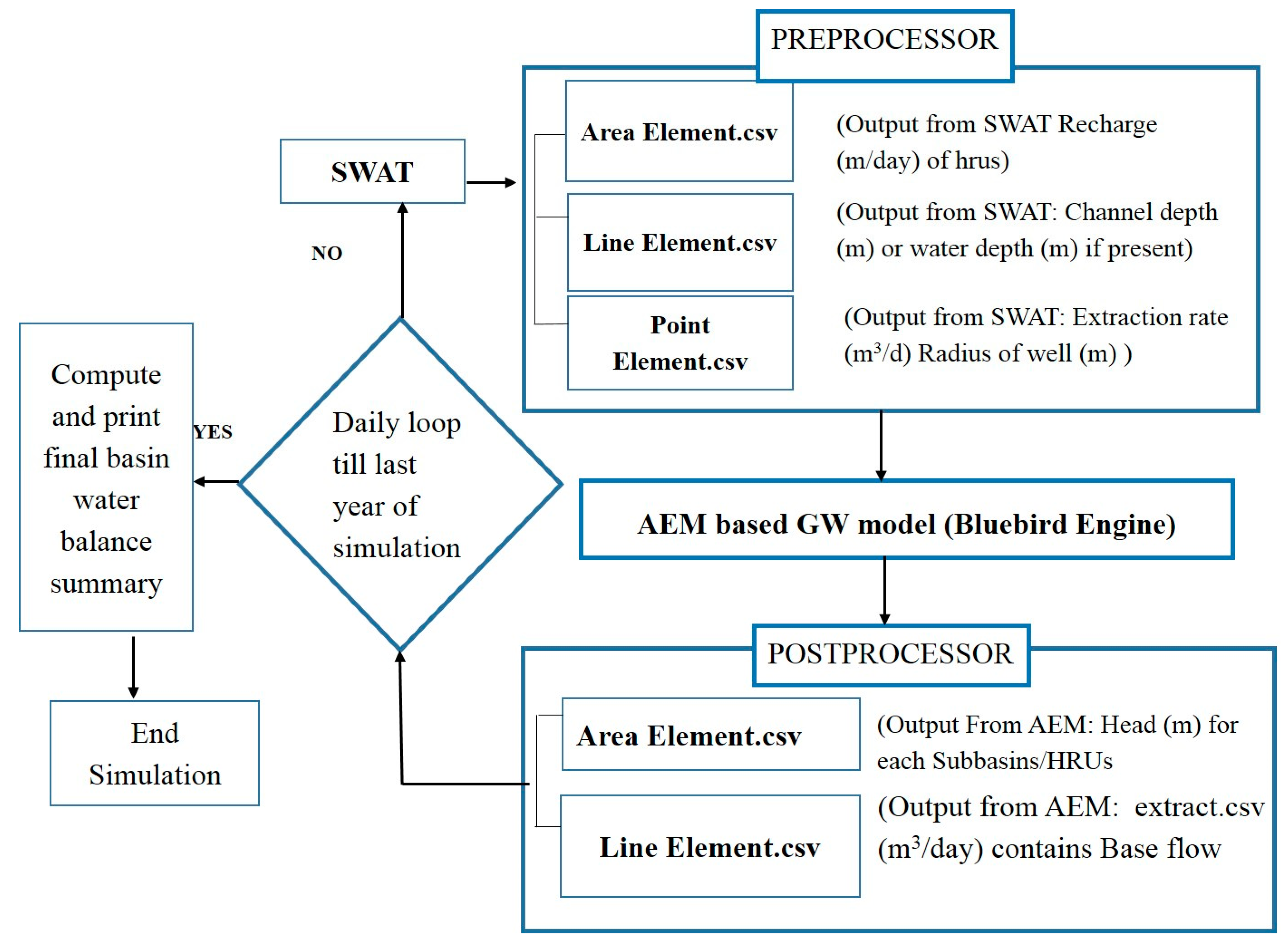
2.3. Structure of SWAT-AEM Linkage
2.4. Conversion of SWAT SW Features to Analytic Elements
2.5. Boundary Conditions for Quasi Steady-State Simulations
2.6. Model Application to the Study Region
Study Area Description
2.7. SWAT model for the San Jacinto River Basin (SJRB)
2.7.1. Model Construction
2.7.2. Model Calibration (SWATCUP)
3. Results and Discussions
3.1. SW-GW Assessment in SWATAEM Model
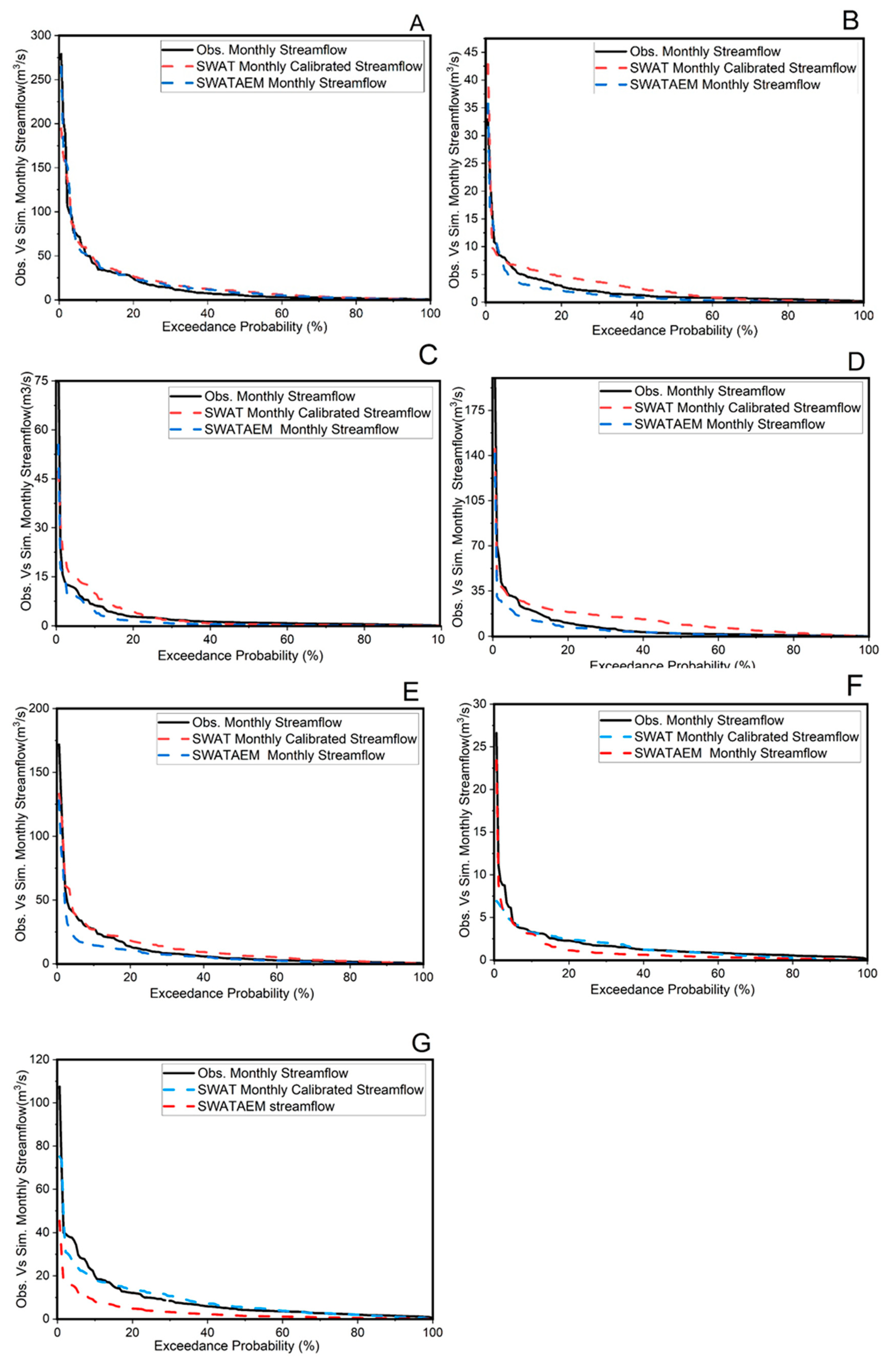
3.1.1. Stream Flow
3.1.2. Ground Water (GW) Levels
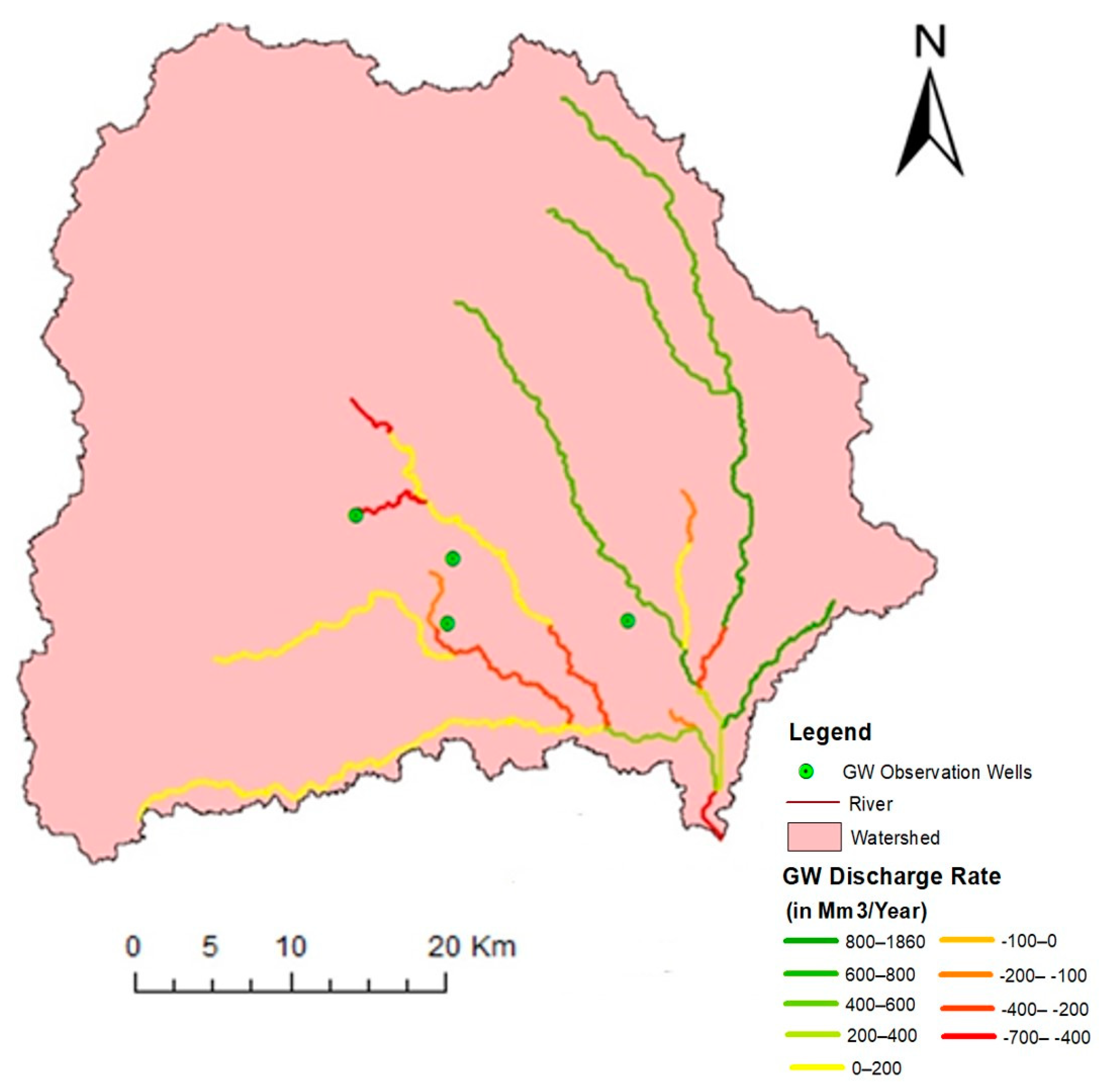
3.1.3. Ground Water Discharge Rates
3.1.4. Overall Water Balance
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Knapp, K.C.; Weinberg, M.; Howitt, R.; Posnikoff, J.F. Water transfers, agriculture, and ground water management: A dynamic economic analysis. J. Environ. Manag. 2003, 67, 291–301. [Google Scholar] [CrossRef]
- de Roo, A.; Bisselink, B.; Beck, H.; Bernhard, J.; Burek, P.; Reynaud, A.; Pastori, M.; Lavalle, C.; Jacobs, C.; Baranzelli, C.; et al. Modelling Water Demand and Availability Scenarios for Current and Future Landuse and Climate in the Sava River Basin; Publications Office of the European Union: Luxembourg, 2016; EUR 27701 EN. [Google Scholar]
- El-Kadi, A.I. Watershed models and their applicability to conjunctive use management. Water Resour. Bull. 1989, 25, 125–137. [Google Scholar] [CrossRef]
- Werner, M.; Reggiani, P.; de Roo, A.; Bates, P.; Sprokkereef, E. Flood forecasting and warning at the river basin and at the European scale. Nat. Hazards 2005, 36, 25–42. [Google Scholar] [CrossRef]
- de Graaf, I.E.M.; Sutanudjaja, E.H.; van Beek, L.P.H.; Bierkens, M.F.P. A high-resolution global-scale groundwater model. Hydrol. Earth Syst. Sci. 2015, 19, 823–837. [Google Scholar] [CrossRef]
- De Lange, W.J. A Groundwater Model of The Netherlands; Tech. Rep.90.066; National Institute for Inland Water Management and Waste Water Treatment: Lelystad, The Netherlands, 1991. [Google Scholar]
- Sutanudjaja, E.H.; van Beek, L.P.H.; de Jong, S.M.; van Geer, F.C.; Bierkens, M.F.P. Calibrating a large-extent high-resolution coupled groundwater-land surface model using soil moisture and discharge data. Water Resour. Res. 2013, 50, 687–705. [Google Scholar] [CrossRef]
- Sophocleous, M. Interactions between Groundwater and Surface Water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Niraula, R.; Norman, L.M.; Meixner, T.; Callegary, J.B. Multi-gauge Calibration for modeling the Semi-Arid Santa Cruz Watershed in Arizona-Mexico Border Area Using SWAT. Air Soil Water Res. 2012, 5, 41–57. [Google Scholar] [CrossRef]
- Xie, X.; Cui, Y. Development and test of SWAT for modelling hydrological processes in irrigation districts with paddy rice. J. Hydrol. 2011, 396, 61–71. [Google Scholar] [CrossRef]
- Azimi, M.; Heshmati, G.A.; Farahpour, M.; Faramarzi, M.; Abbaspour, K.C. Modeling the impact of rangeland management on forage production of sagebrush species in arid and semi-arid regions of Iran. Ecol. Model. 2013, 250, 1–44. [Google Scholar] [CrossRef]
- Ye, L.; Grimm, N.B. Modelling potential impacts of climate change on water and nitrate export from a mid-sized, semiarid watershed in the US Southwest. Clim. Change 2013, 120, 419–431. [Google Scholar] [CrossRef]
- Raneesh, K.Y.; Santosh, G.T. A study on the impact of climate change on stream flow at the watershed scale in the humid tropics. Hydrol. Sci. J. 2011, 56, 946–965. [Google Scholar] [CrossRef]
- Chemingui, A.; Horriche, F. Implementation of a Hydrological Model of Groundwater Recharge for the Chiba Catchment (Cap-Bon, Tunisia); Centre Eau Terre Environment: Quebec City, QC, Canada, 2013. [Google Scholar]
- Mitchell-Bruker, S.; Haitjema, H.M. Modelling steady state conjunctive GW and SW flow with analytic elements. Water Resour. Res. 1996, 32, 2725–2732. [Google Scholar] [CrossRef]
- Jin, X.; Sridhar, V. An Integrated Model Coupling VIC and MODFLOW to Study the Hydrological Prediction at the Snake River Basin; EPSCOR Publications: Albuquerque, NM, USA, 2010. [Google Scholar]
- Arnold, J.G.; Allen, P.M.; Bernhardt, G. A comprehensive surface—GW flow model. J. Hydrol. 1993, 142, 47–69. [Google Scholar] [CrossRef]
- Liu, W.; An, W.; Jeppesen, E.; Ma, J.; Yang, M.; Trolle, D. Modelling the fate and transport of Cryptosporidium, a zoonotic and waterborne pathogen, in the Daning River watershed of the Three Gorges Reservoir Region, China. J. Environ. Manag. 2019, 232, 462–474. [Google Scholar] [CrossRef] [PubMed]
- Markstrom, S.L.; Niswonger, R.G.; Regan, R.S.; Prudic, D.E.; Barlow, P.M. GSFLOW—Coupled Ground-Water and Surface-Water Flow Model Based on the Integration of the Precipitation-Runoff Modeling System (PRMS) and the Modular Ground-Water Flow Model (MODFLOW-2005). In U.S. Geological Survey Techniques and Methods 6-D1; Geological Survey: Reston, VA, USA, 2008; p. 254. [Google Scholar]
- Sophocleous, M.; Perkins, S.P. Methodology and application of combined watershed and ground-water models in Kansas. J. Hydrol. 2000, 236, 185–201. [Google Scholar] [CrossRef]
- Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R.; Haney, E.B.; Neitsch, S.L. Input/Output Documentation, Chapter1; Texas Water Resources Institute: College Station, TX, USA, 2012. [Google Scholar]
- Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R.; Haney, E.B.; Neitsch, S.L. SWAT 2012 Input/Output Documentation; Texas Water Resources Institute: College Station, TX, USA, 2013. [Google Scholar]
- Refsgaard, J.C.; Storm, B. MIKE SHE. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1995; pp. 809–846. [Google Scholar]
- Tian, Y.; Zheng, Y.; Wu, B.; Wu, X.; Liu, J.; Zheng, C. Modeling surface water-groundwater interaction in arid and semi-arid regions with intensive agriculture. Environ. Model. Softw. 2015, 63, 170–184. [Google Scholar] [CrossRef]
- Sudicky, E.A.; Jones, J.P.; Park, Y.J.; Brookfield, A.E.; Colautti, D. Simulating complex flow and transport dynamics in an integrated surface-subsurface modeling framework. Geosci. J. 2008, 12, 107–122. [Google Scholar] [CrossRef]
- Gayathri, K.D.; Ganasri, B.P.; Dwarakish, G.S. A review on hydrological models. In Proceedings of the ICWRCOE Conference, Karnataka, India, 12–14 December 2015; Aquatic Procedia 4. pp. 1001–1007. [Google Scholar]
- Behera, S.; Panda, R.K. Evaluation of management alternatives for an agricultural watershed in a sub-humid subtropical region using a physical process based model. Agric. Ecosyst. Environ. 2006, 113, 62–72. [Google Scholar] [CrossRef]
- Swain, E.D.; Wexler, E.J. A Coupled Surface-Water and Ground-Water Flow Model (MODBRANCH) for Simulation of Stream–Aquifer Interaction: U.S. Geological Survey Techniques of Water-Resources Investigations; Book 6, Chapter A6; U.S. Geological Survey, Information Services: Reston, VA, USA, 1996; p. 125. [Google Scholar]
- Sophocleous, M.A.; Koelliker, J.K.; Govindaraju, R.S.; Birdie, T.; Ramireddygari, S.R.; Perkins, S.P. Integrated numerical modelling for basin-wide water management: The case of the Rattlesnake Creekbasin in south-central Kansas. J. Hydrol. 1999, 214, 179–196. [Google Scholar] [CrossRef]
- Panday, S.; Huyakorn, P.S. A fully coupled physically-based spatially-distributed model for evaluating surface/subsurface flow. Adv. Water Resour. 2004, 27, 361–382. [Google Scholar] [CrossRef]
- Guzha, A.C. Modeling the interaction of surface and sub SW flow by linking TOPMODEL and MODFLOW. Int. J. Water 2013, 7, 191–205. [Google Scholar] [CrossRef]
- Aliyari, F.; Bailey, R.T.; Tasdighi, A.; Dozier, A.; Arabi, M.; Zeiler, K. Coupled SWAT MODFLOW model for large-scale mixed agro urban river basins. Environ. Model. Softw. 2019, 115, 200–210. [Google Scholar] [CrossRef]
- Guzman, J.A.; Moriasi, D.N.; Gowda, P.H.; Steiner, J.L.; Starks, P.J.; Arnold, J.G.; Srinivasan, R. A model integration framework for linking SWAT and MODFLOW. J. Environ. Model. Softw. 2015, 73, 103–116. [Google Scholar] [CrossRef]
- ASCE Task Committee. Criteria for evaluation of watershed models. J. Irrigat. Drain. Eng. 1993, 119, 429–442. [Google Scholar] [CrossRef]
- Abbas, S.; Xuan, Y.; Bailey, R. Improving River Flow Simulation Usinga Coupled Surface-Groundwater Model for Integrated Water Resources Management. EPiC Ser. Eng. 2018, 3, 1–9. [Google Scholar]
- Bailey, R.T.; Wible, T.C.; Arabi, M.; Records, R.M.; Ditty, J. Assessing Regional-Scale Spatio-Temporal Patterns of Groundwater-Surface Water Interactions Using a Coupled SWAT-MODFLOW Model. Hydrol. Processes 2016, 30, 4420–4433. [Google Scholar] [CrossRef]
- Gao, F.; Feng, G.; Han, M.; Dash, P.; Jenkins, J.; Liu, C. Assessment of Surface Water Resources in the Big Sunflower River Watershed using Coupled SWAT-MODFLOW Model. Water 2019, 11, 528. [Google Scholar] [CrossRef]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and application of the integrated SWAT-MODFLOW model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Rathjens, H.; Beiger, K.; Bailey, R. SWATMOD-Prep: Interface for Preparing SWATMODFLOW Simulations, User Manual; Colorado State University: Fort Collins, CO, USA, 2016. [Google Scholar]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development applications, and future Research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Guzman, J.A.; Moriasi, D.N.; Gowda, P.H.; Steiner, J.L.; Arnold, J.G.; Srinivasan, R. An integrated hydrologic modelling framework for coupling SWAT with MODFLOW. In Proceedings of the International SWAT Conference & Workshop 2012, New Delphi, India, 16–17 July 2012. [Google Scholar]
- Strack, O.D.L. Groundwater Mechanics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Haitjema, H.M. Analytic Element Modeling of Groundwater Low; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Haitjema, H.M. Modeling regional ground-water flow in Fulton County, Indiana: Using the analytic element method. Groundwater 1992, 30, 660–666. [Google Scholar] [CrossRef]
- Strack, O.D.L.; Haitjema, H.M.; Melnyk, J. Interactive modelling of the aquifers near the Tennessee-Tombigbee Waterway. In Symposium on Water and Related Land Resource Systems; Ohio.International.Federal.Automation.Control: Cleveland, OH, USA, 1980. [Google Scholar]
- Kelson, V.A.; Hunt, R.J.; Haitjema, H.M. Improving a regional model using reduced complexity and parameter estimation. Ground Water 2002, 40, 132–143. [Google Scholar] [CrossRef]
- WHAEM. Available online: https://www.epa.gov/ceam/wellhead-analytic-element-model-whaem (accessed on 3 July 2016).
- VisualAEM. Available online: https://www.civil.uwaterloo.ca/jrcraig/visualaem/main.html (accessed on 15 March 2014).
- James, R.; Matott, C.L.S. Visual AEM v1.0 Users Manual. Available online: https://www.civil.uwaterloo.ca/jrcraig/visualaem/main.html (accessed on 15 March 2014).
- Fitts, R.; Joshua, G.; Kathaleen, F.; Charles, M.; Seth, M. Analytic Element Modeling of Steady Interface Flow in multilayer aquifers using AnAqsim. Ground Water 2010, 53, 432–439. [Google Scholar] [CrossRef]
- Bakker, M.; Anderson, E.I.; Olsthoorn, N.; Strack, O.D.L. Regional GW modeling of the Yucca Mountain Site using analytic elements. J. Hydrol. 1999, 226, 167–178. [Google Scholar] [CrossRef]
- Bakker, M.; Strack, O.D.L. Analytic Elements for Multiaquifer Flow. J. Hydrol. 2003, 271, 119–129. [Google Scholar] [CrossRef]
- Hunt, R.J. GW modelling applications using the analytic element method. Groundwater 2006, 44, 5–15. [Google Scholar] [CrossRef]
- Soil and Water Assessment Tool, 2015. ArcSWAT Ver. 2012.10_1.18. Available online: http://swat.tamu.edu/software/arcswat/ (accessed on 9 September 2015).
- Hooghoudt, S.B. Bijdrage tot de kennis van enige natuurkundige grootheden van de grond. Versl. Landbouwkd. Onderz. 1940, 46, 515–707. [Google Scholar]
- Smedema, L.K.; Rycroft, D.W. Land Drainage—Planning and Design of Agricultural Drainage Systems; Cornell University Press: Ithica, NY, USA, 1983. [Google Scholar]
- Texas Natural Resource Consevation Commission; Parsons Engineering Science. Report on Surface Water/Groundwater Interaction Evaluation for 22 Texas River Basins; INC: New York, NY, USA, 1999. [Google Scholar]
- TWDB (Texas Water Development Board). Available online: https://s3.amazonaws.com/gw-models/USGS.HAGM.Archive.20131111.Version1.1.zip (accessed on 3 October 2018).
- TWDB (Texas Water Development Board). Available online: https://www3.twdb.texas.gov/apps/reports/WU/SumFinal_CountyPumpage (accessed on 10 July 2018).
- TWDB (Texas Water Development Board). Available online: http://www.twdb.texas.gov/groundwater/data/gwdbrpt.asp (accessed on 15 October 2018).
- TWDB (Texas Water Development Board). Available online: https://www.waterdatafortexas.org/groundwater (accessed on 15 October 2018).
- TWDB (Texas Water Development Board). Available online: https://www3.twdb.texas.gov/apps/reports/WU/SumFinal_CountyReport (accessed on 10 July 2018).
- TWDB (Texas Water Development Board). Available online: https://www.twdb.texas.gov/publications/reports/numbered_reports/doc/R380_AquifersofTexas.pdf (accessed on 16 July 2015).
- U.S. Geological Survey. 1993. Available online: https://apps.nationalmap.gov/downloader/#productSearch (accessed on 20 July 2018).
- Natural Resources Conservation Service, and United States Department of Agriculture.USADA-Cropland Data Layer(CDL). Available online: https://datagateway.nrcs.usda.gov/GDGOrder.aspx (accessed on 3 March 2016).
- Natural Resources Conservation Service, and United States Department of Agriculture. U.S. Generic Soil Map (STATSGO2). Available online: https://sdmdataaccess.sc.egov.usda.gov/ (accessed on 3 March 2016).
- U.S. Geological Survey, Texas Daily Streamflow Current Conditions. Available online: https://waterdata.usgs.gov/tx/nwis/current/?type=flow (accessed on 10 July 2018).
- Abbaspour, K.C. SWAT-CUP-2012: SWAT Calibration and Uncertainty Programs—A User Manual; Swiss Federal Institute of Aquatic Science and Technology: Dubendorf, Switzerland, 2012. [Google Scholar]
- Kollet, S.; Sulis, M.; Maxwell, R.M.; Paniconi, C.; Putti, M.; Bertoldi, G.; Coon, E.T.; Cordano, E.; Endrizzi, S.; Kikinzon, E. The integrated hydrologic model intercomparison project: A second set of benchmark results to diagnose integrated hydrology and feedbacks. Water Resour. Res. 2016, 53, 867–890. [Google Scholar] [CrossRef]
- Mishra, A.; Kar, S. Modelling hydrologic processes and NPS pollution in a small watershed in sub humid subtropics using SWAT. J. Hydrol. Eng. 2012, 17, 445–454. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. J. Am. Soc. Agri. Biol. Eng. 2007, 50, 885–900. [Google Scholar]
- Molina-Navarro, E.; Andersen, H.E.; Nielsen, A.; Thodsen, H.; Trolle, D. The impact of the objective function in multi-site and multi-variable calibration of the SWAT model. Environ. Model. Softw. 2017, 93, 255–267. [Google Scholar] [CrossRef]
- Molina-Navarro, E.; Bailey, R.T.; Andersen, H.E.; Thodsen, H.; Nielsen, A.; Park, S.; Jensen, J.S.; Jensen, J.B.; Trolle, D. Comparison of abstraction scenarios simulated by SWAT and SWAT-MODFLOW. Hydrol. Sci. J. 2019, 64, 434–454. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Muttiah, R.; Bernhardt, G. Automated baseflow separation and recession analysis techniques. Ground Water 1995, 33, 1010–1018. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Automated methods for estimating baseflow and ground water recharge from streamflow records. J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]







| SI.NO | Aquifer Properties | Range of Values |
|---|---|---|
| 1 | Aquifer Conductivity (k) | 2 × 10−5 to 6 m/day |
| 2 | Specific storage (Ss) | 1.819 × 10−5 to 0.20 |
| 3 | Aquifer Thickness (H) | 0.305 to 659.892 m |
| 4 | Base Elevation | −595.399 to 137.902 m |
| Parameters | USGS Stream Flow Gauge Locations | ||||||
|---|---|---|---|---|---|---|---|
| 08068090 | 08070500 | 08071000 | 08070200 | 08068450 | 08068500 | 08069000 | |
| r*_CN2 | −0.0747 | −0.1691 | −0.1467 | −0.168 | −0.1857 | −0.0790 | −0.1493 |
| r*_SOLAWC | −0.0522 | −0.2083 | 0.4003 | 0.481 | 0.4418 | 0.2278 | 0.3543 |
| r*_SOL_K | −0.3912 | 0.4248 | −0.4733 | −0.133 | 0.0023 | 0.1463 | 0.2003 |
| v*_SURLAG | 2.8022 | 5.1423 | 8.0268 | 7.081 | 9.4802 | 8.4587 | 5.6463 |
| v*_ESCO | 0.9179 | 0.7221 | 0.7421 | 0.901 | 0.6551 | 0.6165 | 0.6729 |
| v*_ALPHABF | 0.7961 | 0.5521 | 0.9800 | 0.079 | 0.6170 | 0.6070 | 0.8096 |
| v*_GWDELAY | 29.2607 | 40.996 | 1.5023 | 1.232 | 27.6682 | 22.3273 | 49.6447 |
| r*_GWQMN | 0.1375 | −0.0105 | 0.1177 | −0.115 | −0.0515 | 0.0187 | 0.0519 |
| r*_REVAPMN | −0.1297 | 0.0015 | −0.1837 | 0.161 | −0.1327 | 0.0377 | 0.1395 |
| r*_RECHG_DP | 0.0184 | 0.1525 | 0.1971 | 0.163 | 0.0613 | 0.1152 | 0.0245 |
| v*_GWREVAP | 0.1589 | 0.1297 | 0.1793 | 0.151 | 0.0959 | 0.1366 | 0.0003 |
| Name of Stream Flow Gauge Station | Performance Statistics | SWAT | SWATAEM | ||||
|---|---|---|---|---|---|---|---|
| Daily | Monthly | Performance Rating Based on [71] | Daily | Monthly | Performance Rating Based on [71] | ||
| Peach Ck at Splendora, TX (USGS 08071000) | NSE | 0.520 | 0.644 | Satisfactory | 0.660 | 0.710 | Good |
| R2 | 0.521 | 0.522 | Satisfactory | 0.676 | 0.757 | Good | |
| PBIAS | 25 | 20 | Satisfactory | 8 | 8 | Very Good | |
| Caney Ck nr Splendora, TX (USGS 08070500) | NSE | 0.52 | 0.61 | Satisfactory | 0.664 | 0.73 | Good |
| R2 | 0.492 | 0.669 | Good | 0.599 | 0.767 | Very Good | |
| PBIAS | 28 | 12 | Good | 12 | 6.56 | Good | |
| W Fk San Jacinto Rv abv Lk Houston nr Porter, TX (USGS 08068090) | NSE | 0.412 | 0.517 | Satisfactory | 0.651 | 0.687 | Good |
| R2 | 0.38 | 0.555 | Good | 0.54 | 0.6473 | Good | |
| PBIAS | 31 | 11.04 | Good | 14 | 8.86 | Very Good | |
| E Fk San Jacinto Rv nr New Caney, TX (USGS 08070200) | NSE | 0.52 | 0.72 | Good | 0.57 | 0.804 | Very Good |
| R2 | 0.42 | 0.75 | Good | 0.65 | 0.821 | Very Good | |
| PBIAS | 13.30 | 13.95 | Good | 10.66 | 10.42 | Good | |
| Panther Br nr Spring, TX (USGS 08068450) | NSE | 0.52 | 0.56 | Satisfactory | 0.66 | 0.78 | Very Good |
| R2 | 0.461 | 0.69 | Satisfactory | 0.554 | 0.7473 | Good | |
| PBIAS | 18.0 | 18.20 | Satisfactory | 14 | 9 | Very Good | |
| Spring Ck nr Spring, TX (USGS 08068500) | NSE | 0.527 | 0.628 | Satisfactory | 0.6208 | 0.6405 | Satisfactory |
| R2 | 0.647 | 0.7886 | Very Good | 0.7324 | 0.8734 | Very Good | |
| PBIAS | 18 | 18.89 | Satisfactory | 15 | 14.56 | Good | |
| Cypress Ck nr Westfield, TX (USGS 08069000) | NSE | 0.43 | 0.587 | Satisfactory | 0.64 | 0.68 | Good |
| R2 | 0.5628 | 0.5909 | Good | 0.67 | 0.71 | Good | |
| PBIAS | 20.8 | 18.2 | Satisfactory | 14.29 | 14.28 | Good | |
| Name of Stream Flow Gauge Station | Observed Baseflow | SWAT | Difference (%) | SWATAEM | Difference (%) |
|---|---|---|---|---|---|
| Caney Ck nr Splendora, TX (USGS 08070500) | 0.47 | 0.25 | 46 | 0.38 | 19 |
| W Fk San Jacinto Rv abv Lk Houston nr Porter, TX (USGS 08068090) | 0.44 | 0.32 | 27 | 0.49 | −11 |
| Peach Ck at Splendora, TX (USGS 08071000) | 0.44 | 0.28 | 40 | 0.39 | 11 |
| E Fk San Jacinto Rv nr New Caney, TX (USGS 08070200) | 0.43 | 0.26 | 39 | 0.39 | 9 |
| Panther Br nr Spring, TX (USGS 08068450) | 0.41 | 0.35 | 15 | 0.49 | −19 |
| Spring Ck nr Spring, TX (USGS 08068500) | 0.38 | 0.22 | 42 | 0.30 | 21 |
| Cypress Ck nr Westfield, TX (USGS 08069000) | 0.41 | 0.25 | 39 | 0.34 | 15 |
| Water Balance Components (mm/year) | SWAT Model | SWAT-AEM Model |
|---|---|---|
| Precipitation | 1259.2 | 1259.2 |
| Surface flow | 225.06 | 302.208 |
| Lateral sub surface flow | 3.70 | 4.19 |
| Total Water yield | 403.90 | 337.7 |
| Actual Evapotranspiration | 795.6 | 818.48 |
| Potential Evapotranspiration | 1782.9 | 1782.9 |
| Aquifer recharge | 192.17 | 491.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sangeetha, K.; Narasimhan, B.; Srinivasan, R. A Coupled SWAT-AEM Modelling Framework for a Comprehensive Hydrologic Assessment. Water 2022, 14, 2753. https://doi.org/10.3390/w14172753
Sangeetha K, Narasimhan B, Srinivasan R. A Coupled SWAT-AEM Modelling Framework for a Comprehensive Hydrologic Assessment. Water. 2022; 14(17):2753. https://doi.org/10.3390/w14172753
Chicago/Turabian StyleSangeetha, K., Balaji Narasimhan, and R. Srinivasan. 2022. "A Coupled SWAT-AEM Modelling Framework for a Comprehensive Hydrologic Assessment" Water 14, no. 17: 2753. https://doi.org/10.3390/w14172753
APA StyleSangeetha, K., Narasimhan, B., & Srinivasan, R. (2022). A Coupled SWAT-AEM Modelling Framework for a Comprehensive Hydrologic Assessment. Water, 14(17), 2753. https://doi.org/10.3390/w14172753








