An Indirect Inversion Scheme for Retrieving Toxic Metal Concentrations Using Ground-Based Spectral Data in a Reclamation Coal Mine, China
Abstract
:1. Introduction
2. Materials and Methods
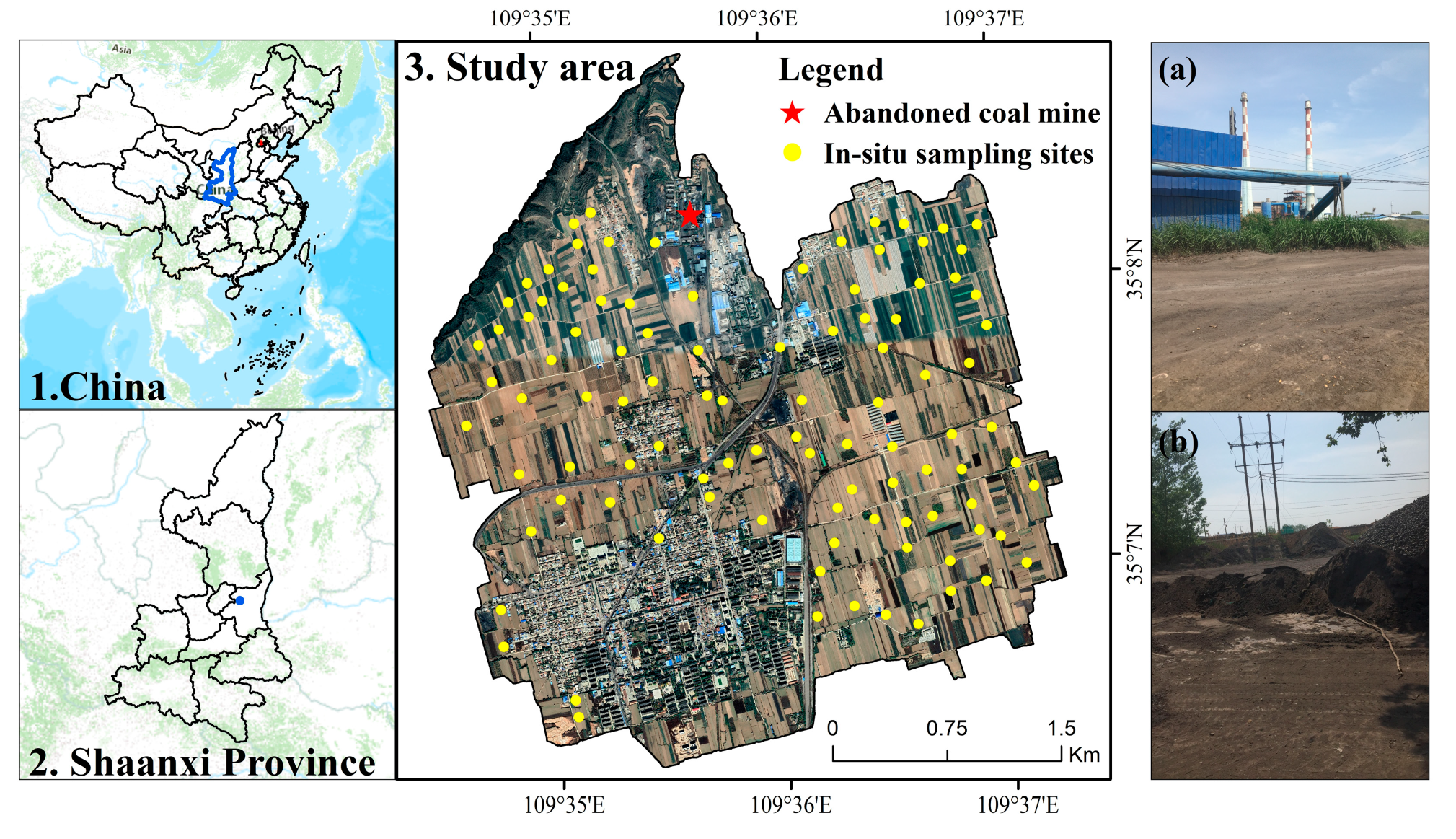
2.1. Study Area
2.2. Soil Sampling and Pretreatment
2.3. Spectral Measurement and Preparation
2.3.1. Spectral Measurement
2.3.2. Spectral Smoothing and Spectral Transformation
2.4. Correlation Analysis for Determining the Characteristic Bands
2.5. Calibration and Validation
2.5.1. Partial Least Squares Regression (PLSR)
2.5.2. Extreme Learning Machine (ELM)
2.5.3. Random Forest (RF)
2.5.4. Support Vector Machine (SVM)
2.5.5. Validation
2.5.6. Software
3. Results
3.1. Statistical Analysis of Heavy Metals in Soil
3.2. Analysis of Soil Spectral Characteristics
3.3. Correlation Analysis of Heavy Metals Concentration in Soil
3.4. Determining the Characteristic Bands for Fe Element Using R2 and CWT
3.5. Estimating Metals Concentration Using RF, PLSR, and ELM Methods
3.5.1. Fe Concentration Estimation
3.5.2. Ni Concentration Estimation
3.6. The Spatial Distribution of Soil Ni Element
4. Discussion
4.1. The Possible Reason for the Accumulation of Heavy Metals in the Study Area
4.2. The Characteristics of Spectral Response for Heavy Metals and the Efficiency of the Spectral Transformation Methods
4.3. The Precision Comparison of Estimation Models Combined with Different Transformation Methods in Inferring Metal Content
4.4. Limitations of This Paper
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Proshad, R.; Kormoker, T.; Mursheed, N.; Islam, M.M.; Bhuyan, M.I.; Islam, M.S.; Mithu, T.N. Heavy metal toxicity in agricultural soil due to rapid industrialization in Bangladesh: A review. Int. J. Adv. Geosci. 2018, 6, 83–88. [Google Scholar] [CrossRef]
- Tan, W.-F.; Zhang, R.; Cao, H.; Huang, C.-Q.; Yang, Q.-K.; Wang, M.-K.; Koopal, L.K. Soil inorganic carbon stock under different soil types and land uses on the Loess Plateau region of China. Catena 2014, 121, 22–30. [Google Scholar] [CrossRef]
- Lamine, S.; Petropoulos, G.P.; Brewer, P.A.; Bachari, N.-E.-I.; Srivastava, P.K.; Manevski, K.; Kalaitzidis, C.; Macklin, M.G. Heavy Metal Soil Contamination Detection Using Combined Geochemistry and Field Spectroradiometry in the United Kingdom. Sensors 2019, 19, 762. [Google Scholar] [CrossRef]
- Wang, F.; Gao, J.; Zha, Y. Hyperspectral sensing of heavy metals in soil and vegetation: Feasibility and challenges. ISPRS J. Photogramm. Remote Sens. 2018, 136, 73–84. [Google Scholar] [CrossRef]
- Guo, B.; Su, Y.; Pei, L.; Wang, X.; Zhang, B.; Zhang, D.; Wang, X. Ecological risk evaluation and source apportionment of heavy metals in park playgrounds: A case study in Xi’an, Shaanxi Province, a northwest city of China. Environ. Sci. Pollut. Res. Int. 2020, 27, 24400–24412. [Google Scholar] [CrossRef] [PubMed]
- Alshahri, F.; El-Taher, A. Assessment of Heavy and Trace Metals in Surface Soil Nearby an Oil Refinery, Saudi Arabia, Using Geoaccumulation and Pollution Indices. Arch. Environ. Contam. Toxicol. 2018, 75, 390–401. [Google Scholar] [CrossRef]
- Guo, B.; Wang, Y.; Pei, L.; Yu, Y.; Liu, F.; Zhang, D.; Wang, X.; Su, Y.; Zhang, D.; Zhang, B.; et al. Determining the effects of socioeconomic and environmental determinants on chronic obstructive pulmonary disease (COPD) mortality using geographically and temporally weighted regression model across Xi’an during 2014–2016. Sci. Total Environ. 2021, 756, 143869. [Google Scholar] [CrossRef]
- Guo, B.; Su, Y.; Pei, L.; Wang, X.; Wei, X.; Zhang, B.; Zhang, D.; Wang, X. Contamination, Distribution and Health Risk Assessment of Risk Elements in Topsoil for Amusement Parks in Xi’an, China. Pol. J. Environ. Stud. 2021, 30, 601–617. [Google Scholar] [CrossRef]
- Naz, A.; Chowdhury, A.; Mishra, B.K.; Karthikeyan, K. Distribution of heavy metals and associated human health risk in mine, agricultural and roadside soils at the largest chromite mine of India. Environ. Geochem. Health 2018, 40, 2155–2175. [Google Scholar] [CrossRef]
- Li, Z.; Ma, Z.; van der Kuijp, T.J.; Yuan, Z.; Huang, L. A review of soil heavy metal pollution from mines in China: Pollution and health risk assessment. Sci. Total Environ. 2014, 468–469, 843–853. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, C.; Li, K.; Zhu, X. Distribution characteristics and pollution assessment of soil heavy metals over a typical nonferrous metal mine area in Chifeng, Inner Mongolia, China. Environ. Earth Sci. 2018, 77, 638. [Google Scholar] [CrossRef]
- Zhang, S.; Shen, Q.; Nie, C.; Huang, Y.; Wang, J.; Hu, Q.; Ding, X.; Zhou, Y.; Chen, Y. Hyperspectral inversion of heavy metal content in reclaimed soil from a mining wasteland based on different spectral transformation and modeling methods. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2019, 211, 393–400. [Google Scholar] [CrossRef] [PubMed]
- Pandit, C.M.; Filippelli, G.M.; Li, L. Estimation of heavy-metal contamination in soil using reflectance spectroscopy and partial least-squares regression. Int. J. Remote Sens. 2010, 31, 4111–4123. [Google Scholar] [CrossRef]
- Cheng, H.; Shen, R.; Chen, Y.; Wan, Q.; Shi, T.; Wang, J.; Wan, Y.; Hong, Y.; Li, X. Estimating heavy metal concentrations in suburban soils with reflectance spectroscopy. Geoderma 2019, 336, 59–67. [Google Scholar] [CrossRef]
- Han, L.; Chen, R.; Zhu, H.; Zhao, Y.; Liu, Z.; Huo, H. Estimating Soil Arsenic Content with Visible and Near-Infrared Hyperspectral Reflectance. Sustainability 2020, 12, 1476. [Google Scholar] [CrossRef]
- Tan, K.; Ma, W.; Chen, L.; Wang, H.; Du, Q.; Du, P.; Yan, B.; Liu, R.; Li, H. Estimating the distribution trend of soil heavy metals in mining area from HyMap airborne hyperspectral imagery based on ensemble learning. J. Hazard. Mater. 2021, 401, 123288. [Google Scholar] [CrossRef]
- Shen, Q.; Xia, K.; Zhang, S.; Kong, C.; Hu, Q.; Yang, S. Hyperspectral indirect inversion of heavy-metal copper in reclaimed soil of iron ore area. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2019, 222, 117191. [Google Scholar]
- Lu, Q.; Wang, S.; Bai, X.; Liu, F.; Wang, M.; Wang, J.; Tian, S. Rapid inversion of heavy metal concentration in karst grain producing areas based on hyperspectral bands associated with soil components. Microchem. J. 2019, 148, 404–411. [Google Scholar]
- Sun, W.; Zhang, X.; Sun, X.; Sun, Y.; Cen, Y. Predicting nickel concentration in soil using reflectance spectroscopy associated with organic matter and clay minerals. Geoderma 2018, 327, 25–35. [Google Scholar] [CrossRef]
- Shi, T.; Chen, Y.; Liu, Y.; Wu, G. Visible and near-infrared reflectance spectroscopy—An alternative for monitoring soil contamination by heavy metals. J. Hazard. Mater. 2014, 265, 166–176. [Google Scholar] [CrossRef]
- Alsbou, E.M.E.; Al-Khashman, O.A. Heavy metal concentrations in roadside soil and street dust from Petra region, Jordan. Environ. Monit. Assess. 2017, 190, 48. [Google Scholar] [CrossRef]
- Zhang, S.; Fei, T.; You, X.; Wan, Y.; Wang, Y.; Bian, M. Two hyperspectral indices for detecting cadmium and lead contamination from arice canopy spectrum. Land Degrad. Dev. 2020, 32, 66–78. [Google Scholar] [CrossRef]
- Wang, J.; Zou, L.; Li, Z.; Mu, H.; Zhou, P.; Yang, J.; Zhao, Y.; Qin, K. A detection method of trace metal elements in black soil based on hyperspectral technol-ogy: Geological implications. J. Geomech. 2021, 27, 418–429. [Google Scholar]
- Chen, T.; Chang, Q.; Clevers, J.G.P.W.; Kooistra, L. Rapid identification of soil cadmium pollution risk at regional scale based on visible and near-infrared spectroscopy. Environ. Pollut. 2015, 206, 217–226. [Google Scholar] [CrossRef]
- Douglas, R.K.; Nawar, S.; Cipullo, S.; Alamar, M.C.; Coulon, F.; Mouazen, A.M. Evaluation of vis-NIR reflectance spectroscopy sensitivity to weathering for enhanced assessment of oil contaminated soils. Sci. Total Environ. 2018, 626, 1108–1120. [Google Scholar] [CrossRef] [PubMed]
- Khosravi, V.; Doulati Ardejani, F.; Yousefi, S.; Aryafar, A. Monitoring soil lead and zinc contents via combination of spectroscopy with extreme learning machine and other data mining methods. Geoderma 2018, 318, 29–41. [Google Scholar] [CrossRef]
- Chakraborty, S.; Weindorf, D.C.; Li, B.; Ali Aldabaa, A.A.; Ghosh, R.K.; Paul, S.; Ali, M.N. Development of a hybrid proximal sensing method for rapid identification of petroleum contaminated soils. Sci. Total Environ. 2015, 514, 399–408. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhang, Y.; Wang, H.; Du, Y. Study on the prediction of soil heavy metal elements content based on visible near-infrared spectroscopy. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2018, 199, 43–49. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.; Shen, R.; Cheng, H.; Chen, Y.; Zhang, Y.; Liu, Y.; Zhou, M.; Yu, L.; Liu, Y.; Liu, Y. Estimating lead and zinc concentrations in peri-urban agricultural soils through reflectance spectroscopy: Effects of fractional-order derivative and random forest. Sci. Total Environ. 2018, 651, 1969–1982. [Google Scholar] [CrossRef] [PubMed]
- Kemper, T.; Sommer, S. Estimate of heavy metal contamination in soils after a mining accident using reflectance spectroscopy. Environ. Sci. Technol. 2002, 36, 2742–2747. [Google Scholar] [CrossRef] [PubMed]
- Hou, L.; Li, X.; Li, F. Hyperspectral-based Inversion of Heavy Metal Content in the Soil of Coal Mining Areas. J. Environ. Qual. 2019, 48, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Sawut, R.; Kasim, N.; Abliz, A.; Hu, L.; Yalkun, A.; Maihemuti, B.; Qingdong, S. Possibility of optimized indices for the assessment of heavy metal contents in soil around an open pit coal mine area. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 14–25. [Google Scholar] [CrossRef]
- Wei, L.; Yuan, Z.; Zhong, Y.; Yang, L.; Hu, X.; Zhang, Y. An Improved Gradient Boosting Regression Tree Estimation Model for Soil Heavy Metal (Arsenic) Pollution Monitoring Using Hyperspectral Remote Sensing. Appl. Sci. 2019, 9, 1943. [Google Scholar] [CrossRef] [Green Version]
- Guo, B.; Zhang, B.; Su, Y.; Zhang, D.; Wang, Y.; Bian, Y.; Suo, L.; Guo, X.; Bai, H. Retrieving zinc concentrations in topsoil with reflectance spectroscopy at Opencast Coal Mine sites. Sci. Rep. 2021, 11, 19909. [Google Scholar] [CrossRef]
- Zhang, B.; Guo, B.; Zou, B.; Wei, W.; Lei, Y.; Li, T. Retrieving soil heavy metals concentrations based on GaoFen-5 hyperspectral satellite image at an opencast coal mine, Inner Mongolia, China. Environ. Pollut. 2022, 300, 118981. [Google Scholar] [CrossRef]
- Meng, X.; Bao, Y.; Ye, Q.; Liu, H.; Zhang, X.; Tang, H.; Zhang, X. Soil Organic Matter Prediction Model with Satellite Hyperspectral Image Based on Optimized Denoising Method. Remote Sens. 2021, 13, 2273. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Fathizad, H.; Ali Hakimzadeh Ardakani, M.; Sodaiezadeh, H.; Kerry, R.; Heung, B.; Scholten, T. Spatio-Temporal Analysis of Heavy Metals in Arid Soils at the Catchment Scale Using Digital Soil Assessment and a Random Forest Model. Remote Sens. 2021, 13, 1698. [Google Scholar] [CrossRef]
- Tan, K.; Wang, H.; Chen, L.; Dud, Q.; Due, P.; Pan, C. Estimation of the spatial distribution of heavy metal in agricultural soils using airborne hyperspectral imaging and random forest. J. Hazard. Mater. 2020, 382, 120987. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, H.; Xie, L.; Li, H.; Huang, L.; Zhao, Y.; Yue, T. Hyperspectral inversion of soil heavy metals in Three-River Source Region based on random forest model. Catena 2021, 202, 105222. [Google Scholar] [CrossRef]
- Dong, H.; Zhao, J.; Xie, M. Heavy Metal Concentrations in Orchard Soils with Different Cultivation Durations and Their Potential Ecological Risks in Shaanxi Province, Northwest China. Sustainability 2021, 13, 4741. [Google Scholar] [CrossRef]
- Wang, X.; Rahman, Z.U.; Lv, Z.; Zhu, Y.; Ruan, R.; Deng, S.; Zhang, L.; Tan, H. Experimental Study and Design of Biomass Co-Firing in a Full-Scale Coal-Fired Furnace with Storage Pulverizing System. Agronomy 2021, 11, 810. [Google Scholar] [CrossRef]
- Wei, X.; Wang, N.; Luo, P.; Yang, J.; Zhang, J.; Lin, K. Spatiotemporal Assessment of Land Marketization and Its Driving Forces for Sustainable Urban–Rural Development in Shaanxi Province in China. Sustainability 2021, 13, 7755. [Google Scholar] [CrossRef]
- Zha, X.; Luo, P.; Zhu, W.; Wang, S.; Lyu, J.; Zhou, M.; Huo, A.; Wang, Z. A bibliometric analysis of the research on Sponge City: Current situation and future development direction. Ecohydrology 2021, 14, e2328. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, X. Estimating soil zinc concentrations using reflectance spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 126–133. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, W.; Cen, Y.; Zhang, L.; Wang, N. Predicting cadmium concentration in soils using laboratory and field reflectance spectroscopy. Sci. Total Environ. 2019, 650, 321–334. [Google Scholar] [CrossRef]
- Liu, W.; Li, M.; Zhang, M.; Long, S.; Guo, Z.; Wang, H.; Li, W.; Wang, D.; Hu, Y.; Wei, Y.; et al. Hyperspectral inversion of mercury in reed leaves under different levels of soil mercury contamination. Environ. Sci. Pollut. Res. Int. 2020, 27, 22935–22945. [Google Scholar] [CrossRef]
- Cheng, T.; Rivard, B.; Sánchez-Azofeifa, G.A.; Feng, J.; Calvo-Polanco, M. Continuous wavelet analysis for the detection of green attack damage due to mountain pine beetle infestation. Remote Sens. Environ. 2010, 114, 899–910. [Google Scholar] [CrossRef]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. Solid Earth 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Dehaan, R.L.; Taylor, G.R. Field-derived spectra of salinized soils and vegetation as indicators of irrigation-induced soil salinization. Remote Sens. Environ. 2002, 80, 406–417. [Google Scholar] [CrossRef]
- Hong, Y.; Shen, R.; Cheng, H.; Chen, S.; Chen, Y.; Guo, L.; He, J.; Liu, Y.; Yu, L.; Liu, Y. Cadmium concentration estimation in peri-urban agricultural soils: Using reflectance spectroscopy, soil auxiliary information, or a combination of both? Geoderma 2019, 354, 113875. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Chen, Y.; Linderman, M.; Mouazen, A.M.; Liu, Y.; Guo, L.; Yu, L.; Liu, Y.; Cheng, H.; et al. Comparing laboratory and airborne hyperspectral data for the estimation and mapping of topsoil organic carbon: Feature selection coupled with random forest. Soil Tillage Res. 2020, 199, 104589. [Google Scholar] [CrossRef]
- Liu, W.; Yu, Q.; Niu, T.; Yang, L.; Liu, H. Inversion of Soil Heavy Metal Content Based on Spectral Characteristics of Peach Trees. Forests 2021, 12, 1208. [Google Scholar] [CrossRef]
- Martens, M.; Martens, H.; Wold, S. Preference of cauliflower related to sensory descriptive variables by partial least squares (PLS) regression. J. Sci. Food Agric. 1983, 34, 715–724. [Google Scholar] [CrossRef]
- Shi, T.; Wang, J.; Chen, Y.; Wu, G. Improving the prediction of arsenic contents in agricultural soils by combining the reflectance spectroscopy of soils and rice plants. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 95–103. [Google Scholar] [CrossRef]
- Dotto, A.C.; Dalmolin, R.S.D.; Ten Caten, A.; Grunwald, S. A systematic study on the application of scatter-corrective and spectral-derivative preprocessing for multivariate prediction of soil organic carbon by Vis-NIR spectra. Geoderma 2018, 314, 262–274. [Google Scholar] [CrossRef]
- Guo, W.; Shang, L.; Zhu, X.; Nelson, S.O. Nondestructive Detection of Soluble Solids Content of Apples from Dielectric Spectra with ANN and Chemometric Methods. Food Bioprocess Technol. 2015, 8, 1126–1138. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Zhang, Y.; Chen, Y.; Yu, L.; Liu, Y.; Liu, Y.; Cheng, H.; Liu, Y. Rapid identification of soil organic matter level via visible and near-infrared spectroscopy: Effects of two-dimensional correlation coefficient and extreme learning machine. Sci. Total Environ. 2018, 644, 1232–1243. [Google Scholar] [CrossRef]
- Lu, Q.; Wang, S.; Bai, X.; Liu, F.; Tian, S.; Wang, M.; Wang, J. Rapid estimation of soil heavy metal nickel content based on optimized screening of near-infrared spectral bands. Acta Geochim. 2020, 39, 116–126. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Guo, B.; Bian, Y.; Zhang, D.; Su, Y.; Wang, X.; Zhang, B.; Wang, Y.; Chen, Q.; Wu, Y.; Luo, P. Estimating Socio-Economic Parameters via Machine Learning Methods Using Luojia1-01 Nighttime Light Remotely Sensed Images at Multiple Scales of China in 2018. IEEE Access 2021, 9, 34352–34365. [Google Scholar] [CrossRef]
- Krogh, A.; Vedelsby, J. Neural Network Ensembles, Cross Validation, and Active Learning. In Proceedings of the International Conference on Neural Information Processing Systems, Denver, CO, USA, 1 January 1994. [Google Scholar]
- Du, Y.; Cui, X.; Xu, Q.; Han, D.; Guo, X.; Cao, G. Spatial Characteristics of Soil Organic Matter and As Content in Source Regions of Yangtze River and Yellow River. Chin. J. Grassl. 2012, 34, 24–29. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Wei, L.; Yuan, Z.; Wang, Z.; Zhao, L.; Zhanng, Y.; Lu, X.; Cao, L. Hyperspectral Inversion of Soil Organic Matter Content Based on a Combined Spectral Index Model. Sensors 2020, 20, 2777. [Google Scholar] [CrossRef] [PubMed]
- CNEMC. The Background Values of Elements in Chinese Soils; China national Environmental Monitoring Center: Beijing, China; China Environmental Science Press: Beijing, China, 1990; pp. 15–505. [Google Scholar]
- Yi, P.; Kheir, R.B.; Adhikari, K.; Malinowski, R.; Greve, M.B.; Knadel, M.; Greve, M.H. Digital Mapping of Toxic Metals in Qatari Soils Using Remote Sensing and Ancillary Data. Remote Sens. 2016, 8, 1003. [Google Scholar]
- Xu, B.B.; Ji, G.S. A Preliminary Research of Geographic Regionalization of China Land Background and Spectral Reflectance Characteristics of Soil. Remote Sens. Environ. China 1991, 6, 142–151. [Google Scholar]
- Pyo, J.; Hong, S.M.; Kwon, Y.S.; Kim, M.S.; Cho, K.H. Estimation of heavy metals using deep neural network with visible and infrared spectroscopy of soil. Sci. Total Environ. 2020, 741, 140162. [Google Scholar] [CrossRef] [PubMed]
- Stevens, A.; Nocita, M.; Tóth, G.; Montanarella, L.; van Wesemael, B. Prediction of Soil Organic Carbon at the European Scale by Visible and Near InfraRed Reflectance Spectroscopy. PLoS ONE 2013, 8, e66409. [Google Scholar]
- Clark, R.N.; King, T.V.V.; Klejwa, M.; Swayze, G.A.; Vergo, N. High spectral resolution reflectance spectroscopy of minerals. J. Geophys. Res. 1990, 95, 12653–12680. [Google Scholar] [CrossRef]
- Madejova, J.; Komadel, P. Baseline studies of the clay minerals society source clays: Infrared methods. Clays Clay Miner. 2001, 49, 410–432. [Google Scholar] [CrossRef]
- Jie, L.; Feng, C.; Zeng, G.; Gao, X.; Zhong, M.; Li, X.; Li, X.; He, X.; Fang, Y. Spatial distribution and source identification of heavy metals in surface soils in a typical coal mine city, Lianyuan, China. Environ. Pollut. 2017, 225, 681. [Google Scholar]
- Guan, Q.; Wang, F.; Xu, C.; Pan, N.; Lin, J.; Zhao, R.; Yang, Y.; Luo, H. Source apportionment of heavy metals in agricultural soil based on PMF: A case study in Hexi Corridor, northwest China. Chemosphere 2017, 193, 189–197. [Google Scholar] [CrossRef]
- Kelepertzis, E. Accumulation of heavy metals in agricultural soils of Mediterranean: Insights from Argolida basin, Peloponnese, Greece. Geoderma 2014, 221–222, 82–90. [Google Scholar] [CrossRef]
- Chen, X.; Kumari, D.; Cao, C.J.; Plaza, G.; Achal, V. A review on remediation technologies for nickel-contaminated soil. Hum. Ecol. Risk Assess. Int. J. 2019, 26, 571–585. [Google Scholar] [CrossRef]
- Boker, A.; Brownell, L.; Donen, N. The Amsterdam preoperative anxiety and information scale provides a simple and reliable measure of preoperative anxiety. Can. J. Anesth. 2002, 49, 792–798. [Google Scholar] [CrossRef] [PubMed]
- Kayande, K.S.; Deshmukh, R.R.; Janse, P.V.; Kayte, J.N. Hyper spectral Analysis of Soil Iron Oxide using Fieldspec4 Spectroradiometer. Int. J. Comput. Sci. Eng. 2018, 6, 395–399. [Google Scholar] [CrossRef]
- Rathod, P.H.; Müller, I.; Van der Meer, F.D.; de Smeth, B. Analysis of visible and near infrared spectral reflectance for assessing metals in soil. Environ. Monit. Assess. 2016, 188, 588. [Google Scholar] [CrossRef] [PubMed]
- Hunt, G.R. Spectral signatures of particulate minerals in the visible and near infrared. Geophysics 1977, 44, 501–513. [Google Scholar] [CrossRef]
- Jin, G.; Fang, W.; Shafi, M.; Wu, D.; Li, Y.; Zhong, B.; Ma, J.; Liu, D. Source apportionment of heavy metals in farmland soil with application of APCS-MLR model: A pilot study for restoration of farmland in Shaoxing City Zhejiang, China. Ecotoxicol. Environ. Saf. 2019, 184, 109495. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Wang, F.; Li, J.; Tiwari, S.; Chen, B. Assessment of trends and emission sources of heavy metals from the soil sediments near the Bohai Bay. Environ. Sci. Pollut. Res. 2019, 26, 29095–29109. [Google Scholar] [CrossRef]
- Huang, Y.; Li, T.; Wu, C.; He, Z.; Japenga, J.; Deng, M.; Yang, X. An integrated approach to assess heavy metal source apportionment in peri-urban agricultural soils. J. Hazard. Mater. 2015, 299, 540–549. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Lu, X.; Chang, Y.; Xue, W. Heavy metal contamination in dust from kindergartens and elementary schools in Xi’an, China. Environ. Earth Sci. 2014, 71, 2701–2709. [Google Scholar] [CrossRef]
- Douglas, R.K.; Nawar, S.; Alamar, M.C.; Mouazen, A.M.; Coulon, F. Rapid prediction of total petroleum hydrocarbons concentration in contaminated soil using vis-NIR spectroscopy and regression techniques. Sci. Total Environ. 2018, 616–617, 147–155. [Google Scholar] [CrossRef] [PubMed]
- Okparanma, R.N.; Mouazen, A.M. Combined Effects of Oil Concentration, Clay and Moisture Contents on Diffuse Reflectance Spectra of Diesel-Contaminated Soils. Water Air Soil Pollut. 2013, 224, 1539. [Google Scholar] [CrossRef]
- Zou, B.; Jiang, X.; Feng, H.; Tu, Y.; Tao, C. Multisource spectral-integrated estimation of cadmium concentrations in soil using a direct standardization and Spiking algorithm. Sci. Total Environ. 2020, 701, 134890. [Google Scholar] [CrossRef]
- Xue, Y.; Zou, B.; Wen, Y.; Tu, Y.; Xiong, L. Hyperspectral Inversion of Chromium Content in Soil Using Support Vector Machine Combined with Lab and Field Spectra. Sustainability 2020, 12, 4441. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Saberioon, M.; Carmon, N.; Boruvka, L.; Ben-Dor, E. Examining the Performance of PARACUDA-II Data-Mining Engine versus Selected Techniques to Model Soil Carbon from Reflectance Spectra. Remote Sens. 2018, 10, 1172. [Google Scholar] [CrossRef]
- Schapire, R.E. Random Forests. Mach. Learn 2001, 45, 5–32. [Google Scholar]
- Sachdeva, S.; Kumar, B. Comparison of gradient boosted decision trees and random forest for groundwater potential mapping in Dholpur (Rajasthan), India. Stoch. Environ. Res. Risk Assess. 2021, 35, 287–306. [Google Scholar] [CrossRef]








| Paraments | Cr | Ni | Zn | Cu | Mn | Fe |
|---|---|---|---|---|---|---|
| Mean | 76.42 | 27.40 | 67.37 | 19.57 | 580.34 | 28,787.56 |
| Standard deviation (SD) | 11.93 | 2.92 | 16.66 | 12.41 | 38.60 | 1761.97 |
| Minimum | 47.70 | 20.07 | 41.65 | 9.60 | 469.50 | 23,839.00 |
| Maximum | 107.50 | 34.12 | 201.50 | 135.00 | 723.00 | 34,223.00 |
| Coefficient of variation (CV, %) | 15.61 | 10.64 | 24.73 | 63.42 | 6.65 | 6.12 |
| Shaanxi soil background value | 62.50 | 28.80 | 69.40 | 21.40 | 557.00 | - |
| Chinese soil background value | 61.00 | 26.90 | 72.40 | 22.60 | 583.00 | - |
| Elements | Mn | Cr | Zn | Ni | Cu | Fe |
|---|---|---|---|---|---|---|
| Mn | 1 | |||||
| Cr | 0.189 | 1 | ||||
| Zn | 0.522 ** | 0.159 | 1 | |||
| Ni | 0.646 ** | 0.296 ** | 0.353 ** | 1 | ||
| Cu | 0.405 ** | 0.182 | 0.876 ** | 0.179 | 1 | |
| Fe | 0.851 ** | 0.213 * | 0.436 ** | 0.741 ** | 0.274 ** | 1 |
| Transform | Model | Calibration Dataset (n = 70) | Validation Dataset (n = 30) | ||
|---|---|---|---|---|---|
| OR | PLSR | 0.44 | 1214.3 | 0.30 | 1674.8 |
| ELM | 0.56 | 1177.6 | 0.55 | 1345.5 | |
| RF | 0.84 | 864.6 | 0.64 | 899.9 | |
| SVM | 0.62 | 977.1 | 0.49 | 1575.5 | |
| SG | PLSR | 0.39 | 1286.7 | 0.36 | 1591.5 |
| ELM | 0.554 | 1035.3 | 0.548 | 1468.0 | |
| RF | 0.85 | 863.4 | 0.64 | 969.7 | |
| SVM | 0.54 | 1143.7 | 0.36 | 1702.1 | |
| Decomposition Scales | Model | Calibration Dataset (n = 70) | Validation Dataset (n = 30) | ||
|---|---|---|---|---|---|
| 1 | PLSR | 0.40 | 1269.6 | 0.36 | 1631.9 |
| ELM | 0.59 | 1172.5 | 0.40 | 1084.7 | |
| RF | 0.83 | 824.1 | 0.60 | 1186.3 | |
| SVM | 0.44 | 1348.6 | 0.39 | 1419.0 | |
| 2 | PLSR | 0.39 | 1374.4 | 0.33 | 1411.2 |
| ELM | 0.54 | 1170.5 | 0.42 | 1591.4 | |
| RF | 0.86 | 806.2 | 0.59 | 1084.6 | |
| SVM | 0.42 | 1435.2 | 0.36 | 1258.3 | |
| 3 | PLSR | 0.39 | 1291.8 | 0.38 | 1569.2 |
| ELM | 0.49 | 1207.9 | 0.37 | 1622.6 | |
| RF | 0.83 | 774.4 | 0.53 | 1376.3 | |
| SVM | 0.43 | 1349.3 | 0.38 | 1504.1 | |
| 4 | PLSR | 0.39 | 1477.1 | 0.32 | 1137.7 |
| ELM | 0.58 | 1211.0 | 0.42 | 1672.5 | |
| RF | 0.86 | 837.0 | 0.68 | 695.0 | |
| SVM | 0.52 | 1245.5 | 0.32 | 1460.0 | |
| 5 | PLSR | 0.38 | 1383.8 | 0.37 | 1418.0 |
| ELM | 0.64 | 1017.3 | 0.46 | 1580.4 | |
| RF | 0.81 | 880.7 | 0.59 | 1096.3 | |
| SVM | 0.47 | 1115.0 | 0.39 | 1776.0 | |
| 6 | PLSR | 0.40 | 1226.6 | 0.32 | 1750.4 |
| ELM | 0.62 | 1149.2 | 0.41 | 1348.6 | |
| RF | 0.81 | 862.7 | 0.58 | 1099.2 | |
| SVM | 0.46 | 1257.0 | 0.30 | 1575.0 | |
| 8 | PLSR | 0.46 | 1397.5 | 0.42 | 1145.9 |
| ELM | 0.62 | 1149.2 | 0.41 | 1348.6 | |
| RF | 0.83 | 758.7 | 0.61 | 1276.0 | |
| SVM | 0.61 | 1074.0 | 0.4 | 1498.9 | |
| 9 | PLSR | 0.45 | 1433.3 | 0.41 | 1143.1 |
| ELM | 0.64 | 1095.1 | 0.47 | 1765.9 | |
| RF | 0.85 | 768.9 | 0.71 | 1019.1 | |
| SVM | 0.66 | 955.1 | 0.41 | 1539.2 | |
| Model | Calibration Dataset (n = 70) | Validation Dataset (n = 30) | ||
|---|---|---|---|---|
| PLSR | 0.60 | 1.63 | 0.51 | 2.55 |
| ELM | 0.59 | 1.92 | 0.52 | 2.53 |
| RF | 0.83 | 1.24 | 0.69 | 1.94 |
| SVM | 0.59 | 1.89 | 0.57 | 2.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Guo, B.; Lei, Y.; Zhang, D.; Guo, X.; Suo, L.; Zhao, Y.; Bian, Y. An Indirect Inversion Scheme for Retrieving Toxic Metal Concentrations Using Ground-Based Spectral Data in a Reclamation Coal Mine, China. Water 2022, 14, 2784. https://doi.org/10.3390/w14182784
Su Y, Guo B, Lei Y, Zhang D, Guo X, Suo L, Zhao Y, Bian Y. An Indirect Inversion Scheme for Retrieving Toxic Metal Concentrations Using Ground-Based Spectral Data in a Reclamation Coal Mine, China. Water. 2022; 14(18):2784. https://doi.org/10.3390/w14182784
Chicago/Turabian StyleSu, Yi, Bin Guo, Yongzhi Lei, Dingming Zhang, Xianan Guo, Liang Suo, Yonghua Zhao, and Yi Bian. 2022. "An Indirect Inversion Scheme for Retrieving Toxic Metal Concentrations Using Ground-Based Spectral Data in a Reclamation Coal Mine, China" Water 14, no. 18: 2784. https://doi.org/10.3390/w14182784
APA StyleSu, Y., Guo, B., Lei, Y., Zhang, D., Guo, X., Suo, L., Zhao, Y., & Bian, Y. (2022). An Indirect Inversion Scheme for Retrieving Toxic Metal Concentrations Using Ground-Based Spectral Data in a Reclamation Coal Mine, China. Water, 14(18), 2784. https://doi.org/10.3390/w14182784







