Modelling Soil Water, Salt and Heat Dynamics under Partially Mulched Conditions with Drip Irrigation, Using HYDRUS-2D
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Design
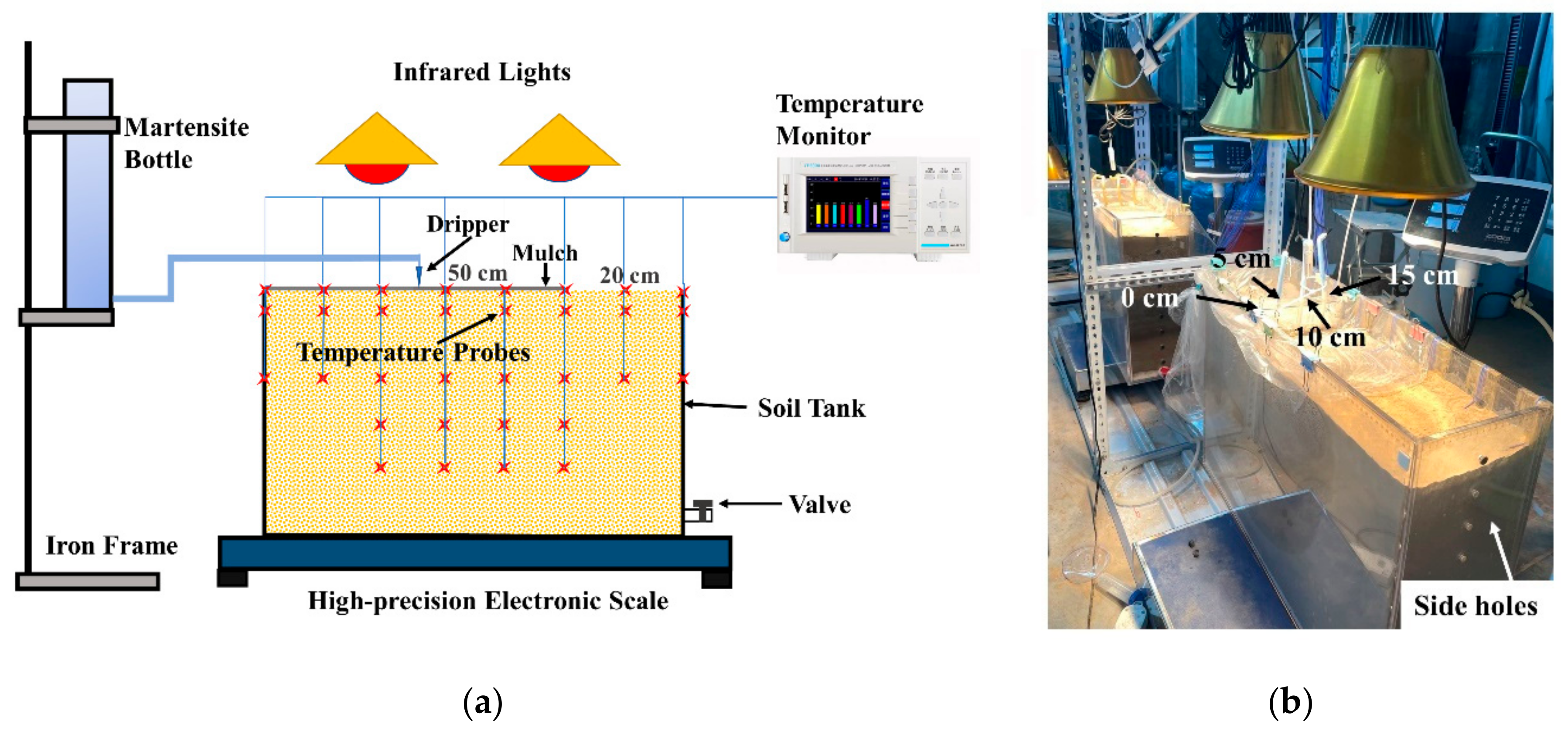
2.2. Monitoring Methods

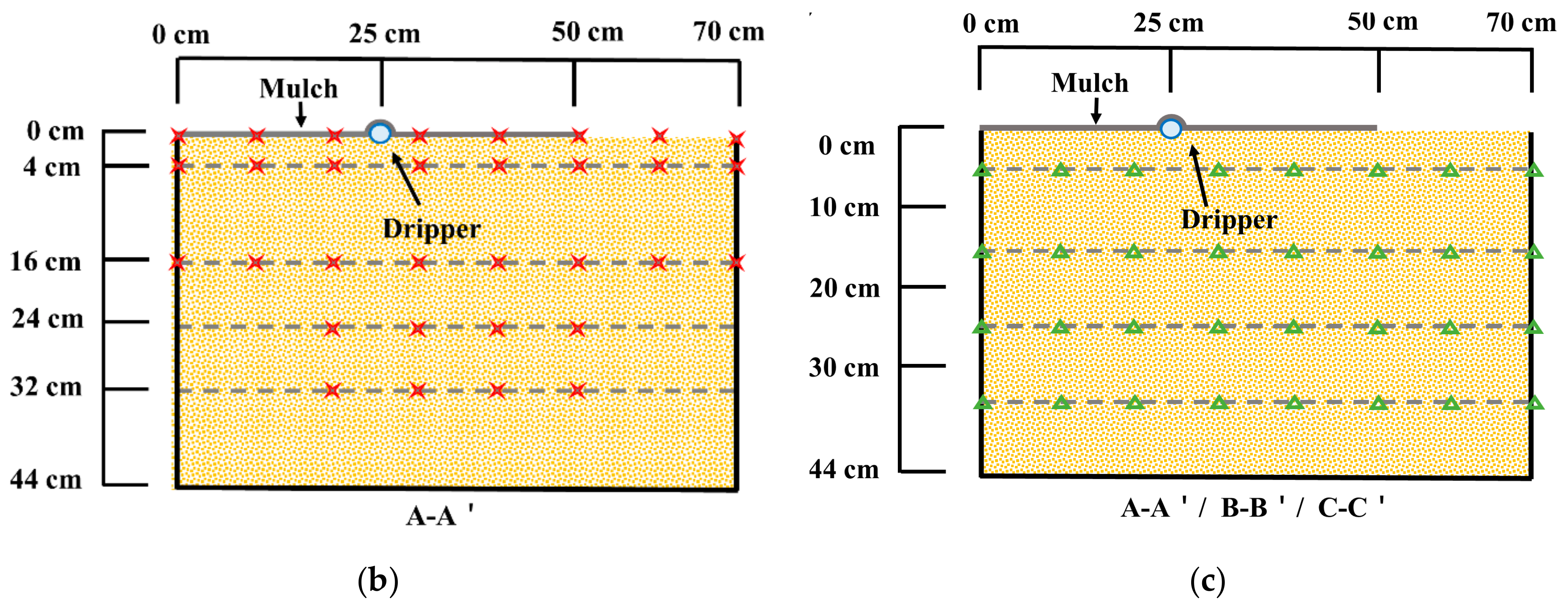
2.3. Model Introduction
2.3.1. Equation of Water Transport
2.3.2. Solute Transport Equation
2.3.3. Heat Transport Equation
2.3.4. Initial and Boundary Conditions
2.3.5. Parameters and Model Calibration/Validation
| Parameters | Value | Source | |||
|---|---|---|---|---|---|
| Soil characteristic parameter | Soil particle composition | Sand | 26.252 | Measured via experiment | |
| Silt | 70.858 | ||||
| Clay | 2.89 | ||||
| 1.55 | |||||
| Soil hydraulic parameters | 0.0353 | Rosetta pedotransfer functions [44] | |||
| 0.42 | |||||
| 0.0072 | |||||
| 1.6613 | |||||
| 1.875 | |||||
| l | 0.5 | ||||
| Solute transport parameters | 26 | Calibrated | |||
| 0.6 | |||||
| 1 | |||||
| 0.05 | |||||
| Heat transport parameters | −0.5519 | Wang et al. [45] | |||
| −4.05 | |||||
| 3.75 | |||||
| Pan et al. [46] | |||||
| Hu et al. [47] | |||||
| 1 | |||||
2.4. Statistical Analysis
3. Results and Discussion
3.1. Results of Model Calibration and Validation
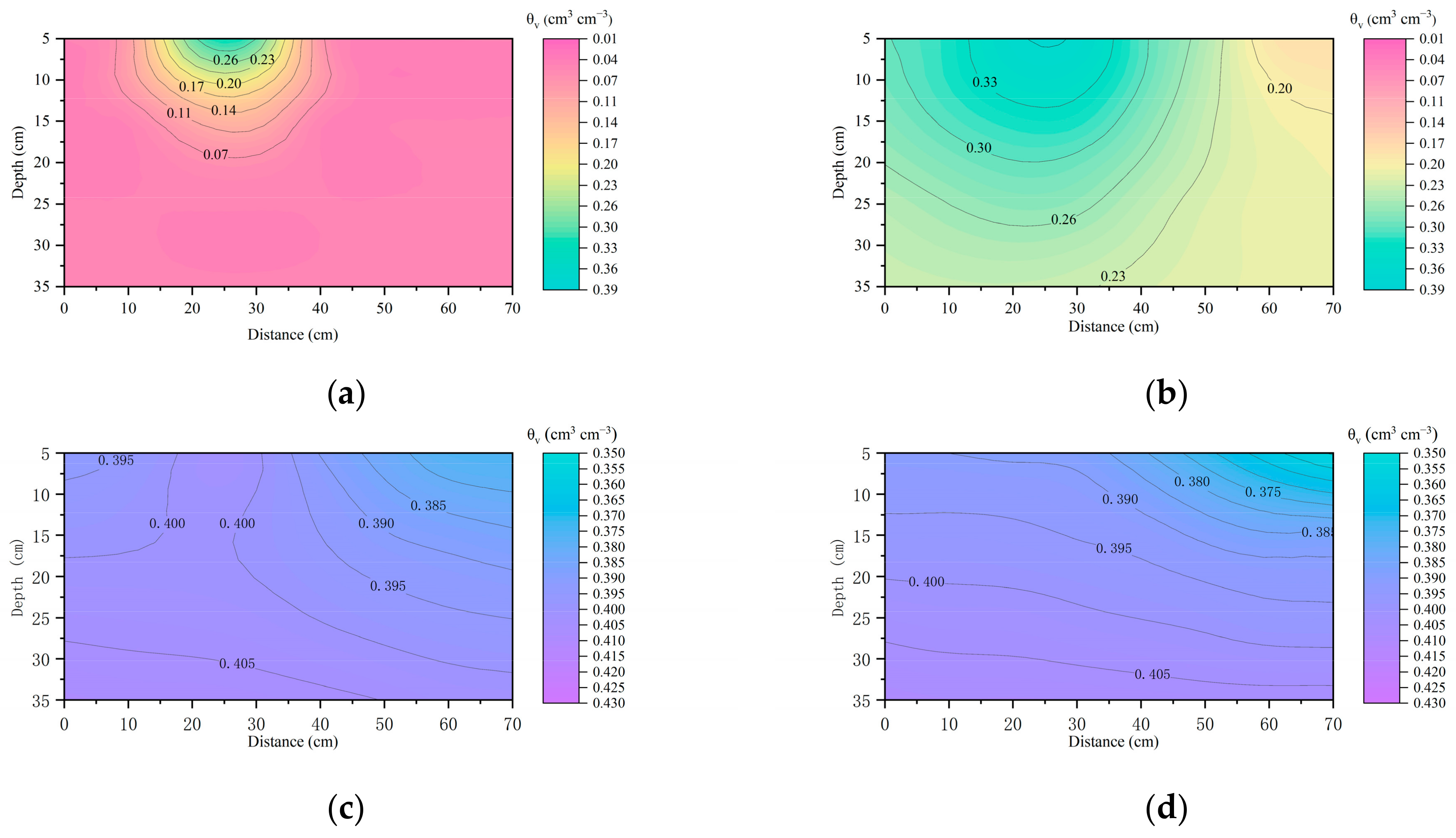
3.2. Water Transport under Various Irrigation Treatments


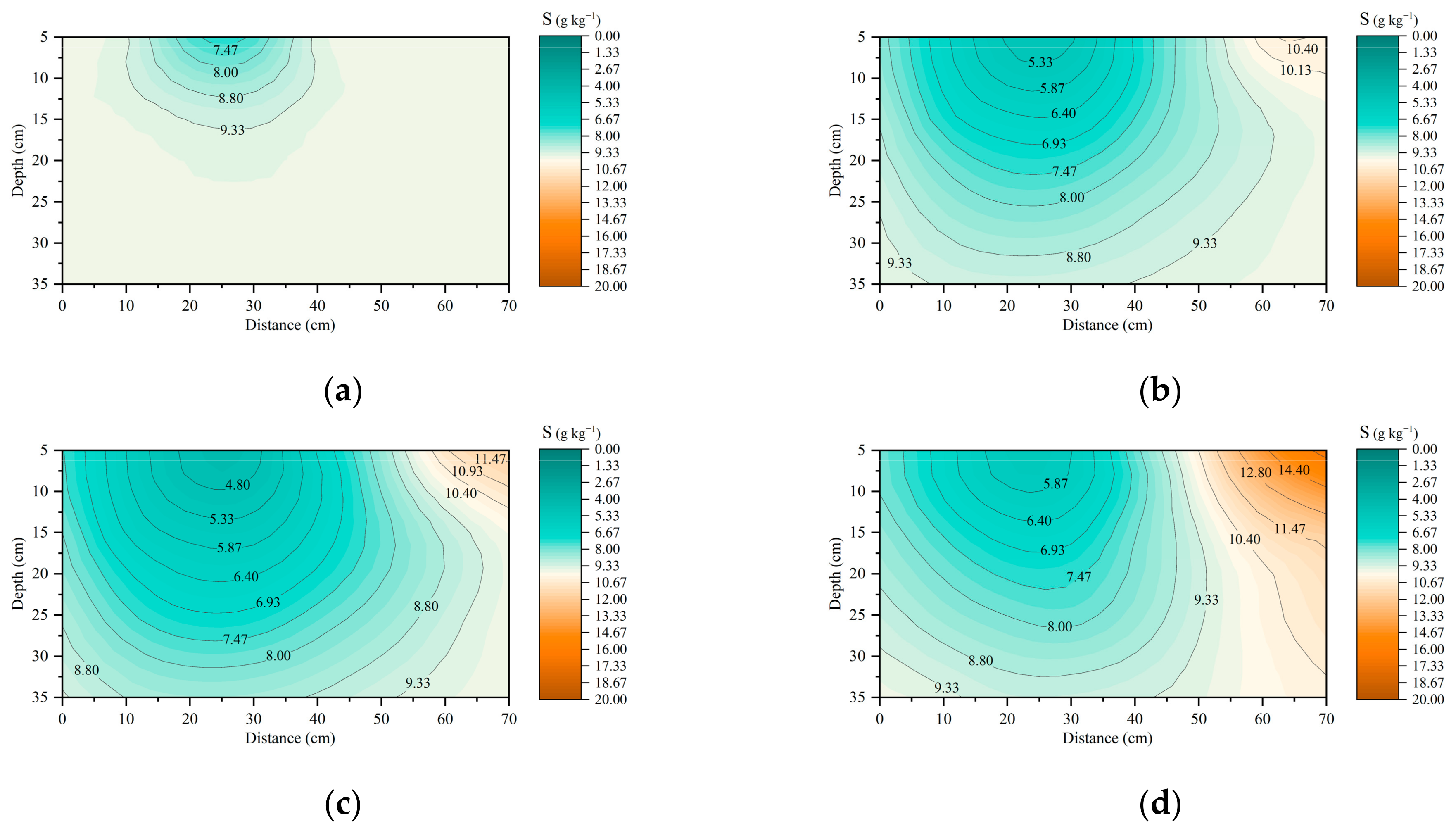
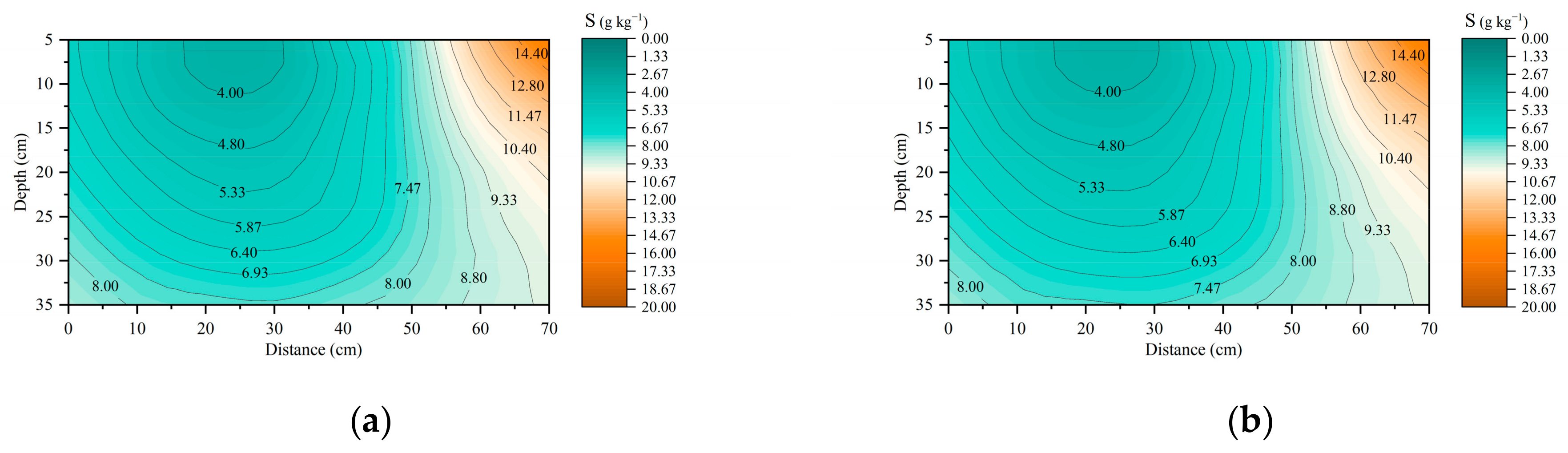
3.3. Salt Transport under Various Irrigation Treatments


3.4. Heat Transport under Various Irrigation Treatments



3.5. Discussion on the Coupling of Water, Salt, and Heat Transport
3.6. Simulation Scenarios


4. Conclusions
- (1)
- The HYDRUS-2D model compared reasonably well with the measured data, demonstrating that it can reflect differences in water, salt, and heat migration in the vertical and lateral directions. For solute transport, compared with instantaneous equilibrium adsorption, kinetic adsorption could better reflect the characteristics of solute transport in this experiment.
- (2)
- Under partially mulched drip irrigation, a significant difference was found in the migration of water, salt, and heat between the mulched and the un-mulched soil area. The un-mulched soil area was drier than the mulched soil area, and it also had higher soil salinity level and higher temperature rise with radiation.
- (3)
- For different irrigation intensities with the same total irrigation amount, lower intensity drip irrigation showed smaller spatial distribution difference for water, and larger spatial distribution differences in salinity and heat at the end of the process. Such treatment can lead to effective desalination in the mulched area; more serious salt accumulation was restricted to the un-mulched soil.
- (4)
- Scenario simulations showed that the total quantity of drip irrigation had an obvious effect on the desalination boundary in the deep soil layer. Drip irrigations with appropriate incremental intensity could improve salt leaching in the root zone, as more water migrates laterally.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- FAO. Land and Plant Nutrition Management Service; FAO: Rome, Italy, 2008; Available online: http://www.fao.org/ag/agl/agll/spush/ (accessed on 16 April 2021).
- Chen, W.; Hou, Z.; Wu, L.; Liang, Y.; Wei, C. Evaluating salinity distribution in soil irrigated with saline water in arid regions of northwest China. Agric. Water Manag. 2010, 97, 2001–2008. [Google Scholar] [CrossRef]
- Mai, W.X.; Tian, C.Y.; Li, C.J. Soil salinity dynamics under drip irrigation and mulch film and their effects on cotton root length. Commun. Soil Sci. Plant Anal. 2013, 44, 1489–1502. [Google Scholar] [CrossRef]
- Mu, H.; Hudan, T.; Su, L.; Mahemujiang, A.; Wang, Y.; Zhang, J. Salt transfer law for cotton field with drip irrigation under mulch in arid region. Trans. Chin. Soc. Agric. Eng. 2011, 27, 18–22. [Google Scholar] [CrossRef]
- Zhao, Y.; Mao, X.; Shukla, M.K.; Tian, F.; Hou, M.; Zhang, T.; Li, S. How does film mulching modify available energy, evapotranspiration, and crop coefficient during the seed—Maize growing season in northwest China? Agric. Water Manag. 2021, 245, 106666. [Google Scholar] [CrossRef]
- He, Q.; Li, S.; Kang, S.; Yang, H.; Qin, S. Simulation of water balance in a maize field under film–mulching drip irrigation. Agric. Water Manag. 2018, 210, 252–260. [Google Scholar] [CrossRef]
- Wang, J.; Tong, L.; Kang, S.; Li, F.; Zhang, X.; Ding, R.; Du, T.; Li, S. Flowering characteristics and yield of maize inbreds grown for hybrid seed production under deficit irrigation. Crop Sci. 2017, 57, 2238–2250. [Google Scholar] [CrossRef]
- Tian, D.; Zhang, Y.; Mu, Y.; Zhou, Y.; Zhang, C.; Liu, J. The effect of drip irrigation and drip fertigation on N2O and NO emissions, water saving and grain yields in a maize field in the North China Plain. Sci. Total Environ. 2017, 575, 1034–1040. [Google Scholar] [CrossRef]
- Cook, H.F.; Valdes, G.S.B.; Lee, H.C. Mulch effects on rainfall interception, soil physical characteristics and temperature under Zea mays L. Soil Tillage Res. 2006, 91, 227–235. [Google Scholar] [CrossRef]
- Ghosh, P.K.; Dayal, D.; Bandyopadhyay, K.K.; Mohanty, M. Evaluation of straw and polythene mulch for enhancing productivity of irrigated summer groundnut. Field Crops Res. 2006, 99, 76–86. [Google Scholar] [CrossRef]
- Ayars, J.E.; Phene, C.J.; Hutmacher, R.B.; Davis, K.R.; Schoneman, R.A.; Vail, S.S.; Mead, R.M. Subsurface drip irrigation of row crops: A review of 15 years of research at the water management research laboratory. Agric. Water Manag. 1999, 42, 1–27. [Google Scholar] [CrossRef]
- Yohannes, F.; Tadesse, T. Effect of drip and furrow irrigation and plant spacing on yield of tomato at dire dawa, Ethiopia. Agric. Water Manag. 1998, 35, 201–207. [Google Scholar] [CrossRef]
- Shao, G.; Cai, H.; Wu, L.; Zhang, Z. Prospect for the development of field drip irrigation under mulch in Xinjiang. Agric. Res. Arid Areas 2001, 19, 122–127. [Google Scholar] [CrossRef]
- Yang, P.; Dong, X.; Wei, G.; Ma, L.; Liu, L. Characteristics of salt deposition under drip irrigation beneath plastic film in arid area. Chin. J. Soil Sci. 2011, 42, 4. [Google Scholar] [CrossRef]
- Wang, Z.; Fan, B.; Guo, L. Soil salinization after long-term mulched drip irrigation poses a potential risk to agricultural sustainability. Eur. J. Soil Sci. 2011, 70, 20–24. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.Y.; Wang, Q.J. Application of drip irrigation technology under membrane in water-saving and salt-controlling irrigation in arid and semi-arid regions. J. Irrig. Drain. 2001, 20, 5. [Google Scholar] [CrossRef]
- Wang, J.; Gong, S.; Xu, D.; Juan, S.; Mu, J. Numerical simulations and validation of water flow and heat transport in a subsurface drip irrigation system using HYDRUS-2D. Irrig. Drain. 2013, 62, 97–106. [Google Scholar] [CrossRef]
- Selim, T.; Berndtson, R.; Persson, M. Simulation of soil water and salinity distribution under surface drip irrigation. Irrig. Drain. 2013, 62, 352–362. [Google Scholar] [CrossRef]
- Zapata-Sierra, A.J.; Roldán-Cañas, J.; Reyes-Requena, R.; Moreno-Pérez, M.F. Study of the Wet Bulb in Stratified Soils (Sand-Covered Soil) in Intensive Greenhouse Agriculture under Drip Irrigation by Calibrating the Hydrus-3D Model. Water 2021, 13, 600. [Google Scholar] [CrossRef]
- Shan, Y.; Wang, Q. Simulation of salinity distribution in the overlap zone with double-point-source drip irrigation using Hydrus-3D. Aust. J. Crop Sci. 2012, 6, 238–247. [Google Scholar]
- Zhao, Y.; Mao, X.; Shukla, M.K. A modified swap model for soil water and heat dynamics and seed—Maize growth under film mulching. Agric. For. Meteorol. 2020, 292–293, 108127. [Google Scholar] [CrossRef]
- Qi, Z.; Hao, F.; Ying, Z.; Zhang, T.; Zhang, A. Spatial distribution and simulation of soil moisture and salinity under mulched drip irrigation combined with tillage in an arid saline irrigation district, northwest China. Agric. Water Manag. 2018, 201, 219–231. [Google Scholar] [CrossRef]
- Bristow, K.L.; Horton, R. Modeling the impact of partial surface mulch on soil heat and water flow. Theor. Appl. Climatol. 1996, 54, 85–98. [Google Scholar] [CrossRef]
- Graefe, J. Simulation of soil heating in ridges partly covered with plastic mulch, part I: Energy balance model. Biosyst. Eng. 2005, 92, 391–407. [Google Scholar] [CrossRef]
- Graefe, J.; Schmidt, S.; Heissner, A. Simulation of soil heating in ridges partly covered with plastic mulch, part II: Model calibration and validation. Biosyst. Eng. 2005, 92, 495–512. [Google Scholar] [CrossRef]
- Zeng, W.Z.; Chi, X.; Wu, J.W.; Huang, J.S. Soil salt leaching under different irrigation regimes: HYDRUS-1D modelling and analysis. J. Arid Land 2014, 6, 44–58. [Google Scholar] [CrossRef]
- Chen, L.; Feng, Q.; Li, F.; Li, C. A bidirectional model for simulating soil water flow and salt transport under mulched drip irrigation with saline water. Agric. Water Manag. 2014, 146, 24–33. [Google Scholar] [CrossRef]
- Ning, S.; Zhou, B.; Shi, J.; Wang, Q. Soil water/salt balance and water productivity of typical irrigation schedules for cotton under film mulched drip irrigation in northern Xinjiang. Agric. Water Manag. 2021, 245, 106651. [Google Scholar] [CrossRef]
- Chen, W.; Li, M.; Qin, W.; Xu, Y.; Nie, J.; Liang, M. Effect of horizontal tillage measures regulatory on soil water and salt distribution under mulched drip irrigation. Trans. Chin. Soc. Agric. Mach. 2020, 51, 276–286. [Google Scholar] [CrossRef]
- Rehemui; Hudan, T.; Mahemut, A.; Zhao, J.H.; Alipujiang, A. Study on the numerical simulation of soil water and salt transport under mulch drip irrigation. Xinjiang Agric. Sci. 2015, 52, 2136–2141. [Google Scholar]
- Šimůnek, J.; Sejna, M.; van Genuchten, M.T. The HYDRUS-2D Software Package for Simulating Two-Dimensional Movement of Water, Heat, and Multiple Solutes in Variable Saturated Media Version 2.0.1GWMCTPS-53; International Ground Water Modeling Center, Colorado School of Mines: Golden, CO, USA, 1999; Available online: https://www.pc-progress.com/Downloads/Pgm_Hydrus2D/HYDRUS2D.PDF (accessed on 10 January 2022).
- Šimůnek, J.; Jacques, D.; Hopmans, J.W.; Inoue, M.; Flury, M.; van Genuchten, M.T. Solute transport during variably saturated flow-inverse methods. In Methods of Soil Analysis: Part 1, Physical Methods, 1st ed.; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America Journal: Madison, WI, USA, 2002; pp. 1435–1449. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, W.; Lü, D.Q.; Wang, Z.R.; Zhang, J.F. Water and salt transport features for salt-effected soil through drip irrigation under film. Trans. Chin. Soc. Agric. Eng. 2000, 16, 54–57. [Google Scholar] [CrossRef]
- Yao, B.; Li, G.; Ye, H.; Li, F. Characteristics of spatial and temporal changes in soil salt content in cotton fields under mulched drip irrigation in arid oasis regions. Trans. Chin. Soc. Agric. Mach. 2016, 47, 11. [Google Scholar] [CrossRef]
- Kandelous, M.M.; Šimůnek, J. Numerical simulations of water movement in a subsurface drip irrigation system under field and laboratory conditions using HYDRUS-2D. Agric. Water Manag. 2010, 97, 1070–1076. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Ippisch, O.; Vogel, H.J.; Bastian, P. Validity limits for the van genuchten-mualem model and implications for parameter estimation and numerical simulation. Adv. Water Resour. 2006, 29, 1780–1789. [Google Scholar] [CrossRef]
- Šimůnek, J.; Huang, K.; Van Genuchten, M.T. The SWMS-3D Code for Simulating Water Flow and Solute Transport in Three-Dimensional Variably Saturated Media Version 1.0; Research Report No. 139; U.S. Salinity Laboratory, USDA, ARS: Riverside, CA, USA, 1995; p. 155. Available online: https://www.ars.usda.gov/arsuserfiles/20361500/pdf_pubs/P1477.pdf (accessed on 12 January 2022).
- Van Genuchten, M.T.; Wagenet, R.J. Two-site/two-region models for pesticide transport and degradation: Theoretical development and analytical solutions. Soil Sci. Soc. Am. J. 1989, 53, 1303–1310. [Google Scholar] [CrossRef]
- Toride, N. Flux-averaged concentrations for transport in soils having nonuniform initial solute distributions. Soil Sci. Soc. Am. J. 1993, 57, 1406–1409. [Google Scholar] [CrossRef]
- Sophocleous, M. Analysis of water and heat flow in unsaturated-saturated porous media. Water Resour. Res. 1979, 15, 1195–1206. [Google Scholar] [CrossRef]
- Šimůnek, J.; Suarez, D.L. Modeling of carbon dioxide transport and production in soil: 1. Model development. Water Resour. Res. 1993, 29, 487–497. [Google Scholar] [CrossRef]
- Chung, S.-O.; Horton, R. Soil heat and water flow with a partial surface mulch. Water Resour. Res. 1987, 23, 2175–2186. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; Van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Q.; Fan, J.; Wang, W. Soil thermal properties determination and prediction model comparison. Trans. Chin. Soc. Agric. Eng. 2012, 28, 78–84. [Google Scholar] [CrossRef]
- Pan, M.; Huang, Q.; Feng, R.; Hang, G. Estimation of hydraulic and thermal parameters in saturated layered porous media based on heat tracing method. J. Hydraul. Eng. 2017, 48, 10. [Google Scholar] [CrossRef]
- Hu, J.H.; Zhao, W.J.; Liu, G.Y.; Hu, J.Z. Numerical Simulation of the Influence of Water and Soil Temperature on Water and Heat Transfer of Sand Mulching Soil under Drip Irrigation. J. Soil Water Conserv. 2020, 34, 349–354. [Google Scholar] [CrossRef]
- Chen, S.; Mao, X.; Shukla, M.K. Evaluating the effects of layered soils on water flow, solute transport, and crop growth with a coupled agro-eco-hydrological model. J. Soils Sediments 2020, 20, 3442–3458. [Google Scholar] [CrossRef]
- Sun, G.; Qu, Z.; Du, B.; Ren, Z.; Liu, A. Water-heat-salt effects of mulched drip irrigation maize with different irrigation scheduling in hetao irrigation district. Trans. Chin. Soc. Agric. Eng. 2017, 33, 144–152. [Google Scholar] [CrossRef]
- Wang, Y.M.; Husan, T.; Yi, P.F.; Zhang, J.Z.; Wu, Z.G.; Xu, F.L. Research on the Moment of Water and Salinity for Drip Irrigation under the Film under Saline and Alkali Soils. China Rural Water Hydropower 2010, 10, 13–17. [Google Scholar]
- Nachshon, U.; Weisbrod, N.; Dragila, M.I.; Grader, A. Combined evaporation and salt precipitation in homogeneous and heterogeneous porous media. Water Resour. Res. 2011, 47, 980–990. [Google Scholar] [CrossRef]
- Wu, Z.D.; Wang, Q.J. Saline water infiltration with different initial moisture contents. Trans. Chin. Soc. Agric. Mach. 2010, 41, 53–58. Available online: http://www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=2010s11&journal_id=jcsam (accessed on 26 July 2022).
- Li, M.; Liu, H.; Zheng, X. Spatiotemporal variation for soil salinity of field land under long-term mulched drip irrigation. Trans. Chin. Soc. Agric. Eng. 2012, 28, 82–87. [Google Scholar] [CrossRef]
- Liu, Q.; Li, W.; Zhao, G.; Jia, Z.; An, W.; Wang, J.; Mu, M. Effects of gravel-sand mulching and irrigation on soil hydrothermal conditions and fruit yield in ecological jujube forests on degraded field. J. Agric. Resour. Environ. 2022. Available online: http://agri.ckcest.cn/topic/downloadFile/d71a6748-c6dc-4e48-b054-82fe7de8760e (accessed on 26 July 2022).
- Wen, W.; Lai, Y.; You, Z. Numerical modeling of water—Heat—Vapor—Salt transport in unsaturated soil under evaporation. Int. J. Heat Mass Transf. 2020, 159, 120114. [Google Scholar] [CrossRef]
- Noborio, K.; Mclnnes, K.J. Thermal conductivity of salt-affected soils. Soil Sci. Soc. Am. J. 1993, 57, 329–334. [Google Scholar] [CrossRef]

| Time (d) | 1 | 4 | 7 | 10 | 13 | 16 | 19 | 22 | 25 | 28 | ||
| Number of irrigation -th | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| Irrigation amount | W1 1 | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 2 | 1 | 1 | 31 |
| W2 1 | 5 | 5 | 5 | 5 | 5 | 2 | 1 | 1 | 1 | 1 | 31 | |
| W1 | W2 | W1 | W2 | W1 | W2 | |
| MAE | 0.0051 | 0.0074 | 1.16 | 1.13 | 1.32 | 1.76 |
| RMSE | 0.0064 | 0.0092 | 1.48 | 1.52 | 1.60 | 2.16 |
| NRMSE (%) | 1.63 | 2.32 | 16.35 | 16.64 | 5.04 | 6.63 |
| 0.67 | 0.70 | 0.66 | 0.54 | 0.79 | 0.71 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, H.; Bo, L.; Mao, X.; Liu, X.; Wang, Y.; Hu, Q. Modelling Soil Water, Salt and Heat Dynamics under Partially Mulched Conditions with Drip Irrigation, Using HYDRUS-2D. Water 2022, 14, 2791. https://doi.org/10.3390/w14182791
Tian H, Bo L, Mao X, Liu X, Wang Y, Hu Q. Modelling Soil Water, Salt and Heat Dynamics under Partially Mulched Conditions with Drip Irrigation, Using HYDRUS-2D. Water. 2022; 14(18):2791. https://doi.org/10.3390/w14182791
Chicago/Turabian StyleTian, Huiwen, Liyuan Bo, Xiaomin Mao, Xinyu Liu, Yan Wang, and Qingyang Hu. 2022. "Modelling Soil Water, Salt and Heat Dynamics under Partially Mulched Conditions with Drip Irrigation, Using HYDRUS-2D" Water 14, no. 18: 2791. https://doi.org/10.3390/w14182791
APA StyleTian, H., Bo, L., Mao, X., Liu, X., Wang, Y., & Hu, Q. (2022). Modelling Soil Water, Salt and Heat Dynamics under Partially Mulched Conditions with Drip Irrigation, Using HYDRUS-2D. Water, 14(18), 2791. https://doi.org/10.3390/w14182791





