Innovative Vulnerability and Risk Assessment of Urban Areas against Flood Events: Prognosis of Structural Damage with a New Approach Considering Flow Velocity
Abstract
:1. Introduction
2. Basic Elements of the Procedure
2.1. Damage Data
2.1.1. EDAC Flood Damage Database
2.1.2. Tsunami Damage Data
2.2. Investigation Areas
2.3. Flood Scenarios
3. Flood Damage and Vulnerability of Buildings
3.1. Damage Scale for Flooding
3.2. Flood Vulnerability Classes
3.3. Prognosis of Structural Damage
3.4. Loss Prediction
4. Improved Prognosis of Structural Damages
4.1. Consideration of Inundation Level and Flow Velocity
- Variant V1 only converts the existing approach from [18] to the six-stage damage scale;
- Variant V2 uses the inundation level (hgl) and flood intensity (Ifl = hgl × vfl) from the so-called “Swiss model”, representing a combination of inundation level and flow velocity but without an extended physical background;
- Variant V3 includes the inundation level (hgl) and the momentum flux (hgl × vfl2) (which is related to the hydrodynamic forces);
- Variant V4 considers only the momentum flux as a physically based input parameter;
- Variant V5 is similar to Variant 3 but weights the influence of the inundation level in a differentiated way.
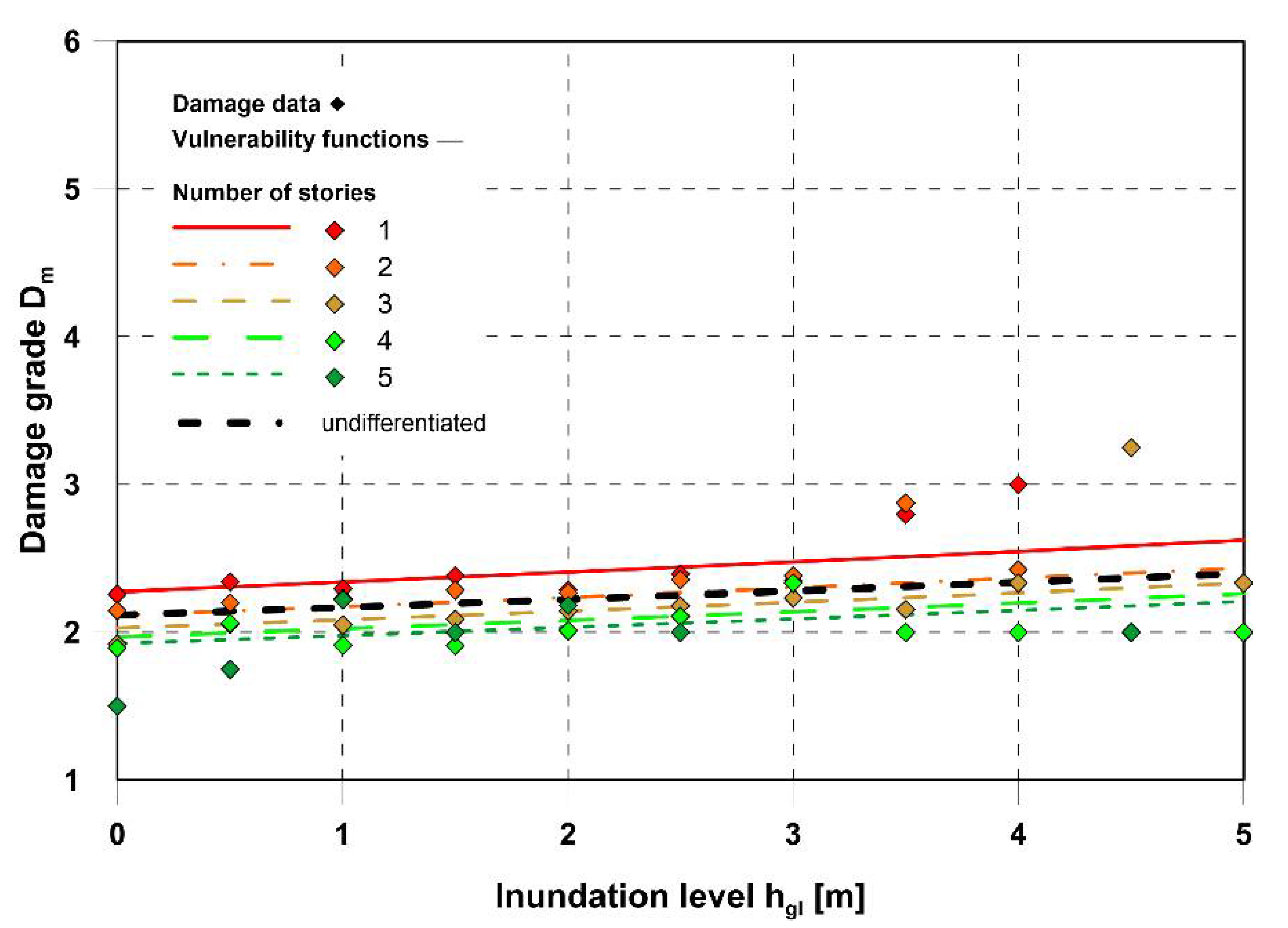
4.2. Consideration of Inundation Level, Flow Velocity and the Number of Storeys
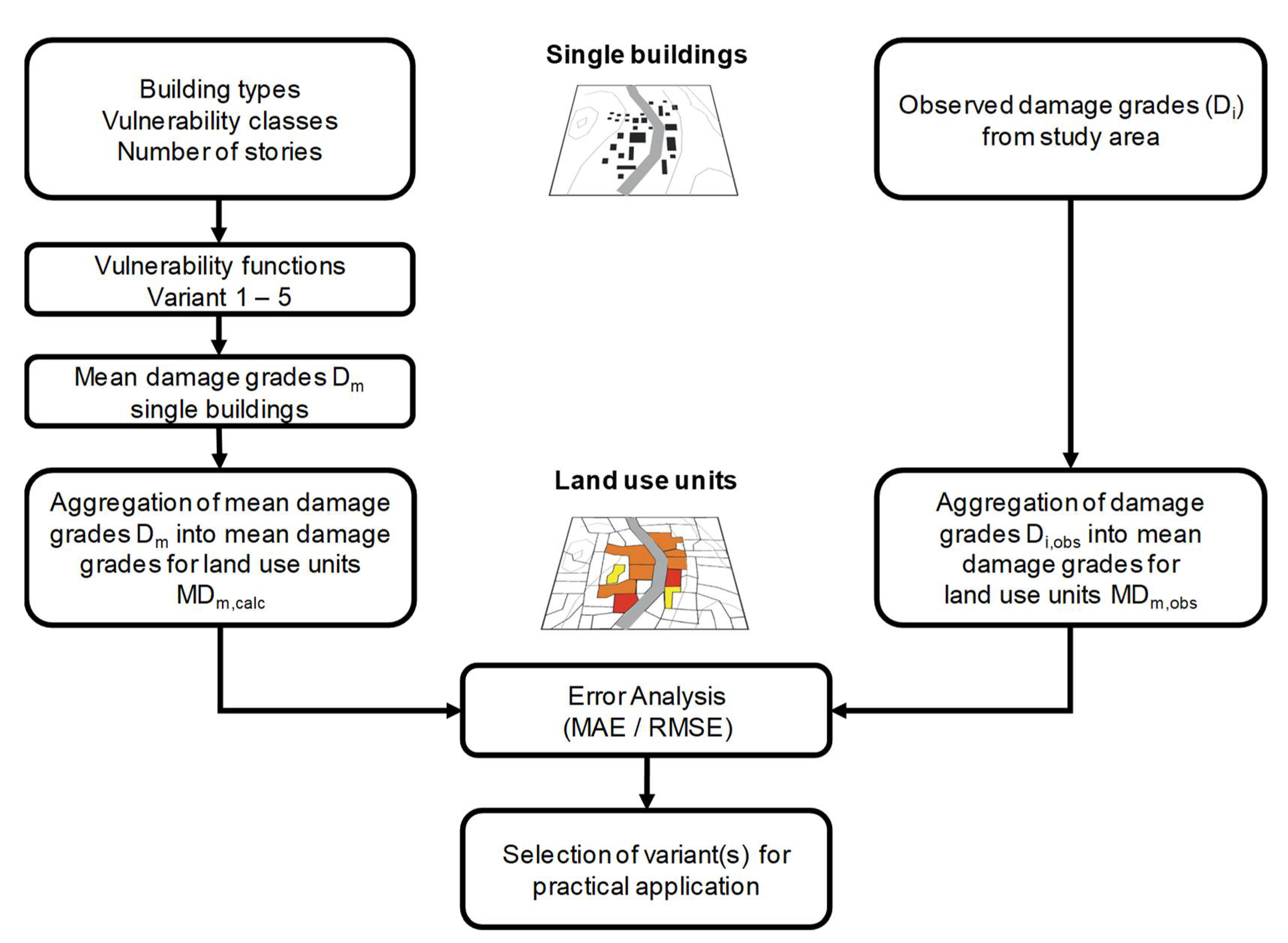
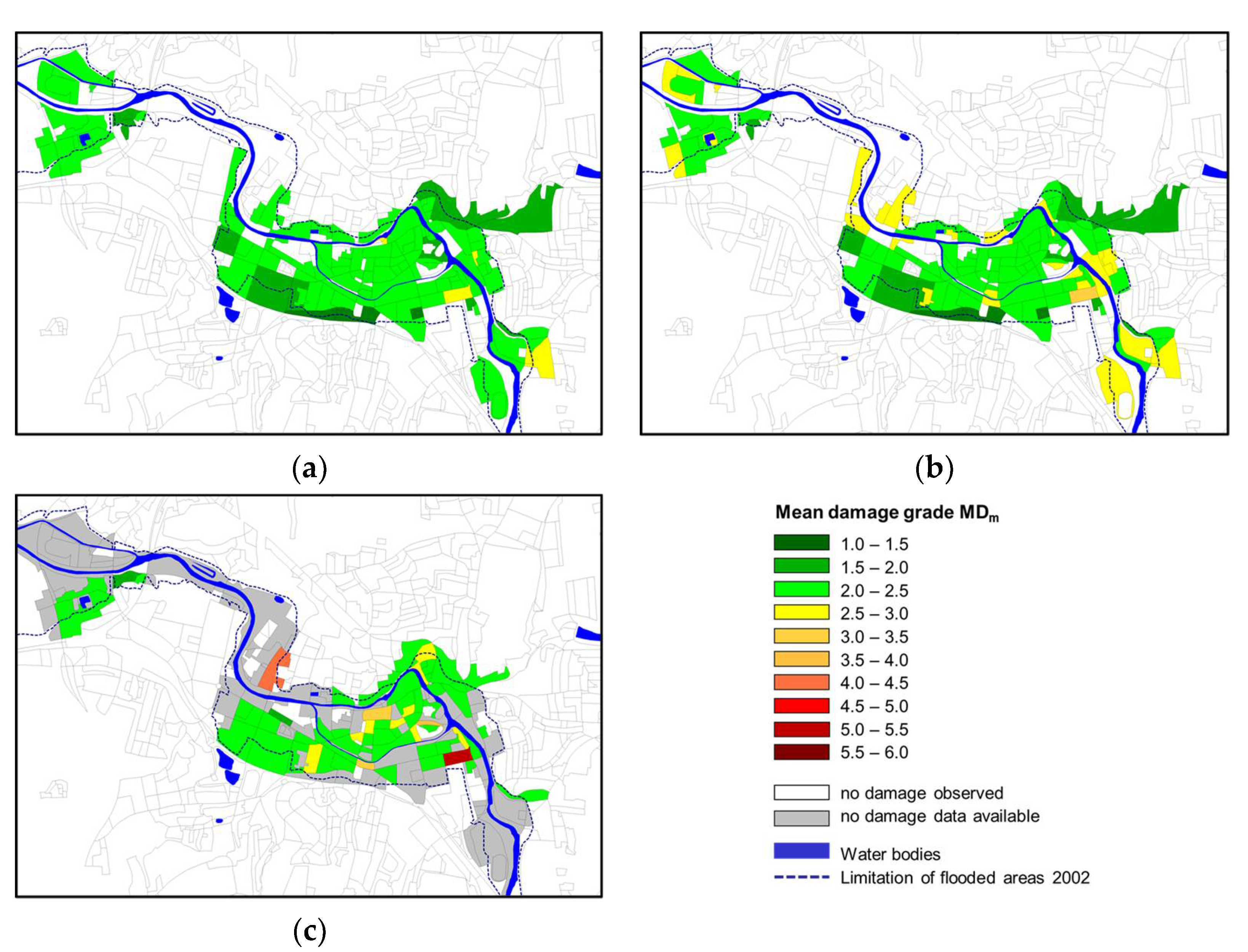
5. Validation of the Improved Model
6. Conclusions
7. Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maiwald, H.; Schwarz, J. Die Sturzflut von Braunsbach—Ingenieuranalyse der Gebäudeschäden. Bautechnik 2016, 93, 925–932. [Google Scholar] [CrossRef]
- Laudan, J.; Rözer, V.; Sieg, T.; Vogel, K.; Thieken, A.H. Damage assessment in Braunsbach 2016: Data collection and analysis for an improved understanding of damaging processes during flash floods. Nat. Hazards Earth Syst. Sci. 2017, 17, 2163–2179. [Google Scholar] [CrossRef]
- Maiwald, H.; Schwarz, J.; Abrahamczyk, L.; Kaufmann, C. Das Hochwasser 2021—Ingenieuranalyse der Bauwerksschäden. Bautechnik 2022, 99, submitted. [Google Scholar]
- Jongman, B.; Kreibich, H.; Apel, H.; Barredo, J.I.; Bates, P.D.; Feyen, L.; Gericke, A.; Neal, J.; Aerts, J.C.J.H.; Ward, P.J. Comparative flood damage model assessment: Towards a European approach. Nat. Hazards Earth Syst. Sci. 2012, 12, 3733–3752. [Google Scholar] [CrossRef]
- Black, R.D. Floodproofing Rural Residences; Report no EDA 77-088; US Department of Commerce, Economic Development Administration: Washington, DC, USA, 1975.
- Sangrey, D.A.; Murphy, P.J.; Nieber, J.L. Evaluating the Impact of Structurally Interrupted Flood Plain Flows; Technical Report No. 98; Cornell University Water Resources and Marine Sciences Center: Ithaca, NY, USA, 1975. [Google Scholar]
- Smith, D.I. Extreme floods and dam failure inundation implications for loss assessment. In Proceedings of the Seminar Natural and Technological Hazards: Implications for the Insurance Industry; University of New England: Armidale, Australia, 1991; pp. 149–165. [Google Scholar]
- Clausen, L.; Clark, P.B. The development of criteria for predicting dambreak flood damages using modelling of historical dam failures. In Proceedings of the International Conference on River Flood Hydraulics; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1991. [Google Scholar]
- Maiwald, H.; Schwarz, J. Ermittlung von Hochwasserschäden unter Berücksichtigung der Bauwerksverletzbarkeit, EDAC-Hochwasserschadensmodell; Scientific Technical Reports 01-11; Zentrum für die Ingenieuranalyse von Erdbebenschäden, Universitätsverlag, Bauhaus-Universität Weimar: Weimar, Germany, 2011. [Google Scholar]
- Maiwald, H.; Schwarz, J. Damage and Loss Prognosis Tools Correlating Flood Action and Building’s Resistance-type Parameters. Int. J. Saf. Secur. Eng. 2015, 5, 222–250. [Google Scholar] [CrossRef]
- Maiwald, H.; Kaufmann, C.; Langhammer, T.; Schwarz, J. A new model for consideration of flow velocity in flood damage and loss prognosis. In Proceedings of the FLOODrisk 2020, 4th European Conference on Flood Risk Management, Online, 22–24 June 2021. Paper PA_11_9. [Google Scholar] [CrossRef]
- Golz, S.; Maiwald, H.; Naumann, T.; Schwarz, J. Innovative Vulnerability and Risk Assessment of Urban Areas against Flood Events: Prognosis of losses with a new approach for synthetic damage functions. Water 2022, 14. in preparation. [Google Scholar]
- Koch, R.; Tritschler, F.; Golz, S.; Wehner, T.; Maiwald, H. Innovative Vulnerabilitäts- und Risikobewertung urbaner Räume gegenüber Überflutungsereignissen: Schadenpotenzialanalyse mit Geodatenbasierten Ansätzen. Hydr. Wasserbewirt. 2023. in preparation. [Google Scholar]
- SAB Information on the Amount of Losses in the Residential Area and on the Commercial Damage in Saxony; Saxonian Relief Bank: Saxony, Germany, 2012; Excel-file.
- Schwarz, J.; Maiwald, H. Ingenieurmäßige Beschreibung der Schadenserwartung von Gebäuden unter Hochwassereinwirkung auf der Grundlage von Verletzbarkeitsklassen; Abschlussbericht zum Projekt 246 143 75 im Auftrag der Landestalsperrenverwaltung des Freistaates Sachsen; Zentrum für die Ingenieuranalyse von Erdbebenschäden, Bauhaus-Universität Weimar: Weimar, Germany, 2009; Excel-file. [Google Scholar]
- Schwarz, J.; Maiwald, H.; Gerstberger, A. Quantifizierung der Schäden infolge Hochwassereinwirkung: Fallstudie Eilenburg. Bautechnik 2005, 82, 845–856. [Google Scholar] [CrossRef]
- Kreibich, H.; Piroth, K.; Seifert, I.; Maiwald, H.; Kunert, U.; Schwarz, J.; Merz, B.; Thieken, A.H. Is flow velocity a significant parameter in flood damage modelling? Nat. Hazards Earth Syst. Sci. 2009, 9, 1679–1692. [Google Scholar] [CrossRef]
- Maiwald, H.; Schwarz, J. Berücksichtigung der Fließgeschwindigkeit bei Hochwasser-Schadensmodellen. Bautechnik 2009, 86, 550–565. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure and Transportation (MLIT). Survey of Tsunami Damage Condition. Available online: http://www.mlit.go.jp/toshi/toshi-hukkou-arkaibu.html (accessed on 5 May 2021).
- Suppasri, A.; Mas, E.; Charvet, I.; Gunasekera, R.; Imai, K.; Fukutani, Y.; Abe, Y.; Imamura, F. Building damage characteristics based on surveyed data and fragility curves of the 2011 Great East Japan Tsunami. Nat. Hazards 2013, 66, 319–341. [Google Scholar] [CrossRef]
- Suppasri, A.; Charvet, I.; Imai, K.; Imamura, F. Fragility curves based on data from the 2011 Tohoku-Oki Tsunami in Ishinomaki City, with discussion of parameters influencing building damage. Earthq. Spectr. 2015, 31, 841–868. [Google Scholar] [CrossRef]
- Grünthal, G.; Musson, R.; Schwarz, J.; Stucchi, M. European Macroseismic Scale 1998. In Cahiers du Centre Européen de Géodynamique et de Séismologie; European Center for Geodynamics and Seismology: Walferdange, Luxembourg, 1998; Volume 15. [Google Scholar]
- Schwarz, J.; Maiwald, H. Prognose der Bauwerksschädigung unter Hochwassereinwirkung. Bautechnik 2007, 84, 450–464. [Google Scholar] [CrossRef]
- Maiwald, H.; Schwarz, J. Unified damage description and risk assessment of buildings under extreme natural hazards. Eur. J. Mason. 2019, 23, 95–111. [Google Scholar] [CrossRef]
- Maiwald, H.; Schwarz, J. Vulnerability assessment of Multi Hazard exposed building types—Development of an EMS-98 based empirical-statistical methodology. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017. Paper No. 2134. [Google Scholar]
- Foytong, P.; Ruangrassamee, A.; Shoji, G.; Hiraki, Y.; Ezura, Y. Analysis of tsunami flow velocities during the March 2011 Tohoku, Japan, Tsunami. Earthq. Spectr. 2013, 29, 161–181. [Google Scholar] [CrossRef]
- Suppasri, A.; Imai, K.; Imamura, F.; Koshimura, S. Comparison of casualty and building damage between Sanriku Ria Coast and Sendai Plain Coast based on the 2011 Great East Japan Tsunami. In Proceedings of the International Sessions in Conference of Coastal Engineering, Santander, Spain, 2–6 July 2012; JSCE, 3. pp. 76–80. [Google Scholar]
- Maiwald, H.; Schwarz, J. Schadensmodelle für extreme Hochwasser—Teil 1: Modellbildung und Validierung am Hochwasser 2002. Bautechnik 2014, 91, 200–210. [Google Scholar] [CrossRef]
- Naumann, T.; Rubin, C. Ermittlung potenzieller Hochwasserschäden in Pirna nach dem gebäudetypologischen VERIS Elbe-Ansatz. In Tagungsband zum DWA-Seminar Hochwasserschadensinformationen: Neues und Bewährtes; Hennef: Hennef, Germany, 2008; pp. 86–101. [Google Scholar]
- Naumann, T.; Golz, S.; Nikolowski, J. Synthetic depth-damage functions—A detailed tool for analyzing flood resilience of building types. In Proceedings of the Final Conference of the COST action C22 Urban Flood Management in cooperation with UNESCO-IHP, Paris, France, 26–27 November 2009. [Google Scholar]
- Schwarz, J.; Maiwald, H.; Kaufmann, C.; Beinersdorf, S. Evaluation of the vulnerability of existing building stocks under single and Multi-Hazard impact. In Proceedings of the 16th European Conference on Earthquake Engineering (ECEE), Thessaloniki, Greece, 18–21 June 2018. Paper 11641. [Google Scholar]
- Schwarz, J.; Maiwald, H.; Kaufmann, C.; Langhammer, T.; Beinersdorf, S. Conceptual basics and tools to assess the multi hazard vulnerability of existing buildings. Eur. J. Mason. 2019, 23, 246–264. [Google Scholar] [CrossRef]
- Planungsgesellschaft Scholz und Lewis mbH. Ergebnisse der 2D-HN-Modellierung Döbeln für den Ist-Zustand 8/2002, Wassertiefen- und Geschwindigkeitsshapes, GRIDS und -TINS; Planungsgesellschaft Scholz und Lewis mbH, Landestalsperrenverwaltung Sachsen: Pirna, Germany, 2009. [Google Scholar]
- Maiwald, H.; Schwarz, J.; Abrahamczyk, L.; Lobos, D. Das Magnitude 8.8 Maule (Chile)-Erdbeben vom 27. Februar 2010—Ingenieuranalyse der Tsunamischäden. Bautechnik 2010, 87, 614–622. [Google Scholar] [CrossRef]
- Maiwald, H.; Schwarz, J. Simulative flood damage modelling taking into account inundation level and flow velocity: Uncertainties and strategies for further refinement. In Proceedings of the 8th International Conference on Flood and Urban Water Management, FRIAR 2022, Online, 6–8 July 2022. [Google Scholar]
- Strangefield, P.; Stopp, H. Floating houses: An adaptation strategy for flood preparedness in times of global change. In Proceedings of the Flood Recovery, Innovation and Reponse IV, Poznan, Poland, 18–20 June 2014. [Google Scholar] [CrossRef]
- Maiwald, H. Ingenieurmäßige Ermittlung von Hochwasserschadenspotentialen im Mikroskaligen Maßstab. Ph.D. Thesis, Bauhaus-Universität Weimar, Weimar, Germany, 2008. Schriftenreihe des Instituts für Konstruktiven Ingenieurbau 011. [Google Scholar]
- Bundesministerium für Verkehr, Bau- und Wohnungswesen. Normalherstellungskosten 2000 (NHK 2000). Available online: https://www.werttax.de/plaintext/downloads/normalherstellungskosten2000nhk2000.pd (accessed on 25 July 2022).
- Statistisches Bundesamt. Preisindizes für die Bauwirtschaft. Fachserie 17, Reihe 4. 2020. Available online: https://www.statistischebibliothek.de/mir/receive/DEHeft_mods_00133218 (accessed on 5 July 2022).
- Charvet, I.; Macabuag, J.; Rossetto, T. Estimating Tsunami-Induced Building Damage through Fragility Functions: Critical Review and Research Needs. Front. Built. Environ. 2017, 3, 36. [Google Scholar] [CrossRef]
- De Risi, R.; Goda, K.; Yasuda, T.; Mori, N. Is flow velocity important in tsunami empirical fragility modeling? Earth. Sci. Rev. 2017, 166, 64–82. [Google Scholar] [CrossRef]
- Farhadi, H.; Najafzadeh, M. Flood Risk Mapping by Remote Sensing Data and Random Forest Technique. Water 2021, 13, 3115. [Google Scholar] [CrossRef]
- Schwarz, J.; Maiwald, H.; Kaufmann, C.; Langhammer, T. Innovative Vulnerabilitäts- und Risikobewertung urbaner Räume gegenüber Überflutungsereignissen INNOVARU; Abschlussbericht Teil II: Projektergebnisse; Bauhaus-Universität Weimar: Weimar, Germany, 2021. [Google Scholar]
- Figueiredo, R.; Schröter, K.; Weiss-Motz, A.; Martina, M.L.V.; Kreibich, H. Multi-model ensembles for assessment of flood losses and associated uncertainty. Nat. Hazards Earth Syst. Sci. 2018, 18, 1297–1314. [Google Scholar] [CrossRef]
- Farhadi, H.; Esmaeily, A.; Najafzadeh, M. Flood monitoring by integration of Remote Sensing technique and Multi-Criteria Decision Making method. Comp. Geosci. 2022, 160, 105045. [Google Scholar] [CrossRef]
- Haddidian, N.M.; Schwarz, J. EMS-98 based damage grade assessment using remote sensing images for cascading events. In Proceedings of the 3rd European Conference on Earthquake Engineering & Seismology (ECEES), Bucharest, Romania, 4–9 September 2022. Paper 6231. [Google Scholar]














| Investigation Area | Buildings Inspected (Affected) 1 | Damage Cases: SAB 2 (EDAC) 3 | Year(s) of Survey | |
|---|---|---|---|---|
| Residential | Total | |||
| Pirna | 1209 (938) | 1405 (1067) | 1148 (366) | 2008 |
| Grimma | 773 (690) | 1280 (1186) | 616 (306) | 2009, 2017 |
| Freital | 1048 (946) | 2096 (1842) | 865 (277) | 2019 |
| Eilenburg | 1041 (1028) | 2184 (2149) | 961 (551) | 2003, 2004 |
| Döbeln | 832 (788) | 1429 (1348) | 681 (276) | 2004 |
| Flöha | 734 (721) | 1872 (1828) | 582 (154) | 2009 |
| Investigation Area | 2D Model Approach | Grid Size (m × m) 1 | Inundation Level hgl (m) 2 | Flow Velocity vfl (m/s) 2 |
|---|---|---|---|---|
| Pirna | detailed | variable | 0–4.1 | 0–5.3 |
| Grimma | detailed | 5 × 5 (hgl) 1 × 1 (vfl) | 0–5.0 | 0–2.7 |
| Freital | detailed | 2 × 2 | 0–3.5 | 0–4.5 |
| Eilenburg | mean roughness | 25 × 25 | 0–3.5 | 0–1.9 |
| Döbeln | detailed | variable | 0–4.7 | 0–2.4 |
| Flöha | mean roughness | 5 × 5 | 0–2.8 | 0–2.3 |
| Damage Grade | Damage | Description | Drawing | Example 1 | |
|---|---|---|---|---|---|
| Structural | Non-Structural | ||||
| D1 | none | light | moisture damage, dirt |  |  |
| D2 | light | moderate | slight cracking of loadbearing walls doors/windows pushed in washing out of foundations contamination replacement of finshings necessary | 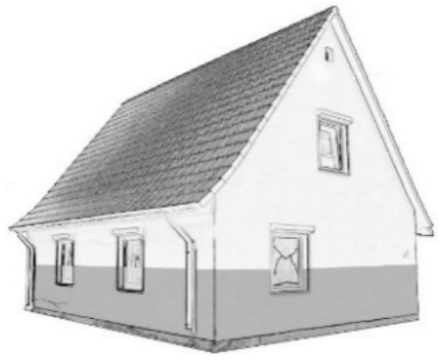 |  |
| D3 | moderate | heavy | larger cracking in loadbearing walls and slabs settlements collapse of non-loadbearing walls replacement of non-loadbearing building elements necessary | 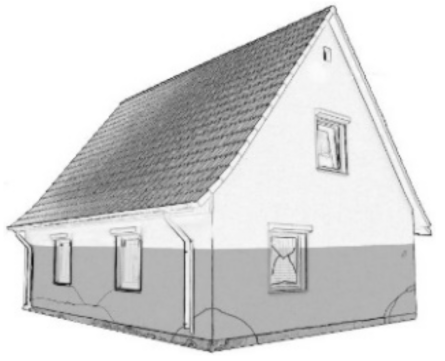 |  |
| D4 | heavy | very heavy | collapse of loadbearing walls, slabs replacement of loadbearing walls, slabs | 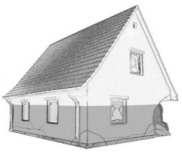 |  |
| D5 | very heavy | very heavy | collapse of larger parts of building | 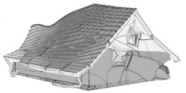 |  |
| D6 | very heavy | very heavy | dislocation: building completely washed away, toppled or displaced from foundation |  |  |
| Building Type | Vulnerability Class HW- | |||||
|---|---|---|---|---|---|---|
| A | B | C | D | E | F | |
| Clay |  | |||||
| Prefabricated timber frame | 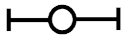 | |||||
| Timber frame with masonry or clay infill | 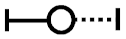 | |||||
| Masonry |  | |||||
| Reinforced concrete |  | |||||
| Flood-resistant design | 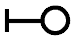 | |||||
| Flood-evasive design |  | |||||
 Most likely vulnerability class.
Most likely vulnerability class.  Probable range.
Probable range.  Range of less probable, exceptional cases.
Range of less probable, exceptional cases.| Variant | VC | Coefficients | Coefficient of Determination (R2) | ||
|---|---|---|---|---|---|
| C1 | C2 | C3 | |||
| V1 | HW-A 1 | 0.351 | −0.730 | - | - |
| HW-B | 0.292 | −0.853 | - | 0.72 | |
| HW-C | 0.238 | −0.914 | - | 0.84 | |
| HW-D 2 | 0.189 | −0.920 | - | 0.76 | |
| V2 | HW-A 1 | 0.255 | 0.066 | −0.572 | - |
| HW-B | 0.135 | 0.053 | −0.621 | 0.78 | |
| HW-C | 0.062 | 0.042 | −0.647 | 0.88 | |
| HW-D 2 | 0.035 | 0.030 | −0.650 | 0.84 | |
| V3 | HW-A 1 | 0.230 | 0.017 | −0.496 | - |
| HW-B | 0.143 | 0.011 | −0.571 | 0.79 | |
| HW-C | 0.090 | 0.007 | −0.623 | 0.85 | |
| HW-D 2 | 0.071 | 0.004 | −0.650 | 0.79 | |
| V4 | HW-A 1 | 0.017 | 0.105 | - | - |
| HW-B | 0.013 | −0.250 | - | 0.74 | |
| HW-C | 0.009 | −0.456 | - | 0.83 | |
| HW-D | 0.005 | −0.512 | - | 0.78 | |
| V5 | HW-A 1,2 | 0.578 | 0.017 | −0.800 | - |
| HW-B 2 | 0.381 | 0.011 | −0.800 | 0.79 | |
| HW-C 2 | 0.264 | 0.007 | −0.800 | 0.86 | |
| HW-D 2 | 0.227 | 0.004 | −0.800 | 0.80 | |
| Variant | VC | Coefficients | |||
|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | ||
| V1 | HW-A | 0.351 | −0.155 | −0.622 | - |
| HW-B | 0.292 | −0.064 | −0.809 | - | |
| HW-C | 0.238 | −0.127 | −0.829 | - | |
| HW-D | 0.189 | −0.074 | −0.869 | - | |
| V2 | HW-A | 0.255 | 0.066 | −0.155 | −0.465 |
| HW-B | 0.135 | 0.053 | −0.064 | −0.577 | |
| HW-C | 0.062 | 0.042 | −0.127 | −0.559 | |
| HW-D | 0.035 | 0.030 | −0.074 | −0.599 | |
| V3 | HW-A | 0.230 | 0.017 | −0.155 | −0.388 |
| HW-B | 0.143 | 0.011 | −0.064 | −0.527 | |
| HW-C | 0.090 | 0.007 | −0.127 | −0.535 | |
| HW-D | 0.071 | 0.004 | −0.074 | −0.599 | |
| V4 | HW-A | 0.017 | −0.155 | 0.212 | - |
| HW-B | 0.013 | −0.064 | −0.206 | - | |
| HW-C | 0.009 | −0.127 | −0.368 | - | |
| HW-D | 0.005 | −0.074 | −0.460 | - | |
| V5 | HW-A | 0.578 | 0.017 | −0.155 | −0.693 |
| HW-B | 0.381 | 0.011 | −0.064 | −0.756 | |
| HW-C | 0.264 | 0.007 | −0.127 | −0.712 | |
| HW-D | 0.227 | 0.004 | −0.074 | −0.749 | |
| Investigation Area | MAE | RMSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| V1 | V2 | V3 | V4 | V5 | V1 | V2 | V3 | V4 | V5 | |
| Döbeln | 0.38 | 0.34 | 0.41 | 0.44 | 0.41 | 0.48 | 0.48 | 0.51 | 0.54 | 0.51 |
| Eilenburg | 0.48 | 0.41 | 0.49 | 0.51 | 0.50 | 0.75 | 0.68 | 0.70 | 0.68 | 0.71 |
| Flöha | 0.23 | 0.26 | 0.34 | 0.44 | 0.33 | 0.32 | 0.34 | 0.40 | 0.50 | 0.40 |
| Freital | 0.28 | 0.24 | 0.28 | 0.43 | 0.26 | 0.42 | 0.38 | 0.41 | 0.52 | 0.40 |
| Grimma | 0.40 | 0.39 | 0.33 | 0.37 | 0.34 | 0.51 | 0.52 | 0.46 | 0.51 | 0.47 |
| Pirna | 0.36 | 0.21 | 0.32 | 0.34 | 0.33 | 0.40 | 0.23 | 0.35 | 0.37 | 0.37 |
| Total | 0.36 | 0.31 | 0.36 | 0.42 | 0.36 | 0.48 | 0.44 | 0.47 | 0.52 | 0.48 |
| Investigation Area | MAE | RMSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| V1 | V2 | V3 | V4 | V5 | V1 | V2 | V3 | V4 | V5 | |
| Döbeln | 0.35 | 0.34 | 0.39 | 0.42 | 0.39 | 0.46 | 0.47 | 0.49 | 0.52 | 0.49 |
| Eilenburg | 0.49 | 0.43 | 0.49 | 0.52 | 0.50 | 0.65 | 0.60 | 0.62 | 0.62 | 0.63 |
| Flöha | 0.25 | 0.30 | 0.34 | 0.45 | 0.34 | 0.31 | 0.36 | 0.40 | 0.50 | 0.40 |
| Freital | 0.27 | 0.24 | 0.26 | 0.41 | 0.25 | 0.42 | 0.39 | 0.40 | 0.50 | 0.39 |
| Grimma | 0.41 | 0.35 | 0.34 | 0.37 | 0.34 | 0.51 | 0.48 | 0.46 | 0.50 | 0.47 |
| Pirna | 0.33 | 0.23 | 0.28 | 0.30 | 0.29 | 0.37 | 0.25 | 0.31 | 0.33 | 0.33 |
| Total | 0.35 | 0.32 | 0.35 | 0.41 | 0.35 | 0.45 | 0.43 | 0.44 | 0.50 | 0.45 |
| No. | Type/ Location | Description | Flow Direction | Scheme |
|---|---|---|---|---|
| 1 | Stand-alone | Direct |  | |
| 2a | Front house | Beginning of a row of houses | Direct/flow around | 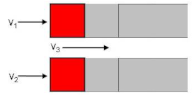 |
| 2b | End house | End of a row of houses | Flow around/circulation | 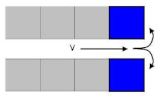 |
| 2c | Front/end house | Beginning/end of a row of houses | Orthogonal/circulation |  |
| 3a | Central house | In the middle of a row of houses | Tangential | 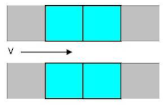 |
| 3b | Central house | In the middle of a row of houses | Direct/orthogonal | 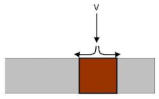 |
| 4 | Corner house | Cross situation | Flow around/circulation | 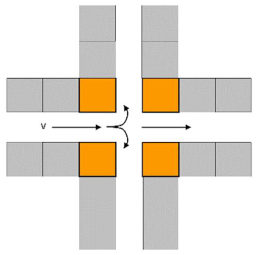 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maiwald, H.; Schwarz, J.; Kaufmann, C.; Langhammer, T.; Golz, S.; Wehner, T. Innovative Vulnerability and Risk Assessment of Urban Areas against Flood Events: Prognosis of Structural Damage with a New Approach Considering Flow Velocity. Water 2022, 14, 2793. https://doi.org/10.3390/w14182793
Maiwald H, Schwarz J, Kaufmann C, Langhammer T, Golz S, Wehner T. Innovative Vulnerability and Risk Assessment of Urban Areas against Flood Events: Prognosis of Structural Damage with a New Approach Considering Flow Velocity. Water. 2022; 14(18):2793. https://doi.org/10.3390/w14182793
Chicago/Turabian StyleMaiwald, Holger, Jochen Schwarz, Christian Kaufmann, Tobias Langhammer, Sebastian Golz, and Theresa Wehner. 2022. "Innovative Vulnerability and Risk Assessment of Urban Areas against Flood Events: Prognosis of Structural Damage with a New Approach Considering Flow Velocity" Water 14, no. 18: 2793. https://doi.org/10.3390/w14182793
APA StyleMaiwald, H., Schwarz, J., Kaufmann, C., Langhammer, T., Golz, S., & Wehner, T. (2022). Innovative Vulnerability and Risk Assessment of Urban Areas against Flood Events: Prognosis of Structural Damage with a New Approach Considering Flow Velocity. Water, 14(18), 2793. https://doi.org/10.3390/w14182793






