Assessing Riverbed Surface Destabilization Risk Downstream Isolated Vegetation Elements
Abstract
:1. Introduction
1.1. Parameters for Sediment Movement
1.2. Sediment Motion around Porous Vegetation
2. Experimental Setup and Protocol
2.1. Experiment Setup
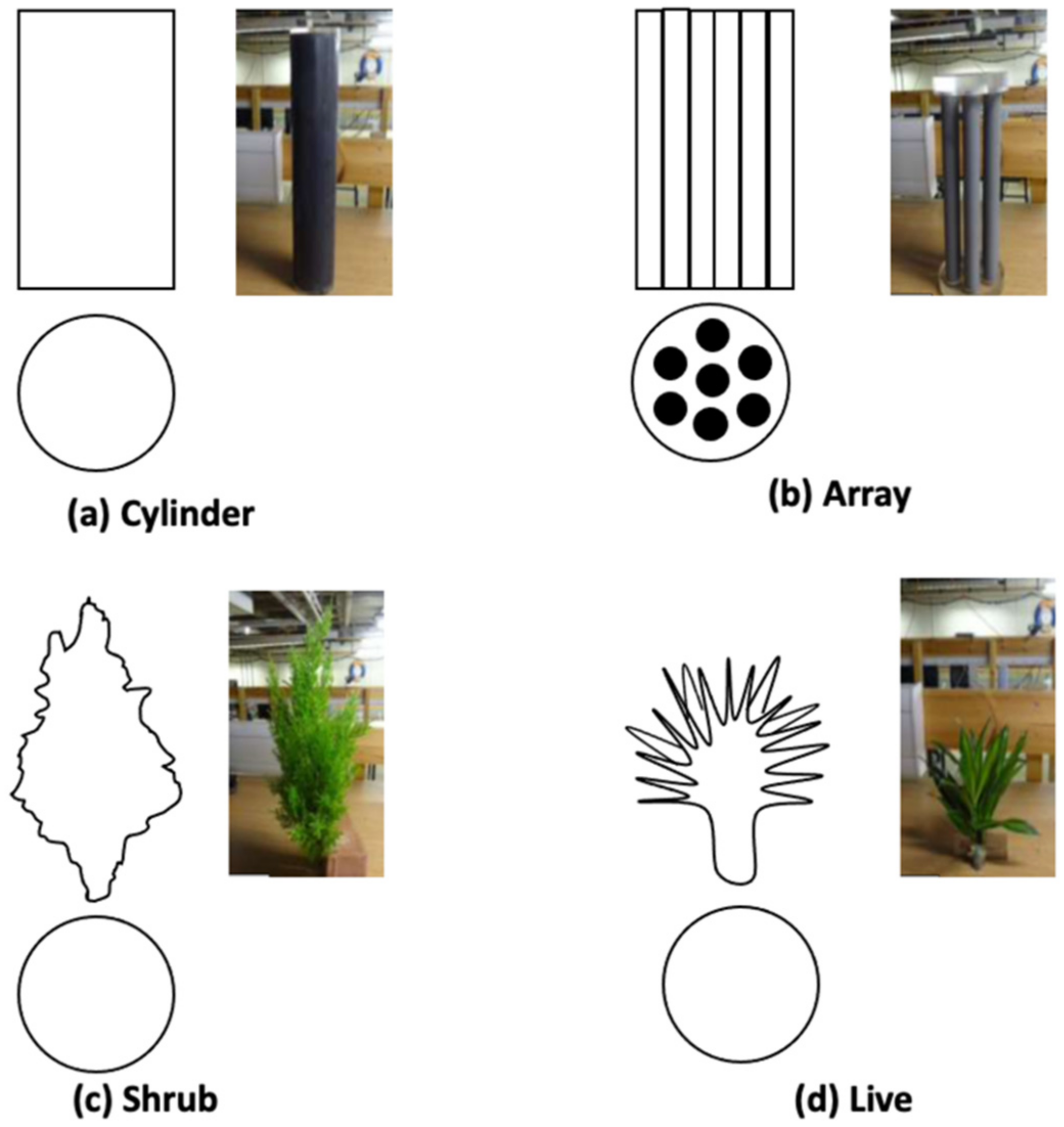
2.2. Vegetation Elements
2.3. Velocity Measurements
2.4. Instrumented Particle and Experimental Arrangement
3. Results
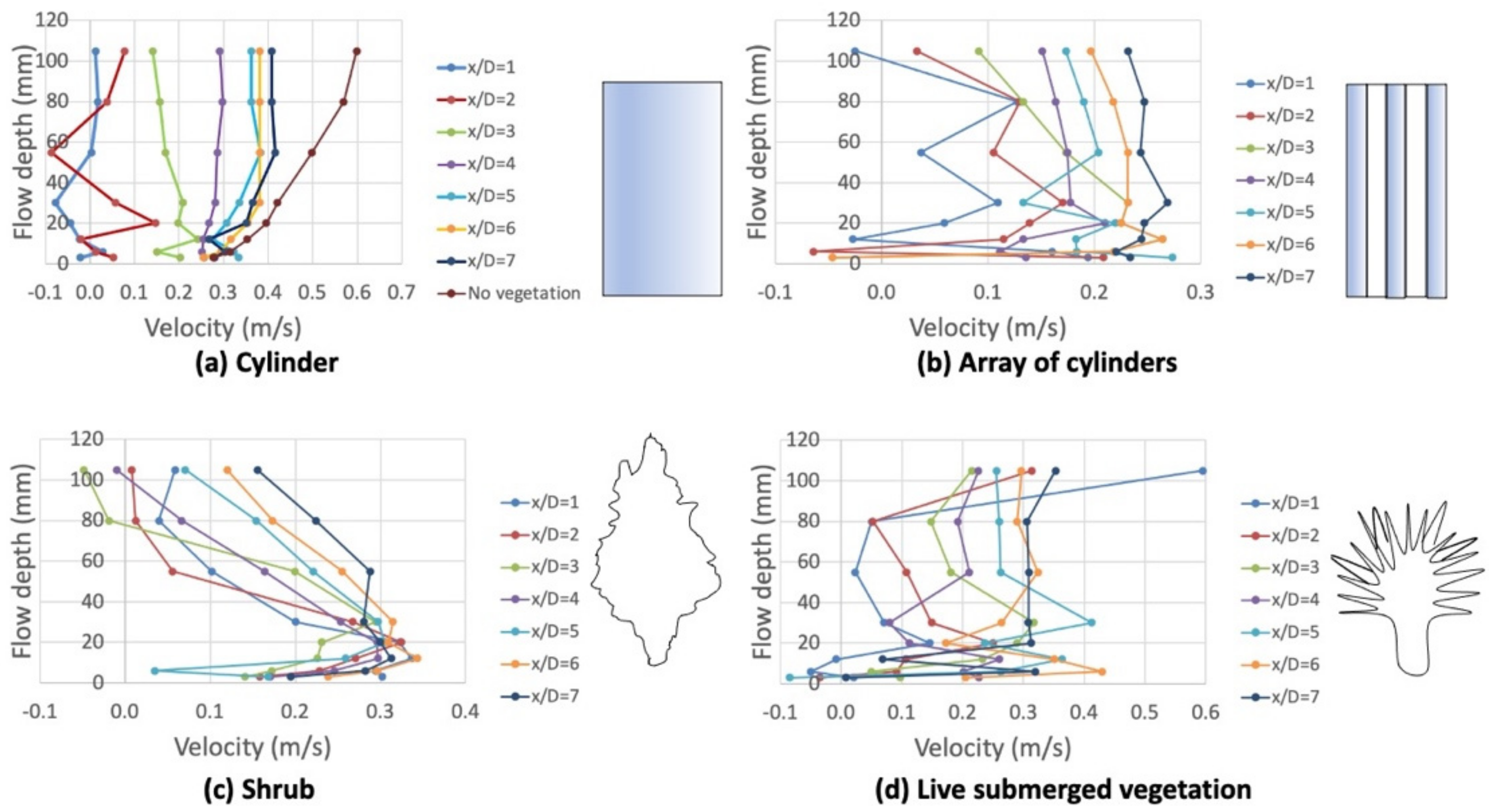
3.1. Flow Structure in the Wake Region of Representative Vegetative Elements
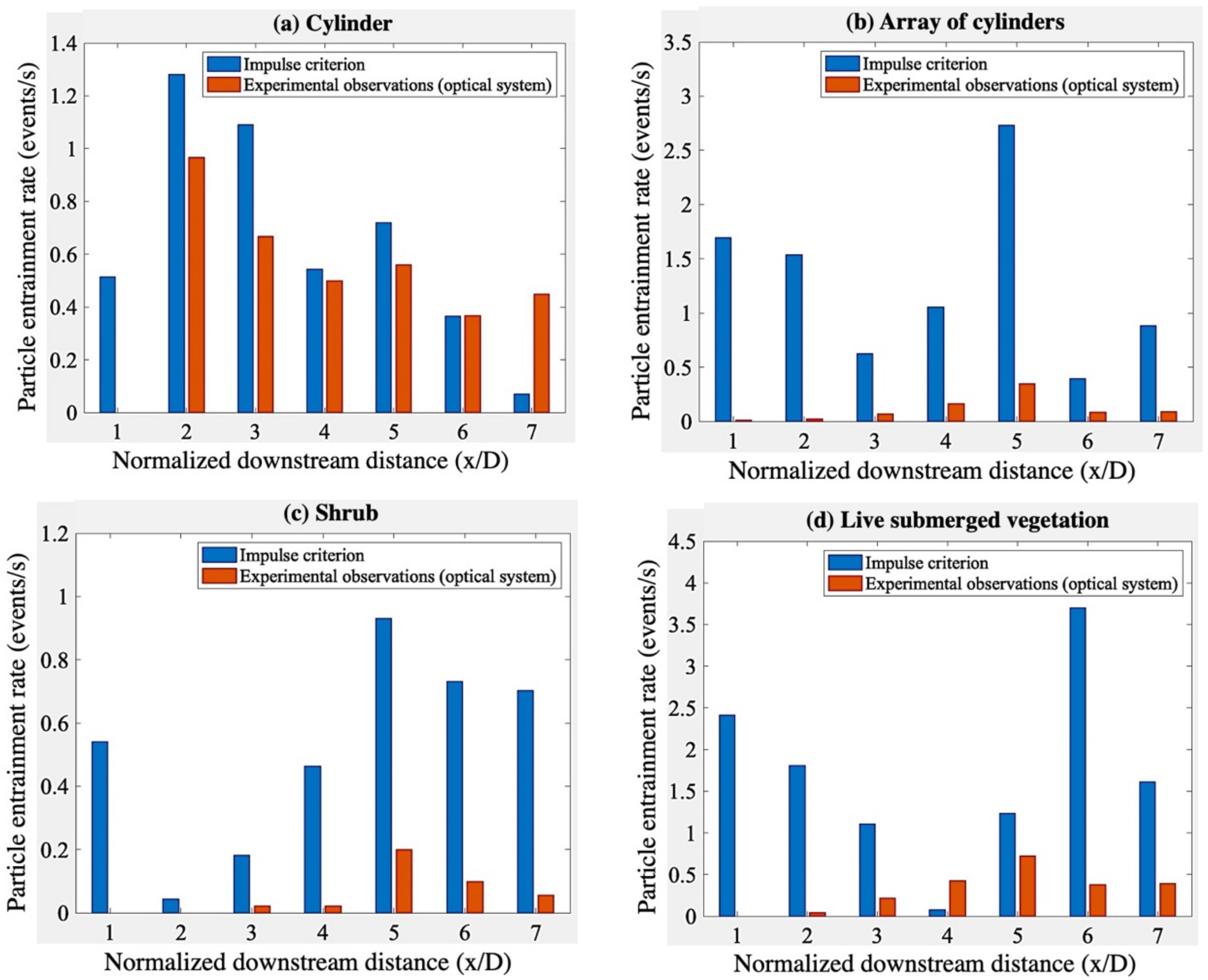
3.2. Particle Entrainment Rate
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notation
| The approaching area of particle to the flow. |
| Buoyancy force. |
| Drag coefficient. |
| Added mass coefficient. |
| Diameter of the solid rod. |
| Bridge pier diameter. |
| Frequency of particle entrainment. |
| Hydrodynamic mass coefficient. |
| Drag force. |
| Lift force. |
| Impulse. |
| Critical impulse. |
| Threshold impulse level. |
| Turbulence kinetic energy. |
| Length of lever arm. |
| Vegetation porosity. |
| Entrainment rate of particle. |
| Time. |
| Flow velocity. |
| Critical velocity. |
| Volume of particle. |
| Weight of particle. |
| Distance downstream pier model. |
| Angle between scour slope and riverbed. |
| Density of water. |
| Riverbed material density. |
| Coefficient. |
| Pivoting angle. |
| Impulse exceedance. |
References
- Pandey, M.; Valyrakis, M.; Qi, M.; Sharma, A.; Lodhi, A.S. Experimental assessment and prediction of temporal scour depth around a spur dike. Intl. J. Sed. Res. 2020, 36, 17–28. [Google Scholar] [CrossRef]
- Michalis, P.; Konstantinidis, F.; Valyrakis, M. The road towards Civil Infrastructure 4.0 for proactive asset management of critical infrastructure systems. In Proceedings of the 2nd International Conference on Natural Hazards & Infrastructure (ICONHIC), Chania, Greece, 23–26 June 2019. [Google Scholar]
- Michalis, P.; Vintzileou, E. The Growing Infrastructure Crisis: The Challenge of Scour Risk Assessment and the Development of a New Sensing System. Infrastructures 2022, 7, 68. [Google Scholar] [CrossRef]
- Forzieri, G.; Feyen, L.; Russo, S.; Vousdoukas, M.; Alfieri, L.; Outten, S.; Migliavacca, M.; Bianchi, A.; Rojas, R.; Cid, A. Multi-hazard assessment in Europe under climate change. Clim. Chang. 2016, 137, 105–119. [Google Scholar] [CrossRef]
- Couper, P.R.; Maddock, I.P. Subaerial river bank erosion processes and their interaction with other bank erosion mechanisms on the river arrow, Warwickshire, UK. Earth Surf. Processes Landf. 2001, 26, 631–646. [Google Scholar] [CrossRef]
- Thorne, C.R.; Hey, R.D.; Newson, M.D. Applied Fluvial Geomorphology for River Engineering and Management; John Wiley & Sons: Chichester, UK, 1997. [Google Scholar]
- Solari, L.; Van Oorschot, M.; Belletti, B.; Hendriks, D.; Rinaldi, M.; Vargas-Luna, A. Advances on modelling riparian vegetation—Hydromorphology interactions. River Res. Appl. 2016, 32, 164–178. [Google Scholar] [CrossRef]
- Hardy, R.J. Fluvial geomorphology. Prog. Phys. Geogr. 2006, 30, 553–567. [Google Scholar] [CrossRef]
- Jarvela, J. Flow resistance of flexible and stiff vegetation: A flume study with natural plants. J. Hydrol. 2002, 269, 44–54. [Google Scholar] [CrossRef]
- Wang, P.; Wang, C.; Zhu, D.Z. Hydraulic Resistance of Submerged Vegetation Related to Effective Height. J. Hydrog. 2010, 22, 265–273. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef]
- Przyborowski, Ł.; Łoboda, A.M.; Bialik, R.J. Effect of two distinct patches of Myriophyllum species on downstream turbulence in a natural river. Acta Geoph. 2019, 67, 987–997. [Google Scholar] [CrossRef] [Green Version]
- Najafzadeh, M.; Oliveto, G. Riprap incipient motion for overtopping flows with machine learning models. J. Hydroinform. 2020, 22, 749–767. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Rezaie-Balf, M.; Tafarojnoruz, A. Prediction of riprap stone size under overtopping flow using data-driven models. Int. J. River Basin Manag. 2018, 16, 505–512. [Google Scholar] [CrossRef]
- Valyrakis, M.; Diplas, P.; Dancey, C.L. Entrainment of coarse grains in turbulent flows: An extreme value theory approach. Water Resour. Res. 2011, 47, W09,512,3399. [Google Scholar] [CrossRef]
- Carollo, F.G.; Ferro, V.; Termini, D. Flow velocity measurements in vegetated channels. J. Hydraul. Eng. 2002, 128, 664–673. [Google Scholar] [CrossRef]
- Poggi, D.; Porporato, A.; Ridolfi, L.; Albertson, J.; Katul, G. The effect of vegetation density on canopy sub-layer turbulence. Bound.-Layer Meteorol. 2004, 111, 565–587. [Google Scholar] [CrossRef]
- Liu, D.; Diplas, P.; Fairbanks, J.D.; Hodges, C.C. An experimental study of flow through rigid vegetation. J. Geophys. Res. 2008, 113, F04015. [Google Scholar] [CrossRef]
- Hopkinson, L.; Wynn, T. Vegetation impacts on near bank flow. Ecohydrology 2009, 2, 404–418. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow and Transport in Regions with Aquatic Vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef]
- Yager, E.; Schmeeckle, M. The influence of vegetation on turbulence and bedload transport. J. Geophys. Res. Earth Surf. 2013, 118, 1585–1601. [Google Scholar] [CrossRef]
- Kitsikoudis, V.; Yagci, O.; Kirca, V.S.O.; Kellecioglu, D. Experimental investigation of channel flow through idealized isolated tree-like vegetation. Environ. Fluid Mech. 2016, 16, 1283–1308. [Google Scholar] [CrossRef]
- Yagci, O.; Strom, K. Reach-scale experiments on deposition process in vegetated channel: Suspended sediment capturing ability and backwater effect of instream plants. J. Hydrol. 2022, 608, 127612. [Google Scholar] [CrossRef]
- Hopkinson, L.; Wynn-Thompson, T. Streambank shear stress estimates using turbulent kinetic energy. J. Hydraul. Res. 2012, 50, 320–323. [Google Scholar] [CrossRef]
- Bouteiller, L.C.; Venditti, J.G. Sediment transport and shear stress partitioning in a vegetated flow. Water Resour. 2015, 51, 2901–2922. [Google Scholar] [CrossRef]
- Shields, A. Anwendung der Ahnlichkeitsmechanik und der Turbulentzforschung die Geshiebebewegung. Ph.D. Thesis, Technical University Berlin, Berlin, Germany, 1936. [Google Scholar]
- Leonard, L.A.; Luther, M.E. Flow hydrodynamics in tidal marsh canopies. Limnol. Oceanogr. 1995, 40, 1474–1484. [Google Scholar] [CrossRef]
- Neumeier, U.; Amos, C.L. The influence of vegetation on turbulence and flow velocities in European salt-marshes. Sedimentology 2006, 53, 259–277. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y. Analytical model for predicting the longitudinal profiles of velocities in a channel with a model vegetation patch. J. Hydrol. 2019, 576, 561–574. [Google Scholar] [CrossRef]
- Link, O.; González, C.; Maldonado, M.; Escauriaza, C. Coherent structure dynamics and sediment particle motion around a cylindrical pier in developing scour holes. Acta Geophys. 2012, 60, 1689–1719. [Google Scholar] [CrossRef]
- Yang, J.Q.; Chung, H.; Nepf, H.M. The onset of sediment transport in vegetated channels predicted by turbulent kinetic energy. Geophys. Res. Lett. 2016, 43, 11,261-11,268. [Google Scholar] [CrossRef]
- Graf, W.H. Hydraulics of Sediment Transport; McGraw-Hill Book, Co.: New York, NY, USA, 1971. [Google Scholar]
- Garde, R.J.; Ranga Raju, K.G. Mechanics of Sediment Transportation Alluvial Stream Problems; Wiley Eastern Ltd.: New Delhi, India, 1987. [Google Scholar]
- Krey, H. Grenzen der Übertragbarkeit der Versuchsergebnisse und Modellähnlichkeit bei praktischen Flussbauversuchen. Z. Angew. Math. Mech. 1925, 5, 484–486. [Google Scholar]
- Neill, C.R. Mean-velocity criterion for scour of coarse uniform bed-material. In Proceedings of the 12th Congress of the International Association for Hydraulics Research, Fort Collins, CO, USA, 11–14 September 1967; Volume 3, pp. 46–54. [Google Scholar]
- Egiazaroff, I.V. Discussion of “Sediment transportation mechanics: Initiation of motion” by V. A. Vanoni et al. J. Hydraul. Div. Am. Soc. Civ. Eng. 1967, 93, 281–287. [Google Scholar]
- Knoroz, V.S. Non-Eroding Velocity for Fine Sand; Hydrotech Construct: Moscow, Russia, 1953; pp. 21–24. (In Russian) [Google Scholar]
- Bagnold, R.A. An empirical correlation of bedload transport rates in flumes and natural rivers. Math. Phys. Sci. 1980, 372, 453–473. [Google Scholar]
- Bettess, R. Initiation of sediment transport in gravel streams. Proc. Inst. Civ. Eng. 1984, 407, 79–88. [Google Scholar]
- Bathurst, J.C. Critical conditions for bed material movement in steep, boulder-bed streams. Erosion and Sedimentation in the Pacific Rim. In Proceedings of the Symposium, Corvallis, OR, USA, 3–7 August 1987; Beschta, R.L., Blinn, T., Grant, G.E., Ice, G.G., Swanson, F.J., Eds.; IAHS Publ. No. 165; IAHS-AISH Publication: Oxfordshire, UK, 1987; pp. 309–318. [Google Scholar]
- Komar, P.D. Entrainment of sediments from deposits of mixed grain sizes and densities. In Advances in Fluvial Dynamics and Stratigraphy; Carling, P.A., Dawson, M.R., Eds.; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 1996; pp. 127–181. [Google Scholar]
- Nelson, J.M.; Shreve, R.L.; McLean, S.R.; Drake, T.G. Role of near-bed turbulence structure in bed load transport and bed form mechanics. Water Resour. Res. 1995, 31, 2071–2086. [Google Scholar] [CrossRef]
- Sumer, B.M.; Chua, L.H.; Cheng, N.-S.; Fredsøe, J. Influence of turbulence on bedload sediment transport. J. Hydraul. Eng. 2003, 129, 585–596. [Google Scholar] [CrossRef]
- Nino, Y.; Garcia, M. Experiments on particle–turbulence interactions in the near-wall region of an open channel flow: Implications for sediment transport. J. Fluid Mech. 1996, 326, 285–319. [Google Scholar] [CrossRef]
- Smart, G.; Habersack, H. Pressure fluctuations and gravel entrainment in rivers. J. Hydraul. Res. 2007, 45, 661–673. [Google Scholar] [CrossRef]
- Feng, Z.; Tan, G.; Xia, J.; Shu, C.; Chen, P.; Yi, R. Two- dimensional numerical simulation of sediment transport using improved critical shear stress methods. Int. J. Sediment Res. 2019, 35, 15–26. [Google Scholar] [CrossRef]
- Diplas, P.; Dancey, C.L.; Celik, A.O.; Valyrakis, M.; Greer, K.; Akar, T. The role of impulse on the initiation of particle movement under turbulent flow conditions. Science 2008, 322, 717–720. [Google Scholar] [CrossRef]
- Tinoco, R.O.; Coco, G. A laboratory study on sediment resuspension within arrays of rigid cylinders. Adv. Water Resour. 2016, 92, 1–9. [Google Scholar] [CrossRef]
- Tinoco, R.; Coco, G. Turbulence as the main driver of resuspension in oscillatory flow through vegetation. J. Geophys. Res. Earth Surf. 2018, 123, 891–904. [Google Scholar] [CrossRef]
- Schmeeckle, M.W.; Nelson, J.M.; Shreve, R.L. Forces on stationary particles in near-bed turbulent flows. J. Geophys. Res. 2007, 112, F02003. [Google Scholar] [CrossRef]
- Gimenez-Curto, L.A.; Corniero, M.A. Entrainment threshold of cohesionless sediment grains under steady flow of air and water. Sedimentology 2009, 56, 493–509. [Google Scholar] [CrossRef]
- Hubble, T.C.T.; Docker, B.B.; Rutherfurd, I.D. The role of riparian trees in maintaining riverbank stability: A review of Australian experience and practice. Ecol. Eng. 2010, 36, 291–304. [Google Scholar] [CrossRef]
- Perona, P.; Molnar, P.; Savina, M.; Burlando, P. An observation-based stochastic model for sediment and vegetation dynamics in the floodplain of an alpine braided river. Water Resour. Res. 2009, 45, W09418. [Google Scholar] [CrossRef]
- Millar, R.G.; Quick, M.C. Effects of bank stability on geometry of gravel rivers. J. Hydraul. Eng. 1993, 119, 1343–1363. [Google Scholar] [CrossRef]
- Czarnomski, N.M.; Tullos, D.D.; Thomas, R.E.; Simon, A. Effects of Vegetation Canopy Density and Bank Angle on Near-Bank Patterns of Turbulence and Reynolds Stresses. J. Hydraul. Eng. 2012, 138, 974–978. [Google Scholar] [CrossRef]
- Wilson, C.A.M.E.; Stoesser, T.; Bates, P.D.; Pinzon, A.B. Open channel flow through different forms of submerged flexible vegetation. J. Hydraul. Eng. 2003, 129, 847–853. [Google Scholar] [CrossRef]
- Sand-Jensen, K. Influence of submerged macrophytes on sediment composition and near-bed flow in lowland streams. Freshw. Biol. 1998, 39, 663–679. [Google Scholar] [CrossRef]
- Wang, C.; Zheng, S.; Wang, P.F.; Hou, J. Interactions between vegetation, water flow and sediment transport: A review. J. Hydrog. 2015, 27, 24–37. [Google Scholar] [CrossRef]
- Jalonen, J.; Järvelä, J. Estimation of drag forces caused by natural woody vegetation of different scales. J. Hydrodyn. Ser. B 2014, 26, 608–623. [Google Scholar] [CrossRef]
- Liu, D.; Diplas, P.; Hodges, C.C.; Fairbanks, J.D. Hydrodynamics of flow through double-layer rigid vegetation. Geomorphology 2010, 116, 286–296. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Yagci, O.; Yildirim, I.; Celik, M.F.; Kitsikoudis, V.; Duran, Z.; Kirca, V.S.O. Clear water scour around a finite array of cylinders. Appl. Ocean. Res. 2017, 68, 114–129. [Google Scholar] [CrossRef]
- Liu, C.; Hu, Z.; Lei, J.; Nepf, H. Vortex structure and sediment deposition in the wake behind a finite patch of model submerged vegetation. J. Hydraul. Eng. ASCE 2018, 144, 04017065. [Google Scholar] [CrossRef]
- Liu, C.; Nepf, H. Sediment deposition within and around a finite patch of model vegetation over a range of channel velocity. Water Resour. Res. 2016, 52, 600–612. [Google Scholar] [CrossRef]
- Valyrakis, M.; Diplas, P.; Dancey, C.L.; Greer, K.; Celik, A.O. The role of instantaneous force magnitude and duration on particle entrainment. J. Geophys. Res. 2010, 115, 1–18. [Google Scholar] [CrossRef]
- Yagci, O.; Celik, M.F.; Kitsikoudis, V.; Ozgur Kirca, V.S.; Hodoglu, C.; Valyrakis, M.; Duran, Z.; Kaya, S. Scour patterns around isolated vegetation elements. Adv. Water Resour. 2016, 97, 251–265. [Google Scholar] [CrossRef]
- Valyrakis, M.; Liu, D.; Turker, U.; Yagci, O. The role of increasing riverbank vegetation density on flow dynamics across an asymmetrical channel. Environ. Fluid Mech. 2021, 21, 643–666. [Google Scholar] [CrossRef]
- SonTek. ADV Field Technical Manual; SonTek/YSI, Inc.: San Diego, CA, USA, 2001. [Google Scholar]
- Al-Obaidi, K.; Xu, Y.; Valyrakis, M. The Design and Calibration of Instrumented Particles for Assessing Water Infrastructure Hazards. J. Sens. Actuator Netw. 9 2020, 3, 36. [Google Scholar] [CrossRef]
- Liu, D.; AlObaidi, K.; Valyrakis, M. The assessment of an Acoustic Doppler Velocimetry profiler from a user’s perspective. Acta Geophys. 2022, 434, 87–89. [Google Scholar] [CrossRef]
- Yagci, O.; Tschiesche, U.; Kabdasli, M.S. The role of different forms of natural riparian vegetation on turbulence and kinetic energy characteristics. Adv. Water Resour. 2010, 33, 601–614. [Google Scholar] [CrossRef]
- Yagci, O.; Karabay, O.; Strom, K. Bleed flow structure in the wake region of finite array of cylinders acting as an alternative supporting structure for foundation. J. Ocean. Eng. Mar. Energy 2021, 7, 379–403. [Google Scholar] [CrossRef]
- Yagci, O.; Kitsikoudis, V.; Celik, M.F.; Hodoglu, C.; Kirca, V.S.O.; Valyrakis, M.; Duran, Z.; Kaya, S. The variation of local scour pattern around representative natural vegetation elements. In Proceedings of the 2016, 36th IAHR Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Diehl, R.M.; Merritt, D.M.; Wilcox, A.C.; Scott, M.L. Applying functional traits to ecogeomorphic processes in riparian ecosystems. BioScience 2017, 67, 729–743. [Google Scholar] [CrossRef]
- Diplas, P.; Celik, A.O.; Dancey, C.L.; Valyrakis, M. Nonintrusive method for detecting particle movement characteristics near-threshold flow conditions. J. Irrig. Drain. Eng. ASCE 2010, 136, 774–780. [Google Scholar] [CrossRef]
- Amina; Tanaka, N. Numerical Investigation of 3D Flow Properties around Finite Emergent Vegetation by Using the Two-Phase Volume of Fluid (VOF) Modeling Technique. Fluids 2022, 7, 175. [Google Scholar] [CrossRef]
- Yager, E.M.; Venditti, J.G.; Smith, H.J.; Schmeeckle, M.W. The trouble with shear stress. Geomorphology 2018, 323, 41–50. [Google Scholar] [CrossRef]
- Celik, A.O.; Diplas, P.; Dancey, C.L.; Valyrakis, M. Impulse and Particle Dislodgement under Turbulent Flow Conditions. Phys. Fluids 2010, 22, 1–13. [Google Scholar] [CrossRef]
- Xu, Y.; Valyrakis, M. Monitoring the potential for bridge protections destabilization, using instrumented particles. In Proceedings of the International Conference on Fluvial Hydraulics River Flow, Delft, The Netherlands, 7–10 July 2020; p. 0144. [Google Scholar]
- Al-Obaidi, K.; Valyrakis, M. Linking the explicit probability of entrainment of instrumented particles to flow hydrodynamics. Earth Surf. Processes Landf. 2021, 46, 2448–2465. [Google Scholar] [CrossRef]
- AlHusban, Z.; Valyrakis, M. Assessing sediment transport dynamics from energy perspective by using the smart sphere. Intl. J. Sed. Res. 2022, in press. [Google Scholar] [CrossRef]
- Alhusban, Z.; Valyrakis, M. Assessing and Modelling the Interactions of Instrumented Particles with Bed Surface at Low Transport Conditions. Appl. Sci. 2021, 11, 7306. [Google Scholar] [CrossRef]












| N | 5 | 13 | 25 | 45 | 69 | NA |
| (%) | 1.25 | 3.25 | 6.25 | 11.25 | 17.25 | 100 |
| Elements | x/D = 1 | x/D = 2 | x/D = 3 | x/D = 4 | x/D = 5 | x/D = 6 | x/D = 7 | |
|---|---|---|---|---|---|---|---|---|
| Emergent | Cylinder | - | 0.976 | 0.667 | 0.500 | 0.561 | 0.367 | 0.450 |
| Array | 0.011 | 0.022 | 0.072 | 0.167 | 0.350 | 0.089 | 0.094 | |
| Shrub | 0.000 | 0.000 | 0.022 | 0.022 | 0.200 | 0.100 | 0.056 | |
| Submerge | Live | 0.000 | 0.044 | 0.217 | 0.428 | 0.722 | 0.383 | 0.394 |
| No vegetation | 0.328 | 0.328 | 0.328 | 0.328 | 0.328 | 0.328 | 0.328 | |
| Elements | x/D = 1 | x/D = 2 | x/D = 3 | x/D = 4 | x/D = 5 | x/D = 6 | x/D = 7 | |
|---|---|---|---|---|---|---|---|---|
| Emergent | Cylinder | 0.514 | 1.282 | 1.091 | 0.544 | 0.719 | 0.366 | 0.070 |
| Array | 1.693 | 1.537 | 0.627 | 1.055 | 2.73 | 0.394 | 0.882 | |
| Shrub | 0.542 | 0.044 | 0.182 | 0.464 | 0.931 | 0.732 | 0.704 | |
| Submerge | Live | 2.414 | 1.806 | 1.106 | 0.076 | 1.234 | 3.7 | 1.613 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Valyrakis, M.; Gilja, G.; Michalis, P.; Yagci, O.; Przyborowski, Ł. Assessing Riverbed Surface Destabilization Risk Downstream Isolated Vegetation Elements. Water 2022, 14, 2880. https://doi.org/10.3390/w14182880
Xu Y, Valyrakis M, Gilja G, Michalis P, Yagci O, Przyborowski Ł. Assessing Riverbed Surface Destabilization Risk Downstream Isolated Vegetation Elements. Water. 2022; 14(18):2880. https://doi.org/10.3390/w14182880
Chicago/Turabian StyleXu, Yi, Manousos Valyrakis, Gordon Gilja, Panagiotis Michalis, Oral Yagci, and Łukasz Przyborowski. 2022. "Assessing Riverbed Surface Destabilization Risk Downstream Isolated Vegetation Elements" Water 14, no. 18: 2880. https://doi.org/10.3390/w14182880
APA StyleXu, Y., Valyrakis, M., Gilja, G., Michalis, P., Yagci, O., & Przyborowski, Ł. (2022). Assessing Riverbed Surface Destabilization Risk Downstream Isolated Vegetation Elements. Water, 14(18), 2880. https://doi.org/10.3390/w14182880









