Economic Analysis of Flood Risk Applied to the Rehabilitation of Drainage Networks
Abstract
:1. Introduction
- The hydrologic study and the runoff model are beyond the scope of this work;
- No changes in the network topology are considered. The actions allowed to improve the network are the replacement of pipes, the installation of storm tanks and the inclusion of hydraulic control elements in the network;
- The networks in which this methodology can be applied must be gravity-fed. Networks with pumping systems are not considered in this study;
- The hydraulic model is considered as a datum; its parameters and initial conditions are not questioned.
2. Materials and Methods
2.1. Optimization Model
2.1.1. Decision Variables
2.1.2. Cost Functions
2.2. Optimization Process
2.2.1. Search Space Reduction
2.2.2. Final Optimization
2.3. Case Studies
2.3.1. Balloon Network
2.3.2. ES-N Network
2.3.3. Investment Costs
2.3.4. Flood Costs
3. Results
3.1. Balloon Network
3.2. ES-N Network
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DV | Decision Variable |
| EAD | Estimated Annual Damage |
| IDF | Intensity–Duration–Frequency |
| LID | Low-Impact Development |
| OF | Objective Function |
| PGA | Pseudo-Genetic Algorithm |
| SS | Search Space |
| SSR | Search Space Reduction |
| SWMM | Storm Water Management Model |
| Nomenclature | |
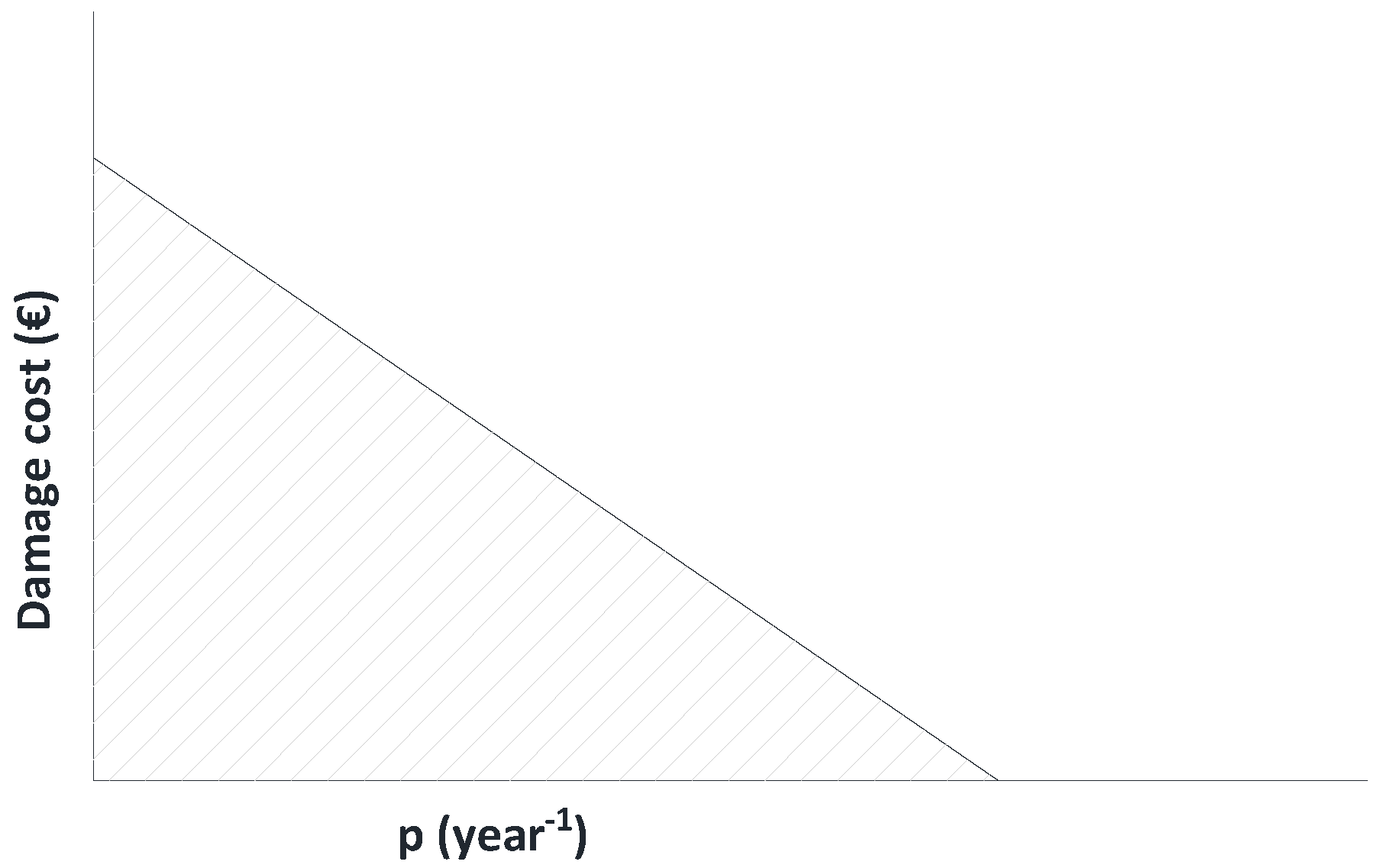
| a | coefficient of the line of the flood cost |
| Ai | flood area |
| b | coefficient of the line of the flood cost |
| Cmax | maximum flood damage cost |
| Cmin | minimum cost of building a storm tank |
| CP (Di) | cost of pipe replacement |
| CT (Vi) | cost of building a storm tank |
| Cv (Di) | cost of installing hydraulic controls |
| Cvar | adjustment coefficient for calculating the cost of storm tank |
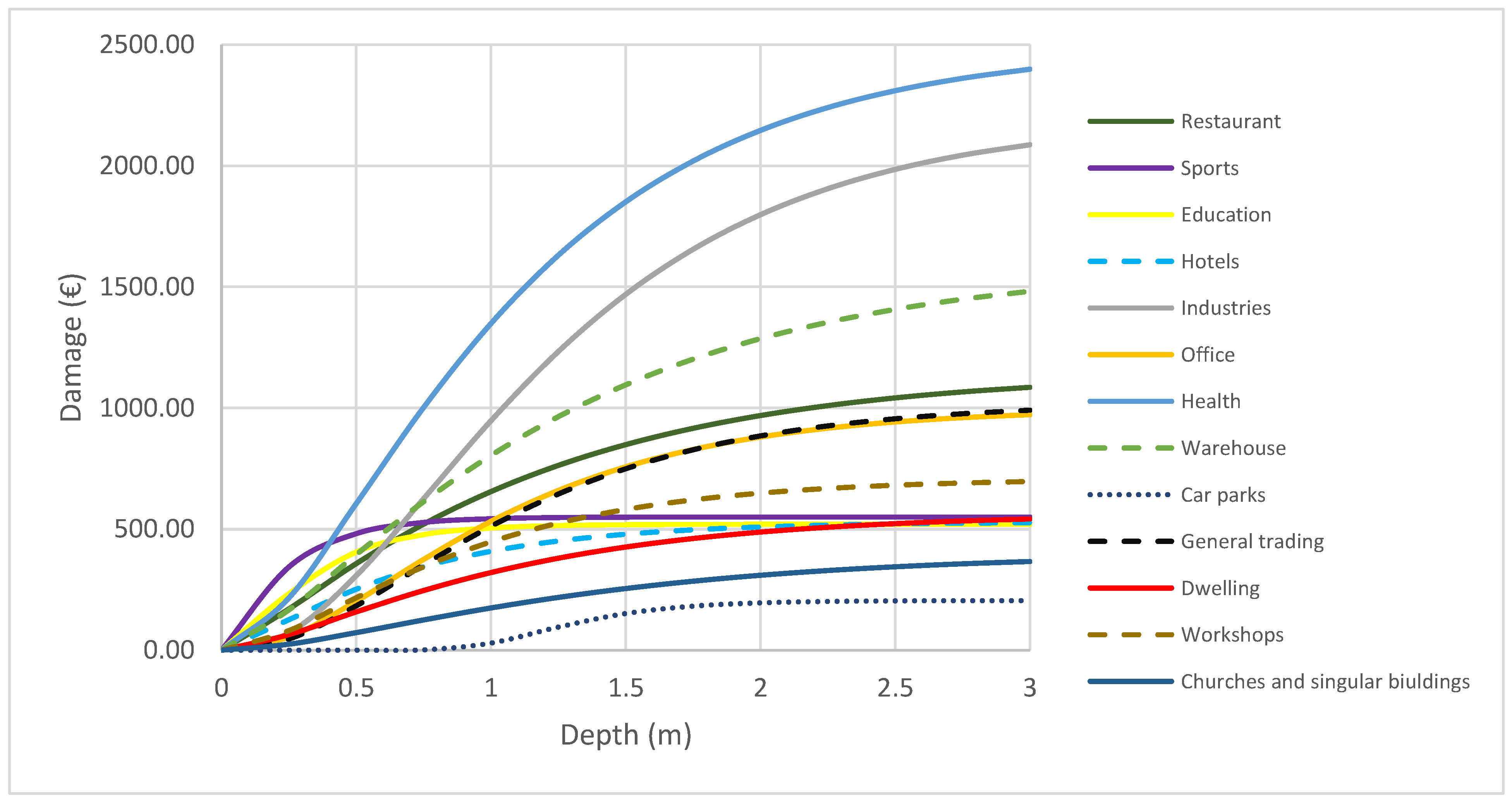
| Cy (yi) | flood damage cost |
| Di | pipe diameter |
| Gmax | convergence criterion |
| Li | pipe length |
| ms | pipes selected to be optimized |
| NDmax | diameter range available |
| ns | nodes selected to be optimized |
| NS | list of options used for nodes |
| NSmax | refined option list for nodes |
| NS0 | coarse option list for nodes |
| Nθ | option list for hydraulic controls |
| p | annual exceedance rate |
| p0 | annual exceedance rate for which flood damage begins to occur |
| r | annual interest |
| t | years to recover the investment |
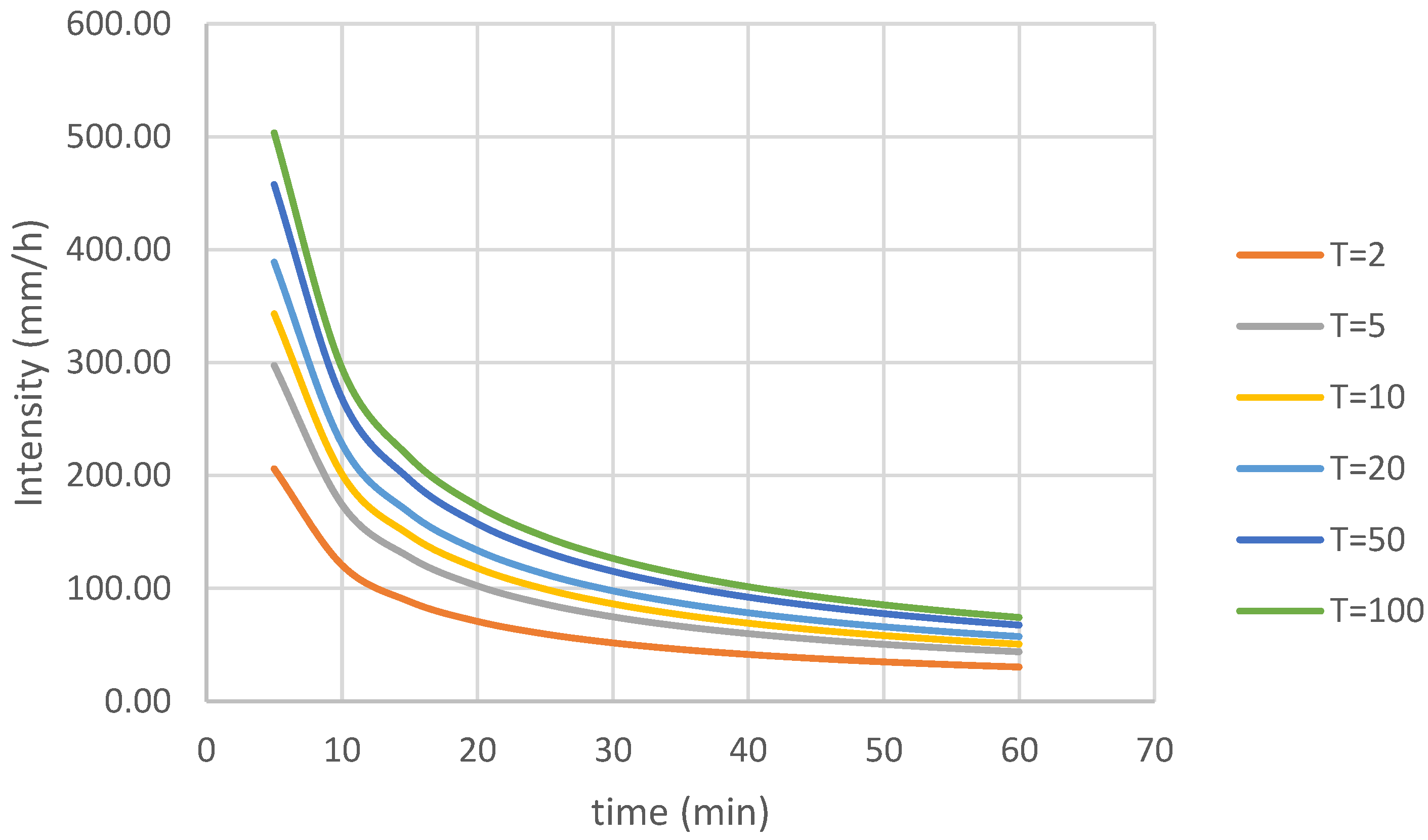
| T | return period |
| Vi | flood volume at the node |
| vs | pipes selected to install hydraulic controls in the optimization process |
| yi | flood depth at node |
| ymax | maximum depth at which the maximum cost of flood damage is reached |
| α | adjustment coefficient for calculating the cost of replacing pipes |
| β | adjustment coefficient for calculating the cost of replacing pipes |
| γ | adjustment coefficient for calculating the cost of replacing pipes |
| ΔND | range of diameters immediately larger than the analyzed pipe |
| Λ | annual amortization factor |
| λ | adjustment coefficient for calculation of flood damage |
| μ | adjustment coefficient for calculating the cost of installing hydraulic controls |
| σ | adjustment coefficient for calculating the cost of installing hydraulic controls |
| υ | adjustment coefficient for calculation of flood damage |
| φ | adjustment coefficient for calculating the cost of installing hydraulic controls |
| ω | adjustment constant for the calculation of the cost of the construction of storm tanks |
References
- Xiong, L.; Yan, L.; Du, T.; Yan, P.; Li, L.; Xu, W. Impacts of Climate Change on Urban Extreme Rainfall and Drainage Infrastructure Performance: A Case Study in Wuhan City, China. Irrig. Drain. 2019, 68, 152–164. [Google Scholar] [CrossRef]
- Salinas-Rodriguez, C.; Gersonius, B.; Zevenbergen, C.; Serrano, D.; Ashley, R. A Semi Risk-Based Approach for Managing Urban Drainage Systems under Extreme Rainfall. Water 2018, 10, 384. [Google Scholar] [CrossRef]
- Szewrański, S.; Chruściński, J.; Kazak, J.; Świąder, M.; Tokarczyk-Dorociak, K.; Żmuda, R. Pluvial Flood Risk Assessment Tool (PFRA) for Rainwater Management and Adaptation to Climate Change in Newly Urbanised Areas. Water 2018, 10, 386. [Google Scholar] [CrossRef]
- Oberascher, M.; Kinzel, C.; Kastlunger, U.; Kleidorfer, M.; Zingerle, C.; Rauch, W.; Sitzenfrei, R. Integrated urban water management with micro storages developed as an IoT-based solution—The smart rain barrel. Environ. Model. Softw. 2021, 139, 105028. [Google Scholar] [CrossRef]
- Szeląg, B.; Suligowski, R.; De Paola, F.; Siwicki, P.; Majerek, D.; Łagód, G. Influence of urban catchment characteristics and rainfall origins on the phenomenon of stormwater flooding: Case study. Environ. Model. Softw. 2022, 150, 105335. [Google Scholar] [CrossRef]
- Olcina, J.; Hernández, M.; Morote, Á.-F.; Eslamian, S. Reducing Flood Risk in Spain: The Role of Spatial Planning. In Flood Handbook, 1st ed.; Eslamian, S., Eslamian, F.A., Eds.; CRC Press: Boca Raton, FL, USA, 2022; pp. 217–226. [Google Scholar]
- Meyer, V.; Becker, N.; Markantonis, V.; Schwarze, R.; Van der Bergh, J.C.J.M.; Bouwer, L.M.; Viavattene, C. Review article: Assessing the costs of natural hazards—State of the art and knowledge gaps. Nat. Hazards Earth Syst. Sci. 2013, 13, 1351–1373. [Google Scholar] [CrossRef]
- Nicklin, H.; Leicher, A.M.; Dieperink, C.; Van Leeuwen, K. Understanding the Costs of Inaction—An Assessment of Pluvial Flood Damages in Two European Cities. Water 2019, 11, 801. [Google Scholar] [CrossRef]
- Mobini, S.; Nilsson, E.; Persson, A.; Becker, P.; Larsson, R. Analysis of pluvial flood damage costs in residential buildings—A case study in Malmö. Int. J. Disaster Risk Reduct. 2021, 62, 102407. [Google Scholar] [CrossRef]
- O’Donnell, E.C.; Thorne, C.R. Drivers of future urban flood risk. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378, 20190216. [Google Scholar] [CrossRef]
- Andrés-Doménech, I.; Montanari, A.; Marco, J.B. Efficiency of storm detention tanks for urban drainage systems under climate variability. J. Water Resour. Plan. Manag. 2012, 138, 36–46. [Google Scholar] [CrossRef]
- Bayas-Jiménez, L.; Martínez-Solano, F.J.; Iglesias-Rey, P.L.; Mora-Melia, D.; Fuertes-Miquel, V.S. Inclusion of Hydraulic Controls in Rehabilitation Models of Drainage Networks to Control Floods. Water 2021, 13, 514. [Google Scholar] [CrossRef]
- Maier, H.R.; Kapelan, Z.; Kasprzyk, J.; Kollat, J.; Matott, L.S.; Cunha, M.C.; Reed, P.M. Evolutionary algorithms and other metaheuristics in water resources: Current status, research challenges and future directions. Environ. Model. Softw. 2014, 62, 271–299. [Google Scholar] [CrossRef]
- Bayas-Jiménez, L.; Martínez-Solano, F.J.; Iglesias-Rey, P.L.; Mora-Meliá, D. Search space reduction for genetic algorithms applied to drainage network optimization problems. Water 2021, 13, 2008. [Google Scholar] [CrossRef]
- Marchi, A.; Salomons, E.; Ostfeld, A.; Kapelan, Z.; Simpson, A.; Zecchin, A.; Maier, H.; Wu, Z.; Elsayed, S.M.; Song, Y.; et al. Battle of the Water Networks II. J. Water Resour. Plan. Manag. 2014, 140, 04014009. [Google Scholar] [CrossRef]
- Mora, D. Design of Water Distribution Networks Using Evolutionary Algorithms. Efficiency Analysis. Ph.D. Thesis, Universitat Politècnica de València, Valencia, Spain, July 2012. (In Spanish). [Google Scholar]
- Schraudolph, N.N.; Belew, R.K. Dynamic Parameter Encoding for Genetic Algorithms. Mach. Learn. 1992, 9, 9–21. [Google Scholar] [CrossRef]
- Sophocleous, S.; Savić, D.; Kapelan, Z. Leak Localization in a Real Water Distribution Network Based on Search-Space Reduction. J. Water Resour. Plan. Manag. 2019, 145, 04019024. [Google Scholar] [CrossRef]
- Freni, G.; La Loggia, G.; Notaro, V. Uncertainty in urban flood damage assessment due to urban drainage modelling and depth-damage curve estimation. Water Sci. Technol. 2010, 61, 2979–2993. [Google Scholar] [CrossRef]
- Zhou, Q.; Mikkelsen, P.S.; Halsnæs, K.; Arnbjerg-Nielsen, K. Framework for economic pluvial flood risk assessment considering climate change effects and adaptation benefits. J. Hydrol. 2012, 414, 539–549. [Google Scholar] [CrossRef]
- Olsen, A.S.; Zhou, Q.; Linde, J.J.; Arnbjerg-Nielsen, K. Comparing methods of calculating expected annual damage in urban pluvial flood risk assessments. Water 2015, 7, 255–270. [Google Scholar] [CrossRef]
- Mora-Melia, D.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Fuertes-Miquel, V.S. Design of Water Distribution Networks using a Pseudo-Genetic Algorithm and Sensitivity of Genetic Operators. Water Resour. Manag. 2013, 27, 4149–4162. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model (SWMM) User’s Manual Version 5.0; U.S. EPA: Cincinnati, OH, USA, 2009. [Google Scholar]
- Martínez-Solano, F.J.; Iglesias-Rey, P.L.; Saldarriaga, J.G.; Vallejo, D. Creation of an SWMM toolkit for its application in urban drainage networks optimization. Water 2016, 8, 259. [Google Scholar] [CrossRef]
- Locatelli, L.; Guerrero, M.; Russo, B.; Martínez-Gomariz, E.; Sunyer, D.; Martínez, M. Socio-Economic Assessment of Green Infrastructure for Climate Change Adaptation in the Context of Urban Drainage Planning. Sustainability 2020, 12, 3792. [Google Scholar] [CrossRef]
- Arnell, N.W. Expected Annual Damages and Uncertainties in Flood Frequency Estimation. J. Water Resour. Plan. Manag. 1989, 115, 94–107. [Google Scholar] [CrossRef]
- Butler, D.; Digman, C.J.; Makropoulos, C.; Davies, J.W. Urban Drainage, 4th ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2018. [Google Scholar]
- Arnbjerg-Nielsen, K.; Fleischer, H.S. Feasible adaptation strategies for increased risk of flooding in cities due to climate change. Water Sci. Technol. 2009, 60, 273–281. [Google Scholar] [CrossRef] [PubMed]
- Reca, J.; Martínez, J.; López, R. A Hybrid Water Distribution Networks Design Optimization Method Based on a Search Space Reduction Approach and a Genetic Algorithm. Water 2017, 9, 845. [Google Scholar] [CrossRef]
- Creaco, E.; Pezzinga, G. Embedding linear programming in multi objective genetic algorithms for reducing the size of the search space with application to leakage minimization in water distribution networks. Environ. Model. Softw. 2015, 69, 308–318. [Google Scholar] [CrossRef]
- Kadu, M.S.; Gupta, R.; Bhave, P.R. Optimal Design of Water Networks Using a Modified Genetic Algorithm with Reduction in Search Space. J. Water Resour. Plan. Manag. 2008, 134, 147–160. [Google Scholar] [CrossRef]
- Martínez-Gomariz, E.; Gómez, M.; Russo, B.; Sánchez, P.; Montes, J.-A. Methodology for the damage assessment of vehicles exposed to flooding in urban areas. J. Flood Risk Manag. 2019, 12, e12475. [Google Scholar] [CrossRef]



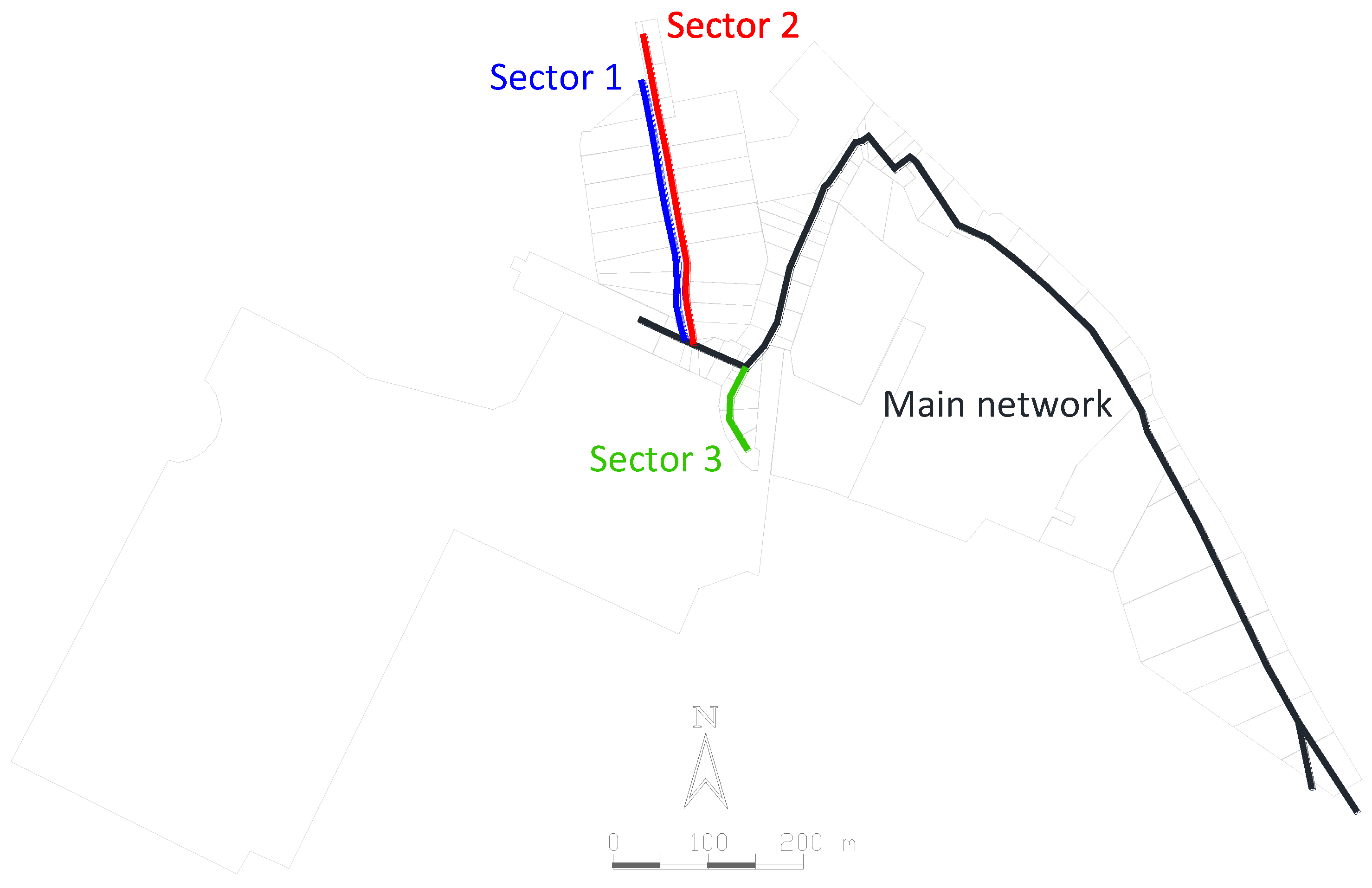








| Sector | Number of Pipes | Number of Nodes | DV | SS | Reduction of SS in Clustering Process |
|---|---|---|---|---|---|
| Sector 1 | 11 | 11 | 33 | 36 | 100% |
| Sector 2 | 12 | 12 | 36 | 40 | 96% |
| Sector 3 | 4 | 4 | 12 | 13 | 100% |
| Main network | 44 | 43 | 130 | 144 | |
| Total | 71 | 70 | 211 | 233 |
| Terms in Objective Function | Pipes | Storm Tank | Hydraulic Control | Flood | Total | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cost per year | 2739 € | 19,727 € | 153 € | 5608 € | 28,227 € | ||||||
| Elements | C5 | C84 | C85 | C86 | N8 | N15 | N16 | N63 | C75 | ||
| Present diameter (m) | 0.70 | 0.70 | 0.70 | 0.70 | |||||||
| Optimized diameter (m) | 1.00 | 1.10 | 1.00 | 1.00 | |||||||
| Volume (m3) | 2496 | 4284 | 5031 | 594 | |||||||
| Head-loss (m) | 72.55 | ||||||||||
| Sector | Number of Pipes | Number of Nodes | DVs | SS | Reduction of SS in Clustering Process |
|---|---|---|---|---|---|
| Sector 1 | 5 | 5 | 15 | 17 | 100% |
| Sector 2 | 2 | 2 | 6 | 7 | 100% |
| Sector 3 | 13 | 13 | 39 | 43 | 100% |
| Sector 4 | 23 | 23 | 69 | 76 | 98% |
| Sector 5 | 24 | 24 | 72 | 79 | 91% |
| Sector 6 | 8 | 8 | 24 | 26 | 100% |
| Sector 7 | 55 | 55 | 165 | 182 | 99% |
| Sector 8 | 8 | 8 | 24 | 26 | 100% |
| Sector 9 | 15 | 15 | 45 | 50 | 100% |
| Sector 10 | 23 | 23 | 69 | 76 | 100% |
| Sector 11 | 25 | 25 | 75 | 83 | 100% |
| Sector 12 | 16 | 16 | 48 | 53 | 97% |
| Sector 13 | 9 | 9 | 27 | 30 | 100% |
| Sector 14 | 5 | 5 | 15 | 17 | 100% |
| Sector 15 | 39 | 39 | 117 | 129 | 97% |
| Sector 16 | 45 | 45 | 135 | 149 | 97% |
| Sector 17 | 4 | 4 | 12 | 13 | 100% |
| Sector 18 | 12 | 12 | 36 | 40 | 75% |
| Sector 19 | 5 | 5 | 15 | 17 | 100% |
| Main network | 49 | 49 | 147 | 162 | |
| Total | 385 | 385 | 1155 | 1271 |
| Terms in Objective Function | Pipes | Storm Tank | Hydraulic Control | Flood | Total | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cost per year | 2672 € | 41,930 € | 125 € | 27,722 € | 72,449 € | |||||||
| Elements | P266 | P293 | P294 | P335 | N71 | N126 | N131 | N161 | N216 | P25 | ||
| N252 | N276 | N308 | N343 | |||||||||
| Present diameter (m) | 0.40 | 0.40 | 0.25 | 0.30 | ||||||||
| Optimized diameter (m) | 0.70 | 0.70 | 0.45 | 0.50 | ||||||||
| Volume (m3) | 1700 | 500 | 750 | 1950 | 1950 | |||||||
| 1100 | 1250 | 1050 | 800 | |||||||||
| Head-loss (m) | 72.55 | |||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayas-Jiménez, L.; Martínez-Solano, F.J.; Iglesias-Rey, P.L.; Boano, F. Economic Analysis of Flood Risk Applied to the Rehabilitation of Drainage Networks. Water 2022, 14, 2901. https://doi.org/10.3390/w14182901
Bayas-Jiménez L, Martínez-Solano FJ, Iglesias-Rey PL, Boano F. Economic Analysis of Flood Risk Applied to the Rehabilitation of Drainage Networks. Water. 2022; 14(18):2901. https://doi.org/10.3390/w14182901
Chicago/Turabian StyleBayas-Jiménez, Leonardo, F. Javier Martínez-Solano, Pedro L. Iglesias-Rey, and Fulvio Boano. 2022. "Economic Analysis of Flood Risk Applied to the Rehabilitation of Drainage Networks" Water 14, no. 18: 2901. https://doi.org/10.3390/w14182901
APA StyleBayas-Jiménez, L., Martínez-Solano, F. J., Iglesias-Rey, P. L., & Boano, F. (2022). Economic Analysis of Flood Risk Applied to the Rehabilitation of Drainage Networks. Water, 14(18), 2901. https://doi.org/10.3390/w14182901










