Flood Uncertainty Estimation Using Deep Ensembles
Abstract
:1. Introduction
2. Related Work
2.1. Flood Estimation
2.2. Uncertainty Estimation in Deep Learning
3. Datasets
- the catchment’s DEM, representing the terrain elevation;
- a spatial differential DEM () comprising of four channels. A DEM can be viewed as a 2D grid whose adjacent columns (c) or rows (r) can be subtracted in four directions: rightward, leftward, downward, and upward. The was obtained using the following equations:where i and j are the row and column index of the DEM.
- the topographic index as the logarithm of the ratio between flow accumulation and local slope. Flow accumulation is related to the upstream drainage area of each raster cell and is computed from the raw DEM using the r.terraflow module in QGIS [70]. The topographic index is commonly used in hydrology as a steady-state wetness index;
- slope, defined as the measure of the rate of change of elevation in the direction of steepest descent. It reflects the steepness of the terrain and is the means by which gravity induces the flow of water;
4. Methodology
4.1. Deep Learning Model
4.2. Predictive Uncertainty Estimation
4.2.1. Epistemic Uncertainty
4.2.2. Aleatoric Uncertainty
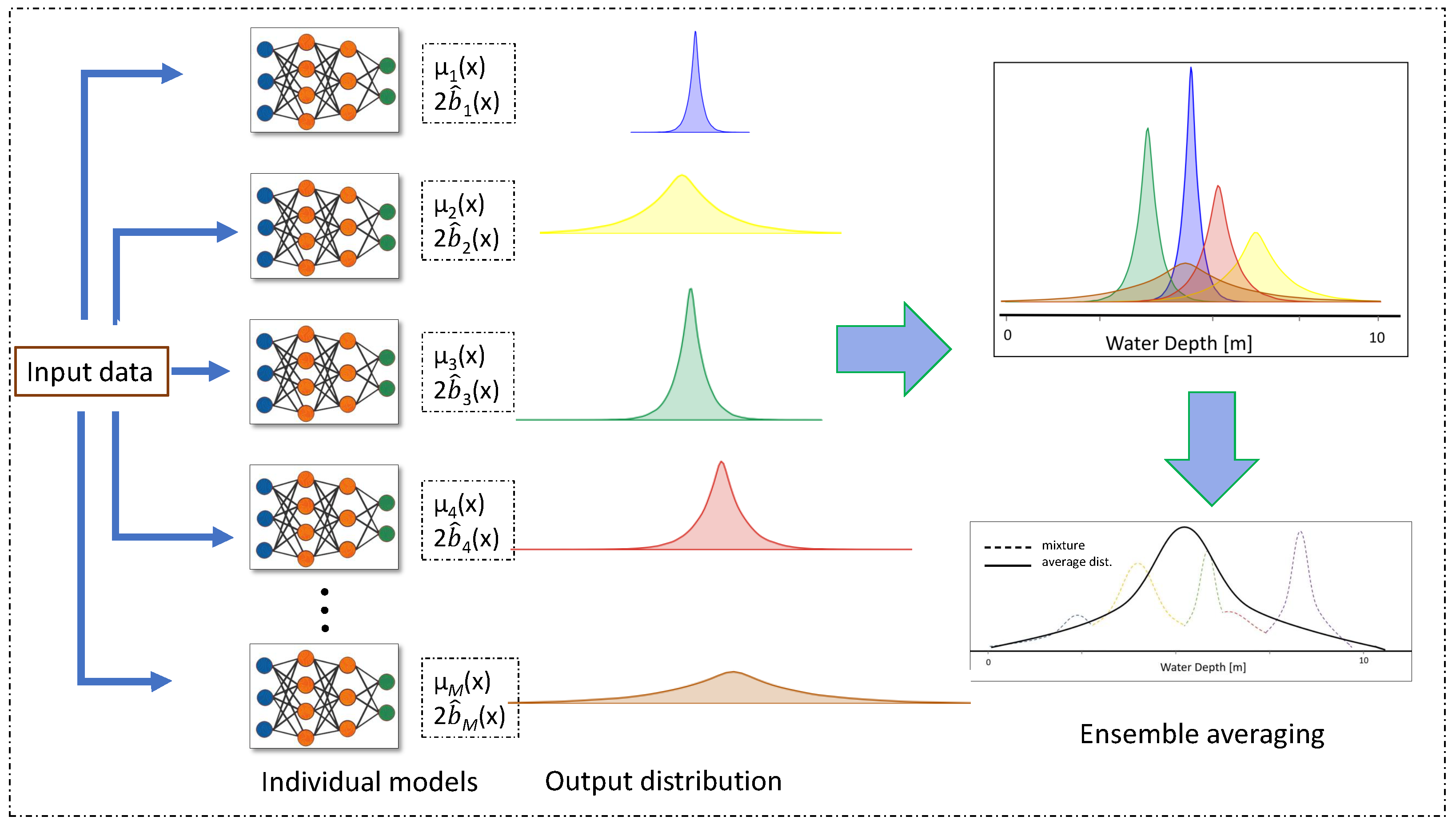
4.2.3. Combining Aleatoric and Epistemic Uncertainty
4.3. Model Training
5. Results
5.1. Hazard Map
5.2. Uncertainty Evaluation
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A





References
- Misra, A.K. Climate change and challenges of water and food security. Int. J. Sustain. Built Environ. 2014, 3, 153–165. [Google Scholar] [CrossRef]
- Rosenzweig, B.R.; McPhillips, L.; Chang, H.; Cheng, C.; Welty, C.; Matsler, M.; Iwaniec, D.; Davidson, C.I. Pluvial flood risk and opportunities for resilience. WIREs Water 2018, 5, e1302. [Google Scholar] [CrossRef]
- Adikari, Y.; Yoshitani, J. Global Trends in Water-Related Disasters: An Insight for Policymakers, 2009. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000181793 (accessed on 23 August 2022).
- Kubal, C.; Haase, D.; Meyer, V.; Scheuer, S. Integrated urban flood risk assessment – adapting a multicriteria approach to a city. Nat. Hazards Earth Syst. Sci. 2009, 9, 1881–1895. [Google Scholar] [CrossRef]
- Leitão, J.P.; Peña-Haro, S. Leveraging Video Data to Assess Urban Pluvial Flood Hazard. 2022. Available online: https://udm2022.org/wp-content/uploads/2021/11/1428_Leitao_REV-4d457576.pdf (accessed on 2 February 2022).
- Plate, E.J. Flood risk and flood management. J. Hydrol. 2002, 267, 2–11, Advances in Flood Research. [Google Scholar] [CrossRef]
- Guo, Z.; Leitão, J.P.; Simões, N.E.; Moosavi, V. Data-driven flood emulation: Speeding up urban flood predictions by deep convolutional neural networks. J. Flood Risk Manag. 2021, 14, e12684. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.; Vaze, J.; Croke, B.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Mark, O.; Weesakul, S.; Apirumanekul, C.; Aroonnet, S.B.; Djordjević, S. Potential and limitations of 1D modelling of urban flooding. J. Hydrol. 2004, 299, 284–299, Urban Hydrology. [Google Scholar] [CrossRef]
- Kim, T.; Yang, T.; Gao, S.; Zhang, L.; Ding, Z.; Wen, X.; Gourley, J.J.; Hong, Y. Can artificial intelligence and data-driven machine learning models match or even replace process-driven hydrologic models for streamflow simulation?: A case study of four watersheds with different hydro-climatic regions across the CONUS. J. Hydrol. 2021, 598, 126423. [Google Scholar] [CrossRef]
- Li, Y.; Martinis, S.; Wieland, M. Urban flood mapping with an active self-learning convolutional neural network based on TerraSAR-X intensity and interferometric coherence. ISPRS J. Photogramm. Remote Sens. 2019, 152, 178–191. [Google Scholar] [CrossRef]
- Berkhahn, S.; Fuchs, L.; Neuweiler, I. An ensemble neural network model for real-time prediction of urban floods. J. Hydrol. 2019, 575, 743–754. [Google Scholar] [CrossRef]
- Gude, V.; Corns, S.; Long, S. Flood Prediction and Uncertainty Estimation Using Deep Learning. Water 2020, 12, 884. [Google Scholar] [CrossRef]
- Löwe, R.; Böhm, J.; Jensen, D.G.; Leandro, J.; Rasmussen, S.H. U-FLOOD—Topographic deep learning for predicting urban pluvial flood water depth. J. Hydrol. 2021, 603, 126898. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, Y.; Wang, H.; Jiang, Z. Depth prediction of urban flood under different rainfall return periods based on deep learning and data warehouse. Sci. Total. Environ. 2020, 716, 137077. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.G.; Izmailov, P. Bayesian Deep Learning and a Probabilistic Perspective of Generalization. In Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 4697–4708. [Google Scholar]
- Gustafsson, F.K.; Danelljan, M.; Schon, T.B. Evaluating Scalable Bayesian Deep Learning Methods for Robust Computer Vision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Kendall, A.; Gal, Y. What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Butler, D.; Digman, C.; Makropoulos, C.; Davies, J.W. Urban Drainage; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Borah, D.K. Hydrologic procedures of storm event watershed models: A comprehensive review and comparison. Hydrol. Process. 2011, 25, 3472–3489. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; Macchione, F. A storm event watershed model for surface runoff based on 2D fully dynamic wave equations. Hydrol. Process. 2013, 27, 554–569. [Google Scholar] [CrossRef]
- Cea, L.; Garrido, M.; Puertas, J. Experimental validation of two-dimensional depth-averaged models for forecasting rainfall-runoff from precipitation data in urban areas. J. Hydrol. 2010, 382, 88–102. [Google Scholar] [CrossRef]
- Fernández-Pato, J.; Caviedes-Voullième, D.; García-Navarro, P. Rainfall/runoff simulation with 2D full shallow water equations: Sensitivity analysis and calibration of infiltration parameters. J. Hydrol. 2016, 536, 496–513. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; García-Navarro, P.; Murillo, J. Influence of mesh structure on 2D full shallow water equations and SCS Curve Number simulation of rainfall/runoff events. J. Hydrol. 2012, 448–449, 39–59. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; Macchione, F. Comparative analysis of overland flow models using finite volume schemes. J. Hydroinformatics 2011, 14, 122–135. [Google Scholar] [CrossRef] [Green Version]
- Xia, X.; Liang, Q.; Ming, X.; Hou, J. An efficient and stable hydrodynamic model with novel source term discretization schemes for overland flow and flood simulations. Water Resour. Res. 2017, 53, 3730–3759. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Costabile, P.; Macchione, F. Enhancing river model set-up for 2-D dynamic flood modelling. Environ. Model. Softw. 2015, 67, 89–107. [Google Scholar] [CrossRef]
- Bradbrook, K.; Lane, S.; Waller, S.; Bates, P. Two dimensional diffusion wave modelling of flood inundation using a simplified channel representation. Int. J. River Basin Manag. 2004, 2, 211–223. [Google Scholar] [CrossRef]
- Chen, A.; Djordjević, S.; Leandro, J.; Savić, D. The urban inundation model with bidirectional flow interaction between 2D overland surface and 1D sewer networks. In Proceedings of the Novatech Sixth International Conference on Sustainable Techniques and Strategies in Urban Water Management, Lyon, France, 25–28 June 2007; pp. 465–472. [Google Scholar]
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Monaghan, J. Simulating Free Surface Flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Ye, J.; McCorquodale, J.A. Simulation of Curved Open Channel Flows by 3D Hydrodynamic Model. J. Hydraul. Eng. 1998, 124, 687–698. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.w. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Hunter, N.M.; Horritt, M.S.; Bates, P.D.; Wilson, M.D.; Werner, M.G. An adaptive time step solution for raster-based storage cell modelling of floodplain inundation. Adv. Water Resour. 2005, 28, 975–991. [Google Scholar] [CrossRef]
- Lhomme, J.; Sayers, P.; Gouldby, B.; Samuels, P.; Wills, M.; Mulet-Marti, J. Recent development and application of a rapid flood spreading method. In Flood Risk Management: Research and Practice; Taylor & Francis Group: London, UK, 2008. [Google Scholar]
- Jamali, B.; Bach, P.M.; Cunningham, L.; Deletic, A. A Cellular Automata Fast Flood Evaluation (CA-ffé) Model. Water Resour. Res. 2019, 55, 4936–4953. [Google Scholar] [CrossRef] [Green Version]
- Hunter, N.M.; Bates, P.D.; Neelz, S.; Pender, G.; Villanueva, I.; Wright, N.G.; Liang, D.; Falconer, R.A.; Lin, B.; Waller, S.; et al. Benchmarking 2D hydraulic models for urban flooding. Proc. Inst. Civ. Eng. Water Manag. 2008, 161, 13–30. [Google Scholar] [CrossRef]
- Neelz, S.; Pender, G. Benchmarking of 2D Hydraulic Modelling Packages SC080035/SR2; Environment Agency: Bristol, UK, 2010. Available online: https://books.google.ch/books/about/Benchmarking_of_2D_Hydraulic_Modelling_P.html?id=ghoZYAAACAAJ&redir_esc=y (accessed on 2 February 2022).
- Guidolin, M.; Chen, A.S.; Ghimire, B.; Keedwell, E.C.; Djordjević, S.; Savić, D.A. A weighted cellular automata 2D inundation model for rapid flood analysis. Environ. Model. Softw. 2016, 84, 378–394. [Google Scholar] [CrossRef]
- Hernandez, O.J.; Alamia, J.A. Precision stabilization simulation of a ball joint gimbaled mirror using advanced MATLAB® techniques. In Proceedings of the IEEE Southeastcon 2009, Atlanta, GA, USA, 5–8 March 2009; pp. 72–77. [Google Scholar] [CrossRef]
- Zhao, G.; Pang, B.; Xu, Z.; Peng, D.; Xu, L. Assessment of urban flood susceptibility using semi-supervised machine learning model. Sci. Total. Environ. 2019, 659, 940–949. [Google Scholar] [CrossRef] [PubMed]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood susceptibility assessment using GIS-based support vector machine model with different kernel types. CATENA 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total. Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Kisi, O.; Choubin, B.; Deo, R.C.; Yaseen, Z.M. Incorporating synoptic-scale climate signals for streamflow modelling over the Mediterranean region using machine learning models. Hydrol. Sci. J. 2019, 64, 1240–1252. [Google Scholar] [CrossRef]
- Sadler, J.; Goodall, J.; Morsy, M.; Spencer, K. Modeling urban coastal flood severity from crowd-sourced flood reports using Poisson regression and Random Forest. J. Hydrol. 2018, 559, 43–55. [Google Scholar] [CrossRef]
- Chang, L.C.; Chang, F.J.; Chiang, Y.M. A two-step-ahead recurrent neural network for stream-flow forecasting. Hydrol. Process. 2004, 18, 81–92. [Google Scholar] [CrossRef]
- Chang, F.J.; Chen, P.A.; Lu, Y.R.; Huang, E.; Chang, K.Y. Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. J. Hydrol. 2014, 517, 836–846. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Towards learning universal, regional, and local hydrological behaviors via machine learning applied to large-sample datasets. Hydrol. Earth Syst. Sci. 2019, 23, 5089–5110. [Google Scholar] [CrossRef]
- Tien Bui, D.; Hoang, N.D.; Martínez-Álvarez, F.; Ngo, P.T.T.; Hoa, P.V.; Pham, T.D.; Samui, P.; Costache, R. A novel deep learning neural network approach for predicting flash flood susceptibility: A case study at a high frequency tropical storm area. Sci. Total. Environ. 2020, 701, 134413. [Google Scholar] [CrossRef]
- Guo, X.; Li, W.; Iorio, F. Convolutional Neural Networks for Steady Flow Approximation. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 481–490. [Google Scholar] [CrossRef]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On Calibration of Modern Neural Networks. In Proceedings of the 34th International Conference on Machine Learning, ICML’17, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1321–1330. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, ICML’16, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 1050–1059. [Google Scholar]
- Tagasovska, N.; Lopez-Paz, D. Single-Model Uncertainties for Deep Learning. In Advances in Neural Information Processing Systems; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Van Amersfoort, J.; Smith, L.; Teh, Y.W.; Gal, Y. Uncertainty Estimation Using a Single Deep Deterministic Neural Network. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; III, H.D., Singh, A., Eds.; 2020; Volume 119, pp. 9690–9700. [Google Scholar]
- Liu, J.Z.; Lin, Z.; Padhy, S.; Tran, D.; Bedrax-Weiss, T.; Lakshminarayanan, B. Simple and Principled Uncertainty Estimation with Deterministic Deep Learning via Distance Awareness. Adv. Neural Inf. Process. Syst. 2020, 33, 7498–7512. [Google Scholar]
- Mukhoti, J.; Kirsch, A.; van Amersfoort, J.; Torr, P.H.S.; Gal, Y. Deterministic Neural Networks with Appropriate Inductive Biases Capture Epistemic and Aleatoric Uncertainty. arXiv 2021, arXiv:2102.11582. [Google Scholar]
- Kopetzki, A.K.; Charpentier, B.; Zügner, D.; Giri, S.; Günnemann, S. Evaluating Robustness of Predictive Uncertainty Estimation: Are Dirichlet-based Models Reliable? In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; Meila, M., Zhang, T., Eds.; 2021; Volume 139, pp. 5707–5718. [Google Scholar]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- MacKay, D.J. Bayesian Methods for Adaptive Models. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1992. [Google Scholar]
- Shen, G.; Chen, X.; Deng, Z. Variational Learning of Bayesian Neural Networks via Bayesian Dark Knowledge. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, Yokohama, Japan, 11–17 July 2020; IJCAI-20. Bessiere, C., Ed.; International Joint Conferences on Artificial Intelligence Organization, 2020; pp. 2037–2043, Main track. [Google Scholar]
- Neal, R.M. Bayesian Learning for Neural Networks; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Wilson, A.G. The Case for Bayesian Deep Learning. arXiv 2020, arXiv:2001.10995. [Google Scholar]
- Ganaie, M.A.; Hu, M.; Tanveer, M.; Suganthan, P.N. Ensemble deep learning: A review. arXiv 2021, arXiv:2104.02395. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ashukha, A.; Lyzhov, A.; Molchanov, D.; Vetrov, D. Pitfalls of In-Domain Uncertainty Estimation and Ensembling in Deep Learning. arXiv 2020, arXiv:2002.06470. [Google Scholar]
- Ghimire, B.; Chen, A.S.; Guidolin, M.; Keedwell, E.C.; Djordjević, S.; Savić, D.A. Formulation of a fast 2D urban pluvial flood model using a cellular automata approach. J. Hydroinformatics 2012, 15, 676–686. [Google Scholar] [CrossRef]
- Innovyze. InfoWorks ICM. 2019. Available online: https://www.innovyze.com/en-us/products/infoworks-icm (accessed on 27 July 2022).
- QGIS Development Team. QGIS Geographic Information System; Open Source Geospatial Foundation. 2022. Available online: https://gis.stackexchange.com/questions/23622/citing-qgis-in-formal-publications#:~:text=A%3A%20To%20cite%20QGIS%20software,qgis.osgeo.org%22 (accessed on 2 February 2022).
- Wilson, J.P.; Gallant, J.C. Terrain Analysis: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Horn, B. Hill shading and the reflectance map. Proc. IEEE 1981, 69, 14–47. [Google Scholar] [CrossRef]
- Zevenbergen, L.W.; Thorne, C.R. Quantitative analysis of land surface topography. Earth Surf. Process. Landforms 1987, 12, 47–56. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Kendall, A. Geometry and Uncertainty in Deep Learning for Computer Vision. PhD Thesis, University of Cambridge, Cambridge, UK, 2018. [Google Scholar]
- Nix, D.; Weigend, A. Estimating the mean and variance of the target probability distribution. In Proceedings of the 1994 IEEE International Conference on Neural Networks (ICNN’94), Orlando, FL, USA, 28 June–2 July 1994; Volume 1, pp. 55–60. [Google Scholar]
- Le, Q.V.; Smola, A.J.; Canu, S. Heteroscedastic Gaussian Process Regression. In Proceedings of the 22nd International Conference on Machine Learning, ICML ’05, Bonn, Germany, 7–11 August 2005; Association for Computing Machinery: New York, NY, USA, 2005; pp. 489–496. [Google Scholar]
- Ronchetti, E.M.; Huber, P.J. Robust Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Hecht-Nielsen. Hecht-Nielsen. Theory of the backpropagation neural network. In Proceedings of the International 1989 Joint Conference on Neural Networks, Washington, DC, USA, 1989; Volume 1, pp. 593–605. [Google Scholar] [CrossRef]
- Song, C.M. Data construction methodology for convolution neural network based daily runoff prediction and assessment of its applicability. J. Hydrol. 2022, 605, 127324. [Google Scholar] [CrossRef]
- Izmailov, P.; Vikram, S.; Hoffman, M.D.; Wilson, A.G. What Are Bayesian Neural Network Posteriors Really Like? CoRR 2021, abs/2104.14421. [Google Scholar]
- Ovadia, Y.; Fertig, E.; Ren, J.; Nado, Z.; Sculley, D.; Nowozin, S.; Dillon, J.V.; Lakshminarayanan, B.; Snoek, J. Can You Trust Your Model’s Uncertainty? Evaluating Predictive Uncertainty Under Dataset Shift. arXiv 2019, arXiv:stat.ML/1906.02530. [Google Scholar]
- Osband, I.; Blundell, C.; Pritzel, A.; Van Roy, B. Deep Exploration via Bootstrapped DQN. In Advances in Neural Information Processing Systems; Lee, D., Sugiyama, M., Luxburg, U., Guyon, I., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2016; Volume 29. [Google Scholar]








| Area | Minimum | Maximum | Maximum | |
|---|---|---|---|---|
| (km) | Elevation (m) | Elevation (m) | Slope (rise/run) | |
| Zurich | 37.36 | 393.7 | 857.3 | 5.77 |
| Lucerne | 10.48 | 430.69 | 602.11 | 24.36 |
| Portugal | 4.23 | 8.81 | 173.94 | 14.77 |
| Dataset | Rainfall Events |
|---|---|
| Training Set | tr5_1, tr20_1, tr50_1, tr2_2, tr10_2, tr20_2, tr50_2, tr5_3, tr10_3, tr100_3 |
| Validation Set | tr100_2, tr2_3 |
| Test Set | tr2_1, tr10_1, tr5_2, tr20_3, tr50_3, tr100_1 |
| Mean Absolute Errors (cm) | |||||
|---|---|---|---|---|---|
| all | >10 cms | >20 cms | >50 cms | >100 cms | |
| Zurich | 2.70 | 10.97 | 19.09 | 33.87 | 51.87 |
| Lucerne | 3.45 | 18.60 | 25.0 | 42.95 | 69.83 |
| Portugal | 0.72 | 7.87 | 10.20 | 18.86 | 21.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaudhary, P.; Leitão, J.P.; Donauer, T.; D’Aronco, S.; Perraudin, N.; Obozinski, G.; Perez-Cruz, F.; Schindler, K.; Wegner, J.D.; Russo, S. Flood Uncertainty Estimation Using Deep Ensembles. Water 2022, 14, 2980. https://doi.org/10.3390/w14192980
Chaudhary P, Leitão JP, Donauer T, D’Aronco S, Perraudin N, Obozinski G, Perez-Cruz F, Schindler K, Wegner JD, Russo S. Flood Uncertainty Estimation Using Deep Ensembles. Water. 2022; 14(19):2980. https://doi.org/10.3390/w14192980
Chicago/Turabian StyleChaudhary, Priyanka, João P. Leitão, Tabea Donauer, Stefano D’Aronco, Nathanaël Perraudin, Guillaume Obozinski, Fernando Perez-Cruz, Konrad Schindler, Jan Dirk Wegner, and Stefania Russo. 2022. "Flood Uncertainty Estimation Using Deep Ensembles" Water 14, no. 19: 2980. https://doi.org/10.3390/w14192980
APA StyleChaudhary, P., Leitão, J. P., Donauer, T., D’Aronco, S., Perraudin, N., Obozinski, G., Perez-Cruz, F., Schindler, K., Wegner, J. D., & Russo, S. (2022). Flood Uncertainty Estimation Using Deep Ensembles. Water, 14(19), 2980. https://doi.org/10.3390/w14192980







